|
BAB2
LANDASAN TEORI
2.1
Computer Vision
Computer vision merupakan
suatu bidang baru yang cukup terkenal
dalam
dunia
ilmu
komputer.
Alan
Turing,
pencetus
artificial
intelligence
dan
salah satu penemu komputer digital, pemah mengatakan bahwa sebuah komputer
digital nantinya dapat memiliki kepintaran dan kemarnpuan untuk mengerti
citra.
Berdasarkan hal tersebut muncullah computer vision sebagai jawabannya.
Computer vision (disebutjuga
machine vision) adalah suatu pembelajaran
dan
pengaplikasian
akan
teori-teori dan
algoritma
yang
mcmpcrbolchkan
komputer
untuk
mengekstraksi dan
menganalisis
informasi spesifik dari sebuah
citra
melalui
. proses komputasi. Computer vision berhubungan erat dengan citra
digital, baik secara individual maupun secara sekuensial.
Tujuan
daripada
computer
vision
adalah
untuk
membuat berbagai
keputusan
penting
mengenai objek-objek
fisik
berdasarkan
citra
yang dimiliki
(Shapiro dan Stockman, 2001). Untuk membuat suatu keputusan mengenai objek
nyata, maka sebelumnya harus dibuat terlebih dahulu bentuk deskripsi dari citra
tersebut.
Setelah
diketahui
bagaimana
deskripsi
citra,
maka
selanjutnya
dapat
diputuskan
teknik
computer
vision apa
yang
dapat
dipergunakan didalam
citra
tersebut.
Bidang
computer vision
merupakan kombinasi
antara
pengolahan citra
(image processing) dan pengenalan pola (pattern recognition) dimana keduanya
|
|
8
berhubungan
dengan
proses
otomatisasi
interpretasi
citra. Contoh
aplikasi
dari
computer
vision adalah
sebagai berikut
:
a.
OCR
(Optical
Character
Recognition)
OCR
berguna
dalam
mengkonversi
informasi
dari bentuk
kertas
menjadi
bentuk
digital.
Dalam
proses
konversi
tersebut,
setiap
bentuk
karakter
dapat
dikenali
dengan
baik oleh
komputer.
Bentuk
aplikasi
ini
dapat
dilihat
dalam
berbagai
peralatan elektronik,
seperti
pada
PDA
(Personal
Digital Assistant).
b.
Object
Detection
Aplikasi
object
detection
berguna untuk
mendeteksi
keberadaan
objek
dalam
.sc:buah 'itru
l.kntuk
aplikasi
ini sering
dipergunakan
dalam
analisis
kesehatan,
seperti
pada
MRI
(Magnetic
Resonance Imaging),
dimana
dapat
memberikan
data
citra
yang
lebih
akurat
yang dapat
mendukung proses
diagnosis penyakit itu
sendiri.
c. Image
compression
Image
compression
berguna
untuk
mengecilkan ukuran
citra
tanpa
mengurangi inti
informasi
yang terkandung
didalamnya.
Bentuk
aplikasi
ini
biasanya
dipergunakan
pada
siaran
televisi
dimana
terjadi
proses
transmisi data
citra
dengan
ukuran
yang
telah
dikompresi
tanpa
adanya
kehilangan
data
yang
menyebabkan informasi
dapat
disampaikan dengan
utuh.
|
 9
2..2
Citra
Citra
merupakan
suatu
bagian
penting
dalam bidang
computer
vision.
Citra berguna sebagai objek utama yang dianalisis dalam
computer
vision.
Untuk
itu harus diketahui terlebih dahulu apakah arti dari citra itu sendiri.
Pengertian dari citra secara umum adalah suatu
fungsi
intensitas cahaya
dua
dimensi
f{x,y)
dimana
x
dan
y
adalah koordinat
posisi
dan
nilai
f
pada
koordinat
(x,y)
disebut dengan
brightness
atau
gray
level
dari citra (Gonzales dan
Woods,
200 I). Bagian
terkecil
dari suatu
citra
disebut
dengan
piksel
(pixel;
picture
element)
yang tersusun dalam
matriks dua
dimensi
pada
layar
monitor
(x.y).
Sebuah citra memiliki baik nilai intensitas maupun nilai RGB.
Citra
dapat
direpresentasikan berdasarkan intensitasnya.
Intensitas yang
disebut sebagai
brightness
(tingkat kecerahan) atau
gray
level
(tingkat keabuan)
biasanya memiliki nilai integer positif mulai dari 0 sampai 255.
Citra juga dapat direpresentasikan dengan
menggunakan
three-chromatic
dari
penglihatan
manusia. dimana
wama
yang
timbul
pada
setiap
bagian kecil
cahaya dibentuk oleh tiga angka. Ketiga angka tersebut terdiri dari wama-wama
primer
(Red
Green
Blue)
yang merupakan wama dasar untuk membuat spektrum
wama.
Nilai
dari
wama
tersebut mulai
dari
0
sampai
255.
Diluar dari
nilai
tersebut maka akan dibulatkan ke nilai terdekat sebab wama
yang muncul tidak
akan berubah lagi.
|
 10
t3
Pengolahan Citra (Image
Processing)
Pengolahan citra (image processing) berhubungan dengan segala bentuk
pemrosesan
informasi
dimana
input
dan
outputnya
adalah
citra.
Proses ini
bertujuan untuk
mendapatkan kualitas
yang
lebih baik dalam bentuk
yang
efisien. Karena cakupan ilmu pengolahan citra cukup luas maka pengolahan
citra
dapat
dibagi-bagi
menjadi
beberapa
sub kategori
seperti
image
enhancement,
image compression, image filtering, image distortion, image display, dan image
colouring.
Pengolahan
citra
terdiri
dari
tiga
tahap
utama.
Tahap
pertama dalam
pengolahan citra
yaitu
menentukan citra digital
yang akan
menjadi
input
untuk
diolah pada
proses
berikutnya.
Tahap
kedua
adalah
tahap
proses
pengolahan
citra.
Di
tahap
ini,
input
yang
berupa citra
digital
tadi
akan
dianalisis dan
dimanipulasi
sesuai
dengan
keinginan
pemakai.
Pertama-tama
akan
dilakukan
analisis dimana dilakukan proses pengekstraksian
informasi
dan
fitur-fitur pada
citra input. Lalu dilakukan
proses manipulasi
dimana dilakukan proses
perubahan nilai dari bagian terkecil pada citra
untuk suatu tujuan tertentu seperti
koreksi
wama, pengubahan
brightness dan
contrast,
pengubahan
ukuran
(scaling), dan pengubahan bentuk objek (warping). Tahap pengolahan citra yang
terakhir
adalah
membuat
output
berdasarkan pengolahan
yang
telah
dilakukan
pada proses sebelumnya menjadi bentuk citra digital kernbali.
|
|
II
Z.4
Kompresi Citra (Image Compression)
Seperti yang sudah disebutkan sebelumnya, salah satu
sub kategori dari
ilmu pengolahan citra adalah kompresi citra (image compression). Inti dan tujuan
utama
dari
proses
kompresi citra
adalah
mengurangi
jumlah
memori
yang
dibutuhkan
untuk
menyimpan suatu
citra.
Biasanya
kompresi
citra
dilakukan
dengan
cara mengurangi
pengulangan
(redundancy)
informasi
yang
ada
pada
citra. Secara
teknis kompresi. citra berhubungan dengan proses
meminimasi
jumlah
bit
yang
dibutuhkan
untuk
merepresentasikan sebuah
citra
dimana
sejumlah nilai piksel ditransformasi ke dalam nilai yang lebih kecil tanpa adanya
kehilangan informasi yang berarti.
Kompresi citra sangat
berguna dalam
pru>-e>
omuru asi
dimana dapat
mempermudah proses transmisilpenyimpanan suatu citra dikarenakan
output
kompresi citra menghasilkan citra yang memiliki
ukuran
lebih kecil dibanding
sebelumnya.
Contoh jelas
proses kompresi citra
adalah sebagai
berikut: suatu
citra yang memiliki resolusi 640x480 dan memiliki tipe wama RGB denganjarak
wama 8 bit membutuhkan
900 kilobytes kapasitas penyimpanan. Jika citra
tersebut dikompres dengan suatu algoritma tertentu
yang
memiliki rasio
20:I,
maka kapasitas penyimpanan yang dibutuhkan hanya 45 kilobytes. Pada contoh
diatas penghematan kapasitas penyimpanan yang berhasil dilakukan adalah
sebesar
855 kilobytes.
Sampai saat
ini,
telah banyak
muncul
metode-metode
kompresi citra yang cukup baik, beberapa diantaranya adalah GIF, JPEG, BMP,
PNG, TGA dan Wavelet.
|
|
12
Pada
era
informasi
ini, kebutuhan
akan
kecepatan
transfer
data
dan
penghematan
kapasitas
penyimpanan
sangatlah
penting
oleh
karena
itu peranan
kompresi
citra
dalam
aplikasi-aplikasi
nyata
sangatlah
dibutuhkan.
Contoh
aplikasi-aplikasi yang
membutuhkan
kompresi
citra
adalah
sebagai
berikut
siaran
tv, radar dan sonar,
teleconference,facsimile, medical
image, dan
multimedia.
..4.1 Teknik Kompresi Citra
Teknik
pengompresan
secara
umum
dibagi
menjadi
2 kategori,
yaitu
lossy
compression
dan
lossless
compression.
a. Lossy Compression
Mctl>Jc: J1mana
!>aal
data sumber
di
kompresi
dan
ketika di
dekompresi
kembali
data
hasil
pengompresan
tidak
dapat
dikembalikan
secara
tepat
sepeni
data
sumbemya.
hanya mendekati
data
sumbemya.
Ukuran file
hasil
dekompresi
lebih
kecil dari
file sumber.
b. Lossless
compression
Metode
dimana
saat
data
di
kompresi
dan
ketika
di
dekompresi
kembali
data
hasil
pengompresan
dapat
dikembalikan
secara
tepat
sama
persis
seperti
data
sumbemya.
Ukuran
file
hasil
dekompresi
sama
dengan
file sumber.
Dalam
pengompresan
citra. yang
biasa
dipergunakan
adalah lossy
compression
dengan
cara
menghilangkan
sejumlah
bit
rate
yang
dipergunakan
pada
citra.
Sayangnya
teknik
ini
tidak
dapat
dilakukan
pada
rasio
tinggi
karena
akan
mengakibatkan
penurunan
kualitas citra.
|
|
13
Yang dapat dilakukan untuk mengatasinya adalah membuat citra
lossless
secara
visual,
tetapi
data
sebenamya
lossy.
Teknik
ini memanfaatkan
ketidaksensitifan
mata kita sehingga pengurangan
kualitas dalam
rasio tertentu
masih dapat ditolerir dan dilihat oleh mata kita seperti citra aslinya.
t.S
Fractal
t.S.l
Definisi Fractal
Fractal
adalah
objek
geometri
yang
bagian-bagiannya mempunyai
persamaan
bentuk
yang
mewakili
bentuk
dasar
objek
itu
sendiri
dalam segala
skala. Bentuk
dari
fractal
adalah
irregular
(tidak teratur) dan kompleksitas
fractal
tidak pemah berubah.
Fractal
memiliki
dua
ciri khas,
yaitu
self-similarity
dan
infinite
detail.
Self-similarity
berarti setiap bagian darifractal
memiliki bentuk dasar yang sama
walau dilihat menggunakan skala apapun. Sedangkan
infinite
detail
berarti setiap
fractal
memiliki
bentuk
dasar
yang
seakan-akan
tidak
habis-habis apabila
diperhatikan. Berbagai bentuk
fractal
yang terkenal antara lain
Sierpinsky
Triangle
dan
Von
Koch Snowflake.
|
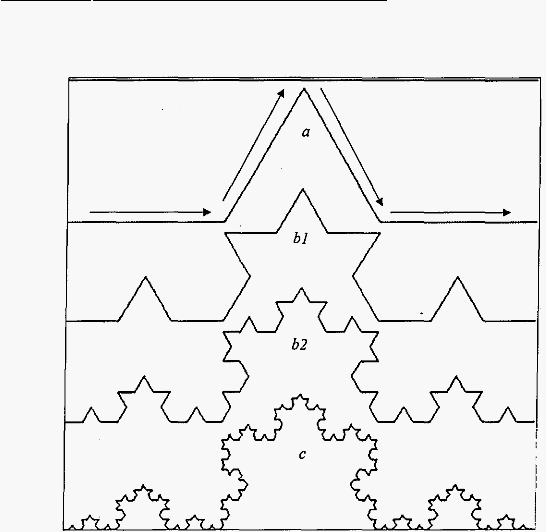 14
Gambar 2.1 Von Koch Snowflake
Perhatikan gambar 2.1. Pada gambar tersebut dapat dilihat
bahwafractal
Von
Koch
Snowflake
mempunyai tiga
buah
objek
penting
yaitu
initiator,
generator
dan
a/tractor.
Bagian berlabel
a
disebut juga sebagai
initiator.
Initiator
dapat dianggap sebagai citra
asli. Fungsi dari
initiator
adalah sebagai
bahan
dasar
untuk
membuat
fractal.
Tanpa
initiator
suatu
fractal
tidak
akan
dapat
terbentuk.
Berdasarkan
definisi
diatas,
initiator
dapat
dianggap
sebagai
bagian terkecil dari sebuahfractal.
Bagian
berlabel
bl
dan
b2
biasa disebut
juga sebagai
generator.
Generator
berasal dari hasil transformasi pola yang ada pada
initiator
ke dalam
bentuk dasar
initiator
itu sendiri. Pada gambar, terlihat jelas bagian
bl
terbentuk
|
 15
dari hasil proses transformasi bagian
a
ke dalam bagian
a
itu sendiri sedangkan
bagian b2 terbentuk dari hasil proses
transformasi bagian bl ke bagian bl
itu
sendiri. Berdasarkan
penjelasan diatas,
generator
dapat
didefinisikan
sebagai
hasil dari transformasi
initiator
ke dalam dirinya sendiri.
Bagian terakhir
adalah
bagian
c.
bagian
c
dapat
disebut juga
sebagai
a/tractor.
Attractor
merupakan basil
akhir
dari
transformasi
yang
dilakukan
generator.
Oleh karena itu
attractor
sering
disebut juga sebagai
fractal
itu
sendiri.
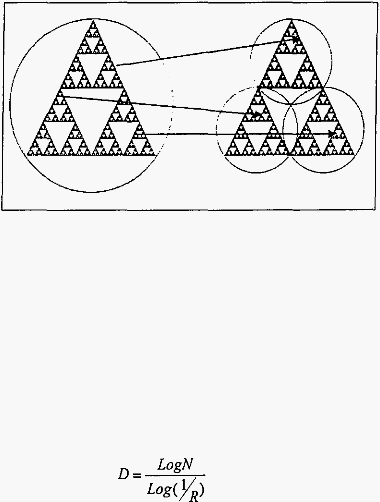
Gambar 2.2 Sierpinsky Triangle
.5.2
Dimensi Fractal
Dimensi.fractal
adalah suatu bilangan real yang menunjukkan derajat
ketidakteraturan
bidang.fractal
tersebut.
Rumus dimensi
.fractal
adalah :
|
 16
Dimana
D
adalah
dimensifractal, N adalah
jumlah
segmen
garis
pada
generator,
dan R
adalah panjang
segmen
garis
pada
generator
dibagi
jarak
titik
awal
dan
akhir
generator.
!.6
IFS (Iterated Function System)
!.6.1
Pengertian IFS
IFS
adalah
suatu
fungsi
iterasi
yang
terdiri
dari
sekumpulan
transformasi-
affine
yang dipilih
sedemikian
rupa
hingga
gabungan
dari
transformasi-affine
tersebut
mendekati
citra
target.
Sifat
dari
IFS
menyerupai
sifat
mesin
fotokopi,
yaitu menyalin kembali suatu
bentuk ke
dalam
posisi dan
ukuran yang
dtinginkan.
Prinsip
terpenting
dalam
IFS adalah
pemetaan
kontraktif
(contractive
mapping)
dimana
setelah
semua
transformasi-affine
ditentukan,
IFS dapat
diterapkan
dengan
mengkodekan
semua
koefisien
transformasi.
Pemetaan
suatu
fungsi
ke dirinya sendiri
dikatakan
kontraktif
bila selisih
nilai
hasil fungsi
pada setiap
iterasi
semakin
kecil. Teorema
pemetaan
kontraktif
menyatakan
bahwa setiap
IFS
memiliki
suatu
unique fixed
point
pada
pemetaan
fungsi
f(x)
=
x
dimana
nilai
itu
merupakan
nilai dari attractor
sebuah
IFS.
Rumus dari
unique fixed point adalah sebagai
berikut :
N
A=Uwn(A)
n=l
Dimana,
A
:Attractor
|
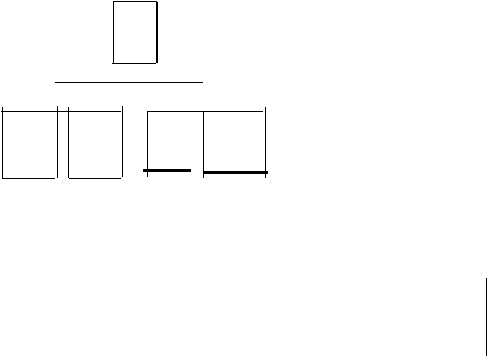 17
N
:
Jumlah
iterasi
W
:
Transformasi
Affine
.6.2 Transformasi-Affine
Transformasi-affine
adalah
transformasi
linier
yang
terdiri
dari
empat
operasi
dasar
yaitu
rotasi, pergeseran,
translasi, dan
penyekalaan.
Transformasi
dinamakan
affine
karena
terdapat
afinitas
(hubungan)
antara
visual
dan
struktural
antara
bentuk
lama dan
bentuk
yang
baru.
D
Kotak
A
/
/
"'\
--.....,_
Rotasl
Pergeseran
Translasl
Penyekalaan
.·""\.
<>
(Jl
b
D
Gam bar 2.3 Bentuk
transformasi-affine dari segi
empat
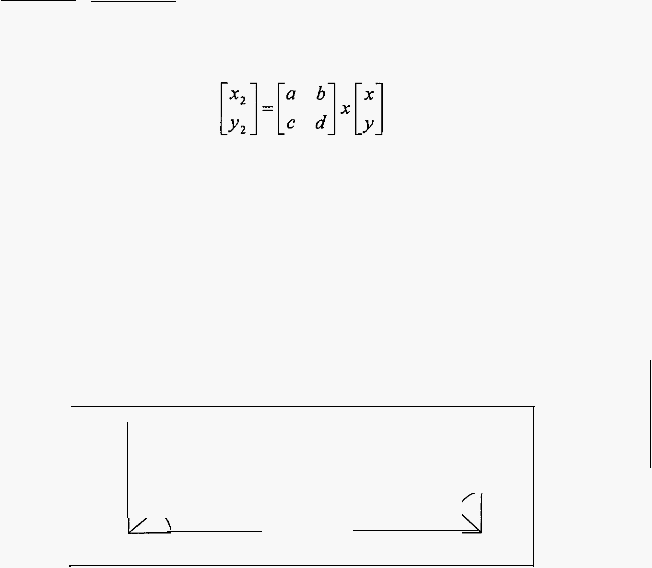
Transformasi
titik-titik
dalam
bidang dapat
dinyatakan
dengan suatu
perkalian
matriks
transformasi
T
dengan
vektor
v
yang
mewakili
koordinat
titik
tersebut.
Koordinat
baru
hasil
transformasi
(x2.Y2)
didapatkan
dengan
melakukan
operasi
perkalian
antara
T
dan
v.
T
=
[:
,
v
=
[;]
|
 18
[
Beberapa bentuk transformasi dasar yaitu :
a. Rotasi (rotation)
Bentuk matrik transformasinya adalah sebagai berikut.
x
2
]
=
[C sq
-
Sin'F] x [x]
Y
2
Szn
q
Cos
F
y
•••••• 00. 00
.t
Sin q
F
CosF
q
Cosq
-Sin
F
Gam bar 2.4 Sin q
dan
Cos F
Dimana
q
adalah
besar sudut
rotasi
terhadap
sumbu
x
dengan arah
berlawanan jarum jam, sedang F
adalah besar sudut rotasi terhadap sumbu y
dengan arah berlawananjarumjam.
b.
Pergeseran (shearing)
Bentuk
dari
transfom1asi
ini
terlihat
seperti
"menarik"
sebagian sisi
objek
geometri ke sebuah arah yang parallel dengan koordinat sisi satunya. Bentuk
matriks shearing adalah sebagai berikut.
|
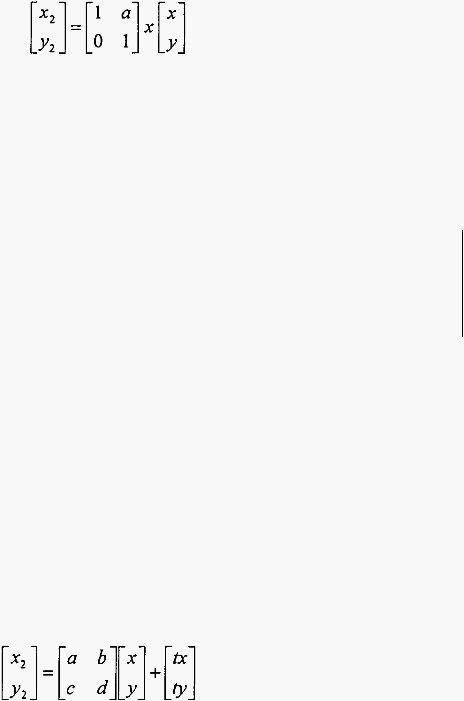 19
[
[
c.
Translasi
(translation)
Titik - titik
sebuah
objek
dapat dipindahkan
dalam
arab
horisontal
sebesar tx
satuan
dan
dalam
arab
vertikal sebesar ty
satuan
dengan
operasi
penjumlahan
sebagai
berikut.
x
2
]
=
[x+
tx]
Y2
y+ty
d.
Penyekalaan
(scaling)
Penyekalaan
diatur
oleh clcmcn diagonal
matrik,
yaitu
nilai
sx
dan
sy.
Bentuk
matrik
transformasinya
adalah sebagai
berikut :
x
2
]
=
[sx
o]
Yz
0
sy
Dari
empat
operasi
transformasi diatas.
yang
dipakai
dalam IFS
hanya
tiga
operasi,
yaitu
penyekalaan,
rotasi
dan
translasi.
Bentuk dari
transformasi-
affine dalam
IFS dinyatakan
dengan :
|
|
20
x2
=ax+by+tx
Y
2
=cx+dy+ty
Dimana
a, b, c, d mewakili operasi penyekalaan dan rotasi, sedangkan
tx
dan ty
mewakili operasi translasi.
.6.3
Teorema Collage
Proses pada IFS adalah proses
untuk
menggenerate suatu fractal dengan
cara
melakukan fungsi iterasi secara kontraktif dengan koefisien affine ke dalam
dirinya sendiri. Proses IFS dapat dianggap sebagai proses pembentukan attractor
dari inilialor. Lalu muncul sebuah pertanyaan baru, "Apakah mungkin proses itu
dibalik, bisakah attraclor dikembalikan menjadi sebuah initiator?". Masalah ini
dikenal dengan inverse problem,
bagaimana dari sebuah fractal kita dapat
melacak
inilialor
yang
mirip
dengan fractal
tersebut.
Dan
muncullah
teorema
collage sebagai solusinya.
Teorema collage menyatakan bahwajika W(J)
mendekati /maka unique
fixed point W(l)
=
W(W(W ..Jf'(l)...)) juga mendekati I.
Gambar W(l) tersusun
dari semua gabungan dari W(J(/)).
7
Kompresi Citra Fractal
Kompresi citra frac!al pertama kali dikenalkan oleh Michael F. Bamsley
pada awal tahun
1980. Lalu dikembangkan oleh
Arnaud
Jacquin
yang akhimya
menciptakan kompresi citra fractal pertama, yaitu Partitioned Iterated Function
Syslem (PIFS). Karena
menggunakan karakteristik
fractal dalam
metode
|
 21
pengompresannya maka
teknik
kompresi
ini
sering
disebut
pula
sebagai
kompresi citra fractal (fractal image compression) atau dapat disingkat menjadi
kompresifractal.
Konsep
dari
kompresi fractal
adalah
merubah
suatu citra
asli
menjadi
koefisien
fractal
menggunakan
teorema
collage
dan
menghasilkan citra
dekompresi dengan cara
melakukan proses IFS terhadap koefisien fractal
tersebut (Bamsley, 1993). Dengan hanya menyimpan.beberapa koe
sienfractal
hasil dari transformasi-affine, maka secara otomatis ukuran data citra akan lebih
kecil dibanding menyimpan keseluruhan citra.
Bamsley
mengemukakan
bahwa
sebuah
fractal
merupakan salinan dari
setiap
initiatornya
sendiri.
Pada
kenyataannya suatu
citra
tidak
benar-benar
memiliki sebuah bagian kecil (initiator) yang sama persis dengan dirinya seperti
pada
fractal.
Tetapi
kemungkinan
bahwa
adanya
kemiripan
bagian
kecil
dari
suatu
citra
dengan
bagian
yang lainnya selalu
ada. Ini
berarti
bahwa kumpulan
initiator
yang
memiliki sifat self-similarity tidak dapat
membentuk keseluruhan
citra asli, namun dapat membentuk bagian tertentu dari citra asli.
Gam bar
2.5
Self-similarity
dari sebuah
citra
|
|
22
Pada
gambar
2.5
dapat ditemukan
bahwa bagian
topi
dari
citra tersebut
sama
dengan
bayangan
topi
yang
terpantul
di
kaca.
lni
menunjukkan
bahwa
sebenamya
kemiripan
(self-similarity)
dalam
sebuah
citra
sebenamya ada
tetapi
tidak disadari.
Teknik
mempartisi
dan
menemukan bagian-bagian
citra terbaik
yang
saling terkoneksi tidaklah mudah.
Sampai
saat ini,
banyak
teknik partisi
citra
yang
telah
dikemba_ngkan.
Diantaranya
adalah
metode
partisi
quadtree
dan
horizontal-vertical.
7.1 Tahapan Kompresi Citra
Fractal
Gambaran umum
tahapan
proses
pada
kompresi
citra
fractal
adalah
sebagai
berikut
:
a.
Skema
Partisi
Skema
partisi
adalah salah
satu
tahapan
yang
sangat
penting.
Pemilihan
metode
skema
partisi
sangat
mempengaruhi
kualitas,
rasio dan
waktu
pengompresan
citra.
Pada
tahap
ini,
suatu
citra
dipartisi
ke
dalam
kumpulan
range
dan
domain.
Bentuk
partisi
dibagi
menjadi
dua
jenis,
yaitu:
I.
Right angled
partition
scheme
dimana
bentuk
partisinya
sesuai
dengan
bentuk
asli
piksel dan
membentuk
sudut
yang
berpotongan
secara
tegak
lurus.
Contoh metode
partisi
ini
adalah.fixed
block, region-based
dan quadtree.
2. Not-right
angled
partition scheme
|
 23
dimana
bentuk
partisinya
tidak
sesuai
dengan
bentuk
asli
piksel
dan
membentuk
sudut
yang
berpotongan
diagonal.
Contoh
metode
partisinya
adalah
triangular
dan de/aunay triangulation.
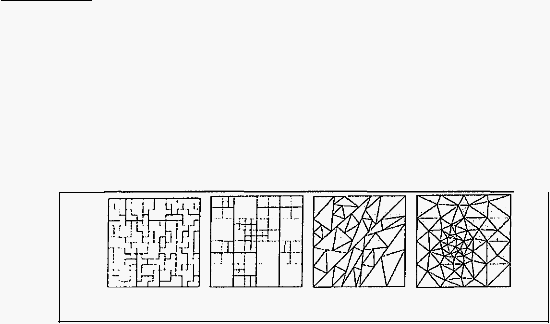
Region-based
Quadtree
Triangular
De/aunay
Trian
/ation
b. Seleksi
Domain
Gambar
2.6 Bentuk partisi
Penentuan
panjang
dan
Iebar
dari
domain
mempengaruhi
kualitas
dan
waktu
kompresi.
Semakin
kecil
ukuran
domain
menyebabkan
kualitas citra
terkomprcsi
makinbaik
namun waktu
kompresi
akan
semakin
lama
dikarenakan
banyaknya
domain
yang diproses,
begitu
juga
sebaliknya.
c.
Transformasi
Blok
Transformasi
blok
adalah
proses
penyekalaan
ukuran
domain
sehingga
sama
dengan
ukuran
range.
Jenis
proses
transformasi
blok
sangat
dipengaruhi
oleh
skema
partisi
yang
dilakukan.
Untuk
skema
partisi
right-angled,
proses
'pengecilan'
domain
dilakukan
dengan
cara mengalikan
domain
dengan
faktor
skala
pengali.
Untuk
mendapatkan nilai
piksel
maka
dilakukan
teknik
averaging
pada
piksel
tetangga.
Sedangkan
pada
skema
partisi
not-right
angled
proses
transformasi
blok
lebih
rumit
karena diperlukan
konversi
bentuk
bagian
dari
bentuk
piksel
ke dalam
bentuk
partisi
poligon yang
diinginkan.
d.
Encoding
|
 24
Pada tahap
ini dilakukan proses penyimpanan dan
pengalokasian koefisien
transformasi-affine, lokasi domain dan lokasi range menjadi bentuk bit.
e. Decoding
Pada tahap decoding, proses IFS dilakukan terhadap koefisien fractal yang
disimpan sehingga membentuk suatu citra hasil kompresi.
,7.2 Range, Domain, dan Domain Pool
Pada
awalnya sebuah
citra
dipartisi
menjadi 2
bagian,
yaitu range dan
domain. Range adalah hasil partisi dari suatu citra dimana setiap bagiannya tidak
boleh saling menimpa (non-overlapped block). Daiamfractal, range disebut juga
initiator yang diperlukan untuk membentuk sebuah attractor.
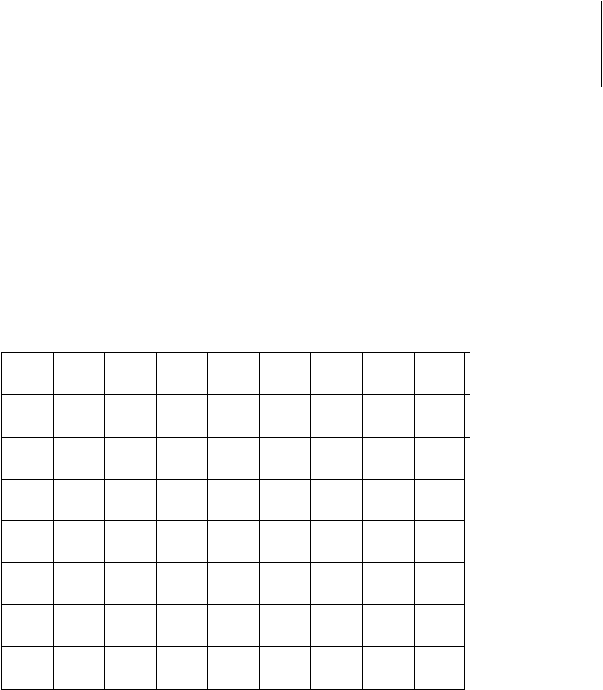
Ril
R12
Rl3
R14
Rln
R21
R22
R23
R24
R2n
Rm 1
Rm2
Rm3
Rm4
Rmn
Gam bar
2.7
Segmentasi
blok range
pada sebuah
citra
|
|
25
Range
pada
umumnya
berbentuk
bujur sangkar,
namun sesungguhnya
tidak ada keharusan
mengenai bentuk dan ukuran range. Pemilihan bentuk serta
ukuran range yang tepat dapat
menghasilkan rasio kompresi yang cukup tinggi,
kualitas citra
yang
masih dapat dipertahankan dan
waktu kompresi yang cukup
rendah.
Bila ukuran range terlalu
besar,
maka
citra basil
proses
kompresi akan
mengalami penurunan kualitas
yang besar,
namun
rl!sio kompresi
yang dicapai
akan
tinggi.
Demikian
sebaliknya
jika
ukuran
range
terlalu
kecil,
maka rasio
kompresi akan rendah namun kualitas citra semakin baik.
Tidak
seperti
range, domain adalah
basil
dari
partisi
citra
yang
boleh
saling
menimpa
antara satu
dengan
yang
lainnya
(orerlapped
block;.
Domain
merupakan
bagian
dari
citra
yang
mirip
dengan
range.
Domain juga
sering
disebut dengan
codebook.
Ukuran dari domain harus lebih besar atau sama dengan range. Aturannya
adalah O<s<l dimana s adalah
faktor skala pengali. Faktor skala pengali
(s)
dari
domain ke range pada umumnya
dibagi menjadi empat ukuran,
yaitu s
E
S
={I I 4,1I 2,3I 4,1}.
Domain dikatakan 2 kali lebih besar dari range jika s = Yz,
domain
dikatakan
4
kali
lebih
besar
dari
range
jika
s
=
Y.,
dan
seterusnya.
Proses
kompresi
dilakukan
dengan
menemukan
pemetaan
transformasi-ajjine
terbaik dari domain ke range.
|
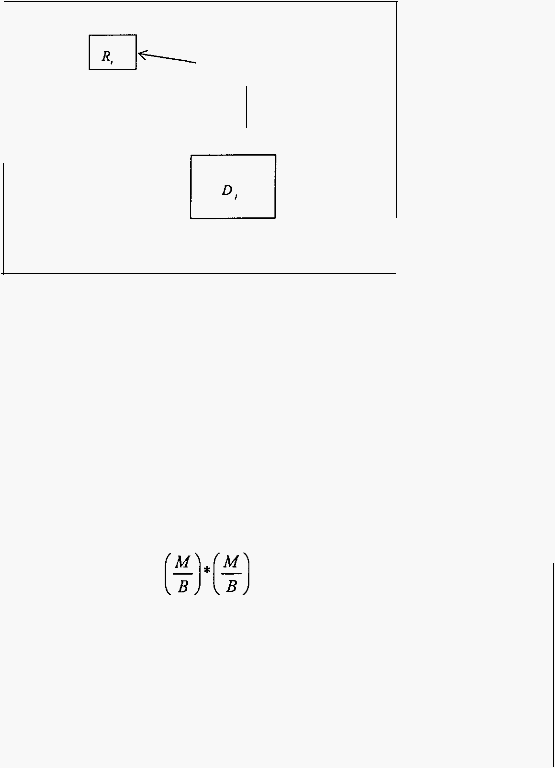 26
BxB
Transformasi
affine
2Bx2B
Gambar 2.8 Transformasi-affine
memetakan domain
ke range
Karena
domain
boleh
saling
bertumpuk,
maka
jumlah
domain
pada citra
dipengaruhi
oleh
step
hori=ontal (,I/;) dan .\/rr
'""tical (61·) yang ditentukan.
Rum us perhitungan
range
dan domain
pada sebuah
citra adalah :
a.
Range
suatu
citra
berukuran
MxM
piksel
dengan
ukuran
range
BxB
piksel akan
memiliki
range
sebanyak
:
b. Domain
Jika
kita tentukan
step
domain
sebesar
6
piksel,
maka
total
domain
yang ada
pada
citra
tersebut
dapat diperoleh
melalui
rumus
berikut
:
(!:_1 ; 2B
+
I)
*
(
M
2B
+
I)
Berikut
adalah
contoh
perhitungan
range
dan domain.
|
|
27
Suatu citra grayscale berukuran 256x256 piksel dengan ukuran range adalah 8x8
piksel. Step horizontal
(oh) dan step
vertical (ov) sebesar
4
piksel. Range baik
vertikal maupun horisontal berjumlah 32 buah. Jumlah range total adalah 32 x 32
=
1024 range. Jumlah domain blok
adalah
61 x 61 =
3721 domain blok.
Dikarenakan ada 8 transformasi-ajjine (4 arah rotasi dan 4 arah
translasi) yang
dilakukan
untuk
mencari domain
terbaik dari suatu range,
maka
pada setiap
range dilakukan
sejumlah
8 x
3721 =
29768 proses. Dengan
jumlah range
sebanyak
I
024 range, maka secara keseluruhan ada 29768 x
I
024
=
30482432
proses. Semakin banyak
proses
yang
dilakukan
berarti
semakin lama waktu
kompresi yang dibutuhkan.
Pcncarian domain
terbaik
dengan
cara
membabi
buta
sangatlah
tidak
efisicn dan memakan waktu. Untuk itu dibutuhkan strategi untuk mengefisienkan
pcncarian
domain
terbaik. yaitu
dengan cara
mengurangi
jumlah domain
yang
dicari. Proses ini disebut dengan domain pool.
Domain
pool atau
virtual codebook adalah beberapa kumpulan
domain
yang dekat
dengan
suatu
range.
Landasan pemikiran
domain pool
menyatakan
bahwa pada
umumnya domain
terbaik
dari
suatu
range terletak
tidak
jauh dari
range
tersebut.
Pada
domain
pool,
pemilihan
domain
terbaik
tidak
dilakukan
pada keseluruhan
domain
yang ada
pada
citra,
melainkan
hanya
pada
domain
pool yang yang bersangkutan.
|
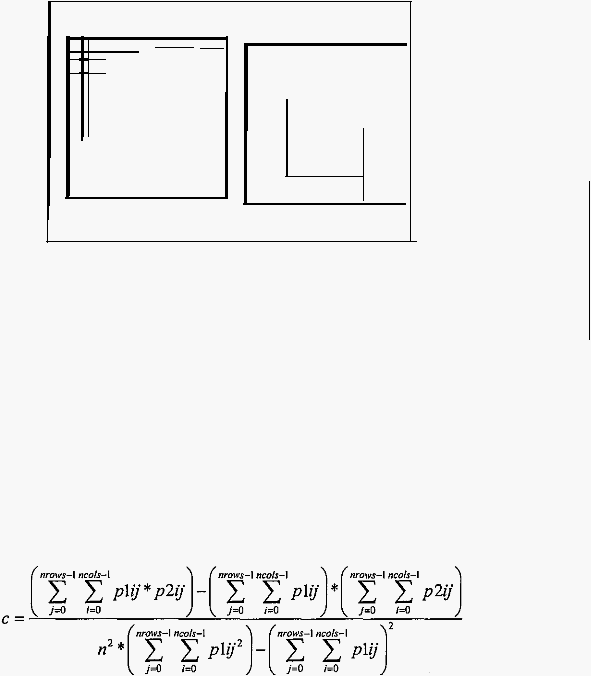 28
TF
n
III
o
Range
Domain
,
•
I
I
•
I
I
-
---
.
w
--
·
-
---
t=Ji=
_i_
:
,
orR,.
T
L+2B
l_
I
•
I
•
•
• •
I
I
J ;
B
/f--1.+2B.-.j
Candia:'te
domain
block
Gambar 2.9 Domain dan
domain pool
pada suatu citra
.7.3
Contrast dan
Brightness
Contrast
menyatakan
tingkat
perbedaan
antara
suatu
wama
dengan
wama
lainnya,
sedangkan
br{ghtness
menyatakan tingkat
keterangan
dari wama
tersebut.
Rumus
penghitungan
nilai
contrast
antara
range
dengan
domain
adalah
sebagai
berikut:
Rumus
penghitungan
nilai
brightness
antara
range
dengan
domain adalah
sebagai
berikut :
1
(nrows-1 ncols-l
nrows-l nco/s-l
J
b=
*
*
:L
:L
p2ij-c*
:L
:L
ptij
(nrows
ncols)
j=O
i=O
j=O
i=O
|
 29
Dimana,
c
:
nilai contrast
b
:
nilai
brightness
pi
:
nilai
piksel
pada sebuah
domain
p2
:
nilai
piksel
pada sebuah
range.
:
jumlah
keseluruhan
piksel
yang
berada
dalam
suatu
range tertentu.
nrows & ncols
ukuran dari
range
atau
domain
.7.4 Nilai Error
Domain
terbaik
yang
paling
mirip
dengan
suatu
ran!?<
J•dap:tt
blla
nilai
error
antara
pasangan
range-domain
tersebut
merupakan
yang
terkecil.
Maksud
dari
nilai
error
adalah
seluruh
selisih
nilai
piksel
yang
ada
antara
pasangan
range
dengan
domain
Rumus
penghitungan
nilai
error
(E)
adalah sebagai
berikut:
E
="L[f(i,
j)-
F(i,
j)f
Dimana,
f(i.j)
Nilai
piksel
range
pada koordinat
i.j
F(i.j)
Nilai
piksel
domain
pada koordinat
i.j
8
Prototyping
Dalam
perancangan
software
aplikasi
untuk evaluasi
digunakan
model
prototyping
di
mana prototyping
merupakan
salah
satu
metodologi
perancangan
aplikasi
yang dapat
digambarkan
dengan
gambar
dibawah
ini.
|
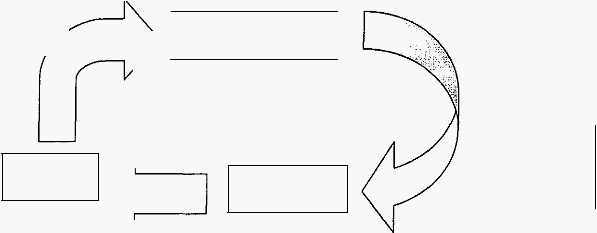 30
Perancangan
Anal isis
kebutuhan
Testing/Imple
mentasi
Prototyping
Model
gam bar 2.10 Prototyping
Model
Gambar
diatas
menjelaskan
bawah
dalam
prototyping
model hasil
perancangan
aplikasi
tidak
lah
selesai
pada
tahap
testing
dan
implementasi,
tetapi
setelah
di
testing
dan
diimplementasikan
akan dilakukan
analisis
kebutuhan
apakah
ada
kekurangan-kekurangan
yang
perlu
disempumakan
dan
kemudian
akan
dilakukan
perancangan
kembali
untuk
menyempumakan
aplikasi
tersebut,
dan
proses
ini terjadi
sampai
aplikasi
menjadi sempuma.
Dalam
penelitian
ini,
perancangan
software
aplikasi
pengujian
metode
yang
dirancang
digunakan model
prototyping
seperti yang
telah
dijelaskan
diatas.
Berdasarkan
analisis
kelemahan
dibawah
maka
akan
dirancang
metode
yang
lebih
efektif
dan
dapat
diimplementasikan
dalam
bentuk
prototype
yang
masih
dapat
dikembangkan
lagi
dengan
menganalisis
kelemahan-kelemahan
yang ada
pada
prototype
hasil
perancangan.
|
|
-------------------------------
31
:.9
Kelemahan Beberapa Metode Partisi Dalam Kompresi Citra Fractal
Kompresi
citra
fractal merupakan
suatu
bentuk
kompresi yang
keefektifannya
tergantung
dari
bentuk
partisi
yang
dipakai.
Bentuk
partisi
inilah
yang
menentukan
ukuran
range
dari
citra.
Bila
ukuran
range
terlalu
besar,
maka
citra
basil
proses
kompresi
akan
mengalami
penurunan
kualitas
yang
besar,
namun
rasio
kompresi
yang
dicapai
akan
tinggi.
Demikian
sebaliknya
jika
ukuran
range
terlalu
kecil,
maka
rasio
kompresi
akan
rendah
namun
kualitas
citra
semakin
baik.
Sampai
saat
ini
telah
banyak
metode partisi
yang
telah
dikembangkan.
Beberapa
diantaranya
yang
sering
dipergunakan
adalah
fixed
block. polygonal,
dan
quadtree.
Metode
fixed block
adalah
bentuk
partisi
yang
paling
sederhana.
Teknjk
ini
mempartisi
piksel
citra
kedalam
range-range
berbentuk
bujur sangkar
yang
memiliki
ukuran
yang
sama
satu
dengan
yang
lain. Jenis
partisi
ini sangat
memboroskan
waktu
pada
saat
pencarian
domain
terbaik
terutama
pada citra
yang
berukuran
besar.
Kelemahan
lain
dari
teknik
ini
adalah
menyamakan
semua
bagian
dari
citra
tanpa
memperhitungkan
karakteristik
dari
citra
itu sendiri.
Metode
polygonal
merupakan
jenis
bentuk partisi
yang
memiliki
bentuk
yang
tidak
biasa.
Teknik
ini
mempartisi
piksel
citra
kedalam
range-range
yang
berbentuk
poligon.
Tetapi
karena
bentuk
partisinya
berbeda
dengan
bentuk
piksel
(square),
maka
partisi
ini
tidak
dapat
dipergunakan
sebelum bentuk
piksel
pada
citra
sesuai
dengan
bentuk
partisinya. Disinilah
kelemahan
utama
dari
metode
polygonal.
Untuk menggunakan
bentuk
partisi
ini kita
memerlukan
suatu alat
|
|
32
penangkap
citra
yang
dimodifikasi
sehingga
dapat
membagi
citra
kedalam
piksel
yang
sesuai
dengan
bentuk
partisi.
Metode
quadtree
adalah
bentuk
partisi
hasil
modifikasi
dari
metode fixed
block.
Teknik awalnya membagi
citra kedalam
range-range
berbentuk
4
bujur
sangkar
yang
sama
besar. Setelah
itu
pada range
yang
memiliki
error
lebih
besar
dari
threshold
akan
dilakukan
partisi
lagi
pada
range
tersebut.
Begitu
pula
dengan
range
didalamnya,
apabila
masih
lebih
besar
dari
threshold
akan dipartisi
kembali.
Tetapi
pada
batasan
maksimum,
partisi
akan
berhenti
dilakukan.
Jenis
partisi
ini
cukup
menghemat
waktu
pada
saat
pemetaan
domain ke
range
sebab
tidak
semua
range
memiliki
ukuran
kecil. Kelemahan
dari
partisi
ini adalah
threshold
yang
dipergunakan
sama
untuk
segala
level
partisi.
Setelah
diteliti,
hal
ini
tidak
efektif
dan
hasil
dari
partisi
menghasilkan banyak
range.
Berdasarkan
analisis
diatas,
metode
quadtree
memiliki
keunggulan
lebih.
Dengan
menggunakan
algoritma
adaptive
threshold
maka
kelemahan
dari quadtree dapat
diatasi.
|
 33
-B
F
(j
H
I
1
R
s.
N
0
T
L
M
v
Q
X
y
.10
Metode Partisi Adaptive Quadtree
.10.1 Skema Partisi Quadtree
Inti
metode partisi
quadtree
adalah
mempartisi
citra
ke dalam 4 sub
node
berbentuk
bujur sangkar
yang
berukuran
sama.
··
(a)
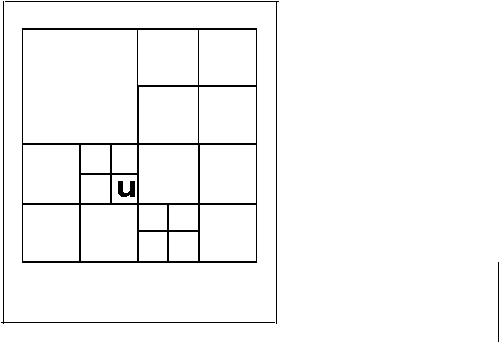
Gam bar 2.11 (a)
Bentuk
representasi citra
menggunakan
metode quadtree
Perhatikan
gambar
2.ll(a). Pada
awalnya citra
A
dibagi
menjadi
4
sub
node
yaitu
B,
C,
D, E
kemudian
node
C
dipartisi
menjadi
4
sub
node
F,G,H,l,
node
D
dibagi
menjadi
4
sub
node
J.
K, L, M,
dan seterusnya.
Hubungan
dalam metode
quadtree
juga
dapat
direpresentasikan melalui
sebuah
tree. Setiap
node
dapat
dibagi
menjadi
empat
sub
node.
Sebuah
quadtree
membagi
range ke
dalam
beberapa level sesuai
ukurannya.
|
 34
--------·-----· 2
R
D
T
U
(b)
t
---
4
V
W
X
Y
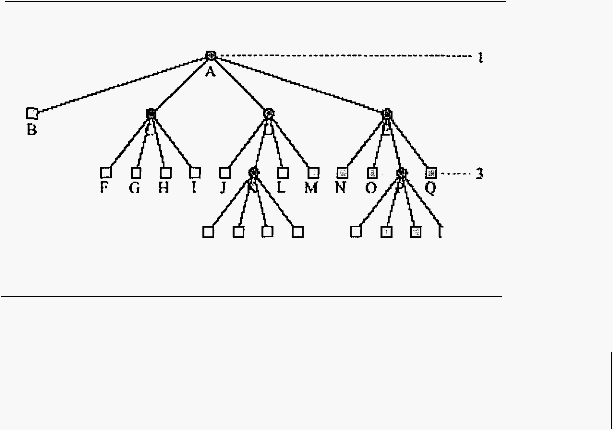
Gam bar
2.11
(b)
Korespondensi dalam suatu
quadtree
Perhatikan gam bar
2. l I (b).
Node
A sebagai root
menunjukkan
repre ente
Sl
re
rti'i
dalam bentuk
quadtree.
Setiap
node
yang
terbagi
menjadi
empat sub
node baru memiliki
level baru
yang
menggambarkan
tingkat
kedalaman
partisinya.
Begitu
pula dengan
sub
node dibawahnya.
Representasi
dari
suatu
citra menggunakan
quadtree
ditentukan
oleh
dua
parameter.
yaitu
level
minimum
dan
level maksimum.
Ukuran quadtree
menentukan
bahwa
suatu
citra
minimal
harus
dipartisi
sampai
level
minimumnya
dan
level
partisi
tidak
boleh
melebihi
level
maksimurnnya.
Level
minimum
adalah
level
dimana
pengkodean
quadtree
dimulai.
sedangkan
level maksimum
adalah
batas maksimal
pengkodean
quadtree.
Pengkodean
quadtree
hanya
dilakukan
di
antara
level
minimum
dan
level
maksimum.
Node
yang
memiliki
level
dibawah
level
minimum
dan
diatas
level
maksimum
tidak akan
dikodekan. Node yang
terpecah memiliki nilai I,
sedangkan
node yang
tidak terpecah
memiliki
nilai
0.
|
|
35
Perhatikan
gambar
2.1!(b),
urutan
pembacaan
struktur
quadtree
menggunakan
breadth first search
dengan
level minimum =
2
dan
level
maksimum
=
4
adalah sebagai
berikut :
A-B-C-D-E-F-G-H-l-J-K-L-M-N-0-P-Q-R-S-T
-U-V-
W-X-Y
Kode
quadtree
yang dihasilkan
adalah
:
I-O-l-l-l-O-O-O-O-O-I-0-0-0-0-l-0-0-0-0-0-0-0-0-0
Tetapi
karena
setelah
mencapai
level
maksimum
sudah
pasti
node tidak
dapat
dibagi
lagi
menjadi
sub
node
baru,
maka
kita
dapat
mengabaikan
kode
di
level
maksimum.
Jadi
kode
quadtree
yang
sudah
dikurangi
dengan
level
maksimumnya
adalah
:
l-0-1-l-l-0-0-0-0-0-l-O-O-O-O-l-O
.10.2
Adaptive Tit res/told
Pada
awalnya
teknik quadtree menggunakan
satu
nilai
threshold
error
tetap
(fixed
threshold).
Namun
teknik
ini
memiliki
kelemahan
karena
satu
nilai
threshold
tetap
tidaklah
cocok
untuk
diaplikasikan
terhadap
ukuran
range
yang
berbeda-beda.
Untuk
itu
dipergunakan
adaptive threshold
dimana
setiap
level
quadtree
memiliki
nilai
threshold
error
yang
berbeda-beda
sesuai
dengan
levelnya.
Teknik
adaptive threshold
sebelumnya telah
diteliti
dan
dibuktikan
bahwa
j
ika
kita
memakai
adaptive threshold
pada
level
quadtree,
maka
kualitas
pengkodean
citra
akan
lebih
baik
daripada
menggunakanjixed threshold
pada
bit
rate yang sama
(Shusterman
dan
Feder, 1994).
|
 36
I
1
-1
Berikut
adalah
tahapan
adaptive
threshold
dan
penggunaannya
dalam
partisi
quadtree,
a.
Untuk setiap
blok
range, cari
koefisien.fractal
terbaik
yang
memiliki
minimal
error
diantara
domain pool-nya.
b. Jika error
minimal lebih besar
dari
initial threshold
dan
level
node
masih
dibawah
maksimum
level, partisi
blok
range
menjadi
empat
bagian
sama
besar.
c.
Initial threshold (eJ)
di
level
pertama
menjadi
menjadi
sub
threshold
bagi
level
selanjutnya.
Rumus
dari
adaptive threshold
adalah sebagai
berikut :
e.=
k.e.
Dimana,
ei
threshold
dari
level
i.
k
nilai
threshold
yang
pas
bagi kondisi
level. Berdasarkan
penelitian
Shusterman
dan
Feder,
nilai
k
yang
paling
tepat
pada
adaptive
threshold
adalah
2.
d.
Ulangi tahap a dan
b
sampai
level
node
memenuhi
batas
maksimum
level.
Metode
partisi
ini
kemudian
lebih
dikenal
dengan
metode
adaptive
quadtree
dimana
menggunakan
partisi
quadtree
dengan
menggunakan
adaptive
threshold.
11
Perancangan Penyimpanan Data
Pada umumnya
kompresi
data pada
citra
berbentuk
sekumpulan
informasi
yang
didapatkan
dari citra yang
disimpan
ke
dalam
bentuk bit-bit.
|
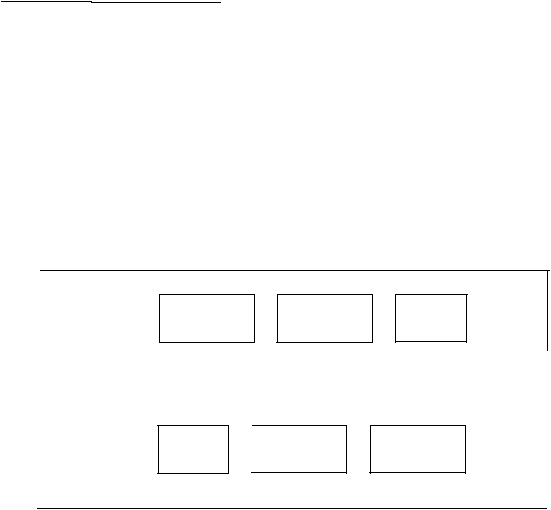 37
Symbols
-
f-+
Symbols
-
f-.
f4-
Setiap
informasi
terdiri
dari
serangkaian
simbol-simbol
yang
akan
diubah
ke
dalam
kode.
Semakin
banyak simbol
maka
semakin
banyak
jumlah
bit
yang
dibutuhkan.
Apabila
metode
kompresi
yang dipakai
cukup
efektif,
maka
akan
menghasilkan kumpulan
kode
yang
ukurannya
lebih
kecil
daripada
ukuran
aslinya.
--=....
Read
Input
Encode
Output
Symbols
Symbols
Code
Output
Decode
Read Input
Symbol
Symbols
Code
Gam bar
2.12
Kompresi
dan dekompresi data
secara
umum
Code
Salah
satu
metode
kompresi
yang
digunakan
dalam
menyimpan
data
adalah
adaptive
arithmetic coding.
Metode
ini
cukup
efisien
karena
dapat
melakukan
kompresi
dengan rasio
lebih dari
40%.
Inti dari
adaptive arithmetic coding
adalah
mengompres
data dengan
mengganti
simbol
dari kode asli
menjadi
simbol
representasi
probabilitas
kemunculan
simbol
tersebut.
Teknik
adaptive arithmetic coding
mengkonversi
keseluruhan
simbol
yang
ada
pacta
suatu
informasi
berdasarkan
nilai
peluang
kemunculan
antara
(0.0
:S
n
<
1.0). Setiap simbol
yang
akan
dikonversi
memiliki
|
 38
perhitungan
probabilitas masing-masing.
Rumus
dasar
dari
adaptive arithmetic
coding
adalah :
P(x)
=
N(x)
+I
N(x)+N(y)+N(z)+ jum
sim
dimana.
p
=
Nilai
probabilitas dari
simbol
x.y.=
=
Simbol-simbol
yang ada
pada suatu
informasi
N
=
Jumlah
dari simbol-simbol
yang sudah di
encode
jum_sim
=
Jumlah
jenis simbol
yang ada
|
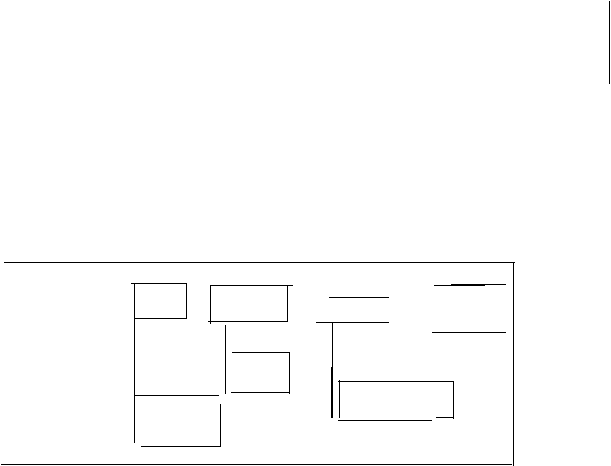 Partisi
Citra
Seleksi
Domain
Pool
Encoding
BAB3
ANALISIS
DAN PERANCANGAN
KOMPRESI
DAN DEKOMPRESI CITRA
.1
Analisis dan Perancangan Kompresi Citra
Kerangka umum dari kompresi
citra menggunakmetode
adaptive
quadtree
dapat dilihat pada gambar 3.1.
Transformasi
4
Blok
File)
Kompresi
r
Adaptive
Quadtree
Adaptive Arithmetic
Encoding
Gambar 3.1
Tahapan kompresi citra metode
quadtree
Pada gambar
diatas,
terdapat tiga
bagian
utama proses kompresi citra.
Ketiga bagian tersebut adalah :
a. Partisi citra
Awalnya
citra
dipartisi
ke
dalam
range-range
menggunakan
adaptive
quadtree.
Lalu
tentukan parameter-parameter
yang
dipergunakan, yaitu
range, domain, dan
domain pool.
b.
Transformasi Blok
|
 40
Untuk
seluruh
domain
akan
dilakukan
transformasi
blok
menggunakan
metode partisi
adaptive quadtree.
Mula-mula
ukuran domain diproses
sehingga
sama
dengan
ukuran
range.
Setelah
itu
dilakukan
proses
pencarian
domain
terbaik dari
range
yang ada
menggunakan
transformasi-affine.
c. Encoding
Pada
proses
encoding,
seluruh
koefisien
yang
ada
dikonver5i
ke
dalam
byte
yang
lebih kecil
menggunakan
algoritl):la
adaptive -arithmetic coding
agar
lebih
menghemat
kapasitas
penyimpanan.
.1.1 Analisis Partisi Citra
Suatu citra
T
berukuran
NxN
akan
dipartisi
m.:nggunakan
mctode
adaptive
quadtree.
Pertama-tama
tentukan terlebih
dahulu
level
minimum
dan
maksimum
dari
suatu
citra.
Setelah
parameter
tersebut
ditentukan,
partisi citra
sampai
batas
level
minimumnya
tercapai. Hasil
partisi
tersebut akan menjadi
range dari citra.
Selanjutnya
akan
dicari
domain
dan
domain pool
dari
setiap
range.
Bentuk
dari
domain
dan
domain
pool
tersebut
adalah
persegi.
Pemilihan
bentuk
persegi
ini
didasarkan
pada
bentuk
dasar
dari
-
piksel
itu
sendiri agar
mempermudah
proses
partisi.
Untuk
mencari
domain
dan
domain
pool
dari
sebuah
range,
terlebih
dahulu
harus
ditentukan empat
parameter
pendukungnya,
yaitu
lx, ly, step
vertical,
dan
step
horizontal.
Parameter
lx
dan
ly
berguna
untuk
menentukan
panjang
dan
Iebar
domain pool.
Sedangkan
step
vertical
dan
step horizontal
|
 41
so
so
j(l
j(l
so
49
,,
"
-
47
47
47
47
-
48
49
so
49
I
I
51
'
.U
"
-17
47
49
49
49
49
so
50
so
50
:!
51
50
49
50
52
52
51
49
48
47
48
49
49
49
49
50
50
so
50
52
52
52
52
50
49
50
52
52
52
52
52
berguna
untuk
menentukan
langkah
pergeseran
pencarian
domain
di
dalam
domain
pool.
Secara
keseluruhan,
keempat parameter
ini berguna
dalam
menentukan
jumlab
domain
yang
ada
pada
domain
pool.
Contoh
perhitungan
domain
dan
domain pool
adalah
sebagai
berikut
:
jika
terdapat
suatu
range
berukuran
B
x
B
dan
diketabui
nilai
s
sebesar
Y,, maka ukuran
domain
adalab
2B
x
2B dan
didapatkan
ukuran
domain pool
sebesar
(2B+lx)
x
(2B+ly).
Domain Pool
Domain
4x4
lx
Range
2x2
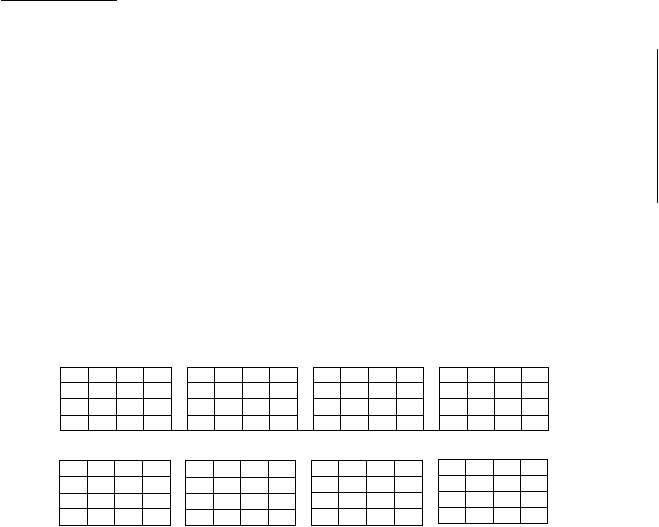
Gambar 3.2 Bentuk citra
sebelum
partisi dengan range 2x2 yang
memiliki domain 4x4
.1.2
Analisis Transformasi
Blok
Setelah
domain
dan
domain pool
didapat.
maka
akan
dilakukan
pencarian
range-domain
terbaik.
Pertama-tama
tentukan terlebih
dabulu
parameter
error
yang
akan
dipergunakan
saat
pemilihan
domain
terbaik.
Ada
dua
jenis
nilai
error
yang
dipakai
saat
penghitungan,
yaitu nilai error
antara
domain-range
dan
nilai
initial error dari threshold.
|
 3
2
I
0
7
6
5
4
II
10
9
8
15
14
13
12
15
II
7
3
14
10
6
2
13
9
5
I
12
8
4
0
12
13
14
15
8
9
10
II
4
5
6
7
0
I
2
3
----------
42
Pemilihan
pasangan
range-domain
dimulai
dengan
mencari domain
terbaik dari domain
pool. Proses akan
dilakukan
menggunakan
step
horizontal
ke
kanan sebanyak
I piksel
(sampai
batas
akhir lx)
dan
step vertical
ke bawah
sebanyak
I piksel
(sampai batas
akhir
ly).
Setelah
itu, proses
pencarian
domain
terbaik
dilakukan
dengan
cara
menghitung
luminansi
dan
menghitung
error
·
antara
range dengan
setiap
domain yang
ada.
Pasangan
range-domain
terbaik
adalah
pasangan
yang
memiliki
nilai
error
terkecil
dari
transformasi-affine
dengan
4
arah
rotasi
dan
4
arah
translasi
diantara
seluruh
domain
blok yang ada
0
I
2
3
12
8
4
0
15
14
13
12
3
7
II
15
4
5
6
7
13
9
5
I
II
10
9
8
2
6
10
14
8
9
10
II
14
10
6
2
7
6
5
4
I
5
9
13
12
13
14
15
15
II
7
3
3
2
I
0
0
4
8
12
(a)
Rotast
4
arah
0
4
8
12
I
5
9
13
2
6
10
14
3
7
II
15
(b) Translast
4
arah
Gam
bar 3.3 (a)
Bentuk rotasi 4 arah, (b) bentuk translasi
4
arah
Setelah
dilakukan
proses
pencarian
domain
terbaik
maka
akan didapatkan
pasangan
range-domain
terbaik. Sesuai
dengan
syarat
partisi
quadtree
bahwa jika
nilai error terkecil
antara
range-domain
lebih besar
dari initial
threshold dan
level
node masih
dibawah
level
maksimumblok range
lalu
dipartisi
menjadi
empat
bagian
sama
besar.
|
 50
50
50
50
50
49
47
47
47
47
48
49
47
47
50
49
51
51
51
51
48
49
49
49
49
49
50
50
50-50
47
47
52
51
50
52
49
48
49
49
49
49
50
49
52
51
47
48
50
50
50
50
52
52
52
52
50
49
52
52
52
52
50
52
------------------
43
Domain Pool
Domain
4x4
lx
Range
2x2
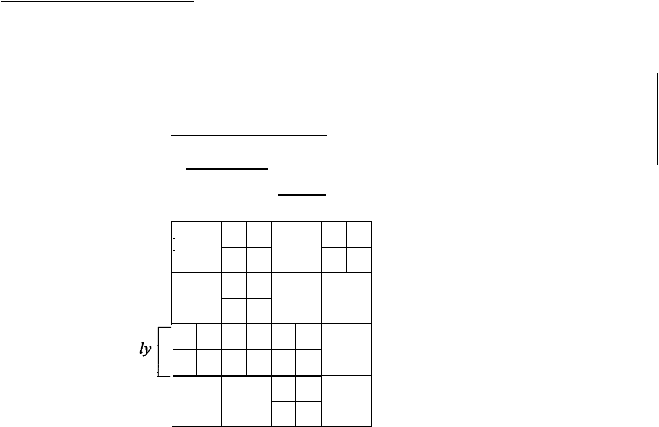
Gambar
3.4
Bentuk
citra
sesudah
partisi
dengan
range 2x2
yang
memiliki
domain
4x4
Setelah
metode partisi
quadtree
dilakukan di
seluruh bagian range maka
akan
didapatkan kumpulan
range (B)
dengan
ukuran
yang
berbeda-beda. Nilai
quadtree
code
lalu
disimpan
untuk
dipergunakan saat
proses
dekompresi
(membentuk range).
Pemetaan
range-domain
terbaik digabungkan
dengan
metode
partisi
quadtree
akan menghasi!kan koefisien yang terdiri dari simetri
affine,
luminansi
(contrast
dan
brightness),
posisi domain, dan
quadtree
code.
1.3
Analisis Encoding
Data koefisien dari proses
quadtree
dan
transformasi-ajjine
masih cukup
besar.
Oleh
karena
itu
untuk
lebih
menghemat
kapasitas
penyimpanan serta
mempertinggi rasio kompresi maka sebelum disimpan, data-data tersebut harus
|
 44
diencode
lagi
menggunakan
algoritma
tertentu.
Algoritma
yang
digunakan
untuk
mengencode
data quadtree code
adalah
adaptive arithmetic coding.
Tiga
konsep
utama
dalam
adaptive arithmetic
coding
adalah
interval
peluang,
symbol occurrence pool
dan
window size.
Symbol occurrence pool
adalah
suatu
wadah
untuk
menampung
simbol-simbol
yang
sudah
muncul
dalam
suatu string saat
proses
encode
atau simbol-simbol
hasil
dari
proses
decode.
Window
size
adalah
banyaknY.a
jumlah
simbol
yang
dapat
ditampung
dalam
symbol
occurrence
pool.
Window
size
ditetapkan
berdasarkan
jumlah
simbol
pada
string
yang
akan
di
encode.
Kegunaan
window size
sangat
terlihatjelas
pada
tahap
decoding.
Berikut
ini
adalah contoh proses
encvJmg mcnggunakan penghitungan
adaptive arithmetic coding.
Suatu string
bccb
dimana
setiap
symbolnya
merupakan
anggota
dari
himpunan
{a,b,c} akan
di
encode
menggunakan
teknik
adaptive
arithmetic coding, maka
langkah
langkah
yang
dilakukan
adalah
sebagai
berikut
:
a.
Inisialisasi
symbol occurrence
pool
sebagai
wadah
kosong
0
= {}
dan
inisialisasi
window size
sebesar
4
(sesuai
jumlah
simbol
yang akan
di
encode)
setelah
itu
peluang
kemunculan
setlap
simbol
anggota
himpunan
{a,b,c}
akan
dihitung
menggunakan
rumus berikut
:
J'v'(a)
+
1
p(
a)
=
-;-:-:-:----;--:'7._:...7;,:-..,.....--,
N(a)
N(b) +
Nfc)
+3"
i\'(c)
+
1
.
N(b)+l
p(b!
=
N(a)
+
N(b)
+
N(c)
+
3:
p(c)
=
'1\(""'
a')'+ N"'
(;,l:i;-)
+'-_...,.\',c..(-:-+·'3
')
Dimana
p
melambangkan
peluang
kemunculan,
N
melambangkan
jumlah
symbol
tertentu
yang ada
dalam
symbol occurrence pool.
Penambahan angka
|
|
45
I
pada
pembilang dan angka
3 pada
penyebut berdasarkan
rumus dasar
peluang, besamya penambahan pada penyebut didasarkan pada jumlah
simbol pada himpunan.
Ketika
meng-encode simbol b
(simbol
pertama dalam
string bccb),
karena
symbol
occurrence pool
(0)
masih kosong
maka N(a)
=
N(b) = N(c) =
0,
sehingga
didapatkan
p(a)
=
p(b)=
p(c)=
113.
Interval
peluang
awal
(0,1)
akan
terbagi
menjadi
tiga
bagian sesuai dengan
besar peluang kemunculan
masing-masing simbol. Interval peluang baru dibentuk berdasarkan peluang
kemunculan simbol
yang di
encode
terhadap
interval peluang sebelumnya.
Pada
tahap
ini
interval
peluang
baru
yang
terbentuk
berdasarkan
peluang
l..c:muncu!an imbol b adalah (low= 0.3333. high=
0.6667). Saat ini, symbol
occurrence pool
(
0)
akan berisi simbol
b
dan dinotasikan sebagai berikut :
O={b}.
b.
Ketika meng-encode simbol c (simbol kedua dalam string bccb), p(a), p(b)
dan p{c) akan dihitung ulang. Karena saat
ini pada symbol occurrence pool
berisi satu simbol b maka N(b) =I
sedangkan nilai N(a) = N(c) = 0 setelah
itu didapatkan p(a)
=
p(c) =
114 dan p(b}
=
2/4. Selanjutnya penghitungan
inter\'al
peluang baru dilakukan berdasarkan peluang simbol
c
.
Kemudian
simbol c dimasukkan
ke
dalam
symbol
occurrence
pool.
Saat
ini
symbol
occurrence pool (0)
berisi 2 simbol
yaitu b dan c:
0
=
{b,c} sedangkan
interval peluang baru yang terbentuk adalah low =
0.5834, high
=
0.6667.
|
|
46
c. Simbol c (simbol ketiga dalam string bccb) di encode. p(a), p(b) dan p(c)
akan dihitung ulang. Karena saat
ini pada symbol occurrence pool berisi dua
simbol, yaitu b dan c
maka N(a) =0 sedangkan nilai N(b) = N(c) = I setelah
itu akan didapatkan p(a) = 1/5, p(b) = p(c) = 2/5. Selanjutnya penghitungan
interval
peluang
baru dilakukan
berdasarkan
peluang
simbol
c
kemudian
simbol
c
dimasukkan
ke
dalam
symbol
occurrence
pool.
Saat
ini
symbol
occurrence pool berisi tiga simbolyaitu satu simbol b dan dua simbol c : 0
=
{b,c,c) sedangkan
interval
peluang
baru yang terbentuk
adalah
low
=
0.6334, high = 0.6667.
d. Simbol b (simbol keempat dalam string bccb) di encode. p(a), p(b) danp(c)
akan dihitung ulang. Karena saat ini pada symbol occurrence pool berisi tiga
simbol, yaitu satu simbol b dan dua symbol c maka N(a) =0 ,nilai N(b) = 1,
N(c) =
2 setelah itu akan didapatkan p(a)
=
116,
p(b)
=
2/6 . p(c)
=
3/6.
Selanjutnya
penghitungan interval peluang
baru dilakukan berdasarkan
peluang
simbol b
kemudian
simbol
b
dimasukkan ke
dalam symbol
occurrence pool. Saat ini symbol occurrence pool berisi empat simbol yaitu
dua simbol b dan dua simbol c : 0
=
{b,c,c,b} sedangkan interval peluang
baru yang terbentuk adalah low = 0.6390, high = 0.650 I. Karena pada tahap
ini jumlah symbol pada symbol occurrence pool sama dengan window size,
maka
proses encode dihentikan kemudian pemilihan sembarang angka
diantara 0.6390 (low terakhir) dan 0.6501 (high terakhir) dilakukan. Misal
angka decimal 0.64 dipilih, maka encoder akan mengirimkan simbol 0.64.
|
 --- ---- ------------
47
LO
0.6667
0.6667
c=1/4
c=215
c=3/6
0.6667
b=2
0.6501
0.3333
b=216
a= 1/4
90
•= 1/6
0.0
0.6334
Gam
bar
3.5
Proses
Penghitungan
Adaptive Arithmetic
Coding
Tahapan
proses encoding
menggunakan adaptive arithmetic coding
adalah sebagai berikut :
Langkah 1
Inisialisasi symbol occurrence pool
0
=
{},
inisialisasi window
size
sesuai
dengan jumlah
simbol
yang akan
di
encode dan
inisialisasi interval peluang dengan low
=
0 dan high
=
I.
Langkah 2
Hitung peluang
masing-masing simbol
yang ada pada himpunan
simbol yang ada.
Langkah 3 Hitung nilai posisi setiap simbol pada
interval
peluang
berdasarkan peluangnya masing-masing
Langkah 4 Encode simbol awal pada string dengan cara
memindahkan
symbol tersebut ke dalam symbol occurrence pool.
Langkah
5
Buat
interval
peluang
yang
baru dengan
nilai
low
dan
high
berdasarkan
nilai posisi low dan high pada simbol yang
di
encode.
Langkah 6
Cek
apakah
jumlah symbol
yang
ada
pada
symbol
occurrence
pool
telah
mencapai window
size. Jika
sudah, pilih
dan simpan
nilai
posisi
antara
low
dan
high
pada
interval peluang terbaru
|
 48
kemudian
akhiri
prosedur
encoding. Jika belum,
ulangi
langkah
ke
2.
2
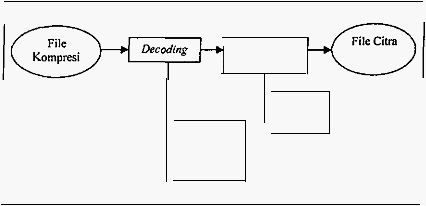
Analisis dan Perancangan
Dekompresi Citra
Kerangka
umum
dari
dekompresi
citra menggunakan
metode
quadtree
dapat
dilihat
pada
gam bar 3.6.
Pcmbentukan
Citra
Adaptiw
Q11odlru
"""-V•n..
.4.rrthWWtl'
Enrodiffg
Gam bar 3.6 Tahapan dekompresi citra metode quadtree
Pada
gambar
diatas,
terdapat
dua
bagian
utama
proses
dekompresi
citra.
Kedua
bagian
tersebut
adalah
:
a.
Decoding
Data
hasil
kompresi
yang
telah
di
encode
harus
dikembalikan
lagi
ke
dalam
bentuk
aslinya
agar
dapat
digunakan
untuk
pembentukan
citra. Proses
ini
dilakukan
dengan
menggunakan
algoritma
adaptive arithmetic
coding.
b.
Pembentukan
citra
Dengan
menggunakan
berbagai
parameter
yang ada
maka
quadtree code
akan
disusun
kembali
pada
citra
baru
sehingga menghasilkan range
dengan
|
|
49
+.\"icl
;\'(c)+
1
ukuran
yang
berbeda. Setelah
itu citra dibentuk dengan
melakukan proses
IFS ke dalam citra baru sesuai denganjumlah
iterasi yang ditentukan.
.
2.1
Analisis Decoding
Data
yang
didapat
dari
file
kompresi
harus
didecode
agar
kembali ke
bentuk semula. Algoritma yang dipakai
untuk memenuhi
hal ini adalah adaptive
arithmetic coding.
Proses decoding
dari
adaptive
arithmetic
coding
merupakan
bentuk
terbalik
dari
proses
encoding. Berikut
ini
adalah
contoh
proses
decoding
menggunakan
penghitungan adaptive arithmetic coding.
Su;,tu sirnbol
0.64
akan
di decode
menggunakan teknik
adaptive
arithmetic
,·uding.
rnaka langkah-langkah yang dilakukan adalah sebagai berikut:
a.
lnisialisasi
symbol
occurrence
pool
sebagai
wadah
kosong
0
= {}
dan
inisialisasi
windows size
sebesar
4
(sesuai
dengan
windows
size
sewaktu
encoding) setelah
itu peluang kemunculan setiap simbol anggota himpunan
{a,b,c} akan dihitung menggunakan rumus:
N(a)
+
1
p(a)
=
=-:----'o-2-'-.-:-:-...,-----,
:\'(a)
+Nib!+
Xi
c)+
3·
p(c)
=
=
.\
'
-
(
-
a
,-
)+
-
--
S
-
(
.
b
-
.
l
,.;.,.:-=-
+
-
3"
b _
N(b)+l
.
.
p(
l-
N(al+N(b)+N(c)+3"
dimana p
melambangkan
peluang
kemunculan,
N
melambangkan
jumlah
simbol
tertentu
yang
ada
dalam
symbol
occurrence pool.
Catatan:
penambahan
angka
l
pada
pembilang
dan angka 3 pada
penyebut
berdasarkan
rumus dasar
peluang,
besamya
penambahan
pada
penyebut
didasarkan pada jumlah simbol pada himpunan.
|
|
50
Decode simbol 0.64 yang pertama dilakukan. Karena symbol occurrence pool
(0) masih kosong maka N{a) = N(b) = N(c) = 0, sehingga didapatkanp{a)
=
p{b)= p(c)= 113. Interval peluang awal (0,1) akan terbagi menjadi tiga bagian
sesuai dengan besar peluang kemunculan masing-masing simbol. Pada tahap
ini
0.64 berada diantara
nilai posisi
low = 0.3333, high =
0.6667
yang
mewakili simbol b. maka simbol b dimasukkan ke dalam symbol occurrence
pool (0) dan dinotasikan sebagai berikut : O={b} sedangkan interval peluang_
baru
yang
terbentuk adalah
low =
0.3333,
high
=
0.6667. Karena jumlah
simbol
pada
symbol occurrence
pool
belum
mencapai window size,
maka
proses decode simbol 0.64 akan terns diulangi
b.
Pada proses decode
simbol 0.64
yang
ke
dua, p(a), p(b) dan
p{c) akan
dihitung ulang.
Karena saat ini
pada symbol occurrence
pool berisi satu
simbol b maka N(b) =! sedangkan nilai N(a) = N(c) = 0 setelah itu
didapatkan
p(a)
=
p(c) = 114
dan p{b) = 2/4. Pada tahap
ini 0.64 berada
diantara
nilai posisi low
=
0.5834,
high =
0.6667
yang
mewakili simbol
c.
maka
simbol
c
dimasukkan
ke dalam
symbol
occurrence
pool
(0)
dan
dinotasikan sebagai berikut :
0
=
{b,c} sedangkan .interval peluang baru
yang terbentuk adalah low = 0.5834, high = 0.6667.
c.
Pada proses
decode
simbol 0.64 yang
ke
tiga, p(a), p{b) dan
p{c) akan
dihitung
ulang.
Karena
saat
ini
pada
symbol
occurrence
pool
berisi dua
simbol, yaitu b dan c maka N(a) =0 sedangkan nilai N(b) = N(c) =
I setelah
|
|
51
itu akan
didapatkan
p(a)
=
115,
p(b)
=
p(c)
=
2/5. Pada tahap ini 0.64
berada
diantara
nilai
posisi
low =
0.6334,
high =
0.6667 yang
mewakili
simbol c. maka simbol c dimasukkan ke dalam symbol occurrence pool (0)
dan dinotasikan sebagai berikut : 0
=
{b.c,c) sedangkan
interval peluang
baru yang terbentuk adalah low =
0.6334, high
=
0.6667.
d.
Pada
proses
decode.. simbol
0.64
yapg ke empat, p(a), p(b)
dan
p(c) akan
dihitung
ulang.
Karena
saat
ini
pada
symbol
occurrence
pool
berisi tiga
simbol, yaitu satu simbol b dan dua simbol c maka N(a) =0 ,nilai N(b) =
I,
N(c)
=
2
setelah
itu akan didapatkan p(a)
=
116. p(b)
=
2/6 ,
p(c)
=
316.
Pada tahap ini 0.64 berada diantara nilai posisi lo11 0.6390. /ugh0.6501
yang
mewakili
simbol
c.
maka
simbol
c
dimasukkan
ke dalam
symbol
occurrence
pool
(0)
dan
dinotasikan
sebagai
berikut
: 0
=
{b.c,c,b}
sedangkan interval peluang baru yang terbentuk adalah low
=
0.6390, high
=
0.650I.
Pada
saat
ini
jumlah
symbol
pada symbol
occurrence
pool
sama
dengan
window
size,
maka
proses decode
dihentikan
dan
string
yang
dihasilkan adalah kumpulan symbol
yang ada pada Jymbol occurrence pool
yaitu string bccb.
Tahapan proses decoding
menggunakan adaptive arithmetic coding
adalah sebagai berikut :
|
|
----
---------------------------
52
Langkah
1
Inisialisasi
symbol
occurrence
pool
0
=
{}, inisialisasi
window
size
sesuai dengan
window
size
yang ada pada
proses
encoding
dan inisialisasi interval peluang dengan
low
=
0
dan
high
=
I.
Langkah
2
Hitung peluang masing-masing simbol
yang ada pada himpunan
simbol yang ada.
Langkah
3
Hi tung nilai
posisi
setiap simbol pada
berdasarkan peluangnya masing-masing
interval
peluang
Langkah
4
Decode
simbol baru dengan cara
memasukkan nilai simbol baru
tersebut
ke dalam
peluang
interval
yang ada,
masukkan
simbol
asli
yang
memiliki
nilai
posisi
yang
mencakup
nilai dari simbol
yan£ di JccoJ,·
l..c dalam
symbol occurrence
pool.
Langkah
5
Buat inten al pcluang yang baru dengan
nilai
low
dan
high
berdasarkan
nilai
posisi
low
dan
high
pada
symbol
asli
yang
terpilih.
Langkah
6
Cek apakah jumlah simbol yang ada pada
symbol
occurrence
pool
Ielah mencapai
window
size.
Jika sudah, akhiri prosedur
decoding.
Pada tahap ini kumpulan simbol yang ada pada
symbol
occurrence
pool
adalah
representasi
dari
kumpulan simbol asli.
Jika bel urn, ulangi langkah ke 2.
3.2.2 Analisis Pembcntukan Citra
Proses pembentukan citra menggunakan proses IFS , yaitu proses yang
dilakukan
berulang-ulang sesuai
jumlah
iterasi
yang
ditentukan.
Untuk setiap
|
|
54
dimasukkan ke dalam domain kemudian dilakukan transformasi-affine terhadap
domain
sesuai
dengan
simetri
yang
ada.
Informasi
koordinat
domain, nilai
luminansi, dan simetri affine untuk setiap range tersimpan pada koefisien.fracta/
yang
terbentuk saat proses kompresi. Hasil dari
proses
ini
adalah
terbentuknya
citra
sementara
pada
iterasi saat
ini.
Sesuai
dengan
jumlah
iterasi
yang
ditentukan,
ulangi
proses
IFS
terhadap setiap
range
yang
ada.
Setelah
iterasi
selesai dilakukan akan terbentuk citra keseluruhan hasil dekompresi.
.3 Penghitungan Kualitas Citra
Citra
hasil
dekompresi akan
mengalami penurunan
kualitas (lossy) dari
citra aslinya. Untuk menghitung seberapa besar perbandingan penurunan
kualitas
citra
(citra
asli
dengan
citra
hasil
dekompresi)
maka
dilakukan proses
penghitungan kualitas citra menggunakan PSNR.
Pada
dasarnya
PSNR
(peak
signal-to-noise ratio)
berguna
untuk
menghasilkan suatu angka
yang dapat mencerminkan kualitas dari sebuah citra.
Teori PSNR mengatakan bahwa semakin tinggi nilai PSNR berarti semakin baik
kualitas citra
hasil dekompresi. Namun dikarenakan angka-angka yang di proses
pada
perhitungan PSNR didapat dari
komputasi nilai
piksel citra asli
dan citra
hasil
dekompresi,
rnaka
sesungguhnya ukuran
PSNR
tidaklah
sesuai
dengan
persepsi
manusia
akan
kualitas citra.
Oleh
karena
itu
nilai
PSNR
yang
lebih
tinggi sesungguhnya belum tentu memiliki kualitas citra yang lebih baik.
Saat
ini,
telah banyak penelitian
mengenai cara
mengukur kualitas citra
berdasarkan persepsi penglihatan manusia, namun
semuanya masih merupakan
|
|
55
perhitungan
yang
masih
sulit
diaplikasikan.
Oleh
karena
itu
PSNR
masih
menjadi
tolak
ukur
penghitungan
kualitas citra
dalam
dunia
computer vision.
Penjelasan
penghitungan
PSNR adalah sebagai
berikut.
Tersedia
suatu
citra
asli
yang
dilambangkan sebagai
f(i,j)
yang
memiliki
NxN
piksel
dan
citra
hasil
dekompresi yang
dilambangkan
sebagai
F{ij).
Untuk
menghitung
nilai
PSNR,
Jangkah
pertama
yang
perlu
dilakukan
adalah
menghitung
nilai
dari
MSE
(mean
squared err01:)
Setelah
itu
dilakukan
penghitungan
bit rate
dan MAX1.
Setelah
mendapatkan
semua
koefisien
yang
dibutuhkan,
maka
penghitungan
PSNR
dapat
dilakukan.
Adapun
rumus-rumus
untuk
penghitungan MSE,
MAX1
dan
PSNR
adalah
sebagai
berikut
:
MSE=
L{j(l.JI-F(l.-!JL'
NxN
B
=
Jumlah _bit
Jumlah _
pxl
MAX
1
=2"-J
PSNR
=
20log
10(
Dimana,
f(i.j)
:
Nilai
piksel citra
asli pada
koordinat
i.j
F(i.j)
: Nilai
piksel citra
hasil
dekompresi
pada koordinat
i.j
Jum/ah
bit
:
Jumlah
bit
Jumlah_pxl :
Jumlah
piksel
B
:
Jumlah
bit
per
piksel
N
:
Resolusi
citra
|
|
56
MSE
MAXI
:
Nilai error keseluruhan citra
:
Nilai piksel maksimum pada citra
PSNR biasanya memiliki nilai yang berkisar diantara 20 sampai 40 dan
biasanya ditulis
menggunakan format desimal dengan 2 angka dibelakang koma
(contoh:
35.46)
dengan
satuan
db
(decibel).
Namun
untuk
menampilkan
data
yang sesungguhnya, maka dalam penelitian ini
nilai PSNR ditulis dengan
lengkap sesuai dengan tipe data yang digunakan dalam program yang dirancang.
|