|
BAB 2
Landasan Teori
2.1 Langkah-Langkah Dalam Merancang Sistem Control
Dalam merancang
suatu
sistem,
diperlukan
suatu
langkah
sistematik
untuk
mendapatkan
konfigurasi,
spesifikasi,
dan identifikasi dari sistem tersebut agar
memperoleh suatu hasil dan proses yang diinginkan. Langkah-langkah tersebut
diantaranya:
•
Langkah pertama, harus mengetahui tujuan dari sistem yang akan dibuat,
sebagai contoh sistem kontrol untuk mengendalikan tiga buah motor DC
yang bekerja secara simultan.
•
Langkah kedua,
menentukan pemodelan-pemodelan apa
yang cocok
untuk digunakan dalam membangun sistem yang ingin di buat.
•
Langkah ketiga,
mensimulasikan pemodelan dari sistem yang di bangun,
apakah dapat berjalan dengan baik atau masih ada yang harus diperbaiki.
•
Langkah
empat
adalah
pengimplementasian
dari
sistem
yang
sudah
di
rancang, yaitu dengan membuat bentuk nyata dari sistem control.
•
Langkah lima adalah tahap akhir dari perancangan yaitu dengan
mengukur tingkat kestabilan dari sistem control. Dan bila tidak ada yang
perlu di perbaiki atau di teliti ulang, maka sistem tersebut sudah baik.
7
|
|
8
2.2 Sistem Control
Definisi
sistem adalah
susunan,
himpunan,
komponen-komponen
fisik
atau
kumpulan benda-benda
yang dihubungkan atau berhubungan sedemikian rupa sehingga
membentuk suatu kesatuan atau keseluruhan. Kata Control itu sendiri adalah mengatur,
mengarah
atau
mengendalikan.
Jadi
sistem
control adalah
hubungan
timbal
balik
komponen-komponen
fisik
yang
membentuk
suatu
konfigurasi
sistem sehingga
memberikan hasil yang diharapkan. Untuk hubungan antara input dan output pada
sistem menunjukan adanya hubungan sebab akibat dari sebuah proses, yang berawal dari
sinyal
input
sampai
menghasilkan
sinyal
output. Maksud
dari
sistem
control adalah
menetapkan atau
mendefinisikan output
dan
input.
Jika
input
dan
output telah
ditentukan,
maka
memungkin
untuk
menetapkan
atau
mendefinisikan sifat dari
komponen-komponen sistem tersebut(SK202-Teori Sistem, Bina Nusantara,2001 ).
2.2.1 Penggolongan Sistem Control
Sistem control digolongkan ke dalam dua kategori umum, yaitu sistem untaian-
terbuka dan sistem untaian-tertutup. (SK202-Teori Sistem, Bina Nusantara,2001 ).
2.2.1.1 Sistem Untaian Terbuka ( Loop Terbuka)
Sistem control untaian-terbuka (lup tebuka) adalah sebuah sistem control yang
tak memiliki umpan balik, sehingga bila terdapat gangguan dari dalam maupun dari luar
maka sistem tak dapat melaksanakan tugas seperti yang diharapkan. Contohnya seperti
alat pemanggang roti automatik dimana waktu yang diperlukan untuk membuat hasil
panggangan yang bagus harus diperkirakan
oleh pemakainya, yang bukan merupakan
bagian
dari
sistem
itu.
Hasil
control
atas
mutu
panggangan
(output)
adalah
dengan
|
 9
penghentian alat pada saat
waktu
yang
telah disetel. (SK202-Teori Sistem,
Bina
Nusantara,2001 ).
Gambar 2.1: Sistem Pengendalian lup terbuka
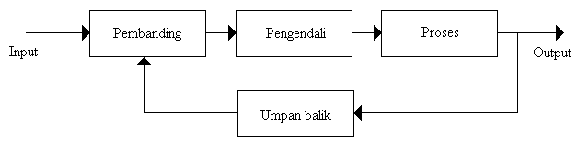
2.2.1.2 Sistem Untaian Tertutup ( Loop Tertutup)
Sistem
control
untaian-tertutup (lup tertutup) adalah sebuah sistem
control
yang
memiliki umpan balik, dimana antara output yang baru dengan sinyal input
yang
dimasukan kedalam sistem akan diselisih. Selisih dari sinyal output dengan sinyal input
tersebut disebut dengan sinyal
umpan balik. Pada sistem
ini sinyal error
yang
merupakan hasil dari selisih antara sinyal output yang baru terjadi dengan dengan sinyal
input yang
dimasukan
ke
dalam sistem akan
dikembalikan ke
pengendali
(controller)
untuk
mengurangi error. Proses tersebut terus dilakukan sampai mendapatkan hasil
output yang diinginkan. Contohnya seperti
mekanisme autopilot pada pesawat terbang.
Sistem
control
lup
tertutup
tersebut
digunakan
untuk
mempertahankan
arah
pesawat
yang telah ditetapkan, tanpa terpengaruh oleh perubahan-perubahan cuaca dan atmosfir.
Inputnya
adalah arah
tertentu
yang bisa disetel pada suatu alat penunjuk dalam panel
pengendalian pesawat,
dan
outputnya adalah
arah
yang
sesungguhnya. Sebuah
piranti
pembanding senantiasa mengamati input dan outputnya. Bila input dan outputnya sudah
sama
maka tak diperlukan tindakan pengendalian.
Bila ada perbedaan antara input dan
|
 10
output,
piranti
pembanding
tersebut
menyalurkan
suatu
isyarat
tindakan
ke
pengendalinya. (SK202-Teori Sistem, Bina Nusantara,2001 ).
Gambar 2.2: Sistem Pengendalian lup tertutup
2.3 Kestabilan Sistem
Kestabilan
sistem dibagi
menjadi
dua yaitu
kestabilan
absolut
dan kestabilan
relatif. Pada kestabilan absolut hanya terdapat dua buah keadaan yaitu stabil
atau tidak
stabil, dan pada kestabilan yang
relatif,
banyaknya
keadaan pun menjadi relatif pula
seiring semakin kompleksnya
sebuah
sistem,
jadi pada
kestabilan relatif
ada
yang
di
sebut kurang stabil, agak stabil, sangat stabil, dan lain lainnya.sebuah sistem yang stabil
adalah sistem yang memiliki respon yang terbatas (bounded). Untuk
memenuhi kriteria
kestabilan, maka sebuah sistem harus mampu untuk mengatasi gangguan dari luar,
dalam artian sistem tersebut dapat mengembalikan ke keadaan pada sebelum terjadinya
gangguan tersebut. (SK214-Sistem Pengaturan dasar, Bina Nusantara, 2001; Pert13 ).
2.4 Beberapa Model Controller
Prinsip
dasar
dari
teknik
controller
bertujuan
untuk
membuat
sebuah
sistem
menjadi
stabil
dan
memiliki
kehandalan
yang tinggi.
Beberapa
macam
teknik
yang
digunakan
diantaranya
adalah
controller
"on” dan
"off", controller
Proporsional,
|
|
11
controller Integral,
controller Proporsional
ditambah
Integral,
controller Proporsional
ditambah
Derivative,
dan
controller
Proporsional
ditambah Integral
ditambah
Derivative. Dalam memilih jenis controller haruslah dipertimbangkan dengan baik
karena berpengaruh pada kestabilan sistem dan tingkat efisiensi dari
sistem yang akan
dibuat.
Dan
untuk
memilih
tentu
saja
harus mengerti
dan
memahami
dari
sistem
pengaturan yang ada dan mengetahui kelebihan dan kekurangannya masing-masing.
2.4.1 " On " " Off " Controller
Dalam controller ini
hanya
terdapat dua buah keadaan
yaitu
"on" atau "off "
dan dapat juga dikatakan "hidup" atau "mati" dan dalam dunia digital biasa di isyaratkan
dengan pengertian angka "0" dan
"1". Jadi pada jenis controller ini
hanya terdapat dua
buah kemungkinan yang sifatnya berlawanan. Bila ditinjau dari segi perancangan sistem,
controller ini
sangat sederhana dibandingkan
jenis
controller
yang
lainnya, dan
masih
banyak
diterapkan
dalam
sistem
pengendalian yang
terdapat
pada
alat-alat
produksi
dalam pabrik.
2.4.2 Proporsional Controller Proporsional ( P )
Pada
Proporsional Controller
sebenarnya
hanyalah
sebuah
penguat
input
sehingga
hasil
pada
output tidak
semakin
mengecil
pada
sebuah
sistem.
Persamaan
matematika dari jenis controller ini adalah
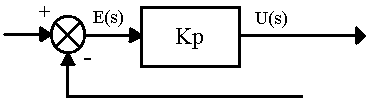
U(t) = Kp . e(t)
Dimana U(t) adalah output
Proporsional Controller
dan e(t) adalah sinyal
error dari
sistem.
Kp adalah
besaran
konstanta
untuk
di
kalikan dengan
sinyal error,
dimana besaran untuk Kp harus dapat di sesuaikan dengan kebutuhannya.
|
 12
0
Gambar 2.3: Blok Diagram Controller Proporsional
Sumber : (Katsuhiko Ogata,1996)
2.4.3 Integral Controller ( I )
Integral
Controller berfungsi
menghasilkan
respon
sistem
yang
memiliki
kesalahan dalam menuju ke keadaan yang di inginkan. Kalau sebuah plant tidak
memiliki unsur integrator , Proporsional Controller tidak akan mampu menjamin output
dari sistem akan
menuju ke keadaan yang di
inginkan. Pada Integral Controller,
nilai
input controller di
kalikan dengan
nilai
error yang
di
integralkan dengan
batasan
atas
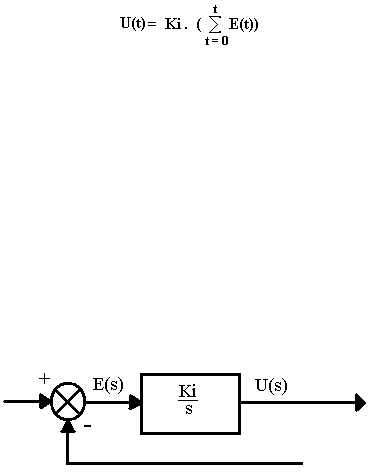
adalah t dan batas bawah adalah 0, sehingga bentuk persamaan matematika-nya menjadi:
U(t) = Ki
t
? e(t) dt
Dimana Ki adalah nilai konstanta yang dapat di ubah ubah sesuai
kebutuhannya. Dan setelah diubah kedalam domain waktu, maka fungsi alih dari
Integral Controller menjadi:
U(s) / E(s) =
Ki / s
atau
|
 13
Pada
controller integral
ini
menghasilkan
output
controller
yang
sebanding
dengan jumlah
error, dan
juga sangat dipengaruhi oleh time sampling, sehingga dari
dari rumus Integral Controller
dapat dilihat bahwa controller
ini dapat membantu
respon
dari
sistem
untuk
memperbaiki
keadaan
error
karena
sifat
dari
controller ini
adalah selalu menjumlahkan nilai error dari saat E(t
0
) sampai E(t), sehingga bila
Proporsional Controller sudah
tidak
mampu
lagi
untuk
memperbaiki
keadaan
error,
maka seiring berjalannya waktu, Integral Controller membantu menaikan respon untuk
menuju ke keadaan yang diinginkan.
Gambar 2.4: Blok diagram Integral Controller
Sumber : (Katsuhiko Ogata,1996)
Ketika digunakan Integral Controller, sistem akan mempunyai beberapa
karakteristik berikut ini:
1. controller output membutuhkan selang waktu tertentu, sehingga Integral
Controller cenderung terlihat memperlambat respon.
2. Ketika sinyal error berharga nol, controller output akan bertahan pada nilai
sebelumnya.
3. Jika sinyal error tidak berharga nol, output akan menunjukkan kenaikan atau
penurunan yang dipengaruhi oleh besarnya sinyal error dan nilai K
i
.
|
 14
4. Konstanta integral K
i
yang berharga besar akan mempercepat hilangnya
offset. Tetapi semakin besar nilai konstanta K
i
akan mengakibatkan
peningkatan osilasi dari sinyal controller output
(Guterus, 1994, p7-4).
2.4.4 Controller Diferensial ( D )
Output dari Diferensial
Controller memiliki
sifat seperti
halnya suatu operasi
derivatif yang
cenderung
meredam respon
untuk menuju ke keadaan
yang diinginkan.
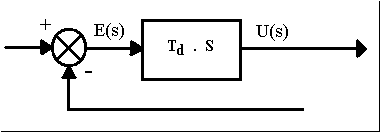
Bentuk persamaan matematika-nya untuk Diferensial Controller adalah:
U(t) = Kd . Td . (de(t)/ dt)
Dimana Kd adalah nilai konstanta yang dapat di ubah-ubah sesuai
kebutuhannya. Dan setelah diubah kedalam domain waktu, maka fungsi alih dari
Integral Controller menjadi:
U(s) / E(s) =
Kd (Td . s)
Atau
U(t) = Kd .[ E(t) – E(t -1)]
Gambar 2.5: Blok Diagram Diferensial Controller
Sumber : (Katsuhiko Ogata,1996)
|
 15
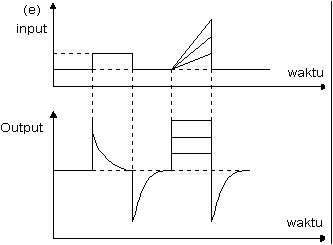
Pada gambar 2.6 menyatakan hubungan antara sinyal input dengan sinyal
output dari Diferensial Controller. Ketika input tidak
mengalami perubahan, controller
output juga
tidak
mengalami
perubahan,
sedangkan
apabila
sinyal
input berubah
mendadak
dan
menaik
(berbentuk
fungsi step),
output menghasilkan
sinyal
berbentuk
impuls.
Jika
sinyal
input
berubah
naik
secara
perlahan
(fungsi
ramp),
output justru
merupakan fungsi step yang besar magnitudnya sangat dipengaruhi oleh kecepatan naik
dari fungsi ramp dan faktor konstanta diferensialnya T
d
(Guterus, 1994, p8-4).
Gambar 2.6: Kurva waktu hubungan input-output Diferensial Controller
Karakteristik Controller diferensial adalah sebagai berikut:
1. Controller ini tidak dapat menghasilkan output bila tidak ada perubahan pada
input nya (berupa sinyal error).
2. Jika sinyal error berubah terhadap waktu, maka output yang dihasilkan
controller tergantung pada nilai Td dan laju perubahan sinyal error.
|
|
16
0
3. Diferensial Controller mempunyai suatu karakter
untuk mendahului,
sehingga controller ini dapat menghasilkan koreksi
yang signifikan sebelum
pembangkit kesalahan menjadi sangat besar. Jadi Diferensial Controller
dapat mengantisipasi pembangkit error, memberikan aksi yang bersifat
korektif, dan cenderung meningkatkan stabilitas sistem (Ogata,, 1997, p240).
Kerja Diferensial Controller hanyalah efektif pada lingkup yang sempit,
yaitu
pada periode peralihan. Oleh sebab
itu
Diferensial Controller tidak pernah digunakan
tanpa ada controller lain dalam sebuah sistem.
2.4.5 Pengontrolan Controller Dengan Integral Dengan Derivative ( PID )
Bila
Proporsional Controller digabungkan
dengan Diferensial Controller
(Derivative) dan
digabungkan
lagi
dengan
Integral
Controller
maka
persamaan
matematika-nya menjadi:
U(t)= [ Kp . e(t)] + [ ( Kp / Ti ).(
t
?
e(t) dt) ] + [Kp . Td . (de(t)/ dt)]
Maka fungsi alih dari pengendalian ini adalah
U(s) / E(s) = Kp .[ 1+ ( 1 / Ti . s) + (Td . s) ]
Dimana Kp adalah penguatan Proporsional, Ti adalah Integral dari waktu dan
Td
adalah
Derivative dari
waktu(Ogata,1996,p203).
Setiap
kekurangan
dan
kelebihan
dari masing-masing controller P, I dan D dapat saling menutupi dengan menggabungkan
ketiganya secara paralel
menjadi Proporsional plus
integral plus diferensial Controller
(Controller PID).
Elemen-elemen
Controller P,
I
dan
D
masing-masing
secara
keseluruhan bertujuan untuk mempercepat reaksi sebuah sistem,
menghilangkan offset
dan menghasilkan perubahan awal yang besar(Guterus, 1994, p8-10).
|
 17
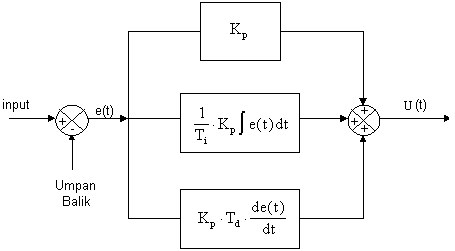
Gambar 2.7: blok diagram Controller Proporsional dengan
Integral dan dengan Derivative ( PID ).
Karakteristik
Controller PID
sangat
dipengaruhi
oleh
kontribusi
besar
dari
ketiga parameter P, I dan D. Penyetelan konstanta Kp, Ti, dan Td akan mengakibatkan
penonjolan sifat dari masing-masing elemen. Satu atau dua dari ketiga konstanta tersebut
dapat disetel lebih menonjol dibanding yang lain. Konstanta yang menonjol itulah akan
memberikan kontribusi pengaruh pada respon sistem secara keseluruhan (Gunterus,
1994, p8-10). Penalaan parameter Controller PID selalu didasari atas tinjauan terhadap
karakteristik
yang
diatur
(Plant). Dengan
demikian
betapapun
rumitnya
suatu
plant,
perilaku plant tersebut harus diketahui terlebih dahulu sebelum penalaan parameter PID
itu
dilakukan.
Karena
penyusunan
model
matematik
plant tidak
mudah,
maka
dikembangkan suatu
metode
eksperimental.
Metode
ini
didasarkan
pada
reaksi
plant
yang dikenai suatu perubahan. Dengan menggunakan metode itu model matematik
perilaku
plant tidak
diperlukan
lagi,
karena
dengan
menggunakan
data
yang
berupa
|
 18
kurva output, penalaan Controller PID telah dapat dilakukan. Penalaan bertujuan untuk
mendapatkan kinerja
sistem
sesuai
spesifikasi perancangan.
Ogata menyatakan
hal
itu
sebagai
alat
control
(tuning controller)
(Ogata,
1997,
p168,
Jilid
2). Agar
persamaan
PID
yang
ingin
digunakan
dapat
di
implementasikan
ke
dalam sistem
diskrit
maka
persamaan
PID
tersebut
harus
di
ubah
kedalam bentuk diskrit terlebih dahulu. Untuk
dapat dijadikan persamaan PID yang diskrit sebelumnya harus di ubah terlebih dahulu
kedalam domain Z. Kemudian dari persamaan PID dalam Domain Z di
ubah kedalam
persamaan PID diskrit dengan cara di laplace-kan.
U(t) =
[U (t-¹)
]+[
(Kp + Ki + Kd) . E(t)]
–[(Kp + 2Kd) . E(t-1)]
+[(Kd) . E(t-2)
]
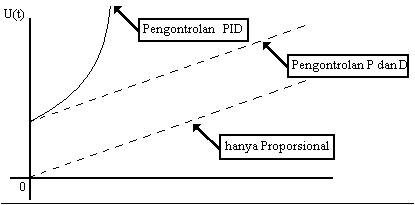
Gambar 2.8: Perbandingan hasil Proporsional Controller ( P )
dengan Proporsional Controller ditambah Derivative ( PD ) dengan
Proporsional ditambah Integral ditambah Derivative ( PID ).
Sumber : (Katsuhiko Ogata,1996)
|
|
19
2.5 Motor DC
Seiring dengan berkembangnya teknologi motor DC, saat ini sangat banyak
sekali
macam-macam
bentuk
motor
DC.
Sehingga
untuk
dapat
mengendalikan
motor
DC dengan baik, perlu diketahui pemodelan matematik dan cara kerjanya dari motor DC
yang akan digunakan. Pada sub bab ini akan di uraikan tentang perkembangan teknologi
motor DC, lalu cara kerja dan persamaan matematik dari motor DC.
2.5.1 Perkembangan Motor DC
Pada
perkembangan
teknologi
motor DC
memang
cukup
membantu
untuk
terciptanya perangkat elektronik yang membutuhkan penggerak, misalnya untuk
memutar pita kaset , untuk memutar kepingan CD, dan lain lainnya. Motor DC dengan
model model lama tidaklah memungkinkan untuk digunakan dalam perangkat
elektronik, karena model-model pada jaman dahulu masih menggunakan sikat dan
komutator, karena pada saat tersebut belum ada motor DC yang menggunakan teknologi
magnet permanen, sehingga bentuk
fisik dari motor DC
itu sendiri
menjadi
lebih besar
dan
membutuhkan
ruang
yang
sangat
besar, tetapi
dengan
menggunakan
teknologi
magnet permanen permasalahan tersebut dapat teratasi dengan baik. Dan seiring
berjalannya waktu, teknologi motor DC pun
menjadi
semakin
baik
dengan
tidak
menggunakan
sikat
dalam motor
DC
sehingga
tidak
perlu
perawatan khusus terhadap
motor DC, dan juga teknik manufaktur yang baik telah menghasilkan sebuah motor DC
yang memiliki rotor
yang tidak lagi terbuat dari besi, sehingga akselerasi yang
didapatkan
menjadi
semakin
baik beserta momen
inersianya
yang
menjadi
lebih
kecil
sehingga dapat membuat rasio torsi inersia yang tinggi dengan konstanta waktu yang
kecil.
Dari
seluruh
perkembangan
yang
ada,
pada
saat
ini
sangatlah
memungkinkan
|
|
20
untuk menggunakan motor DC kedalam perangkat elektronik yang kecil dan perangkat
digital lainnya, bahkan saat ini mampu digunakan dalam membuat robot-robot industri.
2.5.2 Cara Kerja dan Persamaan Matematik dari Motor DC
Cara kerja motor DC yang secara umum adalah mengubah energi listrik
menjadi energi mekanik, dan kekuatan dari gaya memutarnya biasa di sebut torsi. Torsi
yang
dihasilkan
berbanding lurus dengan besarnya arus pada
kumparan
dan
juga
berbanding
lurus dengan besarnya fluks pada
medan
magnetik.
Hubungan antara
torsi,
fluks dan arus dapat dituliskan dalam persamaan sebagai berikut :
T
m
=
K
m
.
?
. i
a
Keterangan :
T
m
= Torsi motor (N-m, lb-ft atau oz-in)
K
m
= Konstanta motor
i
a
= Arus jangkar (Ampere)
?
= Fluks (Weber)
Pergerakan dari motor DC terjadi karena adanya kumparan yang akan bersifat
magnetik ketika diberikan tegangan, dan karena dipengaruhi oleh medan magnetik aktif
yang mengelilingi kumparan tersebut maka kumparan yang tadinya bersifat magnetik
akan
melakukan
gerakan
memutar.
Gerakan inilah
yang
membuat
motor
tersebut
berputar. Pada saat konduktor bergerak pada medan magnetik maka suatu tegangan
dibangkitkan melintasi ujung-ujungnya. Tegangan ini disebut dengan tegangan emf
balik.
Tegangan
tersebut
berbanding
lurus
dengan
kecepatan
batang dan
berlawanan
dengan aliran arus. Hubungan antara emf balik dengan kecepatan sudut sebagai berikut:
e
b
=
K
m
. ? . ?
m
|
|
21
keterangan:
e
b
= emf balik (Volt)
K
m
= Konstanta motor
?
= Fluks (Weber)
?
m
= Kecepatan sudut dari motor (Radian / detik)
2.6 Analog to Digital Converter – ADC
ADC adalah komponen yang digunakan untuk merubah besaran tegangan
analog
kedalam bentuk
digital.
Ada
banyak
konsep
yang
digunakan dalam membuat
ADC,
salah
satu
diantaranya
adalah pendekatan
berangsur-angsur
(Successive
Approximation). Langkah
–
langkah
yang
terdapat
dalam
ADC
adalah
sinyal
analog
disampling
sehingga
sinyal
analog
yang
waktunya
continue menjadi
waktu
diskrit,
kemudian sinyal diskrit tersebut di kuantisasi yang bermaksud untuk membuat nilai dari
sinyal diskrit menjadi sesuai dengan yang ditentukan, setelah nilai pada sinyal diskrit
sudah
dikuantisasi,
maka
langkah
terakhirnya
adalah
melakukan
coding,
dimana
nilai
dari
hasil
kuantisasi
di
ubah kedalam
bentuk
bilangan binary, sehingga
nilai
binary
tersebut dapat digunakan kedalam perangkat diskrit lainnya. Contohnya Modem
(Modulator dan Demulator) adalah salah satu contoh dari suatu alat yang
menggunakan
ADC dimana cara kerjanya modulator (DAC) mengubah sinyal diskrit ke sinyal analog
lalu
sinyal
analog
dikirim
melalui
saluran
komunikasi
ke
ujung
lain
suatu
jaringan
sinyal. Di ujung lain sinyal tersebut dikembalikan ke bentuk asalnya yaitu bentuk diskrit
yang bisa diinterpretasikan oleh komputer. Proses pengubahan ini dinamakan demulasi
(ADC).
|
 22
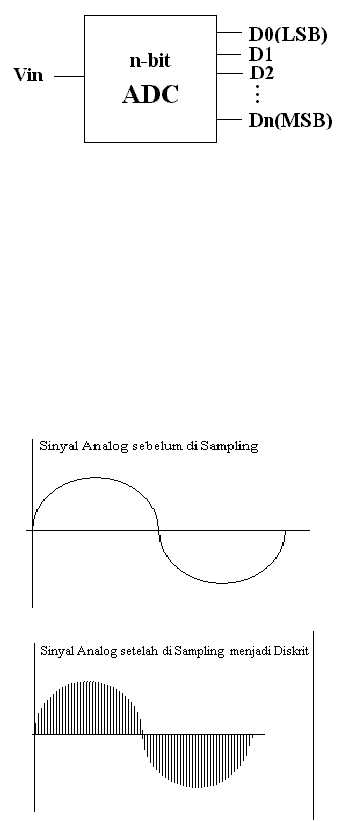
Gambar 2.9 : ADC dengan output n-bit
2.6.1
Sampling
Sampling adalah mengubah sinyal analog yang memiliki waktu yang continue
menjadi
sinyal
yang waktunya diskrit.
Dan
kecepatan
waktu sampling harus
dua
kali
lebih
cepat
dari
frekuensi
tertinggi
pada
sinyal
analog tersebut,
untuk
menghindari
terjadinya efek aliasing.
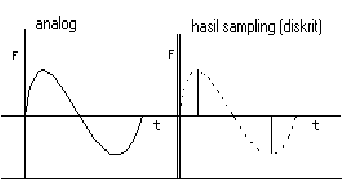
Gambar 2.10: Sinyal Analog sebelum dan sesudah disampling
|
 23
Pada syarat Nyquist dalam pengambilan contoh frekuensi, minimal harus
paling sedikit dua kali dalam satu frekuensi, hal tersebut di
haruskan agar output pada
frekuensi diskrit digital masih mampu untuk mendekati nilai frekuensi pada input.
Gambar 2.11: Sinyal Analog yang memiliki waktu sampling
yang minimum
2.6.2
Quantisasi
Quantisasi
adalah proses dimana
nilai diskrit yang
memiliki
nilai
yang
tidak
bulat
atau
memiliki
nilai
yang
berkoma,
dilakukan
pembulatan dengan
2
cara, yaitu
pemotongan
atau
pembuangan.
(Rounding dan
Dissection)
Bila
menggunakan
cara
Rounding maka
nilai
di
atas
0,5
akan
dibulatkan
keatas.
(cth:
nilai
7,51
dibulatkan
menjadi 8.) dan nilai dibawah 0.5 sampai 0.5 akan dibulatkan kebawah. (cth:
nilai 7,5
dibulatkan
menjadi
7).
Hal
ini
berbeda
degan
cara
Dissection (pemotongan
atau
pembuangan) yaitu berapapun nilai di belakang koma, maka nilai
dibulatkan kebawah
(cth: nilai 7,4 menjadi 7, dan nilai 7,8 tetap dibulatkan kebawah menjadi nilai 7).
|
 24
2.6.3
Coding
Coding adalah proses pengubahan dari
nilai desimal pada sinyal
diskrit
yaitu
menjadikan nilai kedalam bentuk binary, hal ini di lakukan agar
nilai
tersebut dapat di
gunakan
sebagai
data
digital
pada
perangkat digital
lainnya,
karena
pada
dasarnya
perangkat digital hanya beroperasi dalam bilangan binary.
2.6.4
Tahapan dari ADC
Gambar 2.12 : Tahapan konversi dari analog ke sinyal digital
2.6.5
Error dalam ADC
Karena pada ADC juga menggunakan DAC sebagai komponen konversi, maka
error-error yang dapat
terjadi pada DAC juga akan terjadi pada ADC. Beberapa jenis
kesalahan yang sering terjadi pada ADC adalah :
•
Quantization Error
Quantization Error atau ralat quantisasi pada
umumnya sebesar ± ½ LSB.
Quantization Error
ini dapat juga dinyatakan dalam bentuk SNQR (Signal
to Noise Quantization Error), dimana:
SNQR = 20 log (FSR/ I
LSB
)dB
•
Offset Error
Merupakan
error
yang
terjadi
pada
saat
input
diberikan
0
volt,
namun
output diskrit tidak menunjukkan ‘0’.
|
|
25
•
Gain Error
Error ini memberikan output data diskrit (binary) tidak sesuai dengan input
analog.
Akibatnya
FSR
(Full
Scale
Range)
akan
ikut
terpengaruh.
Bila
Gain Error besar maka output FSR akan turun karena besarnya error yang
terjadi, begitu juga sebaliknya.
•
Non-Linearity Error
Error
ini
terjadi akibat
dari adanya
variasi
Offset Error
dan
Gain
Error
sehingga
perbandingan
antara tegangan
input
dengan data
output diskrit
menjadi tidak linear.
•
Differential Non-Linearity Error
Nilai error ini selalu lebih besar dari Quantization Error (maksimum 2 kali
yaitu
sebesar
I
LSB
). Error
ini
adalah
selisih
antara
harga
teoritis dengan
harga
sesungguhnya
untuk
input
range
tertentu.Bila
terjadi
Overlap
maka
akan ada output binary yang hilang.
2.7 Digital to Analog Converter – DAC
DAC merupakan komponen untuk merubah besaran data diskrit kedalam
bentuk analog. DAC terbagi dalam beberapa jenis sesuai dengan cara kerjanya, beberapa
diantaranya adalah : Weighted Resistor dan R-2R.
2.7.1 Weighted Resistor
Resistor
yang
mempunyai nilai
dengan
perbandingan tertentu dipararelkan
secara
bersama-sama
dan
dipasang
pada
input
inverting
sebuah
Op-Amp
sedangkan
|
 26
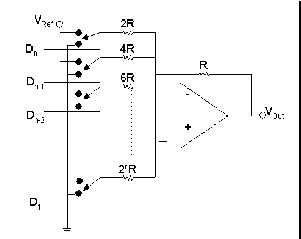
input Non-Inverting dihubungkan ke ground. Perbandingan antara masing-masing
resistor adalah R, 2R, 4R, 6R, dst. Dengan adanya perbandingan tersebut maka nilai
resistor yang dibutuhkan menjadi sangat bervariasi dan menimbulkan masalah dalam
mendapatkannya. Oleh karena
itu konsep R-2R menjadi pilihan
yang lebih baik.
Weighted Resistor memiliki gambaran seperti berikut.
Gambar 2.13: Rangkaian Weighted Resistor
2.7.2 R-2R Ladder
DAC
dengan
konsep
R-2R pada
dasarnya
merupakan
pengembangan
dari
konsep
Weighted Resistor
namun
dengan
cara
penempatan
resistor
yang
lebih
baik
sehingga
nilai
resistor
akan
memenuhi
syarat
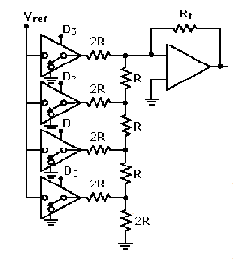
perbandingan.R-2R Ladder
memiliki
gambaran seperti berikut :
|
 27
Gambar 2.14: Rangkaian R-2R Ladder.
Pada
DAC,
jumlah
bit
masukan
akan
mempengaruhi
jumlah
step
(resolusi)
yang dapat dihasilkan, yaitu mengikuti rumus 2
N
dimana N = jumlah bit input.
Sedangkan
V
FS
merupakan
nilai
tegangan maksimum
yang dapat dihasilkan
DAC pada
saat semua data input bernilai 1, namun karena adanya keterbatasan pada sistem diskrit,
maka nilai tegangan maksimum
yang dapat dihasilkan akan kurang dari V
FS
,
yaitu
sebesar V
FS
-
I
LSB
.
Dimana I
LSH
adalah nilai
tegangan yang dapat dihasilkan bila terjadi
perubahan satu step. Nilai I
LSB
didapatkan dari V
FS
/2
N
2.7.3 Error
Beberapa kesalahan yang sering terjadi pada DAC adalah :
•
Accuracy Error
Merupakan error pada ketepatan perubahan nilai tegangan sebesar
I
LSB
pada
saat
terjadi
perubahan
satu
step.
Namun
pada
umumnya, error
sebesar ± ½ LSB adalah dianggap normal. Pada
DAC yang
lebih
baik,
tingkat error akan dapat ditekan
menjadi ±¼ LSB karena
menggunakan
|
|
28
metode A-Law dan µ-Law. Toleransi pada DAC ini adalah seperti halnya
toleransi pada resistor.
•
Absolute Error
Merupakan error
absolute
yang
terjadi.
Besarnya adalah sebesar
Y-X,
dimana
Y
=
output seharusnya,
sedangkan X
=
output yang diperoleh.
Absolute Error ini juga berhubungan sebab akibat pada Accuracy Error
•
Offset Error
Offset Error
ini
adalah
output DAC
yang
tidak
tepat
0
Volt
pada saat
semua input diskrit DAC bernilai ‘0’. Offset Error ini dapat diatasi
dengan penyetelan V
OS
pada Op-Amp yang digunakan sebagai penguat
pada output DAC.
•
Gain Error
Dinamakan juga Scaling Error. Error ini adalah step berubah tidak sesuai
dengan nilai I
LSB
(lebih besar atau lebih kecil dari I
LSB
). Bila input binary
makin besar akan menyebabkan penyimpangan tegangan makin besar
sehingga pada
akhirnya akan
mengakibatkan
Absolute Error
yang
juga
semakin besar.
•
Linearity Error
Linearity Error
merupakan error
pada DAC yang berupa ukuran step
(nilai
I
LSB
) yang
berubah-ubah.
Dengan
adanya
error
ini
maka
nilai
tegangan output dari DAC akan menjadi tidak sesuai (tidak linear)
dengan perbandingan data diskrit yang diberikan kedalam DAC.
|
|
29
2.8 FPGA
FPGA
merupakan
komponen
yang
berfungsi sebagai media untuk
mengimplementasikan
rangkaian diskrit, komponen
ini
memiliki
sifat
yang sangat
fleksibel atau dengan kata lain, arsitektur diskrit yang ada dalam IC ini dapat di bentuk
menjadi rangkaian diskrit seperti apapun dan kemampuannya dibatasi oleh banyaknya
gerbang logika dalam IC tersebut. Dalam perancangan ini FPGA yang tersedia memiliki
gerbang logika sebanyak 400000(Empat Ratus Ribu) gerbang.
2.8.1 Sejarah Perkembangan FPGA
FPGA adalah pengembangan sebuah PLD yang mana sejarah
perkembangannya dikelompokkan menjadi 3 kelas yaitu:
•
SPLD (Simple Programmable Logic Device) Î
SPLD adalah merupakan
PLD dengan teknologi yang sederhana, seperti Read Only Memory (ROM),
Programmable Logic Array (PLA) dan Programmable Array Logic (PAL).
•
CPLD (Complex Programmable Logic Device)
Î
CPLD
adalah
merupakan suatu komponen
logic yang
terdiri atas beberapa PLD dengan
sebuah struktur interkoneksi dalam sebuah chip.
FPGA
dibandingkan
dengan
CPLD,
sebuah
chip FPGA
mengandung
lebih
banyak
logic
block daripada
sebuah
chip
CPLD.
FPGA
menyediakan
struktur
interkoneksi yang besar, yang mendominasi keseluruhan chip.
|
|
30
2.8.2 Keuntungan Menggunakan FPGA
Keuntungan yang dimiliki FPGA sebagai alat perancangan diskrit :
-
Untuk proses perkembangan, rekonfigurasi sirkuit dapat dilakukan dengan
kecepatan yang tinggi dan dapat dilakukan oleh user sendiri.
-
Bisa
melakukan
Parallel
processing
yang
mana dapat
dilakukan
dengan
kecepatan tinggi.
-
Menyediakan
solusi software terintegrasi
untuk
merancang,
mensimulasi,
implementasi dan download ke alatnya.
-
Hasil
sintesis
bisa
disimulasikan,
dimana
hal
tersebut
dapat
pengurangi
resiko kegagalan dalam seluruh rancangan
-
Tersedianya
beberapa
entry
design
sesuai
kebutuhan,
seperti
schematic,
HDL, dan state machine.
-
Hemat biaya dalam aplikasi
2.8.3 Aplikasi Dari FPGA
Sekarang ini sudah terdapat berbagai macam aplikasi dari FPGA diantara-nya
adalah sebagai berikut :
-
Controller protocol komunikasi.
-
Pembuatan satellite.
-
Sistem GPS.
-
Controller PLC.
-
Alat-alat medis.
|
|
31
FPGA yang akan digunakan adalah IC FPGA tipe SPARTAN 3 yang memiliki
400
ribu
gerbang
dan
di
produksi
oleh XILINX. FPGA adalah sebuah
Field
Programming Device (FPD) dimana
mengacu pada tipe IC
yang
memiliki fungsi
yang
dapat menyimpan sebuah sistem elektronik tertentu, dengan batasan banyaknya gerbang
–
gerbang logic yang terdapat didalamnya. Dapat dikatakan FPGA ialah FPD yang
mempunyai struktur yang umum, yang memperbolehkan kapasitas very high logic gate.
FPGA dapat diprogram, hampir sama dengan PLD, yaitu istilah umum untuk IC yang
dapat diprogram dalam
lab
untuk
melakukan
fungsi
yang
kompleks.
Perbedaan
PLD
dengan FPGA biasanya dibatasi perbedaan jumlah
gerbang dan cara
menggunakannya
misalnya PLD memiliki gerbang yang sangat sedikit jumlahnya bila dibandingkan
FPGA yang bisa sampai ribuan sampai ratusan ribu gerbang, juga FPGA biasanya
terkenal untuk membuat rancangan IC. Untuk memasukan sesuatu atau memprogram
suatu sistem kedalam IC FPGA salah
satunya dapat di gunakan software dari XILINX
yang bernama "XILINX ISE WEBPACK 6.1" dan untuk mensimulasikan sistem atau
model
rangkaian
diskrit
yang hendak
dibuat dapat
menggunakan software
pendukung,
seperti
"ModelSim XE
II 5.7c" atau program simulator
lainnya. Bahasa pemrograman
yang digunakan dalam merancang arsitektur diskrit pada FPGA adalah VHDL
(VHSIC
Hardware
Description Language)
atau
dapat
juga
dengan
menggunakan
bahasa
pemrograman
lainnya seperti
"VERILOG". Pada board FPGA tipe Spartan 3
terdapat
tiga buah expansion connector yang berfungsi sebagai power output dan I/O yang dapat
pakai sebagai input atau output data diskrit. Pada
IC FPGA seri XC3S-400-ft256
ini,
memiliki total I/O sebanyak 100 pin. Interconnection untuk Xilinx FPGAs terdiri dari
jalur-jalur konduktor (single leght dan long line) yang mana terdapat switch matrix yang
|
|
32
sebagai penghubung jalur-jalur konduktor tersebut secara
horizontal dan
vertical
yang
terletak di antara CLB (Configurtable Logic Block) dan IOB (Input Output Block)
2.8.4 Pengenalan VHDL
HDL
(Hardware
Description Language)
adalah
bahasa
pemrograman
untuk
memodelkan hardware diskrit. VHSIC adalah singkatan dari Very High Speed Integrated
Circuit.
Jadi
VHDL
adalah
VHSIC
Hardware
Description Language
dimana
bahasa
pemrograman ini sangat populer digunakan untuk memodelkan arsitektur diskrit yang
memiliki kecepatan proses data yang tinggi. Sehingga dengan terbitnya
bahasa
pemrograman
ini,
seorang
designer perangkat
diskrit
akan
lebih
leluasa
dalam
menciptakan arsitektur diskritnya, karena dengan menggunakan bahasa VHDL, seorang
designer dapat
langsung
mensimulasikan
rancangannya
dan
langsung
dapat
di
implementasi kedalam FPGA dalam waktu
yang sangat singkat. Menurut Perry,
Douglas,
berikut
ini
adalah komponen-komponen dasar
VHDL
yang
digunakan
pada
hampir semua deskripsi :
-
Entity
Sebuah entity adalah komponen penyusun yang paling dasar dimana tingkatan
yang
paling
tinggi
dari
sebuah
rancangan
adalah
entity top
level. Bila
rancangan
berbentuk tingkatan atau hierarki maka deskripsi top level akan memiliki deskripsi lower
level yang terkandung di dalamnya.
-
Arsitektur
Semua entity yang dapat disimulasi mempunyai deskripsi arsitektur. Arsitektur
tersebut menjelaskan perilaku dari entity tersebut. Sebuah entity tunggal dapat memiliki
|
|
33
beberapa arsitektur. Sebuah arsitektur mungkin berupa behavioral, sementara yang
lainnya berupa deskripsi structural dari desain tersebut.
-
Proses
Proses
adalah
bagian
paling dasar
dalam
VHDL
untuk
melakukan
pengeksekusian. Semua deskripsi VHDL pengoperasiannya ditampilkan dalam simulasi,
prosesnya dapat dipisahkan ke dalam satu proses atau banyak proses.
2.8.5 Beberapa Syntax yang terdapat dalam VHDL
1) Case Insensitive
2) Komentar diawali dengan ‘--’
3) Statement diakhiri dengan ‘;’
4) List dipisahkan dengan ‘,’
5) Signal assignment menggunakan ‘<=‘
6) Variable assignment menggunakan ‘:=‘
7) Penamaan identifier:
a) Dapat menggunakan huruf, angka, dan ‘_’
b) Diawali dengan huruf
2.8.6 Data Object
1)
Signal, menggambarkan kabel
yang dapat
memiliki
nilai
yang dapat
berubah-ubah sejalan dengan waktu.
2)
Variable, berfungsi
sama seperti
variabel pada
bahasa
pemrograman
konvensional, dengan nilai yang berubah sejalan dengan urutan statement.
|
|
34
3)
Constant, sebagai konstanta yang harus diinisialisasi dengan suatu nilai dan
tidak dapat berubah nilainya.
2.8.7
Standard Data Types
1) Integer
2) Real
3) Boolean
4) Character
5) Bit
6) Bit_Vector
7) Time
8) String
9) Natural
10) Positive
2.8.8 IEEE Standard Logic Type std_logic
1)
‘U’
->
Uninitialized
2)
‘X’
->
Forcing unknown
3)
‘0’
->
Forcing 0
4)
‘1’
->
Forcing 1
5)
‘Z’
->
High Impedance
6)
‘W’
->
Weak unknown
7)
‘L’
->
Weak 0
8)
‘H’
->
Weak 1
|
|
35
9)
‘-’
->
Don’t care
2.9 Op-Amp
Op-Amp (Operational Amplifier) adalah suatu rangkaian terpadu yang tersusun
dari berbagai komponen semikonduktor lainnya, dimana fungsi utama dari op-amp
adalah
untuk
melakukan
operasi-operasi
aritmatik, integrasi dan penguatan. Op-amp
sudah
dikemas
dalam bentuk
IC
(teknologi
rangkaian
terpadu)
dan
mengambil
sinyal
dalam bentuk (tegangan listrik) yang di input melalui jalur V
in
yang disediakan di dalam
komponen tersebut untuk dikuatkan dengan dengan sumber daya yang tersedia, dan
kemudian
di
output
hasil
penguatannya
melalui
jalur
outputnya. Keuntungan
dari
penggunaan OP-AMP ini adalah ukuran kecil, kehandalan tinggi, harga lebih murah,
lebih kebal terhadap temperatur yang berlebihan, dan tegangan serta arus offset lebih
rendah.
Oleh
karena
itu,
Op-amp
lebih
sering
digunakan
dibandingkan
dengan
Transistor.
Karena
transistor
mempunyai
kelemahan,
yaitu
nilai penguatan
rendah
dan
mudah dipengaruhi oleh temperatur yamg berlebihan.
2.9.1 Karateristik Op-Amp yang ideal
•
Bati tegangan : 8
Besarnya bati Av = Vo/Vin atau Av(dB) = 20 Log Av. Bila nilai bati tegangan
adalah tak berhingga maka nilai Vo akan besar sekali dibandingkan dengan Vin.
|
|
36
•
Lebar pita : 8
Bila lebar pita adalah tidak
berhingga
maka
op-amp
dapat
bekerja
pada
frekuensi
yang
besar,
bila
semakin
besar
lebar
pita
maka
op-amp
tersebut
semakin
bagus.
•
Hambatan input : 8
Semakin besar hambatan input maka Vin = Vsg ,karena hambatan output sangat
kecil maka hambatan output dapat diabaikan dan menyebabkan tidak ada tegangan yang
terbuang.
•
Hambatan output : 0
Semakin
kecil
nilai
hambatan
output maka
penguatan
yang
dihasilkan
akan
semakin besar.
•
Offset dan drift : 0
Tegangan offset terjadi karena input sebuah op-amp dihubungkan dengan bumi,
dan
oleh
karena
transistor
masukkan
mempunyai
harga
Vbe
yang
berbeda. Drift
merupakan offset yang dipengaruhi suhu.
•
CMRR
:
8
CMRR
(Common
Mode
Rejection Ratio)
merupakan
perbandingan
dari
bati
tegangan diferensial dengan bati tegangan ragam sekutu.Semakin tinggi CMRR maka
makin baik penguat diferensial tersebut.
•
Slew Rate : 0
Slew
rate
merupakan
nilai
tercepat
dimana
output dapat
berubah.
Perubahan
maksimum dari
tegangan output Salah satunya
yang
terpenting dari semua spesifikasi
|
 37
yang mempengaruhi operasi AC, dari sebuah op-amp karena besaran tersebut membatasi
kepatuhan AC pada frekuensi tinggi.
2.9.2 Macam-Macam Penguatan
Pada
sebuah Op-Amp
yang berfungsi sebagai
penguat,
terbagi
menjadi
dua
macam penguatan, yaitu Penguat pembalik dan penguat tak membalik.
•
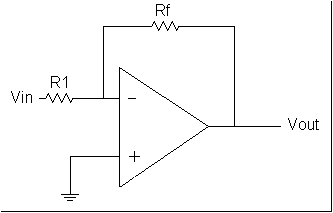
Penguat membalik
Penguat membalik adalah suatu rangkaian op-amp dimana sumber tegangannya
diambil dari kaki inverting op-amp.
•
Penguat tak membalik
Penguat tak membalik adalah suatu rangkaian op-amp dimana sumber
tegangannya diambil dari kaki non inverting op-amp.
|
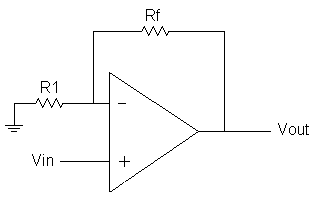 38
2.9.3 Cara kerjanya dari Penguatan Operasional
Kerja dari Op-Amp
adalah Penguat operasional
mempunyai 2
terminal
input
yaitu tegangan V1 dan V2, dimana V1 disebut terminal masukan tanpa pembalik (non
inverting) sedangkan
V2
disebut
terminal
masukan
pembalik
(inverting).
Penguatan
antara
V0 dan V1 positive (+)
dihasilkan oleh
terminal
non pembalik (non
inverting)
sedangkan penguatan antara Vo dan V2 negative (-) dihasilkan oleh terminal pembalik
(inverting). Sebuah
penguat
dengan
satu
ujung
dianggap
sebagai
peristiwa
khusus
dimana,
salah
satu
terminal
masuk
digroundkan. Hampir
semua OP-AMP hanya
mempunyai
satu
terminal output.
Bila
penguatan
dengan
hambatan
sama
besar,
hubungan
langsung
dari
output menuju
input,
menghasilkan
penguatan
satu.
Dalam
konfigurasi
tak
membalik
ini
tegangan output sama
dengan
tegangan
input dan
penguatan sama dengan 1.
Berbagai
tipe penguatan digunakan dalam rangkaian dasar.
Salah satu fungsi yang penting untuk diingat adalah hubungan polaritas masukan
terhadap output. Bila input membalik lebih negative dibandingkan dengan
masukan tak
membalik,
maka outputnya-pun negative. Demikian pula jika masukan
membalik
lebih
negative dibadingkan
dengan
masukan
tidak
membalik,
maka
output
akan
bernilai
positive.
|
|
39
2.10 Sensor Posisi
Pada
sebuah
sistem
loop tertutup,
kehadiran
sensor
sangatlah
di
butuhkan,
karena sensor bekerja sebagai pembaca fungsi output untuk dimasukan kembali kedalam
sistem. Pada perancangan sistem ini output dari dari sistem berupa posisi putaran motor
sehingga
untuk
membaca
posisi
pada
poros putaran
dapat
digunakan
potensiometer
dengan cara menghubungkan tuas potensiometer langsung dengan poros putaran lengan
yang
ingin
dilihat
posisinya. Karena
pada
output
sistem adalah posisi
lengan
dalam
satuan
derajat
kemiringan,
maka
untuk
membaca posisi tersebut dapat digunakan
potensiometer
linear,
yang
besaran
hambatannya
dapat diubah dengan
memutar
tuas
pada potensiometer. Potensiometer
ini dapat bekerja
sebagai sensor, karena perubahan
hambatan dapat mengubah tegangan dan arus yang melewatinya, sehingga sistem dapat
membaca posisi lengan dengan
melihat perubahan arus dan tegangan
yang disebabkan
oleh poros putaran lengan yang menggerakan tuas potensiometer. Sehingga dengan
rumus pembagi
tegangan dan hamabatan, maka output tegangan yang dihasilkan dalam
bentuk sinyal
analog, dapat
di
konversikan
kedalam diskrit
dengan bantuan IC
ADC
(Analog To Digital Converter).
|