 5
BAB 2
LANDASAN TEORI
2.1. Struktur Beton Bertulang
2.1.1. Pengertian dan Definisi Beton Bertulang
Beton bertulang adalah gabungan antara beton dan tulang baja. Beton merupakan
campuran antara semen, pasir, kerikil dan air
yang setelah mengeras membentuk massa
padat. Sedangkan beton bertulang adalah beton yang ditulangi dengan
luas dan
jumlah
tulangan tertentu untuk mendapatkan penampang yang berdasarkan asumsi bahwa kedua
material bekerja bersama – sama dalam menahan gaya yang bekerja.
Gambar 2.1. Kolom beton bertulang
( Sumber : Reinforced Concrete Mechanics and Design )
|
 6
2.1.2. Tipe – Tipe Kolom
Secara umum kolom beton bertulang ada 3 macam menurut bentuknya yaitu :
a. Kolom
berbentuk
bujursangkar
atau
persegi
panjang
dengan
tulangan
memanjang dan pengikat lateral terpisah (sengkang).
b. Kolom berbentuk lingkaran dengan tulangan melingkar dengan pengikat lateral
terus ( spiral ).
c. Kolom dengan bentuk tak tentu dengan tulangan mengikuti bentuk tak tertentu
tersebut.
(a)
(b)
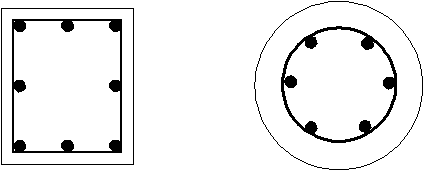
Gambar 2.2 (a) Kolom persegi dengan tulangan sengkang; (b) kolom lingkaran dengan
tulangan melingkar ( Sumber : Reinforced Concrete Mechanics and Design )
|
 7
(a)
(b)
Gambar 2.3 (a) Kolom persegi dengan tulangan sengkang; (b) Kolom lingkaran
dengan tulangan spiral
2.1.3. Tujuan Perencanaan Struktur Beton
Struktur harus memenuhi 4 (empat) kriteria utama yaitu :
1. Ketetapan
Pengaturan
Ruang,
bentang,
ketinggian
plafon,
akses
dan
arus
lalu
lintas
harus memenuhi
kebutuhan
pemakai.
Struktur
harus sesuai
dengan
lingkungan dan Estetika.
2. Ekonomi
Biaya total struktur tidak boleh malampaui anggaran dari pemilik.
3. Persyaratan struktur.
Hal ini meliputi 2 (dua) aspek utama :
a. Struktur harus cukup kuat sehingga dapat menerima semua beban dengan
aman.
b.
Struktur tidak
boleh
melendut,
terangkat,
bergetar
atau
retak
sehingga
menggangu fungsi dari bangunan tersebut.
4. Desain
struktur
harus sedemikian
sehingga
memerlukan
pemeliharaan
minimum dam pemeliharaan tersebut dapat dilaksanakan secara sederhana.
|
|
8
2.1.4. Proses Desain
Proses
desain
adalah
proses
pengambilan
keputusan
yang
berurutan
dan
berulang, 3 tahap utamanya adalah :
1. Penentuan kebutuhan dan prioritas pemilik
Semua bangunan atau struktur lain dibangun sesuai dengan kebutuhan. Pemilik atau
pemakai
seharusnya
terlibat
pada
penentuam fungsi
estetika,
anggaran
yang
diperlukan, dan penyelesaian bangunan yang cepat.
2. Pengembangan Konsep Proyek
Berdasarkan kebutuhan
dan
prioritas
pemilik
dapat
dikembangkan berbagai
kemungkinan anggaran. Rencana anggaran awal dapat menjadi pilihan terakhir
untuk memenuhi prioritas kebutuhan pemilik sesuai dengan anggaran yang tersedia.
Selama tahap ini dapat dipilih konsep seluruh struktur. Ukuran elemen struktur dapat
diestimasi
dari
hasil
analisis besaran
momen ,
gaya
geser dan
gaya
aksial.
Tahap
desain struktur ini adalah untuk memenuhi kriteria desain yang berhubungan dengan
ketepatan, ekonomi, dan pemeliharaan.
3. Perencanaan masing – masing sistim
Setelah dipilih konsep struktur secara umum maka dapat direncanakan sistim,
struktur yang meliputi 3 (tiga) langkah utama, yaitu :
a.
Analisis
struktur
untuk
menghitung
atau
menentukan
harga
momen
dan
gaya
aksial dalam struktur.
b. Merancang ukuran tiap elemen sehingga dapat menahan gaya – gaya tersebut.
c. Menyiapkan gambar kerja dan spesifikasi.
|
 9
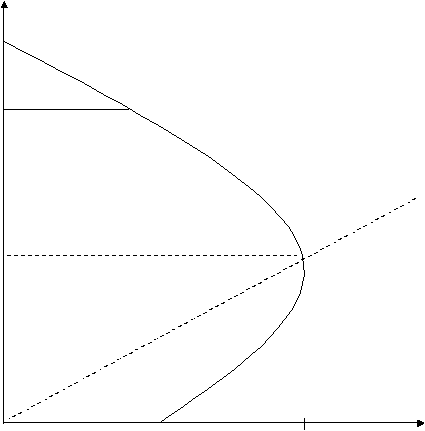
2.1.5 Diagram interaksi dari beban aksial – momen lentur
P
0
P
n
(maks)
P(kN)
Compresion
Controls
Region
P
b
Tension
Controls
Region
0
M
n
M
b
M(kNm)
Gambar 2.4 Diagram interaksi dari beban aksial dan momen lentur
2.1.6 Asumsi Perencanaan Kolom
Asumsi – asumsi yang dipakai dalam perencanaan kolom adalah sebagai
berikut :
1. Regangan tekan beton maksimum = 0,003.
2. Regangan pada beton dan tulangan proportional terhadap jarak garis netral.
3. Tegangan tarik dari beton diabaikan dan tidak ikut diperhitungkan.
4. Tegangan pada baja tulangan f
s
=
e.E
s
=
f
y.
|
 10
2.1.7 Perhitungan Gaya – Gaya Aksial dan Momen Lentur
Gambar 2.5 Penampang kolom dengan tulangan atas dan bawah
Jika Kolom dibebani secara bertahap dari mulai nilai beban yang ringan sampai
beban batas aman,
maka kolom
mengalami keadaan
lentur.
Proses
peningkatan beban
berakibat
terjadinya kondisi
tegangan dan
regangan
yang
berbeda
pada
tahapan
pembebanan pola yang berbeda
ini dinyatakan dalam sifat elastis dan plastis. Rasio /
perbandingan antara
momen
lentur M
n
terhadap beban aksial dinyatakan sebagai
eksentrisitas e, di mana :
M
e
=
n
P
n
Terdapat tiga kondisi utama yang membedakan
pola tegangan dan regangan yaitu
kondisi
seimbang, kondisi beton
retak
dan
kondisi
tulangan
leleh.
Kondisi
seimbang
adalah kondisi di mana beton dan tulangan bekerja di bawah batas aman, kondisi beton
retak adalah kondisi di
mana beton retak karena
nilai regangan pada serat beton sama
dengan atau melebihi regangan hancur beton yaitu 0,003. Kondisi tulangan leleh adalah
kondisi
tulangan
leleh
karena
regangan
tulangan
lebih
kecil
regangan batas
tulangan
baja, bergantung pada luas tulangan baja.
|
 11
e' = 0.003
e' = 0.003
e' = 0.003
C
b
C
b
C
b
Titik
seimbang
Titik
seimbang
Titik
seimbang
(a)
(b)
(c)
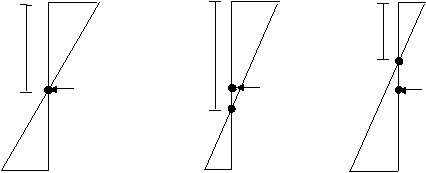
Gambar 2.6 Diagram tegangan – regangan (a) kondisi seimbang; (b) kondisi beton
retak; (c) kondisi tulangan leleh
Dengan
adanya
momen,
kolom
akan
melentur
sehingga
timbul
tegangan
tekan
dan
tarik
pada
tepi
–
tepi
serat
luar
dalam
arah
momen
kerjanya.
Bergantung
pada
besaran relative dari beban aksial dan
momen lenturnya, maka kolom akan
mengalami
keruntuhan dalam berbagai pola yaitu :
1.
Keruntuhan Tarik ( Tension Failure )
Keruntuhan terjadi diawali dengan lelehnya tulangan pada sisi serat tarik.
2.
Keruntuhan Tekan ( Compresion failure )
Keruntuhan tekan terjadi diawali dengan lelehnya beton pada sisi serat tekan.
3.
Keruntuhan Seimbang ( Balance
failure )
Keadaan
di
mana
keruntuhan
tekan
dan
tarik
terjadi
secara
simultan/bersamaan.
|
 12
(a)
(b)
Gambar 2.7 (a) kolom karena keruntuhan tekan; (b) kolom karena keruntuhan tarik
(sumber : pelajaran dari gempa dan tsunami )
Beban
aksial
nominal dinyatakan dengan
P
n
dan
beban aksial
nominal
dalam
keadaan
seimbang
dinyatakan
dengan
P
b
,
maka
3
macam
pola
keruntuhan
tersebut
di
atas dapat ditulis sebagai berikut :
1. P
n
<
P
b
----> Keruntuhan Tarik.
2. P
n
=
P
b
----> Keruntuhan Seimbang
3. P
n
>
P
b
----> Keruntuhan Tekan.
Jika
suatu
gaya
normal
bekerja
pada
suatu
kolom pendek
yang
mempunyai
tulangan atas dan bawah, maka dapat dilihat berbagai kasus
sehubungan dengan lokasi
gaya normal terhadap titik berat plastisnya :
1. Gaya Tekan Aksial ( P
0
) :
Adalah kasus di mana secara teoritis dianggap bekerja suatu gaya aksial yg besar
atau bertitik
tangkap pada
titik
berat plastisnya,
tidak
ada
momen
lentur
dan
|
 13
g
E
eksentrisitas bekerja, e = o, M = 0. Dengan besar reduksi kekuatan untuk
P
0
=
0,8.
Untuk mencari P
0
digunakan rumus :
P
0
=
0,85. f
c
'.
(
A
-
A
st
)
+
f
y.
.A
st
P
0
=
Kuat beban aksial nominal ( N )'
A = Luas Bruto Penampang kolom ( mm² )
f
c
'
=
Kuat Tekan Beton yang disyaratkan ( mpa )
A
st
=
Luas Total tulangan longitudinal ( mm² )
f
y
=
Tegangan leleh tulangan yang disyaratkan ( mpa )
2. Gaya Aksial Nominal Maksimum yang Diizinkan Pn ( max ) :
Adalah kasus di mana gaya normal yang bekerja pada penampang mengandung
eksentrisitas minimum sesuai dengan Standar Tatacara
yang berlaku yaitu
0,7. P
0
.
3. Kondisi Keadaan Seimbang ( P
b
, M
b
)
Pada kasus
ini keadaan seimbang dicapai di
mana regangan tekan beton
f
y
mencapai
0,003 dan regangan tarik tulangan mencapai
e =
secara
y
s
bersamaan, dengan demikian keruntuhan beton terjadi bersamaan pada saat
tulangan mengalami pelelehan. Dengan reduksi kekuatan 0,7 untuk P
b
dan M
b.
Untuk mencarinya digunakan rumus :
-
Kuat beban aksial
|
 14
y
P
b
=
0,85. f
c
'.a
b
.b
+
A
s
'. f
s
'
-
A
s
.
f
y
f
s
'
=
e
s
'.Es
a
b
=
ß1
.
C
b
ß1
=
0,85 – 0,008 ( f
c
'
–
30 )
C =
600 .d
b
600
+
f
(c
-
d
'
)
e
'
=
b
.0,003
c
b
P
b
=
Kuat beban aksial kondisi seimbang ( N )
a
b
=
Tinggi balok tegangan tekan ( mm )
d
=
Jarak tulangan terluar ke serat tepi beton ( mm )
f
s
'
=
Tegangan leleh tulangan yg terjadi ( mpa )
E
s
=
modulus elastisitas besi (200.000 mpa)
d' = selimut ( mm )
b
=
lebar penampang ( m )
A
s
'
=
luas tulangan desak ( mm² )
A = luas tulangan tarik ( mm² )
-
Momen Lentur
M
=
0,85. f
a
'.a .
?
y
-
b
?
+
A
'. f
'
(
y
-
d
)
-
A
.
f
.
(
d
-
y
)
?
b
c
b
?
y
=
h
2
?
2
?
s
s
s
y
|
 15
M
b
=
Momen Lentur pada saat seimbang ( Nm )
y
=
titik berat penampang ( mm )
h
=
panjang penampang ( mm )
4. Kondisi Lentur Murni
Adalah kasus di mana secara teoritis gaya
normal
yang bekerja P = 0 disertai
dengan momen lentur M
n.
Dengan reduksi kekuatan untuk M
n
adalah 0,7.
Untuk mencarinya digunakan rumus :
?
?
a
?
?
M
n
=
A
s
.f
y
.?d-
?
?
?
?
?
2
?
?
Karena
gaya aksial
yang bekerja sama dengan 0
maka
untuk mencari a
digunakan rumus :
a
=
A
s
.
f
y
0,85. f
c
'.b
M
n
=
Momen Lentur Murni ( Nm )
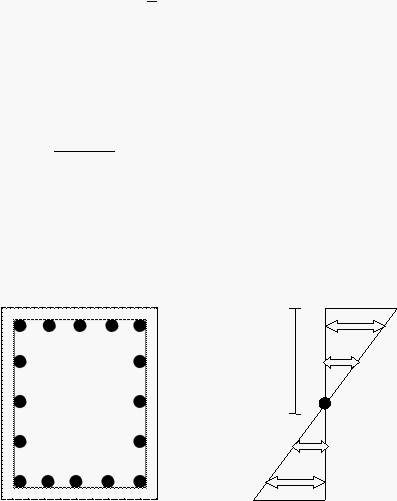
Untuk penampang bujursangkar dan persegi panjang yang mempunyai tulangan
di empat sisinya seperti gambar 2.8
C
b
e
st3
e
st4
e
sc2
e
sc1
(a)
(b)
Gambar 2.8 (a) kolom dengan tulangan di semua sisi; (b) diagram tegangan - regangan
|
 16
?
g
Menggunakan rumus :
P
0
=
0
,
85
.
f
c
'.
(
A
-
A
st
)
+
f
y
.
.
A
st
n
n
P
b
=
0,85 f
. f
c
'.a
b
.b
+
?
A
sn
'. f
scn
'
-
?
A
sn
.
f
stn
n
=1
n
=1
?
?
n
n
M
b
=
0,85. f
c
'.a
b
.? y
-
a
b
?
+
?
A
sn
'. f
scn
'
(
y
-
d
sc
)
+
?
A
sn
.
f
stn
(
d
st
-
y
)
?
2
?
n=1
n=1
?
?
?
?
n
n
M
=
A
.
f
.
?
d
-
?
a
?
?
+
?
A
'. f
'
(
y
-
d
)
+
?
A
.
f
(
d
-
y
)
n
s
y
?
?
?
2
?
?
sn
n
=
1
scn
sc
sn
n
=
1
stn
st
Untuk lingkaran diasumsikan perhitungan menggunakan
perhitungan persegi
panjang dengan tulangan hanya di dua sisi yaitu atas dan bawah dengan asumsi :
-
panjang persegi panjang = 0,8 x diameter lingkaran
-
lebar persegi panjang = luas lingkaran / panjang persegi panjang
-
d' =
(lebar persegi panjang - (diameter lingkaran - selimut ))
2
contoh :
lingkaran dengan diameter 20 cm dengan selimut 4 cm maka diasumsikan
Panjang persegi panjang = 0,8 x 20 cm
=
16 cm
3,14
.
(20)
2
Lebar persegi panjang =
19,63 -
(20 - 4)
4
16
=
19,63 cm
d' =
=
3,63cm
2
|
|
17
Contoh Soal :
Diketahui suatu kolom bujursangkar 400
mm
x
400 mm dengan 4 batangan tulangan
diameter 32 mm. Mutu beton
f
c
'
=
30 MPa dan baja
f
y
= 400 Mpa dibebani dengan
gaya tekan rencana Pu = 1500 Kn dan
momen rencana Mu = 180 kN. Apakah kolom
tersebut mampu untuk menahan gaya dan momen rencana tersebut ?
Jawab :
d = 400 – 50 – 10 – 32/2 = 324 mm
A
s
=
A
s
'
=
0,01 x 400 x 324 = 1296 mm²
A
s
=
A
s
'
=
2D - 32 = 1608 mm²
b = 400 mm ; h = 400 mm; d' = 76 mm
*Titik P-M pada beban sentris
P
0
=
0,85. f
c
'.
(
A
-
A
st
)+
f
y.
.A
st
=
(0,85 x 30 x ((160000-3216) + (3216 x 400)
=
5284392N= 5284 kN
P
0
maks = 0,8 x P
0
=
4227 kN
Batas maksimum yang diizinkan (P
a
)
adalah 0,7 dari P
0
maks
P
a
=
0,7 .4227 = 2959 kN
*Titik P-M pada beban seimbang
P
b
=
0,85. f
c
'.a
b
.b
+
A
s
'. f
s
'
-
A
s
.
f
y
=
1629,859N dan dengan F 0,7 maka
F0,7 = 1141kN.
|
 18
?
?
?
?
M = 0,85. f
'.a
.
?
y
-
a
b
?
+
A
'. f
'
(y - d)
-
A
.
f
.
(
d
-
y
)
b
c
b
?
2
?
S
s
s
y
=
350,46 kNm dan dengan F 0,7 maka
F0,7 = 245 kNm.
*Titik P-M pada keadaan lentur murni
P
n
=
0
M
=
A.f .
(
d-
a
)
n
s y
2
=
1608 x 400 ( 324 – (63,059/2))
=
188,12 kNm, dan dengan F0,7 untuk lentur murni,maka
FM
un
=
132 kNm
* Titik P-M pada C = 295 mm > C
b
: keruntuhan tekan
e
s
'= 0,003.
295 - 76
=
295
0,00222
f
s
'
= e
s
'. E
s
=
0,00222 x 200000 > 400 Mpa
f
s
'
= f
y
= 400 Mpa
e
s
=
0,003.
324
-
295
295
=
0,0029492
f
s
= e
s
. E
s
= 0,00294 92 x
200000 = 58,983 Mpa
a
b
= 0,85 x 295 = 250,75 mm
P
b
=
0,85. f
c
'.a
b
.b+ A
s
'. f
s
'-A
s
.
f
y
= 3106 kN dengan F 0,7 , maka
P
b
= 2174 kN
M
=
0,85. f
'.a .
?
y
-
a
b
?
+
A
'. f
'
(
y
-
d
)
-
A f
. f
.
(
d
-
y
)
b
c
b
?
2
?
S
s
s
y
|
 19
?
?
= 282,38 kNm dengan F 0,7 , maka
= 198 kNm
* Titik P-M pada C = 108 mm < C
b
:
keruntuhan tarik
e
s
'= 0,003.
108
-
76
108
=
8,8889x10
-
4
f
s
'
= e
s
'. E
s
=
8,8889x10
-4
x 200000 = 177,7778 Mpa
e
s
=
0,003.
324
-
108
108
=
0,006
f
s
= e
s
. E
s
= 0,006 x 200000 = 1200 Mpa > 400 Mpa
f
s
= f
y
= 400 Mpa
a
b
= 0,85 x 108 = 91,80 mm
P
b
=
0,85. f
c
'.a
b
.b
+
A
s
'. f
s
'
-
A
s
.
f
y
= 579 kN dengan F 0,7 , maka
P
b
= 405 kN
M
=
0,85. f
'.a .
?
y
-
a
b
?
+
A
'. f
'
(
y
-
d
)
-
A f
. f
.
(
d
-
y
)
b
c
b
?
2
?
S
s
s
y
=
259,50 kNm dengan F 0,7 , maka
= 182 kNm
|
 20
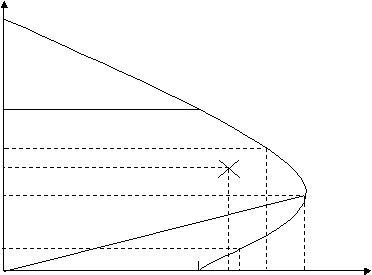
Grafiknya :
4227
P(Kn)
2959
2174
1500
1141
405
0
M
(kNm)
132
180
182
198
245
Gambar 2.9 Diagram Interaksi beban aksial dan momen lentur
Gaya tekan rencana dan momen rencana masih masuk didalam grafik, jadi kolom
tersebut masih dapat menahan gaya dan momen tersebut.
2.2 Fungsi Parabola
2.2.1. Definisi Parabola
Parabola adalah himpunan titik – titik P yang berjarak sama dari garis arah l tetap
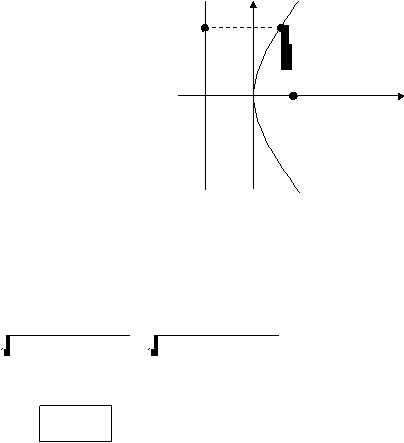
(garis arah) dan fokus F – yaitu, yang memenuhi hubungan
|PF| = |PL|
oleh karena parabola itu simetrik terhadap sumbunya, kita dapat menempatkan satu dari
sumbu koordinat misal sumbu x pada sumbu simetri kurva tersebut. Kita ambil fokus F
di sebelah kanan titik asal, misalnya di ( p , 0 ). Garis arah kita ambil di sebelah kirinya
dengan persamaan x = -p. Dengan demikian, puncak parabola
ada di titik asal sistem
koordinat.
|
 21
L = (-p,y)
P(x,y)
F(p,0)
x
= - p
Gambar 2.10 Parabola
dari syarat |PF|=|PL| dan rumus jarak, kita peroleh
(
x
-
p)
2
+
(
y
-
0)
2
=
(
x
+
p)
2
+
(
y
-
y)
2
setelah ruas kiri dan kanan dikuadratkan dan kemudian disederhanakan, kita peroleh
y²
= 4px
2.2.2. Bentuk Umum Persamaan Parabola
Bentuk umum persamaan parabola adalah fungsi kuadrat yang ditulis
dengan :
y
=
ax
2
+
bx +
c
dengan a ? 0.
2.2.3. Sifat – sifat Parabola
Parabola dengan persamaan
y
=
ax
2
+
bx
+
c
; a ? 0 mempunyai sifat :
(i).
Parabola terbuka keatas jika a>0 dan terbuka kebawah jika a < 0.
(ii). Parabola memotong
sumbu
y
pada
x
=
0. Titik potong
dengan
sumbu
y
adalah
(0, c)
.
|
 22
?
2
(iii). Jika D > 0 maka parabola memotong sumbu x di dua titik
Jika D = 0 maka parabola menyinggung sumbu x.
Jika D < 0 maka parabola tidak memotong dan tidak menyingung sumbu x.
Dengan D adalah diskriminan dan D = b
2
–
4ac.
Titik potong dan titik singgung dengan sumbu x diperoleh pada y = 0.
(iv). Parabola mempunyai sumbu simetri dengan persamaan
x
=
-
b
2a
(v). Parabola mempunyai titik ekstrim yaitu
?
-
b
,
-
D
?
?
?
2a
4a
?
untuk a > 0 maka titik ekstrim adalah titik minimum dan untuk a < 0 maka titik ekstrim
adalah titik maksimum.
2.2.4. Menentukan Persamaan Parabola
Persamaan
parabola
dapat
ditentukan jika diketahui tiga titik sembarang yang
dilalui parabola, atau titik potong dengan sumbu X dan satu titik sembarang yang dilalui
parabola.
(i).
Jika diketahui
tiga titik
yang dilalui,
maka persamaan parabola dapat dinyatakan
dengan
y
=
ax
2
+
bx
+
c
.
(ii). Jika diketahui titik – titik potong dengan sumbu X, misalnya
(x
1
,0
)
dan
(
x
2
,0
)
dan
satu
titik
yang
dilalui
maka
persamaan
parabola
dapat
dinyatakan
dengan y
=
a
(x
-
x
1
)(x
-
x
2
)
.
(iii).
Jika diketahui
titik ekstrim parabola misalnya
(x
e
,
y
e
)
dan
satu titik
yang dilalui
maka persamaan parabola dapat dinyatakan dengan
y
-
y
e
=
a
(x
-
x
e
)
|