15
Sumber
Keragama
n
Sebelum dikoreksi (JK dan JHK)
Setelah dikoreksi terhadap
pengaruh X
db
XX
XY
YY
db
JK
KT
F
hit.
Total
n-1
JKT(XX)
JKT(XY)
JKT(YY)
Kelompok
r-1
JKK(XX)
JKK(XY)
JKK(YY)
Perlakuan
a-1
JKP(XX)
JKP(XY)
JKP(YY)
Galat
dbT-dbK-
dbP
JKG(XX)
JKG(XY)
JKG(YY)
dbG-
JKGt
KTG
Perlakuan+
Galat
dbG+
dbP-1
JK(P+G)
-
Perlakuan
terkoreksi
-
-
-
-
dbP
JKPt
KTP
Fhit
Jumlah Kuadrat Kelompok (JKK)
2
r
?
r
a
?
?
X
i
?
??
X
ij
?
2
r
?
r
a
?
?
Y
i
?
??
Y
ij
?
r
?
r
a
??
r
a
?
?
X
Y
?
?? X
??
?? Y
?
i
i
i
?
i
j
ij
??
i
j
ij
?
-
a
r.a
Jumlah Kuadrat Perlakuan (JKP)
2
a
?
r a
?
?
X
j
?
??
X
ij
?
2
a
?
r
a
?
?
j
?
??
ij
?
Y
²
?
Y
?
j
-
?
?
a
?
r
a
??
r
a
?
?
X
j
Y
j
?
?? X
ij
??
?? Y
ij
?
=
j
-
?
i
j
??
i
j
?
r
r.a
Jumlah Kuadrat Galat (JKG)
JKT(XX)–JKK(XX)
-
JKP(XX)
JKT(YY)–JKK(YY)–
JKP(YY)
JKT(XY)-JKK(XY)-JKP(XY)
Tabel 2.1 Rumus Jumlah Kuadrat RAK Satu Faktor
Rumus pada
tabel 2.1 di atas kemudian digunakan untuk ditampilkan pada
tabel
analisis peragam seperti pada tabel 2.2.
1
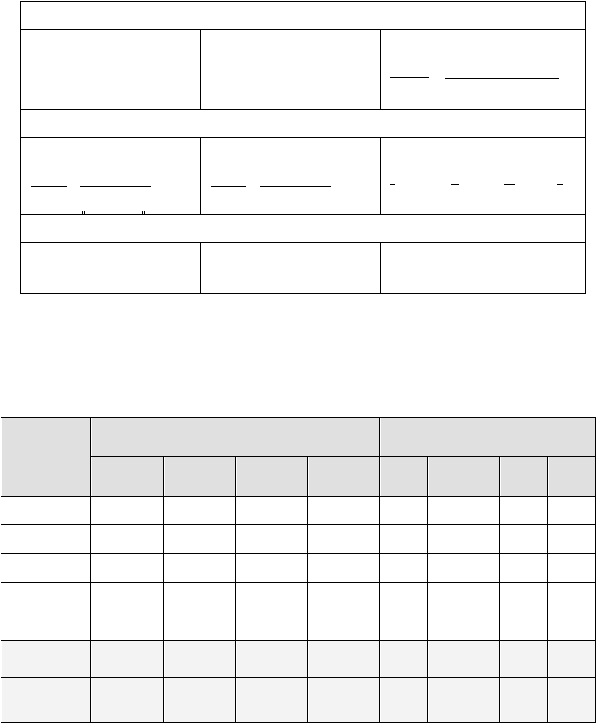
Tabel 2.2 Tabel Analisis Peragam RAK Satu Faktor
Pendugaan koefisien regresi
b
YX
=
JKG (XY) / JKG (XX)