|
?
?
1
?
BAB 2
LANDASAN TEORI
2.1
Matriks
2.1.1
Pengertian Matriks
Definisi dari matriks adalah benda (bangun) matematika yang berisi objek-objek
(bisa
berupa
bilangan,
fungsi,
dll.)
yang
tersusun
dalam baris-baris
dan kolom-kolom
yang
memenuhi
sifat
bahwa
setiap
barisnya
atau
kolomnya
berisi
objek-objek
yang
sama banyaknya. Untuk menyatakan suatu matriks dapat dipakai huruf cetak besar atau
miring seperti: A, B, atau Z. Susunan dari matriks A yang memiliki m buah baris dan n
buah kolom adalah sebagai berikut.
?
a
a
L
a
?
?
11
12
1n
?
A
=
?
a
21
a
22
L
a
2
n
?
?
?
M
M
?
O
M
?
?
?
a
m1
a
m
2
L
a
mn
?
Berikut adalah contoh sebuah matriks A yang memiliki tiga buah baris dan tiga
buah kolom.
Contoh 1:
?
2
?
?
4
?
10
1
3
?
?
-
1
2
?
= A
5
?
Objek-objek
pada
matriks
disebut
unsur
(elemen)
dari
matriks,
biasa
ditulis
dengan huruf cetak kecil miring berindeks dua seperti: a
ij
,
b
ij
,
c
ij
,
dan lain-lain di mana i
|
|
6
?
7
?
?
5
?
adalah indeks yang menyatakan letak baris dan j adalah indeks yang menyatakan letak
kolom dari matriks tersebut.
Contoh 2: Pada matriks A contoh sebelumnya, angka 5 terdapat pada baris ketiga
dan kolom kedua ditulis sebagai a
32
.
Indeks pertama menunjuk pada baris, dan indeks
kedua menunjuk pada kolom.
Kumpulan elemen-elemen dimulai dari elemen kiri atas dan secara diagonal ke
elemen kanan bawah, disebut diagonal utama.
2.1.2
Ukuran dan Bentuk Matriks
Ukuran
dari
matriks
merupakan
salah
satu sifat
penting
dari
matriks
yang
menyatakan banyaknya baris dan kolom. Sebuah
matriks dengan m baris dan n kolom
disebut sebagai matriks m kali n, ditulis
m
×
n
. Bila dua buah matriks memiliki baris dan
kolom yang sama banyaknya, maka kedua matriks tersebut memiliki ukuran yang sama
(misalkan 3
×
2
).
Contoh 3: Kedua matriks di bawah ini memiliki ukuran yang sama.
?
1
6
?
?
p
?
?
?
10
?
?
?
6
2
?
,
?
-
2
7
?
?
1
?
?
-
3
?
Sifat penting lain dari sebuah matriks adalah bentuknya. Untuk matriks M
m
x
n
:
Jika
m=n,
matriks
tersebut
dikatakan
matriks
bujur
sangkar.
Matriks
A
pada
Contoh 1 di atas, adalah contoh sebuah matriks bujur sangkar.
Jika m=1 (satu) maka matriks disebut matriks baris.
Jika n=1 maka matriks disebut matriks kolom.
|
|
7
?
5?
Contoh 4:
(1
-
2
5
)
disebut matriks baris, sedangkan
?
?
adalah matriks
?
3
?
kolom.
2.1.3
Jenis Matriks dan Operasi Aljabar pada Matriks
Untuk
dapat
diterapkan
pada
penyelesaian masalah pada bidang pengetahuan
lainnya,
maka perlu diberikan arti tentang kesamaan dua
matriks,
jumlah dua
matriks,
perkalian antar bilangan dengan matriks, perkalian dua matriks, dan lain-lain, yang akan
diberikan pada bagian ini.
Kesamaan Dua Matriks
Definisi: Dua matriks disebut sama, jika keduanya mempunyai ukuran sama dan
dua elemen yang seletak pada kedua matriks nilainya sama.
?
1
Contoh 5: Perhatikan matriks-matriks: A =
?
?
6
4
?
?
1
?
, B =
?
2
?
?
3
4
?
?
, dan C =
2
?
?
1
2
?
?
3
4
0
?
?
. Di antara ketiga matriks di atas tidak ada yang sama
-
1
?
A
?
C
sebab
ukurannya tidak sama,
A
?
B
sebab ada unsur yang seletak (yaitu baris ke-2, kolom
pertama) pada kedua matriks tersebut yang nilainya tidak sama.
Penjumlahan Dua Matriks
Definisi:
Jika
A dan
B
dua
matriks
yang
berukuran
sama,
maka
A+B adalah
matriks berukuran sama dengan ukuran A dan setiap unsurnya sama dengan jumlah dari
dua unsur di A dan B yang seletak.
|
|
8
?
1
?
1
?
?
?
2
?
1
?
?
?
3
?
?
?
?
?
?
1
?
Contoh 6: A =
?
6
?
4
3
?
?
2
3
?
?
?
2
7
?
,B =
?
6
9
?
1
?
?
1
?
?
4
?
, C =
?
9
?
?
2
?
?
-
1
?
?
. Maka berlaku:
?
1
4
3?
?
2
7
?
?
?
1
?
?
1
+
2
?
?
4
+
7
3
+
1
?
?
?
3
11
4
?
?
?
A
+
B
=
?
6
2
3
?
+
?
6
9
4
?
=
?
6
+
6
2
+
9
3
+
4
?
=
?
12 11
7
?
.
Sedangkan
?
2
5
?
?
3
-
2
?
?
2
+
3
5
-
2
1
+
1
?
?
5
3
?
A
+
C
dan B + C tidak terdefinisi.
Sifat:
A+B=B+A
(hukum komutatif penjumlahan)
A+(B+C)=(A+B)+C (hukum assosiatif penjumlahan)
Perkalian antara Bilangan dengan Matriks
Definisi: Jika A suatu matriks dan r suatu bilangan kompleks, maka perkalian rA
adalah matriks yang ukurannya sama dengan ukuran A dan setiap unsurnya adalah unsur
di A dikalikan dengan r.
Contoh 7:
?
2
1
?
3
?
?
3 × 2
?
?
3
×
1
3
×
3
?
?
6
?
?
3
9
?
?
3
?
4
-
1
2
?
=
?
3
×
4
3
×
(
-
1)
3
×
2
?
=
?
12
-
3
6
?
?
10
5
?
?
3
×
10
3
×
5
3
×
1
?
?
30
15
?
Sifat: rA=Ar
r(B+C)=rB+rC
(r+s)C=rC+sC
(rs)C=r(sC)=s(rC)
|
|
9
Pengurangan Dua Matriks
Pengurangan
dua
matriks
didefinisikan dengan
menggunakan
definisi
dari
penjumlahan dua
matriks dan perkalian antara bilangan dengan
matriks,
yaitu: Jika A
dan B dua matriks yang berukuran sama, maka
A
-
B
= A + (-1)B
Contoh 8:
?
1
4
6
?
?
5
0
1
?
Perhatikan matriks–matriks:
A
= ?
?
7
?
,
2
3
?
B
=
?
?
?
-
2
3
2
?
?
-
5
0
Maka
-
B
=
?
-
1
?
?
,
?
2
-
3
-
2
?
?
1
4
6
?
?
-
5
0
-
1
?
?
-
4
0
5
?
dan selanjutnya A -
B
= ?
7
?
+ ?
2
3
2
?
= ?
3
2
9
?
-
1 1
?
?
?
-
-
?
?
?
Perkalian Dua Matriks
Definisi: Jika A matriks berukuran
m
×
k
dan B berukuran
k
×
n
maka perkalian
AB adalah matriks beruukuran m × n
yang memenuhi syarat sebagai berikut:
Untuk mendapatkan unsur dari AB yang terletak pada baris ke-i dan kolom ke-j,
perhatikan baris ke-i dari matriks A dan kolom ke-j dari matriks B, selanjutnya kalikan
unsur-unsur yang seletak pada baris dan kolom tersebut, kemudian jumlahkan, hasilnya
merupakan unsur dari matriks AB tersebut di atas.
Dengan kata lain, bila C=AB maka untuk C
ij
=
?
A
ik
B
kj
k
semua i dan j.
Walaupun ada beberapa matriks yang memiliki sifat AB=BA, secara umum sifat
komutatif perkalian matriks tidak berlaku.
|
|
10
?
3
Contoh 9:
Perhatikan
matriks-matriks:
?
1
2
3
?
A
=
?
?
,
?
3
4
0
?
?
3
?
B
=
?
1
?
8
2
1
-
1
5
3
-
1
2
?
?
2
?
.
Maka
?
?
?
1
×
3
+
2
×
1
+
3
×
8
AB
=
?
?
3
×
3
+
4
×
1
+
0
×
8
1
×
2
+
2
×
(
-
1)
+
3
×
3
3
×
2
+
4
×
(
-
1)
+
0
×
3
1
×
1
+
2
×
5
+
3
×
(
-
1)
3
×
1
+
4
×
5
+
0
×
(
-
1)
1× 2 +
2
×
2
+
3
×
3
?
?
29
9
8
15
?
?
=
?
?
3
×
2
+
4
×
2
+
0
×
3
?
?
13
2
23
14
?
Contoh 10:
?
1
4
?
?
2
7
?
Perhatikan
matriks-matriks:
A
= ?
6
?
,
B
=
?
2
6
?
.
Maka
9
?
?
?
?
?
1× 2 +
4
×
6
1× 7 + 4 × 9
?
?
26
43
?
AB
= ?
?
=
?
?
sedangkan
?
6
×
2
+
2
×
6
6
×
7
+
2
×
9
?
?
24
60
?
?
2
×
1
+
7
×
6
2
×
4
+
7
× 2
?
?
44
22
?
BA = ?
?
=
?
?
, berarti
AB ?
BA
.
?
6
×
1
+
9
×
6
6
×
4
+
9
×
2
?
?
60
42
?
Sifat:
A(BC)=(AB)C
(hukum asosiatif perkalian)
A(B+C)=AB+AC
(hukum distributif) (B+C) A
=BA+CA
(hukum distributif)
r(BC)=(rB)C=B(rC) dengan r adalah bilangan skalar
Transpose Matriks
Definisi: Jika A matriks berukuran
m
×
n
,
maka matriks transpose dari matriks A
(ditulis C=A
T
)
adalah matriks berukuran
n
×
m
yang
unsur baris ke-i kolom ke-j nya
|
|
11
?
0
T
adalah unsur baris ke-j dan kolom ke-i dari matriks A untuk setiap i dari 1 sampai n dan
j dari 1 sampai m.
Ketika
kita
melakukan
transpose
matriks,
baris
ke-i
menjadi
kolom ke-i,
dan
kolom ke-j menjadi baris ke-j.
Setiap matriks dapat di-transpose.
?
1
?
Contoh 11
?
2
?
5
6
?
?
?
1
3
?
=
?
?
?
6
?
2
5
?
?
3
0
?
Sifat:
(
A
T
)
T
= A
(A +
B
)
T
= A
T
+
B
T
(AB)
T
=
B
T
A
T
Bila A
T
=A maka A disebut matriks simetris dan A
ij
=A
ji
untuk semua i dan j.
Jika
A
T
=
-
A
maka A disebut matriks skew-simetris dan
A
ij
=
-
A
ji
untuk
semua i dan j.
Elemen
diagonal
utama dari
matriks
skew-simetris
haruslah
bernilai 0,
karena
A
ii
=
-
A
ii
=
0.
Matriks Nol
Suatu
matriks
dengan
semua
unsurnya
nol,
disebut
matriks
nol,
diberi
notasi
O
mxn
(
m
×
n
ukurannya).
|
|
12
?
0
?
1
?
?
Contoh 12
?
0
0
?
?
0
0
0
?
?
0
0
0
?
?
?
O
2×2
=
?
0
?
,
O
2×3
= ?
0
0
0
?
,
O
3×3
=
?
0
0
0
0
?
.
?
?
?
?
?
0
0
?
Misalkan A matriks berukuran
m
×
n
dan O adalah matriks nol berukuran
m
×
n
,
maka berlaku A + O = O + A = A. Jadi matriks nol berperan mirip seperti bilangan real
0 untuk operasi penjumlahan.
Matriks Satuan (Identitas)
Matriks bujur sangkar
I
n×n
yang diagonal
utamanya
hanya berisi 1 dan
unsur
lainnya yang tidak pada diagonal hanya bilangan 0, disebut sebagai matriks
satuan/identitas
n
×
n
.
Contoh 13
?
1
0
?
?
1
0
0
?
?
?
I
2×2
=
?
0
?
,
I
3×3
=
?
0
1
1
0
?
, dll.
?
?
?
0
0
?
Misalkan A matriks berukuran
n
×
n
dan I adalah matriks satuan berukuran sama,
maka berlaku
I
nxn
·
A
=
A
=
A
·
I
nxn
.
Jadi matriks satuan berperan mirip seperti bilangan
real 1 (satu) untuk operasi perkalian.
Invers Matriks
Misalkan
A
matriks
bujur
sangkar,
matriks
B
yang
memenuhi
AB
=
BA
=
I
,
disebut
sebagai
invers
dari
A,
sedangkan
matriks A
yang
mempunyai
invers
disebut
sebagai matriks tak singular atau invertibel.
|
|
13
?
Contoh 14
?
4
3
?
?
1
-
3
?
Matriks
B
= ?
?
1
?
merupakan
invers dari
matriks
1
?
A
= ?
?
-
1
?
, sebab
4
?
?
4
3? ?
1
-
3?
?
1
0
?
?
1
-
3? ? 4
3?
?
1
0
?
berlaku:
AB = ?
1
?
·
?
1
1
?
=
?
4
0
?
, dan BA = ?
1
-
1
?
·
?
4
1
?
=
?
?
.
1
0
1
?
?
?
-
?
?
?
?
?
?
?
?
?
Sedangkan
matriks
?
3
C
=
?
?
5
0
?
?
tidak
mempunyai
invers.
Sebab
andaikan
0
?
terdapat
matriks
D
=
?
d
11
?
d
21
d
12
?
?
d
22
?
adalah
invers
dari
matriks
C,
maka D
·
C
=
?
d
11
d
12
?
?
3
0
?
?
3d
11
+
5d
12
0
?
?
1
0
?
?
?
·
?
?
=
?
?
?
?
?
tidak
mungkin
menjadi
matriks
?
d
21
d
22
?
?
5
0
?
?
3d
21
+
5d
22
0
?
?
0
1
?
satuan.
Dalil berikut
menunjukkan bahwa setiap
matriks tak singular
mempunyai tepat
satu invers.
Dalil 1 (Ketunggalan Invers): Jika A dan B kedua-duanya matriks invers dari C,
maka A=B.
Bukti:
Karena A invers dari C, maka AC = I. Kemudian kalikan kedua ruas persamaan
tersebut dengan B, didapat:
(
AC)B
=
IB
=
B
. Karena
(
AC)B
=
A(CB)
=
AI
=
A
, maka didapat bahwa
A
=
B
.
Simbol lain untuk
menyatakan
invers dari
matriks A adalah
A
-1
.
Jadi didapat:
A
·
A
-1
=
I
dan
A
-1
·
A
=
I
|
 14
c
?
?
?
?
Contoh 15
Diberikan
matriks
?
a
A
=
?
?
c
b
?
?
,
ad - bc ?
0
d
?
dan
a, b, c, d ? R . Tunjukan bahwa
1
1
?
d
?
d
-
b
?
?
-
b
?
?
A
-
=
?
?
=
?
ad - bc
ad - bc
?
.
ad - bc
?
-
c
a
?
-
c
?
a
?
?
?
ad
-
bc
ad
-
bc
?
Mudah ditunjukan bahwa
?
a
b
?
1
A
·
A
-1
= ?
?
.
?
d
-
b
?
?
?
=
1
?
a
?
b
??
d
??
-
b
?
?
?
d
?
ad - bc
?
-
c
a
?
ad
-
bc
?
c
d
??
-
c
a
?
1
?
ad
-
bc
0
?
?
1
0
?
=
?
?
=
?
?
=
I
.
ad
-
bc
?
0
ad
-
bc
?
?
0
1
?
Juga
1
?
d
-
b
??
a
b
?
1
?
ad - bc
0
?
?
1
0
?
A
-1
·
A
=
?
??
?
=
?
?
=
?
?
=
I
.
ad - bc
?
-
c
a
??
c
d
?
ad - bc
?
0
ad - bc
?
?
0
1
?
Dengan
demikian,
maka
untuk
matriks
?
a
A
=
?
?
c
b
?
?
,
ad - bc ?
0
dan
d
?
1
1
?
d
?
d
-
b
?
?
-
b
?
?
a, b, c, d ? R . Inversnya adalah
A
-
=
?
?
=
?
ad
-
bc
ad
-
bc
?
ad
-
bc
?
-
c
a
?
-
c
?
a
?
?
?
ad
-
bc
ad
-
bc ?
Berikut ini diberikan dalil yang mengatakan bahwa perkalian
dari
dua
matriks
yang tak singular adalah juga matriks tak singular, dan cara
untuk
mendapatkan
invers
dari perkalian dua matriks.
|
|
15
Dalil 2:
Jika A dan B dua matriks tak singular, maka AB tak singular dan
(AB)
-1
=
B
-1
A
-1
Bukti:
Apabila kita dapat
menunjukkan bahwa
(AB)
·
(
B
-1
A
-1
)
=
(B
-1
A
-1
)
·
(AB)
=
I
,
maka kita telah menunjukkan kedua hal tersebut di atas.
Perhatikan bahwa karena A dan B tak singular, maka
A
-1
dan
B
-1
ada, juga:
AB
·
(B
-1
A
-1
)
=
((
AB
)
·
B 1
-1
)
·
A
-1
=
A
·
(
B
·
B
-1
)
·
A
-1
=
A
·
I
·
A
-1
=
A
·
A
-1
=
I
Dengan cara yang sama,
(B
-1
A
-1
)
·
AB
=
((
B
-1
A
-1
)
·
A
)
·
B
=
B
-1
·
(
A
-1
·
A
)
·
B
=
B
-1
·
I
·
B
=
B
-1
·
B
=
I
Dalil
di
atas dapat diperluas
untuk
tiga
(atau lebih)
buath matriks.
Jadi
akan
didapat hal berikut:
Perkalian dari matriks-matriks tak singular akan menghasilkan matriks tak
singular. Invers dari perkalian matriks sama
dengan perkalian invers masing-masing
matriks dengan urutannya dibalik.
Contoh 16
?
3
2
?
?
8
5
?
?
30
19
?
A
=
?
1
?
,
B
=
?
1
3
?
,
AB
=
?
2
11
?
.
Dengan
memakai
cara
menentukan
7
?
?
?
?
?
?
invers
matriks
2
×
2
seperti
pada
contoh
sebelumnya,
didapat:
?
1
-
2
?
? 2
2
-
5?
?
7
-
19 ?
A
-1
= ?
?
,
B
-1
=
?
?
,
dan
(AB)
-1
= ?
?
.
Juga
didapat,
?
-
1
3
?
?
-
3
8
?
?
-
11
30
?
|
|
16
?
2
-
5
?
? 1
-
2
?
?
7
-
19 ?
B
-1
·
A
-1
=
?
?
·
?
?
=
?
?
.
Jadi tampak
(AB)
-
1
=
B
-1
·
A
-1
sesuai
?
-
3
8
?
?
-
1
3
?
?
-
11
30
?
dengan dalil 2.
Matriks Berpangkat
Jika A matriks bujur sangkar dan n bilangan asli, maka
A
n
= A
·
A L · A
· L · A
sebanyak n buah, dan
A
0
=
I
.
Lagi, jika A matriks tak singular, maka
A
-
n
=
(
A
-1
)
n
=
A
-1
·
A
-1
·
L
·
A
-1
sebanyak n buah.
Dalil 3:
Jika A matriks tak singular, maka
(i).
A
-1
matriks tak singular, dan
(A
-1
)
-1
= A
(ii).
A
n
matriks tak singular,
(
A
n
)
-1
=
(A
-1
)
n
, berlaku untuk n
=
0,1,2,L
(iii).
Untuk setiap bilangan real tak nol r, matriks rA tak singular; dan
(rA)
-1
=
1
A
-1
r
Bukti:
(i).
Karena berlaku
dan
(
A
-1
)
-1
=
I
A
-1
A
=
AA
-1
=
I
,
maka didapat bahwa
A
-
1
tak singular
(ii).
Untuk n = 0,1 pembuktian nya adalah trivial.
Untuk n = 2,3,... kita gunakan dalil 2 yang diperluas untuk n buah
matriks.
|
 17
?
1
0
-
5
?
2
7
13
?
0
?
5
9
?
?
0
0
4
?
3
5
0
0
?
?
7
4
1
0
?
6
?
?
?
(iii).
Karena r bilangan real tak nol, maka berlaku
?
1
1
?
?
1
?
1
?
1
-1
?
?
1
?
-1
(rA)
·
?
A
-
?
=
?
r
·
?
A A
· A
-
=
1
·
I
=
I
.
Juga
?
A
?
·
(
rA
)
=
?
r
?
·
A
A
=
1
·
I
=
I
,
?
r
?
?
r
?
?
r
?
?
r
?
sehingga didapat
rA matriks tak singular, dan
(rA)
-1
=
1
A
-1
r
Matriks Hessenberg
Sebuah
matriks
disebut
matriks
Hessenberg
atas
jika
semua
elemen di bawah
subdiagonal
hanya
bilangan
0 atau
a
ij
=
0
untuk
i
> j + 1,
dan
disebut
matriks
Hessenberg bawah
jika
semua elemen
di
atas
superdiagonal
berupa
bilangan
0
atau
a
ij
=
0
untuk
i
<
j
-
1
.
Contoh 17
?
Matriks A
=
?
B
=
?
9
?
?
0
-
3
6
2
8
?
7
?
adalah matriks Hessenberg bawah.
?
10
?
2.1.4
Determinan
Jika A adalah matriks berukuran
n
× n , determinan dari A, ditulis det(A), adalah
bilangan yang kita asosiasikan untuk matriks A. Determinan biasanya didefinisikan
dengan cara kofaktor atau cara permutasi, dan kita akan mendefinisikannya dengan cara
kofaktor. Kita akan mulai dengan definisi det(A) jika A adalah matriks berukuran 2
×
2
.
|
 18
?
ij
Definisi:
Jika
A
=
?
a
11
?
a
21
a
12
?
?
.
Determinan
dari
matriks
A
adalah
a
22
?
det( A) =
a
11
a
22
-
a
12
a
21
.
Untuk memudahkan penulisan determinan biasanya ditulis dengan menggunakan
garis vertikal:
det( A) =
a
11
a
21
a
12
a
22
Contoh 18
Determinan
untuk
matriks
?
1
2
?
A
=
?
?
?
-
1
3
?
adalah
1
det( A) =
-
1
2
=
1 3 -
· 3 -
2(-1) = 5 . Sedangkan determinan untuk matriks
3
?
3
4
?
B
=
?
?
?
6
8
?
3
adalah det(B) =
6
4
=
3 8 -
· 8 -
4
·
6
=
0
8
Sekarang kita akan mendefinisikan determinan dari matriks berukuran
n
×
n
sebagai
jumlah
berbobot
(weighted
sum)
dari
determinan
matriks
berukuran
[(
n
-
1
)×
(n - 1
)]
. Sebelumnya kita akan memberikan definisi untuk minor dan kofaktor.
Definisi:
Jika
A
matriks
berukuran
n
×
n
,
dan
M
rs
menyatakan
matriks
berukuran
[(
n
-
1
)
×
(n
-
1
)] yang didapat dengan menghapus baris ke-r dan kolom ke-s dari matriks
A, maka M
rs
disebut matriks minor dari A, dan bilangan det(M
rs
)
disebut minor dari
a
rs
.
Lagi, bilangan
A
ij
=
(
-
1
)
i
+
j
det
(
M
)
disebut kofaktor (atau minor bertanda).
|
 19
5
ij
Contoh 19
?
1
-
1
2
?
?
?
Untuk matriks
A
=
?
2
?
3
-
3
?
?
Tentukan matriks minor
M
11
,
M
23
,
dan M
32
.
?
4
5
1
?
Juga hitung kofaktor
A
11
,
A
23
, dan
A
32
.
Dengan menghapus baris pertama dan kolom pertama untuk matriks A, kita dapat
?
3
-
3?
M
11
:
M
11
=
?
?
?
.
Dengan cara
yang sama,
matriks minor
1
?
M
23
dan
M
32
adalah
?
1
-
1
?
?
1
2
?
M
23
=
?
4
?
dan
M
32
=
?
?
.
5
2
-
3
?
?
?
?
Kofaktor yang bersesuaian, A
ij
=
(
-
1
)
i
+
j
det
(M
)
didapat sebagai berikut:
A
11
A
23
=
(
-
1
)
1+1
3
5
=
(
-
1
)
2+3
1
4
-
3
=
3
+
15
=
18
1
-
1
=
-
(5
+
4)
=
-
9
5
A
32
=
(-1)
3+ 2
1
2
2
=
-(-3 - 4) =
7
-
3
Kita akan menggunakan kofaktor untuk mendefinisikan determinan.
Definisi:
Jika A matriks berukuran
n
×
n
, maka
determinan dari
matriks A adalah
det( A)
=
a
11
A
11
+
a
12
A
12
+
L
+
a
1n
A
1n
, dengan
A
1
j
adalah kofaktor dari a
1
j
,
1
=
j
=
n
.
|
 20
?
?
?
Contoh 20
?
1
2
?
0
2
?
?
Hitung det( A) , di mana
A
=
?
-
1
2
?
-
3
2
?
3
1
?
-
1
0
?
.
?
?
2
-
3
-
2
1
?
Dengan
menggunakan
definisi
determinan
di
atas,
maka
det( A)
=
a
11
A
11
+
a
12
A
12
+
a
13
A
13
+
a
14
A
14
=
A
11
+
2
A
12
+
2
A
14
. Kofaktor A1
3
tidak perlu
dihitung, karena a1
3
= 0.
A
11
2
3
=
(
-
1
)
1+1
2
-
1
-
3
-
2
1
-
1
0
=
2
-
2
1
0
2
-
3
1
-
3
0
2
+
1
1
-
3
-
1
=
-
15
-
2
-
1
3
1
?
-
-
-
-
?
A
12
=
(- 1
)
1+ 2
-
3
-
1
0
=
-
?
-
1
1
-
2
0
3
0
3
-
3
+
1
1
2
1
2
1
?
=
-18
-
2
?
2
-
2
1
?
?
-
1
2
3
?
-
-
-
-
?
A
=
(- 1
)
1+ 4
-
3
2
-
1
=
-
?
-
1
2
1
3
1
3
-
2
+
3
2
?
=
-6 .
14
2
-
3
-
2
?
-
3
-
2
2
-
2
2
-
3
?
Maka det( A)
=
A
11
+
2
A
12
+
2
A
14
=
-
15
-
36
-
12
=
-
63 .
Catat bahwa dalam contoh ini, penghitungan determinan matriks berukuran 4
×
4
lebih sederhana karena adanya bilangan nol pada a
13
. Jelas, bila kita memiliki prosedur
untuk menciptakan bilangan nol, kita dapat menyederhanakan penghitungan determinan
karena kofaktor yang bersesuaian untuk bilangan tersebut tidak perlu dihitung.
2.1.5 Cara Mencari Invers Matriks
Ada beberapa
cara
untuk
mencari
invers
matriks.
Cara
khusus
untuk
mencari
|
|
21
invers matriks untuk matriks berukuran 2 × 2
telah dijelaskan di muka. Sedangkan untuk
|
 22
?
6
?
?
?
?
?
?
?
matriks
berukuran
n
×
n
,
dapat
dilakukan
dengan
melakukan
eliminasi
Gauss-Jordan
atau dengan
metode adjoint. Di bawah
ini
adalah cara
mencari
invers
matriks dengan
metode adjoint
.
Misalkan A adalah matriks
n
×
n Invers dari matriks A atau
. Invers dari matriks A atau
A
-1
dapat dicari
dengan rumus:
A
-1
=
1
K
T
, dengan K adalah matriks kofaktor dari A.
det( A)
sedangkan yang dimaksud dengan matriks adjoint adalah matriks K
T
Contoh 21
Hitung invers dari matriks A, di mana
?
1
?
A
=
?
0
?
1
2
3
?
?
4
5
?
0
?
?
24
?
5
-
4
?
?
Matriks kofaktor dari A adalah
?
-
12
3
?
-
2
-
5
2
?
,
dan determinan dari A adalah
4
?
?
24
-
12
-
2
?
?
12
-
6
-
1
?
-1
1
?
?
11
11
?
5
3
11
?
5
?
22, maka
A
=
?
5
22
3
-
5
?
=
?
22
22
-
22
?
?
-
4
2
4
?
-
2
1
?
11
11
2
?
11
?
2.2
Nilai Eigen dan Vektor Eigen
2.2.1
Definisi
Definisi: Secara formal, kita mendefinisikan nilai eigen dan vektor eigen sebagai
berikut:
Misalkan A adalah matriks
n
×
n
.
|
|
23
Vektor
v
?
C
n
,
v
tidak nol, disebut suatu
vektor eigen dari A apabila terdapat
bilangan
?
,
?
?
C sehingga berlaku:
Av
=
?
v
Bilangan
?
disebut
nilai
eigen
(nilai karakteristik) dari A,
vektor v
disebut
suatu vektor eigen (vektor karakteristik) yang berkorespondensi dengan ? .
Spektrum A, dinotasikan
s
(
A) , adalah kumpulan dari semua nilai eigen
untuk
matriks A.
Kata eigen didapat dari bahasa Jerman eigen yang berarti “karakteristik”.
Sebuah nilai eigen dari sebuah matriks biasanya direpresentasikan dengan huruf
Yunani
?
(dibaca lamda).
Definisi: Suatu vektor eigen disebut vektor eigen dominan dari sebuah matriks
jika vektor eigen itu bersesuaian dengan nilai eigen dengan
modulus terbesar untuk
matriks tersebut. Nilai eigen dengan modulus terbesar dari sebuah matriks disebut nilai
eigen dominan.
2.2.2 Cara Menghitung Nilai Eigen dan Vektor Eigen
Dari definisi di atas, maka
?
v
-
Av
=
0
(
?
I
-
A)v = 0
dengan I adalah matriks identitas.
Tetapi
(?I
-A)
adalah
sebuah
matriks,
jadi
kita
berusaha
menyelesaikan
persamaan Bv=0 di
mana
B=(?I-A), dan karena v adalah sebuah
vektor tak nol,
maka
hanya
mempunyai
solusi
taknol
jika
|B|
=
det(B) adalah 0.
Jadi
untuk
mencari
nilai
eigen, kita beri
nilai |?I-A|=0 dan mencari solusi untuk ?. Persamaan
|?I-A|=0 disebut
|
|
24
?
1
1
?
?
4
0
?
?
persamaan
karakteristik,
sedangkan
suku
banyak
|?I-A|
disebut
suku
banyak
karakteristik. Akar-akar dari persamaan ini adalah nilai eigen.
Untuk mencari vektor eigen, kita mensubtitusi nilai eigen yang sudah didapat ke
dalam persamaan
Av
=
?
v
,
atau kernel dari
(
?
I
-
A)
,
yaitu
(
?
I
-
A
)v
=
0
.
Maka kita
akan dapat mencari v yaitu vektor eigen yang bersesuaian dengan nilai eigen
?
.
Ruang
jawab dari sistem persamaan linear
(
?
I
-
A
)v = 0 disebut ruang karakteristik dari A yang
berkorespondensi dengan ?.
Catat bahwa kita tidak memasukkan vektor nol( 0 ) kedalam vektor eigen, karena
vektor nol adalah solusi trivial untuk
Av = ?v
dan tidak terlalu penting untuk dibahas.
Sebagai
tambahan, jika
vektor
nol
diikutkan,
maka akan
ada
tidak
berhingga
banyak
nilai eigen, karena setiap nilai
?
memenuhi
A0
=
?
0
.
Contoh
22
Misalkan
kita
ingin
mencari
nilai
eigen
untuk
matriks
?
0
1
?
A
=
?
1
1
?
-
1
0
-
1
?
?
0
?
.
?
?
Pertama kita hitung suku banyak karakteristik untuk matriks A:
?
?
?
p( x) = det(
?
I
-
A) = det
?
-
1
-
1
?
-
1
1 ?
?
0
?
= ?
3
-
2
?
2
-
?
+
2
?
?
-
1
?
Suku banyak tersebut dapat difaktorisasi menjadi p(?) = (? - 2)(? - 1)(? + 1).
Maka nilai eigen dari A adalah 2,1, dan -1.
Contoh 23: Cari nilai eigen dan vektor eigen untuk matriks
?
1
-
3
3
?
?
?
A
=
?
3
-
5
3
?
?
6
-
6
?
|
 25
?
?
?
4
?
?
?
?
Dengan cara mengekspansi
?
I
-
A
=
0
, kita dapat mencari nilai eigen:
?
?
0
?
0
?
?
1
?
?
-
3
3
?
?
?
?
-
1
3
?
-
3
?
?
?
0
?
0
?
-
?
3
-
5
3
?
=
?
-
3
?
+
5
-
3
?
=
?
0
0
?
?
6
-
6
?
?
-
6
6
?
-
4
?
(
?
+
2
)
2
(
?
-
4
)
=
0
Maka, nilai eigen dari matriks A adalah -2 dan 4.
Sekarang kita akan mencari vektor eigen untuk matriks A.
?
v
1
?
?
?
Misal
v
=
?
v
2
?
adalah
vektor
eigen
untuk
matriks
A
yang
berkorespondensi
?
?
?
v
3
?
dengan nilai eigen
?
=
-2 . Maka:
(?
I
-
A
)
v
=
0
?
?
-
1
3
-
3
??
v
1
?
?
0
?
?
??
?
?
?
?
-
3
?
+
5
-
3
??
v
2
?
=
?
0
?
, dan untuk
?
=
-
2 menjadi:
?
??
?
?
?
?
-
6
6
?
-
4
??
v
3
?
?
0
?
?
-
3
3
-
3 ? v
?? v
?
?
0
?
?
-
3v
+
3v2
-
3v
=
0
?
??
1
?
?
?
1
3
?
?
-
3
3
-
3
??
v
2
?
=
?
0
?
,atau
?
-
3v
1
+
3v
2
-
3v
3
=
0
?
??
?
?
?
?
?
-
6
6
-
6
??
v
3
?
?
0
?
?
-
6v
1
+
6v
2
-
6v
3
=
0
,atau v
1
-
v
2
+
v
3
=
0
, atau v
1
=
v
2
-
v
3
.
Himpunan jawab dari sistem persamaan linear homogen di atas, adalah:
|
 26
?
?
?
?
v
2
-
v
3
?
?
?
?
1
?
?
-
1?
?
?
?
?
?
?
?
?
?
?
?
H
1
=
??
v
2
?
v
2
,
v
3
real
?
=
?
v
2
?
1
?
+
v
3
?
0
?
v
2
,
v
3
?
R
?
??
?
?
?
?
?
?
?
?
?
?
v
3
?
?
?
?
0
?
?
1
?
?
?
1
?
?
-
1
?
?
?
?
?
Jadi vektor: v
=
v
2
?
1
?
+
v
3
?
0
?
dengan sedikitnya satu di antara v
2
atau v
3
tidak
?
?
?
?
?
0
?
?
1
?
nol, adalah vektor eigen dari A yang berkorespondensi dengan
?
=
-
2
.
?
v
1
?
?
?
Misal
v
=
?
v
2
?
adalah
vektor
eigen
untuk
matriks
A
yang
berkorespondensi
?
?
?
v
3
?
dengan nilai eigen
?
=
4
. Maka:
(?
I
-
A
)
v
=
0
?
?
-
1
3
-
3
??
v
1
?
?
0
?
?
??
?
?
?
?
-
3
?
+
5
-
3
??
v
2
?
=
?
0
?
, dan untuk
?
=
4
menjadi:
?
??
?
?
?
?
-
6
6
?
-
4
??
v
3
?
?
0
?
?
3
3
-
3?? v
?
?
0
?
?
3v1
+
3v2
-
3v
=
0
?
??
1
?
?
?
3
?
?
-
3
9
-
3
??
v
2
?
=
?
0
?
, atau
?
-
3v
1
+
9v
2
-
3v
3
=
0
?
??
?
?
?
?
?
-
6
6
6
??
v
3
?
?
0
?
?
-
6v
1
+
6v
2
+
6v
3
=
0
, atau
?v
1
+
3v
2
-
v
3
=
0
, atau
?
v
1
=
v
2
?
2v
2
-
v
3
=
0
?
v
3
=
2v
2
Himpunan jawab dari sistem persamaan linear homogen di atas, adalah:
|
 27
?
?
v
2
?
?
?
?
1
?
?
?
?
?
?
?
?
?
?
H
2
=
??
v
2
?
v
2
?
R
?
=
?
v
2
?
1
?
v
2
?
R
?
??
?
?
?
?
?
?
?
?
2v
2
?
?
?
?
2
?
?
?
1
?
?
?
Jadi
vektor:
v
=
v
2
?
1
?
,
dengan
v
2
?
0
adalah
vektor
eigen
dari
A
yang
?
?
?
2
?
berkorespondensi dengan
?
=
4
.
?
?
1
?
?
-
1?
?
Himpunan
H
=
?
?
?
?
?
?
1
+
ß
0
a
,
ß
?
R
adalah
ruang
karakteristik
dari A
1
?
a
?
?
?
?
?
?
?
?
?
?
?
?
?
0
?
?
1
?
?
yang berkorespondensi dengan
?
=
-
2
.
?
?
1
?
?
Sementara
H =
?
?
?
?
1
a
?
R
adalah
ruang
karakteristik
dari
A
yang
2
?
a
?
?
?
?
?
?
?
?
?
2
?
?
berkorespondensi dengan
?
=
4
.
Bila
matriks
yang
ingin
dihitung
cukup
kecil
ukurannya,
kita
dapat
menggunakan cara di atas (menyelesaikan persamaan karakteristik) untuk mencari nilai
dan
vektor eigen. Sayangnya, metode
ini
memiliki keterbatasan. Suku banyak secara
umumnya, untuk orde
n
>
4
tak dapat diselesaikan dengan barisan terbatas (dibuktikan
oleh teorema Abel-Ruffini). Terdapat algoritma mencari akar suku banyak yang efisien
untuk suku banyak berorde tinggi. Namun, mencari akar dari karakter suku banyak ini
mungkin ill-condition.walaupun nilai eigen yang dicari well-condition. Untuk alasan ini,
maka metode ini jarang digunakan.
|
|
28
Dengan demikian,
maka untuk matriks ukuran besar, kita harus menggunakan
metode numerik, seperti metode Power atau metode QR.
2.3
Metode Power
Ide
dasar
dari
metode
ini
adalah
mencari
vektor awal b
(bisa
saja
merupakan
perkiraan vektor eigen atau vektor acak) dan menghitung secara iteratif. Kecuali matriks
nol yang digunakan sebagai vektor awal, hasilnya akan konvergen ke vektor eigen yang
bersesuaian dengan nilai eigen dominan. Dalam praktiknya, vektor harus
dinormalisasikan setiap iterasi. Namun demikian, iterasi dengan Metode Power kurang
begitu berguna. Konvergensinya lambat kecuali untuk matriks khusus, dan tanpa
modifikasi, metode ini hanya dapat mencari nilai eigen dominan (juga vektor eigen yang
bersesuaian). Namun demikian, kita dapat mengerti
beberapa algoritma
mencari
nilai
eigen yang lebih baik sebagai variasi atau berdasar dari Metode Power.
Metode
Power secara
umum cukup
lambat.
Khususnya
untuk
nilai
eigen
yang
besarnya cukup dekat dengan nilai eigen dominan.
2.4
Metode QR
Untuk
menyelesaikan permasalahan
mencari
nilai
eigen
pada
suatu
matriks A,
yang biasa dilakukan adalah dengan mereduksi matriks tersebut menjadi matriks segitiga
T
melalui serangkaian transformasi ortogonal, dan lalu mencari nilai eigen untuk matriks
T. Transformasi yang dilakukan pada A memastikan bahwa nilai eigen pada matriks A
dan T adalah sama.
|
|
29
A
Teorema 1
Misalkan
A,B,S
adalah
matriks
berukuran
n
×
n
.
Bila
B
=
S
-1
AS ,
maka
nilai
eigen dari matriks A dan B adalah sama.
Bukti:
Cukup
dibuktikan
bahwa
A
dan
B
memiliki
suku
banyak
karakteristik
yang
sama.
Untuk t sembarang,
p
B
(t )
=
det(tI
-
B)
=
det(tS 1S
-1S
-
S 1
-1
AS )
=
det S ¹
-¹
(tI
-
A)S
=
det S
-1
det(tI -
A)
det S =
(det S )
-1
det S det(tI -
A) =
det(tI -
A) = p
(t )
Teorema 2
Misalkan A,B,S adalah
matriks berukuran
n
×
n
.
Bila
B
=
S
-1
AS , dan
x
?
C
n
merupakan vektor eigen dari matriks B yang berkorespondensi dengan
?
?
s
(B) , maka
Sx merupakan vektor eigen dari matriks A yang berkorespondensi dengan
?
.
Bukti:
Karena
B
=
S
-
1
AS
dan
Bx
=
?
x
, maka
S
-
1
ASx
=
?
x
atau
ASx
=
?
Sx . Juga
karena
S
tidak
singular
dan
x
?
0
,
Sx ?
0
,
maka Sx
merupakan
vektor
eigen
dari
matriks A.
Salah satu cara menyelesaikan masalah nilai eigen dengan transformasi seperti di
atas adalah metode QR. Dasar dari metode QR untuk mencari nilai eigen dari matriks A
adalah fakta bahwa matriks real n
×
n
dapat ditulis menjadi:
A = Q R , dengan QR adalah faktorisasi dari A
|
|
30
T
di
mana
Q
adalah
matriks
ortogonal dan
R
adalah
matriks
segitiga atas.
Metode
ini
efisien untuk menghitung semua nilai eigen untuk sebuah matriks.
Konstruksi matriks Q dan R adalah sebagai berikut. Matriks-matriks P1,P2, …,P
n-
1
dikonstruksikan
sedemikian
sehingga
P
n 1
-1
P
n- 2
L
P
2
P
1
A
=
R
adalah
matriks
segitiga
atas.
Matriks-matriks
ini dapat dipilih sebagai
matriks ortogonal
dan disebut
matriks
householder. Bila kita memilih
Q
=
P
n
-1
P
n- 2
L
P
2
P
1
Maka kita memiliki Q
T
A
= R dan
QQ
T
A
= QR
IA = QR
A = QR
Sedangkan
cara
mengkonstuksikan
matriks
P
adalah
sebagai
berikut.
Pertama
kita
mendefinisikan
barisan
matriks
A1
,A2
,…,A
m
,…, Q1,Q2
,…,Q
m
,…, dan
R1,R2,…R
m
,…
dengan proses berikut:
Langkah pertama:
Set A1
=
A, Q1 = Q dan R
1
= R
Langkah kedua:
Pertama set A2
=
R1
Q1; lalu faktorkan A2
sebagai A2
=
Q2R2
(faktorisasi QR dari
A2)
|
 31
Langkah ketiga:
Pertama set A3
=
R2
Q2; lalu faktorkan A3
sebagai A3
=
Q3R3
(faktorisasi QR dari
A3)
Langkah ke-m:
Set A
m
= R
m-1
Q
m-1
;
lalu faktorkan A
m
sebagai A
m
=
Q
m
R
m
(faktorisasi QR dari A
m
)
Pada langkah ke-k, matriks A
k
kita dapat, pertama dengan menggunakan Q
k-1
dan
R
k-1
dari langkah
sebelumnya; kedua, A
k
difaktorkan
menjadi Q
k
R
k
.
Jadi
faktorisasi QR
terjadi di setiap langkah. Matriks A
m
akan condong menjadi matriks segitiga atau hampir
segitiga. Jadi nilai eigen dari A
m
akan menjadi mudah dihitung.
Teorema 3
Misalkan A adalah matriks segitiga atas/bawah berukuran
n
×
n Nilai eigen dari
. Nilai eigen dari
matriks A adalah elemen-elemen diagonal dari matriks A.
Bukti:
?
a
×
×
×
×
?
Misalkan
?
11
?
0
A
=
?
0
?
?
M
?
a
22
0
M
×
×
a
33
×
M
O
?
×
?
×
?
adalah
matriks
segitiga
atas.
Maka
?
M
?
?
?
0
0
0
L
a
nn
?
persamaan karakteristiknya adalah
?
-
a
11
0
0
M
0
×
?
-
a
22
0
M
0
×
×
?
-
a
33
M
0
×
×
×
×
×
×
O
M
L
?
-
a
nn
=
0
.
Dengan
menguraikan determinan, kita dapat
(
?
-
a
11
)(
?
-
a
22
)L(
?
-
a
nn
)
=
0
.
|
 32
?
M
M
M
O
M
?
?
0
0
a
ˆ
n3
L
a
ˆ
nn
?
a
a
~
?
?
0
L
?
23
Ide dari faktorisasi QR adalah mencari P1 yang, jika dikalikan dari sebelah kiri
dengan matriks A, akan menghasilkan nol di bawah a
11
.
Yang kita inginkan adalah,
?
a
a
L
a
?
?
a
a
L
a
?
?
11
12
1n
?
?
11
12
1n
?
?
a
21
a
22
L
a
2
n
?
?
0
a
22
L
a
2
n
?
P
1
?
?
=
?
?
?
M
M
O
?
M
?
?
M
?
?
M
O
=
M
?
?
?
a
n1
a
n
2
L
a
nn
?
?
0
a
n
2
L
a
nn
?
Setelah didapat, kita mencari P2 yang akan menghasilkan:
?
a
a
L
a
?
?
aˆ
?
11
a
ˆ
12
a
ˆ
13
L
a
ˆ
1n
?
?
?
11
?
0
12
a
22
1n
?
?
0
L
a
2
n
?
?
a
ˆ
22
a
ˆ
23
L
a
ˆ
2
n
?
?
P
2
P
1
A
=
P
2
?
?
M
?
M
O
=
M
?
=
?
0
?
?
0
a
ˆ
33
L
a
ˆ
3n
?
?
0
a
n
2
L
a
nn
?
?
?
Proses ini terus berlanjut sampai kita punya
?
a
~
a
~
a
~
L
a
~
?
11
12
~
22
13
1n
~
2
n
?
P
P
L
P
P
A
=
R
=
?
0
0
a
~
L
a
~
?
n 1
-
n
-
2
2 1
?
33
3n
?
?
M
M
?
M
O
M
?
~
?
?
0
0
0
L
a
nn
?
Metode QR adalah algoritma iteratif yang diterapkan pada serangkaian
transformasi
ortogonal Q
i
pada
matriks tridiagonal
T
sedemikian
sehingga
matriks
T
konvergen pada matriks diagonal D. Matriks D
memiliki nilai eigen
yang sama dengan
matriks T,
maka
nilai eigen dari T adalah elemen diagonal dari D. Sebagai tambahan,
perkalian dari transformasi Q
i
adalah matriks yang kolom-kolomnya adalah vektor eigen
dari T. Metode ini disebut QR karena untuk setiap iterasi, dekomposisi QR pada matriks
A
i
(A
i
=
QR di mana Q
T
Q = I dan R adalah matriks segitiga atas) dikerjakan. Pseudocode
dan flowchart untuk metode QR diberikan di bawah ini.
|
|
33
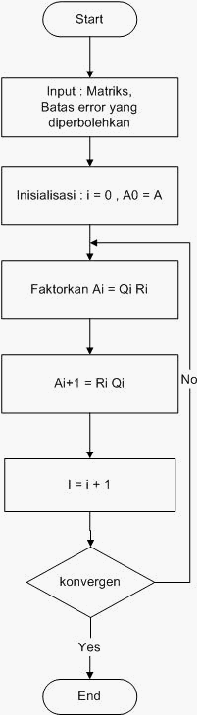
Pseudocode Algoritma QR(A)
1.
i = 0
2.
A
0
= A
3.
ULANGI
4.
Faktorkan A
i
= Q
i
R
i
5.
A
i+1
= R
i
Q
i
6.
i = i + 1
7.
SAMPAI konvergen
|
 34
Gambar 2.1. Flowchart Algoritma QR
|
|
35
Q
=
?
Q
Setelah konvergen, matriks A
n
adalah matriks segitiga dengan nilai eigen A
adalah
elemen
diagonal,
dan
matriks
n
j
=1
j
memiliki
kolom-kolom
yang
merupakan vektor eigen untuk masing-masing nilai eigen.
2.5
Metode QR dengan Hessenberg
Ada cara yang lebih sederhana untuk mencari
nilai eigen dan
vektor eigen dari
sebuah matriks, yaitu dengan mengubah matriks tersebut menjadi bentuk Hessenberg,
lalu dilakukan metode QR.
Perubahan matriks menjadi bentuk Hessenberg harus dilakukan dengan
transformasi
similar
untuk
menjamin
nilai
eigen
tetap
sama
dan
vektor
eigen
dapat
diketahui, yaitu mencari matriks H dimana
H
=
Q
-1
AQ , dengan H merupakan matriks
Hessenberg dan A merupakan matriks yang ingin diketahui nilai eigen dan vektor
eigennya..
Untuk memudahkan komputasi, akan digunakan transformasi householder untuk
mencari matriks Q
Definisi: Misalkan
u
?
R
n
,
u
?
0
dan
I
n×n
merupakan matriks identitas. Matriks
Q
=
I
-
2
u
T
u
uu
T
disebut matriks householder.
Setelah matriks
H
diketahui,
maka akan digunakan
metode QR
untuk
mencari
nilai dan vektor eigen matriks H.
|
|
36
2.6
Dinamika Populasi
Dinamika
populasi
adalah
ilmu
yang
mempelajari
perubahan
dalam jumlah,
komposisi usia, berat, dan sebagainya dalam satu atau beberapa populasi.
Pada awalnya dinamika populasi adalah cabang utama dari
matematika biologi,
dan
didominasi
oleh
studi demografi
yaitu ilmu
yang
mempelajari
populasi
manusia,
struktur dan perubahannya. Namun pada perkembangan selanjutnya, dinamika populasi
tidak hanya mempelajari manusia saja, tetapi juga hewan dan tumbuhan.
Ukuran populasi biasanya dipengaruhi oleh tiga faktor utama
, yaitu tingkat
kelahiran/natality, tingkat pertumbuhan/growth rate, tingkat kematian/mortality. Tingkat
perpindahan (imigrasi atau emigrasi) juga merupakan salah satu faktor, tetapi biasanya
tidak diukur.
Cara memodelkan dinamika populasi dapat dilakukan dengan sudut pandang
individual (i-state) di mana kita menelusuri individual-individual dengan karakteristik
yang berbeda (misalkan usia, strata, ukuran, dsb.) atau dapat dilakukan dengan sudut
pandang populasi (p-state) di mana kita
mencirikan populasi dengan fungsi kepadatan
(misalkan distribusi usia, atau ukuran, dsb.). Model populasi dasar
mencirikan populasi
dengan
sebuah
variabel
p-state
Salah satu contohnya adalah
dengan
memodelkan
pertumbuhan
populasi
dengan
variabel
usia. Model
tersebut
menjelaskan
gambaran
populasi yang ada, dan perkiraan gambaran populasi tersebut di masa yang akan datang.
2.7
Model Pertumbuhan Leslie
Model ini pertama dijelaskan oleh Lotka pada tahun 1920-an dan
diformalisasikan
pada 1940-an oleh
Leslie. Model ini berdasar pada tingkat bertahan
hidup (survival) dan kesuburan (fecundity) berdasarkan umur.
|
|
37
p
i
Kemungkinan bertahan hidup(survive) dari umur i ke umur i+1
f
i
Banyaknya anak per individual pada umur i
n
i
(t)
Banyaknya individual pada kelas umur i pada waktu t.
Kita mengambil n
0
sebagai banyaknya individual yang baru lahir. Jadi:
T
n
0
(t
+
1)
=
?
n
i
(t ) f
i
,
i
=0
di
mana T adalah umur
maksimum seorang
individual dapat
hidup. Banyaknya
individu dalam kategori umur lainnya ditentukan oleh banyaknya individual yang
bertahan hidup dari tahun sebelumnya. Khususnya,
n
i
(t + 1) = p
i
-1
n
i
-1
(t)
Secara keseluruhan, hal ini menjelaskan demografi dari populasi, dengan asumsi
untuk saat
ini bahwa p
i
dan f
i
tidak bervariasi dari tahun
ini ke
tahun berikutnya. Ini
dapat ditulis dalam bentuk matriks sebagai
?
n
o
(t
+
1) ?
?
f
0
f
1
f
2
K
f
T
?? n
0
(t ) ?
?
?
?
??
?
?
n
1
(t + 1)
?
?
p
0
0
0
L
0
??
n
1
(t )
?
?
n
(t
+
1)
?
=
?
0
p
0
L
0
??
n
(t )
?
?
M
?
?
0
?
?
?
0
p
2
O
0
??
M
?
??
?
?
n
T
(t + 1)
?
?
0
0
0
p
T
-1
0
??
n
T
(t )
?
Singkatnya,
n(t ) = An(t - 1) = A
t
n(0)
Model inilah yang biasa disebut Model Matriks Leslie. Matriks Leslie memiliki
tingkat kesuburan di baris pertama dan tingkat bertahan hidup di subdiagonal, sedangkan
elemen
lainnya adalah 0. Tetapi representasi matriks
yang lebih umum
untuk jenis
ini
|
|
38
dapat memenuhi kebutuhan untuk model yang lebih luas di mana subpopulasi yang
berubah-ubah sifatnya seiring waktu. Perlu dicatat bahwa tingkat bertahan hidup dalam
contoh di
atas
memberikan
informasi
yang
cukup
banyak,
bersama
dengan
interaksi
yang mungkin terjadi di antara subpopulasi, dan antara subpopulasi dengan lingkungan.
Ini mungkin dibutuhkan untuk kasus tertentu, tetapi tergantung pada bagaimana populasi
global dibagi, kita dapat memliki parameter yang lebih spesifik mengenai hubungan
antara
satu subpopulasi dengan
state sebelumnya atau antara state sebelumnya dengan
subpopulasi lainnya
Sifat-sifat yang penting dari matriks Leslie antara lain, adalah:
1.
Seluruh kelas umur diidentifikasi,
masing-masing dengan tingkat kesuburan dan
bertahan hidup mereka masing-masing.
2.
Setiap
anggota dari kelas umur
memiliki kemungkinan
yang sama
untuk
bertahan hidup ke tahun berikutnya, dan memroduksi keturunan yang sama
banyaknya.
3. Linier – Populasi akan berkembang atau menyusut secara geometris.
4. Seluruh kelas umur bertumbuh (atau menyusut) dalam tingkat yang sama.
5. Pertumbuhan awal bergantung pada struktur umur dari populasi.
6.
Reproduksi
awal
memiliki
kontribusi
yang
lebih
banyak
daripada
tingkat
pertumbuhan populasi daripada tingkat reproduksi akhir. Pada manusia, seorang
wanita
yang memiliki
tiga
orang
anak
dimulai
dari
umur
15
tahun
memiliki
kontribusi yang sama dengan wanita yang memiliki lima orang anak dimulai dari
umur 30 tahun.
|
|
39
2.8
Analisis Nilai Eigen terhadap Model Pertumbuhan Leslie
Kita akan memperhatikan bagimana nilai eigen dan vektor eigen dari matriks
transfomasi pada Model Pertumbuhan Leslie digunakan untuk mempermudah
perhitungan.
Ketika kita dapat memilih beberapa vektor sebagai vektor basis (satu untuk tiap
dimensi dari ruang), kita tentu ingin agar kita dapat menulis vektor sebagai kombinasi
linier dari vektor-vektor basis tersebut. Dalam hal ini, sembarang vektor x dapat ditulis
sebagai jumlah ‘bobot’ dari sembarang vektor (basis) b:
n
x
=
?
w
i
b
i
,
i
di
mana nilai w
i
adalah skalar
untuk setiap i. Walaupun kita dapat
menuliskan
sembarang
vektor sebagai
vektor basis (asal bukan kelipatan dari
vektor basis lainnya),
kita akan menuliskan vektor basis dengan vektor eigen. Salah satu alasan yang ingin
difokuskan adalah, dengan menuliskan vektor eigen sebagai vektor basis akan
menyederhanakan perhitungan untuk transformasi yang akan dilakukan secara berulang-
ulang
untuk
sebuah
vektor.
Untuk
memperjelas,
ingat
bahwa
transformasi
berulang
n
kali
dalam
bentuk
Ax
berarti
A
n
x. Ini
adalah
apa
yang
akan
kita
cari
apabila
kita
membaharui
nilai secara
berulang-ulang
menggunakan
persamaan
diferensial,
di
mana
x
t+1
=Ax
t
.
Tentu
akan
lebih
sulit
untuk
menghitung
secara
langsung
A
n
;
bahkan
untuk
mendapat
nilai
tersebut kita perlu melakukan seluruh perkalian
matriks,
yang terlebih
sulit lagi untuk matriks berukuran besar. Tentu akan lebih mudah bila operasi pangkat
yang dilakukan bukan untuk matriks yang mungkin berukuran besar, tetapi hanya untuk
bilangan skalar. Ini adalah apa
yang kita dapat apabila kita menggunakan
vektor eigen
sebagai vektor basis.
|
|
40
Tetapi sebuah
matriks berorde
n
× n
belum tentu memiliki
tepat n buah vektor
eigen.
Kekurangan
lainnya
adalah
adanya
trade off
pada
beban
perhitungan
karena
adanya
fakta bahwa kita
harus mengetahui bagaimana cara menulis
ulang vektor awal
dalam suku vektor eigen. Dengan kata lain, kita harus mengetahui nilai eigen dan vektor
eigen
yang
beresuaian;
lalu
kita
harus
mencari
bobot
yang
tepat
untuk
menyatakan
vektor tersebut dalam suku-suku vektor eigen.
Cara
mencari
nilai
dan
vektor
eigen
telah
dijabarkan
di
muka,
yaitu
dengan
menggunakan algoritma QR.
Setelah kita mengetahui nilai dan vektor eigen, langkah terakhir adalah mencari
bobot. Ingat bahwa sebuah vektor x dapat ditulis sebagai bobot dari vektor eigen, yang
juga dapat ditulis sebagai:
x =
t =
Ew
t
di mana E adalah matriks yang kolom-kolomnya adalah vektor eigen yang telah
kita dapatkan, dan w adalah
vektor yang
mengandung bobot
yang kita cari. Vektor w
dapat dicari dengan mengalikan kedua ruas dengan E
-1
,
yang berarti
E
-1
Ew
t
=
Iw
t
=
w
t
yang sama dengan
E
-1
x
t
,
yang akan kita hitung. Dengan
vektor eigen
yang telah kita
dapat, dan bobot telah kita dapatkan, kita dapat
menyatakan
vektor x yang ingin kita
cari dalam suku-suku vektor eigen.
Ada
alasan
lain
mengapa
kita
ingin menghitung nilai eigen, terlepas dari
kebutuhan
untuk
mencari
vektor eigen,
yaitu bahwa kita sedang berusaha menghitung
A
n
x
dengan cara yang lebih
mudah. Untuk
mendapat
nilai ini, kita perlu
tiga
hal yang
|
|
41
i
i
telah kita dapat sebelumnya:
vektor eigen,
nilai eigen, dan bobot. Sekarang kita dapat
membicarakan vektor x dalam suku-suku vektor eigen A. Karena:
A
n
x
=
n
A
n
?
i
w
i
e
i
(dengan e
i
adalah vektor eigen ke-i dari A), dan juga
A
=
?
i
untuk setiap e
i
(dari definisi
nilai eigen), maka kita dapat menulis:
n
n
=
?
=
?
i
i i
A
n
x
A
n
w
e
i
?
n
w
e
i
Persamaan terakhir adalah yang ingin kita cari selama ini. Ini adalah cara untuk
menghitung
vektor x setelah
ditransformasi
n-kali oleh
A, tanpa
melakukan
perkalian
dengan A. Dari
sudut
yang
lain, akan
menjadi
lebih
nyata bila kita
mendapatkan
nilai
dan vektor eigen dari matriks transformasi, kita sebenarnya memiliki hal yang akan
memberitahu kita tingkah laku ke depan dari sistem yang akan dijelaskan dari state awal
x
0
dan sebuah matriks transformasi A.
2.9
Rekayasa Piranti Lunak
2.9.1
Definisi Rekayasa Piranti Lunak
Menurut pendapat Pressman (1991, p.6), terdapat tiga macam pengertian piranti
lunak , yaitu:
1.
Instruksi-instruksi
(program
komputer)
yang
ketika
dijalankan
akan
menghasilkan fungsi dan performa yang diinginkan.
2.
Suatu kumpulan struktur data yang memungkinkan program untuk memanipulasi
informasi.
|
 42
3.
Suatu dokumen-dokumen
yang menggambarkan operasi dan kegunaan dari
program.
Sedangkan
rekayasa
piranti
lunak
menurut Pressman (1991,
p.20)
merupakan
penggunaan prinsip-prinsip rekayasa
untuk
mendapatkan piranti
lunak yang ekonomis,
dapat diandalkan, dan dapat dijalankan dengan efisien pada mesin yang ada.
Gambar 2.2
Lapisan-lapisan Rekayasa Piranti Lunak
Rekayasa Piranti
Lunak adalah teknologi yang berlapis. Dari
gambar 2.2, setiap
rekayasa
piranti
lunak
harus
berpijak
pada kualitas.
Dasar dari
rekayasa piranti
lunak
adalah
proses.
Proses
rekayasa
piranti lunak
merupakan
perekat
dari
teknologi
dan
membuat pengembangan dari piranti lunak menjadi rasional. Metode rekayasa piranti
lunak menyediakan
teknis pembuatan sebuah piranti lunak seperti perancangan proyek
dan
estimasi,
menganalisa
kebutuhan
sistem,
perancangan
struktur data, prosedur
algoritma,
arsitektur
program,
pengkodean,
dan
pemeliharaan.
Alat
(tools) rekayasa
piranti lunak menyediakan layanan yang otomatis atau semi otomatis untuk proses dan
metode.
|
 43
2.9.2
Model Rekayasa Piranti Lunak
Model
rekayasa piranti
lunak
yang
digunakan
adalah Linear Sequential
Model
Seringkali disebut sebagai siklus hidup klasik (Classic Life Cycle) atau waterfall model.
Model ini memberikan pendekatan-pendekatan yang sistematik dan berurutan
(sequential)
dalam
pengembangan
suatu
software.
(Pressman,
2001,
p28).
Model
ini
merupakan model yang paling banyak digunakan.
Gambar 2.3
Model Sekuensial Linear
Tahapan-tahapan
yang terdapat dalam Linear Sequential Model adalah sebagai
berikut:
•
System Engineering And analysis (Rekayasa dan analisa sistem).
Karena software
merupakan bagian dari
sistem
yang
lebih
besar,
maka
setiap
pekerjaan
dimulai
dari
penentuan
kebutuhan
untuk
keseluruhan
elemen
sistem
dan kemudian
mengalokasikan beberapa dari kebutuhan tersebut pada software.
Sistem
Engineering dan
analysis
meliputi
pengumpulan
kebutuhan
pada
level
sistem dengan jumlah yang sedikit dari desain top level dan analisa.
|
|
44
•
Software Requirement Analysis (Analisis kebutuhan piranti lunak).
Analisis kebutuhan piranti lunak
merupakan kebutuhan
untuk
memperoleh
proses
yang intensif dan terfokus pada spesialisasi dari software. Untuk
mengerti
karakteristik
dari
program yang
akan
dibuat,
maka
pengembang
software harus
mengerti
dan
memahami kebutuhan-kebutuhan software, seperti
fungsi apa saja yang diperlukan, performa software dan antar muka software.
•
Design (Perancangan)
Perancangan
software merupakan
proses
dengan
langkah
yang
cukup
banyak
yang
terfokuskan
pada
4
atribut
penting
dari
program, yaitu
struktur
data,
arsitektur software, detil prosedur, dan karakteristik dari antarmuka.
•
Coding (Pengkodean)
Coding merupakan langkah untuk menerjemahkan design ke dalam bentuk yang
dapat dikenali oleh mesin (komputer). Jika pada
tahap design
difokuskan pada
hal-hal yang detil, maka pada tahap coding difokuskan pada hal yang mekanik.
•
Testing (Pengujian)
Testing merupakan
langkah
yang digunakan
untuk
menguji program yang telah
dibuat
apakah
telah
sesuai dengan analisis, kebutuhan dan desain seperti yang
telah
direncanakan
sebelumnya.
Testing juga
dimaksudkan
untuk
mencari
kesalahan-kesalahan yang mungkin ada.
•
Maintenance (Pemeliharaan)
Maintenance merupakan suatu langkah yang digunakan untuk menjaga dan
memelihara program yang telah dibuat agar tetap berfungsi dengan baik.
|
|
45
2.10
UML (Unified Modelling Language)
UML adalah suatu bahasa standar untuk menulis cetak biru (rancangan) piranti
lunak.
UML
dapat
digunakan
untuk
memvisualisasi
(visualizing), menspesifikasikan
(specifying),
membentuk (constructing), dan
mendokumentasikan
(documenting) sistem
piranti lunak (Booch et al, 1999, p13).
Booch, Jacobson dan Rumbaugh menyatakan ada tiga tujuan dibentuknya UML,
yaitu:
1.
Untuk
memodelkan sistem,
dari
konsep
menjadi suatu
objek
yang
dapat
dijalankan dengan menggunakan teknik berorientasi objek.
2.
Untuk
menempatkan masalah
yang sifatnya skalar ke dalam sistem yang
rumit
dan bertujuan kritis.
3.
Untuk
membuat sebuah bahasa
pemodelan
yang
bisa digunakan
oleh
manusia
dan mesin.
Berikut adalah beberapa diagram-diagram dalam UML:
1.
Class Diagram
Class diagram mengambarkan kumpulan class, interfaces dan collaboration
serta relationships ketiganya (Booch et al, 1999, p25).
Beberapa komponen class diagram antara lain:
•
Class
Sebuah class adalah kumpulan objek
yang
mempunyai
attributes, operations,
relationships dan semantics yang sama (Booch et al, 1999, p49).
Class dapat merepresentasikan hal fisik (seperti
pelanggan, produk,
buku),
hal
konseptual
(seperti
pesanan, pinjaman,
pemesanan) atau hal organisasi (seperti
perusahaan atau departemen).
|
 46
Class digambarkan dengan
sebuah
kotak
persegi panjang.
Notasi
class
terdiri
dari 3 bagian yaitu nama class, attribute dan operation.
Gambar 2.4 Notasi class
•
Relationships
i.
Generalization
Menggambarkan
hubungan class yang
umum
dengan
class
yang khusus
yang dikenal dengan hubungan subclass/superclass atau child/parent.
ii.
Association
Menggambarkan
hubungan
struktural
antara class.
Pada association,
terdapat multiplicity dan aggregation.
Multiplicity menggambarkan
berapa
banyak
objek
yang
mungkin
terhubung dari suatu hubungan association. Multiplicity
dinotasikan
dengan 1 atau 1..1, * atau 0..*, 0..1, 1..* atau bilangan tertentu di masing-
masing ujung garis association. Misalkan:
Gambar 2.5 Contoh multiplicity
Aggregation adalah association yang mempunyai hubungan “bagian dari”.
Misalkan:
|
 47
Gambar 2.6 Contoh aggregation
2.
Use Case Diagram
Use case diagram
menggambarkan
sekumpulan use case dan actor serta
hubungan antara keduanya.
Beberapa komponen dari use case diagram:
•
Actor
Actor mewakili
peran
pengguna
dalam
hubungannya
dengan
use
case.
Actor
dapat saja berupa seorang manusia, alat perangkat keras atau sistem lain.
Gambar 2.7 Notasi actor
•
Use case
Use case menjelaskan sekumpulan urutan, di
mana
masing-masing urutan
mewakili interaksi “benda” di luar sistem (actor) dengan sistem itu sendiri
(Booch et al, 1999, p220). Sebuah use case mewakili sebuah functional
|
 48
requirement dari sistem secara keseluruhan. Use case menggambarkan apa yang
dilakukan oleh sistem, bukan bagaimana sistem melakukannya.
Gambar 2.8 Notasi use case
•
Flow of events
Flow of events menggambarkan perilaku sistem dengan kalimat yang jelas
sehingga bisa dimengerti dengan mudah oleh orang di luar sistem.
•
Include
Include relationship di antara use case-use case berarti sebuah use case dasar
memasukkan
perilaku
dari use
case
lain
secara
eksplisit.
Include
relationship
digunakan untuk menggambarkan use case yang berulang.
Gambar 2.9 Contoh include relationship
•
Extend
Extend
relationship di
antara
use
case-use
case
berarti
use
case
dasar
memasukkan perilaku dari use case
lain
secara tidak langsung. Extend
relationship digunakan untuk menggambarkan variasi dari tingkah laku normal.
|
 49
Gambar 2.10 Contoh extend relationship
3.
Activity Diagram
Activity Diagram menggambarkan flow (aliran) dari sebuah aktivitas ke aktivitas
lainnya dalam sistem.
Komponen
Keterangan
Initial
state,
yaitu
menyertakan
awal
dimulainya
suatu
aktivitas.
Final state, yaitu menyatakan berakhirnya suatu aktivitas.
State,
menggambarkan aktivitas yang merepresentasikan
kinerja dari suatu operasi
Pada
transition dapat
dituliskan ekspresi
sebagai
guard
(kondisi yang menentukan aliran kontrol, ditandai dengan
tanda “[ ]”).
Decision, menggambarkan
kontrol
dari aliran
yang
bersifat
kondisional.
Forking dan joining dipergunakan untuk menggambarkan
aliran kontrol yang berjalan secara paralel atau bersamaan.
Tabel 2.1 Tabel notasi activity diagram
|
|
50
4.
Statechart Diagram
Statechart
Diagram
menggambarkan sebuah state
machine,
yang terdiri dari
state, transition, event dan aktivitas (Booch et al, 1999, p25). Statechart diagram hampir
sama dengan activity diagram. Keduanya sama-sama menggambarkan flow of control.
Bedanya
activity diagram
menggambarkan
flow
of
control dari
suatu
aktivitas
ke
aktivitas, sedangkan statechart diagram menggambarkan flow of control dari suatu state
ke state lainnya.
|