|
BAB 2
LANDASAN TEORI
2.1
Pengertian Persediaan
Menurut Smith
dan
Skousen
dalam bukunya
Intermediate
Accounting
sebagai
berikut:
“Barang-barang yang dimiliki
untuk dijual
dalam kegiatan
normal
perusahaan,
serta
untuk
perusahaan
manufaktur,
barang-barang yang
tengah
diproduksi
atau
ditempatkan di dalam produksi.”
Menurut
Ikatan
Akutan
Indonesia (IAI)
dalam
prinsip
akuntansi Indonesia
menyatakan
bahwa
istilah
persediaan
digunakan
untuk
menyatakan
barang
berwujud
yang:
a. tersedia untuk dijual (barang dagang/barang jadi)
b. masih dalam proses produksi untuk diselesaikan kemudian dijual (barang dalam
proses/pengolahan)
c. akan dipergunakan untuk produksi barang-barang jadi yang akan dijual (bahan
baku dan bahan pembantu) dalam rangka kegiatan normal usaha.
Jadi
dapat disimpulkan bahwa
yang dimaksud dengan persediaan barang adalah
semua
barang
yang
terdapat
di
perusahaan,
maupun
barang-barang yang
berada
di
perjalanan dan barang-barang yang dititipkan ke pihak lain.
|
|
6
2.2
Fungsi dan Penggolongan Persediaan
Persediaan
merupakan
unsur
dari
harta
lancar (current assets)
yang besar
nilainya, selain itu persediaan merupakan harta yang peka terhadap waktu, penurunan dan
kenaikan harga pasar, pencurian, dan sebagainya.
Persediaan berfungsi juga sebagai kontinuitas eksistensi suatu perusahaan dengan
mencari
keuntungan/laba
untuk
kontinuitas perusahaan tersebut.
Dengan demikian
ada
beberapa
alasan
yang
menyebabkan perusahaan
untuk
menanggani persediaan
dengan
serius, antara lain:
a. Untuk meningkatkan efesiensi operasional
Persediaan
barang
sangat
penting
dalam
meningkatkan efesiensi
operasional,
misalnya proses
A
memerlukan bahan
baku
X1 untuk
menghasilkan barang
Y1,
sedangkan
proses B memerlukan
bahan baku yaitu Y1 yang dihasilkan
oleh
proses A. Apabila proses A kehabisan persediaan bahan baku, maka proses B juga
tidak
dapat
beroperasi. Seandainya persediaan
selalu
tersedia
maka
efesiensi
operasional akan terlaksana.
b. Memberikan respon yang cepat kepada pelanggan
Permintaan pelanggan akan
dapat
terpenuhi
jika
barang
yang
diinginkan
pelanggan selalu tersedia.
c. Antisipasi terhadap situasi dan kondisi tertentu
Pengaturan
persediaan barang sangat diperlukan
untuk
mengantisipasi
terhadap
kemungkinan
yang
mungkin
terjadi,
misalnya
keterlambatan pengiriman
dari
pemasok, mesin rusak, dan sebagainya.
|
|
7
Menurut Sofjan
Assauri
jenis
persediaan dilihat dari
fungsinya dapat
dibedakan
menjadi:
a. Batch stock atau Lot size inventory
b. Fluctuantion stock
c. Anticipation stock
Batch stock atau
lot
size
inventory
merupakan persediaan
yang diadakan karena
melakukan
pembelian atau
pembuatan bahan-bahan/barang-barang
dalam
jumlah
lebih
besar
dari
jumlah
yang
dibutuhkan pada
saat
itu.
Hal
ini
dilakukan
untuk
memperoleh
potongan
harga
dan
penghematan
biaya
angkutan.
Tetapi,
dengan
pembelian
barang
dalam
jumlah
besar
mengakibatkan investasi
juga
besar,
biaya
sewa
gudang
pun
bertambah, serta resiko penyimpanannya juga besar.
Fluctuantion
stock
adalah
persediaan untuk
menghadapi fluktuasi,
seperti:
permintaan konsumen dan keterlambatan pengiriman yang tidak dapat diramalkan. Oleh
karena itu perlu adanya persediaan untuk mengatasi hal tersebut.
Anticipation
stock
merupakan persediaan yang
diadakan
untuk
menghadapi
fluktuasi
yang
dapat
diramalkan, misalnya:
permintaan
akan
meningkat
pada
saat
menjelang hari raya, dan lain-lain.
Menurut
Wilson
dan
John
B.
Campbell
penggolongan persediaan
dilihat
dari
kegiatan perusahaan dapat dibedakan menjadi empat golongan, yaitu:
a. Persediaan bahan baku (Raw Material Inventory)
b. Persediaan bahan baku pembantu (Supplies Inventory)
c. Persediaan barang setengah jadi (work In Prosess Inventory)
d. Persediaan barang jadi (Finished Goods Inventory)
|
|
8
Persediaan
bahan
baku
hanya
terdapat
pada
perusahaan
yang
membeli
barang
pada pemasok untuk diproses
lebih lanjut sehingga menjadi barang jadi. Misalnya kayu,
papan dan cat merupakan bahan baku dari perusahaan mebel, dsb.
Persediaan bahan baku pembantu digunakan sebagai bahan pelengkap (tambahan)
untuk membantu kelancaran jalannya proses produksi. Misalnya: pensil, kertas, alat-alat
pemotong, alat-alat kantor
lainnya yang digunakan
untuk
membantu berjalannya fungsi
organisasi di dalam perusahaan.
Persediaan barang
setengah
jadi
merupakan
bagian
dari
produk
akhir
yang
memerlukan proses lebih lanjut. misalnya: Kain pada industri pakaian.
Persediaan barang jadi merupakan barang-barang yang telah selesai diproses dan
siap untuk dijual ke pasar.
2.3
Biaya Dalam Persediaan
Tujuan
manajemen persediaan
adalah
untuk
menyediakan jumlah material yang
tepat,
tenggang waktu
(lead
time)
yang
tepat
dan
biaya
rendah.
Biaya
persediaan
merupakan keseluruhan biaya operasi atas sistem persediaan. Biaya persediaan
didasarkan pada parameter yang relevan dengan jenis biaya sebagai berikut:
a. Biaya pembelian (purchase cost)
b. Biaya pemesanan (ordering cost / setup cost)
c. Biaya simpan (carrying cost / holding cost)
d. Biaya kekurangan persediaan (stockout cost / penalty cost)
|
|
9
Biaya pembelian adalah harga per unit item yang dibeli dari pihak luar, atau biaya
produksi per unit apabila diproduksi
dalam perusahaan.
Biaya per unit akan selalu
menjadi bagian dari biaya item dalam persediaan. Untuk pembelian item dari luar, biaya
per
unit
adalah
harga
beli
ditambah
biaya
pengangkutan. Sedangkan
untuk
item
yang
diproduksi didalam perusahaan biaya per unit adalah termasuk biaya tenaga kerja, bahan
baku.
Biaya pemesanan adalah biaya yang berasal dari pembelian pesanan dari pemasok
atau biaya persiapan (setup cost) apabila item diproduksi di dalam perusahaan. Biaya ini
diasumsikan tidak
akan
berubah
secara
langsung
dengan
jumlah
pesanan.
Biaya
pemesanan
dapat
berupa:
biaya
membuat
daftar
permintaan,
menganalisis pemasok,
membuat pesanan pembelian, dan
sebagainya. Sedangkan biaya persiapan dapat berupa
biaya
yang
dikeluarkan akibat
perubahan
proses
produksi,
pembuatan
jadwal
kerja,
persiapan sebelum produksi dan pengecekan kualitas.
Hal-hal yang perlu diperhatikan berkaitan dengan pemesanan persediaan, antara
lain:
a. Berapa biaya permintaan untuk setiap item selama satu tahun? Seandainya, rata-
rata
permintaan adalah
60
permintaan setiap
bulan,
maka
ada
720
permintaan
selama satu tahun.
b. Perkirakan waktu dan biaya yang dibutuhkan dalam mengirim pesanan pembelian
kepada pemasok setiap tahunnya.
c. Perkirakan waktu dan biaya penerimaan pesanan selama satu tahun tersebut.
d. Perkirakan waktu dan biaya pembukuan, pengiriman cek, amplop, dan
sebagainya.
|
|
10
Biaya simpan adalah biaya yang dikeluarkan atas investasi dalam persediaan dan
pemeliharaan maupun
investasi sarana fisik untuk menyimpan persediaan. Biaya simpan
dapat berupa: biaya modal, pajak, asuransi, sewa gudang dan sebagainya.
Biaya kekurangan persediaan adalah konsekuensi ekonomis atas kekurangan dari
luar
maupun
dari
dalam
perusahaan. Kekurangan dari
luar
terjadi
apabila
pesanan
konsumen
tidak
dapat
dipenuhi.
Sedangkan
kekurangan dari
dalam
terjadi
apabila
depertermen yang
satu
tidak
dapat
memenuhi
permintaan
dari
departemen
yang
lain.
Kekurangan persediaan dapat mengakibatkan kehilangan kesempatan untuk mendapatkan
keuntungan bahkan kehilangan kepercayaan dari pelanggan.
Tujuan dari
manajemen persediaan adalah meminimumkan biaya, oleh karena itu
perusahaan perlu mengadakan analisis untuk menentukan tingkat persediaan yang paling
ekonomis.
2.4
Peramalan Permintaan (Forecasting)
Peramalan
merupakan
alat
bantu
yang penting
dalam perencanaan
yang
efektif
dan
efisien
khususnya
dalam
bidang
ekonomi.
Peramalan
merupakan suatu
proses
perkiraan tingkat permintaan yang diharapkan untuk suatu produk atau beberapa produk
dalam periode waktu tertentu pada masa yang akan datang.
Peramalan merupakan prediksi, proyeksi atau estimasi tingkat kejadian yang tidak
pasti
dimasa
yang
akan
datang.
Dalam
peramalan
digunakan data
historis
yang
telah
dimiliki untuk diproyeksikan ke dalam suatu
model. Dengan menggunakan model
tersebut diharapkan dapat memperkirakan keadaan pada masa yang akan datang.
|
 11
Sumber: Zulian Yamit, Manajemen Persediaan, (Yogyakarta:Ekonisia,1999,p.17)
Faktor-faktor
umum
yang
mempengaruhi
permintaan
suatu
perusahaan,
antara
lain:
a. Kondisi umum bisnis dan ekonomi
b. Reaksi dan tindakan pesaing
c. Tindakan pemerintah
d. Kecenderungan pasar
e. Inovasi teknologi.
Banyak
jenis
metode
peramalan, secara
umum
metode
peramalan
dapat
diklasifikasikan dalam dua kategori utama, yaitu
metode kuantitatif dan kualitatif.
Metode kuantitatif dapat dibagi ke dalam deret berkala atau runtun waktu (times series),
indikator
ekonomi,
dan model ekonometri.
Sedangkan
metode
kualitatif
berupa
pengumpulan pendapat.
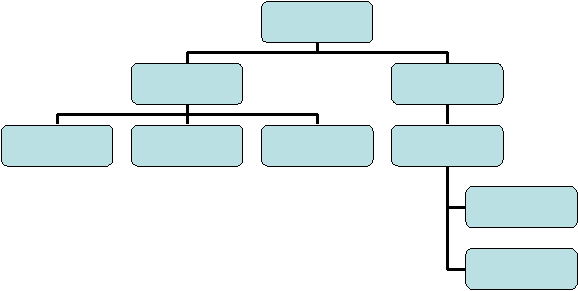
Metode
Peramalan
Kuantitatif
(Statistikal)
Kualitatif
(Judmental)
Analisis Runtun
Waktu
Indikator
Ekonomi
Model
Ekonometri
Pengumpulan
Pendapat
Pendapat Ahli
Survei Pasar
Gambar 2.1 Kualifikasi Metode Peramalan
|
|
12
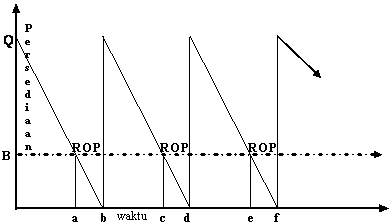
dengan Q. Dengan tingkat penggunaan tetap, persediaan akan habis dalam waktu tertentu.
2.5
Permintaan Independen Model Deterministik
2.5.1
Sistem Pemesanan Jumlah Tetap
Salah satu alasan utama mengapa perusahaan mempunyai persediaan adalah agar
perusahaan dapat membeli atau membuat produksi dalam jumlah yang paling ekonomis.
Informasi
yang
dibutuhkan
untuk
menentukan kebijakan
persediaan
optimum
adalah
parameter sebagai berikut:
a. Permintaan
b. Biaya Persediaan
c. Tenggang Waktu (lead time)
Dalam model deterministik, semua parameter tersebut dapat diperhitungkan
secara tepat, dengan kata lain jumlah permintaan dan biaya persediaan diasumsikan dapat
ditentukan secara pasti. Demikian pula terhadap tenggang waktu pemesanan diasumsikan
konstan.
Pertanyaan mendasar yang harus dijawab dalam sistem persediaan adalah, berapa
banyak
dan
kapan
melakukan
pemesanan. Untuk
menjawab
kedua
pertanyaan seperti
tersebut
sangat
tergantung
pada
parameter: permintaan,
biaya
persediaan dan tenggang
waktu.
2.5.2
Economic Order Quantity (EOQ)
Jumlah
pemesanan
yang
dapat
meminimukan total
biaya
persediaan
disebut
Economic Order Quantity (EOQ). Secara klasik model diperlihatkan pada gambar 2.2, di
mana Q adalah jumlah pembelian dan ketika pemesanan diterima jumlah persediaan sama
|
 13
Ketika persediaan hanya tinggal sebanyak kebutuhan tenggang
waktu, pemesanan
kembali
(reorder point =
ROP)
harus dilakukan. Pada
gambar
2.2 tersebut pemesanan
kembali
pada
titik
ROP.
Garis
vertikal
menunjukkan
penerimaan
pesanan
ketika
persediaan nol, dengan demikian rata-rata persediaan adalah (Q + 0)/2 atau Q/2.
Gambar 2.2 Model Persediaan
Sumber: Zulian Yamit, Manajemen Persediaan, (Yogyakarta:Ekonisia,1999,p.48)
Jika tidak terjadi kekurangan persediaan, maka total biaya persediaan per
tahun
dicari dengan rumus berikut.
Total biaya = biaya pembelian + biaya pemesanan + biaya simpan
TC (Q) = PR + (CR/Q) + (HQ/2)
Total biaya pembelian = P x R
Total biaya pemesanan = C x (R/Q)
Total biaya simpan = HQ/2
|
 14
*
Dimana
:
R
=
jumlah kebutuhan dalam unit
P
=
biaya pembelian per unit
C
=
biaya pemesanan setiap kali pesan
H
=
biaya simpan per unit per tahun
Q
=
jumlah pemesanan dalam unit
T
=
persentase total biaya simpan per tahun
Untuk
memperoleh biaya
minimum setiap kali pemesanan dapat dilakukan
dengan cara
mencari turunan total biaya terhadap jumlah pemesanan(Q) dan disamakan
dengan nol.
dTC (Q)
=
H
-
CR
dQ
2
Q
2
Dari persamaan tersebut dapat ditentukan rumus EOQ sebagai berikut:
Q
*
=
2CR
=
H
2CR
PT
Dari EOQ tersebut dapat diketahui
jumlah
frekuensi pemesanan selama satu tahun (F)
dan waktu interval antara pemesanan (V), dengan cara sebagai berikut:
F
=
R
=
HR
Q
*
2C
V
=
1
=
Q
=
2C
F
R
HR
Pemesanan kembali (reorder
point) ditentukan berdasarkan kebutuhan selama
tenggang
waktu
pemesanan. Jika
posisi
persediaan cukup
untuk
memenuhi
permintaan selama
tenggang waktu pemesanan, maka pemesanan kembali harus dilakukan sebanyak Q
*
unit.
|
 15
Formula
berikut
ini
dapat
digunakan untuk
menentukan kapan
melakukan pemesanan
kembali apabila tenggang waktu pemesanan L ditentukan dalam bulan mau pun minggu.
B
=
RL
=
ROP
unit
12
B
=
RL
=
ROP unit
52
Jika jumlah pemesanan kembali (B) lebih kecil dari jumlah pemesanan (Q) atau B < Q,
maka tidak akan pernah terjadi kekurangan persediaan. Jika jumlah pemesanan kembali
(B)
lebih besar dari
jumlah pemesanan
(Q) atau
B
>
Q, maka akan terjadi kekurangan
persediaan dalam setiap pemesanan.
Total biaya minimum per tahun dapat ditentukan dengan mengganti Q dengan Q
*
yang terdapat dalam rumus total biaya minimum per tahun:
TC(Q
*
)
= PR +H Q
*
2.5.3 Analisis Sensitivitas Dalam EOQ
Analisis sensitivitas
digunakan
untuk
menentukan
bagaimana
pengaruh
perubahan atau kesalahan data dalam parameter terhadap EOQ. Dalam sistem pemesanan
jumlah
tetap, jumlah
pemesanan dapat
meminimumkan total biaya variabel per tahun.
Secara matematik dapat dirumuskan sebagai berikut:
Q
*
=
2CR
H
Dalam rumus tersebut, total biaya variabel (TVC) per tahun tidak termasuk dalam biaya
pembelian dan diasumsikan pula tidak ada diskon dan kekurangan persediaan.
|
 16
TVC (Q)
= biaya pesan + biaya simpan
= CR/Q + HQ/2
TVC (Q
*
)
= CR/ Q
*
+ H Q
*
/2 = HQ
*
Jika diasumsikan bahwa kesalahan dalam parameter R,H dan C masing-masing disebut
XR, X
H
dan XC, maka model EOQ nya adalah:
Q
=
2CR
X
C
X
R
=
Q
*
X
C
X
R
H
X
H
X
H
Dimana :
Q
= jumlah pemesanan dengan parameter kesalahan
Q
*
= Economic Order Quantity (EOQ)
XR
= estimasi permintaan/permintaan aktual = faktor kesalahan kebutuhan
XC
= estimasi biaya pesan/biaya pesan aktual = faktor kesalahan biaya pesan
X
H
= faktor kesalahan biaya simpan
Untuk menentukan sensitivitas total biaya variabel per tahun akibat adanya
kesalahan dalam penentuan parameter, dapat dilakukan dengan cara memasukkan faktor
kesalahan dalam rumus sebagai berikut:
TVC (Q)
-
TV (Q
*
)
=
TVC (Q
*
)
X
C
X
R
X
h
-
1
2.5.4
Model Backorder
Backorder terjadi ketika permintaan pelanggan tidak dapat dipenuhi dari
persediaan yang ada dan pelanggan menyetujui untuk menunggu pengiriman pesanan
berikutnya.
|
|
17
2.6
Macam Cara Pemesanan (Model Deterministik)
2.6.1
Periodik Order Quantity (POQ)
POQ menentukan jumlah
periode
permintaan.
POQ
menggunakan
logika
yang
sama dengan EOQ, tetapi POQ mengubah jumlah
pemesanan menjadi jumlah periode
pemesanan. Hasilnya adalah interval pemesanan tetap dengan bilangan bulat (integer).
Untuk
menentukan
jumlah
pemesanan
sistem POQ cukup
dengan
memproyeksikan
jumlah kebutuhan setiap periode.
2.6.2
Part Period Algorithm
Metode
Part
Period
Algorithm
(PPA) digunakan
untuk
menentukan
jumlah
pemesanan berdasarkan keseimbangan antara biaya pesan dan biaya simpan. Oleh karena
itu metode ini disebut juga part period balancing atau
total
biaya
terkecil.
Metode
ini
menyeleksi
jumlah periode
untuk
mencukupi pesanan tambahan berdasarkan akumulasi
biaya simpan dan biaya pesan.
2.7
Optimasi Persediaan dengan Metode Power Approximation
Pada sistem
persediaan di mana permintaan tidak dapat dipenuhi maka akan
terjadi distribusi permintaan dan tenggang waktu (lead time) antara tempat pemesanan ke
tempat
tujuan.
Pada
umumnya
distribusi
permintaan dan
tenggang
waktu
bersifat acak
(random),
oleh
karena
itu
metode klasik EOQ tidak
akan efisien untuk
menyelesaikan
masalah seperti itu. Oleh karena itu diperlukan suatu metode yang dapat digunakan untuk
mengatasi hal tersebut. Metode PA yang dikembangkan oleh Ehrhardt dan Mosier
|
 18
?
digunakan untuk mengatasi masalah distribusi permintaan dan tenggang waktu yang
bersifat acak (random).
2.7.1
Metodologi Power Approximation
Robert memperbaharui teori EOQ untuk menandai batasan dari kebijakan optimal
K dan p yang bernilai besar. Robert mengikuti kebijakan parameter optimal s* dan D =
S*-s*, di mana D* meningkat sangat besar.
D* =
2Kµ
h
+
o
(
D
*
),
EOQ
(1)
8
?
(
x
-
s*
)
d
f
(
x;L+1
)
=
D*
+o
(
D*
)
,
?
p
?
s*
?
1+
?
?
h
?
(2)
Di mana ?(.;n) adalah fungsi distribusi kumulatif dari penyimpangan permintaan sebesar
kelipatan n. Karena D* sama dengan tak terhingga maka o(D*)/D* konvergen terhadap
nol. Ketika distibusi permintaan dibakukan, akan diperoleh ?(.) sebagai fungsi distribusi
standar, yaitu:
F
(x; L + 1
)
=
?
{[x - (
L
+
1
)µ
]/s
[s
L
+
1
]},
Sehingga persamaan (2) menjadi:
8
F u
(u
) =
?
(
x
-
u d
)d
?
(
x) =
u
D
*
?
?
p
?
?
?
1
+
?
s
?
?
h
?
L
+
1
?
?
+
o(D*),
(3)
Di mana u =
[
s
*
-
(
L
+
1
)µ
]
s
L
+
1
Dari persamaan (1) dan (3) diperoleh persamaan perkiraan yang optimal.
D
=
2K
µ
,
h
(4)
|
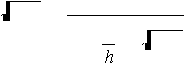 19
?
?
1+
?
S
= L +1
(
)
µ
+
s
?
?
L
+1 G
?
?
?
?
?
?
?
?
D
p
?
?
?
?
s
?
?
?
?
?
?
,
L
+1
?
?
?
(5)
Di
mana
G(x) = F
-1
(x) dan S
merupakan
jumlah persediaan
yang sedang dipesan,
sedangkan s merupakan jumlah persediaan yang ada ditambah dengan jumlah yang
sedang dipesan.
Kesulitan perhitungan terletak
pada perhitungan fungsi G(.). Salah satu cara untuk
menghitungnya adalah dengan mengasumsikan bahwa permintaan berdistribusi normal.
Dengan
demikian,
fungsi
G(.)
dapat
dihitung dengan mengunakan metode iterasi
atau
fungsi perkiraan rasional. Dalam hal ini pendekatan yang dilakukan adalah mengunakan
analisis
numerik,
untuk
menyesuaikan
sederetan power terhadap
fungsi
G(.),
dengan
menggunakan kebijakan optimal sebagai data. Selajutnya digunakan regresi untuk
melakukan penyesuaian parameter yang terdapat pada persamaan (4) dan persamaan (5).
Sebelum membahas
lebih
lanjut
mengenai
model
regresi,
akan
disajikan data-data
yang
akan
digunakan
seperti
yang
ada
didalam tabel
inventory
di
bawah
ini.
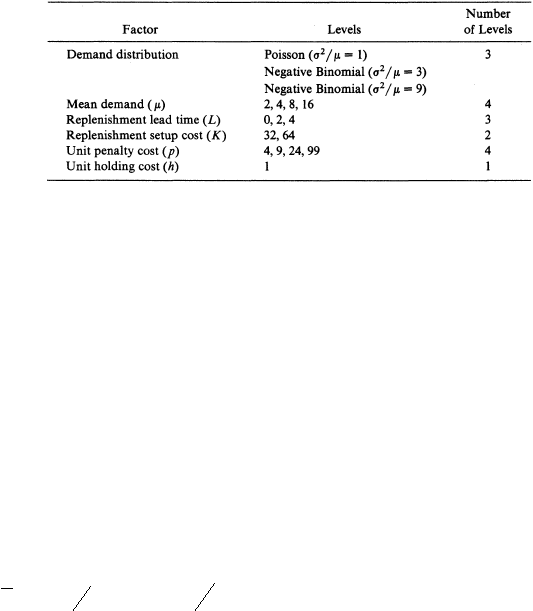
Tabel
inventory yang terdiri dari 288 item, digunakan agar menghasilkan data untuk dianalisis.
Tabel 1 berisi daftar pengaturan parameter. Ada beberapa jenis distribusi permintaan
yang digunakan: Poisson dan negative binomial dengan variance-to-mean ratio dari 3
dan 9. Dari tiap-tiap distribusi permintaan diberikan empat nilai rata-rata: 2, 4, 8, dan 16
dan
tiga
nilai
yang
berikan
pada
lead time: 0, 2, dan 4. Selama
fungsi
biaya
linier
terhadap
parameter
K,
p
dan h,
maka nilai
dari
biaya penyimpanan
berupa parameter
berulang, diatur agar tetap menjadi kesatuan. Biaya penalty
adalah 4, 9, 24 dan 99 dan
biaya pemesanan adalah 32 dan 64. Biaya pengisian
ulang (c) tidak ditetapkan karena
|
 20
h
h
e
tidak akan mempengaruhi perhitungan optimal.
Berikut
ini adalah kombinasi dari
parameter yang tercakup dalam tabel 288 item persediaan.
Tabel 1.1 Sistem Parameter
Dengan
menggunakan
algoritma
Veinot
dan
Wagner,
diperoleh
hasil
perhitungan
yang optimal dari 288 item barang. Hasil perhitungan nilai s dan S, merupakan data yang
akan dipergunakan untuk penyesuaian regresi. Kebijakan optimal memiliki nilai harapan
berkisar atara 4 sampai 82, akhir periode yang tertunda berkisar dari 0.006 sampai 0.9,
frekuensi yang tertunda berkisar antara 0.0009 dan 0.19 dan frekuensi pemesanan
berkisar 0.08 sampai 0.39.
2.7.2
Perkiraan untuk Nilai D
*
Hal
yang pertama
yang
dilakukan
adalah
membuat
regresi
model
untuk D*.
Nilai
optimal D = S-s. Dengan mengeneralisasi persamaan (4) ke bentuk multiplikatif.
D = C
µ
a
(
K
)
ß
(L
+
1)
?
(s )
d
?
?
p
?
?
?
?
(6)
Adapun
C, a, ß, ?, d, dan e adalah konstanta. Variabel µ dan K/h pada persamaan (6)
sama dengan Variabel µ dan K/h pada persamaan (4), sedangkan variabel lainnya tidak
muncul pada persamaan (4). Variabel-variabel yang ada pada persamaan (6) merupakan
|
|
21
faktor multiplikatif sederhana. Kemudian, (L+1) digunakan untuk menggantikan L
karena
inilah
cara
untuk
menunjukkan
tenggang
waktu
dalam bentuk
analitik
untuk
memperoleh biaya yang diharapkan.
Dengan
mengambil
model linier dari persamaan (6) dan menggunakan regresi least-
square
untuk
memperoleh
hasil
yang
sesuai dengan D*.
Kemudian, diuji
hasilnya
dan
dipilih bentuk
yang
sesuai. Variabel p/h dihilangkan karena nilai dari e mendekati
nol.
Akhirnya diperoleh nilai optimal dari approximation D*.
?
K
?
0.498
D* = 1.463
µ
0.364
?
?
[(
L
+
1
)
s
2
]
0.0691
(7)
?
h
?
Eksponen K/h mirip dengan eksponen pada persamaan Wilson Lot-size yakni 0.5,
konstanta
1.463
juga
mirip
dengan
konstanta
pada
Wilson Lot-size
yakni 1.414, hanya
nilai dari
rata-rata permintaan yang tidak signifikan dengan persamaan Wilson Lot-size.
Selain itu, terdapat variabel yang baru yaitu: L dan varian.
2.7.3 Perkiraan untuk nilai S
*
Dengan menggunakan
persamaan (5), dibentuk
sebuah
model
regresi
untuk
memperoleh
perkiraan perhitungan
reorder point s
*
yang
optimal.
Kemudian
dilakukan
perhitungan nilai s dari setiap 228 item dengan meminimumkan ekspektasi biaya total per
periode dan persamaan
(7) digunakan
untuk
mengatur
(S-s), akan menghasilkan suatu
data
baru
untuk
analisis.
Nilai
baru
ini
dinamakan
s
p
*
. Pendekatan
ini
menggunakan
persamaan
(5)
yang
diperoleh
dari
turunan parsial
dari
ekspektasi
biaya
total
yang
mengacu pada nilai s yang diatur sehingga sama dengan nol.
Persamaan (5) merupakan approximation nilai terbaik dari s pada saat menggunakan nilai
tertentu dari D. Langkah-langkah optimalisasinya adalah sebagai berikut.
|
 22
?
p
p
p
p
?
D
p
y
=
,
?
?
p
?
?
?
?
1
+
h
?
s
L
+
1
?
?
?
?
?
Di mana D
p
diperoleh dari persamaan (7).Untuk setiap 288 item yang dihitung dari nilai y
dan untuk:
u
*
=
[s
*
-
(L + 1)
µ
]
s
L
+
1
Dicari kecocokan dengan persamaan (5) dengan mengunakan model
u
*
=
G(
y)
+
e
,
Di mana e adalah suatu error. Berikut ini adalah suatu fungsi yang mewakili fungsi G(.)
m
G
n,m
(
y
)
=
?
Ai
(n, m)
y
i
/
2
,
i
=
n
Di mana A
i
(n,m) adalah koefisien yang dihasilkan dari regresi n dan m; Dengan menguji
24 model
yg dilakukan dalam
rentang
n
=
0, -1,
-2
dan
m
=
1, 2,
…,
8.
Hasil
yang
diperoleh dari n = 1 dan m = 1 adalah:
u
*
=
A
1
+
A
2
y
+
A
3
y
+
e
Cara
termudah
untuk
menghasilkan korelasi dengan
data
adalah
mensubstitusi
G
-1,1
(.)
terhadap G(.) ke persamaan (5) untuk memperoleh perkiraan yang optimal.
s =
(
L
+
1
)
µ
+
s
?
L
+
1
?
?
?
A
1
?
+ A
2
+ A
3
y
y
?
(8)
Dengan menggunakan persamaan (8) ditetapkan suatu urutan analis regresi . hal pertama
yang dilakukan adalah melakukan regresi terhadap konstanta A1, A2
,
dan A3; kemudian
|
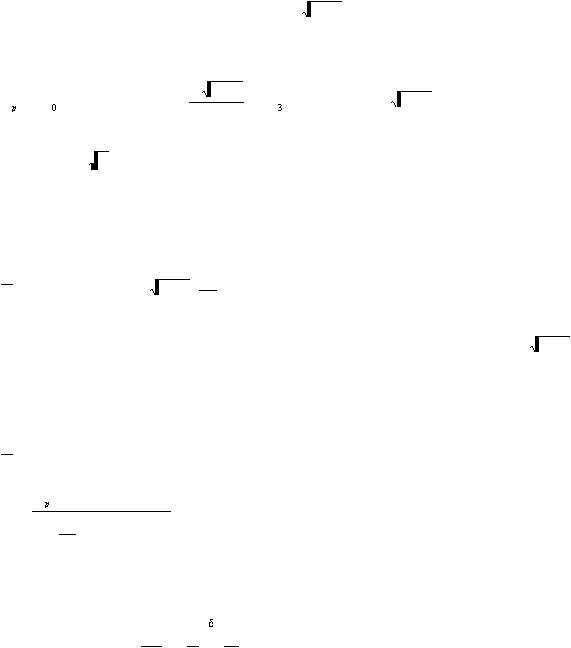 23
?
1
?
3
4
?
1
?
s
e
dilakukan pernyesuaian terhadap pengali
s
L
+
1
dan yang terakhir, kita sesuaikan
kembali terhadap konstanta A1, A2
, dan A3; Model regresi yang dihasilkan adalah:
s
*
=
C
+
C
1
[(
L
+
1
)
µ
]
+
C
2
?
L
+
1
?
+
C
[(
L
+
1
)
s
]
+
C
4
[s
L
+
1
Z
]+ e
,
(9)
?
z
?
Di mana
z
=
y
dan e adalah suatu error. Misalkan a
0
,a1
,…,a
4
merupakan nilai dari C
0
,
C1,…,C
4
, maka regresi least-square yang disubstitusi dari persamaan (9) akan
menghasilkan bentuk nilai optimal s.
s
=
a
0
+
a
1
(L
+
1
)
µ
+
s
L
+
?
a
2
+
a
+
a
z
?
(10)
?
z
?
Pengujian secara detil dari setiap data akan terbukti dengan penyesuaian faktor s
L
+
1
.
Penyesuaian ini dilakukan dengan cara, mengantikan faktor dengan variabel f dan
penyelesaian dengan persamaan (10) untuk nilai yang dari f akan menghasilkan
s1
= s
p
*
.
[
s
*
-
a
f
=
0
?
a
2
-
a
(
L
+
1
)
µ
]
?
?
+ a
3
+
a
4
z
?
?
z
?
Kemudian dicari bentuk perkiraan dari fungsi f:
?
s
2
f
=
?
C
(L +1)
a
µ
ß
?
?
?
?
p
?
?
?
?
?
K
?
?
?
,
?
µ
?
?
h
?
?
h
?
Di mana ? adalah suatu error, dan C, a, ß, ?, d, dan e adalah konstanta. Notasi-notasi ini
dikonversikan ke model linear dengan mengambil logaritmanya dan regresi least-square
digunakan untuk mengatur konstanta-konstantanya.
Setelah
menghilangkan
variabel-
variabel yang tidak signifikan dan melakukan pengelompokkan terhadap data yang mirip,
maka akan diperoleh.
|
 24
µ
f a
[
(L
+
1
)
µ
]
0.416
?
?s
2
?
0.603
?
?
=
q
?
persamaan (9) dapat diubah menjadi:
*
?
q
?
s
p
=
C
0
+
C
1
[
(
L
+
1
)
µ
]
+
C
2
?
?
+
C
3
[
q
]
+
C
4
[
qz
]
+
e
.
(11)
?
z
?
Dengan
menggunakan regresi least-square untuk
melakukan penyesuaian data dan
menghilangkan penyimpangan yang terjadi serta hal-hal yang tidak siqnifikan. Akhirnya
kita melakukan penyesuaian ulang untuk menentukan Power Approximation s
0.416
?
s
2
0.603
?
?
0.220
?
s
p
=
(
L
+
1
)
µ
+
[(
L
+
1
)
µ
]
?
?
?
µ
?
?
?
z
+
1.142
-
2.866z
?
?
(12)
2.7.4
Power Approximation
Dari
persamaan
(7)
dan
(12)
akan
dihasilkan
approximation
(s
p
,S
p
) untuk
kebijakan (s,S) yang optimal. Berdasarkan teori yang menganggap bahwa nilai parameter
K
dan p adalah besar,
maka Wagner, O’Hogan dan
Lundh telah
meneliti
teori Wilson
yang diubah oleh Robert, ternyata teori tersebut sangat baik diterapkan pada
approximation
D*, dimana
K/h bernilai besar dan relatif
terhadap µ, tetapi untuk K/h
bernilai kecil tidak
mendekati nol. Oleh karena
itu, perubahan teori empiris Robert juga
dapat digunakan untuk mendapatkan Power Approximation yang baik.
Ketika D
p
/µ bernilai cukup kecil (kecil dari 1.5), S
p
dibandingkan dengan angka
kritis tunggal akan menghasilkan nilai yang optimal jika K sama dengan nol. Dua angka
terkecil digunakan
pada
kebijakan
S, sehingga memperpendek jarak yang memisahkan
antara S dan s. Angka kritis tunggal akan optimal jika permintaan berdistribusi normal
dan K sama dengan nol, sehingga S
0
S
0
=
(
L
+
1
)
µ
+
?s
L
+
1
Dimana ? adalah solusi untuk:
|
 25
)
?
? ?
?
?1 +
?
0.187
µ
0.187
µ
(
p
2
-8
?
?
?
exp
-
x
2
2
?
dx
=
(
p
+
h
)
Dengan mengasumsikan
µ
L
=
(
L
+
1)
µ
dan
s
L
=
s
L
+
1
,
maka Power Approximation
didefiniskan.
D
1.463
µ
0.364
?
K
?
0.498
+
s
0.138
=
?
?
(14)
p
?
h
?
L
?
z
=
?
D
p
0.5
?
?
?
?
(15)
?
?
?
?
p
?
?
?
s
L
?
h
?
?
?
0.832
?
s
2
?
?
0.220
?
S
p
=
µ
L
+
s
L
?
?
?
?
?
?
z
+
1.142 - 2.866 z
?
?
(16)
2.7.5
Revisi Metode Power Approximation
Pada penulisan diatas, power approximation merupakan suatu perkiraan kebijakan
(s,S) yang optimal . tetapi terdapat dua kekurangan yaitu, mengenai prilaku ketika suatu
unit dipilih untuk mengukur permintaan yang bervariasi dan pada saat varian permintaan
bernilai
sangat
kecil.
sehingga
metode
ini perlu direvisi
untuk
mengatasi
kekurangan
yang terjadi.
Dengan
mengasumsikan bahwa kebijakan (s,S) optimal, dan
persediaan y kecil
atau
sama
dengan
s
dan pesanan sejumlah
S-y
ditempatkan. Power approximation
merupakan
algoritma
perhitungan
sederhana
untuk
memperkirakan
nilai
yang
optimal
dari kebijakan (s,S). Algoritma ini hanya membutuhkan informasi dari rata-rata
permintaan dan varian permintaan.
Adapun persamaan yang diperoleh dari pengujian diatas adalah sebagai berikut.
D
1.463
µ
0.364
?
K
?
0.498
+
s
0.138
=
?
?
(1)
p
?
h
?
L
0.832
?
s
2
?
?
0.220
?
S
p
=
µ
L
+
s
L
?
?
?
?
?
?
z
+
1.142 - 2.866 z
?
?
(2)
|
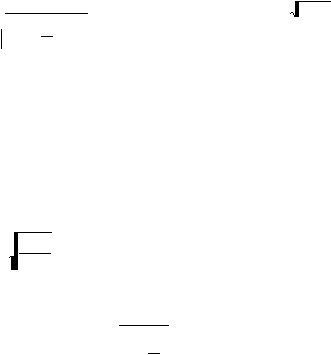 26
?
? ?
?
?1 +
?
?
?
?
z
=
?
D
p
0.5
?
?
?
?
,
µ
L
=
(
L
+
1)
µ
dan
s
L
=
s
L
+
1
.
(3)
?
?
?
?
p
?
?
?
s
L
?
h
?
?
?
Pada umumnya dalam Power approximation diatur s = s
p
dan
S = s
p
+D
p
.
Persamaan
(1),(2),
dan
(3)
diperoleh
dengan
menyesuaikan dengan persamaan
yang dikembangkan oleh Robert. Beliau telah
membuktikan bahwa kebijakan parameter
optimal s* dan D = S*-s* adalah sebagai berikut.
D*
=
2K
µ
h
+
o
(
D
*
),
EOQ
(4)
8
?
(x
-
s*
)df(
x;L
+
1
)
=
D*
+
o
(D*),
?
p
?
s*
?1
+
?
?
h
?
(5)
Ada pun ?(.;n) adalah fungsi distribusi kumulatif dari penyimpangan permintaan sebesar
kelipatan n. Karena D* sama dengan tak terhingga
maka o(D*)/D* konvergen terhadap
nol.
Persamaan
(4)
dan
(5)
digunakan
untuk
mendapatkan model
regresi
yang
telah
disesuaikan dengan
tabel
inventory
persediaan
288
item.
Oleh
karena
itu
persamaan
(1),(2), dan (3) merupakan hasil numerik dari penurunan dari persamaan (4) dan (5).
2.7.6 Alasan dan Metode yang Dipakai untuk Revisi
Seperti
alasan
yang
dikemukan
diatas,
bahwa
terdapat
dua
kekurangan pada
rumusan
sebelumnya yaitu,
mengenai prilaku ketika suatu
unit
dipilih
untuk
mengukur
permintaan yang
bervariasi
dan
pada
saat
varian
permintaan bernilai
sangat
kecil,
khususnya jika nilai K sangat besar. Permasalahan yang timbul dari persamaan (1) diatas
adalah, nilai D
p
akan
lenyap karena s²
mendekati
nol. Keakuratan dari persamaan (1)
|
 27
(
)
ß
?
1
+
s
L
µ
L
z
?
?
h
p
?
2
2
?
tidak
akan
begitu
berdampak kecuali
varian
permintaan bernilai sangat
kecil
karena
eksponen pada persamaan (1) hanya
0.069.
Tetapi,
persamaan (1)
harus
berlaku dalam
keadaan
apa
pun
karena
berdampak
pada
nilai
varian
permintaan. Bagaimanapun
juga
perubahan
kecil
yang
terjadi
kadang-kadang
dapat
menimpulkan dampak
di
dalam
statistika. Seperti halnya dalam pengaturan perkiraan batas bawah varian pada persamaan
(1)
dapat
mempengaruhi
nilai
D
p.
penyesuaian
prilaku
batas
bawah
varian diperoleh
dengan membentuk model regresi seperti dibawah ini.
?
D
=
a
µ
a
K
?
?
h
?
?
,
(6)
Di mana a,a,ß, dan ?
merupakan konstanta yang dipakai untuk
memperoleh data yang
optimal.
Kekurangan dari perumusan sebelumnya muncul ketika unit permintaan berubah.
Jika unit permintaan berubah karena disebabkan oleh suatu faktor (misalkan f), kemudian
s
p
dan D
p
harus diubah
dengan
cara yang
sama.
Oleh
karena
itu, jika
µ
'
=
f
µ
dan
s
'
=
f
s
, kemudian D
'
=
fD dan
s'
=
fs .
Perbaikan dilakukan dengan menahan regresi untuk D dan s. Pada persamaan(6),
dengan sederhana dibentuk a=1-ß. Kemudian, jika µ = fµ dan s = fs,
maka K=K dan
h=h/f, dengan
memastikan bahwa D=fD. Regresi
untuk s sangat
mudah diubah, dengan
mengunakan model
s
p
=
a
0
µ
L
+
s
?
a
1
+
a
?
+
a
3
?,
(7)
?
z
?
?
?
D
p
z
=
?
?
s
p
0.5
?
?
?
?
,
(8)
?
?
L
?
?
?
?
?
|
 28
dimana:
D
p
µ
= Jumlah pesanan per tahun
= rata-rata permintaan per tahun
P
= biaya penalty
K
= biaya pemesanan barang
h
= biaya simpan per unit barang per tahun
s
L
z
= varian permintaan selama tenggang waktu (lead time)
= varian dari rata-rata
µ
L
= rata-rata permintaan selama tenggang waktu (lead time)
(
p
L
L
?
?
L
D
p
ditentukan oleh persamaan (6) untuk memperoleh kebijakan data yang optimal.
Karena z tidak berdimensi, s
p
bersifat homogen pada unit permintaan.
Dengan menggunakan persamaan (6) dan (7) berdasarkan tabel 1 diatas. Maka persamaan
di bawah ini digunakan untuk mengantikan persamaan (1),(2), dan (3) untuk
menghasilkan data yang akurat.
D
=
1.30
µ
0.494
K
p
h
)
0.506
(
1
+
s
2
µ
2
)
0.116
,
?
z
=
?
D
p
?
s
L
P
?
?
?
?
?
h
?
?
0.5
,
S
=
0.973
µ
+
s
?
0.183
+
1.063 -
2.192 z
?
?
z
?
|
|
29
Contoh:
Diketahui bahwa jumlah permintaan untuk barang AC mobil (Ferrule ½) per tahun
adalah 100 unit, biaya pemesanan Rp.30.000,-
dan biaya simpan Rp.5000,-. Apabila
permintaan tidak
dapat terpenuhi, maka akan ada biaya ekstra yang harus dikeluarkan
(penalty
cost)
sebesar
Rp.
15.000,-.
Hitunglah
frekuensi
pemesanan pembelian
selama
satu tahun (350
hari kerja) dan kapan
melakukan pemesanan kembali
jika
lead time 14
hari dan simpangan baku sebesar 0.5 %.
Jawab :
Menggunakan metode power approximation
K = 30.000
h = 5.000
P = 15.000
µ= 100 unit
L1=14 hari
L = 14/350 (per tahun)
L = 0.04
s
= (0.005)(100)
s
= 0.5
s
2
L
= (L+1)s²
s
2
L
= (0.04+1)(0.5)
2
s
2
L
= 0.26
|
 30
(
?
?
?
?
L
µ
L
= (L+1) µ
µ
L
= (0.04+1) (100)
µ
L
= 104
D = 1.30µ
0.494
K
p
h
)
0.506
(1 + s
2
µ
2
)
0.116
D
=
1.30
(100
)
0.494
(
30000
5000
)
0.506
(
1
+
3.75 100
2
)
0.116
D
p
=
31.3
Maka banyaknya barang
yang
harus dipesan (Q) adalah sebanyak 31
untuk setiap kali
pemesanan.
Untuk banyaknya frekuensi pemesanan (F) adalah sebagai berikut.
S
p
F
=
D
p
?
0.183
?
S
p
=
0.973
µ
L
+
s
L
?
?
?
+
1.063
-
2.192z
?
z
?
0.5
?
z
=
?
?
?
31
0.26 15000)
(15000)
?
?
5000
?
z
=
4.5
S
p
=
0.973(104) +
0.26
?
0.183
+
1.063 - 2.192(4.5)
?
S
p
=
96.7
F
=
96.7
31.3
?
4.5
?
F
=
3.1
Reorderpoint (B)
B
=
(SpxL
1
)
350
|
 31
B
=
(96.7
x14)
350
B
=
3.87
Maka reorderpointnya adalah 4. Jadi sebelum jumlah persediaan tinggal 4 buah, maka
barang sudah harus dipesan.
Metode EOQ
D
=
2Kµ
h
2
(30000)(100)
D
=
5000
D
=
34.6
Untuk banyaknya frekuensi pemesanan (F) adalah sebagai berikut
F
=
µ
D
F
=
100
34.6
F
=
2.89
Reorderpoint (B)
(
µ
)(L)
B
=
350
(100)(14)
B
=
350
B
=
4
|