|
BAB 2
LANDASAN TEORI
2.1
Demografi
2.1.1
Pengertian Demografi
Demografi berasal
dari
bahasa
Yunani
yang
berarti:
“Demos”
adalah
rakyat atau
penduduk
dan
“Grafein”
adalah
menulis.
Maka
demografi
adalah
tulisan-tulisan atau
karangan-karangan mengenai
rakyat
atau
penduduk. Istilah
ini
dipakai
untuk
pertama
kalinya
oleh
Achille
Guillard
dalam
karangannya yang
berjudul
“Elements
de
Statistique
Humaine on Demographic Compares” pada tahun 1885.
Donald J.Bogue (1973) dalam bukunya yang berjudul “Principles
of Demography” memberikan definisi demografi sebagai berikut:
“Demografi
adalah
ilmu
yang
mempelajari secara
statistik
dan
matematik tentang
besar,
komposisi
dan
distribusi
penduduk
dan
perubahan-perubahannya sepanjang
masa
melalui
bekerjanya
lima
komponen
demografi, yaitu
kelahiran
(fertilitas),
kematian
(mortalitas), perkawinan,
migrasi, dan mobilitas sosial.”
Jadi
dapat
disimpulkan bahwa
demografi
adalah
suatu
pembelajaran atas
dinamika
populasi
manusia.
Analisis
demografis
dilakukan
untuk
mengestimasi nilai-nilai
dari
parameter dasar
di
bidang
demografi seperti angka fertilitas (kelahiran) dan angka mortalitas
|
|
(kematian)
yang digunakan
untuk mengindikasikan cara suatu populasi
akan berkembang
menurut ukuran dan struktur usia, selama sepanjang
masa, berdasarkan
hasil
pengumpulan
data baik melalui
sensus
maupun
sistem registrasi vital.
2.1.2
Mortalitas
Mortalitas atau
kematian
merupakan salah
satu
di
antara
tiga
komponen demografi yang dapat mempengaruhi perubahan penduduk. Dua
komponen lainnya adalah fertilitas dan migrasi. Alasan pengadaan asuransi
jiwa
terutama disebabkan oleh
kerugian
yang
diakibatkan oleh
kematian,
dengan fakta bahwa sangat sulit
untuk memprediksi kapan seseorang akan
meninggal bahkan dengan kesehatan yang baik.
Meskipun
kita
tidak
dapat
memastikan kapan
seseorang
akan
meninggal tetapi kita tahu bahwa cepat atau lambat setiap orang pasti akan
meninggal.
Jika
kita
menggunakan asumsi
bahwa
kondisi
yang
menyebabkan terjadinya kematian
di
waktu
yang akan
datang
tidak
akan
berbeda secara
radikal dengan kondisi pada beberapa waktu
yang lampau
hingga
saat
sekarang, maka
kita
dapat
membuat
prediksi
secara
umum
berkenaan dengan
kematian
yang
akan
datang.
Kita
dapat
memprediksi
sebagai contoh, beberapa orang
yang terpilih secara acak dari sekelompok
besar orang, dapat diperkirakan akan meninggal dalam suatu periode waktu
tertentu, meskipun kita tidak dapat mengatakan secara pasti mana individu
yang akan meninggal pada waktu tersebut.
|
 Angka
kematian atau
death
rate
adalah
suatu
nilai probabilitas
bahwa seseorang yang telah mencapai
usia tertentu akan meninggal dalam
waktu
satu
tahun.
Tinggi
rendahnya angka
kematian
dipengaruhi oleh
berbagai faktor,
misalnya struktur
umur,
jenis
kelamin, jenis
pekerjaan,
status
sosial
ekonomi,
keadaan
lingkungan dan sebagainya (Dasar-Dasar
Demografi, 2004,
p8).
Beberapa
ukuran angka
kematian
yang
sederhana
antara lain:
a. Angka Kematian Kasar (Crude Death Rate)
Angka ini
menunjukkan jumlah orang
yang
meninggal per 1000
penduduk. Secara konvensional dinyatakan dengan rumus:
CDR =
D
·
k
P
dimana:
D
=
Jumlah kematian pada tahun X
P
=
Jumlah penduduk pada pertengahan tahun X
k
=
1000
b.
Angka Kematian Menurut Umur (Age Specific Death Rate)
Angka
ini
menyatakan banyaknya
kematian
pada
kelompok
umur
tertentu (biasanya 0, 1-4, 5-9, 10-14, 15-19, dan seterusnya) per
1000
penduduk dalam kelompok
umur
yang
sama,
sehingga dalam bentuk
rumus dapat dinyatakan dengan:
ASDR
i
=
D
i
·
k
P
i
dimana:
D
i
=
Jumlah kematian dari penduduk kelompok umur i
|
 pada tahun X
P
i
=
Jumlah penduduk kelompok umur i pada pertengahan
tahun X
k
=
1000
c. Angka Kematian Bayi (Infant Mortality Rate)
Angka ini menunjukkan banyaknya kematian pada bayi di bawah usia 1
tahun per 1000 kelahiran. Angka kematian bayi dapat dirumuskan
sebagai berikut:
IMR =
D
0
·
k
B
dimana:
D
0
=
Jumlah kematian bayi di bawah usia 1 tahun selama
tahun X
P
i
=
Jumlah kelahiran hidup selama tahun X
k
=
1000
Berkaitan
dengan
hal
ini,
lahir
mati
(fetal
death)
tidak
dimasukkan
dalam level lahir maupun mati.
2.2
Life Table
2.2.1
Pengertian Life Table
Life table yang sering disebut juga dengan mortality table adalah
sebuah
alat
analisa
mortalitas
yang
sering
digunakan dan
hasilnya
memuaskan para ahli demografi. Sebuah life table
dikonstruksikan secara
matematis
untuk
memberikan
deskripsi
secara
lengkap
mengenai angka
|
|
kematian
dan
harapan
hidup
serta
menunjukkan pola
mortalitas
dari
sekumpulan orang
yang
dilahirkan
pada
waktu
yang
sama
(cohort)
berdasarkan usia yang telah dicapainya. Dalam perindustrian asuransi jiwa,
para
ahli aktuaria
berfokus
pada analisa
mortalitas
serta
penyusunan life
table
untuk
diaplikasikan pada
perhitungan
premi
serta
resiko
guna
memperoleh keuntungan sebanyak mungkin bagi perusahaan. (Daykin,
1995, p8).
Life
table
merupakan sebuah
matriks
persegi
panjang,
yang
menunjukkan perubahan masing-masing fungsi di dalamnya melalui kolom,
berdasarkan
usia
yang
ditunjukkan
melalui
baris. Pada
dasarnya,
terdapat
dua jenis life table yang berbeda menurut panjang interval
yang digunakan
untuk
menampilkan
umur.
Complete
life
table
disusun
berdasarkan
umur
dengan
interval
satu
tahun.
Sedangkan abridged
life
table
disusun
berdasarkan umur
dengan
interval
yang
lebih
panjang,
biasanya
berupa
kelompok usia 0 tahun (baru lahir), 1-4 tahun, 5-9 tahun, 10-14 tahun, 20-
24 tahun, dan seterusnya.
Pada umumnya
komponen
atau fungsi-fungsi
standar
yang
terdapat dalam suatu life table adalah sebagai berikut:
a. Umur tepat (Exact Age) = x
Komponen
ini menunjukkan
bahwa anggota
cohort yang dimaksud
telah
menjalani
hidup
selama
tepat
x
tahun
atau
pada
saat
tersebut
berada pada ulang tahunnya ke-x.
b.
Interval umur (Age interval) = n
|
 n
x
Nilai
ini
merupakan selisih
antara
nilai
umur
x
dengan
umur
x
berikutnya. Pada
abridged
life
table kelompok
umur
disusun dengan
menggunakan interval tertentu, yaitu
interval 1 tahun
untuk
umur 0-<1
tahun, kemudian interval 4 tahun untuk umur 1-4 tahun, dan selanjutnya
menggunakan interval 5 tahun untuk umur 5-9 tahun, 10-14 tahun, dan
seterusnya sampai pada ? yaitu
umur
tertinggi
yang
membatasi umur
pada life table. Kelompok umur pertama dan kedua tidak menggunakan
interval
5
tahun
dikarenakan khusus dan
pentingnya angka
kematian
bayi (Epidemiological Bulletin, p3).
c. Probabilitas kematian antara umur tepat x tahun dan x+n tahun
(Probability of death between age x and age x+n) =
n
q
x
Nilai
probabilitas ini
dihitung
berdasarkan angka
kematian
pada
kelompok
umur tertentu, sehingga dirumuskan sebagai berikut di
bawah ini.
q
=
n
·
n
M
x
n
x
1
+
n(1
-
a
)
n
M
x
n
a
x
merupakan
angka
rata-rata
tahun
yang
dijalani
hidup
oleh
orang
yang
berumur
x
yang
meninggal
pada
umur antara
x
dan x+n.
Meski
tidak dicantumkan dalam life table tetapi nilai ini sangat penting dalam
perhitungan.
Nilai
n
a
x
diperoleh
melalui
fraksi dari
interval
terakhir
kelompok umur, biasanya digunakan
n
n
a
x
=
, sehingga nilai
n
a
x
2
untuk kematian pada kelompok
umur dengan
interval 5
tahun =
2,5.
|
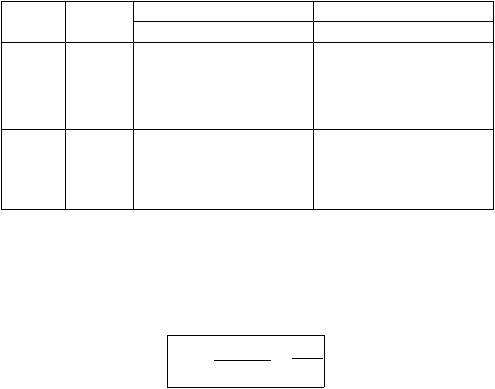 Namun
untuk
kelompok umur
0
dan
1-4
tahun
digunakan nilai
n
a
x
berdasarkan IMR (Infant Mortality Rate) disesuaikan dengan zone
life
table
seperti
yang
disajikan pada
Tabel
2.1
di
bawah
ini.
Perlu
diperhatikan bahwa Indonesia mempunyai angka IMR dibawah 0,1.
Tabel 2.1
Tabel Nilai Faktor Pemisah Untuk Usia 0 dan 1-4
IMR
Zones
Age 0
Age 1 - 4
Men
Women
Both
Men
Women
Both
>
0.1
North
East
South
West
0.33
0.35
0.35
0.29
0.31
0.31
0.33
0.35
0.35
0.33
0.35
0.35
1.558
1.570
1.570
1.313
1.324
1.324
1.240
1.239
1.239
1.352
1.361
1.361
<
0.1
North
East
South
West
0.0425
0.05
0.05
0.0025
0.01
0.01
0.0425
0.05
0.05
0.0425
0.05
0.05
1.859
1.733
1.733
1.614
1.487
1.487
1.541
1.402
1.402
1.653
1.524
1.524
Sumber: Life Tables: A Technique to Summarize Mortality and Survival, 2000
Jika nilai l
x
dan l
x+n
terlebih dahulu diketahui, maka dapat digunakan
rumus di bawah ini:
n
q
x
=
l
x
-
l
x
+
n
l
x
=
n
d
x
l
x
Jika kelompok umur terakhir pada life table
menggunakan interval tak
terhingga maka probabilitas kematian
8
q
?
=
1.
d.
Jumlah orang yang berhasil mencapai umur tepat x tahun
(Numbers of survival from birth to exact age x) =
l
x
Nilai
ini digunakan
untuk
memperkirakan proporsi dari
individu
yang
bertahan
hidup
hingga
umur
awal
dari
kelompok umurnya. Seiring
bertambahnya umur maka jumlah orang yang bertahan hidup pun
|
 berkurang. Secara umum nilai ekspektasi jumlah orang yang hidup pada
umur x dirumuskan sebagai berikut:
l
x
+
n
=
l
x
(¹
-
n
q
x
)
Dimulai dari
l
0
disebut sebagai radiks life table, yaitu merupakan
jumlah
orang
pada
saat
tepat
lahir
yang
akan
diikuti
sampai
semua
orang tersebut meninggal. Nilainya ditentukan secara sembarang karena
besar
kecilnya tidak
akan
mempengaruhi interpretasi
tabel
kematian,
biasanya ditentukan 100.000 atau 1.000.000. Tentunya life table dapat
dimulai dari umur berapapun (a) sehingga radiks dituliskan dengan
l
a
.
e. Jumlah kematian antara umur tepat x tahun dan x+n tahun
(Number of deaths between age x and age x+n) =
n
d
x
Angka ini menunjukkan banyaknya kematian dari
l
x
yang terjadi antara
umur x hingga umur x+n tahun. Angka ini biasanya hanya digunakan
dalam perhitungan dan tidak selalu ditampilkan pada life table.
n
d
x
=
l
x
-
l
x
+
n
n
d
x
=
l
x
·
n
q
x
f.
Angka kematian antara umur tepat x tahun dan x+n tahun
(Central death rate between age x and age x+n) =
n
M
x
Nilai
ini disebut
juga age specific
(central) death rate,
menunjukkan
rata-rata kematian pada kelompok umur x tahun dan x+n tahun, atau
|
 L
banyaknya
kematian per
jumlah
“tahun orang”
hidup
antara
umur
x
tahun dan x+n tahun, sehingga dirumuskan seperti di bawah ini.
M
=
n
d
x
n
x
n
x
g.
Jumlah tahun orang hidup yang dijalani antara umur tepat x dan x+n
(Number of person-years lived between the exact age x and age x+n) =
n
L
x
Nilai
ini merupakan ekspektasi jumlah dalam
“tahun orang” (person-
years) dari l
x
orang yang berumur tepat x yang
menjalani hidup
hingga
umur x+n. Seorang anggota cohort yang
mengalami hidup
mulai dari
awal umur x hingga umur x+1 berarti menjalani dan mengkontribusikan
1
“tahun orang hidup” (person-years lived) pada nilai
n
L
x
.
Jika terdapat
dua orang
yang mengalami
hal tersebut
berarti
menjalani
2 “tahun
orang
hidup”.
Namun tidak semua
orang bisa
menjalani hidup
hingga
akhir
periode.
Jika
seseorang mengalami hidup
hanya
hingga
pertengahan periode tersebut, berarti menjalani 0,5 “tahun orang hidup”.
Besarnya
nilai
n
L
x
diperkirakan dengan
penduduk
pada
pertengahan
periode, sehingga perkiraannya dapat dilakukan dengan
menggunakan
rumus di bawah ini.
n
L
x
=
n
(l
x
+
l
x+
n
)
2
Karena kematian
bayi
lebih
banyak
terjadi
pada
saat
segera
setelah
kelahirannya, diasumsikan bahwa 70% diantara kematian bayi terjadi
|
 sebelum bayi berumur ½ tahun,
maka khusus untuk 1
L
0
diperkirakan
dengan menggunakan persamaan di bawah ini.
1
L
0
=
0,3
l
0
+
0,7
l
1
Jika nilai
n
L
x
diperkirakan dengan menggunakan nilai
n
a
x
dan
n
d
x
,
maka
dapat digunakan rumus di bawah ini.
n
L
x
=
n
·
l
x
+
n
+
n
a
x
·
n
d
x
h.
Jumlah tahun orang hidup setelah umur tepat x tahun
(Number of person-years lived after the exact age x) = T
x
T
x
adalah perkiraan jumlah
“tahun orang”
yang dijalani
hidup oleh l
x
orang sejak umur tepat x sampai semuanya meninggal.
8
T
x
=
?
n
L
x
n=1
i.
Angka harapan hidup pada saat umur tepat x tahun
(Life expectancy at exact age x) = e
x
Nilai ini menunjukkan angka perkiraan rata-rata tahun hidup yang
masih
akan
dijalani
oleh
anggota
cohort
setelah
ia
mencapai ulang
tahunnya
yang
ke-x.
Dengan
membagi jumlah
“tahun
orang”
yang
dijalani
hidup
oleh
l
x
orang
sejak
umur
x
hingga
meninggal dengan
dengan banyaknya orang pada umur x, maka dapat diperoleh perkiraan
angka harapan hidup. Secara umum dirumuskan dengan:
|
 x
8
?
n
L
x
T
e
=
n
=
1
=
x
l
x
l
x
Jadi perkiraan bahwa seseorang yang berumur x tahun akan meninggal
adalah pada umur x +
e
x
tahun. Angka harapan hidup dibedakan
menurut
jenis
kelamin
untuk
menunjukkan ikhtisar
secara
statistik
terhadap perbedaan mortalitas pria dan wanita untuk semua umur.
e
0
adalah
harapan
hidup saat
lahir atau
life expectancy at birth adalah
perkiraan rata-rata tahun yang akan dijalani oleh suatu cohort pada saat
dilahirkan.
2.2.2
Model Life Table
Para
ahli demografi pada
masa
awal
mencoba
untuk
melukiskan
dalam bentuk
matematika,
variasi
dari angka
kematian berdasarkan
usia,
terutama
peningkatan resiko
atas
kematian
setelah
masa
kanak-kanak.
Kesulitan dialami pada saat
mencoba untuk
menggambarkan karakteristik
resiko
kematian
selama
sepanjang
kehidupan
berdasarkan usia
sebagai
bentuk U atau J melalui satu fungsi matematika.
Karena kesulitan inilah
maka para ahli
melakukan pendekatan lain
dalam
membuat
model
mortalitas atau
model
life
table.
Pendekatan
dilakukan
dengan
mengkaitkan resiko
kematian
tidak
hanya berdasarkan
usia saja
melainkan mengkaitkan resiko pada
usia tertentu dengan resiko
|
|
yang diamati pada usia lanjut atau dengan resiko yang diamati pada
populasi lain dengan usia yang sama.
Menurut United
Nations
(1983,
p12),
hingga
saat
ini
telah
dikembangkan
sekurang-kurangnya empat
sistem
dari
model
life
table
untuk
menambah
pilihan
sistem
life table yang
mempermudah atas dasar
perhitungan dan
penentuan
tingkat
resiko
kematian
yang
dikalkulasikan
pada
populasi
yang
sebenarnya.
Sistem-sistem ini
berbeda-beda
disesuaikan dengan pengalaman para ahli
selama proses pembuatan sistem
model
life
table
tersebut, sehingga
model life
table
yang
satu
mungkin
lebih
sesuai digunakan daripada
model
life
table
yang
lain
untuk kasus
tertentu. Model-model life table yang telah dikembangkan, antara lain:
a. United Nations life tables
Model
life
table
yang pertama
dikembangkan oleh
Population
Division dari United Nations Secretariat pada era 1950-an, berdasarkan
pengamatan
atas
kumpulan158
life
table
untuk
masing-masing jenis
kelamin. Model
life table
ini menggunakan sistem
parameter
tunggal.
Dengan
mengetahui hanya
satu
parameter
mortalitas,
yaitu
1
q
0
atau
tingkat
index
yang ekuivalen
maka dapat
menyusun
sebuah
complete
life table.
Pada
model
life
table
ini
terdapat banyak
kelemahan.
Ditemukan banyak
kesalahan
pada
koefisien
regresi
yang
diestimasi
dikarenakan 158
life table yang
diobservasi
mempunyai kualitas
yang
berbeda. Pada tabel-tabel yang berasal dari negara-negara berkembang
|
|
ditemukan
banyak
kekurangan data
mortalitas
yang
seharusnya
tidak
boleh dimasukkan dalam kumpulan tabel
yang diobservasi. Selain
itu,
sistem
parameter tunggal
dinilai
tidak
cukup
memadai
melihat
banyaknya jenis
kasus
yang
ditemukan
pada
dunia
nyata.
Karena
kelemahan-kelemahan
tersebut
maka
kemudian
muncul
model-model
life table lainnya meskipun melalui pendekatan yang hampir sama.
b.
Coale and Demeny regional life tables
Model
regional
life
table
Coale
dan
Demeny pertama kali
dipublikasikan pada
tahun
1966,
berasal
dari
192
life
table
yang
terseleksi
untuk
masing-masing jenis
kelamin
pada
populasi
yang
sebenarnya. Life table Coale dan
Demeny
merupakan
model life
table
yang
paling
banyak
digunakan
dikarenakan dapat
merepresentasikan
berbagai pola
mortalitas
yang ada tanpa membutuhkan informasi
yang
terlalu
lengkap
mengenai
suatu
populasi.
Penjelasan lebih
lanjut
mengenai life
table
Coale dan Demeny
akan disajikan
pada
sub
bab
berikutnya.
c. Ledermann’s system life tables
Model
life
table
ini
dikembangkan
oleh Sully
Ledermann
dan
Jean
Breas
dengan
menggunakan analisis
faktor
untuk
mengidentifikasikan variabel-variabel
yang
terpenting
atau
faktor-
faktor yang menimbulkan variasi berdasarkan pengamatan atas 154 life
table. Database
yang
digunakan oleh
mereka
hampir
identik dengan
yang telah digunakan sebelumnya pada model life table United Nations.
|
|
Oleh karena itu, model life table ini memiliki kelebihan dan kekurangan
yang sama dengan
model
life table United Nations. Selain itu, sistem
Ledermann
sendiri
sulit
untuk
diaplikasikan pada
negara-negara
berkembang dikarenakan variabel
bebas
yang
digunakan
atau
angka
yang
akan
dimasukkan ke
dalam
tabel
tidak
dapat
dengan
segera
diestimasi menggunakan teknik tak langsung yang telah ada.
d.
Brass logit system life table
Model
life
table
yang
dikemukakan oleh
William
Brass
dan
rekan-rekannya
ini
dikenal
dengan
sistem
logit,
yang
mencoba
untuk
menghubungkan secara
matematis
dua
life table
yang berbeda. Brass
menemukan
bahwa
dengan
mentransformasikan nilai
probabilitas
bertahan
hidup
sampai
usia
x
(l
x
),
maka
terdapat
hubungan linear
dengan
probabilitas tersebut
pada
life
table
yang
berbeda.
Ketergantungan
yang
rendah
terhadap
tipe
data
membuat sistem
logit
berbeda dengan sistem-sistem yang telah digunakan pada berbagai
model life table.
Pada umumnya model life table yang sering digunakan adalah
model
regional
life
table
Coale-Demeny. Dalam
kasus
ini
kita
menggunakan model west karena menurut McDonald (1978) bahwa setelah
dirinya
melakukan
penelitian
yang
memakan waktu
lebih
dari tiga tahun
untuk
sepuluh
wilayah
di
Indonesia
maka
menurutnya lebih
sesuai
menggunakan life
table
model
west
daripada
model
life
table
lainnya
(UGM, p11).
|
|
2.2.3
Life Table Coale-Demeny
Ansley J. Coale dan Paul Demeny memperkenalkan model regional
life table pada tahun 1966. Model ini berasal dari pengamatan mereka atas
kumpulan 192 life table menurut jenis kelamin
yang dicatat dari populasi
yang
sebenarnya. Tabel-tabel ini
merupakan
hasil
seleksi dari
326
tabel
yang
telah dikumpulkan sebelumnya. Keseluruhan 192 tabel
tersebut
berasal dari data registrasi vital dan dari hasil enumerasi secara menyeluruh
terhadap
populasi-populasi yang
berkenaan.
Sebagian
besar
tabel-tabel
mencakup seluruh
negara
tetapi
beberapa
yang
merepresentasikan
pengalaman mortalitas
pada
wilayah
pinggiran
(sub
region)
juga
diikutsertakan, terutama
yang
menunjukkan karakteristik
khusus
yang
bertahan sepanjang waktu.
Analisa lebih lanjut terhadap tabel-tabel tersebut menunjukkan
empat
pola
kematian yang
secara
jelas
berbeda.
Pola-pola tersebut
kemudian
dikelompokkan dengan
nama
North,
South,
East,
dan
West
disesuaikan dengan predominansi negara-negara Eropa dalam wilayah yang
bervariasi
pada
tiap-tiap
level
tersebut.
Adapun
penjelasan mengenai
masing-masing pola tersebut adalah sebagai berikut:
a. Model East
Life table
yang termasuk dalam pola ini
berasal dari Austria, Jerman,
Italia bagian utara, serta beberapa dari Cekoslovakia dan Polandia. Jika
pola
dari
tabel-tabel tersebut
dibandingkan
dengan
pola standar
yang
diperoleh dari sebagian besar tabel, maka deviasi dari pola standar akan
|
|
menunjukkan bentuk U, yang menunjukkan angka kematian yang
relatif tinggi pada usia bayi dan pada usia tua di atas 50 tahun.
b.
Model North
Life table yang masuk dalam level ini berasal dari Islandia, Norwegia,
Swedia.
Karakteristik
pola
ini
adalah
angka kematian
pada
usia
bayi
yang
terhitung rendah
dirangkai dengan
angka kematian yang
relatif
tinggi pada usia kanak-kanak dan angka kematian pada usia 50 tahun ke
atas
yang
menurun jauh
di
bawah
standar.
Populasi yang
memperlihatkan pola kematian seperti
ini diasumsikan karena populasi
tersebut
terkena
endemi
tuberkulosis, sehingga
model
ini
direkomendasikan untuk digunakan pada populasi dimana sering timbul
endemi penyakit.
c. Model South
Pola
yang
termasuk
level
ini
ditunjukkan oleh
life
table dari
negara
Spanyol, Portugal, Italia bagian selatan. Pola kematian dalam
level ini
mempunyai karakteristik angka
kematian
yang
tinggi
sampai dengan
usia 5 tahun, kemudian angka kematian yang rendah dari usia kira-kira
40 tahun hingga 60 tahun, dan kemudian meninggi pada usia di atas 65
tahun sesuai dengan standar.
d.
Model West
Model
ini
berdasarkan
tabel
residual
dimana
pola
kematiannya tidak
menyimpang secara sistematis dari pola standar. Karakteristik
|
|
khususnya adalah angka kematian yang cenderung tinggi pada usia 20
tahun hingga 50
tahun. Model
ini berasal dari paling banyak populasi
dengan
berbagai
angka
keragaman wilayah
dan
kasus,
sehingga
dianggap
dapat
menggambarkan pola
kematian
secara
umum.
Model
west
ini
direkomendasikan sebagai
pilihan
pertama
dalam
merepresentasikan angka kematian dan digunakan oleh banyak
negara
terutama pada negara-negara berkembang.
2.3
Metode Trussel
2.3.1
Pengertian Metode Trussel
Selain beberapa angka kematian
yang telah dijelaskan
sebelumnya
di
atas,
ukuran
kematian
lainnya
yang
sering
digunakan adalah
level
mortalitas, yaitu suatu fungsi life table yang menunjukkan tingkat kematian.
Level
mortalitas
mempunyai
hubungan
terbalik
dengan
infant
mortality
rate. Level mortalitas saling berbeda antara kelompok penduduk satu
dengan kelompok penduduk lainnya.
Untuk mengukur
level mortalitas terdapat dua macam cara
yang
biasa
digunakan, yaitu
cara
langsung
(direct
method)
dan
cara
tidak
langsung
(indirect
method).
Cara
langsung
mengumpulkan keterangan
mengenai kematian
yang
terjadi
selama
kurun
waktu
tertentu
biasanya
setahun
sebelum
waktu
wawancara dan
membagi
angka
tadi
dengan
penyebut yang tepat, biasanya jumlah penduduk. Data seperti itu
dinamakan current mortality.
|
|
Cara
tidak
langsung
adalah
dengan
menggunakan informasi
tertentu yang tidak berhubungan langsung dengan data kematian, misalnya
struktur
umur
penduduk, komposisi anggota rumah
tangga,
jumlah
anak
lahir
hidup
dan
jumlah anak
yang
masih
hidup
yang
kemudian
dikonversikan dengan
metode
tertentu.
Pada
kebanyakan
negara
berkembang, data statistik kelahiran dan kematian yang lengkap serta dapat
diandalkan dari hasil pencatatan sipil masih sangat sulit diperoleh. Hal ini
dikarenakan sistem pencatatan sipil pada negara-negara berkembang masih
kurang baik. Oleh karena itu, telah dikembangkan berbagai metode untuk
mengestimasi harapan
hidup
yang
menggunakan data
selain
dari
catatan
sipil. Sebagian besar metode menggunakan
data dari hasil sensus dan
survei demografi.
Pada
tahun
1964
untuk
pertama kalinya
Brass
memperkenalkan
suatu
metode tak langsung untuk
mengestimasi probabilitas kematian pada
beberapa
usia anak-anak dengan
mengkonversikan proporsi
kematian
dari
anak yang
lahir
hidup pada wanita dengan kelompok umur 15-19, 20-24,
dan
seterusnya.
Metode
ini
kemudian
dikembangkan oleh
beberapa
ahli
kependudukan, yaitu
Sullivan pada
tahun
1972,
kemudian
Trussel
pada
tahun 1975, dan beberapa metode lainnya (BPS, 2001, p57).
Brass
memperkirakan probabilitas
kematian
dengan
mengalikan
data proporsi anak yang sudah meninggal di antara anak yang masih hidup
pada wanita menurut kelompok umur (dengan rentang 5 tahun-an) dengan
suatu faktor pengali untuk menyesuaikan
dengan faktor non-mortalitas
yang mempengaruhi nilai proporsi kematian anak. Perhitungan ini
|
 menghasilkan suatu ukuran kematian anak yang diartikan sebagai
banyaknya anak yang meninggal per 1000 kelahiran sebelum anak tersebut
mencapai usia x =1, 2, 3, 5, 10, 15, 20 tahun atau diberi simbol
q(1), q(2),
q(3),
q(5),
q(10), q(15), dan
q(20). Bentuk dasa® dari persamaan tersebut
adalah:
q( x)
=
k
(i)
·
D
(i)
dimana: q
(x)
=
probabilitas kematian sejak lahir hingga umur x tahun
k
(i)
=
faktor pengali untuk masing kelompok umur ibu
D
(i)
=
proporsi anak meninggal untuk tiap kelompok umur ibu
i = indeks untuk kelompok umur dari ibu
Kemudian
James
Trussel
mengembangkan metode
Brass
dan
mengadakan pendekatan
dengan
cara
regresi
untuk
memperoleh faktor
pengali
k(i),
yaitu
menggunakan rasio
paritas
P
(1)
/P
(2)
dan
P
(2)
/P
(3)
sekaligus
yang
kemudian dikalikan dengan koefisien tertentu.
P
(1)
,
P
(2)
,
P
(3)
adalah rata-rata paritas untuk wanita usia 15-19 tahun untuk P
(1)
,
20-
24
tahun untuk P
(2)
, dan
25-29 tahun untuk P
(3)
.
Para ahli
demografi
mendefinisikan paritas sebagai
jumlah anak yang
lahir
hidup dari seorang
wanita, sehingga
rata-rata paritas berarti rata-rata jumlah anak yang
lahir
hidup per wanita. (UN, 1983, p8)
k
(i)
=
a
(i)
+
b
(i)
(P
(1)
/
P
(2)
)
+
c
(i)
(P
(2)
/
P
(3)
)
Trussel
menyediakan satu set koefisien a(i),
b(i),
c
(i)
untuk
kelompok
usia
ibu
15-19 tahun
hingga
45-49 tahun,
berdasarkan empat
|
|
model
regional
life
table
Coale-Demeny, yaitu:
North,
South,
East,
dan
west. Selain
itu terdapat pula satu set koefisien untuk penghitungan waktu
rujukan
t(x)
yang
diperkirakan berdasarkan rasio
paritas
di
atas,
yang
selanjutnya dikonversikan ke kalender masehi.
Untuk
model
yang
dikembangkannya, Trussel
memakai
asumsi
perubahan kematian yang sesuai untuk digunakan di Indonesia (BPS, 2001,
p58). Dari segi
metodologi, pendekatan ini
membuat metode Trussel lebih
baik dari metode Brass dan Sullivan yang hanya memakai salah satu rasio
paritas saja (UN, 1983, p74).
2.3.2
Perkiraan Level Mortalitas
Pada
model
regional life
table
Coale
dan
Demeny terdapat
beberapa
level
mortalitas. Coale
dan
Demeny
menyusun secara
umum
keempat
model
regional
life
table
masing-masing ke
dalam
25
level
abridged
life
table,
beserta pula
nilai probability
of
surviving from
birth,
l(x),
untuk penentuan
level mortalitas, berdasarkan jenis kelamin
laki-laki
(male),
perempuan
(female)
dan
tanpa
membedakan jenis
kelamin
(both
sexes).
Jika data untuk estimasi
yang ada telah diklasifikasikan menurut
jenis
kelamin,
maka
lebih
tepat
menghitung level
mortalitas
dengan
menggunakan
nilai
l(x)
untuk
masing-masing jenis
kelamin.
Dan
level
mortalitas
untuk
kombinasi kedua
jenis
kelamin
(both
sexes)
tidak
diperlukan lagi karena
jika telah
diperoleh
level-level untuk
kedua
jenis
|
 kelamin secara tersendiri, maka level mortalitas kombinasi tidak akan
memberikan informasi apapun (UN, 1983, p81).
Dalam
memperkirakan level
mortalitas yang akan digunakan
untuk menentukan life table perlu dilakukan beberapa langkah perhitungan
mortalitas anak. Langkah pertama adalah menghitung P
(1)
,
P
(2)
,
P
(3), yaitu
nilai
rata-rata
paritas
per
wanita
(average parity
per
woman).
Rata-rata
paritas P
(1) menunjukkan
jumlah anak yang lahir hidup pada wanita dengan
kelompok umur
15-19
tahun, 20-24
tahun
untuk
P
(2)
,
dan
25-29 tahun
untuk P
(3)
per jumlah seluruh wanita pada kelompok usia
tersebut
.
Secara
umum dirumuskan dengan:
P(i)
=
CEB(i)
FP
(i)
dimana CEB(i) adalah jumlah anak
yang
lahir hidup (children ever born)
pada
wanita
kelompok umur
i,
dan
FP(i)
adalah
jumlah
seluruh
wanita
dalam kelompok umur i tanpa memperhatikan status perkawinannya. Nilai i
menunjukkan kelompok umur, i=1 untuk kelompok umur 15-19 tahun, i=2
untuk kelompok umur 20-24 tahun, dan seterusnya.
Langkah kedua adalah menghitung D(i), yaitu proporsi anak yang
meninggal untuk tiap kelompok umur ibu, didefinisikan juga sebagai rasio
anak yang meninggal (children dead) terhadap anak yang pernah dilahirkan
hidup menurut kelompok umur ibu.
D
(i)
=
CD
(i)
CEB(i)
|
 Nilai
proporsi
tersebut
dapat
juga
dicari
dengan
menggunakan
nilai rata-rata paritas per jumlah wanita dan nilai rata-rata anak yang masih
hidup (average number of
children
still living) per jumlah wanita sesuai
dengan kelompok umurnya.
D(i) =
1
-
average CSL
(i)
average CEB
(i)
Langkah berikutnya adalah menghitung
nilai
faktor pengali k(i)
dengan menggunakan persamaan berikut:
k
(i)
=
a
(i)
+
b
(i)
(P
(1)
/
P
(2)
)
+
c
(i)
(P
(2)
/
P
(3)
)
Koefisien a
(i),
b
(i),
c
(i)
yang diperlukan untuk mengestimasi faktor pengali
tersebut disajikan dalam Tabel 2.2 di bawah sesuai dengan model life table
yang
akan
digunakan, yaitu
model
west.
Metode
Trussel
membatasi
perhitungan kematian anak dengan menggunakan kelompok umur ibu dari
15-19 tahun sampai 45-49 tahun.
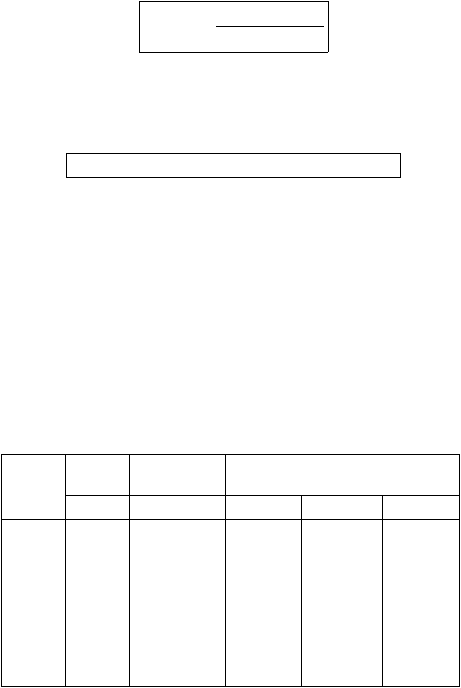
Tabel 2.2
Koefisien untuk Estimasi Faktor Pengali Kematian Anak,
Varians Trussel untuk Model West, Diklasifikasikan
Menurut Usia Ibu
Age
Group
Index
Mortality
Ratio
Coefficients
i
q(x)/D(i)
a(i)
b(i)
c(i)
15 - 19
20 - 24
25 - 29
30 - 34
35 - 39
40 - 44
45 - 49
1
2
3
4
5
6
7
q(1)/D(1)
q(2)/D(2)
q(3)/D(3)
q(5)/D(4)
q(10)/D(5)
q(15)/D(6)
q(20)/D(7)
1,1415
1,2563
1,1851
1,1720
1,1865
1,1746
1,1639
-2,0700
-0,5381
0,0633
0,2341
0,3080
0,3314
0,3190
0,7663
-0,2637
-0,4177
-0,4272
-0,4452
-0,4537
-0,4435
Sumber: Manual X Indirect Techniques For Demographic Estimation, 1983
|
 Langkah
keempat
adalah
menghitung probabilitas kematian
dan
probabilitas bertahan
hidup.
Perkiraan
probabilitas kematian
untuk
umur
tepat x tahun, q(x), diperoleh dengan mengalikan nilai
D(i) dengan faktor
pengali k(i), dirumuskan sebagai:
q( x)
=
k
(i)
·
D
(i)
Setelah
nilai
q(x)
diperoleh,
nilai
probabilitas
menjalani
hidup
sejak
lahir
hingga
umur
x,
l(x),
yang
merupakan
komplemen
dari
q(x),
dapat langsung dihitung dengan menggunakan persamaan di bawah ini.
l
(x) = 1.0 -
q(x)
Langkah selanjutnya adalah
mengkonversikan nilai l(x) ke sistem
level
mortalitas
Coale-Demeny
melalui
interpolasi
nilai
tersebut
dengan
nilai
l(x)
model
west
untuk
menentukan level
mortalitas
untuk
tiap
kelompok
umur.
Sehingga
berdasarkan nilai
rata-rata
level
mortalitas
tersebut dapat ditentukan perkiraan harapan hidup suatu cohort untuk setiap
kelompok umur.
2.4
Angka Harapan Hidup Personal
Angka harapan hidup (life expectancy) personal berarti berapa lama
waktu
yang
tersisa
bagi
seseorang
untuk
menjalankan hidup.
Walaupun
umur
seseorang adalah relatif dan hanya Tuhan Yang Maha Esa yang dapat menentukan,
namun
secara
statistika
kita
dapat
memperkirakan
berapa
besar
angka
harapan
hidup tersebut.
|
|
Harapan hidup setiap orang berbeda-beda dikarenakan faktor-faktor yang
mempengaruhi kematian
(mortality
risk
factors)
seseorang
tidak
sama.
Resiko
kematian
penduduk laki-laki
biasanya
lebih
tinggi
daripada
resiko
kematian
penduduk wanita.
Para
ahli
kesehatan dari
berbagai
institusi
kesehatan seperti
National
Center for Health Statistic dan Institute of Behavioral Science di Amerika Serikat,
Bandolier
di
Inggris
melakukan
penelitian
dan
diperoleh
beberapa
faktor
dasar
yang
mempengaruhi angka kematian dan
kemudian dijadikan sebagai acuan bagi
ahli
aktuaria
untuk
mengkalkulasi angka
kematian dan
harapan
hidup dari calon
tertanggung atau nasabah yang kemudian digunakan untuk menentukan besar
premi yang harus ditanggungkan pada calon tertanggung tersebut.
Untuk memperoleh informasi dari calon tertanggung mengenai informasi
kesehatannya
yang
berkaitan
dengan
faktor-faktor
yang
mempengaruhi angka
kematian
tersebut
maka
pada
saat
seseorang hendak
menjadi
nasabah
sebuah
perusahaan asuransi,
akan
dilakukan
wawancara terhadap
calon
tertanggung
tersebut untuk mendapatkan informasi seperti nama
lengkap, umur, jenis kelamin,
berat
badan,
tinggi
badan,
pendidikan
terakhir,
status bekerja,
status pernikahan,
kebiasaan berolahraga, kebiasaan merokok, dan kebiasaan
minum
minuman keras
atau mengkonsumsi alkohol
yang akan diisikan pada Surat Permohonan Asuransi
Jiwa
(SPAJ)
bagi
orang
dewasa.
Ini
merupakan
hal-hal
dasar
yang
diperlukan
untuk menyusun sebuah proposal yang memberikan gambaran berapa besar premi
yang
harus
ditanggungkan kepada
nasabah
yang
akan
berpengaruh
terhadap
perlindungan yang diperoleh. Semakin sehat seseorang maka semakin tinggi angka
|
|
harapan
hidup
orang
tersebut,
sehingga
premi
yang
harus
ditanggung
semakin
ringan dan perlindungan yang diperoleh semakin besar.
2.4.1
Tolak Ukur Angka Kematian
Beberapa
faktor
yang
mempengaruhi tingkat
resiko
kematian
seseorang
dan
diikutsertakan dalam
perhitungan
angka
harapan
hidup
personal calon terganggung sesuai dengan SPAJ adalah sebagai berikut:
a)
Usia (Age)
Orang
yang
berusia
20 tahun
tentunya memiliki harapan
hidup
lebih
lama
dibandingkan yang
telah
berusia
50
tahun.
Seiring
dengan
pertambahan
umur
manusia,
kesehatannya cenderung
menurun
dan
resiko terhadap kematian semakin meningkat.
b)
Jenis Kelamin (Sex)
Banyak statistik menunjukkan bahwa kaum pria
memiliki harapan
hidup yang lebih rendah dan resiko kematian yang diakibatkan penyakit
dan kecelakaan yang lebih besar dibandingkan wanita.
Perbedaan angka
harapan
hidup
sejak
lahir
antara pria
dan
wanita
di
Amerika
pada
tahun
2000
mencapai 5,4
tahun
dimana
kaum
pria
mempunyai
angka
kematian
yang
lebih
tinggi
untuk
masing-masing
dari sepuluh penyebab terbesar kematian sesuai dengan penelitian yang
dituangkan pada
buku Trends
in the
Leading
Causes of Death
(2004,
p3).
|
|
Menurut
penelitian lembaga
h2g2
(2005)
pria
lebih
agresif
dan
mempunyai kapasitas
mengambil
resiko
yang
lebih
besar,
selain
itu
tingkat
testosteron
yang
tinggi
pada
pria
membuat
mereka
beresiko
lebih besar untuk penyakit jantung dan stroke pada usia lanjut. Adanya
hormon estrogen pada wanita dapat mengurangi resiko kematian dini.
c)
Body Mass Index (BMI)
BMI dipengaruhi oleh berat dan tinggi badan, yang menunjukkan
tingkat
obesitas seseorang, merupakan salah satu faktor untuk
memprediksi resiko terkena penyakit dan kematian. BMI normal berada
di antara 18,5 dan 24,9. Orang yang mempunyai BMI di bawah atau di
atas
normal
untuk
semua
kelompok umur
baik
pria
maupun
wanita
berpeluang besar
terserang
penyakit
dan
meninggal
dunia.
Tingginya
angka
kematian banyak
dihubungkan dengan pengaruh
dari
obesitas,
seperti
kasus
mati
mendadak
dan
penyumbatan darah
pada
jantung
karena
kegagalan fungsi
pompa
darah.
Beberapa
penyakit
yang
dihubungkan dengan
kelebihan
berat
badan dan
obesitas,
antara
lain
cardiovascular, hipertensi,
radang
tulang
persendian
(osteoarthritis),
beberapa
kanker,
diabetes.
Penyakit
pembuluh darah
dan
jantung
(cardiovascular) berada pada urutan teratas sebagai penyebab kematian
terbesar di Indonesia.
Menurut hasil penelitian E. Calle et
al. (The New England Journal of
Medicine, 1999, 341: p1097-1105), sesuai dengan meningkatnya BMI,
resiko terhadap kematian juga meningkat. Pria dan wanita yang obesitas
|
|
dengan
BMI
30.0
atau
lebih,
mengalami
peningkatan
resiko terhadap
kematian masing-masing sebesar 250% dan 200%. Pada kebalikannya,
kekurangan
berat
badan
(underweight)
pada
pria
dan
wanita
dengan
BMI 18.5 atau kurang, resiko kematiannya juga meningkat sebesar 26%
dan 36%.
d)
Pendidikan Terakhir (Education Ended)
Banyak penelitian telah menemukan bahwa pendidikan yang ditempuh
seseorang
mempengaruhi gaya
hidup
dan
kebiasaan
sehat orang
tersebut dan
merupakan faktor
yang berbanding terbalik dengan angka
kematian.
Semakin
tinggi
jenjang pendidikan
yang
berhasil
ditempuh
maka semakin sadar dalam menjaga kesehatan dirinya.
Menteri
Negara Pemberdayaan Perempuan
Meutia
Hatta
mengatakan
bahwa tingginya angka kematian ibu pada saat melahirkan di Indonesia
adalah dikarenakan pendidikan yang rendah sehingga tidak tahu tentang
cara-cara
menjaga
kesehatannya dan
bayinya
saat
hamil.
(Media
Indonesia Online, 2006)
e)
Status Pernikahan (Marital Status)
Menurut penelitian Center
for
the
Study of Aging
(1998)
ditemukan
bahwa
orang-orang yang
hidup
dalam
pernikahan
mempunyai angka
kematian yang
lebih
rendah
pada
usia
50-an,
60-an,
dan
70-an
dibandingkan dengan
mereka
yang
tidak
hidup
dalam pernikahan baik
tidak
pernah
menikah, cerai
maupun
duda
atau
janda.
Untuk
orang-
orang
yang bercerai,
resiko kematiannya
yang
lebih
tinggi
terutama
|
|
disebabkan oleh kesehatan mereka yang lebih buruk.
Diketahui bahwa
kesehatan
yang
baik
mengurangi resiko
terhadap
kematian
dan
pada
keadaan
tertentu,
menikah
membawa kontribusi bagi
kesehatan yang
baik melalui gaya hidup yang lebih baik.
f)
Status Bekerja (Employment Status)
Resiko
kematian sangat
berkaitan dengan
gaya
hidup
seseorang
didefinisikan melalui
usia,
jenis
kelamin,
kelas
sosial
dan
status
pekerjaan.
Pekerjaan
seseorang
menentukan karakteristik sosial
ekonominya serta mempengaruhi gaya hidup dan kebiasaan sehat orang
tersebut.
Mempunyai pekerjaan
berarti
mempunyai penghasilan.
Berdasarkan penelitian P.Krueger et al. (Sociological Forum, vol.18(3),
p465-482) penghasilan yang diperoleh dari bekerja ataupun wiraswasta
memprediksikan mortalitas
yang rendah pada
usia
muda,
pertengahan
dan pada usia
tua. Mitchell et al. (1997) menemukan bahwa seseorang
dengan
usia
pertengahan
tua
yang
merupakan
pengangguran jika
kembali bekerja akan menurunkan resiko terhadap kematiannya.
g)
Aktivitas Fisik (Physical Activity)
Aktivitas
fisik
yang
dimaksud adalah
kebiasaan untuk
berolahraga.
Olahraga
yang
dilakukan secara
teratur
dan
seimbang sangat
menunjang
kesehatan
seseorang. Olahraga
jika
dilakukan
secara
rutin
dan
dalam
porsi
yang
benar
dapat
memperlancar
aliran
darah
serta
|
|
menyeimbangkan kadar kolesterol dalam darah sehingga resiko terkena
penyakit cardiovascular akan semakin rendah.
Berdasarkan penelitian Wannamethee (Archives of Internal Medicine,
1998, p2433-2440), seorang pria berusia 50 tahun mempunyai peluang
89% untuk hidup hingga umur 65 tahun tanpa penyakit jantung, stroke
atau diabetes jika dia tidak pernah merokok, aktif secara fisik atau rajin
berolahraga dan
tidak
kelebihan
berat
badan.
Sebaliknya
jika
orang
tersebut merokok, kurang aktif dan sangat kelebihan berat badan orang
tersebut hanya mempunyai peluang sebesar 42%.
h)
Status Merokok (Smoking Status)
Jika
dibandingkan dengan
mereka
yang
tidak
merokok,
orang
yang
merokok
menghadapi resiko
yang lebih besar terserang
oleh berbagai
penyakit yang banyak diantaranya membawa kematian. Penyakit TBC
dan
infeksi
saluran pernafasan
bawah
yang
terutama disebabkan
oleh
merokok menempati urutan kedua dan ketiga sebagai penyebab kasus
kematian di
Indonesia. Selain
itu
merokok juga
berpengaruh terhadap
BMI
dan
meningkatkan resiko
terjangkitnya penyakit pembuluh darah
dan
jantung
(cardiovascular) yang
menempati
urutan
teratas
sebagai
penyebab kasus kematian di Indonesia.
Orang
yang
berhenti
merokok,
khususnya sebelum umur
50
tahun,
mempunyai
harapan
hidup
lebih
besar
daripada
mereka
yang
masih
terus
merokok. Sebuah studi
menemukan bahwa seseorang setelah 15
tahun berhenti merokok, angka resiko terkena penyakit cardiovascular
|
|
pada
orang
tersebut
mendekati angka
resiko
pada
orang
yang
tidak
pernah
merokok. Menurut
jurnal
kesehatan seperti
Morbidity and
Mortality Weekly Report dari National Center of Health Statistics,
secara
umum
perokok
mempunyai resiko
70%
lebih
besar
terkena
penyakit
cardiovascular dibandingkan
non-perokok.
Orang
yang
merokok lebih
dari
atau
sebanyak dua
bungkus
setiap
harinya
mempunyai resiko
dua
atau
tiga
kali
lebih
besar
terkena
penyakit
cardiovascular.
i)
Status Kebiasaan Minum (Drinking Status)
Suatu studi pada
negara-negara di mana penderita alkoholisme cukup
banyak, diperoleh angka kematian akibat sirosis
liver (suatu penyakit
hati
yang
kronis
dan
berbahaya)
sangat
tinggi,
sedangkan kematian
yang terkait dengan
alkoholisme seperti kecelakaan
lalu
lintas akibat
sopirnya menggunakan alkohol berjumlah 25.000 kematian, akibat
bunuh diri dan pembunuhan 15.000 angka kematian setiap tahunnya.
Suatu penelitian lain di
negara barat yang melibatkan 90.000 pria dan
wanita yang diikuti selama 10 tahun, menunjukkan bahwa pada orang
yang meminum alkohol 6 gelas sehari akan meningkatkan resiko
kematian 2 kali dibandingkan
orang yang tidak meminum
alkohol.
Ditemukan bahwa resiko kematian mulai meningkat apabila meminum
alkohol 2-3 gelas sehari dan meningkat tajam mulai 6 gelas sehari.
Berdasarkan
pendapat
Bachtiar
(Banjarmasin Post
Online,
2000),
penggunaan alkohol di
Indonesia dengan
indikasi medis relatif sangat
|
|
kecil
dibandingkan dengan
penggunaannya
secara
luas
di
masyarakat
sebagai
minuman.
Penderita
alkoholisme di
Indonesia
cukup
banyak
meskipun belum ada data konkret
mengenai hal
tersebut,
namun
proporsi
kematian
yang
diakibatkan oleh
kecelakaan
dan
luka
serius
terus meningkat setiap tahunnya dan menempati urutan kelima terbesar
penyebab kasus kematian di Indonesia.
2.4.2
Penyesuaian Personal Life Table
Menurut
general
life table
untuk
penduduk
suatu
daerah
seperti
yang telah dijelaskan sebelumnya, setiap anggota cohort
memiliki harapan
hidup
yang
sama.
Jika
disesuaikan
berdasarkan
faktor-faktor yang
mempengaruhi angka kematian, maka akan diperoleh angka harapan hidup
secara personal.
Dengan
menggunakan nilai-nilai koefisien
untuk
masing-
masing
faktor
tersebut,
dapat
disusun
life
table
yang
disesuaikan untuk
personal.
Koefisien
yang
disediakan
disesuaikan dengan
level
yang
ada
untuk
masing-masing
faktor
tersebut.
Menurut
beberapa
jurnal
kesehatan
seperti
Morbidity and
Mortality
Weekly
Report
dari
National
Center
of
Health Statistics, The New England Journal of Medicine dan Handbook of
Population,
faktor-faktor
yang
mempengaruhi angka
kematian
masing-
masing dibagi ke dalam beberapa level seperti yang dijelaskan di bawah ini.
Faktor umur dibagi menjadi level umur 20-24 tahun, 25-29 tahun,
30-34 tahun,
demikian seterusnya
dengan
interval
5
tahun
sampai
pada
umur 80-84 tahun, dan dibatasi dengan level terakhir 85 tahun ke atas.
|
|
World
Health
Organization (1997)
membagi
Body
Mass
Index
menjadi
6
level,
yaitu
normal
untuk
nilai
BMI
18,5
–
24,9,
kekurangan
berat
(under
weight)
untuk
BMI kurang dari
18,5,
kelebihan berat
(over
weight) untuk
BMI
25,0
–
29,9,
obesitas
tingkat
1
(obese class 1) untuk
BMI 30,0 – 34,9, obesitas tingkat 2 (obese class 2) untuk BMI 35,0 – 39,9,
dan terakhir obesitas tingkat 3 (obese class 3) untuk BMI lebih dari 40,0.
Pendidikan terakhir dibagi menjadi tiga level berdasarkan
lamanya
jenjang pendidikan yang ditempuh,
yaitu sekolah
menengah atau
kurang (secondary or less) untuk mereka yang hanya menempuh
pendidikan dasar dan
menengah selama 11
tahun atau
kurang. Kemudian
level sekolah tinggi (high school degree) untuk mereka yang tamat sekolah
menegah atas, dan
mencapai gelar S1 atau
lebih
(college graduate) untuk
mereka yang telah lulus sekolah tinggi atau universitas.
Faktor
status
pernikahan
dikelompokkan
menjadi
level
menikah
(currently married), belum menikah (never married) juga termasuk mereka
yang
tidak pernah
menikah, dan
level cerai,
juda
atau
janda
(previously
married).
Level untuk status bekerja adalah pekerja (employed) bagi mereka
yang
mempunyai sumber
penghasilan atau
pekerjaan
tetap
baik
sebagai
karyawan
suatu
perusahaan maupun
sebagai
wiraswasta, tidak
bekerja
(unemployed) bagi
mereka
yang
tidak
mempunyai
pekerjaan
tetap,
dan
bukan angkatan
pekerja
(not
in the
labor force)
untuk orang-orang
yang
sudah pensiun dan tidak mampu bekerja.
|
|
Aktivitas fisik atau kebiasaan berolahraga dibagi menjadi tiga level,
yaitu cukup aktif (about as active) untuk mereka yang melakukan olahraga
secara teratur sekurang-kurangnya sekali dalam
seminggu,
misalnya
jalan
pagi
sejauh
3
km
dalam
satu
minggu.
Selanjutnya orang-orang yang
termasuk level sangat aktif (more active) adalah
mereka yang
melakukan
olahraga secara rutin dalam porsi yang
lebih banyak,
misalnya melakukan
senam
aerobik
selama
30
menit
sekurang-kurangnya tiga
kali
dalam
seminggu. Terdapat juga level kurang aktif (less active) untuk orang-orang
yang tidak suka berolahraga.
Status
merokok
dibagi
sesuai
dengan
konsumsi rokok
per
hari
menjadi level non-perokok untuk orang yang tidak pernah merokok,
perokok yang merokok kurang dari 1 bungkus per hari (current <1),
perokok 1 hingga kurang dari 2 bungkus per hari (current 1 - <2), perokok
lebih
dari
2
bungkus per
hari
(current
2+). Juga
terdapat
level
untuk
ex-
perokok kurang dari 1 bungkus per hari (former <1), ex-perokok 1 hingga
kurang
dari
2
bungkus
per
hari
(former
1
-
<2), ex-perokok lebih
dari
2
bungkus
per
hari
(former
2+).
Dalam
perhitungannya level
non-perokok
menggunakan koefisien yang sama dengan level ex-perokok kurang dari 1
bungkus per hari.
Terdapat empat
level
untuk
status
minum atau
kebiasaan
mengkonsumsi minuman
beralkohol,
yaitu
tidak
minum
(abstain
from
drinking)
untuk
orang-orang yang
berpantang
atau
tidak
mengkonsumsi
alkohol,
kadang-kadang (infrequent
drinker)
untuk
orang-orang
yang
mengkonsumsi alkohol namun tidak sering dan dalam jumlah paling
|
 banyak
satu
gelas
kecil
dalam
sehari
yang
biasanya untuk
pengobatan
tertentu.
Level
selanjutnya adalah
sering
minum
(current drinker)
untuk
mereka
yang
mempunyai kebiasaan
minum
dan
secara
teratur
mengkonsumsi alkohol baik harian maupun mingguan, dan kemudian level
sudah
berhenti minum (former
drinker) untuk
orang
yang
telah
menghentikan kebiasaannya mengkonsumsi alkohol.
Dengan
menggunakan model
regresi
logistik
(logistic regressions
model) dapat dihitung angka kematian (death rate) untuk personal menurut
faktor-faktor
tersebut di atas.
Regresi
logistik
digunakan apabila
variabel
dependen
atau variabel hasil yang digunakan
bersifat dichotomy,
yaitu
hanya
memiliki dua kemungkinan. Model dari persamaan regresi logistik
dituliskan sebagai berikut:
P(Y
=
1| x)
=
e
ß
0
+ß
1
x
ß
+ß
1
+
e
0 1
x
P(Y=1|x) adalah probabilitas variabel dependen Y bernilai 1 untuk
variabel
independen
x
yang
diberikan.
Y
bersifat
dichotomy jadi
hanya
bernilai 1 atau 0. Dengan menggunakan transformasi logit pada persamaan
di atas diperoleh:
ln
?
P
?
=
z = ß +
ß
x
?
1
-
P
?
0
1
?
?
Dalam kasus
ini kita
menghitung probabilitas terjadinya kematian
untuk
seseorang
berdasarkan
pengaruh
faktor-faktor
resiko
yang
tersedia,
yaitu death rate atau angka kematian. Dalam life table, angka kematian ini
|
|
dinotasikan dengan
n
M
x
.
Sehingga P(Y=1|X) =
n
M
x
,
Y
bernilai 1
untuk
|
 kasus
terjadinya kematian dan
sebaliknya bernilai 0
untuk kasus bertahan
hidup,
X
adalah
variabel
faktor-faktor
yang
mempengaruhi terjadinya
kematian. Dengan demikian persamaannya dapat dituliskan kembali seperti
berikut ini:
e
z
n
M
x
=
z
1
+
e
Untuk memudahkan
perhitungan,
persamaan
angka kematian
disesuaikan menjadi bentuk fungsi sigmoid seperti berikut:
1
n
M
x
=
-
z
1
+
e
Pada
gambar
2.1
di
bawah
ditunjukkan gambar
kurva
dari
persamaan regresi
logistik
dimana
variabel
yang
dihasilkan pasti
mempunyai nilai lebih besar atau sama dengan 0 dan lebih kecil atau sama
dengan 1. Kurva tersebut menunjukkan bahwa nilai hasil mendekati 0 dan 1
secara bertahap atau
gradual terhadap x, dan semakin
mendekati 0
atau 1
perubahan
nilai
hasil terhadap
x
menjadi
semakin kecil.
Kurva tersebut
dikatakan berbentuk S.
Gambar 2.1
Kurva Dua Dimensi Persamaan Regresi Logistik
|
|
Karena
faktor
yang
mempengaruhi (variabel
independen)
angka
kematian terdapat
lebih
dari
satu
dan
dengan
berbagai
level,
maka
digunakan model multiple logistic regression dengan design variables (atau
dummy variables). Logit dari persamaan tersebut
menurut
model multiple
logistic regression menjadi:
z = ß
0
+
ß1 x1
+
ß
2
x
2
+
ß3
x
3
+
... + ß
n
x
n
dimana
ß
0
,
ß
1,...
ß
n
adalah koefisien regresi logistik atau disebut juga
koefisien beta dan
x
1
,x2,...
x
n
adalah variabel independen, yaitu faktor-faktor
yang mempengaruhi angka kematian
seperti yang telah dijelaskan
sebelumnya di atas.
Sistem
registrasi
vital
merupakan standar
emas
untuk
mengumpulkan
data mortalitas dimana registrasi tersebut dilakukan
menurut
umur
dan
jenis
kelamin. Sistem registrasi vital
dengan
tingkat
kelengkapan yang tinggi sudah diterapkan di negara-negara maju jadi untuk
memperoleh data
mortalitas
yang
lengkap
menjadi
mudah.
Di
negara-
negara
berkembang sistem
registrasi
vital
semacam
ini
yang
lengkap
dan
akurat belum dapat ditemukan. (UN, 2005, p154)
Indonesia belum memiliki sistem registrasi vital yang lengkap, oleh
karena itu data koefisien regresi logistik dan nilai konstan yang digunakan
untuk
menghitung
angka
kematian
personal
dalam
perancangan ini
diperoleh dari
hasil
penelitian
kependudukan National
Center
for
Health
Statistics (NCHS) atas kombinasi faktor-faktor yang
mempengaruhi angka
kematian. Berikut adalah nilai koefisien yang digunakan:
|
 Tabel 2.3
Koefisien Regresi Logistik dari Faktor-Faktor yang
Mempengaruhi Angka Kematian
Variable
Beta-
Coeft.
Variable
Beta-
Coeft.
Sex
Marital Status
female
ref
Currently Married
ref
male
0,394
Previously Married
0.173
Age
Never Married
0.252
20-24
1
Employment Status
25-29
-0.026
Employed
Ref
30-34
0.206
Unemployed
0.516
35-39
0.525
Not in the labor force
0.540
40-44
1.104
Physical Activity
45-49
1.284
More active
-0.231
50-54
1.794
About as active
Ref
55-59
2.236
Less active
0.314
60-64
2.736
Smoking Status
65-69
2.984
Current 2+
1.318
70-74
3.432
Current 1 - <2
0.945
75-79
3.770
Current <1
0.879
80-84
4.313
Former 2+
0.661
85+
4.959
Former 1 - <2
0.559
Body Mass Index
Former <1
0.174
Under weight
0.426
Never
ref
Normal
Ref
Drinking Status
Over weight
0.014
Abstain from drinking
-0.061
Obese class 1
0.046
Infrequent drinker
Ref
Obese class 2
0.211
Former drinker
0.195
Obese class 3
0.440
Current drinker
0.229
Education
Constant
-7.120
11 years or less
0.249
High School Degree
0.068
Any College
ref
Sumber: Combining Prevalence and Mortality Risk Rates, 2002
Selanjutnya nilai
angka kematian
yang
diperoleh
dimasukkan ke
dalam
fungsi-fungsi standar
lain
dalam
life
table
seperti
yang
telah
dijelaskan pada subbab 2.2.1 guna menyusun sebuah personal life table.
2.5
Paradigma Rekayasa Piranti Lunak
Rekayasa piranti lunak menurut Fritz Bauer (Pressman, 1992, p23) adalah
penetapan
dan pemakaian
prinsip-prinsip
rekayasa
dalam
rangka mendapatkan
|
|
piranti
lunak
yang
ekonomis,
yaitu
terpercaya dan
bekerja
efisien
pada
mesin
(komputer). Menurut Pressman (1992, p24) rekayasa piranti lunak mencakup tiga
elemen yang mampu mengontrol proses pengembangan piranti lunak, yaitu:
a)
Metode-metode (Methods), berfungsi untuk
menyediakan cara-cara teknis
untuk membangun piranti lunak.
b)
Alat-alat
bantu
(Tools),
mengadakan dukungan
otomatis
atau
semi
otomatis
untuk
metode-metode seperti
CASE
(Computer Aided
Software Engineering)
yang
mengkombinasikan software,
hardware,
dan
software
engineering
database.
c)
Prosedur-prosedur (Procedures), merupakan pengembangan dari metode dan
alat bantu.
Dalam
perancangan piranti
lunak
(software)
dikenal
istilah
Classic
Life
Cycle,
yaitu
serangkaian
kegiatan
yang
dilakukan
selama
masa
perancangan
software, diantaranya:
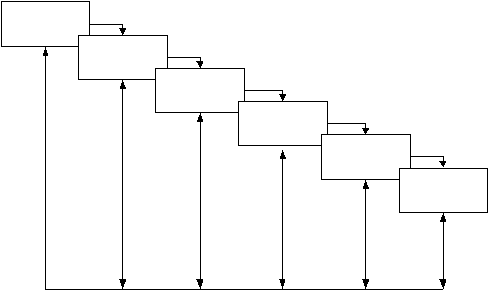
1.
Rekayasa sistem (System engineering)
Tahap awal perancangan piranti lunak adalah rekayasa sistem yang akan
dibangun dengan menetapkan kebutuhan-kebutuhan elemen sistem.
2.
Analisa kebutuhan piranti lunak (Analysis)
Sebelum merancang sebuah sistem, harus
terlebih dahulu
mengetahui
kebutuhan, informasi beserta spesifikasi piranti lunak.
3.
Perancangan (Design)
|
 Tahap
perancangan
ini
menitikberatkan pada
tiga
komponen program,
yaitu
struktur data, arsitektur piranti lunak dan prosedur detail.
4.
Pengkodean (Coding)
Pada tahap ini hasil rancangan diterjemahkan ke bahasa yang dimengerti oleh
mesin dalam bentuk program-program.
5.
Pengujian (Testing)
Sebelum
diaplikasikan, suatu
piranti
lunak
harus
diuji
terlebih
dahulu
agar
keluaran yang dihasilkan oleh sistem sesuai dengan yang diharapkan.
6.
Pemeliharaan (Maintenance)
Pemeliharaan
piranti
lunak
dilakukan
untuk
mengantisipasi peningkatan
kebutuhan pengguna akan fungsi-fungsi baru.
Gambar 2.1
Classic Life Cycle
|
 2.6
State Transition Diagram (STD)
State
Transition Diagram
merupakan
sebuah
alat
pemodelan
yang
digunakan untuk mendeskripsikan sistem
yang memiliki ketergantungan terhadap
waktu.
STD
merupakan suatu
kumpulan
keadaan
atau
atribut
yang
mencirikan
suatu keadaan pada waktu tertentu.
STD terdiri dari tiga komponen utama, yaitu:
1.
State, disimbolkan dengan
State
menggambarkan suatu
keadaan
sebagai
hasil
dari
suatu tindakan.
Terdapat dua jenis state, yaitu state awal dan state akhir.
2.
Arrow, disimbolkan dengan
Arrow menunjukkan transisi state dengan label ekspresi atau aturan.
3.
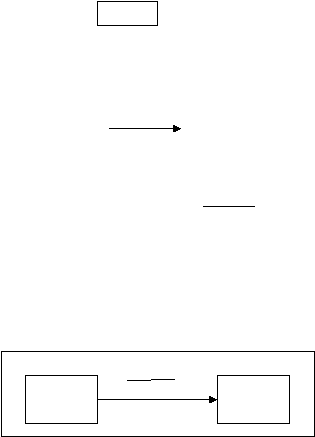
Condition and Action, disimbolkan dengan
condition
action
Condition adalah suatu event pada lingkungan eksternal yang dapat dideteksi
oleh sistem, sedangkan action adalah
yang dilakukan oleh sistem bila terjadi
perubahan state.
condition
action
State 1
State 2
Gambar 2.2
Komponen Utama STD
2.7
Penelitian yang Relevan
“Palestinian Society in Gaza, West Bank and Arab Jerusalem. A Survey of
Living Conditions” oleh Marianne Heiberg and Geir Øvensen pada tahun 1993 dan
|
|
1994.
Dalam
penelitian
tersebut,
para
penulis
menggunakan
metode
Trussel
dan
model west Coale-Demeny untuk
mengestimasi probabilitas kematian pada
umur
tepat 1 tahun dan 5 tahun dan harapan hidup pada saat lahir (estimates of
probability of dying by exact age 1 and 5 and life expectancy at birth in common
indices) dimana menurut mereka metode Trussel merupakan prosedur yang paling
standar digunakan.
“The 2000 Guyana Multiple Indicator Cluster Survey” oleh The Bureau of
Statistics Guyana yang dibiayai oleh UNICEF pada bulan Juli tahun 2001. Isi bab
2
dari
laporan
ini
berupa
hasil
estimasi kematian pada
bayi
dan
anak
balita
(estimates
of
infant and under
five
mortality)
dengan
menggunakan teknik
tidak
langsung berupa metode Trussel.
“Perancangan Program
Aplikasi
Perhitungan
Harapan
Hidup
Penduduk
Suatu
Daerah dengan Menggunakan Metode
Brass” oleh
David
Halim Wijaya
di
Universitas Bina
Nusantara
pada
tahun
2004.
Penulis
tersebut
dengan
menggunakan metode
Brass
memperoleh
harapan
hidup
untuk penduduk Jakarta
adalah 68,6 tahun untuk laki-laki dan 72,5 tahun untuk perempuan.
“Report on
Advanced Demographic Techniques” oleh
Delphine
Gay
dan
Napaporn Chayovan di Universitas Chulalongkorn, Bangkok pada bulan Oktober
2004.
Laporan
ini
berisi
mengenai
pembahasan
metode-metode demografi
yang
standar
dimana metode yang digunakan untuk analisa mortalitas adalah
menggunakan life table dengan metode Coale dan Trussel.
“Impact
of
a
Self-reliance Programme
on
Family Planning
Activities
in
Bangladesh” oleh
M. Nurul
Islam, M. Mujibur
Rahman, M. Kabir, S.A.
Mallick
yang
dipublikasikan
di
Asia-Pacific Population
Journal,
Vol.
6,
No.
1.
Dalam
|
|
menyusun
laporan
ini, para
penulis
mengestimasi probabilitas kematian q(x) dari
menggunakan metode Trussel dan life table Coale-Demeny model west. Diperoleh
kesimpulan bahwa
harapan
hidup bagi
bayi
yang baru
lahir
adalah
50,0
tahun
dengan angka kematian 119 per 1000 kelahiran pada area terprogram. Sedangkan
pada area tidak terprogram diperoleh harapan hidup bayi adalah 47,6 tahun dengan
angka kematian 132 per 1000 kelahiran. Selain itu juga digunakan regresi logistik
untuk menganalisa faktor-faktor yang mempengaruhi.
|