|
BAB 2
LANDASAN TEORI
2.1. Persediaan
2.1.1. Tujuan Pengendalian Persediaan
Memperoleh tingkat persediaan optimal dengan menjaga keseimbangan antara
biaya karena persediaan yang terlalu banyak dengan biaya karena persediaan yang terlalu
sedikit.
2.1.2. Jenis-Jenis Permintaan
•
Deterministic dan Stochastic
Deterministic berarti permintaan
yang
akan
datang
untuk
suatu
barang diketahui
secara
pasti.
Sedangkan
Stochastic
berarti
permintaan
yang
akan
datang
untuk
suatu
barang masih bersifat tidak pasti/acak.
•
Independent dan Dependent demand
Independent demand adalah permintaan suatu barang
yang tidak terpengaruh oleh
permintaan barang yang lain/tidak dipengaruhi oleh kondisi pasar. Sedangkan Dependent
demand adalah permintaan yang disebabkan oleh permintaan barang yang lain.
|
|
7
2.1.3. Jenis-Jenis Biaya Persediaan
•
Biaya Pembelian atau Purchasing Cost
Biaya pembelian terdiri dari dua jenis biaya. Pertama, kalau harga pembelian adalah
tetap maka ongkos per satuan adalah tetap tanpa melihat jumlah yang dibeli. Kedua kalau
ada diskon maka harga per satuan berubah-ubah tergantung pada jumlah pembelian.
•
Biaya Pengadaan atau Ordering Cost
Kategori biaya
ini
mencakup beberapa
jenis
biaya
yang
sudah
umum
diketahui.
Ordering cost terdiri dari biaya pemeriksaan awal, biaya pemesanan, biaya penerimaan
dan pemeriksaan akhir, biaya kuitansi-kuitansi dan dokumen lainnya untuk menjamin
lancarnya arus barang, biaya telpon dan lain-lain.
Pada
umumnya,
ordering
cost berkurang
atau
bertambah
sesuai
dengan
jumlah
pesanan. Hal ini berarti bahwa dalam banyak hal berlaku “akan lebih murah jika barang
dipesan lebih banyak”, karena
pesanan
tidak
terlalu
sering. Akan
tetapi
hal
ini
akan
menimbulkan kasus baru yaitu bertambahnya biaya penyimpanan.
•
Biaya Penyimpanan atau Holding Cost atau Carrying Cost
Holding cost terdiri dari semua biaya yang berhubungan dengan biaya penyimpanan
barang dalam gudang. Biaya ini
meliputi bunga modal yang tertanam dalam persediaan,
sewa gedung, asuransi, pajak, biaya bongkar-muat, harga penyusutan, harga kerusakan,
dan penurunan harga. Biasanya biaya ini sebanding dengan jumlah persediaan di dalam
gudang.
•
Biaya Kekurangan Stok atau Stock Out atau Shortage Cost
Biaya ini timbul akibat tidak terpenuhinya kebutuhan pelanggan. Kalau pelanggan
mau
menunggu,
maka biaya
ini timbul dari pengadaan yang
terburu-buru. Tetapi kalau
|
|
8
langganan tidak rela menunggu, maka biaya ini terjadi akibat kehilangan laba dan lebih-
lebih
lagi kehilangan
kepercayaan. Biaya
jenis
ini
umumnya
mendapat
perhatian
yang
sungguh-sungguh, karena akibatnya tidak segera
terasa
walaupun
secara
lambat
laun
merusak.
2.1.4. Model Economic Order Quantity (EOQ)
Model persediaan yang paling sederhana adalah barang yang dipesan dan disimpan
hanya satu macam, kebutuhan/permintaan per periode diketahui dan barang yang dipesan
segera dapat tersedia.
Model persediaan yang sederhana memakai parameter berikut ini.
k
= ordering cost per pesanan,
A
= jumlah barang yang dibutuhkan dalam 1 periode (misalkan 1 tahun),
c
= procurement cost per unit barang yang dipesan,
h = holding cost per satuan nilai persediaan,
T = waktu antara satu pemesanan dengan lainnya.
Tujuan
model
ini adalah untuk menentukan
jumlah setiap kali pemesanan (Q) sehingga
total annual cost dapat diminimumkan.
Total annual cost = ordering cost + holding cost + procurement cost
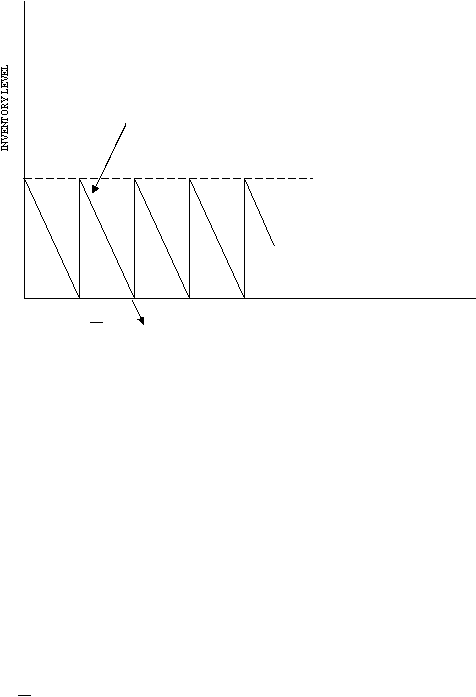
Secara grafis model persediaan yang sederhana tersebut dapat digambarkan sebagai
berikut.
|
 9
Slope = -A
Q
T
=
Q
A
Order point
TIME
Gambar 2.1 Model persediaan sederhana
Sumber : Dasar-Dasar Operations Research (2000,p209)
Gambar
2.1 dapat membantu penyusunan
model
matematisnya. Sejumlah Q unit
barang dipesan secara periodik. Order point merupakan saat siklus persediaan yang baru
dimulai dan yang lama
berakhir. Setiap siklus
persediaan
mempunyai periode waktu
selama T,
artinya
setiap T
hari
(atau
minggu,
bulan
dan
lain-lain)
pemesanan
kembali
dilakukan. Lamanya T sebanding dengan kebutuhan selama satu periode (A) yang dapat
dipenuhi oleh Q.
Jadi,
T
=
Q
A
Slope-A dapat dipakai sebagai penunjuk jumlah persediaan dari waktu ke waktu dengan
melihat
garis-garis
lurus yang
memiliki slope
tersebut.
Sekali
lagi
karena
barang
yang
dipesan diasumsikan dapat segera tersedia. Setiap siklus persediaan dapat dilukiskan
dalam bentuk segitiga dengan tinggi Q dan alas T.
|
 10
Ordering
cost
tergantung
pada
frekuensi
pemesanan
dalam satu
periode (tahun).
Frekuensi pemesanan tergantung pula pada dua hal yaitu jumlah barang yang dibutuhkan
selama satu periode (tahun) A dan jumlah setiap kali pemesanan Q
Sehingga: frekuensi pemesanan =
A
.
Q
Dengan mengalikan A/Q dengan biaya setiap order yakni k, akan diperoleh
?
?
Annual ordering cost = ?
A
?k .
?
Q
?
Komponen biaya kedua
adalah holding cost yang ditentukan oleh jumlah barang yang
disimpan dan
lamanya barang disimpan. Setiap hari jumlah barang
yang disimpan akan
berkurang,
yang berarti
lamanya penyimpanan berbeda antara satu
unit barang dengan
unit barang yang lain. Karenanya perlu diperhatikan tingkat persediaan rata-rata. Karena
persediaan bergerak dari Q unit ke
nol
unit
dengan
tingkat
pengurangan
yang
konstan
(slope-A) maka persediaan rata-rata untuk setiap siklus adalah:
Persediaan rata-rata = Q / 2 .
Holding
cost
dihitung
berdasarkan
satuan
nilai
persediaan
dan procurement
cost
(c),
sehingga:
Annual holding cost (per unit barang) = hc,
Jadi :
?
Q
?
Annual holding cost = hc?
?
.
?
2
?
Holding cost dapat pula dicari dengan bantuan Gambar 2.1 sebagai berikut.
Luas segitiga = ½ alas x tinggi = ½ T x Q = ½ TQ.
|
 11
Bila T
=
Q
,
maka:
A
? Q
?
?
2
?
luas segitiga =
1
?
?
Q
=
1
?
Q
?
=
1
TQ .
2
?
A
?
2
?
A
?
2
Bila holding cost per unit barang = hc,
Maka
?
Q
2
?
Holding cost (per siklus) = hc?
?
.
Apabila
?
2
A
?
A
adalah jumlah siklus persediaan dalam satu periode (tahun) maka
Q
?
Q
2
?
A
Annual holding cost
=
hc
?
?
x
2
A
Q
?
?
?
Q
?
=
hc
?
?
.
?
2
?
Setelah komponen biaya kedua (holding cost) diketahui, procurement cost dapat dihitung
pula. Dalam satu periode (tahun) dibutuhkan A unit barang, sehingga:
Annual procurement cost = Ac.
Dengan
menggabungkan
ketiga komponen
biaya persediaan yang telah
dihitung
di
atas, maka:
?
?
?
?
Total annual cost
=
?
A
?
k
+
hc?
Q
?
+
Ac .
?
Q
?
?
2
?
Tujuan model
ini
adalah untuk
memilih
nilai Q yang
mengandung semua biaya di
atas
serendah-rendahnya.
Tetapi,
yang
perlu diperhatikan hanyalah biaya-biaya yang
relevan saja.
Biaya
yang ketiga, Ac, dapat diabaikan karena biaya tersebut tidak
|
 12
tergantung pada
frekuensi pemesanan. Karena
itu tujuan daripada
model persediaan
ini
adalah:
?
A ?
?
Q
?
Minimumkan TC =
?
?
h
+
hc
?
?
,
Q
?
?
?
2
?
di mana TC adalah total biaya yang relevan.
Persamaan
TC di atas
merupakan
sebuah ekspresi secara matematis yang disebut
sebagai fungsi tujuan. Besarnya TC tergantung pada besarnya order quantity atau Q yang
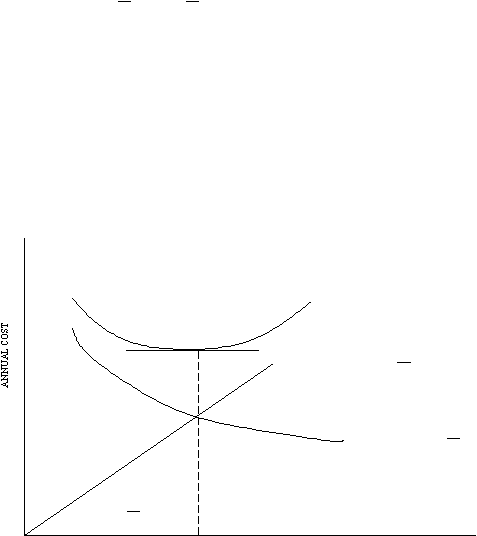
dipilih. Gambar 2.2 di bawah ini
menunjukkan bagaimana TC dinyatakan secara
grafis
dengan sumbu tegak mewakili annual cost dan Q pada sumbu datar.
TC
?
Q
?
MINIMUM
Holding cost hc ?
?
?
2
?
?
?
Ordering cost ?
A
?k
?
Q
?
T
=
Q
A
0
Q
*
Q
Gambar 2.2 Komponen-komponen biaya persediaan
Sumber: Dasar-Dasar Operations Research (2000,p213)
Total
annual cost
mengandung
dua
komponen,
yakni
annual ordering
cost
dan
annual holding cost. Kedua komponen ini juga digambarkan pada Gambar 2.2. Karena
TC adalah hasil penjumlahan kedua komponen tersebut, tinggi kurva TC pada setiap titik
Q merupakan hasil penjumlahan tinggi kedua komponen tersebut secara vertikal.
|
|
13
Annual ordering cost mempunyai bentuk geometris seperti hiperbola. Apabila
dilihat
kembali
bahasan
terdahulu, jelas
bahwa
setiap pemesanan
akan
mengakibatkan
beban biaya sebesar k, tanpa
memandang
jumlah barang
yang dipesan (Q). Jadi,
makin
kecil
Q berarti makin sering pemesanan dilakukan, dan
makin besar pula biaya
pemesanan yang dikeluarkan. Sebaliknya, bila Q makin
besar
berarti
makin
jarang
pemesanan dilakukan dan
makin
kecil
pula annual ordering cost
yang
menjadi beban.
Akibatnya apabila digambarkan
secara
grafis
maka
makin besar Q (bergeser ke kanan),
makin menurunlah kurva ordering cost.
Annual holding cost digambarkan sebagai sebuah garis lurus. Hal ini disebabkan
karena
komponen
ini
secara
langsung
tergantung pada tingkat persediaan rata-rata.
Tampak bahwa garis ini dimulai dan
titik
Q=0, di
mana tingkat persediaan adalah nol.
Makin besar jumlah barang yang dipesan maka
makin besarnya tingkat persediaan rata-
rata. Akibatnya
holding
cost akan
meningkat
secara
proporsional,
dan
digambarkan
dengan garis dengan slope yang sama.
Solusi
optimal daripada
fungsi tujuan
ditemukan
pada saat
total annual relevant
cost
minimum. Pada saat tersebut, jumlah
pemesanan yang optimal akan dinyatakan
dengan Q*. Secara grafis, solusi optimal ditemukan pada saat slope dari kurva TC adalah
nol.
Secara matematis, Q* (jumlah pemesanan yang optimal) dapat dihitung sebagai berikut.
Persamaan TC diturunkan, kemudian disamakan dengan nol.
|
 14
?
?
?
?
TC
= ?
A
?
k
+
hc
?
Q
?
?
Q
?
?
2
?
dTC
=
-
A
dQ
Q
2
k
+
hc
=
0
2
kemudian
A
k
=
hc
Q
2
2
Q
2
hc
=
2
Ak
Q
2
=
2
Ak
hc
Q*
=
2
Ak
.
hc
Q*
kadang-kadang
disebut
sebagai
Economic
Order
Quantity
(EOQ).
Persamaan
ini disebut Wilson Formula, yang berasal dari nama orang yang mula-mula
mengemukakannya.
Apabila Q* telah ditemukan, waktu pemesanan kembali dapat dihitung pula dengan:
T
*
=
Q
*
.
A
Kebijaksanaan persediaan telah terpecahkan dengan diketahui berapa dan bilamana
pemesanan harus dilakukan agar biaya yang ditanggung menjadi minimal. Besarnya
annual
relevant
cost
dapat
dihitung
dengan
mengganti
Q
pada
persamaan TC
dengan
nilai Q*.
Apabila
dilihat
kembali
Gambar
2.2, jelas
terlihat bahwa Q*
dicapai pada saat
holding cost sama dengan ordering cost. Hal ini dapat pula dibuktikan secara matematis
sebagai berikut.
|
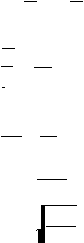 15
2
?
?
?
?
hc
?
Q
?
=
?
A
?
k
?
2
?
Q
?
Q
?
2
=
k
A
hc
Q
Q
=
k
2
A
hc
Q
2
=
2
Ak
hc
Q* =
2
Ak
.
hc
2.1.5. Reorder Point
Adalah saat bilamana pemesanan kembali harus dilakukan agar barang yang
dipesan datang tepat pada saat dibutuhkan. Reorder point
ditentukan dengan
mempertimbangkan dua variabel yaitu lead time (L) dan tingkat kebutuhan per hari (U).
Secara kasar
reorder point
merupakan
hasil
kali
L
dan
U ditambah
dengan
sejumlah
tertentu sebagai safety stock.
2.1.6. Safety Stock
Adalah persediaan pengaman yang besarnya tergantung pada kebijaksanaan
manajemen masing-masing perusahaan.
|
 16
2.1.7. Model Pembelian dalam Jumlah Banyak
2.1.7.1. Quantity Discounts
•
All Units Quantity Discounts
Ketika
Quantity Discounts ditawarkan,
fungsi objektif
adalah
mencari
total
cost
minimum pada kurva total cost. Tetapi kurva total cost tidak kontinyu, sehingga turunan
pertamanya
bukan
merupakan
biaya
minimum
sebagaimana
yang
berlaku
pada
kasus
non-discounts.
Quantity
Discounts
menciptakan
diskontinuitas
pada
kurva total
cost.
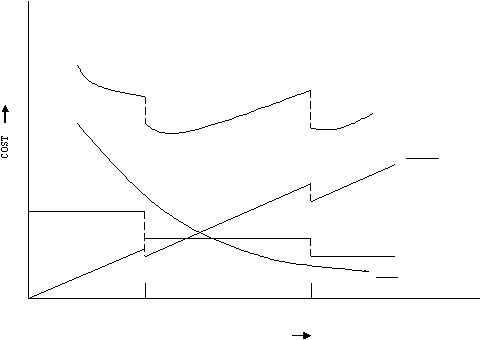
Gambar 2.3 menunjukkan suatu situasi dengan two price breaks.
TC (Q)
PFQ
2
U
1
U
2
ORDER QUANTITY (Q)
CR
PR
Q
Gambar 2.3 Biaya persediaan: all-units quantity discounts
Sumber : Principles of Inventory and Materials Management (1994,p107)
Nilai biaya
minimum
dapat
merupakan
suatu
nilai diskontinuitas atau
yang
turunannya sama dengan nol sebagaimana ditentukan melalui EOQ.
Dengan all units quantity discounts, pembeli diperlihatkan dengan suatu daftar
harga yang terdiri dari sejumlah j, di mana harga satu unit adalah sama untuk seluruh unit
|
|
17
?
dalam suatu pemesanan dan harga semakin menurun seiring dengan meningkatnya
jumlah pesanan. Purchase cost suatu unit barang diperlihatkan sebagai berikut.
?
P
0
untuk U
0
=
Q
<
U
1
,
?
P
1
untuk U
1
=
Q
<
U
2
,
P
i
=
?
?
?
?
P
untuk U
=
Q
<
U
,
?
j
j
j
+
1
di mana U1
<
U2
<…< U
j
adalah
urutan
jumlah barang
(dalam
bilangan bulat) tempat
price breaks terjadi. U
0
adalah jumlah minimum yang dibeli (biasanya nilainya satu), dan
U
j+1
adalah jumlah
maksimum
yang dibeli (biasanya tak terbatas). P
i
merupakan
purchase cost unit barang yang ditetapkan berdasarkan jumlah pemesanan barang dalam
interval U
i
hingga U
i+1
di mana P
0
>
P1
>
… >
P
j
.
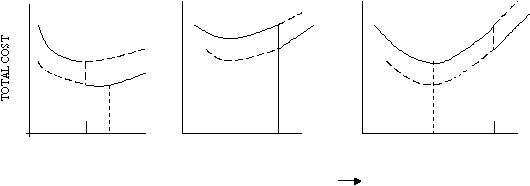
Gambar 2.4 menunjukkan tiga kemungkinan kondisi yang mungkin ada pada
single
price
break.
Bagian kurva total
cost yang tebal relevan, sedangkan bagian
yang
bergaris putus-putus tidak relevan. Kurva yang tebal menunjukkan fungsi biaya,
sedangkan
kurva
yang bergaris
putus-putus
mewakili
luasnya
fungsi
biaya
ke
dalam
wilayah
yang
nonapplicable. Permasalahannya
adalah
menemukan
nilai
terendah
pada
kurva
yang
dibentuk
oleh bagian
yang
tebal. Karena
diskontinuitas dari
kurva,
jumlah
dengan
biaya terkecil
tidak
dapat
selalu
ditemukan
melalui diferensiasi.
|
 18
Case 1
Case 2
Case 3
U1
U1
U1
QUANTITY
Gambar 2.4 All-units quantity discounts
Sumber : Principles of Inventory and Materials Management(1994,p108)
Dengan all units quantity discounts, ada kurva total cost yang terpisah untuk setiap
harga unit barang. Masing-masing kurva hanya diterapkan pada satu bagian dari interval
jumlah dengan harga yang valid. Hasilnya adalah sebuah kurva total cost dengan
langkah-langkah diskontinu pada kuantitas price break. Walaupun kurva untuk
masing-
masing
harga
barang
mempunyai
nilai
yang
minimum
tetapi
belum
tentu
valid. Suatu
EOQ valid apabila berada dalam interval jumlah barang yang berdasarkan pada purchase
cost
unit barang tersebut. Ketika holding
costs diperlakukan sebagai
nilai pecahan dari
suatu purchase cost unit barang, setiap kurva akan memiliki EOQ yang berbeda.
Purchase cost yang lebih rendah menghasilkan holding costs yang lebih rendah dan EOQ
yang
lebih
besar.
Karena
setiap bagian
dari
kurva
total
cost
diminimalisasi baik
pada
EOQ mau pun jumlah pada suatu price break, jumlah barang yang diambil agar total cost
optimum adalah EOQ yang feasible dan pada setiap price break.
|
|
19
?
•
Incremental Quantity Discounts
Pada situasi ini, pembeli dihadapkan pada sebuah daftar
harga yang diurut
berdasarkan
interval jumlah barang yang akan dibeli, sehingga purchase cost suatu unit
barang akan diberikan sesuai dengan cost pada interval
yang sudah ditentukan tersebut.
Purchase cost
satu
unit
barang
akan
menjadi
lebih
murah
apabila
jumlah
pembelian
barang semakin banyak. Daftar harga yang diberikan adalah sebagai berikut.
?
P
0
?
U
0
=
Q
=
U
1
-
1,
?
P
1
?
U
1
=
Q
=
U
2
-
1,
P
i
=
?
?
?
?
P ? U
=
Q
=
U
?
j
j
j
+1,
Di mana U1
<
U2 <…< U
j
adalah urutan jumlah barang (dalam bilangan bulat) pada saat
price break terjadi dan P
0
>
P1 > …> P
j
.
Berdasarkan daftar harga di atas, purchase cost
untuk
suatu
unit Q tidak
konstan
melainkan
berdasarkan pada
interval di
mana
U
i
=
Q
<
U
i
+1
. Purchase cost pada sejumlah Q adalah sebagai berikut.
M
i
=
D
i
+
P
i
Q
,
dengan
i
D
i
=
?
(U
e
-
1)(P
e-1
-
P
e
).
e=1
Karena semua unit barang tidak dibeli pada purchase cost yang sama, D
i
adalah purchase
cost
tambahan
dikarenakan
tidak
membeli
tiap-tiap
Q
unit
pada
P
i
.
Purchase cost
tambahan ini adalah sebuah konstanta untuk memesan sejumlah Q lain dalam interval U
i
hingga
U
i+1
. Dengan
demikian
D
i
adalah
ordering
cost tambahan
karena setiap
pemesanan yang dilakukan terkena biaya. Purchase cost per unit adalah
|
 20
?
?
i
i
M
i
=
D
i
Q
Q
+
P
i
.
Dengan demikian total cost per tahun untuk sejumlah Q barang adalah
TC(Q) = purchase cost + order cost + holding cost
=
?
P
+
D
i
?
CR
?
R
+
+
FQ
?
P
+
D
i
?
?
?
Q
?
Q
2
?
Q
?
=
P
R
+
(C
+
D
i
)R
+
P
i
FQ
+
FD
i
.
i
Q
2
2
Kurva total cost untuk setiap purchase cost adalah cembung. Jumlah barang
yang
mempunyai biaya
minimum diperoleh melalui
turunan pertama dari total cost tahunan
sama dengan nol yang menghasilkan:
dTC (Q)
=
-
(C + D
i
)R
+
P
i
F
=
0,
dQ
Q
2
2
Qi* =
2R(C + Di)
PiF
?
i
?
2R
?
C
+
?
(U
e
-
1)(P
e-1
-
P
e
)
?
=
?
e=1
?
P
i
F
di mana i = 1, 2,…, j. Dengan demikian
formula di atas
merupakan bentuk EOQ yang
dimodifikasi dengan biaya tambahan yang ditambahkan pada order cost.
Karena kurva total cost
pada incremental
discounts bersifat
kontinyu,
maka total
cost minimum akan selalu terdapat pada sebuah EOQ yang valid. Meskipun sebuah EOQ
valid tetapi EOQ tersebut belum tentu optimal, valid EOQ yang lebih besar belum tentu
lebih
layak
dibanding
dengan
valid EOQ
yang
lebih
kecil
lainnya.
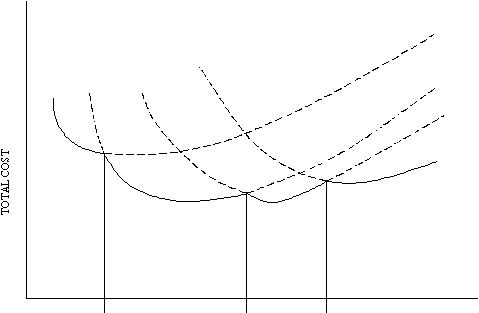
Seperti
yang
ditunjukkan pada Gambar 2.5, setiap EOQ yang valid mungkin merupakan ukuran yang
optimum sehingga setiap EOQ yang valid harus diperiksa. Ukuran yang optimum
|
 21
ditentukan
melalui perhitungan total cost per tahun pada setiap EOQ yang valid. Suatu
EOQ dikatakan valid apabila
U
i
=
Q
i
*
<
U
i
+1
(Nilai EOQ harus berkisar di antara
interval jumlah pada setiap price break).
TC (Q
0
)
TC (Q
1
)
TC (Q
2
)
TC (Q
3
)
U
1
U
2
U
3
QUANTITY
Gambar 2.5 Incremental quantity discounts
Sumber : Principles of Inventory and Materials Management(1994,p112)
2.1.7.2. Special Sale Prices
Seorang
supplier
mungkin akan
memberikan
potongan
harga
(discount)
sewaktu-
waktu
pada
suatu
barang,
khususnya saat kegiatan pengisian gudang (regular
replenishment cycle)
dilakukan.
Alasan
memberikan
potongan
harga
tersebut
dapat
disebabkan karena adanya kompetisi/perang
harga
di
pasar,
mau
pun
hanya
sekedar
mengurangi
jumlah barang di
gudang. Reaksi yang
logis dari pembeli
sewaktu tawaran
ini diberikan pada saat regular replenishment adalah memesan lebih banyak barang agar
memperoleh
keuntungan.
Jika
special order
tersebut
disetujui,
maka
manajer
harus
menentukan berapa jumlah optimum yang harus dipesan.
|
 22
s
Asumsikan
ketika
pemesanan dilakukan, supplier
akan
memberikan pengurangan
harga pada barang. Harga reguler sebuah barang adalah P, tetapi harga pembelian
sekarang menjadi P - d, di mana d adalah pengurangan harga barang. Karena special sale
hanya sementara waktu, harga barang akan kembali menjadi P. Jumlah pesanan sebelum
dan sesudah pengurangan harga adalah: Q*
=
2CR
.
PF
Untuk
memperoleh
hasil
optimal
special order,
perlu
dimaksimalkan
perbedaan
biaya selama periode waktu
Q
ˆ
/
R
dengan
mau pun tanpa special order. Situasi
persediaan secara grafik dapat digambarkan seperti pada Gambar 2.6. Biaya total (total
cost) selama periode Q
ˆ
/
R
,
ketika tawaran special order diambil pada harga P-d, adalah
sebagai berikut.
total cost = purchase cost +
holding cost + order cost,
TC = (P -
d
)Q
ˆ
+
Q
ˆ
2
(P - d
)
FQ
ˆ
+
C
R
=
(P
-
d
)Q
ˆ
+
(P
-
d
)FQ
ˆ
2
2R
+
C.
|
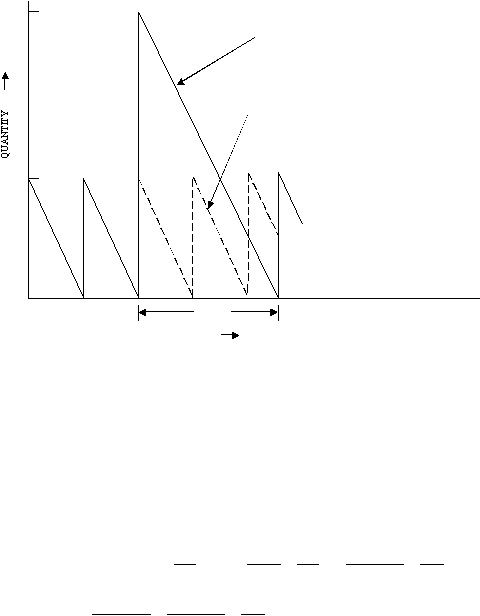 23
Q
ˆ
Special Order
No Special Order
Q
*
Q
ˆ
/
R
TIME
Gambar 2.6 Special sale price
Sumber: Principles of Inventory and Materials Management(1994,p114)
Jika special order tidak diambil selama
Q
ˆ
/
R
, total cost ketika pesanan pertama
dilakukan saat
harga
P-d
dan
seluruh
pesanan
kemudian
yang
dilakukan
saat
harga P
adalah sebagai berikut.
TC
n
=
(P
-
d
)Q *
+
P(Q
ˆ
-
Q*)
+
Q
*
(P
-
d
)
2
FQ *
+
2R
Q
*
PF
2
(Q
ˆ
-
Q*)
+
R
CQ
ˆ
Q
*
=
PQ
ˆ
-
dQ *
-
dF (Q*)
2
2R
PFQ * Q
ˆ
+
2R
CQ
ˆ
+
Q
*
d = pengurangan harga barang,
P = biaya pembelian (purchase cost) barang sebelum diskon,
C
= biaya pemesanan (order cost) per pesanan,
F = pecahan biaya penyimpanan (holding cost) per tahun,
R = permintaan (demand) tahunan dalam unit,
Q* = jumlah pesanan ekonomik (EOQ) dalam unit,
|
 24
?
?
Q
ˆ
= ukuran special order dalam unit.
Untuk
mendapatkan special order
yang optimal, perbedaan total cost
harus
dimaksimalkan, sehingga turunan pertama sama dengan nol.
g
=
TC
n
-
TC
s
= penghematan biaya special order
?
2
?
ˆ -
(
)
ˆ
2
(
*)
2
=
?
d
+
C
?Q -
P
-
d FQ
-
dQ * -
dF
Q
-
C,
?
Q
*
?
2R
2R
dg
=
d
+
2C
-
(P
-
d
)FQ
ˆ
=
0,
dQ
ˆ
Q
ˆ
*
=
Q
*
dR
(P -
d
)F
R
+
PQ *
=
ukuran optimum special order
P
-
d
Ketika potongan
harga barang adalah
nol (d=0),
maka
formula
untuk
ukuran
special
order yang optimum kembali ke formula EOQ dan penghematan biaya bernilai nol
(g=0). Dengan
menggantikan
Q
ˆ
dengan
Q
ˆ
*
pada formula penghematan biaya g,
maka
penghematan biaya optimum yang diperoleh adalah: g* =
C
(P - d )
?
Q
ˆ
*
-
1
?
.
?
?
P
?
Q
*
?
Karena g* selalu positif, maka special order tetap boleh dilakukan ketika
suatu diskon
barang ditawarkan selama waktu regular replenishment.
Formula
pengoptimalisasi
pada
special order
di
atas
mengasumsikan
bahwa
pemberian
potongan
harga
terjadi
saat
regular
replenishment (ketika
stock
position
mencapai reorder
point). Dalam
beberapa
kasus, potongan
harga ditawarkan sebelum
regular replenishment. Dengan demikian manajer harus memutuskan apakah special
order
tetap
dilakukan
atau
tidak. Jika
special order
dilakukan
sebelum
waktu
regular
replenishment dan stock position masih
tersedia q unit, formula optimasi adalah sebagai
berikut.
|
 25
?
Q
ˆ
*
=
dR
(P
-
d
)F
+
PQ *
-
q,
P
-
d
?
?
?
g* =
C
?
?
Q
ˆ
*
?
2
?
?
?
?
-
1
?
.
?
?
?
?
?
?
?
P
P
-
d
?
?
Q
*
?
?
?
?
?
Dalam
situasi
ini,
menerima
tawaran
special
order
tidak
selalu
menguntungkan.
Penghematan
biaya
hanya
bernilai
positif
ketika
ukuran
special
order
melebihi
P
/(P
-
d
)
kali EOQ. Keputusan
untuk melakukan special order
untuk
Q
ˆ
*
jika
Q
ˆ
*
>
P
/(P - d ) Q*. Jika
Q
ˆ
*
=
P
/( P -
d Q*, abaikan special order dan lakukan
) Q*, abaikan special order dan lakukan
pemesanan pada Q* pada waktu regular replenishment.
Sebagai tambahan, formula
untuk
Q
ˆ
*
diperoleh dari lead time sama dengan nol. Jika lead time tidak sama dengan
nol,
stock position q pada saat
special order dilakukan
harus
dikurangi
dengan
permintaan lead time (reorder point).
2.1.7.3. Known Price Increases
Supplier biasanya memberitahukan bahwa kenaikan harga suatu barang akan terjadi
pada beberapa waktu yang akan datang. Respon yang logis dari pembeli adalah memesan
barang lebih banyak agar memperoleh keuntungan dari harga sekarang yang masih
murah.
Jika
pemesanan
dilakukan
sebelum harga
naik,
tanggungjawab
manajer
adalah
menentukan berapa banyak jumlah pesanan yang harus dilakukan.
Asumsikan bahwa
harga sebuah barang akan naik sejumlah k pada suatu
waktu t1
.
Pembelian barang sebelum t
1
masih bernilai P, tetapi pembelian sesudah t1
akan bernilai
P + k. Dengan demikian, jumlah pembelian sebelum kenaikan harga diberitahukan
adalah:
|
 26
Q*
=
2CR
= EOQ sebelum harga naik.
PF
Karena seluruh pembelian berikutnya akan dihitung pada harga baru (P+k), maka jumlah
pesanan optimal akan menjadi:
Q
*
=
2CR
(P + k )F
=
Q
*
P
P
+
k
=
EOQ setelah harga naik.
Jika dianggap bahwa replenishment lead time adalah nol, keadaan known price dilukiskan
oleh Gambar 2.7. Kenaikan
harga terjadi
sebelum stock position mencapai batas tanda
penghabisan,
dan
bukan
saat
regular
replenishment. Seperti
yang
ditunjukkan
dengan
garis
yang bercetak tebal, suatu special order
Q
ˆ
dilakukan pada waktu t
1
,
ketika stock
position berjumlah q unit. Pembelian berikutnya akan terjadi pada waktu t
3
setelah waktu
lalu
(Q
ˆ
+
q)
/
R
(setelah special order
dan
stock
position
telah
habis).
Jika
tidak
ada
special order yang dilakukan, pembelian selanjutnya akan terjadi pada waktu t
2
,
setelah
waktu
lalu q/R (setelah stock position dikosongkan). Untuk
memperoleh
ukuran special
order
yang
optimal,
diperlukan
maksimalisasi
perbedaan biaya
dari
t1
hingga
t
3
atau
selama (Q
ˆ
+
q) / R
dengan mau pun tanpa special order.
Total cost selama periode
(Q
ˆ
+
q) / R
ketika suatu special order dibeli pada harga P
per unit barang, adalah sebagai berikut.
total cost
=
purchase cost
+
holding cost
+
order cost
TC
=
PQ
ˆ
+
Q
ˆ
PF
q
+
Q
ˆ
PF
Q
ˆ
+
q
PF
q
+
C
s
R
2
R
2
R
=
PQ
ˆ
+
PFqQ
ˆ
+
PFQ
ˆ
+
PFq
+
C
.
R
2R
2R
|
 27
Q
Q
+
2
a
Jika tidak ada special order
yang dilakukan selama
(Q
ˆ
+
q)
/
R
,
maka total cost ketika
seluruh pesanan dibeli pada harga P+k adalah sebagai berikut.
Q
ˆ
Q
*
*
a
q
t
1
t
2
t
3
TIME
Gambar 2.7 Known price increase
Sumber : Principles of Inventory and Materials Management(1994,p118)
TC
n
=
(
P
+
k Q
)Q
ˆ
+
a
(P
+
k
)F
Q
ˆ
2
R
+
q
PF
2
q
CQ
ˆ
*
a
=
(P
+
k
)Q
ˆ
+
(P
+
k
)FQ
a
Q
ˆ
+
PFq
+
CQ
ˆ
=
(P
+
k
)Q
ˆ
+
2R
(P + k )FQ
*
Q
ˆ
R
2R
*
PFq
2
+
,
2R
k
= known price increases,
P
= biaya pembelian (purchase cost) barang sebelum kenaikan harga,
C
= biaya pemesanan (order cost) per pesanan,
F
= nilai pecahan holding cost tahunan,
R
= permintaan (demand) tahunan dalam unit,
q = stock position dalam unit ketika special order dilakukan,
|
 28
?
a
?
Q
-
-
Q* = EOQ sebelum kenaikan harga,
*
= EOQ setelah kenaikan harga,
Q
ˆ
= ukuran special order dalam unit,
ˆ Q
/ Q
*
*
Q Q
a
= jumlah pesanan dengan ukuran
Q
a
selama t
2
hingga t
3.
Untuk
mendapatkan
ukuran special
order
yang
optimal
(Q
ˆ
*) ,
perbedaan dalam
total cost harus dimaksimalkan, sehingga turunan pertama harus sama dengan nol.
g
=
TC
n
-
TC
s
=
penghematan biaya special order
?
=
?
k
+
(P
+
k
)FQ
*
PFq
?
ˆ
?
PFQ
ˆ
2
-
C,
?
R
R
?
2R
dg
(P
+
k
)FQ
*
PFq
PFQ
ˆ
a
dQ
ˆ
=
k
+
kR
-
-
R
R
R
(P
+
k Q
)Q
*
=
0,
Q
ˆ
*
=
+
a
-
q.
PF
P
Dengan
menggantikan
Q
ˆ
dengan
Q
ˆ
*
dalam bentuk penghematan biaya untuk g,
penghematan biaya optimum dapat diperoleh:
?
?
?
?
?
?
?
?
g*
C
?
P
?
Q
ˆ
*
?
-
1
?
=
C
??
Q
ˆ
*
?
-
1
?
.
=
?
P
+
k
?
Q
*
?
?
?
?
Q
*
?
?
?
?
a
?
?
?
?
?
?
Suatu
special order
Q
ˆ
*
menyebabkan penghematan biaya jika dan hanya jika g* > 0,
dan
hal
ini
hanya
terjadi
jika
Q
ˆ
*
/
Q
*
lebih besar dari satu.
Dengan
demikian,
suatu
special order
haruslah
dilakukan
hanya
jika
ukuran
special order
lebih
besar
dari Q*
(EOQ pada harga barang P).
Ukuran special order tersebut diperoleh dari suatu replenishment dengan lead time
sama dengan
nol.
Jika lead
time
tidak
sama
dengan
nol,
maka
stock
position q
pada
|
 29
?
?
?
?
waktu special order dilakukan haruslah dikurangi dengan permintaan lead time (reorder
point).
Bentuk optimasi
untuk
special order seperti di atas, diasumsikan bahwa kenaikan
harga
terjadi
ketika
stock
position bernilai
positif
dan
tidak
ada
kesempatan
untuk
menunggu regular replenishment. Jika special order dilakukan pada
saat regular
replenishment (ketika stock position mencapai reorder point), bentuk optimasinya adalah:
Q
ˆ
*
=
kR
(P +
k
)Q
*
+
a
,
PF
P
2
g* = C
?
Q
ˆ
*
?
-
1 .
?
Q
*
?
Karena g* selalu positif, maka suatu special order layak dilakukan ketika suatu kenaikan
harga dijumpai selama regular replenishment.
2.1.8. Kendala-Kendala Pembelian dalam Jumlah Banyak
•
Working Capital Restrictions
Jika working capital restrictions membatasi besarnya investasi terhadap persediaan
sebesar J dolar, maka penentuan tingkat persediaan yang terbaik dapat ditentukan dengan
metode Lagrange-multipliers. Permasalahannya dapat dinyatakan sebagai berikut.
Minimumkan G = order cost + holding cost
n
?
R C
Q
P
F
?
=
?
?
i
+
i i
?
i
=1
?
Q
i
2
?
n
dengan kendala g
=
?
P
i
Q
i
=
J
.
i
=1
2
Dari
permasalahan
minimalisasi
dengan
satu
batasan
masalah,
persamaan
Lagrangian dapat dirumuskan sebagai berikut:
|
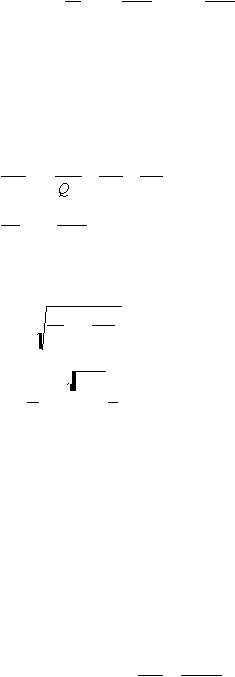 30
2
?
i
2
?
?
n
R
n
?
n
?
h
=
C
?
i
+
F
?
P
i
Q
i
+
??
?
P
i
Q
i
-
J
?
.
i
=1
Q
i
i
=1
2
?
i
=1
2
?
Untuk
meminimalisasi
fungsi
objektif
G
dengan
kendala
g
memerlukan
minimalisasi h
untuk
mendapatkan Q
i
dan ?.
Hal
ini dapat dicapai dengan
menghitung
turunan parsial yang nilainya disamadengankan nol.
?h
?
Q
i
=
-
CR
i
i
+
FP
i
+
?
P
i
2
2
=
0,
?h
n
P
Q
=
i i
??
2
-
J
=
0.
i
=1
Persamaan yang di atas menghasilkan Q
i
dan ? dengan rumusan sebagai berikut.
Q
*
=
2CR
i
,
(F
+
?
)P
i
?
n
?
C?
?
?
=
? =1
i
P
i
R
i
?
?
-
F .
2
J
2
•
Storage Restrictions
Jika storage space restrictions membatasi jumlah maksimum persediaan sebesar W
kaki
kubik,
maka
penentuan
tingkat
persediaan yang terbaik dapat diperoleh dengan
menggunakan
metode Lagrange multipliers. Permasalahannya
dapat dinyatakan
sebagai
berikut.
Minimumkan G
=
order cost
+
holding cost
n
?
R
C
Q
P
F
?
=
?
?
i
i
+
i i
?
i
=1
?
Q
i
2
?
n
dengan kendala g
=
?
w
i
Q
i
i
=1
=
W
,
W = total volume penyimpanan untuk seluruh barang dalam persediaan,
w
i
= ruang penyimpanan yang diperlukan untuk masing-masing unit dari barang i.
|
 31
2
i
i
=
i
Dari
permasalahan
minimalisasi
dengan
satu
kendala
masalah,
persamaan
Lagrangian dapat dirumuskan sebagai berikut.
n
R
n
P
Q
?
n
?
h
=
C
?
i
+
F
?
i
+
?
?
?
w
i
Q
i
-
W
?
.
i
=
1
Q
i
i
=
1
2
?
i
=
1
?
Untuk meminimumkan fungsi objektif G ditempuh cara sebagai berikut.
?
h
?
Q
i
=
-
CR
i
i
+
FP
i
2
+
?
w
i
=
0,
?
n
?
?
(
g
-
W
)
=
??
?
w
i
Q
i
-
W
?
=
0,
di mana
?
i
=1
?
?
=
0
jika g
-
W
<
0,
?
>
0
jika g - W = 0.
Dari persamaan di atas, persamaan untuk Q
*
dapat diperoleh.
*
2CR
i
.
FP
i
+
2
?
w
i
Dengan
menguji
nilai
?
yang berbeda,
dimungkinkan
penentuan
jumlah
pesanan
yang optimum yang memenuhi persyaratan kendala g.
•
Working Capital and Storage Restrictions
Masalah
akibat
keterbatasan
working
capital
mau
pun storage
space juga
dapat
merupakan kendala suatu sistem persediaan. Jika
investasi persediaan dibatasi
sebesar J
dolar
dan
storage
space maksimum
untuk
persediaan
adalah
W
kaki
kubik,
tingkat
persediaan yang terbaik dapat
diperoleh
dengan
menggunakan
Lagrange
multipliers
dengan KuhnTucker. Permasalahannya dapat dinyatakan sebagai berikut.
|
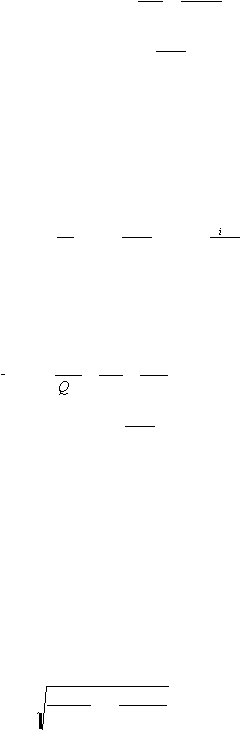 32
i
i
?
?
?
i
i
2
Minimumkan G
=
order cost
+
holding cost
n
?
R C
Q
P
F
?
=
?
?
i
i
+
i i
?
i
=
1
?
Q
i
2
?
n
P
Q
1
dengan kendala g
=
i
=
1
n
i i
=
J
,
2
dengan kendala g
2
=
?
w
i
Q
i
i
=1
=
W
.
Dari masalah minimalisasi dengan dua kendala tersebut maka persamaan
Lagrangian dapat dikembangkan menjadi:
n
R
n
P
Q
?
n
P
Q
?
?
n
?
h
=
C
?
i
+
F
?
i
+
?
1
?
?
-
J
?
+
?
2
?
?
w
i
Q
i
-
W
?.
i
=1
Q
i
i
=1
2
?
i
-1
2
?
?
i
=1
?
Untuk
meminimumkan
fungsi
objektif
G
dengan
dua
kendala
ditempuh
cara
sebagai
berikut.
?
h
?
Q
i
=
-
CR
i
i
+
FP
i
2
+
?
1
P
i
2
+
?
2
w
i
=
0,
?
n
P
Q
?
?
1
(
g
1
-
J
)
=
?
1
?
?
?
i
=1
i i
-
J
?
=
0,
2
?
?
n
?
?
2
(
g
2
-
W
)
=
?
2
?
?
w
i
Q
i
-
W
?
=
0,
di mana
?
i
=1
?
?
1
=
0
jika g
1
-
J
<
0,
?
1
>
0
jika g
1
-
J
=
0,
?
2
=
0
jika g
2
-
W
<
0,
?
2
>
0
jika g
2
-
W
=
0.
Persamaan untuk Q
*
dapat diperoleh:
Q
*
=
2CR
i
.
i
FP + ?
P
+ ?
w
i
1
i
2
2 i
Substitusikan persamaan Q
*
ke dalam kedua persamaan di atas, sehingga diperoleh:
|
 33
?
Q
?
?
?
?
?
=
?
?
n
2CR P
2
?
1
?
i i
-
J
=
0,
2
?
i
=1
FP
i
+
?
1
P
i
+
2
?
2
w
i
?
?
n
2CR w
2
?
?
2
?
?
FP
+
?
P
+
?
w
-
W
?
=
0.
?
i
=1
i
i
1 i
i
2
2 i
?
Dengan menguji kombinasi yang berbeda dari nilai ?
1
dan ?2
,
memungkinkan untuk
menentukan jumlah pesanan optimum
*
yang
memenuhi persyaratan dari batasan g1
dan g2. Proses dimulai dengan ?1 dan ?2
diberi nilai awal nol, kemudian salah satu ? tetap
bernilai
konstan
sedangkan ?
yang lain ditambahkan nilainya
sedikit demi
sedikit, dan
begitu juga sebaliknya.
2.2. Alat Bantu Perancangan
2.2.1. State Transition Diagram (STD)
STD digunakan untuk menggambarkan jalannya suatu program. Notasi yang
digunakan adalah sebagai berikut.
State bentuk seperti kotak persegi panjang
yang berfungsi menunjukkan kegiatan
atau keadaan atau atribut yang menjelaskan bagian tertentu dari program.
Kondisi
Aksi
Anak
panah
berarah
menunjukkan
perubahan
state yang
disebabkan
oleh
aksi
terhadap
kondisi
tertentu.
Kondisi
merupakan
suatu
event yang
dapat
dideteksi
oleh
sistem,
misalnya sinyal,
interupsi atau data. Hal
ini akan
menyebabkan perubahan dari
|
|
34
satu state ke state lain atau satu aktivitas ke aktivitas lainnya. Aksi merupakan hal yang
dilakukan oleh sistem jika terjadi perubahan state atau merupakan reaksi terhadap
kondisi. Aksi dapat menghasilkan output, tampilan pesan pada layar, kalkulasi atau
kegiatan lainnya.
2.2.2. Database
Adalah
kumpulan
dari
data-data
yang
saling
berhubungan
antara
satu
dengan
yang lain, yang dirancang untuk menyimpan informasi bagi kepentingan suatu organisasi.
|