|
7
BAB II
LANDASAN
TEORI
2.1 Pemeliharaan atau
Maintenance
2.1.1 Pengertian Pemeliharaan
Pemeliharaan
atau
dalam
istilah
asingnya
disebut
maintenance adalah
kegiatan untuk memelihara atau menjaga fasilitas / peralatan pabrik dan mengadakan
perbaikan
atau
penyesuaian
/
penggantian yang
diperlukan
supaya
terdapat
suatu
keadaan operasi produksi
yang memuaskan sesuai dengan apa yang direncanakan. (
Assauri, 1980, hal 89)
Sedangkan maintanability didefinisikan sebagai kemungkinan komponen atau sistem
yang
jatuh
atau rusak
akan diperbaiki
pada kondisi
tertentu
dalam
suatu periode
waktu
saat
pemeliharaan dilakukan sesuai
dengan
prosedur
yang telah
ditentukan
(
Ebeling, 1997 hal 6 ).
Kegiatan
pemeliharaan
atau
maintenance
merupakan
kegiatan
yang penting
dalam
suatu
industri agar
produksi
dapat berjalan
lancar.
Dalam
usaha untuk
dapat
menggunakan terus
fasilitas
atau
peralatan
–
peralatan
produksi
agar
kontinuitas
produksi dapat terjamin, maka dibutuhkan kegiatan- kegiatan pemeliharaan dan
|
|
8
perawatan
yang meliputi kegiatan pengecekan, meminyaki dan perbaikan atau
reparasi
atas
kerusakan-
kerusakan
yang
ada
serta
penggantian
spare
part
atau
komponen yang
terdapat
pada
fasilitas
tersebut.
Semua
kegiatan
ini
sebenarnya
merupakan tugas maintenance.
Tugas – tugas atau kegiatan maintenance adalah : ( Sofyan Assauri,1980 )
Pemeriksaan (inspection), yaitu tindakan yang ditujukan terhadap sistem atau mesin
untuk mengetahui apakah sistem berada pada kondisi yang diinginkan.
Servis
(service),
yaitu
tindakan
yang
betujuan
untuk
menjaga kondisi
suatu
sistem
yang biasanya telah diatur dalam buku petunjuk pemakain sistem.
Penggantian
komponen
(replacement),
yaitu
tindakan
penggantian komponen
yang
dianggap
rusak
atau
tidak
memenuhi
kondisi
yang
diinginkan. Tindakan
penggantian
ini
mungkin
dilakukan
secara
mendadak
atau
dengan
perencanaan
pencegahan terlebih dahulu.
Repair,
yaitu
tindakan
perbaikan
minor yang
dilakukan pada
saat
terjadi
kerusakan
kecil.
Overhaul,
yaitu tindakan
perbaikan
besar-besaran
yang
biasanya dilakukan diakhir
periode tertentu.
2.1.2 Tujuan pemeliharaan
Tujuan utama fungsi pemeliharaan adalah : ( Sofyan Assauri, 1980, hal 89)
1. Kemampuan produksi dapat memenuhi sesuai dengan rencana produksi.
|
|
9
2. Menjaga kualitas pada tingkat yang
tepat untuk memenuhi apa yang dibutuhkan
oleh produk itu sendiri dan kegiatan produksi yang tidak terganggu.
3. Untuk
membantu
mengurangi
pemakaian
dan
penyimpangan
yang
ada
di
luar
batas
dan
menjaga
modal
yang diinvestasikan dalam
perusahaan
selama
waktu
yang
ditentukan
sesuai
dengan
kebijaksanaan perusahaan
mengenai
investasi
tersebut.
4. Untuk
mencapai
tingkat
biaya
pemeliharaan
serendah
mungkin
dengan
melaksanakan kegiatan maintenance secara efektif dan efisien keseluruhannya.
5. Menghindari kegiatan maintenance yang dapat membahayakan pekerja.
6. Mengadakan
suatu kerja sama
yang
erat dengan
fungsi –
fungsi
utama lainnya
dari
suatu
perusahaan dalam
rangka
untuk
mencapai
tujuan
utama perusahaan,
yaitu tingkat keuntungan atau return of investment yang sebaik mungkin dan total
biaya yang rendah.
2.1.3 Jenis
–Jenis
Pemeliharaan
Bedasarkan jenisnya pemeliharan terbagi atas dua yaitu reactive maintenance
dan proactive maintenance.
2.1.3.1 Reactive Maintenace
Yang termasuk dengan reactive
maintenance
adalah corrective
maintenance.
Corrective
maintenance
merupakan kegiatan pemeliharaan setelah adanya peralatan
atau mesin yang rusak atau break down. Perawatan
ini
dilakukan
pada
pabrik –
pabrik
yang menggunakan permesinan
yang tidak
mahal karena biasanya
|
|
10
melengkapinya dengan
mesin
cadangan
yang
selalu
siap
sehingga bila
mesin
yang
beroperasi mengalami kerusakan dapat digantikan. Breakdown Maintenace dilakukan
setelah peralatan rusak dan tidak ada pencegahan. Jenis pemeliharaan ini mempunyai
kelemahan yaitu bila mesin rusak mendadak maka otomatis kegiatan produksi
berhenti
dan
menimbulkan waktu
mengganggur (
idle
)
mesin
untuk
diperbaiki
sehingga target produksi mungkin tidak tercapai.
2.1.3.2 Proactive Maintenance
Proactive maintenance merupakan pemeliharaan yang dilakukan secara
terencana tanpa menunggu mesin rusak terlebih dahulu sehingga dapat meminimasi
terjadinya downtime akibat kerusakan mesin. Yang termasuk dalam praoctive
maintenance adalah :
1. Preventive Maintenance
Preventive maintenance adalah kegiatan perawatan yang dilakukan secara
terjadwal, umumnya secara periodik, di mana sejumlah tugas pemeliharaan
seperti inspeksi, perbaikan, penggantian, pembersihan, pelumasan, dan
penyesuaian dilakukan.
Tujuan preventive maintenance adalah untuk meningkatkan performansi
peralatan. Semua fasilitas yang mendapatkan preventive maintenance akan
terjamin kelancaran kerjanya dan selalu diusahakan dalam kondisi atau keadaan
yang siap digunakan untuk setiap operasi atau proses produksi. Preventive
maintenance umumnya dilakukan berdasarkan data kerusakan di masa lalu di mana
umumnya data kerusakan suatu sistem memiliki hubungan yang erat dengan
|
|
11
distribusi statistik tertentu. Karena itulah dalam pelaksanannya, preventive
maintenance memiliki hubungan erat dengan realibility dan maintainability
engineering.
Dalam
prakteknya
preventive maintenance
yang
dilakukan
oleh
suatu
perusahaan
pabrik dapat dibedakan
menjadi
dua
yaitu
routine
maintenance
dan
periodic
maintenance.
Routine maintenance
adalah
kegiatan
pemeliharaan
dan
perawatan yang dilakukan secara
rutin
misalnya setiap hari. Sebagai contoh dari
kegiatan routine
maintenance adalah pembersihan fasilitas / peralatan, pelumasan
(
lubrication
)
atau pengecekan olinya serta pengecekan
isi
bahan bakarnya dan
mungkin termasuk pemanasan ( warming up ) dari mesin – mesin selama
beberapa
menit
sebelum
dipakai
beroperasi sepanjang hari
sedangkan
periodic
maintenance adalah kegiatan pemeliharaan dan perawatan yang dilakukan secara
periodik
atau
dalam
jangka
waktu
tertentu,
misalnya
setiap satu
minggu sekali
lalu
meningkat
setiap
bulan
sekali dan akhirnya
setiap
setahun
sekali.
Periodic
maintenance dapat dilakukan pula dengan memakai lamanya jam kerja mesin atau
fasilitas produksi
tersebut sebagai
jadwal
kegiatan,
misalnya
setiap
seratus
jam
kerja mesin sekali dan seterusnya. Jadi sifat kegiatan maintenance ini tetap secara
periodik atau berkala. Kegiatan periodic
maintenance
ini adalah jauh
lebih berat
daripada
kegiatan routine
maintenance.
Sebagai
contoh
dari
kegiatan periodic
maintenance adalah pembongkaran carburator ataupun pembongkaran alat – alat
di bagian sistem aliran bensin, penyetelan katup –
katup pemasukan dan
|
|
12
pembuangan cylinder mesin dan pembongkaran mesin / fasilitas
tersebut
untuk
penggantian pelor roda ( bearing ) serta service dan overhaul besar ataupun kecil.
2. Predictive Maintenance
Menurut Harold Amrine (1982, hal 234), predictive maintenance atau
diagnostic maintenance adalah pemeliharaan yang dilakukan melalui analisa secara
fisik terhadap peralatan / komponen dengan bantuan pengukuran instrumen
tertentu seperti alat pengukur getaran, amplitudo meter, temperatur pengukur suara,
dll untuk mendeteksi kerusakan sedini mungkin.
2.2
Keandalan atau
Reliability
Keandalan atau
reliability
adalah
probabilitas
sebuah
komponen
atau
sistem
akan
dapat
beroperasi sesuai
fungsi
yang
diinginkan untuk
suatu
periode
waktu
tertentu ketika digunakan di bawah kondisi operasi yang telah ditetapkan. ( Ebeling,
1997, hal 5). Reliability merupakan probabilitas ketidakgagalan dalam suatu waktu.
Keandalan didefinisikan sebagai suatu kemungkinan bahwa sistem atau hasil
produksi dapat berperan / berguna pada keadaan yang memuaskan pada suatu waktu
periode yang telah ditentukan jika dipergunakan pada suatu kondisi operasi yang
telah ditetapkan (Gunawan, 1997)
2.3
Ketersediaan atau
Availibility
|
 13
Ketersediaan atau availability adalah probabilitas sebuah komponen /
sistem
beroperasi sesuai
fungsi
yang
diinginkan untuk suatu
periode
waktu
tertentu
ketika
digunakan di bawah kondisi operasi yang telah ditetapkan. ( Ebeling, 1997, hal 6).
Availabilitas juga dapat diinterpretasikan sebagai persentase waktu operasi
dari sebuah komponen atau sistem selama interval waktu tertentu atau persentase
komponen yang beroperasi pada waktu tertentu. Perbedaannya dengan reliabilitas
adalah bahwa availabilitas adalah probabilitas bahwa komponen saat ini dapat
beroperasi meskipun sebelumnya komponen tersebut pernah rusak/ gagal dan telah
dipulihkan atau dikembalikan pada kondisi operasi yang normal. Karena itu
availabilitas sistem tidak pernah lebih kecil nilainya daripada nilai reliabilitasnya.
Availabilitas merupakan nilai yang lebih sering digunakan pada komponen/ sistem
yang dapat diperbaiki karena memperhitungkan baik kegagalan/ kerusakan maupun
perbaikan.
2.4
Fungsi
Keandalan
Keandalan merupakan probabilitas bahwa sebuah sistem ( komponen) akan
berfungsi dengan baik hingga periode t dalam kondisi operasi yang ditetapkan. Dapat
digambarkan sebagai berikut :
R(t) = Pr {T
t }..............................................................................(2.1)
dimana :
R
(t)
=
fungsi keandalan dengan R(t)
0, R(0) = 1, dan lim
t
R(t) = 0
|
 14
T
=
variabel acak time to failure ( waktu saat terjadinya kerusakan sistem atau
komponen ) dan T
0
Dengan memasukkan fungsi kepadatan peluang, maka :
R(t) = 1 – F(t) ............................................................................(2.2)
t
R(t )
1
f
(t)dt .........................................................................(2.3)
0
R(t )
f
(t )dt
...........................................................................(2.4)
t
Untuk 0 = R(t) = 1 dan
0 = F(t) = 1
(Ebeling Charles., hal 23)
2.5
Hazard Rate
Function
Hazard rate function sering kali disebut pula failure rate ( laju kerusakan )
atau instantaneous
failure rate ( laju kerusakan sesaat). Fungsi ini menggambarkan
probabilitas bahwa suatu peralatan akan rusak pada interval waktu berikutnya,
sedangkan sampai saat t, alat tersebut masih dalam kondisi baik. Dilambangkan
dengan
(t).
( Ebeling, 1997, hal 29).
|
 15
s
Kondisi kemungkinan komponen baru akan rusak antara selang waktu t dan t
+
s dinyatakan sebagai : P{ t < T = t + s}. Untuk menyatakan bahwa komponen tetap
bekerja sampai sekarang adalah :
P{ t < T = t + s | T > t }................................................................................(2.5)
Dengan mengingat teori probabilitas :
P{A | B}
P{A
B}
.................................(2.6)
P{B}
Pada kasus tertentu A
B , A
B = A , sehingga
P{A | B}
P{A}
.....................(2.7)
P{B}
Dinyatakan sebagai
P{t
T
t
s | T
t}
P{t
T
t
s}
F
(t
s)
F (t )
P{T
t}
R(t )
Kita membaginya dengan s dan s mendekati nol
1
F
(t
s)
F (t)
f
(t )
lim
s
0
R(t )
.................................................................................(2.8)
R(t )
(t)
f
(t )
1
F (t )
f
(t )
............................................................................................(2.9)
R(t )
dimana :
(t) adalah fungsi laju kerusakan
f (t) adalah fungsi kepadatan peluang
R
(t) adalah fungsi keandalan
|
|
16
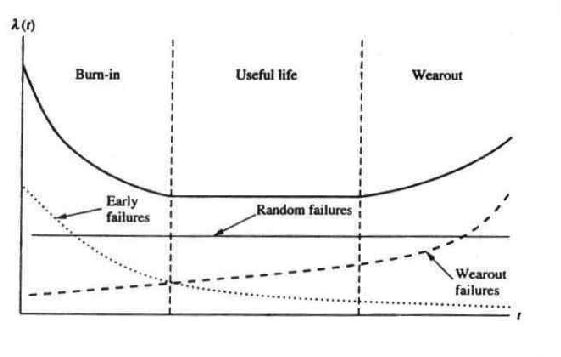
2.5.1 Bathtup Curve
Bentuk penting dari
hazard rate function adalah bathtub curve. Sistem yang
laju kerusakannya berbentuk bathtub curve, mengalami laju kerusakan yang menurun
pada siklus awal, diikuti dengan laju kerusakan konstan dan kemudian laju kerusakan
yang meningkat. Bathtub curve menunjukkan tiga daerah yang memiliki laju
kerusakan yang berbeda, yaitu : ( Ebeling, 1997, hal 31)
Daerah I : Fase Kerusakan Awal ( Startup Failure atau Early Failure )
Laju kerusakan pada tahap ini terus menurun yang diawali dengan tingkat
laju kerusakan yang cukup tinggi pada awal operasi yang kemudian terus
menurun yang diistilahkan dengan DFR ( Decreasing Failure Rate ).
Kerusakan yang terjadi pada fase ini dapat disebabkan oleh berbagai
penyebab, seperti kesalahan proses manufaktur yang diatasi dengan
percobaan acceptance dan pengontrolan pada awal operasi.
Daerah II: Fase Umur Pakai yang Berguna ( Chance Failure atau Useful Life)
Tahap ini ditandai dengan laju kerusakan yang konstan atau CFR ( Constant
Failure Rate). Kesalahan- kesalahan operasional merupakan penyebab dari
kerusakan pada fase ini sehingga pelaksanaan operasi yang tepat dapat
mengatasi kerusakan yang terjadi.
Daerah III: Fase Keausan ( Wear- out Failure)
Fase ini memiliki laju kerusakan yang terus meningkat atau IFR (Increasing
Failure Rate) yang disebabkan oleh berakhirnya umur pakai peralatan. Untuk
|
 17
mengurangi laju kerusakan harus dilakukan perbaikan perawatan
pencegahan.
Gambar 2.1. Kurva Bathtub ( Ebeling , 1997, hal 31)
Secara keseluruhan, perawatan pencegahan dapat mengurangi laju kerusakan
yang terjadi. Namun demikian untuk daerah I ( burn in ) dan II ( useful life )
sebaiknya perawatan pencegahan yang dilakukan bukan berupa penggantian
pencegahan karena tindakan ini tidak dapat mengurangi probabilitas kerusakan yang
terjadi. Tindakan penggantian pencegahan yang dilakukan akan sia – sia. Penggantian
pencegahan hanya dilakukan untuk mengurangi laju kerusakan pada daerah III (
wearout). Sedangkan kebijaksanaan perawatan yang lebih umum, seperti overhaul,
pelumasan, dan pembersihan dapat diterapkan untuk ketiga daerah tersebut.
|
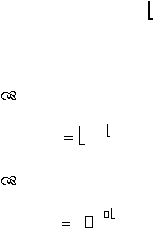 18
2.6
Distribusi
Kerusakan
Distribusi kerusakan dibagi menjadi dua jenis yaitu berdasarkan laju kerusakan
konstan atau tetap dan laju kerusakan tidak tetap ( naik atau turun ) berdasarkan
waktu. Untuk laju kerusakan tetap menggunakan distribusi eksponensial sedangkan
untuk laju kerusakan tidak tetap terdiri dari distribusi weibull, normal, dan lognormal.
2.6.1 Distribusi
Eksponensial
Distribusi eksponensial ini adalah distribusi yang paling populer digunakan
dalam teori keandalan. Distribusi ini digunakan untuk menghitung keandalan dari
distribusi kerusakan yang memiliki laju kerusakan konstan. Distribusi ini memiliki
laju kerusakan yang tetap terhadap waktu, dengan kata lain probabilitas terjadinya
kerusakan tidak tergantung pada umur alat. Distribusi eksponensial merupakan
distribusi yang paling mudah untuk dianalisa. Parameter yang digunakan dalam
distribusi eksponensial adalah
, yaitu rata – rata kedatangan kerusakan yang terjadi.
Fungsi – fungsi dari distribusi eksponensial adalah : (Ebeling, 1995, hal 42)
Probability density function
:
f
(t )
e
t
....................................................................................(2.10)
Cummulative density function
:
F
(t)
1
e
t
.....................................................................................(2.11)
|
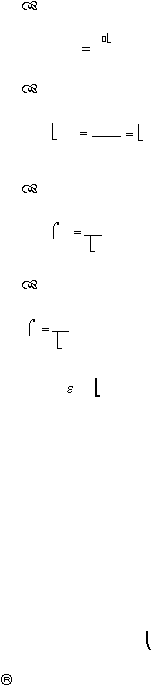 19
Reliability function
:
R(t)
e
t
...........................................................................................(2.12)
Hazard rate
function
:
t)
(t)
f
(t)
...................................................................................(2.13)
R(t)
Variansi
:
2
1
2
...............................................................................................(2.14)
Standar deviasi
:
1
...............................................................................................(2.15)
untuk t
0,
> 0; dimana t adalah waktu.
2.6.2
Distribusi
Weibull
Distribusi Weibull merupakan distribusi yang
paling banyak digunakan untuk
waktu kerusakan karena distribusi ini digunakan baik untuk laju kerusakan yang
meningkat maupun laju kerusakan yang menurun. Dua parameter yang digunakan
dalam distribusi ini adalah
yang disebut dengan parameter skala (scale parameter)
dan
yang disebut parameter bentuk ( shape parameter).
Fungsi – fungsi dalam distribusi Weibull adalah : (Ebeling, 1997, hal 59)
|
 20
2
Probability density function
:
1
t
/
f
(t )
t
e
.......................................................................(2.16)
Cummulative density function
:
¹
F
(t )
1
e
...................................................................................(2.17)
Reliability function
:
1
R(t )
e
........................................................................................2.18)
Hazard rate
function
:
t
1
t)
(t)
...................................................................................(2.19)
Variansi
:
2
1
2
2
1
1
........................................................20)
untuk
> 0,
> 0, x > 0, t
0
Distribusi Weibull ini sering digunakan dalam menentukan tingkat kegagalan.
Yang menentukan hal ini adalah nilai parameter
yang berkaitan dengan laju
kerusakan yang akan terjadi. Nilai – nilai
yang menunjukkan hal ini ditunjukkan
dalam Tabel 2.1:
( Ebeling, 1995, hal 63-64)
Tabel 2.1.
Nilai – nilai Parameter
dalam Distribusi Weibull
|
 21
Nilai
Laju Kerusakan
0 < ß < 1
Pengurangan laju kerusakan (DFR)
ß
= 1
Distribusi eksponensial (CFR)
1 < ß < 2
Peningkatan laju kerusakan (IFR), Konkaf
ß
= 2
Distribusi Rayleigh
ß
> 2
Peningkatan laju kerusakan (IFR), Konveks
3 = ß = 4
Peningkatan laju kerusakan (IFR), mendekati distribusi normal, simetris
Bila
( parameter bentuk ) memperngaruhi bentuk kurva ( laju kerusakan
naik atau turun ), maka
( parameter skala ) mempengaruhi nilai tengah dan sebaran
dari distribusi tersebut. Dengan bertambahnya
, nilai reliabilitas pada waktu tertentu
juga akan meningkat, yang berarti menurunnya laju kerusakan.
2.6.3
Distribusi
Normal
Distribusi normal dapat digunakan untuk memodelkan fenomena keausan.
Parameter yang digunakan adalah
( nilai tengah ) dan
( standar deviasi ).
Distribusi ini juga cocok untuk model kelelahan dan fenomena wear out mesin.
Karena hubungannya dengan distribusi lognormal, distribusi ini juga digunakan untuk
menganalisa probabilitas lognormal. (Ebeling, 1995, hal 69)
Fungsi – fungsi yang digunakan dalam distribusi normal adalah :
Probability density function
:
1
1
(t
)²
f
(t)
exp
2
2
2
.........................................................(2.21)
untuk : -
< t <
|
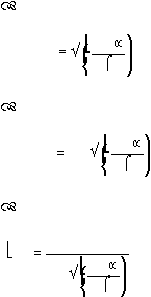 22
Cummulative
density function
:
t
F
(t )
..................................................................................(2.22)
Reliability function
:
t
R(t )
1
.............................................................................(2.23)
Hazard rate
function
:
t)
(t)
f
(t )
t
............................................................................(2.24)
1
2.6.4 Distribusi
Lognormal
Dalam distribusi ini dikenal adanya dua buah parameter, yaitu s sebagai
parameter bentuk ( shape parameter
) dan t
med
sebagai parameter lokasi ( location
parameter ) yang merupakan nilai tengah dari waktu kerusakan. Distribusi ini
dimengerti hanya untuk nilai t positif dan lebih sesuai daripada distribusi normal
dalam hal kerusakan. Seperti halnya distribusi Weibull, distribusi lognormal ini dapat
mempunyai berbagai bentuk. Seringkali dijumpai bahwa data yang sesuai dengan
distribusi Weibull sesuai pula dengan distribusi Lognormal. ( Ebeling,1995, hal 73)
Fungsi – fungsi yang digunakan dalam distribusi Lognormal :
|
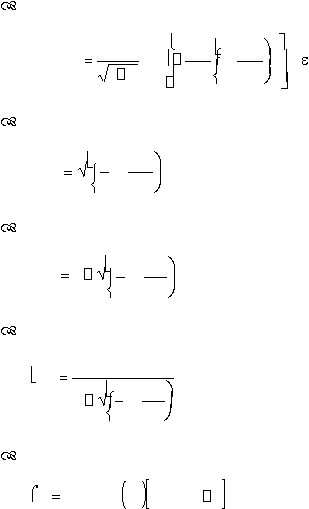 23
2
Probability density function
:
f
(t )
1
exp
1
ln
t
t
0
..................................(2.25)
2
st
2
2s
t
med
Cummulative density function
:
F
(t)
1
ln
t
..........................................................................(2.26)
s
t
med
Reliability function
:
R(t)
1
1
ln
t
.......................................................................(2.27)
s
tmed
Hazard rate
function
:
(t )
f
(t )
1
t
.......................................................................(2.28)
1
s
ln
tmed
Variansi
:
2
t
2
med
exp
s
2
exp(s
2
)
1
.........................................................(2.29)
Dimana : s adalah parameter bentuk ( shape parameter
)
t
med
adalah parameter lokasi ( location parameter
)
2.7
Identifikasi Distribusi
Pengidentifikasian
distribusi
dapat
dilakukan
dalam
tiga
tahap
yaitu
mengidentifikasi distribusi kandidat, estimasi parameter dan
uji goodness-of-fit.
|
 24
i
i
Perincian
mengenai
masing-masing
tahap diberikan pada
uraian berikut (
Ebeling,
1997, hal 359) :
2.7.1
Identifkasi distribusi kandidat
Identifikasi
distribusi
dapat
dilakukan
dengan dua
metode
yaitu
Probability
Plot dan metode Least-Square. Dengan Probability Plot dibuat dengan garis titik-titik
(t
i
,
F(t
i
)). Bila data tersebut menghampiri suatu distribusi, maka grafik yang terbentuk
akan
berbentuk
garis
lurus.
Probability
Plot
ini
juga
digunakan bila jumlah
sampel
terlalu kecil atau data yang digunakan tidak lengkap. Namun demikian metode Least-
Square Curve Fitting
lebih akurat dibanding dengan Probability Plot karena tingkat
subjektivitas untuk menilai kelurusan garis menjadi berkurang. Dengan metode
Least-Square Curve Fitting, distribusi
yang
terpilih
adalah distribusi yang
Index Of
Fit-nya terbesar.
Perhitungan umum pada metode Least Square-Curve Fiting, yaitu:
Nilai tengah kerusakan ( Pattrick O’ Connor, 1996, hal 70) :
F(t
i
)
=
i
0,3
n
0,4
...................................................................(2.30)
dimana : i adalah data waktu ke-t
n adalah jumlah data kerusakan
Index Of Fit (Walpole, 1995, hal 664) :
n
n
n
S
xy
=
n
x
i
y
i
x
i
y
i
......................................(2.31)
i
1
i
1
i
1
n
n
S
xx
=
n
x
2
x
....................................................(2.32)
i
1
i
1
|
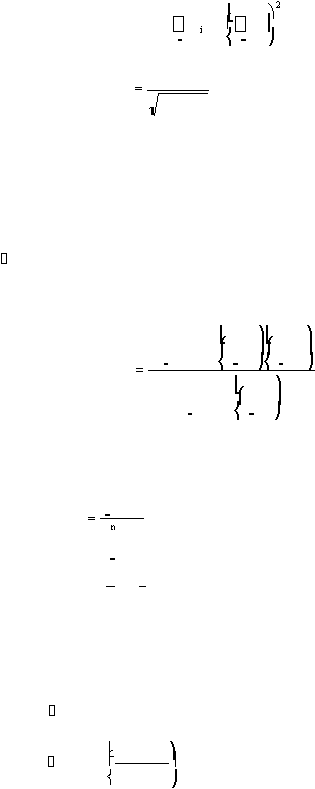 25
i
n
n
S
yy
=
n
y ²
y
...................................................(2.33)
i
1
i
1
S
xy
r
.....................................................................(2.34)
S
xx
xS
yy
dimana : n adalah jumlah kerusakan yang terjadi
r adalah index of fit
Gradien ( Walpole, 1995, hal 611) :
Untuk distribusi Weibull, Normal dan Lognormal :
n
n
n
n
x
i
y
i
x
i
y
i
b
i
1
i
1
i
1
2
..........................................(2.35)
n
2
n
n
x
i
x
i
i
1
i
1
Untuk distribusi Eksponensial ( Ebeling, 1997, hal 364) :
n
x
i
y
i
b
i
1
................................................................................(2.36)
x
i
2
i
1
Intersep a =
y
b x ....................................................................................(2.37)
Sedangkan perhitungan khusus untuk tiap distribusi yaitu :
a. Distribusi Eksponensial ( Ebeling, 1997, hal 363)
x
i
=
t
i
dimana t
i
adalah data ke-i.....................................................(2.38)
y
i
=
ln
1
.............................................................................(2.39)
1
F (t
i
)
|
 26
Parameter:
b ..............................................................................................(2.40)
MTTF=
1
.......................................................................................(2.41)
b
b. Distribusi Weibull ( Ebeling, 1997, hal 367)
x
i
=
ln t
i
dimana t
i
adalah data ke-i ...............................................(2.42)
y
i
=
ln ln
1
.........................................................................(2.43)
1
F (t
i
)
Parameter:
b dan
e
(
/
)
.................................................(2.44)
c. Distribusi Normal ( Ebeling, 1997, hal 370)
x
i
=
t
i
dimana t
i
adalah data ke-i ....................................................(2.45)
y
i
=
z
i
=
1
[F (ti)]
ti
............................................................(2.46)
Parameter:
1
dan
a
........................................................(2.47)
b
b
d. Distribusi Lognormal ( Ebeling, 1997, hal 371)
x
i
=
ln ( t
i
)
dimana t
i
adalah data ke-i ............................................(2.48)
1
1
y
i
=
z
i
=
1
[F (ti)]
ln t
ln t
med
.......................................(2.49)
s
s
Parameter : s
1
dan t
b
med=
e
s
.....................................................(2.50)
2.7.2
Pendugaan Parameter
|
 27
r
Estimasi
parameter
dengan
Maximum Likelihood
Estimator
(MLE)
memberikan
hasil
estimasi yang
lebih akurat dibandingkan perhitungan parameter –
parameter
pada Least
Square-Curve
Fitting.
Estimasi
parameter
untuk
tiap-tiap
distribusi menggunakan perhitungan sebagai berikut :
Distribusi Eksponensial ( Ebeling, 1997, hal 376)
Baik untuk data lengkap maupun data sensor, parameter
diperoleh dari :
r
T
...........................................................................................(2.51)
dimana : r = n = jumlah kerusakan
T = Total waktu Kerusakan
Distribusi Weibull ( Ebeling, 1997, hal 377)
Parameter
diperoleh dari persamaan berikut :
r
t
i
ln t
i
r
g
(
)
i
1
1
1
ln ti
0 ..........................................(2.52)
t
r
i
1
i
1
Penyelesaian persamaan diatas tidak dapat diselesaikan secara analitis, maka
harus
diselesaikan
secara
numerik
dengan
metode
Newton Rhapson
untuk
memecahkan permasalahan non linear dengan menggunakan persamaan :
g
(
j
)
dimana
g x)
' x)
dg ( x)
j
1
j
g (
' (
)
dx
|
 28
2
yang harus dipecahkan secara iterasi sampai mencapai nilai
ß
j
yang
maksimum (atau nilai g(ß) yang mendekati nol).
Maka terlebih dahulu adalah mencari turunan pertama dari g(ß) yaitu
r
r
r
t
ln
2
t
t
t
ln t
i
g (
' (
)
i
1
i
i
i
1
i
i
1
1
r
2
t
i
1
untuk
membantu
mempermudah penyelesaian
iterasi
metode Newton
Rhapson maka disarankan nilai ß
j
awal yang digunakan adalah nilai ß yang
didapat melalui metode Least Square.
r
1
/
Sedangkan parameter
diperoleh dari
1
t
..................(2.53)
r
i
1
dimana : r = n =jumlah data kerusakan
t
i
=
data waktu kerusakan ke –i
Distribusi Normal ( Ebeling, 1997, hal 378)
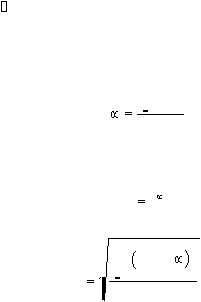
Estimasi parameter distribusi Normal menggunakan perhitungan :
n
(ti
t )
2
x =
i
1
..........................................................(2.54)
n
1
2
n
1
s²
n
n
(ti
t)
2
;
dengan s²
=
i
1
n
1
.............................(2.55)
dimana : t
i
=
data junlah kerusakan ke-i
|
 29
n = jumlah unit yang diamati
Distribusi Lognormal
Estimasi parameter distribusi Lognormal menggunakan perhitungan :
n
ln t
i
i
1
...........................................................................(2.56)
n
t
med
e
................................................................................(2.57)
n
ln t
i
2
s
i
1
.......................................................................(2.58)
n
1
dimana : t
i
= data waktu kerusakan ke-i dan n = jumlah unit yang diamati
2.7.3
Uji Goodness Of Fit
Langkah
terakhir
dalam pemilihan
distribusi
secara teori
adalah
dengan
uji
statistik
yaitu
Goodness
Of Fit.
Uji
ini
dilakukan
dengan
membandingkan
antara
hipotesis
nol
(H
0
) yang
menyatakan
bahawa
data
kerusakan
mengikuti
distribusi
pilihan dan
hipotesis
alternatif (H1) yang
menyatakan bahwa
data
kerusakan
tidak
mengikuti distribusi pilihan.
Pengujian ini merupakan perhitungan statistik yang didasarkan pada sampel
waktu kerusakan. Statistik ini kemudian dibandingkan dengan nilai kritis yang
diperoleh dari tabel. Secara umum, apabila pengujian statistik ini kurang dari nilai
kritis, maka H
0
diterima. Sebaliknya, bila nilai pengujian statistik ini lebih besar
daripada nilai kritis, maka H1
diterima.
|
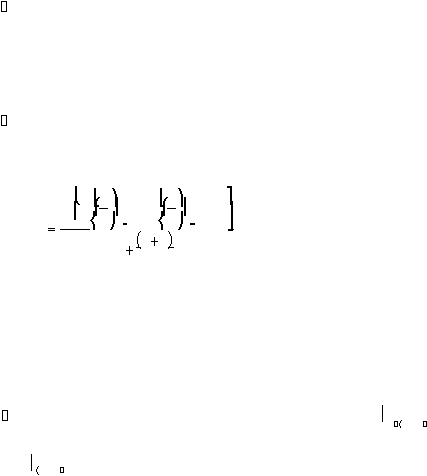 30
1
1
o
1
/ 2,
r
1
/ 2, r
1
Pada dasarnya ada dua jenis
uji
Goodness Of Fit yaitu uji
umum (General
Test)
dan
uji
khusus
(Specific Test).
Uji
umum
dapat
digunakan
untuk
menguji
beberapa distribusi sedangkan uji khusus masing-masing hanya dapat menguji satu
jenis
distribusi.
Dibandingkan
dengan
uji
umum, uji
khusus lebih
akurat
dalam
menolak suatu distribusi yang tidak sesuai. Uji umum
yaitu uji Chi-Square. Uji
khusus terdiri dari :
1. Bartlett’s Test untuk Distribusi Eksponensial ( Ebeling,1997, hal 399)
Hipotesis untuk uji ini adalah
H
0
= Data berdistribusi eksponensial
H1 = Data tidak berdistribusi eksponensial
Uji statistiknya adalah :
r
r
2r
ln
ti
ln ti
B
r
t
1
1
r
t
1
r
1
6r
................................................(2.59)
dimana : ti adalah data waktu kerusakan ke-i
r adalah jumlah kerusakan
B
adalah nilai uji statistik untuk uji Bartlett’s Test
H
diterima apabila nilai B jatuh dalam wilayah kritis
2
<
B
<
2
, dimana
:
distribusi chi-square memiliki r
–
1
derajat
kebebasan.
|
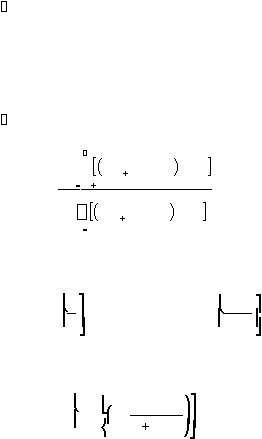 31
2. Mann’s Test untuk Distribusi Weibull ( Ebeling,1997, hal 400)
Distribusi ini dikembangkan oleh Mann, Schafer dan Singpurwalia pada tahun
1974.
Hipotesis untuk melakukan uji ini adalah
:
H
0
=
Data berdistribusi Weibull
H1 = Data tidak berdistribusi Weibull
Uji Statistiknya adalah :
r
1
k
1
ln t
i
1
ln
t
i
/
M
i
M =
i
k1
1
k1
k
2
ln t
i
1
ln t
i
/
Mi
i
1
.....................................................(2.60)
dimana :
r
r
1
k1 =
k2
=
............................................(2.61)
2
2
M
i
=
Z
i+1
-
Z
i
...................................................................................(2.62)
i
0.5
Zi = ln
ln
1
............................................................(2.63)
n
0.25
dimana : M adalah nilai uji statistik untuk Mann’s Test
t
i
adalah data waktu kerusakan ke-i
t
i+1
adalah data waktu kerusakan ke-(i+1)
[x] adalah bilangan integer dari x
r = n adalah jumlah unit yang diamati
i
adalah nomor data kerusakan (1,2,3,…,n)
|
 32
i
H
0
diterima bila M
< F
crit
(
,v1,v2)
.
Nilai F
crit
diperoleh dari
tabel
distribusi F dengan v
1
=
2 k2
dan v2 = 2 k
1.
3. Uji
Kolmogorov-Smirnov
Test
untuk Distribusi Normal
dan Lognormal
(Ebeling,1997, hal 400)
Uji ini dikembangkan oleh H.W. Lilliefors pada tahun 1967.
Hipotesis untuk uji ini adalah :
H
0
=
Data berdistribusi Normal (Lognormal)
H1 = Data tidak berdistribusi Normal (Lognormal)
Uji statistiknya adalah :
D
n
= max {D1, D2
}
dimana :
D1
=
max
t
i
t
i
1
.........................................................(2.64)
1
i
n
s
n
D2 = max
1
i
n
t
i
t
..............................................................(2.65)
n
s
Untuk distribusi normal :
n
ln ti
t
i
t
2
t
i
1
n
s²
=
i
1
.......................................... (2.66)
n
1
dimana : t
i
adalah data waktu antar kerusakan ke-i
t
adalah data waktu antar kerusakan
s adalah standar deviasi
n adalah banyaknya data kerusakan
|
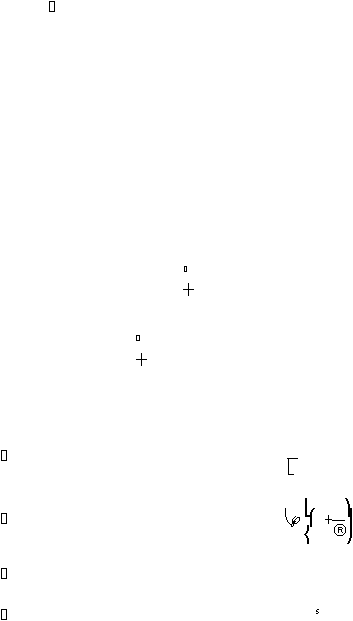 33
H
0
diterima bila D
n
<
D
crit
.
Sebaliknya, bila tidak maka tolak H
0
.
Nilai
D
crit
diperoleh dari tabel critical value
for the Kolmogorov-Smirnov
Test for normality (Lilliefors Test).
2.8
Mean Time To Failure
Mean Time To Failure ( MTTF) adalah rata- rata atau
nilai ekspektasi dari
probability density function f(t) yang diperoleh dari ( Ebeling, 1997, hal 26) :
MTTF = E(T) =
t. f (t )dt .............................................................(2.67)
00
MTTF =
R(t )dt ...........................................................................(2.68)
00
Perhitungan MTTF untuk masing-masing distribusi adalah sebagai berikut :
Distribusi Eksponensial
:
MTTF =
1
..............................................(2.69)
1
Distribusi Weibull
:
MTTF =
1
.................................(2.70)
Distribusi Normal
:
MTTF = µ................................................(2.71)
Distribusi Lognormal
:
MTTF = t
2
med
e
/
2
.....................................(2.72)
2.9
Mean
Time To Repair
Distribusi dari data waktu perbaikan adalah hal yang perlu diketahui terlebih
dahulu
sebelum
dapat
menentukan nilai
tengah
dari
fungsi
probabilitas waktu
perbaikan. Distribusi
yang sering
digunakan untuk
data
waktu
perbaikan
(MTTR)
|
 34
adalah
distribusi
lognormal
dan
eksponensial. Penentuan
atau
pengujian distribusi
dilakukan dengan cara
yang
sama
seperti
yang
telah dijelaskan pada
bagian
sebelumnya. MTTR diperoleh dari
( Ebeling, 1997, hal 192) :
MTTR
t.h(t )dt
1
(1
H (t ))dt
.............................................................(2.73)
0
0
dimana : h(t) adalah fungi kepadatan peluang untuk data waktu perbaikan.
H(t) adalah fungsi distribusi kumulatif untuk data waktu perbaikan.
Perhitungan MTTR untuk masing-masing distribusi adalah sebagai berikut :
Distribusi Eksponensial
:
MTTR =
1
..............................................(2.74)
Distribusi Lognormal
:
MTTR = t
2
med
e
/
2
....................................(2.75)
2.10
Model
Penentuan
Penggantian
Pencegahan
Optimal
Berdasarkan Kriteria Minimasi
Downtime
Penggantian pencegahan
dilakukan
untuk
menghindari
terhentinya
mesin
akibat
kerusakan komponen.
Untuk
melakukan tindakan perawatan
ini,
maka
harus
diketahui
interval
waktu antara
tindakan penggantian (t
p
)
yang
optimal dari
suatu
komponen sehingga dicapai minimasi downtime yang maksimal.
Pada model ini terdapat dua jenis model standar bagi permasalahn
penggantian
yang
dikemukakan
oleh
Jardine,
yaitu
model
Block
Replacement dan
model Age
Replacement.(
Jardine, 2001, hal 291- 292)
Adapun kedua model tersebut adalah sebagai berikut :
|
 35
1. Model Block Replacement
Pada
model
ini,
tindakan
penggantian
dilakukan
pada
suatu
interval
yang
tetap
serta
digunakan adanya
suatu
konsistensi
terhadap
interval
penggantian
pencegahan yang telah ditentukan walaupun sebelumnya telah terjadi penggantian
yang disebabkan karena adanya kerusakan.
Pelaksanaan dari
model ini
adalah
melakukan penggantian karena kerusakan
yang
terjadi dalam
interval (
0,
t
p
)
dengan
mengabaikan
frekuensi penggantian
yang terjadi selama selang
interval waktu tersebut, serta
melakukan penggantian
pencegahan
pada
setiap
selang
waktu
t
p
sekali
secara
konstan,
dengan
mengabaikan umur komponen.
Dalam
model
ini
akan
terdapat
kemungkinan dimana
komponen
yang
baru
dipasang setelah penggantian kerusakan
harus
mengalami penggantian lagi
pada
saat tiba waktu penggantian pencegahan harus dilakukan dalam kurun waktu yang
berdekatan.
Model ini terdapat pada gambar berikut :
Gambar 2.2. Model Block Replacement
(
Jardine, 2001, hal 291)
D(t
p
)
=
EkspektasiDowntimekarenaKerusakan
DowntimekarenaPenggantianPencegahan
PanjangSiklus
|
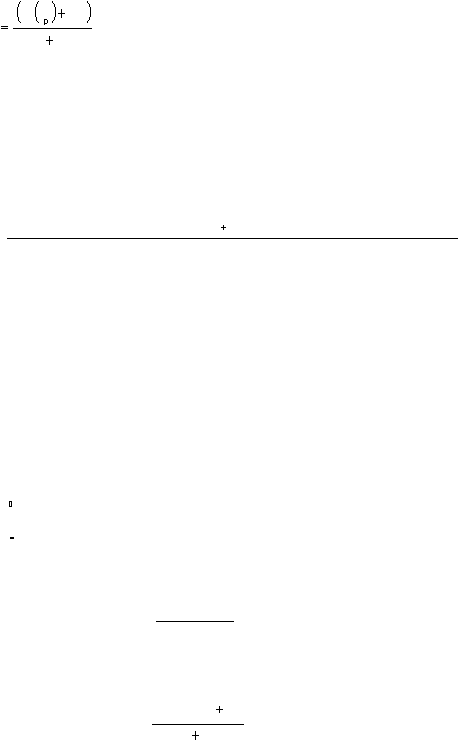 36
p
H
t
T
D(t
p
)
t
p
T
p
.............................................................................................(2.76)
dimana: t
p
=
interval waktu penggantian pencegahan
D(t
p
)
=
total downtime per unit waktu
H(t
p
)
=
ekspektasi jumlah kerusakan pada interval (0,t) = E[N(t)]
D(t
p
)
=
T
p
=
waktu untuk melakukan penggantian pencegahan
EkspektasiDowntimekarenaKerusakan
DowntimekarenaPenggantianPencegahan
PanjangSiklus
Downtime karena kerusakan =
Jumlah kerusakan pada interval (0,t
p
)
x waktu yang dibutuhkan untuk
penggantian kerusakan
=
H(t
p
)
x T
f
..................................................................................(2.77)
dimana T
f
adalah waktu perbaikan kerusakan komponen
H(t) =
Fr(t )
r
1
adalah ekspektasi jumlah kerusakan pada interval (0,t) dapat dihitung
dengan Transformasi Laplace, sehingga diperoleh:
H*(s) =
f
*
(s)
s[1
f
*
(s)]
........................................................(2.78)
Jadi,
D(t
p
)
=
H
(t
p
).T
f
T
p
......................................................(2.79)
t
p
T
p
b. Model Age
Replacement
|
 37
Pada
model
ini
tindakan
penggantian pencegahan dilakukan
pada
saat
pengoperasiannya sudah
mencapai umur yang diterapkan yaitu sebesar t
p
,
jika dalam
selang waktu t
p
tidak mengalami kerusakan. Jika sistem mengalami kerusakan
sebelum
t
p
,
maka
dilakukan
penggantian sebagai
tindakan
corrective.
Perhitungan
umur tindakan penggantian t
p
dimulai dari awal lagi dengan acuan dari
waktu
mulai
beroperasinya sistem
kembali
setelah
dilakukan
tindakan
perawatan
corrective
tersebut.
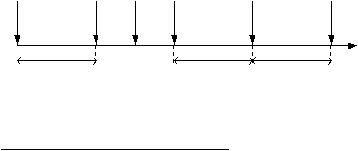
Model ini dapat dilihat pada gambar di bawah ini:
Gambar 2.3. Model Age Replacement ( Jardine, 2001, hal 294)
D(t
p
)
=
TotalEkspektasiDowntimeperSiklus
EkspektasiPanjangSiklus
............................................(2.80)
Total Ekspektasi downtime per siklus (EDS) =
Downtime yang
terjadi
pada
siklus
pencegahan
(preventive
cycle)
x
probabilitas terjadinya siklus pencegahan + ekspektasi downtime yang
terjadi pada siklus kerusakan (failure cycle) x probabilitas terjadinya siklus
kerusakan.
Atau:
Total ekspektasi downtime per siklus (EDS) = T
p
. R(t
p
)
+
T
f
. [1-R(t
p
)]..............(2.81)
|
 38
Ekspektasi panjang siklus kerusakan (EPS) =
Panjang
siklus
pencegahan x
probabilitas terjadinya
siklus
pencegahan +
ekspektasi
panjang
siklus
kerusakan
x
probabilitas terjadinya
siklus
kerusakan
Atau :
Ekspektasi panajang siklus kerusakan (EPS) =
(t
p
+
T
p
)
. R(t
p
)
+
(M(t
p
)
+
T
f
)
. [1-R(t
p
)].................................................(2.82)
Jika
f(t)
merupakan
fungsi
mean
time
to
failure maka
probabilitas
terjadinya
siklus
pencegahan
[R(t
p
)]
adalah
sama
dengan
probabilitas
munculnya
kerusakan
setelah waktu t
p
yang ditunjukkan oleh daerah yang diarsir. Sesuai dengan yang telah
dibahas sebelumnya mengenai fungsi keandalan, maka:
R(t
p
)
f
(t )dt ........................................................................................(2.83)
tp
Nilai tengah dari distribusi waktu kerusakan (Mean Time to Failure = MTTF) dari
suatu distribusi adalah sebagai berikut :
t
f
(t )dt ....................................................................................................(2.84)
dimana pada distribusi
normal selang
waktu kerusakan ini
merupakan rata-rata dari
distribusi
tersebut. Jika penggantian pencegahan dilakukan pada waktu t
p
maka nilai
tengah dari distribusi kerusakannya [M(t
p
)] adalah sebagai berikut:
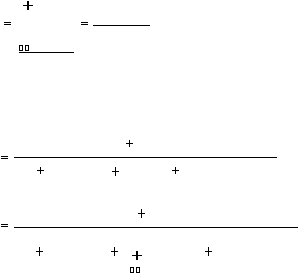
|
 39
M
(t
p
)
tp
t
f
(t
)dt
1
R(t
p
)
MTTF
1
R(t
p
)
...................................................................(2.85)
Jadi total dowmtime per unit waktu adalah:
T
p
.R(t
p
)
T
f
.[1
R(t
p
)]
D(t
p
)
...................................(2.86)
(t
p
T
p
).R(t
p
)
[M (t
p
)
T
f
].[1
R(t
p
)]
D(t
p
)
T
p
.R(t
p
)
T
f
.[1
R(t
p
)]
tp
(t
p
T
p
).R(t
p
)
[
tf (Tt )dt]
T
f
.[1
R(t
p
)]
.............................(2.87)
dimana:
T
f
= waktu untuk melakukan perbaikan kerusakan komponen
T
p
= waktu untuk melakukan penggantian pencegahan
t
p
= panjang interval waktu antara tindakan perawatan pencegahan
f(t) = fungsi kepadatan peluang dari waktu kegagalan komponen
2.11
Interval Waktu Pemeriksaan Optimal
Selain penggantian pencegahan maka pemeriksaan (inspeksi) juga diperlukan
dalam Preventive Maintenance untuk meningkatkan Availability. Tujuan dari inspeksi
adalah
untuk
mencegah
kegagalan
yang
tidak
terdeteksi
terutama
pada
saat
mesin
tidak
beroperasi
yang disebabkan
oleh korosi atau
kerusakan mekanik. Yang harus
diingat adalah bahwa
inspeksi
dapat
meningkatkan
Availability tetapi
tidak
dapat
meningkatkan reliabilitas.
|
 40
Tindak pemeriksaan juga bertujuan untuk meminimasi downtime mesin akbat
kerusakan yang terjadi secara tiba-tiba. (Jardine, hal 108). Konstruksi model interval
waktu pemeriksaan optimal tersebut adalah :
1.
1
= waktu rata-rata perbaikan
2.
1
= waktu rata-rata pemeriksaan
i
Menurut Jardine (hal 109) total downtime per unit waktu
merupakan
fungsi
dari frekuensi pemeriksaan (n) dan dinotasikan dengan D(n) yakni
D(n) = downtime untuk perbaikan kerusakan dan downtime untuk
pemeriksaan
D(n) =
(n)
n
....................................................................................(2.88)
i
Keterangan :
?(n) = laju kerusakan yang terjadi
n
= Jumlah pemeriksaan per satuan waktu
µ
= Berbanding terbalik dengan 1/µ
i
= Berbanding terbalik dengan 1/i
Diasumsikan bahwa laju kerusakan berbanding terbalik dengan jumlah pemeriksaan :
|
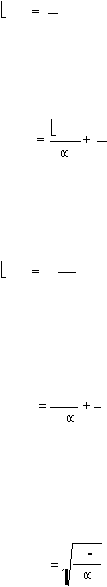 41
(n)
k
.................................................................................................(2.89)
n
dan karena
D(n)
(n)
n
.....................................................................................(2.90)
i
maka
(n)
k
n
2
..........................................................................................(2.91)
dan
D(n)
k
n
2
1
.....................................................................................(2.92)
i
dimana : k = nilai konstan dari jumlah kerusakan per satuan waktu sehingga diperoleh
:
n
k
i
....................................................................................(2.93)
2.12
Perhitungan
Peningkatan
Reliability
pada
Mean
Time
to
Failure Tanpa dan
Dengan
Preventive
Maintenance
|
|
42
Peningkatan keandalan dapat ditempuh dengan cara pemeliharaan
pencegahan.
Perawatan
pencegahan
dapat
mengurangi
pengaruh
wear
out dan
menunjukkan
hasil yang
signifikan terhadap
umur
mesin. Model keandalan berikut
ini
mengasumsikan
sistem kembali
ke kondisi
baru setelah
menjalani pemeliharaan
pencegahan. Keandalan pada saat t dinyatakan sebagai berikut : (Ebeling, 1997,
hal
204)
R
m
(t) = R(t)
untuk 0 = t = T....................(2.94)
R
m
(t)
n
= R(T) . R(t – T) untuk T = t = 2T.................(2.95)
Dimana :
T
: interval waktu penggantian pencegahan kerusakan.
R
m
(t)
:
menyatakan keandalan (reliability) dari sistem dengan pemeliharaan
pencegahan.
R(t)
: menyatakan keandalan sistem tanpa pemeliharaan pencegahan.
R(T)
: peluang dari keandalan hingga pemeliharaan pencegahan pertama.
R(t-T) : peluang dari keandalan antara waktu t – T
setelah sistem
dikembalikan pada kondisi awal pada saat T.
Secara umum persamaannya adalah sebagai berikut :
R
m
(t) = R(T)
n
. R(t – nT) untuk nT = t = ( n+1)T dan n = 0,1,2, ...........(2.96)
dimana :
R(T)
n
: probabilitas keandalan hingga n selang waktu pemeliharaan.
R(t – nT)
: probabilitas keandalan untuk waktu t-nT dari pemeliharaan
pencegahan yang terakhir.
Untuk laju kerusakan yang konstan : R(t) = e
-?t
maka :
|
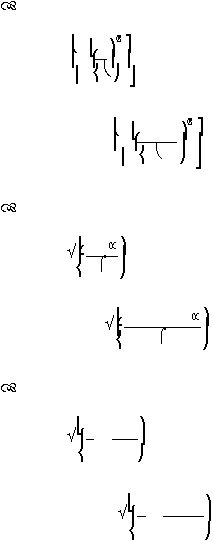 43
R
m
(t) = (e
-?t
)
n
. e
-?t(t-nT)
...............................................................................(2.97)
R
m
(t) = e
-?t
. e
-?t
. e
?t
= e
-?t
= R(t)...............................................................(2.98)
Ini membuktikan bahwa bila dilakukan preventive maintenance pada
distribusi eksponensial yang laju kerusakannya konstan, tidak menghasilkan dampak
apapun atau tidak ada peningkatan reliability seperti yang diharapkan.
Di bawah ini terdapat model keandalan untuk masing- masing distribusi yaitu
Distribusi Weibull ( Ebeling, 1997, hal 205)
T
R(t)= exp
..................................................................................(2.99)
t
nT
R( t – nT) = exp
.............................................................(2.100)
Distribusi Normal
t
R(t) = 1
.................................................................................(2.101)
(t
nT )
R( t – nT) = 1
.............................................................(2.102)
Distribusi Lognormal ( Ebeling, 1997, hal 206)
R(t) = 1
1
ln
t
.............................................................................(2.103)
s
t
med
R( t – nT) = 1
1
ln
t
nT
...............................................................(2.104)
s
t
med
|
|
44
m
R (t )
R(t )
Peningkatan keandalan =
x100% ....................................................(2.105)
R(t )
2.13
Penelitian
Relevan
Penelitian relevan yang menjadi bahan referensi penulis adalah “ Usulan
Penerapan Preventive Maintenance untuk meningkatkan availibility dan reliability
berdasarkan minimasi downtime .“ Penelitian ini dilakukan pada PT. Dynaplast, TBK
dan dilakukan oleh Sjakti Dewi ( 2003 ). Hasil dari penelitian ini adalah setelah
dilakukan penerapan preventive maintenace pada mesin maka reliability meningkat.
|