|
BAB 2
LANDASAN TEORI
2.1 Objek Fraktal
Fraktal memiliki dua arti yang saling berhubungan. Dalam penggunaan sehari-hari,
fraktal adalah bentuk yang dibentuk secara berulang atau self-simiar. Atau dengan kata lain,
sebuah bentuk yang mirip pada semua tingkat pembesaran. Karena alasan ini objek fraktal
seringkali
dianggap
“rumit
tidak
berhingga
–
infinitely
complex.”
Dalam sudut
pandang
matematika,
fraktal
adalah
objek yang
memenuhi spesifikasi
teknis tertentu. Spesifikasi
ini
adalah:
Dimensi Hausdorff > Dimensi Topologi (Mandelbrot, 1983, p361)
Objek-objek dengan spesifikasi ini sudah lama dikenal jauh sebelum kata fraktal ini di
definisikan. Objek-objek ini dapat ditemukan dalam kerajinan primitif di benua Afrika.
Konsep self-similar sudah timbul sejak abad ke 17. Pada tahun 1960, Benoit Mandelbrot mulai
mempelajari
konsep self-similar dan pada
tahun 1975
mulai
mempopulerkan istilah fraktal.
Asal usul penggunaan kata fraktal adalah:
”Fraktal berasal dari bahasa Latin, yaitu kata sifat “fractus” dan kata kerja “frangere”.
“Frangere”
berarti
memecah:
membuat
fragmen-fragmen
yang
tidak
beraturan.
Sebagai tambahan untuk istilah terfragmen (seperti dalam fraksi (fraction) atau
refraksi
(refraction)),
“fractus”
juga
berarti
tidak
teratur
atau
terfragmentasi,
tetapi
juga dapat berarti dimensi
fraksional (fractional dimensional). Keduanya berarti
terbagi dalam bentuk fragmen.” (Mandelbrot, 1983, p15)
5
|
|
6
Menurut Mandelbrot, (Mandelbrot, 1983, p16) fraktal
adalah
bentuk
geometri kasar
yang
terfragmentasi, dapat dibagi dalam beberapa bagian, dan tiap bagian merupakan
tiruan
dalam ukuran yang sama besar atau lebih kecil dari bentuk asli keseluruhannya.
Berdasarkan uraian tersebut, fraktal dapat dikatakan sebagai objek geometri yang
serupa dengan dirinya sendiri pada semua ukuran skala perbesarannya.
2.1.1 Sifat Objek Fraktal
Objek fraktal mempunyai sifat-sifat dasar yang membedakan objek-objek fraktal
dengan objek-objek geometri pada umumnya, yaitu:
y
Self-similarity, atau sifat keserupaan diri. Sifat ini berarti suatu objek fraktal terdiri dari
banyak tiruan yang sama, dari objek fraktal itu sendiri, dengan ukuran yang lebih kecil
terkubur di dalam bentuk aslinya. Dengan kata lain, terdapat kesamaan di dalam
bagian-bagian objek dibanding keseluruhan objek fraktal itu sendiri.
y
Infinite detail,
atau detil
yang
tak
berhingga.
Sifat
ini berarti
bahwa
semakin
objek
fraktal diperbesar akan didapatkan bentuk objek yang lebih mendetil. Detil dari objek
fraktal tidak terlihat langsung, tetapi akan muncul secara bertahap ketika objek fraktal
tersebut
dilihat
‘semakin
dekat’
dengan perbesaran.
Setiap
tahap
perbesaran
yang
semakin meningkat akan memunculkan detil-detil baru. Karena itu sifat ini juga berarti
bahwa objek fraktal tidak terpengaruh dengan ukuran skala, tidak mempunyai variasi
penskalaan (invariance of scale).
|
 7
(a)
(b)
Gambar 2.1 Segitiga Sierpinski
Sebagai
contoh,
segitiga
Sierpinski, salah satu jenis objek fraktal, pada
Gambar
2.1
ditunjukkan
dalam dua
macam ukuran
perbesaran.
Pada
Gambar
2.1(b),
yang
merupakan
perbesaran dari Gambar
2.1(a), terlihat detil-detil tambahan yang bentuknya serupa dengan
bentuk objek pada Gambar 2.1(a). Jika gambar semakin diperbesar, detil- detil baru akan terus
muncul.
2.1.1.1 Dimensi Objek Fraktal
Di
awal
bab
ini
didefinisikan
fraktal
memiliki
sifat:
dimensi
Hausdorff
>
dimensi
Topologi. Untuk itu diperlukan pengertian mengenai kedua dimensi tersebut.
Pada awalnya manusia mengenal dimensi paling dasar, sebuah dimensi klasik yang
seringkali disebut dimensi Euclidean. Dimensi ini adalah dimensi yang terdiri dari:
-
Garis dikenal
sebagai
satu dimensi,
atau
dimensi
dimana
diperlukan
satu
parameter
untuk menemukan sebuah titik. Seperti di gambarkan pada Gambar 2.2.
Gambar 2.2 Garis
|
 8
-
Bidang datar dikenal sebagai dua dimensi, atau dimensi dimana yang memerlukan dua
parameter untuk menentukan sebuah titik. Contohnya (x1
,y
1
), (x2
,y
2
), (x3
,y3) dan (x
4
,y
4
).
Contoh dua dimensi digambarkan pada gambar 2.3.
Gambar 2.3 Bidang Datar
-
Gambar 2.4 menggambarkan contoh bentuk bangun ruang. Bangun ruang dikenal
sebagai tiga dimensi, atau dimensi yang memerlukan tiga buah parameter untuk
menentukan
sebuah
titik
di
dalamnya.
Contohnya
(x1,y1,z1
), (x2
,y2,z2
), (x3
,y
3
,z3
),
(x
4
,y
4
,z
4
)
dan seterusnya.
Gambar 2.4 bangun ruang
Dari
pengertian
dimensi Euclidean, dapat diambil kesimpulan bahwa sebuah garis
merupakan satu dimensi, bidang datar merupakan dua dimensi, dan bangun ruang merupakan
tiga dimensi dan pada umumnya ruang Euclidean
sebagai n-dimensi. Atau, dimensi dari
sebuah ruang sama dengan jumlah parameter real yang diperlukan untuk menunjukkan titik
yang berbeda pada ruang.
|
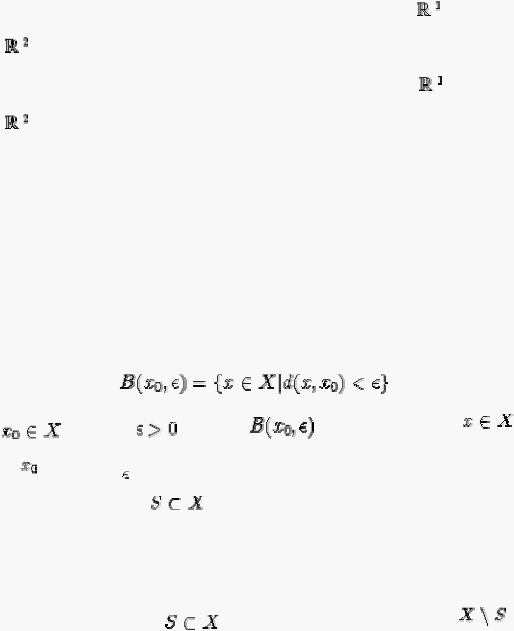 9
Pandangan dimensi euclidean mendapat sanggahan pada akhir abad ke-19 oleh dua
penemuan berikut:
•
Cantor set membuktikan adanya korespondensi satu-satu antara
(satu dimensi) dan
(dua dimensi).
•
Konstruksi Peano mengenai pemetaan
yang berkelanjutan dari
(satu dimensi) ke
(dua dimensi).
Sanggahan ini menunjukkan bahwa pandangan mengenai dimensi belum cukup kuat.
Pada awal abad ke 20, ahli matematika menemukan definisi yang tepat mengenai dimensi.
Definisi ini disebut dimensi topologi.
Sebagai permulaan perlu dimengerti mengenai open set dan closed set. Dalam sebuah
ruang metrik X didefinisikan (Barnsley, 1994, p12):
Open ball:
sebuah open ball dalam X adalah sebuah subset dalam bentuk
Untuk
dan radius
.
Artinya,
mengandung semua
dengan
jarak dari
kurang dari
.
Open: sebuah subset
adalah open jika
merupakan arbitrary union dari open
balls dalam X.
Artinya tiap titik dalam S dikelilingi oleh open ball
yang seluruhnya
berada di dalam X.
Closed: sebuah subset
adalah closed jika komplemennya dalam X
adalah open. Hal ini juga bisa digambarkan dengan mengatakan bahwa titik manapun
di dalam X yang merupakan limit dari deretan titik dalam S harus terkandung dalam S.
|
 10
Dalam ruang topologi X, dianggap bahwa tidak ada distance function, tetapi dianggap
apa yang merupakan open subsets. Artinya dimiliki sekelompok
dari subset X yang disebut
open subsets dari X. Kelompok ini harus memiliki tiga aksiom dasar topology:
•
Baik X dan
open.
•
Union dari open set apapun juga open.
•
Simpangan dari open set apapun adalah open.
Sebuah
subset S
dari
ruang topologi X
mewarisi
sebuah
topologi
dari
X.
dikatakan open jika ada open subset
seperti
. Ini disebut topologi
subspace pada S. Kemudian ada konsep lain yang berhubungan yaitu:
Covering: Sebuah covering dari subset S adalah kumpulan
dari open subset dalam X
dimana union-nya mengandung semua S.
Refinement: Sebuah refinement dari covering
dari S adalah covering lainnya berupa
dari S dimana tiap set B dalam
berada dalam beberapa set dalam set A dalam
.
Jadi set dalam
lebih kecil dari set dalam
dan
memberikan cakupan
yang lebih
rinci dari S.
Coverings
berperan
penting
dalam definisi dimensi
topologi
dan dimensi
Hausdorff.
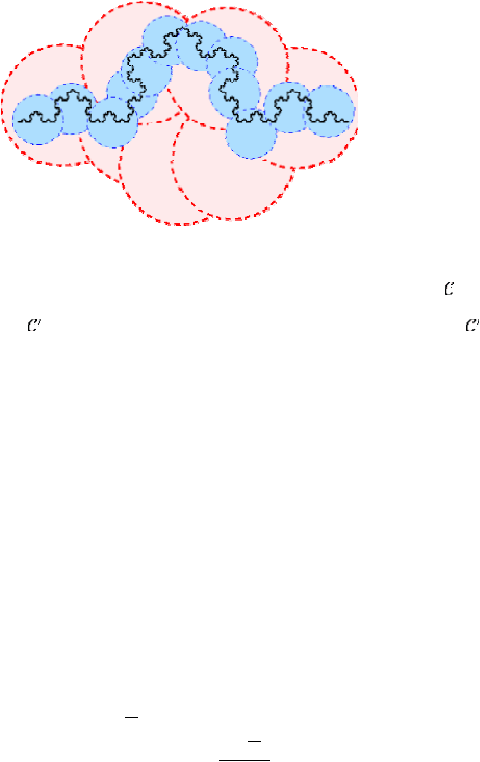
Sebagai
contoh,
pada
Gambar
2.5
ditunjukkan
covering
dari
kurva
Koch
dalam
warna
merah
dengan
garis
merah
putus-putus
yang menunjukkan batas dari lingkaran open, dan
refinement
dari
dengan warna biru. Terlihat bagaimana tiap lingkaran biru berada dalam
beberapa lingkaran merah, dan kurva Koch berada dalam union dari kedua covering.
|
 11
Gambar 2.5 Covering dari kurva Koch
Sebuah ruang topologi X memiliki dimensi topologi sebesar m jika tiap covering dari
X
memiliki refinement dimana tiap titik dari X berada pada paling besar m+1 set pada
,
dan m adalah paling kecil dari bilangan bulat ini. Gambar 2.5
menunjukkan gambaran untuk
menemukan refinement dari covering dari kurva Koch dimana tiap titik dari kurva berada pada
paling
banyak
dalam dua
set
pada
kurva Koch,
yang
menunjukkan
mengapa
kurva
koch
memiliki dimensi topologi bernilai 1.
Dimensi Hausdorff, didefinisikan oleh Felix Hausdorff (1868-1942), adalah dimensi
dengan definisi: Untuk objek apapun dengan ukuran (P) yang terdiri dari objek-objek dengan
ukuran (p), dan jumlah objek (N) yang dapat dimasukkan ke dalam objek
yang lebih besar
sama dengan rasio ukuran (P/p) dipangkatkan dimensi Hausdorff (d). (Tucek, 2006, p1)
d
?
?
log n
N
= ?
P
?
?
p
?
atau d
=
?
P
?
log
?
?
?
p
?
|
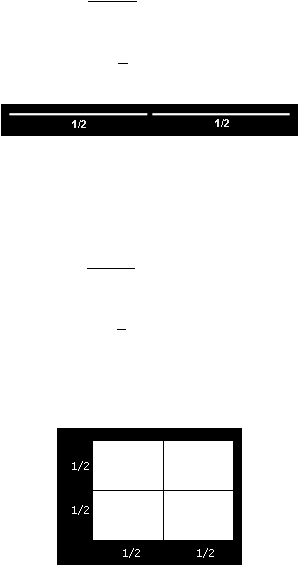  12
Sebelum
memulai
dengan
objek
fraktal,
dicontohkan
dengan objek
sederhana. Pada
Gambar 2.6 sebuah garis (satu dimensi) dengan (P) 2cm dibagi menjadi dua, akan didapatkan
dua buah garis (N) dengan (p) 1cm. Apabila Rumus diatas diaplikasikan.
d
=
log 2
log
?
2
?
maka
d
=
1
?
?
?
1
?
Gambar 2.6 Garis dibagi dua
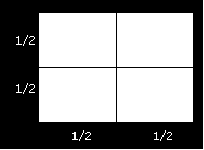
Sedangkan pada Gambar 2.7 sebuah bidang persegi dengan sisi (P) 2cm dibagi dua,
didapatkan empat (N) buah persegi dengan sisi (p) 1cm.
d
=
log 4
log
?
2
?
maka
d
=
2
?
?
?
1
?
Gambar 2.7 Bidang persegi dibagi empat
|
 13
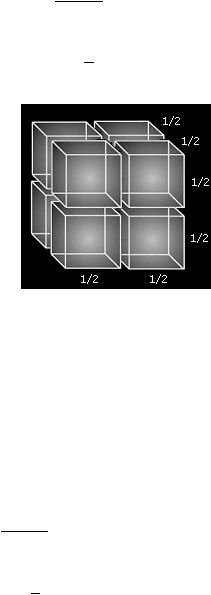
Terakhir, pada Gambar 2.8 tiap sisi sebuah kubus dengan sisi (P) 2cm dibagi dua, akan
menghasilkan delapan (N) buah kubus dengan sisi (p) 1 cm.
d
=
log 8
log?
2
?
maka
d
=
3
?
?
?
1
?
Gambar 2.8 Kubus dibagi delapan
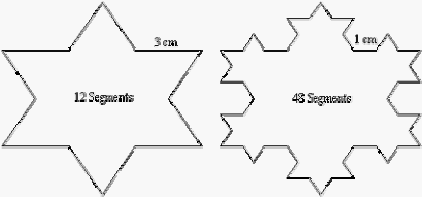
Sekarang persamaan diatas diaplikasikan dengan sebuah objek fraktal. Sebagai contoh
digunakan
kurva
Koch pada
Gambar
2.9.
Dengan
segmen
garis
yang
panjangnya
3cm (P),
dibuat
kurva
Koch,
yang
berbentuk bintang yang terdiri dari
12 segmen. Jika kurva ini
ditingkatkan dan
menggunakan segmen
garis dengan panjang 1cm
(p), jumlah segmen garis
yang digunakan meningkat menjadi 48 segmen garis. N = 48 segmen dibagi 12 segmen.
d
=
log 4
log?
3
?
maka
d
=
1.2618595071429
?
?
?
1
?
Hasilnya kurva Koch pada Gambar 2.9 memiliki dimensi 1.2618595071429. Jadi
kurva Koch memiliki dimensi Hausdorff > dari dimensi topologi (1.261859071429 > 1).
|
 14
Gambar 2.9 Kurva Koch
2.1.1.2 Klasifikasi Objek Fraktal
Fraktal diklasifikasikan berdasarkan kemiripannya dengan diri sendiri atau self-
similarity. Ada tiga jenis self-similarity dalam fraktal:
y
Exact self-similarity — bentuk terkuat self-similarity;
fraktal tampak sama persis pada
ukuran dan rasio berbeda. Fraktal yang dibuat oleh iterated function systems biasanya
menghasilkan jenis ini.
y
Quasi-self-similarity
—
bentuk
yang
lebih
lemah
dari
self-similarity;
fraktal
tampak
mirip (tetapi
tidak sama persis) pada
ukuran dan rasio yang berbeda. Fraktal
Quasi-
self-similar terdiri dari bentuk yang lebih kecil dari seluruh fraktal dalam bentuk yang
terdistorsi. Fraktal seperti ini biasanya dibuat dengan cara recurrence relations.
y
Statistical self-similarity — bentuk
self-similarity yang paling
lemah;
fraktal jenis
ini
memiliki ukuran numerik atau statistik yang dipertahankan pada ukuran dan rasio yang
berbeda. Sebenarnya ini bentuk fraktal yang
paling
dasar karena semua
fraktal
pasti
memiliki
bentuk
self-similarity
karena
fraktal
adalah ukuran
numerik
yang
dipertahankan pada ukuran apapun. Fraktal seperti ini biasanya di buat dengan Random
Fractal.
|
|
15
Perlu dicatat
bahwa
tidak
semua
objek
yang self-similar
adalah
fraktal
–
contohnya
garis nyata (garis Euclidean) berbentuk self-similar,
tetapi
karena
dimensi
Hausdorff dan
dimensi topologinya sama-sama bernilai satu, garis tersebut tidak termasuk fraktal.
2.1.2 Teori Chaos
Teori Chaos adalah adalah
teori
yang
menggambarkan pergerakan
rumit
dan
tidak
dapat ditebak atau dinamika sebuah sistem yang mudah berubah dari kondisi inisialnya.
Sistem Chaos
dapat
dijelaskan
secara
matematika
karena
mengikuti
hukum tertentu.
Tapi
karena sifat
berubah-ubahnya
akan tampak
acak bagi
mata
awam.
Teori
Chaos
merupakan
suatu bentuk perkembangan dari teori sistem dinamis (dynamical system), yang memfokuskan
pembahasan pada gerakan-gerakan yang sangat kompleks (highly complex motions) yang
dikenal dengan nama gerakan keotik (chaotic motions). Hal ini ditemukan oleh Henri Poincaré
sekitar tahun 1890-an dalam usahanya membuktikan kestabilan sistem tata surya (solar
system).
Poincaré menyatakan:
“Mungkin terjadi bahwa perbedaan kecil pada kondisi awal menghasilkan perbedaan
yang
sangat
besar
pada
fenomena
akhirnya.
Sebuah
kesalahan
kecil di awal akan
menghasilkan kesalahan besar di akhir. Hal
ini
menyebabkan prediksi
menjadi
mustahil (Microsoft Corporation, 2005, p243).”
Teori
sistem dinamis
sendiri
merupakan
cabang
ilmu
matematika
yang
membahas
berbagai
gerakan
(motion)
dalam berbagai
sistem yang
terbentuk
dan
senantiasa
berubah
berdasarkan aturan-aturan yang sederhana. Teori ini ditemukan pertama kali oleh Isaac
|
 16
Newton, sekitar abad ketujuhbelas, untuk memperagakan pergerakan sistem tata
surya,
bersamaan dengan teori gravitasi universalnya (universal gravitation) (Abraham, 2004, p16).
Chaos
terjadi
didalam suatu
sistem
dinamis,
yaitu
jika
dua
buah
titik
acak
yang
mendekati
titik
pemicu
(starting point) terbagi-bagi secara eksponensial, sehingga hasil
akhirnya menjadi tidak dapat diprediksi.
Fraktal juga merupakan salah satu dari sekian banyak topik menarik dalam teori
Chaos. Contohnya, pada Gambar 2.9, adalah jenis
fraktal dengan
metode Strange Attractor
dari persamaan
logistik (logistic equation),
yang
dapat
dilihat
pada Gambar 2.9(a)
berikut,
serupa dengan diagram bifurkasi dari metode Chaos pada Gambar 2.9(b)
Gambar 2.9 (a)
Gambar 2.9 (b)
Gambar 2.10 Perbandingan antara Fraktal dengan Chaos 2.9 (a) Objek Fraktal Strange
Attractors dan Persamaan Logistik, 2.9 (b) Diagram Bifurkasi
Fraktal berhubungan erat dengan chaos karena keduanya sama-sama merupakan sistem
yang kompleks, yang memiliki sifat-sifat yang jelas. Fraktal dan chaos, keduanya tidak sama,
walaupun fraktal sendiri sering kali dibentuk dari chaos.
Devaney (Devaney, 1990, p35)
mendefinisikan suatu
fungsi
sebagai chaotic function
jika fungsi tersebut cenderung tergantung pada kondisi-kondisi inisial,
jika
fungsi
tersebut
transitif secara topologis, dengan titik-titik periode yang padat dan teratur. Dengan kata lain,
sebuah
fungsi
merupakan
chaotic
function jika
fungsi
tersebut
tidak terduga, tidak dapat
diperkirakan, tidak dapat didekomposisi, tetapi tetap mengandung keteraturan. Sedangkan
|
|
17
Allgood
dan Yorke
mendefinisikan chaos
sebagai
jalur, garis,
atau
kurva yang
tidak
stabil
baik secara eksponensial maupun menurut periodenya (Strohbeen, 2006, p14).
Perilaku Chaotic sering dijumpai pada berbagai sistem seperti jaringan listrik,
penyebaran penyakit, laser, ritme jantung, aktivitas listrik pada otak, cairan, populasi binatang
dan reaksi kimia.
2.1.3 Metode Pembuatan Fraktal
Ada
beberapa
teknik
yang
biasa
digunakan untuk
membuat
fraktal.
Teknik-teknik
tersebut adalah:
y
Metode Iterated Function Systems
y
Metode Iterated Complex Polynomial
y
Metode L-system
y
Metode Strange Attractor
2.1.3.1 Metode Iterated Function System
Iterated
function systems
atau
IFS adalah sebuah
metode pembentukan
fraktal
yang
divisualisasikan ke dalam bentuknya seperti sekarang oleh John Hutchinson dan di populerkan
oleh Michael Barnsley dalam buku Fractals Everywhere.
Fraktal yang dibentuk dari IFS dapat berada pada dimensi spasial manapun (pada
dimensi
apapun).
Tetapi
biasanya
fraktal
IFS
di hitung
dan
di
gambar
pada
dua
dimensi.
Sebuah
fraktal
IFS
adalah
hasil dari
sebuah
persamaan set
rekursif.
Fraktal IFS tediri dari
union atau gabungan dari beberapa tiruan dirinya
sendiri.
Masing-masing
tiruan
ini
di
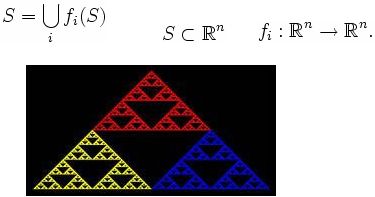
transformasikan oleh sebuah fungsi (function system). Contoh utama adalah Sierpinski gasket.
|
 18
Fungsi ini biasanya contractive yang berarti fungsi ini membawa titik-titik menjadi lebih dekat
dan membuat objek menjadi lebih kecil. Oleh karena itu bentuk fraktal IFS terdiri dari
beberapa tiruan objek yang lebih kecil dan saling tumpang tindih, yang masing-masing juga
terdiri
tiruan dirinya
sendiri.
Hal
ini
berlangsung secara tak hingga. Inilah yang membuat
fraktal IFS self similar. Hal ini dapat dilihat pada Gambar 2.11
Umumnya,
dimana
dan
Gambar 2.11 Sierpinski gasket dengan IFS
Secara umum ada dua metode dalam membentuk fraktal IFS. Metode pertama adalah
Supercopier dan metode kedua adalah metode Chaos game.
IFS Supercopier merupakan pendekatan yang menerapkan konsep mesin fotokopi
khusus yang memproduksi citra baru I1 dari citra awal I
0
.
Citra I
1
ini merupakan superposisi
dari beberapa reduksi citra I
0
.
Kemudian citra I1
diproses lagi dengan mesin fotokopi tersebut
untuk memproduksi citra I2
.
Proses ini dilakukan berulang-ulang hingga didapatkan citra- citra
baru (I3
,
I
4
,
…, I
k
)
yang merupakan komposisi bentuk yang lebih kecil dari citra awalnya.
Sedangkan metode Chaos Game, atau
yang
dikenal
dengan
nama
Algoritma
Iterasi
Acak (Random Iteration Algorithm) memberikan konsep nonrekursif yang sederhana untuk
memproduksi
gambar dari attractor IFS. Konsep ini
menghilangkan kebutuhan akan
memori
komputer
yang besar dalam
membentuk Fraktal IFS. Chaos Game sendiri
merupakan salah
satu bentuk penerapan dari teori Chaos.
|
 19
2.1.3.2 Metode L-System
Fraktal L-system dikembangkan oleh seorang ahli biologi, Lindenmayer, yang bekerja
dengan ragi dan jamur berfilamen dan meneliti pola pertumbuhan berbagai jenis ganggang
(algae), seperti
bakteri Anabaena
catenula. L-system awalnya di bentuk
untuk menyediakan
deskripsi
formal
perkembangan
organisme
multisel
yang sederhaha, dan
menggambarkan
hubungan antar
sel
tumbuhan. Kemudian,
sistem ini diperluas untuk menggambarkan jenis
tumbuhan yang lebih tinggi dan struktur dahan yang rumit
Perilaku rekursif L-system mengarah pada self similarity. Hal ini menyebabkan
bentuk-bentuk
natural
seperti
fraktal
mudah di
gambarkan
dengan
L-system.
Bentuk
tumbuhan dan bentuk organisme lainnya cukup
mudah untuk di definisikan karena dengan
memperbesar
tingkat
perulangan,
bentuk
ini akan tumbuh
dan
menjadi
lebih
rumit.
Contoh
hasil fraktal L-system digambarkan pada Gambar 2.12.
Gambar 2.12 Contoh hasil fraktal L-system
2.1.3.3 Metode Iterated Complex Polynomial
Metode Iterated Complex Polynomial digunakan
untuk menggambarkan bentuk-
bentuk fraktal yang menerapkan perhitungan bilangan kompleks. Contoh fungsi
perhitungannya
adalah
Julia
set
dan
Mendlebrot set. Penelitian pertama
tentang
metode
ini
dilakukan oleh Julia (1918) dan Fatou (1919-1920).
|
 20
Gambar 2.13 Mandelbrot set Metode Iterated Complex Polynomial
2.1.3.4 Metode Strange Attractor
Metode strange attractor, berhubungan erat dengan konsep space of phase
dan
attractor. Space of phase adalah ruang yang memiliki koordinat dari variabel yang digunakan
pada persamaan yang mendeskripsikan gerak. Untuk setiap pergerakan keotik, attractor
adalah sebuah garis dengan panjang tak terbatas, tapi selalu berisi dalam bagian yang terbatas
dari
space of phase. Tipe attractor
inilah
yang disebut dengan strange
attractor. Strange
attractor
ini
terbukti
juga
mempunyai
struktur
fraktal.
Hal
ini
dapat
dilihat
dari
bentuknya
yang tak beraturan yang
merupakan
garis-garis
yang tak terputus dengan detil-detil yang tak
berhingga. Strukturnya tampak sangat rumit. Contoh bentuk fraktal yang dapat dibuat dengan
menggunakan metode ini dapat dilihat pada Gambar 2.14.
Gambar 2.14 Kurva Simpanim metode Strange Attractor
|
 21
2.1.4 Fraktal Dalam Kehidupan Sehari-Hari
Fraktal digunakan hampir di setiap bidang ilmu. Beberapa metode fraktal digunakan
pada
bidang biologi
dan
obat-obatan,
seperti dalam pemodelan
sel, protein, struktur
kromosom, bentuk DNA, enzim dan
tumbuhan.
Bentuk-bentuk
fraktal sering dianggap mirip
dengan bentuk-bentuk yang ada di bidang biologi, seperti bentuk Julia set yang dianggap mirip
dengan bentuk sel, atau bentuk daun pakis yang
mendetil dengan menggunakan
metode IFS,
sehingga
untuk
menggambarkan
bentuk-bentuk biologi
pada
komputer
dapat
menggunakan
salah satu metode fraktal.
Selain aplikasi di bidang biologi,
fraktal juga digunakan untuk memperkirakan grafik
bursa
saham,
melukiskan seismic. Dari penerapan-penerapan ini, musik fraktal merupakan
bentuk
penerapan
yang
terkenal.
Dalam pembuatannya,
musik
fraktal
dapat
menerapkan
algoritma yang biasa digunakan untuk melukiskan suatu bentuk fraktal.
Di bidang
lainnya, fraktal juga dimanfaatkan dalam
proses pembuatan permainan di
komputer.
Banyak
bentuk-bentuk
fraktal
yang
dimanfaatkan
dalam pembuatan
permainan
seperti Bush yang digunakan sebagai bentuk tumbuhan di dalam permainan, dan Dragon curve
yang
dapat
dijadikan
suatu
peta
wilayah
dalam
permainan. Sebagai
contoh,
Gambar
2.15
menunjukkan
contoh
peta permainan
yang
digambar dengan
menggunakan
fraktal
Dragon
Curve.
Gambar 2.15 Peta Permainan dengan Dragon Curve
|
|
22
Algoritma fraktal juga dapat digunakan dalam membuat permainan itu sendiri. Selain
geometri
fraktal,
musik
fraktal yang
unik
juga digunakan sebagai
lagu
tema pengiring
yang
mengisi permainan di komputer. Fraktal juga sedang dikembangkan sebagai metode kompresi
gambar. Diharapkan kompresi dengan menggunakan metode fraktal dapat membuat kompresi
yang jauh lebih kecil dari metode kompresi yang ada saat ini.
Fraktal
juga
dimanfaatkan di bidang konstruksi
untuk
membuat
antena
yang
sangat
kompak dan optimal
untuk penggunaan komunikasi microwave maupun komunikasi selular.
Fraktal juga dimanfaatkan dalam fracture mechanics atau ilmu
memprediksi kerusakan atau
adanya retakan pada sebuah bangunan
2.2 Musik
Kata 'musik' berasal dari bahasa Yunani, mousike. Menurut Kamus Besar Miriam-
Webster, istilah musik (music) berarti (1) suatu komposisi atau kombinasi berbagai bunyi atau
suara (sound); (2) seni bunyi-bunyian, atau kumpulan bunyi atau suara.
Sound (suara) dihasilkan dari getaran, baik udara maupun benda-benda padat. Ketika
getaran itu bersifat tidak teratur, maka suara itu adalah noise; ketika getaran tersebut teratur,
maka suara itu disebut tone atau nada. Musik tergantung
dari nada, tidak termasuk
noise
(seperti
bunyi
simbal,
tabrakan,
piring
pecah, dan
lain-lain). Getaran
yang
pelan
akan
menghasilkan nada dan bunyi yang rendah (low), getaran yang cepat akan menghasilkan suara
yang lebih tinggi (high). Pada prakteknya suara musik berkisar antara 40 – 40000 getaran per
detik (hertz). Frekuensi dari getaran akan menghasilkan bunyi yang sering disebut pitch. Pitch
digunakan sebagai standar tinggi rendah dari sebuah tone atau nada.
|
 23
2.2.1 Tangga Nada
Komposisi bunyi atau suara tersebut merupakan kombinasi deretan frekuensi bunyi
yang berbeda-beda di dalam suatu interval nada yang disebut dengan satu oktaf. Istilah 'oktaf'
dapat diartikan 'jarak' antara nada dasar dan nada oktafnya atau nada kedelapannya. Istilah ini
digunakan, misalnya untuk menetapkan luas suara piano atau luas suara seseorang. Satu oktaf,
terdiri dari delapan (oktal) tingkat nada, yaitu dari nada do sampai nada do yang lebih tinggi.
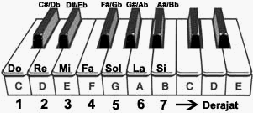
Secara keseluruhan, satu oktaf terdiri dari dua belas nada, nada C, C#, D, D#, E, F, F#, G, G#,
A, A#, dan B.
Gambar 2.16 Satu Oktaf Nada pada Tuts Piano
Gambar 2.16
menunjukkan
gambaran satu oktaf pada sebagian tuts-tuts (keys) piano.
Piano mempunyai 88 tuts, sedangkan keyboard biasa mempunyai 61 tuts. Semua nada disusun
secara continue dari yang terendah (sisi kiri) ke yang tertinggi (sisi kanan). Tuts putih, dalam
urutan dari kiri, disebut dengan nama huruf C D E F G A B, sedangkan yang hitam dinamakan
C# atau Db; D# atau Eb; F# atau Gb; G# atau Ab; A# atau Bb.
Jarak antara dua tuts putih adalah whole-tone atau satu nada, kecuali E-F dan B-C', dua
bagian
itu
berjarak semitone
atau halftone atau
setengah
nada.
Setiap semitone
mempunyai
perbedaan
frekuensi sekitar 1.059463hz.
Tuts
hitam
memisahkan
dua
tuts
putih,
jarak
tuts
putih ke tuts
hitam, dalam
hal ini
C-C#; D-
Eb; F-F#;G-
G#;A-A#, adalah semitone. Jarak
antar nada atau tone ini disebut interval.
|
|
24
Gambar 2.16
juga
menunjukkan 'derajat' pada nada dasar C diwakili dengan angka 1
sampai dengan 7. Pada Gambar 2.16 juga digambarkan solmisasi (solmization). Solmisasi
adalah nada yang pertama kali digunakan oleh Guido d'Arezzo (Italia, 1025), dengan nama ut
re mi fa sol la untuk 6 nada dari hexachord, pada awal abad XVII nada si ditambahkan dan
nada ut diganti menjadi nada do.
Antara C ke C' ada 11 tuts (baik hitam maupun putih). Satu oktaf (one octave) adalah
jarak terdekat antara dua nada yang sama tapi berbeda pitch, yang dipisahkan oleh 12
semitones atau bisa juga dibilang 11 tuts. Misalnya C ke C' atau E ke E', dan seterusnya. Jika
disebutkan dua oktaf
maka pengertiannya sama,
hanya saja dibedakan oleh (12x2) semitones
atau 24 semitones, begitu dengan tiga oktaf dan seterusnya.
Pada
Gambar
2.16
terdapat
tanda
#
dan
b.
Tanda
'b'
(flat atau
mol),
artinya
nada
tersebut diturunkan semitone. Misalnya Eb, artinya nada E diturunkan semitone menjadi
Eb.
Sebenarnya
tanda
flat atau
mol
bukanlah
huruf 'b',
tapi
.
Sedangkan
tanda
'#'
(sharp
atau
cruis), artinya nada
tersebut dinaikkan semitone. Misalnya F#, artinya F dinaikkan semitone
menjadi F#. C# dan Db; D# dan Eb; F# dan Gb; G# dan Ab; serta A# dan Bb disebut
enharmonic, yang artinya berbeda tanda dan huruf tetapi memberikan bunyi yang sama. Tanda
“
'
”
menunjukkan
tingkat
oktaf.
Misalnya
C',
berarti
C
satu
oktaf
lebih tinggi
dari
C.
Kebalikannya 'C, berarti C satu oktaf lebih rendah dari C. Tanda ''' juga menunjukkan nada
tertentu telah melewati C'.
Urutan
nada
pada
tangga
nada ditentukan
oleh nada dasar tangga nada tersebut dan
jenis tangga nada, apakah tangga nada mayor (major) atau minor. Tangga nada mayor adalah
tangga nada yang memiliki nilai interval nada 1 – 1 – ½ - 1 – 1 – 1 – ½. Tangga nada minor
|
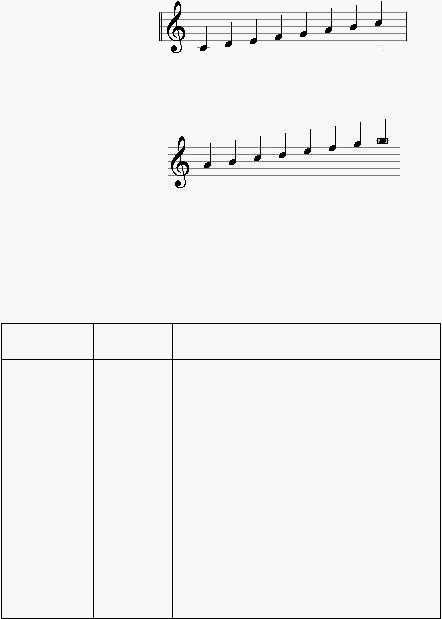 25
adalah tangga nada yang memiliki nilai interval nada 1 – ½ – 1 – 1 – ½ – 1 – 1. Tangga nada
paling dasar pada tangga nada mayor adalah (C = do) dan pada tangga nada minor (A = do).
Gambar 2.17 Tangga nada C Mayor pada not balok
Gambar 2.18 tangga nada A minor pada not balok
Pada Tabel 2.1 dan Tabel 2.2 dijelaskan urutan tangga nada mayor dan minor.
Tangga nada mayor
Tangga
Nada
Nada
Dasar
Urutan Nada
(7b)
(6b)
(5b)
(4b)
(3b)
(2b)
(b)
Natural
(#)
(2#)
(3#)
(4#)
(5#)
(6#)
(7#)
Cb
Gb
Db
Ab
Eb
Bb
F
C
G
D
A
E
B
F#
C#
Cb - Db - Eb - Fb - Gb - Ab - Bb - Cb
Gb - Ab - Bb - Cb - Db - Eb - F - Gb
Db - Eb - F - Gb - Ab - Bb - C - Db
Ab - Bb - C - Db - Eb - F - G - Ab
Eb - F - G - Ab - Bb - C - D - Eb
Bb - C - D - Eb - F - G - A - Bb
F
-
G
-
A
-
Bb - C - D - E - F
C
-
D
-
E
-
F
-
G
-
A
-
B
-
C
G
-
A
-
B
-
C
-
D
-
E
-
F# - G D
-
E
-
F# - G - A - B - C# - D A -
B
-
C# - D - E - F# - G# - A
E
-
F# - G# - A - B - C# - D# - E
B
-
C# - D# - E - F# - G# - A# - B
F# - G# - A# - B - C# - D# - E# - F#
C# - D# - E# - F# - G# - A# - B# - C#
Tabel 2.1 Tangga nada mayor
|
 26
Tangga nada minor
Tangga
Nada
Nada
Dasar
Urutan Nada
(7b)
(6b)
(5b)
(4b)
(3b)
(2b)
(b)
Natural
(#)
(2#)
(3#)
(4#)
(5#)
(6#)
(7#)
Ab
Eb
Bb
F
C
G
D
A
E
B
F#
C#
G#
D#
A#
Ab - Bb - Cb - Db - Eb - Fb - Gb - Ab
Eb - F - Gb - Ab - Bb - Cb - Db - Eb
Bb - C - Db - Eb - F - Gb - Ab - Bb
F
-
G
-
Ab - Bb - C - Db - Eb - F
C
-
D
-
Eb - F - G - Ab - Bb - C
G
-
A
-
Bb - C - D - Eb - F - G
D
-
E
-
F
-
G
-
A
-
Bb - C - D
A
-
B
-
C
-
D
-
E
-
F
-
G
-
A
E
-
F# - G - A - B - C - D - E
B
-
C# - D - E - F# - G - A - B
F# - G# - A - B - C# - D - E - F# C#
-
D# - E - F# - G# - A - B - C# G# -
A# - B - C# - D# - E - F# - G#
D# - E# - F# - G# - A# - B - C# - D#
A# - B# - C# - D# - E# - F# - G# - A#
Tabel 2.2 Tangga nada minor
Not dan nada (tone atau note) pada dasarnya adalah sama yaitu menunjukkan satu
karakter
suara dengan pitch tertentu. Beberapa
not tunggal dapat dirangkaikan dengan
tinggi
rendah yang berbeda. Rangkaian semacam ini disebut melodi.
|
|
27
2.2.2 Chord
Chord adalah dua atau lebih nada yang digunakan
pada
waktu
sama
atau
hampir
bersamaan. Chord terdiri dari sebuah
nada dasar
yang memberi
nama
utama chord tersebut
dan satu atau
lebih
nada lainnya. Nama kedua dari chord ditentukan dari nama nada selain
nada dasar pada chord tersebut. Chord yang
paling banyak
digunakan
adalah
chord
mayor,
chord minor, chord mayor minor atau yang dikenal sebagai chord ke tujuh, chord mayor ke
tujuh dan chord minor ke tujuh.
Susunan nada masing-masing jenis chord adalah sebagai berikut:
•
Chord mayor terdiri dari sebuah nada dasar, nada pada tangga nada mayor ketiga
dan
nada kelima. Contoh: chord C mayor terdiri dari nada C – E – G, dimana C
adalah
nada
dasar,
E
adalah
nada
ketiga
setelah
C
pada tangga
nada
mayor.
G
adalah nada kelima sesudah C
•
Chord
minor
terdiri dari sebuah nada dasar, nada pada tangga nada
minor ketiga
dan nada kelima. Contoh: chord C minor terdiri dari nada C – D# - G, dimana C
adalah nada
dasar,
Eb
adalah
nada
ketiga
setelah C
pada
tangga
nada
minor.
G
adalah nada kelima.
•
Chord
mayor
minor atau yang
lebih dikenal sebagai chord ke 7 terdiri dari chord
mayor yang ditambahkan nada minor ketujuh. Contoh: chord C7 terdiri dari nada C
–
E
–
G
–
Bb.
C
–
E
–
G
merupakan
nada-nada dari chord
C
mayor dan
Bb
merupakan nada ketujuh setelah C pada tangga nada minor.
•
Chord mayor ke 7 terdiri dari chord mayor yang ditambahkan nada mayor ketujuh.
Contoh: chord C7 terdiri dari nada C – E – G – B. C – E – G merupakan nada-nada
|
 28
dari chord C
mayor dan B
merupakan
nada ketujuh setelah C pada
tangga nada
mayor.
•
Chord minor ke 7 terdiri dari chord minor yang ditambahkan nada minor ketujuh.
Contoh: chord C7 terdiri dari nada C – Eb – G – Bb. C – E – G merupakan nada-
nada dari chord C minor dan
Bb
merupakan
nada ketujuh setelah C pada tangga
nada minor.
2.2.3 Tempo
Melodi memerlukan rangkaian nada yang memiliki perbedaan panjang
dan pendek
nada. Pada notasi balok, panjang pendeknya nada oleh bentuk atau wujud not-notnya, dan tiap
bentuk
not
mempunyai
nilai
tertentu.
Nilai
not
ini
dihitung dengan
satuan
hitungan
yang
disebut dengan ketukan.
Gambar 2.19 Nilai ketukan not
Secara umum nilai ketukan not bernilai 4 ketuk, 2 ketuk, 1 ketuk dan seterusnya. Pada
notasi balok, panjang not dapat diperpanjang dengan menambahkan sebuah titik. Titik ini akan
menambahkan nilai not sebesar 50% dari nilai not awal. Pada notasi angka, penambahan nilai
atau
panjang
ketukan diwujudkan
dengan
menambah
titik di
belakang
not
yang ditambah.
Sebagai contoh, jika
not bernilai 4 ketuk maka dalam not angka
untuk nada do akan ditulis
menjadi (1 . . .).
Dalam
musik,
kecepatan
lagu
mempengaruhi
bagaimana
lagu
tersebut
dinyanyikan
dan
apa
yang
di
sampaikan
oleh
lagu..
Istilah
untuk
menyatakan
kecepatan
lagu
dikenal
|
 29
dengan tempo. Pencipta lagu atau komponis, biasanya telah menetapkan tempo lagunya. Jika
diperlukan perubahan kecepatan di tengah-tengah lagu, dapat memakai perubahan tempo.
Terdapat delapan istilah tempo yang sering digunakan, yaitu seperti yang terdapat pada
Tabel 2.3.
Tingkat Kecepatan
Istilah Tempo
Kecepatan Ketukan
(per menit)
Lambat Sekali
Lambat
Sedang
Cepat
Cepat Sekali
Largo
Lento
Adagio
Andante
Moderato
Allegro
Vivace
Presto
40 - 60
60 – 66
66 – 76
76 – 108
108 – 120
120 – 160
160 – 184
184 – 208
Tabel 2.3 Istilah Tempo Utama
Delapan istilah tempo tersebut mewakili kecepatan ketukan setiap not per menitnya.
Dua
istilah yang pertama dan dua
istilah yang
terakhir
lebih sering digunakan dalam
musik
instrumental.
2.2.4 Musik Fraktal
Musik fraktal adalah musik yang merupakan
hasil
proses
rekursif
dimana
sebuah
algoritma diaplikasikan berulang kali untuk memproses output sebelumnya. Dalam pandangan
yang
lebih
luas,
semua
bentuk
musik,
dalam
tingkat
mikro
maupun
makro
dapat
di
buat
dengan proses ini.
Ada
beberapa
cara
untuk
membuat
musik fraktal
yang
merupakan
bentuk
dari
komposisi berdasarkan algoritma. Komposisi berdasarkan algoritma bergantung pada
algoritma
untuk menentukan
fitur-fitur lagu. Pada bentuk paling dasar, algoritma digunakan
|
|
30
untuk menentukan nada apa saja yang dimainkan beserta urutannya. Dalam bentuk yang lebih
rumit algoritma digunakan
untuk
menentukan kekuatan atau volume sebuah
not, tempo dan
panjangnya not.
Algoritma telah digunakan untuk membuat komposisi selama berabad-abad.
Contohnya, prosedur yang digunakan untuk
menentukan
suara
utama
dalam western
counterpoint
dapat
dipermudah
menjadi
determinan
algoritma.
Ada
dua
macam bentuk
komposisi algoritma.
Banyak algoritma yang tidak memiliki relevansi langsung terhadap musik digunakan
oleh composer sebagai inspirasi untuk musiknya. Diantaranya adalah algoritma fraktal IFS, L-
system. Bahkan algoritma
dengan data yang acak seperti nilai sensus, koordinat system
informasi geografi telah digunakan untuk interpretasi musik.
Sukses atau tidaknya prosedur-prosedur ini dalam menghasilkan musik yang baik
sangat
bergantung
pada
system mapping
yang
digunakan
oleh
komposes
untuk
menerjemahkan informasi
non-musik menjadi data stream musik
yang acak. Salah satu cara
yang banyak digunakan adalah dengan mengambil suatu angka dengan algoritma kemudian
angka tersebut di mod dengan 88. Kemudian hasil mod tersebut digunakan untuk menentukan
not mana yang akan dimainkan. Untuk penentuan not mana yang dimainkan, diasumsikan
bahwa angka 0 adalah ‘C’ , angka 1 adalah ‘C#’, angka 2 adalah ‘D’ dan seterusnya hingga
angka
ke
88
‘C’.
Untuk
mendapatkan
hasil yang
lebih
melodic
dapat
range
nada
dapat
diperkecil dari 88 menjadi 2 oktaf atau 25 (nada C hingga C’’).
Atau dapat juga dengan
membatasi
not
yang dipilih agar berada dalam sebuah chord tertentu pada
tiap beberapa bar.
Misalnya bar pertama diisi dengan chord C Mayor berarti not yang dimainkan adalah C – E –
G kemudian bar kedua diisi dengan chord DMayor7 (D – F# – A – C#) dan seterusnya.
|
|
31
2.2.5 MIDI
MIDI,
adalah
singkatan
dari
Musical
Instrument
Digital
Interface.
Dalam ilmu
komputer, MIDI adalah standar serial interface yang memungkinkan koneksi antara
synthesizer musik, instrumen musik dan komputer. Standar MIDI dibuat berdasarkan bagian
perangkat
keras
dan
bagian
penggambaran
cara dimana
musik
dan
suara
di
encode
dan
dikomunikasikan antara perangkat MIDI. MIDI port adalah bagian perangkat keras dari
standar ini yang menentukan tipe saluran
input/output. MIDI port menentukan tipe kabel
tertentu, sebuah kabel MIDI, yang terhubung ke port tersebut. Ada tiga tipe port yang
ditentukan oleh spesifikasi MIDI,
yaitu,
MIDI
In,
MIDI
Out,
dan
MIDI
Thru.
Sebuah
synthesizer atau perangkat MIDI lainnya menerima pesan MIDI melalui port MIDI In. pesan
MIDI
ini
juga
dikirimkan
lagi
melalui
port
MIDI
Thru sehingga
perangkat
lainnya
dapat
menerima pesan tersebut. Perangkat MIDI dapat mengirim pesan mereka sendiri ke perangkat
lainnya melalui port MIDI Out.
Informasi
yang
dikirimkan
antar perangkat MIDI
berada
dalam bentuk
yang disebut
MIDI
message,
yang
mengkodekan
aspek-aspek
suara
seperti
pitch dan
volume
sebagai
informasi digital sebesar 8-bit bytes. Perangkat MIDI
dapat digunakan untuk membuat,
merekam dan
memainkan
musik.
Dengan
menggunakan
MIDI,
komputer,
synthesizer,
dan
sequencer dapat saling berhubungan, apakah untuk mengendalikan tempo atau mengendalikan
musik
yang
dibuat oleh perangkat
lainnya
yang juga
terhubung. Adanya
standarisasi
MIDI
oleh
produsen synthesizer terkemuka
cukup berpengaruh
dalam suksesnya
komputer
dalam
profesi musik.
|
    32
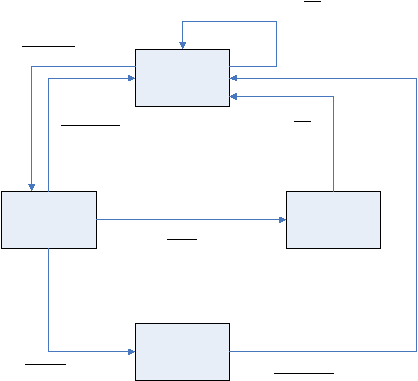
2.3 State Transition Diagram
State
transition
diagram (STD)
atau
yang
juga dikenal
sebagai behavioral
modeling
adalah
prinsip
operasional
untuk
semua
kebutuhan
metode
analisis. STD
menggambarkan
perilaku
dari sebuah
sistem dengan
menunjukkan
kondisi
(state) dan kejadian
(event)
yang
menyebabkan
sistem berubah
kondisi.
Lebih
lanjut,
state
transition
diagram
menunjukkan
tindakan apa (contohnya aktivasi proses) yang dijalankan sebagai hasil dari sebuah kejadian
tertentu. State
digambarkan dengan
kotak.
Alur
kendali
digambarkan
dengan
tanda
panah
memasuki dan keluar dari proses individu. Contoh dari STD digambarkan pada gambar 2.20.
Gambar 2.20 contoh STD pada software fotocopy
|
 33
2.4 Flowchart
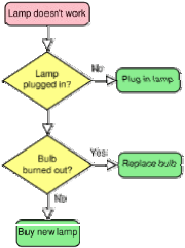
Flowchart adalah representasi skematik dari sebuah algoritma atau proses. Biasanya flowchart
digambarkan dengan symbol – symbol berikut:
•
Symbol awal dan akhir, digambarkan sebagai kapsul, oval atau kotak dengan sudut
tumpul. Biasanya symbol ini berisi kata "Start" atau "End", atau frase lainnya yang
menunjukkan awal ataupun akhir dari sebuah proses
•
"Flow of control" atau alur kendali pada ilmu computer digambarkan dengan panah.
Sebuah panah berasal dari sebuah symbol menunjuk ke symbol lainnya untuk
menggambarkan tahapan alur kendali.
•
Langkah proses digambarkan dengan kotak. Kotak tersebut berisi perintah sederhana
•
Input/Output, digambarkan dengan jajaran genjang.
•
Kondisi digambarkan dengan limas atau diamond. Biasanya mengandung pertanyaan
dengan True/False.
Contoh flowchart digambarkan pada Gambar 2.21:
Gambar 2.21 Contoh Flowchart
|
|
34
2.5 Borland Delphi 6
Borland
Delphi
merupakan
perangkat
lunak
yang
dikembangkan
oleh
Borland
dan
Delphi versi 6.0 ini merupakan pengembangan dari versi-versi sebelumnya.
Borland Delphi, atau yang lebih sering disebut Delphi, menggunakan bahasa
pemrograman Pascal.
Delphi
merupakan
salah satu perangkat lunak yang banyak digunakan
oleh para programmer dunia saat ini. Dukungan Delphi terhadap control Active-X dan VCL
(Visual
Component
Library)
menjadikan
kompiler
ini
mudah
digunakan
dan
cukup
andal
untuk membangun program aplikasi Windows.(Nugroho, 2002, p1)
Delphi mengenkapsulasi fungsi-fungsi Windows API (Application Programming
Interface)
yang
terkenal
rumit
ke dalam fungsi, kelas,
atau
objek baru
yang
menjadi
lebih
mudah
digunakan.
Dengan
Delphi,
seorang
programmer
dapat
membuat
program dengan
interface
yang
menarik
secara
lebih
cepat dan
mudah
dengan
memanfaatkan
komponen-
komponen VCL yang telah disediakan.
Sebagai
salah
satu
perangkat
pemrograman
berorientasi
objek
yang
handal,
Delphi
juga merupakan perangkat aplikasi database berbasis Windows, dengan kemampuan untuk
menggunakan bahasa SQL.
Saat ini komputer tidak hanya menangani informasi tetapi juga menampilkan gambar
di layar, menjalankan video, atau memperdengarkan suara. Delphi juga dapat memanfaatkan
multimedia
untuk
mengeluarkan suara atau
musik. Umumnya Delphi akan
memanggil
prosedur PlaySound dari komponen TMediaPlayer untuk memainkan sebuah file tipe wave
(ekstension WAV) atau memainkan suara sistem. Tipe file multimedia yang lain adalah MIDI.
File
MIDI
yang
menyimpan
suara
berisi
data
mengenai
alat
musik
yang
dimainkan,
dan
|
|
35
berapa
lamanya
musik
tersebut. Keuntungan
MIDI adalah
ukuran
filenya
jauh
lebih kecil
daripada file wave (Martina, 2000, p298-299).
Untuk
dapat
membuat
dan
mengkomposisi serta
memainkan
file
MIDI,
Delphi
membutuhkan komponen tambahan, antara lain yaitu komponen TMidiGen. TMidiGen
merupakan komponen yang dirancang oleh Alan Warriner yang dapat membantu dalam
membuat
kreasi
sederhana
efek
suara dan
rangkaian
not
dan
nada
di
dalam aplikasi tanpa
membutuhkan file-file ataupun sumber eksternal. TMidiGen merangkaikan data MIDI tersebut
di dalam memory. TMidiGen ini menyediakan 175 macam instrumen alat musik yang
mungkin disediakan dari sound card, penyesuaian volume suara, metode yang sederhana
dalam memainkan not-not tunggal, merangkaikan nada-nada dalam bentuk string, pengaturan
durasi sampai 10mS, dan lain sebagainya (Warriner, 2004, p1).
|