 6
BAB II LANDASAN
TEORI
2.1
Konsep Dasar Rekayasa Piranti Lunak
Konsep
ini pertama kali diperkenalkan oleh Fritz
Bauer,
yang menerapkan
beberapa
syarat dalam
merekayasa suatu piranti
lunak
yang kita
buat
sehingga dapat
berjalan secara
efisien dan optimal dalam komputer.
Dalam membuat sebuah rekayasa piranti lunak terdapat lima
paradigma / model
proses,
The
Classic
Life
Cycle
atau
yang
biasa
dikenal
dengan Waterfall
Model,
Prototyping Model, Fourth Generation Techniques (4GT), Spiral Model, dan Combine
Model. Pada pembahasan ini akan digunakan Waterfall Model.
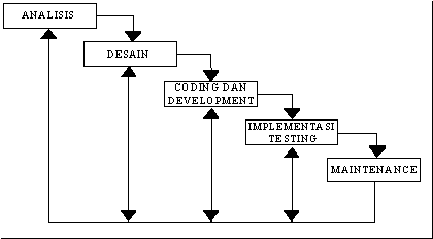
Menurut Presman,
ada
enam
tahapan
dalam
Waterfall
Model,
seperti
gambar
dibawah ini:
2.1 Gambar model Waterfall
2.1.1
Analisis sistem
Tahapan
ini
dimulai
dengan
menganalisis
semua elemen-elemen
yang
dibutuhkan oleh sistem oleh karena perangkat lunak merupakan bagian dari suatu
|
|
7
sistem yang lebih besar dan perangkat lunak tersebut berinteraksi dengan
elemen-elemen lain seperti hardware, dan manusia. Analisis yang dilakukan pada
tahap
ini
adalah
untuk
mengetahui
kebutuhan
user,
fungsi-fungsi
atau
fasilitas
seperti
apa
saja
yang
dibutuhkan, dan
bagaimana
interface
dari
piranti
lunak
tersebut.
2.1.2 Desain Sistem
Setelah perancangan program dianalisis
maka
tahap
selanjutnya
adalah
dengan
membuat
desain
dari
sistem
yang
akan dirancang.
Proses
perancangan
desain
ini
menterjemahkan
kebutuhan
ke dalam
sebuah
representasi
perangkat
lunak yang dapat dinilai kualitasnya sebelum dilakukan pengkodean.
2.1.3 Pengkodean ( Coding )
Tahapan
dimana
mentransformasikan rancangan
atau
desain
yang
telah
dibuat menjadi sebuah kode atau bentuk yang dimengerti oleh mesin dengan cara
membuat program.
2.1.4 Pengujian ( Testing )
Tahap
pengujian perlu
dilakukan agar
output
yang
dihasilkan oleh
program sesuai dengan yang diharapkan. Pengujian dilakukan secara menyeluruh
hingga semua perintah dan fungsi telah diuji.
2.1.5 Pemeliharaan ( Maintenance )
Kebutuhan
pemakai
dari
suatu
program
selalu
saja
meningkat sehingga
piranti lunak yang telah selesai dibuat perlu dipelihara dengan cara mengupdate
kebutuhan pemakai terhadap fungsi -fungsi khusus.
|
|
8
2.2
Sinyal
Suatu sinyal didefinisikan sebagai besaran fisik yang berubah-ubah menurut
waktu, ruang, atau variabel bebas lain.
2.2.1
Elemen Dasar Dalam Pemrosesan Sinyal
Pada kehidupan sehari-hari dikenal banyak sinyal. Sebagian besar sinyal
yang
ditemukan dalam
sains
dan
teknologi
di
alam
adalah
sinyal
analog,
contohnya suara. Suara dapat diubah dan dimanipulasi dengan peralatan digital
apabila
dikonversi
dahulu
menjadi
bentuk
digital
menggunakan circuit
yang
dinamakan ADC
(Analog-to-Digital Converter).
Ketika menggunakan mikrofon
untuk merekam suara ke komputer, digunakan Analog-to-Digital Converter
untuk mengkonversi suara yang merupakan gelombang analog menjadi informasi
digital
yang
tersimpan dalam
format
wav.
Ada
beberapa
alasan
mengapa
gelombang analog diubah menjadi gelombang digital, salah satunya karena
noise. Noise adalah suara bising atau berisik yang dihasilkan dari sekeliling suara
asal
namun
tidak
dikehendaki. Sejak
gelombang
analog
digunakan,
banyak
keluhan tentang adanya noise saat gelombang analog terkirim.
Sinyal
digital
hanya
mengenal dua
digit
angka,
yaitu
nol
dan
satu,
sehingga nilai yang bukan nol dan satu dibuang. Oleh karena itu noise yang tidak
perlu saat diolah oleh sinyal digital bisa dibuang. Keuntungan lain menggunakan
sinyal
digital adalah sinyal
digital
bisa
mengompres data
menjadi
file
dengan
ukuran
yang
lebih
kecil.
Berikut
akan dibahas
mengenai
bagaimana cara
kerja
Analog-to-Digital Converter .
Agar
suatu
sinyal dapat
diproses
secara digital, sinyal
itu
harus
diskrit
waktunya dan
nilai-nilainya
harus diskrit
(harus
dijadikan sinyal
digital). Jika
|
 9
sinyal
yang akan diproses
berbentuk analog, sinyal dikonversikan dahulu
menjadi
sinyal digital.
Caranya
dengan
sampling sinyal
analog
pada
saat
yang
diskrit, guna
menghasilkan sinyal
waktu diskrit. Lalu
nilai-nilainya dikuantisasi
ke suatu himpunan bernilai diskrit. Kuantisasi adalah proses
mengkonversi suatu
sinyal
bernilai
kontinu
menjadi
sinyal
bernilai
diskrit.
Kuantisasi
merupakan
dasar suatu proses pendekatan
yang dilakukan
dengan
pembulatan
atau
pemotongan.
x
a
(t)
x(n)
x
q
(t)
Sampling
Pengkuantisasi
Pengkodean
01011...
Sinyal
analog
Sinyal waktu
diskrit
Sinyal
terkuantisasi
Sinyal
digital
Gambar 2.1 Bagian dasar konverter analog ke digital
Inti
dari
koversi analog
to
digital
adalah proses
yang
terdiri
dari
tiga
langkah utama sebagai berikut.
1. Sampling. Merupakan konversi suatu sinyal waktu-kontinu
menjadi
suatu
sinyal
waktu-diskrit yang
diperoleh
dengan
mengambil sampling sinyal
waktu-kontinu pada saat diskrit. Jadi
jika
x
a
(t) adalah
masukan
terhadap
sampling,
maka
keluarannya
adalah x
a
(nT) = x(n) dengan T dinamakan selang sampling.
2. Kuantisasi. Merupakan konversi
sinyal
yang
bernilai-kontinu
waktu-diskrit
menjadi
sinyal
bernilai-diskrit, waktu-diskrit. Nilai
setiap
sampling
sinyal
digambarkan
dengan
suatu
nilai
terpilih
dari himpunan berhingga nilai-nilai yang mungkin. Selisih antara
|
 10
sampling x(n) yang tidak terkuantisasi dengan keluaran x
q
(n) yang
terkuantisasi dinamakan Galat Kuantisasi (Quantization Error).
3. Pengkodean. Dalam proses pengkodean, setiap nilai diskrit
x
q
(n)
digambarkan dengan suatu barisan biner.
A.
Sampling Sinyal Analog
Ada
beberapa
cara
untuk
mengambil sampling
sinyal
analog.
Tetapi
yang
lebih sering
digunakan adalah
sampling
periodik:
x(n) =
x
a
(nT) dengan x(n) adalah sinyal
waktu diskrit yang diperoleh
dengan
mengambil sampling-sampling
sinyal
analog
x
a
(T)
setiap
T
detik.Gambar 2.1
merupakan
contoh
pengambilan
sinyal
analog
dari
waktu
ke
waktu,
di
mana
sumbu
“y”
menyatakan tegangan
sedangkan
sumbu “x” menyatakan waktu.
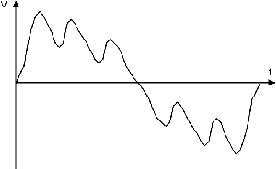
Gambar 2.2 Gelombang Analog
Setiap contoh yang diambil dikonversi ke dalam bentuk angka,
berdasarkan nilai tegangannya.
|
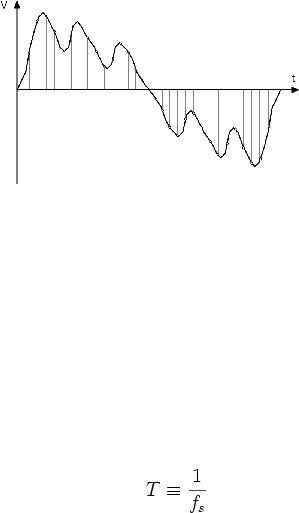 11
Gambar 2.3 Sampling Point
Sampling
Point
(T)
adalah
titik-titik dalam
sinyal
analog
yang
diambil sebagai
contoh
perwakilan
basarnya
nilai
tegangan.
Sedangkan
sampling rate (f
s
)
adalah besarnya frekuensi yang menentukan banyaknya
nilai
yang
diambil tiap
detik.
Jarak
dari
setiap
sampling
point
dapat
dihitung dengan rumus:
Sebagai contoh, jika sampling rate yang digunakan 22.050 Hz
itu berarti
bahwa dalam satu detik, contoh nilai yang diambil sebanyak 22.050 buah.
Jarak dari setiap sampling point akan menjadi 1 / 22.050 detik atau 45.35
µs
.
Nilai
dari
setiap
sampling
point
akan
disimpan dalam
variabel
dengan
panjang yang
konstan sesuai
dengan
bit-nya.
Jika
digunakan
delapan bit,
maka nilai yang dihasilkan berkisar 0 sampai 255 (2
8
=
256)
dengan nilai minimum 0 dan nilai maksimum 255. Jika digunakan enam
|
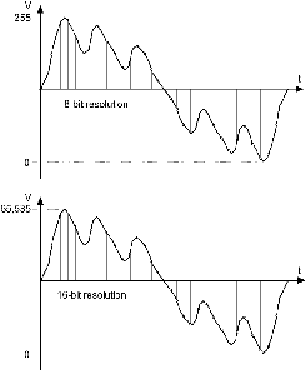 12
belas bit, maka nilai yang akan disimpan berkisar 0 sampai 65535 (2¹
6
=
65536) dengan nilai minimum 0 dan nilai
maksimum 65535
(lihat
gambar 2.3).
Gambar 2.4 Perbandingan resolusi 8-bit dengan 16-bit
Analog-to-Digital
Converter
membagi sumbu
“y”
menjadi “n”
bagian
antara
nilai
maksimum dan
minimum
dari
signal
analog;
“n”
merupakan
variabel.
Jika
ukuran
variabel
terlalu kecil,
maka
dua
sampling point yang berdekatan akan
memiliki representasi digital yang
sama,
sehingga
tidak sesuai dengan
sinyal analog
yang
asli
dan
gelombang yang dihasilkan tidak memiliki kualitas yang bagus. Kualitas
|
|
13
suara
dengan
tingkat
noise
yang
diinginkan dapat
dihitung
dengan
menggunakan SNR (signal-to-noise ratio)
SNR = 6,02 x n + 1,76 dB
Semakin tinggi angka SNR, kualitas suara yang dihasilkan semakin
bagus. Analog-to-Digital Converter dengan 8 bit menghasilkan SNR 49,9
dB, sedangkan jika digunakan 16 bit maka dihasilkan SNR 98 dB (hampir
tidak ada noise).
Untuk
mengembalikan suara
yang sudah
diproses
secara
digital
kembali
ke bentuk
analog
diperlukan
sebuah
circuit yang
dinamakan
DAC
(Digital-to-Analog
Converter).
Pada Digital-to-Analog
Converter
angka yang berupa digit dikembalikan ke dalam bentuk tegangan. Namun
gelombang yang
dihasilkan oleh
Digital-to-Analog
Converter
tidak
sempurna
karena
signal digit
tersebut
hanya
mengambil
beberapa
nilai
dari
gelombang aslinya,
sehingga
Digital-to-Analog
Converter
hanya
menghubungkan nilai-nilai yang ada (lihat gambar 2.4).
Jadi
semakin banyak
sampling
point
yang
diambil
dari
signal
analog, semakin tinggi pula sampling rate, maka hasil konversi ke bentuk
analognya akan
semakin
mendekati bentuk aslinya. Kerugiannya adalah
jika
sampling
rate
terlalu
tinggi,
dibutuhkan tempat
penyimpanan data
yang lebih banyak juga.
Oleh karena itu harus diketahui dengan tepat banyaknya sampling
rate yang
dibutuhkan
agar
tempat
penyimpanan
data
yang
digunakan
tidak terlalu banyak
namun sinyal analog yang dihasilkan dari konversi
sinyal digital
mendekati bentuk aslinya. Ada teorema yang
untuk
|
 14
menghitung dengan tepat sampling rate yang paling sesuai, yaitu Nyquist
-
Shannon Sampling Theorem. Teori Nyquist mengatakan bahwa
sebuah
sinyal sample dapat dikembalikan ke bentuk semula jika samping rate (f
s
)
minimum dua kali
frekuensi tertinggi (B)
yang ada pada sinyal
tersebut.
Teori Nyquist dinotasikan dengan f
s
>
B
atau sama dengan B < f
s
/2, di
mana 2B dinamakan Nyquist rate dan
f
s
/2 dinamakan Nyquist frequency.
Gambar 2.5 Sinyal yang sudah dikonversi ke digital
dan dikonversi lagi ke analog
B. Kuantisasi Sinyal Analog
Sinyal digital
adalah deretan
angka-angka
sampling
yang
setiap
angkanya
digambarkan dengan
angka
digit
berhingga.
Proses
pengkonversian
suatu
sinyal
amplitudo-kontinu waktu-diskrit
menjadi
sinyal
digital
dengan
menyatakan
setiap
nilai
sampling sebagai
suatu
|
|
15
angka digit dinamakan kuantisasi. Kesalahan yang terjadi selama proses
kuantisasi dinamakan kesalahan kuantisasi atau quantization error.
Kesalahan
kuantisasi
dihasilkan dari
selisih
antara
nilai
terkuantisasi dan
nilai
sampling
yang sebenarnya. Kuantisasi
merupakan
pemotongan
nilai
yang
diterima
setelah
melakukan sampling
dengan
pembulatan
ke
bawah.
Proses
pengkuantisasian selalu
mengurangi
informasi
yang akan masuk ke tahap selanjutnya,
karena proses
kuantisasi merupakan proses yang tidak dapat kembali lagi (irreversible)
atau proses yang tidak ada inversinya.
C.
Pengkodean Sampling Terkuantisasi
Proses pengkodean saat konversi dari analog ke digital dilakukan
dengan memberikan nilai pada setiap
tingkatan dengan
nilai
yang
unik.
Jika ada L tingkatan, maka diperlukan pula L angka biner yang berbeda.
Dengan panjang kata b bit, maka akan dihasilkan jumlah 2
b
angka biner
yang berbeda, sehingga akan terdapat 2
b
=
L, atau b = log2L. Jadi jumlah
bit
yang diperlukan
dalam
pengkodean adalah
nilai
integer
yang
lebih
besar dari atau sama dengan log
2
L.
2.2.2
Ekstraksi Suara
Ekstraksi
suara
merupakan
pengambilan contoh
suara
yang
sudah
mengalami tahap
tertentu
agar
dapat
diolah
dan
dianalisis. Sinyal
suara
merupakan sinyal quasi stationer, sinyal yang bereaksi
lambat terhadap waktu.
Sebagai contoh
sebuah
sinyal
suara
yang
diambil
dalam jangka
waktu
cukup
pendek (antara 5 sampai 100 ms), karakteristiknya hampir stasioner. Namun jika
|
|
16
dimbil
dalam
jangka
waktu
yang
cukup
lama
(kurang
lebih 0,2
detik)
maka
karakteristiknya akan berubah sesuai dengan karakteristik suara yang diucapkan.
A.
Mel Cepstrum Coefficients
Mel
Cepstrum
didasarkan pada
variasi
yang
diketahui
pada
lebar
pita kritis telinga manusia terhadap frekuensi. Cepstrum digunakan untuk
memisahkan
sinyal-sinyal
yang
berurutan
dan
mengestimasi isi
dari
spektrum suara. Mel Cepstrum digunakan untuk meningkatkan kecepatan
pengenalan, yaitu dengan kemampuannya dalam menghaluskan spektrum
dengan menghilangkan variasi turunan dari spektrum. Mel cepstrum
sering disebut juga dengan “spektrum berdasarkan mel”.
Mel adalah satuan pengukuran tekanan diterima atau frekuensi dari
sebuah
nada.
Mel
ini
tidak
menanggapi frekuensi
nada
secara
linear
seperti sistem pendengaran manusia yang tidak menerima frekuensi
secara
linear. Menurut buku
Fundamentals
of
Speech
Recognition
halaman 184, pada tahun 1940 Stevens dan Volkman secara bebas
memilih
frekuensi
1000
Hz
dan
menetapkan ini
sebagai
“1000
mels”.
Tekanan
yang
dinyatakan dalam
mel
sacara
kasar
sebanding
dengan
jumlah sel saraf yang berakhir pada membran basilar dari telinga bagian
dalam,
menghitung dari
ujung
apikal
ke
titik
rangsangan
maksimal
sepanjang membran (Stephens and Bate, 1996, hal. 238).
B.
Hamming Windows
Hamming windows
merupakan proses
membuat windows pada tiap
frame yang
ada
untuk
meminimalisasi sinyal
yang
tidak
kontinyu
pada
awal
dan
akhir
frame. Jika
didefinisikan windows
sebagai
|
|
17
?
w(n),
0
=
n
=
N
-
1
,
di
mana N adalah jumlah sampel dalam tiap frame,
maka hasil yang berupa sinyal dari windowing adalah
y
l
(n) =
x
l
(n)w(n),
0
=
n =
N
-
1
Secara umum Hamming windows yang digunakan, mempunyai
notasi:
w(n)
=
0.54
-
0.46 cos
?
2
p
n
?
?
,
0
=
n
=
N
-
1
?
N
-
1
?
2.3
Transformasi Fourier
2.3.1
DFT (Discrete Fourier Transform)
Discrete Fourier Transform atau DFT merupakan alat bantu utama dalam
pemrosesan
sinyal
digital.
Pada
dasarnya DFT
menerima
input
berupa
sinyal
waktu
diskrit
dan
menghasilkan transformasi
frekuensi
diskrit.
Sinyal
input
disebut
berada dalam
waktu
domain
(time
domain),
karena
sinyal
yang
memasuki DFT disusun dari pengambilan sampling berdasarkan waktu tertentu.
Istilah
domain
frekuensi
digunakan
untuk
menggambarkan amplitudo
dari
gelombang
sinus
dan
cosinus
yang
merupakan
pecahan
dari
sinyal
input
pada
DFT. DFT
disebut juga sebagai
suatu
himpunan dari N
sampling {F(k)} untuk
suatu deret berhingga {f(n)} dengan panjang
lebih kecil daripada N. Besaran N
sampling {F(k)} menggambarkan secara keseluruhan deret {f(n)} dalam domain
frekuensi. Persamaan umum DFT yang sering digunakan adalah
N
-1
F
(k
)=
?
f
(n)
e
-i 2pnk / N
n
=0
, k = 0,1,2,..., N - 1
dan inversinya
|
|
18
1
e
N
-
1
f
(
n
)
=
?
F
(
k
)
i
2pnk / N
N
k
=0
, n = 0,1,2,..., N - 1
Domain
frekuensi dan
domain
waktu
pada
dasarnya mengandung
informasi yang sama, hanya saja digambarkan dalam bentuk yang berbeda. Jika
diketahui salah
satunya
maka
yang
lainnya
dapat
dihitung. Jika
diketahui
domain waktu dari suatu sinyal, proses perhitungan untuk menjadikan domain
frekuensi
disebut
dekomposisi analisis,
forward
DFT atau
juga disebut
DFT.
Jika
diketahui
domain
frekuensi,
proses
perhitungan disebut
dengan
sintesis
atau invers DFT.
Banyak
sample dalam
domain
waktu
dapat direpresentasikan dengan
variabel N, di mana N adalah bilangan bulat positif dan biasanya kuadrat dari 2
(2
n
)
seperti 128, 256, 512, 1024, dan lain-lain.
2.3.2
FFT (Fast Fourier Transform)
FFT (Fast Fourier Transform) merupakan algoritma yang menerapkan
DFT
dengan
lebih
cepat
dan
efisien,
dibanding
dengan
perhitungan yang
dilakukan
secara
konvensional oleh
DFT.
Secara
umum
perhitungan FFT
digunakan untuk
mengubah sinyal
digital
menjadi
sinyal analog.
Sedangkan
IFFT (Invers Fast Fourier Transform) digunakan untuk mengubah sinyal
analog menjadi sinyal digital. FFT tidak
melakukan perhitungan transformasi
yang berbeda dari DFT, hanya mengurangi jumlah kalkulasi yang dibutuhkan.
Persamaan matematika yang digunakan adalah
8
F
(
f
)=
?
f
(
t
)
e
-i 2pft
dt
-8
Dan invers dari FFT dinotasikan
8
f
(t
)=
?
F
( f
)
e
i
2pft
df
-8
|
|
19
di mana i adalah akar kuadrat dari -1, sering disebut juga dengan bilangan
imaginer.
2.4
Kuantisasi Vektor
2.4.1
Pendahuluan
Kuantisasi vektor termasuk self-organizing maps (SOM) yang merupakan
aplikasi dari
jaringan saraf tiruan (neural
network).
Jaringan saraf tiruan adalah
sistem
pemroses
informasi
yang
memiliki
karakteristik mirip dengan
jaringan
saraf
biologi.
Jaringan
saraf
tiruan
ini
dibentuk
sebagai
generalisasi model
matematika dari jaringan saraf biologi, dengan asumsi sebagai berikut:
•
Pemrosesan informasi terjadi pada banyak elemen sederhana
(neuron)
•
Sinyal dikirimkan di antara neuron-neuron melalui penghubung-
penghubung.
•
Penghubung antar neuron memiliki bobot yang akan memperkuat
atau memperlemah sinyal (penentuan bobot dilakukan dengan
training).
•
Untuk menentukan
output, setiap neuron menggunakan
fungsi
aktivasi dari jumlah
inputan
yang diterima.
Besarnya output
ini
kemudian dibandingkan dengan batas ambang.
Kuantisasi
vektor
menggunakan
strategi pelatihan
tanpa supervisi
yang
tepat
digunakan
dalam
pengenalan pola
(pattern
recognition)
dengan
model
jaringan layar tunggal. Pada pelatihan dengan supervisi (supervised learning) ada
pasangan
data
yang
berfungsi
sebagai
“guru”
untuk
melatih
jaringan
hingga
|
 20
diperoleh hasil
yang
terbaik.
Sedangkan pada
pelatihan
tanpa
supervisi
(unsupervised
learning) tidak ada “guru”
yang
mengarahkan proses
pelatihan.
Namun
dalam
pelatihannya, perubahan
bobot
jaringan
dilakukan
berdasarkan
parameter tertentu dan jaringan dimodifikasi menurut ukuran parameter tersebut.
Layar
input
menerima
data-data
eksternal
sedangkan
layar
kompetitif berisi
neuron-neuron
yang
saling
berkompetisi agar
memperoleh
kesempatan
untuk
merespon sifat-sifat yang ada dalam data masukan. Neuron
yang memenangkan
kompertisi
akan memperoleh sinyal yang berikutnya diteruskannya. Bobot
neuron pemenang akan dimodifikasi sehingga lebih menyerupai data masukan.
Pada
self-organizing
maps (SOM),
neuron
ditempatkan
pada pola
yang
biasanya berdimensi satu atau dua. Disain dari kuantisasi vektor digunakan untuk
mengatasi
masalah
pengintegrasian berdimensi
banyak.
Kuantisasi
vektor
merupakan
metode
pengompresan data
dengan
prinsip
pendekatan
sinyal
amplitudo
continuous
pada
sinyal
digital
dengan
meminimalisasi hilangnya
informasi yang ada.
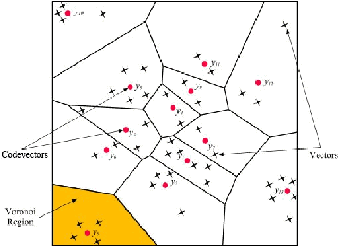
Gambar 2.6 Kuantisasi
Vektor Dua Dimensi
|
 21
Titik
yang
berupa
bintang
merupakan vector,
sedangkan titik
besar
merupakan
codevector.
Daerah
yang
dibatasi
oleh
garis
dinamakan Voronoi
region,
dan
kumpulan dari codevectors dinamakan codebook (gambar 2.5).
2.4.2 Desain Perumusan Masalah
Saat merumuskan masalah, pertama-tama ada urutan training yang terdiri dari M
vektor sumber:
T
=
{x
1
,x2,...,x
M
}
Gambar 2.7 Gambaran Umum Pencocokan Suara
Sumber: http://www.willamette.edu/~gorr/classes/ competitive.html
Urutan
training
ini
bisa
diperoleh dari
database
yang
besar.
Jika
sumbernya
merupakan sinyal suara,
maka
urutan
training-nya
berupa
rekaman suara dari
beberapa
orang
yang
berbeda.
Sumber
kuantisasi
vektor
dapat
berdimensi k
dengan notasi:
x
m
=
(x
m,1
,x
m,2
,...,x
m,k
),
di mana m = 1,2,...,M
Codebook (C) merupakan kumpulan dari N codevectors yang dinotasikan
dengan:
C
=
{c1
,c2,...,c
N
}
|
 22
?
Karena setiap codevectors berdimensi k, maka:
c
n
=
(c
n,1
,c
n,2
,...,c
n,k
),
di mana n = 1,2,...,N
Voronoi region
yang berhubungan dengan codevectors c
n
disimbolkan dengan
S
n
,
dan P menandakan bagian dari ruang, dengan notasi:
P = {S1
,S2
,...,S
N
}
Jika
sumber
vektor
x
m
berada
pada
Voronoi
region S
n
,
maka
nilai
pendekatannya adalah c
n
yang dinotasikan dengan:
Q(x
m
)
=
c
n
,
jika x
m
€ S
n
Diasumsikan bahwa ukuran kuadrat error penyimpangan, rata-ratanya adalah:
D
avg
=
1
x
m
-
Q(x
m
)
2
Mk
2.4.3
Kondisi Optimal
Untuk
mendapatkan nilai
rata-rata
yang
maksimal,
harus
dipenuhi
dua
macam kondisi. Yang
pertama adalah kondisi nearest
neighbour
yang
berarti
bahwa daerah Voronoi S
n
harus terdiri dari semua vektor yang lebih dekat
dengan c
n
daripada dengan codevector yang lain. Notasinya adalah:
Sn = { x :
x
-
cn 2
=
x
-
cn
'
2
?n ' = 1,2,...,N }
Yang kedua
adalah
kondisi
centroid,
di
mana
codevector
c
n
harus
merupakan
rata-rata dari
semua
vektor training yang berada pada Voronoi
region S
n
.
Pada
penerapannya, harus dipastikan bahwa minimal ada satu vektor training yang ada
pada setiap Voronoi region (agar penyebut pada rumus tidak pernah nol).
?
xm
?Sn
xm
Notasinya:
cn =
?
xm
?Sn
1
n = 1,2,...,N
|
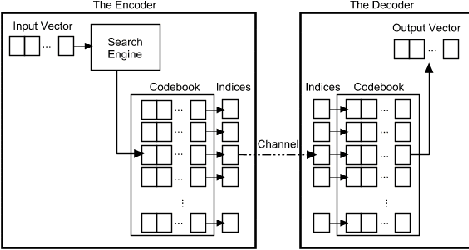 23
2.4.4
Desain Algoritma Linde-Buzo-Gray (LBG)
Proses kuantisasi vektor merupakan teknik pencocokan pola. Setiap
vektor
di-encode
dan
dibandingkan dengan
sekumpulan
vektor
yang
sudah
disimpan, disebut
dengan
codevectors
atau
pola.
Setiap
pola
akan
digunakan
untuk menampilkan vektor masukan yang diidentifikasi sama dengan pola
yang
ada. Pola
yang paling mendekati dengan codebook,
kumpulan pola
yang sudah
disimpan,
akan
dipilih berdasarkan proses
encoding
yang sesuai
dengan
ketepatan pengukuran.
Gambar 2.8 Encoder dan Decoder Dalam Kuantisasi Vektor
Algoritma
LBG
merupakan algoritma
yang
dilakukan
berulang-ulang
untuk
mendapatkan dua
kondisi optimal,
yaitu kondisi
nearest
neighbour
dan
kondisi
centroid.
Saat
pertama
kali
dijalankan, algoritma
ini
butuh
sebuah
inisialisasi codebook
C
(0)
,
yang
diperoleh
dengan
metode
splitting.
Metode
splitting merupakan metode yang membagi codevector menjadi dua bagian. Dua
codevector
inilah
yang
menjadi
inisialisasi codebook
untuk
pertama
kali.
Kemudian setelah kedua codevector terbentuk, mereka terbagi dua lagi menjadi
|
 24
M
c
*
c
c
?
n
?
n
D
m
*
M
M
empat
dan
proses
tersebut kembali
berulang
sampai
jumlah
codevector
yang
diinginkan terbentuk.
Disain algoritma LBG:
1.
Masukkan nilai pada T.
1
M
2.
Beri nilai pertama pada N, N=1, lalu hitung
c =
?
x
m
1
m
=1
*
1
* 2
Kemudian hitung
Dave
=
M
?
x
m
-
c
1
k
m=1
3.
Proses membagi jadi 2 : Untuk i = 1,2,...,N tetapkan nilai
(
0)
i
= 1+ ?)
(1+ ?)
c
i
c
N
+i
=
(1- ?)
c
i
(
0)
*
Set N Å 2N
4.
Proses iterasi : pertama tetapkan
D
(0
)
=
D
*
. Beri nilai index i = 0.
ave
ave
i. Untuk m = 1,2,..,M, cari nilai minimum dari
x
m
-
(i)
2
n
Untuk semua n = 1,2,…,N. biarkan n*
menjadi index yang mencapai
nilai minimum. Set
Q
(
x
)=
c
(
i
)
m
n*
ii. Untuk n = 1,2,…,N, perbaharui codevector
(i +1
)
=
n
Q
(
x
m
)=
c
(
i
)
x
m
Q
(
x
m
)=
c
(
i
)
1
iii. Set
i
=
i
+
1.
iv. Hitung
(i
)
=
ave
1
?
M
k
m
=
1
x
m
-
Q
(
x
)
2
v.
Jika
(
D
(i -1
)
-
D
(i
)
)
/
D
(i -1)
>?
, kembali ke langkah (i).
ave
ave
ave
|
|
25
*
cn
vi. Set
*
D
ave
(
i
)
=
D
ave
untuk n = 1,2,..,N, set
c
n
=
(i
)
sebagai nilai akhir dari
codevectors
5.
Ulangi langkah 3 dan 4 sampai tercapai jumlah codevectors yang
diinginkan.
|