|
BAB 2
LANDASAN TEORI
2.1 Gambaran Umum Traveling Salesman Problem
Traveling Salesman
Problem secara
umum
merupakan masalah
optimasi
yang
kompleks
di
mana
dengan
bertambahnya
variabel
secara
linear
maka
waktu
yang
dibutuhkan
untuk
memecahkan masalah
itu bertambah secara eksponensial. Misal:
algoritma A, jumlah kota N, waktu yang dibutuhkan T. Maka untuk jumlah kota 2N
tidak
bisa
dikatakan
membutuhkan waktu
2T
untuk
algoritma
A.
Hal
ini
mengakibatkan 2 alternatif pengembangan algoritma. Yang pertama algoritma yang
berusaha
menemukan perjalanan
yang
mendekati
optimal
tetapi
dapat
dilakukan
dengan
waktu yang singkat.
Yang kedua mengembangkan optimasi
algoritma
yang
benar-benar
mencari
solusi
yang
terbaik
dari
permasalahan Traveling
Salesman
Problem.
Permasalahan Traveling
Salesman
Problem
ada
2
macam,
yaitu
symmetric
Traveling Salesman
Problem atau
yang
biasa
disebut dengan
Traveling Salesman
Problem saja dan asymmetric Traveling Salesman Problem. Jika 2 kota yang
menjadi tujuan dalam suatu perjalanan, maka masalah perjalanan ini bisa dikatakan
dengan
mudah
sekali.
Untuk symmetric
Traveling
Salesman
Problem
perjalanan
3
kota
juga
masalah
yang
mudah
dipecahkan. Jumlah
kombinasi
perjalanan
yang
dihasilkan untuk kasus asymmetric Traveling Salesman Problem adalah (n-1)!.
Untuk
melihat
mengapa itu bisa
terjadi, pilihlah kota
yang mana saja
secara bebas
sebagai kota pertama, kemudian ada (n-1) kota yang bisa dipilih sebagai kota yang
|
 9
kedua untuk dikunjungi, (n-2) kota yang yang bisa dipilih sebagai kota yang ketiga
untuk dikunjungi, begitu seterusnya sampai semua kota habis dikunjungi dan
kembali ke
kota awal. Pada kasus
symmetric Traveling Salesman
Problem, jumlah
kombinasi
perjalanannya adalah
setengah
dari
jumlah
kombinasi
perjalanan
asymmetric Traveling Salesman Problem yaitu (n-1)!/2 untuk n > 3 (Dakin, 1996).
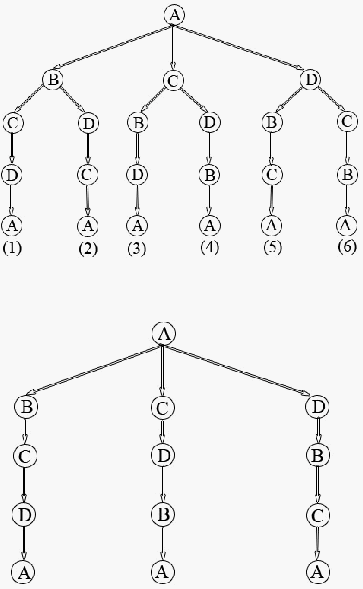
Gambar 2.1 kombinasi kemungkinan solusi ATSP untuk 4 kota
Gambar 2.2 kombinasi kemungkinan solusi tsp untuk 4 kota
|
 10
Dapat
diambil
kesimpulan
bahwa
jumlah
kombinasi n
kota
untuk
masalah
Traveling Salesman Problem adalah ½ kali jumlah kombinasi n kota untuk masalah
asymmetric Traveling Salesman Problem.
Jumlah semua
kombinasi untuk
n
kota
pada kasus
tsp
adalah
(n-1)!/2.
tabel
di
bawah
ini
menunjukkan banyaknya jumlah kombinasi pada
sejumlah kota.
Dengan
melihat data tersebut, maka permasalahan Traveling Salesman Problem untuk
jumlah kota
yang besar adalah permasalahan yang sangat kompleks dan sulit untuk
dipecahkan. Jadi
untuk memecahkan Traveling Salesman Problem diperlukan suatu
algoritma
yang
pada
intinya
adalah
mengurangi
pengecekan terhadap
semua
kombinasi yang mungkin.
Jumlah kota (n)
Jumlah kombinasi
5
12
6
60
7
360
8
2520
9
20160
10
181440
11
1814400
12
19958400
13
239500800
Tabel 2.1 Banyaknya Kombinasi Traveling Salesman Problem dari n Kota
|
|
11
Perancangan program
aplikasi
ini
digunakan
untuk
menentukan tour
Traveling
Salesman
Problem terpendek dimana
setiap
node-nya
memiliki
edge
yang
menghubungkan ke
node
lainnya
dengan
nilai
bobot
yang
sudah
disimpan
di
database.
2.2 Alternatif Pemecahan Masalah
Pada
skripsi
ini,
pembahasan difokuskan
pada
pemecahan
masalah
untuk
symmetric Traveling
Salesman
Problem
atau
selanjutnya
akan
disebut
Traveling
Salesman Problem. Ada beberapa alternatif untuk menyelesaikan
Traveling
Salesman Problem sebagai salah satu masalah optimasi kombinatorial, seperti
dengan pendekatan Algoritma Genetik,
Tabu Search dan
masih banyak
lagi. Untuk
menyelesaikan Traveling
Salesman
Problem
di
sini
akan
digunakan
algoritma
Metropolis. Pemilihan
algoritma
Metropolis
sebagai
metode
yang
digunakan
didasarkan pada beberapa pertimbangan sebagai berikut:
1.
Kemampuannya
untuk
menghindar
dari
terperangkapnya solusi
dalam
local
minima
atau memungkinkan penyelesaian Traveling Salesman untuk
mendapatkan absolute minimum.
2. Algoritma Metropolis relatif sederhana sehingga komputasinya lebih efisien dan
tidak banyak memakan kinerja komputer.
2.3 Deskripsi Teori
2.3.1 Graph
Menurut
Witala
(1987,
p178),
graph
adalah
sebuah
pasangan berurutan
(V,E), di
mana
V
adalah
himpunan vertex/node/titik, dan
E
adalah
himpunan
edge/garis yang menghubungkan antara vertex satu dengan vertex yang lain.
|
 12
Edge
pada
graph dapat
memiliki
bobot/nilai,
di mana
bobot
tersebut
dapat
mewakili
jarak,
biaya,
waktu
dan
sebagainya. Graph
yang
demikian
disebut
weighted
graph,
yaitu
merupakan graph
yang
digunakan
dalam
merepresentasikan Traveling Salesman Problem.
Edge
pada
graph
juga
dapat
memiliki
arah,
graph
demikian disebut
directed graph/digraph. Pada digraph, edge (a,b) merupakan sebuah edge dari
a
ke b, di
mana
vertex
a
disebut
initial
vertex (source) dan vertex
b
disebut
terminal vertex
(sink) dari
edge tersebut. Jadi
edge (a,b)
tidak sama
dengan
edge (b,a),
yang
implementasinya dalam Traveling Salesman Problem disebut
Asymmetric Traveling Salesman Problem. Sebaliknya pada undirected graph,
edge
(a,b)=edge
(b,a)
dalam
Traveling
Salesman
Problem
disebut
Symmetric
Traveling Salesman Problem.
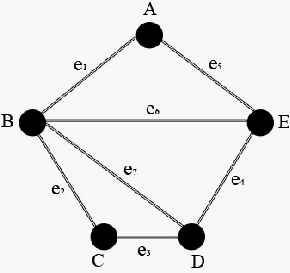
Gambar 2.3 adalah contoh sebuah undirected graph di
mana V = {A, B,
C, D, E} dan E={e1, e
2
,
e
3
,
e
4
,
e
5
,
e
6
,
e
7
}.
Gambar 2.3 Undirected Graph
|
 13
Degree
dari
suatu
vertex
adalah
banyaknya
edge
yang
bertemu
pada
vertex
tersebut.
Untuk
digraph,
dikenal
indegree
dan
outdegree. Indegree
adalah
banyaknya edge
yang
masuk
ke
suatu
vertex,
sedangkan outdegree
adalah
banyaknya
edge
yang keluar
dari suatu
vertex.
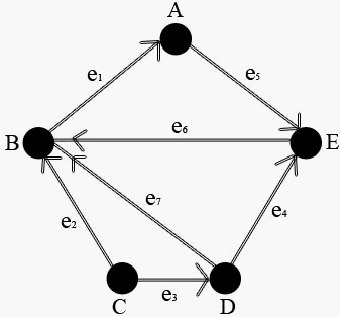
Gambar 2.4 adalah
contoh sebuah digraph, di mana V = {A,B,C,D,E} dan E={(A,E), (B,A), (C,B)
(C,D) (D,B) (D,E) (E,B)}. Pada gambar 2.4, vertex B memiliki 3 indegree dan
1 outdegree.
Gambar 2.4 Directed Graph
Beberapa istilah yang berhubungan dengan edge dan vertex:
a. walk, yaitu lintasan yang mungkin dari vertex awal ke vertex tujuan contoh
walk dari vertex B ke vertex E pada gambar 2.3 adalah (B,D,E), (B,E),
(B,C,D,E,A)
dan
sebagainya. Vertex dan
edge
yang
sama
dapat
ditelusuri kembali.
|
|
14
b. trail,
adalah
walk
yang
semua
edge-nya
berbeda.
Trail
dapat
melalui
vertex yang sama berulang kali hanya
jika
melewati edge yang berbeda.
Contoh trail dari B ke E pada gambar 2.3 adalah (B, D, E), (B, A, E, D, B,
E), dan sebagainya.
c. path, yaitu walk yang semua vertex-nya berbeda kecuali vertex awal dan
vertex akhir sama. Contoh path dari B ke E pada gambar 2.3 adalah (B, A,
E), (B, C, D, E) dan sebagainya.
d. cycle (closed
path),
yaitu path
yang
dimulai dan diakhiri pada
vertex
yang sama (vertex awal = vertex tujuan). Contoh cycle pada
gambar 2.3
adalah (B,A,E,D,C,B).
Traveling
Salesman
Problem
sendiri
merupakan special
case
dari
Hamiltonian
cycle atau Hamiltonian path. Hamiltonian cycle mempunyai definisi yang sama
dengan Traveling Salesman
Problem.
Sebuah
Hamiltonian cycle
mengunjungi
setiap
verteks
tepat
satu
kali,
kecuali
verteks
awal dan akhir
yang
muncul
dua
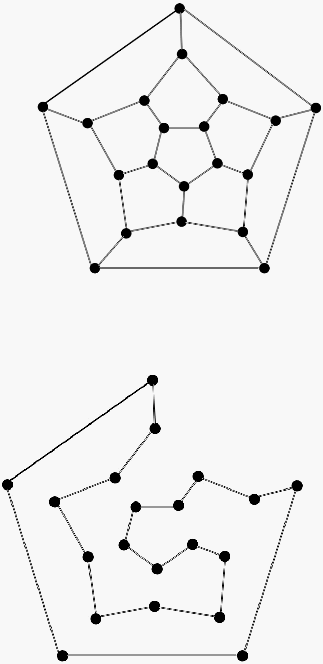
kali. yang secara garis besar dapat digambarkan sebagai berikut:
|
 15
Gambar 2.5 Graph Teka-Teki Hamiltonian Cycle
Gambar 2.6 Hamiltonian Cycle Dari Gambar 2.5
2.3.2 Traveling Salesman Problem
2.3.2.1 Definisi Traveling Salesman Problem
Traveling Salesman Problem dapat didefinisikan sebagai berikut:
ada 1 set kota {C1, C2
,
C3, … C
n
}
dan d{C
i
,
C
j
}
adalah jarak antara kota
|
|
16
ke i dan kota ke j. Tujuannya adalah menemukan urutan p dari rumus
berikut untuk mendapatkan nilai yang paling minimal
?
d C
(C
?
(i )
,
C
?
(i )
)
+
d
(C
?
(
N
)
,
C
?
(1)
)
Hasil dari rumus tersebut disebut sebagai panjang dari perjalanan
seorang
salesman
mengunjungi kota-kota
sesuai
urutan
?,
di
mana
setelah
mengunjungi semua
kota
salesman
tersebut
akan
kembali
ke
kota awal.
Permasalahan Traveling Salesman
Problem ada 2
macam,
yaitu
Symmetric Traveling Salesman Problem atau yang biasa disebut dengan
Traveling Salesman Problem saja dan Asymmetric Traveling Salesman
Problem. Jika Symmetric Traveling Salesman Problem, maka d{C
i
,
C
j
}
=
d{C
j
,
C
i
}, sedangkan jika Asymmetric Traveling Salesman Problem
maka d{C
i
,
C
j
}
?
d{C
i
,
C
j
}
untuk 1 = i, j = n (Johnson dan McGeoch,
1995).
Traveling Salesman Problem adalah salah satu
masalah optimasi
yang
merupakan
NP-complete
problem
(non
deterministic
polynomial
complete),
yaitu
suatu
permasalahan di
mana
dengan
bertambahnya
variabel secara linear maka waktu yang diperlukan untuk memecahkan
masalah itu bertambah secara eksponensial. Hal ini sering disebut juga
dengan combinatorial explosion.
Selain
itu
sulitnya
menyelesaikan Traveling
Salesman
Problem
sebagai
salah
satu
masalah
optimasi
yang
cukup
kompleks juga
disebabkan ruang solusi (solution space) yang mungkin untuk
|
|
17
kebanyakan masalah optimasi terlalu besar dan kemungkinan terjadinya
pencarian yang
tidak
terarah
cukup
besar
sehingga
sulit
untuk
dipecahkan
atau
diselesaikan. Teknik
pencarian
solusi
tingkat
tinggi
untuk
memangkas
atau
menyederhanakan
ruang
pencarian
juga
tidak
menjamin
dihasilkannya suatu
solusi
yang
optimal.
Dengan
kata
lain,
sulit
mendesain
suatu
teknik
pemecahan masalah
yang
efektif
untuk
menyelesaikan masalah optimasi seperti Traveling Salesman Problem.
Hoffman dan Wolfe (1985),
mendefinisikan Traveling Salesman
Problem sebagai berikut:
“The traveling salesman
problem
(TSP) is one which has commanded
much attention of mathematicians and computer scientists specifically
because it is so easy to describe and so difficult to solve. The problem
can simply be stated as: if a traveling salesman wishes to visit exactly
once each of a list of m cities (where the cost of traveling from city i to
city j is C
ij
)
and then return to the home city, what is the least costly
route the traveling salesman can take?”
Berdasarkan definisi
di
atas,
traveling
salesman
problem
merupakan suatu masalah yang mudah dideskripsikan namun sulit
untuk
diselesaikan, yaitu
masalah
bagaimana
menentukan
jarak
terpendek dalam perjalanan melwati titik-titik tertentu di mana satu titik
harus
dilalui satu
kali
dan
hanya boleh
dilalui satu
kalo
saja
dan
perjanalan harus
berakhir dengan kembali ke
titik pertama. Dalam hal
ini titik-titik tersebut merupakan kota-kota dalam suatu wilayah tertentu.
Menurut Karla Hoffman, George Mason University dan Manfred
Padberg, New
York
University ,
yang
diambil
langkah
pertama dalam menyelesaikan Traveling Salesman Problem adalah
|
|
18
dengan
menggunakan formula
matematika
dengan
graph
sebagai
strukturnya, di
mana setiap
kota dinotasikan dengan sebuah
node dan
jarak antar kota digambarkan dengan garis (arcs atau edges). Kemudian
panjang dari sebuah perjalanan merupakan hasil penjumlahan dari jarak
antar kota-kota yang dilalui.
2.3.2.2 Algoritma Untuk Memecahkan Traveling Salesman Problem
Beberapa algoritma yang
sudah
pernah
dipakai
untuk
memecahkan
masalah Traveling Salesman
Problem adalah
Algoritma Genetik, Algoritma
Ant
Colony
Optimization, Algoritma
Tabu
Search,
Algoritma
Neural
Nertwork, dan lain-lain.
Berbagai pendekatan untuk
menyelesaikan Traveling Salesman Problem
juga
telah
digunakan. Berikut
ini
dijelaskan
secara
singkat
mengenai
pendekatan-pendekatan atau
metode-metode
yang pernah
digunakan
dalam
menyelesaikan traveling salesman problem:
a. Pendekatan random search/exhaustive search
Random search merupakan teknik pencarian solusi secara acak. Semakin
besar ruang solusi (solution space) akan
memperkecil kemungkinan
untuk mendapatkan solusi yang baik. Oleh karena itu mencari secara acak
suatu solusi yang baik adalah seperti
mencari jarum di dalam tumpukan
jerami.
Exhaustive search
tidak
dapat
digunakan
untuk
NP-complete
problem karena ruang pencarian (search space) nya sangat besar.
b. Pendekatan riset operasional
1. Enumerative search
a. Mathematical programming
|
 19
Mathematical programming
adalah
salah
satu
teknik
yang
digunakan
untuk
mengoptimasi suatu
fungsi
yang
dibatasi
oleh
variabel bebas.
Linear programming
dan
integer
programming
adalah dua contoh pendekatan yang pernah digunakan.
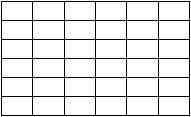
b. Metode Greedy
Terdapat
n
input,
dimana
didapatkan suatu
subset
dari
n
input
tersebut yang
memenuhi persyaratan tertentu. Setiap subset
yang
memenuhi
persyaratan disebut
feasible
solution.
Suatu
feasible
solution
yang
dapat
memaksimalkan atau
meminimalkan
objective function disebut optimal solution. Penerapannya dalam
Traveling Salesman Problem bisa digambarkan dalam contoh
berikut:
A
B
C
D
E
A
-
1
2
7
5
B
1
-
4
4
3
C
2
4
-
1
2
D
7
4
1
-
3
E
5
3
2
3
-
Algoritma Greedy untuk traveling salesman problem:
(1). Pilih kota awal
(2). Pilih kota tujuan dengan biaya termurah
(3). Ulangi langkah 2, sehinga seluruh kota dikunjungi dan tidak
ada kota yang dikunjungi lebih dari satu kali.
(4). Kembali ke kota awal.
Bila algoritma ini dijalankan, dengan A sebagai kota awal, maka
didapat:
|
|
20
Cost (A-B) = 1
Cost (B-E) = 3
Cost (E-C) = 2
Cost (C-D) = 1
Cost (D-A) = 7
+
Total
=
14
Pada
metode
ini,
keputusan
yang diambil adalah keputusan
optimal saat itu atau local optimality, dan selalu tunduk pada satu
keputusan, yaitu bila diputuskan harus naik maka selanjutnya
harus
naik
terus,
sebaliknya bila
diputuskan harus
turun
maka
selanjutnya harus terus turun.
c.
Dynamic Programming
Dynamic programming adalah implicit enumerative search
method yang
dapat
dilihat
sebagai teknik
divide
and
conquer.
Untuk
menyelesaikan masalah
yang besar, dilakukan pemecahan
masalah
tersebut
menjadi
bagian-bagian yang
lebih
kecil
yang
independen. Untuk
masalah
optimasi
yang
kompleks
seperti
Traveling
Salesman
Problem,
langkah-langkah penyelesaiannya
adalah sebagai berikut:
(1) Bangun fungsi obyektif yang berdasarkan prinsip optimality.
(2) Gambarkan persoalan dengan digraph.
(3) Tentukan matriks adjacency.
(4) Cari lintasan (tour) yang cost-nya minimum.
|
|
21
Untuk
masalah
Traveling
Salesman
Problem yang
kompleks,
pendekatan ini tidak efektif bila
jumlah kota banyak (lebih besar
dari 20 kota).
d. Branch and Bound
Metode ini
juga
merupakan implicit enumerative search
method.
Pendekatan
ini
terdiri
dari
dua
prosedur
utama
yaitu
branching
dan bounding. Branching adalah proses mempartisi masalah yang
besar
menjadi dua
atau
lebih
masalah kecil
(subproblem),
sedangkan Bounding adalah proses menghitung batas bawah pada
solusi
optimal
dari
subproblem
yang
bersangkutan. Langkah-
langkah
untuk
penyelesaian Traveling
Salesman
Problem-nya
adalah sebagai berikut:
(1) Gambarkan masalahnya dengan digraph G = (V, E).
(2) C
ij
yaitu cost pada edge (i, j) dan C
ij
=
8
jika (i,j) e E.
(3) Mengunakan
metode
Branch
and
Bound
untuk
membangun
ruang solusi pohon.
(4) Menggunakan fungsi pembatas
untuk
menentukan simpul
hidup atau simpul
mati, dan seterusnya, hingga didapat solusi
yang diinginkan.
2. Heuristic Search
Salah
satu
pendekatan
pada
pemrograman adalah
dengan
mengembangkan heuristic,
kemudian
memperbaikinya. Seperti
halnya
banyak
istilah,
heuristic
pernah
mempunyai arti
yang
tepat
yang kemudian dikaburkan karena pemakaian yang berlebih-lebihan.
|
|
22
Istilah
datang
dari
bahasa
yunani
heurisko
(“menemukan”) dan
berhubungan dengan eureka (“saya telah menemukannya”). Heuristic
yang diilhami dari alam diperoleh dari ilmu fisika, biologi dan sosial,
yang
disesuaikan dengan
masalah
yang
ingin dipecahkan.
Beberapa
cara yang digunakan dalam heuristic adalah:
(1) Menggunakan sejumlah percobaan yang diulang-ulang.
(2) Menggunakan sejumlah
“agent” (neurons, particles,
chromosomes, ants, etc).
(3) Menerapkan suatu
sistem kompetisi pada
sejumlah
agent
yang
saling bekerja sama.
(4) Menanamkan suatu prosedur dengan memanfaatkan parameter
heuristic untuk menghasilkan suatu solusi.
Contoh heuristic sebagai berikut:
a.
Tabu Search
Tabu
Search
merupakan
salah
satu
evolutionary heuristic
yang
meng-update satu
solusi
tunggal.
Tabu
Search
dimulai
dengan
membuat solusi acak dan secara berturut-turut pindah (move) ke
salah
satu
tetangganya.
Setiap kali
suatu
move
dilakukan, solusi
sebelumnya akan dimasukkan ke dalam suatu daftar yang disebut
tabu list. Dari suatu solusi yang diberikan, tidak semua neighbour
(tetangga)
dapat
dicapai.
Setiap
perpindahan
membawanya
pada
solusi
terbaik yang
berada
di
sekitarnya,
tetapi
jika
perpindahan
itu ada di dalam tabu list
maka hanya diterima jika dapat
|
|
23
menurunkan nilai dari fungsi obyektif sampai di bawah level yang
telah dicapai sejauh ini (aspiration level).
b. Algoritma Genetik
Algoritma Genetik adalah suatu bentuk algoritma pencarian
yang
berdasarkan mekanisme
seleksi
alam
dan
sifat-sifat
genetika
alamiah (Goldberg, 1989, p1).
Pendekatan dengan
menggunakan
algoritma
Genetik
sampai
saat
ini
merupakan salah
satu
pendekatan yang
paling
banyak
digunakan
dalam
penelitian-
penelitian
untuk
menyelesaikan masalah
optimasi.
Untuk
menyelesaikan masalah
dengan
algoritma
Genetic
harus
dibuat
representasi dari solusi yang
mungkin dalam ruang permasalahan
yang diberikan, yaitu dengan
membuat suatu populasi awal
yang
berisi
representasi solusi-solusi yang
mungkin.
Setelah populasi
awal
terbentuk, algoritma
Genetik
akan
bekerja
meniru
proses
evolusi
alamiah
untuk
mencari
solusi
yang
diinginkan. Sulitnya
menentukan
nilai
parameter-parameter yang
optimal
menyebabkan
pencarian
solusi
menggunakan algoritma
Genetik
membutuhkan waktu yang relatif lama.
c. Algoritma Local Search
Algoritma ini
dapat
digunakan untuk
mengubah sebuah
rute
perjalanan
menjadi
rute perjalanan
yang
lain. Mula-mula dicari
suatu perjalanan yang mungkin, kemudian algoritma tersebut akan
melakukan
operasi
seacara
berulang-ulang di
mana
masing-
masing operasi tersebut mengurangi panjang rute perjalanan pada
|
|
24
tiap perulangan sampai mencapai sebuah rute perjalanan di
mana
operasi-operasi yang
dilakukan
sudah
tidak
menghasilkan
perbaikan
lagi
(panjang
rute
perjalanan sudah
optimal).
Penggunaan
algoritma
ini
menyebabkan
waktu
yang
dibutuhkan
dalam
melakukan
operasi
pengulangan
untuk
mencari
panjang
rute
perjalanan yang optimal
juga relatif
lama
jika
jumlah
kota
yang dikunjungi makin banyak.
d. Algoritma Nearest Neighbour
Seorang salesman
memulai perjalanannya dari sebuah kota
dan
kemudian
melanjutkan perjalanannya dengan
mengunjungi kota
berikutnya
yang
terdekat dengan kota awal. Dari kota kedua,
ia
mengunjungi
kota
berikutnya
yang
terdekat
yang
dalam
perjalannannya
belum pernah dikunjungi, begitu seterusnya
sampai semua kota telah dikunjungi dan kemudian salesman
tersebut kembali ke kota awal di mana ia memulai perjalanannya.
Hal
ini
merupakan heuristic
yang
hampir
setiap
orang
menjumpainya. Mungkin
hal
ini
mirip dengan kegiatan seorang
salesman yang sebenarnya. Namun demikian, hal
ini merupakan
heuristic yang jelek karena beberapa kota yang tidak begitu jauh,
dilewati dan kemudian dikunjungi pada saat-saat akhir
yang
akibatnya jaraknya berubah menjadi lebih jauh dan biayanya lebih
mahal.
Meskipun
biasanya
agak
jelek,
perjalanan
dengan
nearest
neighbor hanya melakukan
sedikit kesalahan,
tetapi pada saat
|
|
25
yang sama
memiliki bagian
yang
panjang
yang
menghubungkan
node-node
dengan jarak yang terpendek.
Oleh karena itu,
beberapa
perjalanan dengan
nearest
neighbor dapat
dijadikan
sebagai perjalanan awal
yang dapat
menghasilkan perbaikan bagi
metode lain.
2.3.2.3 Aplikasi Traveling Salesman Problem
Sebagian
besar
pekerjaan
yang
menggunakan Traveling
Salesman
Problem
tidak
dimotivasi
oleh
aplikasi-aplikasi yang
secara
langsung
mengunakan Traveling Salesman Problem dalam kegiatan sehari-hari, tetapi
oleh
fakta
bahwa Traveling Salesman Problem
menyediakan platform yang
ideal untuk mempelajari
metode-metode
umum
yang dapat diaplikasikan
pada berbgai
macam
masalah
optimasi.
Namun
demikian, tidak
dikatakan
bahwa Traveling Salesman Problem tidak dapat menemukan aplikasi-aplikasi
dalam berbagai bidang. Memang
sejumlah aplikasi
langsung dari Traveling
Salesman
Problem
membawa kehidupan ke
area
penelitian
dan
membantu
untuk menghubungkan ke dunia pekerjaan di masa depan yang canggih.
2.3.2.3.1 Bidang Transportasi Dan Logistik
Traveling Salesman Problem muncul secara alami sebagai
sub
masalah dalam
berbagai aplikasi
transportasi
dan
logistik,
sebagai contoh menyusun rute bis sekolah untuk menjemput anak-
anak dalam
area sekolah.
Aplikasi
bis ini merupakan
aplikasi
lama
yang
penting
dan
sangat
berarti
dalam sejarah
Traveling
Salesman
Problem, terlebih
ketika
menyediakan motivasi
untuk
Merrill
Flood,
salah
seorang
perintis
riset
Traveling
Salesman
|
|
26
Problem pada
tahun
1940.
Aplikasi
kedua
Traveling
Salesman
Problem
pada
tahun
1940-an
yang
melibatkan
transportasi alat
pertanian dari 1
lokasi ke
lokasi lainnya untuk mengecek keadaan
tanah,
memelopori pelajaran
matematika di
Bengal
oleh
P.C.Mahalanobis dan di Iowa oleh R.J.Jessen. Aplikasi Lain yang
baru-baru
ini
melibatkan
pengantaran
makanan
ke rumah-rumah
orang,
rute
perjalanan
truk
untuk
pengambilan pos
bingkisan
parcel, dan lain sebagainya.
Aplikasi
berikutnya
yaitu
permasalahan arah
pergerakan
kendaraan pada kompetisi Whizzkids’96. Permasalahannya terdiri
dari
pencarian rute
terbaik
untuk
4
pengantar koran
dalam
mengantarkan koran
ke
120
pelanggan
mereka.
Tim
yang
beranggotakan
David
Applegate,
William
Cook,
Sanjeeb
Dash
dan
Andre
Rohe
menerima hadiah
5000
Gulden
dari
firma
teknologi informasi untuk solusi mereka pada Februari 2001.
2.3.2.3.2
Bidang Penjadwalan
Walaupun
kebanyakan aplikasi
transportasi merupakan
setting
yang
alami
untuk
Traveling Salesman
Problem,
kemudahan dari
model
tersebut
telah
membawa
ke
berbagai
macam aplikasi
yang menarik di
area lain. Sebuah contoh klasik
yaitu penjadwalan suatu mesin untuk membor lubang-lubang pada
papan
sirkuit
atau
pada
proyek lain.
Pada
masalah ini
lubang-
lubang yang akan dibor merupakan kota-kota, dan biaya
|
|
27
perjalanan
adalah waktu yang diperlukan untuk memindahkan
kepala pengebor dari satu lubang ke lubang berikutnya.
2.3.2.3.3
Bidang Antariksa
Suatu tim insinyur dari Hernandez Engineering di
Houston
dan
dari
Universitas
Brigham Young
telah
bereksperimen
menggunakan Chainded
Lin
Kerningham
untuk
mengoptimasikan rangkaian dari benda-benda angkasa yang akan
diambil
gambarnya pada
program
NASA
Starlight
Space
Inferometer yang dikemukakan. Tujuan akhir dari studi ini adalah
untuk
meminimalkan penggunaan bahan
bakar dalam
mengambil
target dan gambar pergerakan untuk pasangan satelit yang terlibat
dalam misi (dilihat dari konsep Traveling Salesman Problem
maka
sebagai
kotanya
adalah
benda-benda angkasa
yang
akan
diambil gambarnya dan biaya perjalanannya adalah jumlah bahan
bakar yang dibutuhan untuk
memindahkan posisi dari 1 image ke
image berikutnya ).
2.3.2.3.4
Bidang Elektronik
Contoh
aplikasinya
yaitu
penempatan kabel
untuk
mengantar tenaga
listrik
ke
peralatan
elektronik yang
dihubungkan oleh fiber optik menuju ke rumah-rumah.
Sebuah
pabrik
semi
konduktor
menggunakan konsep
Traveling
Salesman
Problem
untuk
mengoptimasi pembacaan
(scan)
rangkaian
dalam sirkuit
gabungan. Pembacaan rangkaian
tersebut
melalui
sebuah chip
untuk
tujuan
testing
dan
|
 28
meminimalkan jarak sangat berguna untuk alasan waktu dan
tenaga.
2.3.2.3.5
Bidang Biologi
Grup dari
AT
&
T
(www.att.com)
menggunakan konsep
Traveling
Salesman
Problem
untuk
menghitung rangkaian DNA
dalam
sebuah
proyek
penelitian teknik
genetik.
Pada
aplikasi
tersebut, suatu rangkaian DNA dengan panjang masing-masing k,
dilekatkan pada
sebuah
rangkaian
universal
(di
mana
masing-
masing
dari
rangkaian
yang
ditargetkan
mengandung sebuah
bagian
dari
rangkaian
universal) dengan
tujuan
untuk
meminimalkan panjang dari rangkaian universal. Di sini kota-kota
dalam
Traveling
Salesman
Problem adalah
rangkaian yang
ditargetkan dan
biaya
perjalanan adalah k
dikurangi
maksimum
dari rangkaian yang sama.
2.3.2.3.6
Bidang Jaringan
Konsep
Traveling
Salesman
Problem
digunakan
pada
sebuah alat untuk mendesain jaringan dengan fiber optik pada Bell
Communication Research
(sekarang
Telcordia
(www.telcordia.com)).
Aspek
Traveling Salesman
Problem
pada
masalah tersebut muncul
dalam routing
dari sonnet
rings,
yang
menyediakan
hubungan
komunikasi
melalui
suatu
set dari
sonet
(Synchronous
Optical
Network)
yang
terorganisasi pada
sebuah
ring. Struktur ring menyediakan mekanisme cadangan dalam
|
|
29
rangka
mengatasi
kegagalan
hubungan,
karena
arus data yang
padat dapat diarahkan ke ring seberang.
2.3.3 Algoritma Metropolis
Algoritma
Metropolis
adalah
pengembangan dari
metode
Simulated
Annealing. Metode Simulated Annealing dianalogikan dengan termodinamika,
terutama dengan cara bagaimana cairan membeku dan mengkristal, atau proses
memanasi
kemudian
mendinginkan
logam.
Pada
saat
temperatur
dalam
keadaan
tinggi,
molekul-molekul dari
cairan
bergerak
dengan
bebas
tanpa
tergantung
satu
sama
lain.
Jika
cairan
didinginkan secara
perlahan
maka
mobilitas panas hilang. Atom-atom sering dapat berbaris sendiri dan
membentuk kristal murni yang teratur sepanjang jarak miliaran kali dari ukuran
satu atom dalam semua arah. Kristal ini
adalah kondisi minimum energi untuk
sistem
ini.
Fakta
yang
mengagumkan adalah
sistem
yang
didinginkan
secara
perlahan, akan dapat menemukan keadaan energi
minimum. Jika cairan
logam
didinginkan secara cepat, tidak akan mencapai keadaan ini tetapi akan berakhir
dengan polycrystalline atau keadaan amorphous yang
mempunyai energi
yang
lebih tinggi.
Kelebihan
dari
Algoritma
Metropolis
dibandingkan dengan
metode
lainnya
adalah kemampuannya untuk
menghindar dari terperangkapnya solusi
dalam local minima atau dengan kata lain Algoritma Metropolis adalah metode
yang
paling
memungkinkan penyelesaian
Traveling
Salesman
untuk
mendapatkan absolute minimum.
|
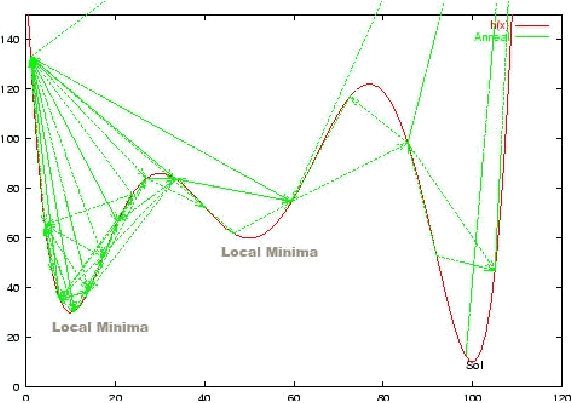 30
Gambar 2.7 Absolute Minimum
Ide
dasar
dari
Algoritma
Metropolis mengambil ide
yang
sama
untuk
mensimulasi atom
dalam
satu
ekuilibrium.
Algoritma
metropolis
digunakan
untuk
mendapatkan konfigurasi
ekuilibrium
dari
koleksi
atom
pada
temperature yang
diberikan.. Hubungan
antara
algoritma
metropolis dan
minimalisasi secara
matematis
pertama
kali
dituliskan
oleh
Pincus.
Namun
Kirkpatrick
mengembangkannya sebagai
teknik
optimalisasi
untuk
permasalahan-permasalahan kombinatorial. Sekarang ini Algoritma Metropolis
sudah banyak diaplikasikan untuk pemecahan masalah optimasi kombinatorial.
Dalam
Algoritma
Metropolis,
suatu
state
(kombinasi dari
satu solusi) dapat
diterima dengan kemungkinan:
|
|
31
?
-
?
E
?
P
=
exp?
?
T
?
, dengan ketentuan:
?
?E adalah selisih energi saat ini dengan energi sebelumnya
T
adalah temperature
Algoritma Metropolis dapat dijabarkan sebagai berikut:
1. Bangkitkan state awal S
0
.
2. Hitung energi E
0
pada S
0
.
3. Update State S dengan aturan update sesuai permasalahan menjadi S
i
.
4. Hitung energi E
i
.
5. Bangkitkan bilangan acak berdistribusi uniform p = [0,1].
6. Jika P = exp(-?E/T), state diterima; jika tidak, state ditolak.
7. Turunkan T dengan fungsi cooling schedule tertentu.
8. Ulangi langkah ke 3 sampai mencapai kriteria berhenti.
Berikut
ini adalah pseudocode dari Algoritma Metropolis yang akan digunakan untuk
memecahkan masalah Traveling Salesman Problem:
initialize temperature
repeat
for i := 1 … ntemps do
mencoba melakukan swapping dari pasangan titik secara acak
delta := current_cost – trial_cost
if delta > 0 then
buat swap menjadi permanent
increment good_swaps
else
|
|
32
m:= angka acak dengan jangkauan [0 ... 1]
p:= exp(delta/temperature)
if m < p then
ubah swap jadi permanent
increment good_swaps
end if
end if
end for
temperature := factor * temperature
until (temperature < finaltemp)
Dalam mempelajari pseudocode dari algoritma tersebut ada beberapa notasi yang
digunakan yaitu:
1. Cost merupakan fungsi objektif atau biaya dari solusi permasalahan optimasi
tersebut, yaitu jarak.
2. delta merupakan perbedaan antara solusi yang lama dengan solusi yang baru,
dalam
permasalahan Traveling
Salesman
Problem,
merupakan
perbedaan
jarak antar rute yang lama dengan rute yang baru.
3.
T
(Iinitial
Temperature)
merupakan kontrol
parameter. Initial
temperature
harus cukup panas atau temperaturnya tinggi sehingga diharapkan pada solusi
final diperoleh suatu solusi yang optimal.
4. factor (Cooling Ratio)
merupakan konstanta yang berguna
untuk
melakukan
penurunan temperature, dengan jangkauan 0 sampai 1.
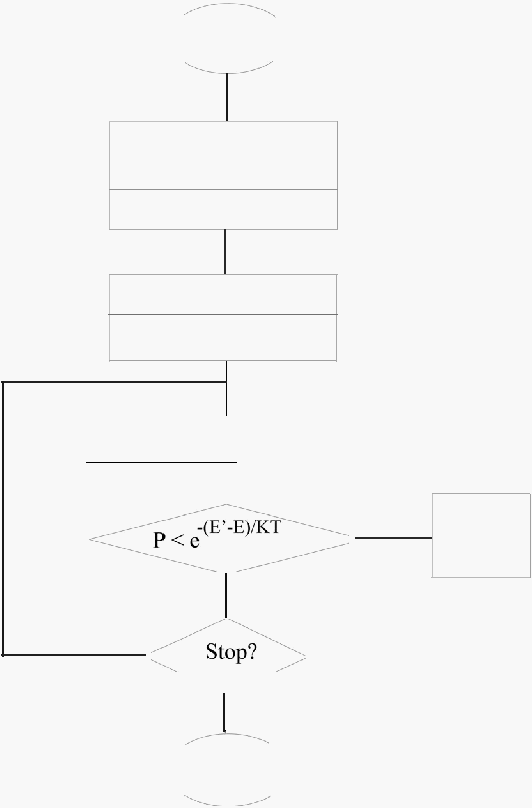
Berikut ini adalah flowchart dari algoritma Metropolis:
|
 33
Start
Membangkitkan
State
Awa] (S)
Hitung
Energi
E
Update
State
Hitung
Energi
E'
angkitkan
bil. acak
p=[O,IIJ
ya
S
-!}
S'
E
-!}
E'
tidak
----------
tidak
ya
Selesai
Garnbar 2.8 Flowchart
Algoritrna
Metropolis
|
|
34
2.4 Rekayasa Piranti Lunak
Piranti
lunak
adalah produk
dan
juga
alat
untuk
mengirimkan sebuah produk
(Pressman, 2001).
Sebagai
produk,
piranti
lunak
memuat
potensi
komputer
dalam
piranti
keras
komputer.
Sebagai
alat
untuk
mengantarkan produk,
piranti
lunak
bekerja sebagai basis kontrol dari komputer (sistem operasi), komunikasi informasi
(jaringan), dan kreasi serta kontrol dari program lain.
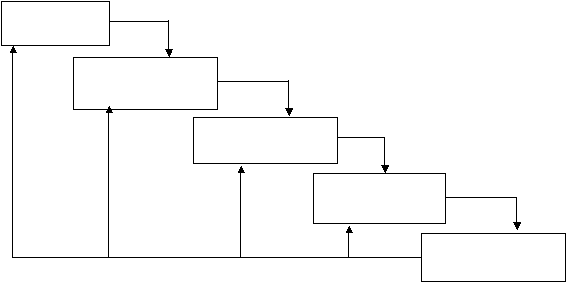
Salah satu cara perancangan piranti lunak adalah dengan menggunakan waterfall
model (model air terjun). Menurut Sommerville (1996, p9-10), tahap – tahap utama
dalam
Waterfall
model
dapat
digambarkan dalam
aktivitas
dasar
pengembangan
seperti berikut ini:
1. Analisis Kebutuhan
Pada
tahap
ini,
dianalisis
apakah
yang
menjadi
kebutuhan dan
yang
menjadi
tujuan dari dibuatnya piranti lunak ini.
2. Desain sistem dan piranti lunak
Proses desain sistem terbagi dalam kebutuhan perangkat keras dan piranti lunak.
Hal
ini
menentukan
arsitektur
piranti
lunak
secara
keseluruhan.
Desain
piranti
lunak
mewakili fungsi
sistem
piranti
lunak
dalam suatu
bentuk
yang
dapat
ditransformasikan ke dalam satu atau lebih program yang dapat dieksekusi.
3. Implementasi dan pengujian unit
Dalam
tahap
ini,
desain
piranti
lunak
direalisasikan dalam
suatu
himpunan
program atau unit –
unit program. Pengujian
unit
mencakup kegiatan
verifikasi
terhadap setiap unit sehingga memenuhi syarat spesifikasinya.
4. Integrasi dan pengujian sistem
|
 35
Unit program secara individual diintegrasikan dan diuji sebagai satu sistem yang
lengkap untuk memastikan bahwa kebutuhan piranti lunak telah terpenuhi.
Setelah pengujian, sistem piranti lunak disampaikan kepada pengguna.
5. Pengoperasian dan Pemeliharaan
Secara
normal,
walaupun
tidak
selalu
diperlukan,
tapi
merupakan
tahap
siklus
hidup
yang terpanjang.
Sistem
telah
terpasang
dan
sedang
dalam
penggunaan.
Pemeliharaan mencakup perbaikan kesalahan yang tidak ditemukan dalam tahap-
tahap
sebelumnya, meningkatkan implementasi unit – unit sistem dan
mempertinggi pelayanan sistem sebagai kebutuhan baru yang ditemukan.
Analisis
Kebutuhan
Desain sistem dan
piranti lunak
Implementasi dan
pengujian unit
Integrasi dan
pengujian sistem
Pengoperasian dan
pemeliharaan
Gambar 2.9 Waterfall Model
2.5 Alat Bantu Perancangan
2.5.1 State Transition Diagram (STD)
State transition
diagram
menggambarkan jalannya
suatu
program dalam
kondisi tertentu. Notasi yang digunakan adalah sebagai berikut.
|
 36
State
menunjukkan
satu
atau
lebih
kegiatan
atau
keadaan
atau
atribut
yang menjelaskan bagian tertentu dari program.
kondisi/aksi
Anak panah berarah menunjukkan perubahan state yang disebabkan oleh
aksi
(action) terhadap
kondisi
(condition)
tertentu.
Kondisi
merupakan
suatu
event
pada
lingkungan eksternal
yang
dapat
dideteksi
oleh
suatu
sistem,
misalnya sinyal,
interupsi, atau data. Hal ini akan
menyebabkan perubahan
dari suatu state ke state
yang
lainnya atau satu
aktivitas ke aktivitas lainnya.
Aksi
merupakan
hal
yang dilakukan oleh
sistem
jika
terjadi
perubahan
state
atau
merupakan
reaksi
terhadap
kondisi.
Aksi
dapat
menghasilkan output,
tampilan pesan pada layar, kalkulasi atau kegiatan lainnya.
2.5.2 Pseudocode
Pseudocode adalah suatu bahasa pemprograman yang
informal dan
sangat
fleksibel,
yang tidak dimaksudkan untuk dieksekusi pada
mesin, tetapi
hanya
digunakan
untuk mengatur pemikiran pemprogram sebelum
melakukan
pengkodean (Page-Jones.1980, p11).
Pseudocode dapat
merupakan
alternatif
lain
dalam
perancangan
perangkat
lunak di
samping alat-alat bantu
berupa diagram.
Tidak
ada
|
|
37
standarisasi dalam
hal
penulisan
pseudocode. Pemprogram dapat
menulisnya
dalam
bahasa
apa
saja
yang
mereka
suka,
dipadukan dengan
bahasa
pemprograman tertentu.
Pemprogram
juga
bebas
menggunakan teknik
dan
aturannya sendiri. Aturan untuk menulis
pseudocode sebagai berikut:
•
Pernyataan ditulis dalam bahasa Inggris sederhana.
•
Setiap perintah ditulis pada baris tersendiri.
•
Kata kunci atau indentasi (penulisan
yang
menjorok ke dalam)
digunakan untuk menandai struktur kontrol khusus.
•
Setiap bimbingan perintah ditulis dari atas ke bawah dengan hanya
satu awal dan satu akhir program.
•
Kumpulan pernyataan-pernyataan dapat dibentuk dalam modul-modul
yang diberi nama tertentu.
|