|
Bab 2
TINJAUAN PUSTAKA
2.1. Daya Dukung Tanah Lempung
Daya dukung tanah adalah parameter tanah yang berkenaan dengan kekuatan tanah
untuk menopang suatu beban di atasnya. Daya dukung tanah dipengaruhi oleh jumlah air
yang terdapat di dalamnya, kohesi tanah, sudut geser dalam, dan tegangan normal tanah.
Daya
dukung
ultimit
didefinisikan sebagai
tekanan
terkecil
yang
dapat
menyebabkan keruntuhan geser pada tanah pendukung tepat di bawah dan di sekeliling
pondasi. Daya dukung ultimit suatu tanah terutama di bawah beban pondasi dipengaruhi
oleh
kuat
geser
tanah. Nilai
kerja
atau nilai
izin
untuk
desain akan
ikut
mempertimbangkan karakteristik kekuatan dan deformasi.
Sebagian
besar
teori
daya
dukung
dikembangkan berdasarkan
teori
plastisitas
dimana
tanah
dianggap
berkelakuan sebagai
bahan
yang
bersifat
plastis.
Paham
ini
dikenalkan oleh Prandtl
(1921)
yang
mengembangkan persamaan dari
analisis kondisi
aliran.
Teori
ini
kemudian
dikembangkan oleh
Terzaghi
(1943),
Meyerhof
(1955),
Hansen (1970), Vesic (1975) dan lainnya. Paham analisa perhitungan daya dukung tanah
lempung
yang dikembangkan para ahli
tersebut mengasumsikan tanah
lempung dalam
keadaan undrained. Teori ini dikembangkan dari persamaan Mohr-Coulomb :
t
=
c
+s
tan
f
(2.1.)
dimana :
t
=
tahanan geser tanah
c
=
kohesi tanah
7
|
 8
2
2
f
=
sudut geser dalam tanah
s
=
tegangan normal tanah
2.1.1
Analisa Prandtl
Prandtl
mengembangkan
persamaan
dari
analisis
kondisi
aliran
yang
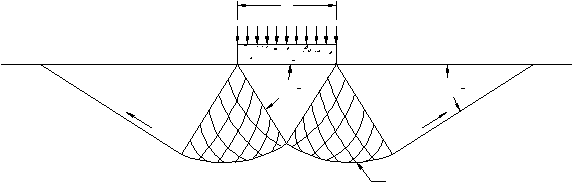
diasumsikan seperti gambar berikut.
B
g
a
b
f
45° +
f
45° -
f
c
d
e
Spiral Log
Gambar 2.1. Bidang Keruntuhan Daya Dukung Pondasi
di Permukaan Tanah Menurut Prandtl (1920)
(Sumber : Joseph E. Bowles, 1991)
Bagian
melengkung dari
busur
ed
atau
ce
dianggap sebagai
bagian
dari suatu spiral
logaritmis. Suatu
keseimbangan plastis terjadi di atas permukaan gdcef sedangkan sisi
tanah lainnya berada dalam keseimbangan elastis.
Berdasarkan teori plastisitas yang dikembangkannya, Prandtl menyelesaikan
permasalahan daya dukung
ultimit pada pondasi di atas
lempung jenuh dalam kondisi
tak terdrainase (f
u
=
0) dengan kekuatan geser c
u
secara eksak sebagai berikut.
q
u
=
(
p
+
2)c
u
=
5,14
c
u
(2.2)
|
|
9
2.1.2
Analisa Terzaghi
Terzaghi
melakukan
analisa kapasitas
dukung
tanah
dengan
beberapa
asumsi,
antara lain:
•
Pondasi berbentuk memanjang tak berhingga
•
Tanah di bawah dasar pondasi adalah homogen
•
Tahanan geser tanah di atas dasar pondasi diabaikan
•
Dasar pondasi kasar
•
Bidang keruntuhan terdiri dari lengkung spiral logaritmis dan linier
•
Baji
tanah
yang
terbentuk
di
dasar
pondasi
dalam
kedudukan
elastis
dan
bergerak bersama-sama dengan dasar pondasi
•
Pertemuan antara sisi baji tanah dan dasar pondasi
membentuk sudut
geser
dalam tanah f
•
Berlaku prinsip superposisi atau prinsip penggabungan
•
Berat tanah di atas dasar pondasi digantikan dengan beban terbagi rata
sebesar
p
o
=
D
f
.
?
,
dengan D
f
adalah kedalaman dasar pondasi dan
?
adalah
berat volume tanah di atas dasar pondasi.
Menurut Terzaghi, daya dukung ultimit didefinisikan sebagai beban maksimum
per
satuan
luas
dimana
tanah
masih
dapat
menopang
beban
tanpa
mengalami
keruntuhan. Pemikiran Terzaghi ini dinyatakan dalam persamaan:
P
u
q
u
=
A
(2.3)
dimana:
q
u
=
daya dukung ultimit
|
 10
P
u
=
beban ultimit
A
=
luas pondasi
Pada analisa daya dukung Terzaghi bentuk pondasi diasumsikan sebagai
memanjang tak berhingga yang diletakkan pada tanah homogen dan dibebani dengan
beban
terbagi
rata
q
u
.
Beban
total
pondasi
per
satuan
panjang
P
u
merupakan
beban
terbagi
rata q
u
yang
dikalikan
dengan
lebar
pondasi
B.
Karena
adanya
beban
total
tersebut, pada tanah yang terletak tepat di bawah pondasi akan membentuk suatu baji
tanah yang menekan tanah ke bawah yang digambarkan sebagai berikut. Gerakan baji
menyebabkan tanah di sekitarnya bergerak, yang
menghasilkan
zona geser di kiri dan
kanan dengan tiap-tiap zona terdiri dari dua bagian yaitu bagian geser radial yang
berdekatan dengan baji dan bagian geser linier yang merupakan kelanjutan dari bagian
geser radial.
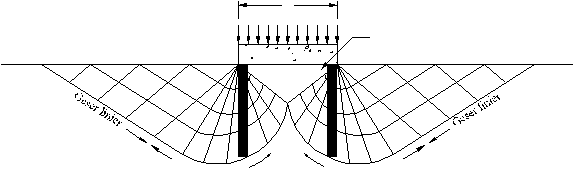
B
Baji
Geser
radial
Geser radial
Gambar 2.2. Pembebanan Pondasi dan Bentuk Bidang Geser
(Sumber : Hary C.H., 2002)
Terzaghi mengembangkan teori keruntuhan plastis Prandtl dalam evaluasi daya
dukung sehingga keruntuhan yang terjadi dalam analisanya dianggap keruntuhan geser
umum.
|
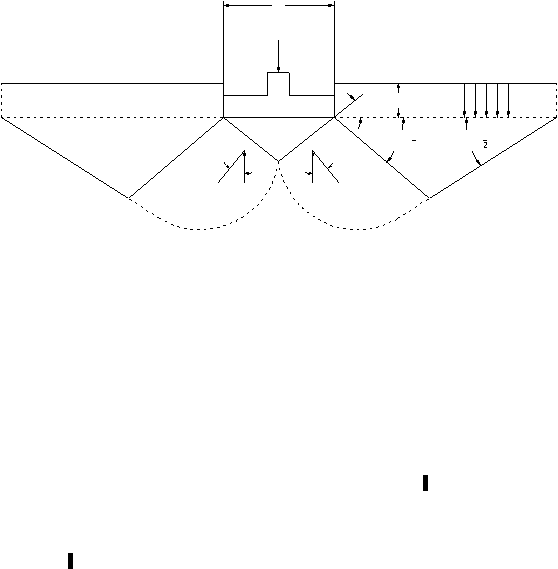 11
2
B
Pu
ß
=
?
(analisis Terzaghi)
A
B
H
C
I
D
ß
Df
45° -
f
45° +
f
?Df
F
Pp
Pp
III
II
G
?
?
III
E
Gambar 2.3. Bentuk Keruntuhan Dalam Analisa Daya Dukung
(Sumber : Hary C.H., 2002)
Baji tanah ABD pada zona I merupakan zona elastis. Bidang AD dan BD
membentuk sudut
ß
terhadap normal horisontal H. Zona II merupakan zona radial
sedangkan
zona III
merupakan
zona
pasif
Rankine.
Lengkung
DE
dan
DG
dianggap
sebagai lengkung spiral logaritmis dan bagian EF dan GH merupakan garis lurus. Garis-
garis
BE,
FE,
AG,
dan
HG
membentuk
sudut
sebesar
(45
°
-
f
2)
terhadap
normal
horisontal
H.
Baji
tanah
yang
terbentuk
dalam
tanah
membentuk sudut
sebesar
a
=
45
°
+ f
2
terhadap horizontal.
Berdasarkan batas yang dibuat oleh sudut tersebut,
dapat diketahui kedalaman maksimum pengaruh baji tanah.
Dalam kondisi keruntuhan geser umum, pada permukaan baji zona I, yaitu pada
bidang AD dan BD, tekanan pasif P
p
akan bekerja jika beban per satuan luas diterapkan.
Bidang AD dan BD
tersebut mendorong tanah di belakangnya, yaitu bagian-bagian
BDEF dan ADGH, sampai tanahnya mengalami keruntuhan. Tekanan ke bawah akibat
beban pondasi P
u
ditambah berat baji tanah pada zona I ditahan oleh tekanan tanah pasif
P
p
pada bagian AD dan BD. Tekanan tanah pasif membentuk sudut gesek dinding (wall
|
 12
friction) d dengan
garis normal
yang melintas di bidang AD dan BD. Karena gesekan
yang terjadi adalah
antara tanah dengan tanah, maka d =
f
(f
adalah sudut geser dalam
tanah).
Untuk per meter panjang pondasi pada saat terjadinya keseimbangan batas maka:
P
u
=
2P
p
cos(ß -
f
)
+
2(BD)c sin
ß
-
W
(2.4)
BD =
B
(2 cos
ß
)
dengan:
P
p
=
tekanan pasif total yang bekerja pada bagian AD dan BD
W
=
berat baji tanah ABD per satuan panjang =
1
4
B
2
?
tan
ß
c
=
kohesi tanah
ß
=
sudut antara bidang BD dan BA
Terzaghi
mengasumsikan bahwa ß =
f
sehingga
nilai
cos(
ß
-
f
)
=
1. Karena bidang-
bidang AD dan BD membentuk sudut
f
dengan horisontal maka arah P
p
vertikal.
Berdasarkan keterangan di atas, tekanan tanah ultimit berubah sebagai berikut.
P
u
=
Bq
u
=
2P
p
+
Bc tan
f
-
1
4
B
2
?
tan
f
(2.5)
Tekanan tanah pasif total (P
p
)
adalah
jumlah tekanan pasif akibat kohesi
tanah, berat
tanah dan beban terbagi rata, yaitu:
P
p
=
P
pc
+
P
pq
+
P
p?
(2.6)
dimana:
P
pc
=
tahanan tanah pasif dari komponen kohesi c
P
pq
=
tahanan tanah pasif akibat beban terbagi rata di atas dasar pondasi
P
p?
=
tahanan tanah pasif akibat berat tanah
|
 13
Tekanan tanah pasif
yang bekerja tegak
lurus arah normal P
p
tegak lurus
terhadap bidang
BD adalah:
P
=
H
[cK
+ p K
]
+
1
?
K
?
?
H
2
?
p?
?
(2.7)
p
tegak lurus
sin
a
pc
0
pq
2
?
sin
a
?
Dengan
H
=
1
2
B
tan
f
a
=
sudut antara bidang DB dan BF
=
180
°
-
f
K
pc
=
koefisien tekanan tanah pasif akibat kohesi tanah
K
pq
=
koefisien tekanan tanah pasif akibat beban terbagi rata
K
p?
=
koefisien tekanan tanah pasif akibat berat tanah
Nilai
koefisien-koefisien
tekanan
tanah
pasif
tersebut tidak tergantung
pada
H
dan ?.
Kombinasi dari persamaan-persamaan di atas adalah sebagai berikut.
P
=
B
[
cK
+
p
K
]
+
1
?
B
2
?
tan
f
?
K
(2.8)
p
2
cos
2
f
pc
0
pq
8
?
cos
2
f
?
p
?
?
Gesekan yang terjadi antara tanah dengan tanah pada bidang BD mengakibatkan arah
tekanan tanah pasif P
p
miring sebesar d. Karena d =
f
,
maka:
P
pm
P
p
=
cos
d
=
P
pm
cos
f
(2.9)
P
pm
adalah
tekanan
tanah
pasif
miring.
Beban
ultimit
dari
hasil
substitusi
persamaan
tekanan tanah pasif ke persamaan tekanan tanah ultimit adalah sebagai berikut.
?
K
pc
?
?
K
pq
?
1
2
?
K
p?
?
P
u
=
Bc
?
cos
2
f
+
tan
f
?
+
Bp
o
?
cos
2
f
?
+
4
?
B
tan
f
?
cos
2
f
-
1
?
(2.10)
?
?
?
?
?
?
|
 14
?
Tekanan-tekanan
tanah
pasif
akibat
kohesi
P
pc
dan
beban
terbagi
rata
P
pq
diperoleh
dengan menganggap tanah tidak mempunyai berat (? = 0). Karena ? = 0,
P
u
=
P
pc
+
P
pq
dinyatakan sebagai persamaan berikut.
?
K
pc
?
?
K
pq
?
P
pc
+
P
pq
=
Bc
?
cos
2
f
+
tan
f
?
+
Bp
0
?
cos
2
f
?
(2.11)
?
?
?
?
=
BcN
c
+
Bp
0
N
q
atau
q +
q
=
1
(P
+
P
)
=
cN
+ p
N
(2.12)
c
q
B
pc
pq
c
0
q
dengan qc
dan q
q
adalah tekanan tanah pasif per satuan luas dari komponen kohesi dan
beban
terbagi
rata
p
0
.
Nilai-nilai
Nc
dan
N
q
diperoleh
Terzaghi
dari
analisa
Prandtl
(1920) dan Reissner (1924) yang besarnya:
?
a
2
?
N
c
=
cot
f
?
2
cos (45
2 (45
°
+
f
-
1
?
2
?
(2.13)
N =
a
=
N tan
f
+
1
dengan nilai a = e 3p
(3p
4-p
2) tan
f
(2.14)
q
2
cos
2
(45
°
+
f
2)
c
Apabila tanah
yang diamati merupakan tanah yang
tidak berkohesi (c = 0) dan
tanpa
beban merata di atasnya (q = 0) maka persamaan perhitungan tekanan tanah pasif hanya
mempertimbangkan akibat dari berat tanah.
2
?
K
p?
?
P
p?
=
1
4
?
B
tan
f
?
cos
2
f
-
1
?
=
B
×
1
2
?
BN
?
(2.15)
?
?
|
 15
Jika P
p?
dinyatakan sebagai tahanan tanah pasif per satuan luas dari akibat berat tanah q
?
maka:
q
?
=
P
p?
=
1
2
?
BN
?
dengan nilai
N
?
tan
f
?
=
?
K
p?
2
?
-
1
?
(2.16)
B
2
?
cos
f
?
Terzaghi tidak memberikan nilai-nilail K
p?
maka digunakan persamaan pendekatan dari
Cernica (1995):
K
p?
=
3
tan
2
{45° + 1 2 (
f
+
33°)
}.
(2.17)
Daya
dukung
ultimit
memperhitungkan
kohesi
tanah,
beban
terbagi
rata
dan
berat volume tanah ( q
u
=
q
c
+
q
q
+
q
?
).
Berdasarkan persamaan tersebut,
Terzaghi
membuat persamaan umum daya dukung ultimit pondasi memanjang sebagai berikut.
q
u
=
cN
c
+ p
0
N
q
+
0,5?
BN
?
(2.18)
Karena
p
o
=
D
f
.
?
, persamaan di atas menjadi
q
u
=
cN
c
+
D
f
?
N
q
+
0,5
?
BN
?
(2.19)
Dimana:
q
u
=
daya dukung ultimit untuk pondasi memanjang (kN/m²
)
c
=
kohesi tanah (kN/m2
)
D
f
=
kedalaman pondasi yang tertanam di dalam tanah (m)
?
=
berat volume tanah (kN/m³
)
p
o
=
D .
f
?
=
tekanan overburden pada dasar pondasi (kN/m²)
Nc
=
faktor daya dukung tanah akibat kohesi tanah
N
q
=
faktor daya dukung tanah akibat beban terbagi rata
N
?
=
faktor daya dukung tanah akibat berat tanah
|
 16
'
Nilai
faktor
daya dukung
ini
merupakan
fungsi
dari sudut
geser dalam tanah
f
dari
Terzaghi (1943).
q
u
adalah beban total maksimum per satuan luas ketika pondasi akan
mengalami
keruntuhan
geser. Beban total tersebut terdiri dari beban-beban struktur, pelat pondasi
dan
tanah
urugan
di atasnya.
Analisa
daya dukung tersebut
berdasarkan
pada kondisi
keruntuhan
geser umum dari suatu bahan yang bersifat plastis dan
tidak terjadi
perubahan volume dan kuat geser oleh adanya keruntuhan tersebut.
Gerakan baji tanah ke bawah pada tanah
yang mengalami regangan yang besar
sebelum mencapai
keruntuhan
geser
mungkin
hanya
memampatkan
tanah
tanpa
menimbulkan regangan yang cukup untuk menghasilkan keruntuhan geser umum.
Menurut
Terzaghi, tidak ada analisis rasional sebagai pemecahannya. Oleh karena itu
Terzaghi memberikan koreksi empiris pada perhitungan faktor daya dukung pada
kondisi keruntuhan geser umum
yang digunakan untuk perhitungan daya dukung pada
keruntuhan
geser
lokal. Nilai
c'
=
2
3
c
dan
f
'
=
arc
tan(2 3 tan
f
)
digunakan sebagai
koreksi
tersebut
sehingga
persamaan
umum
daya
dukung
ultimit
pada
pondasi
memanjang pada keruntuhan geser lokal menjadi:
q
u
=
2
3
cN
c
+
p
0
N
q
'
+
0,5
?
BN
?
'
(2.20)
Persamaan daya dukung pondasi
di
atas hanya dapat
digunakan
untuk
perhitungan daya
dukung
ultimit
pondasi
memanjang.
Oleh
karena
itu
Terzaghi
memberikan pengaruh faktor bentuk terhadap daya dukung ultimit yang didasarkan yang
didasarkan pada analisa pondasi memanjang sebagai berikut.
|
|
17
•
Untuk pondasi bujur sangkar
:
q
u
=
1,3cN
c
+
p
0
N
q
+
0,4
?
BN
?
•
Untuk pondasi lingkaran
:
q
u
=
1,3cN
c
+
p
0
N
q
+
0,3
?
BN
?
•
Untuk pondasi persegi panjang :
q
u
=
cN
c
(1 + 0,3 B
L) + p
0
N
q
+
0,5
?
BN
?
(1
-
0,2 B
L)
dimana:
q
u
=
daya dukung ultimit untuk pondasi memanjang (kN/m²
)
c
=
kohesi tanah (kN/m2
)
D
f
=
kedalaman pondasi yang tertanam di dalam tanah (m)
?
=
berat volume tanah yang dipertimbangkan terhadap posisi
muka air
tanah
(kN/m³)
p
o
=
D .
f
?
=
tekanan overburden pada dasar pondasi (kN/m²)
B
=
lebar atau diameter pondasi (m)
L
=
panjang pondasi (m)
Persamaan daya dukung Terzaghi mengabaikan kuat geser tanah di atas pondasi
dan
hanya
cocok
untuk
pondasi dangkal dengan
D
f
=
B. Oleh karena
itu,
kesalahan
perhitungan untuk pondasi yang dalam menjadi besar.
|
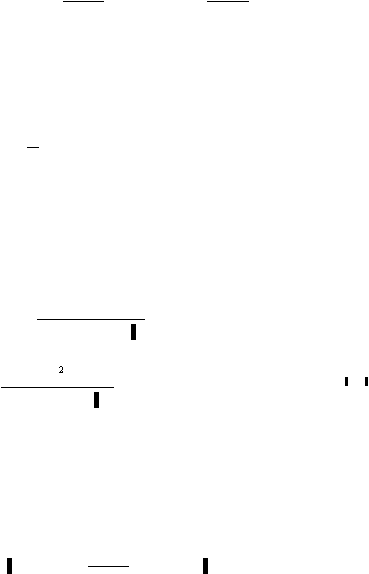
 18
Gambar 2.4. Grafik Hubungan
f
dan N
?
,
Nc
, N
q
Menurut Terzaghi (1943)
(Sumber : Braja M. Das, 1984)
2.1.3
Analisa Skempton
Analisa Skempton (1951) terbatas pada persamaan daya dukung ultimit pondasi
dan hanya pada lempung jenuh. Analisanya menyatakan bahwa perhitungan pondasi
tersebut harus memperhatikan faktor-faktor bentuk dan kedalaman pondasi.
Pada sembarang kedalaman pondasi empat persegi panjang yang
terletak pada
tanah lempung, Skempton memberikan faktor pengaruh bentuk pondasi s
c
sebesar
(1 + 0,2 B
L) . Faktor kapasitas dukung Nc untuk bentuk pondasi tertentu diperoleh dari
mengalikan faktor bentuk pondasi s
c
dengan Nc
pada pondasi yang besarnya dipengaruhi
oleh kedalaman D
f
.
|
|
19
Kondisi-kondisi yang merupakan analisa Skempton antara lain:
•
Pondasi di permukaan (D
f
= 0)
Nc
(permukaan)
=
5,14
(untuk pondasi memanjang)
Nc
(permukaan)
=
6,20
(untuk pondasi lingkaran dan bujur sangkar)
•
Pondasi pada kedalaman 0 < D
f
< 2,5B
?
N
c
=
?1 +
?
D
f
0,2
B
?
?
N
c permukaan
( permukaan
)
?
•
Pondasi pada kedalaman D
f
> 2,5B
Nc = 1,5 Nc
(permukaan)
Analisa
Skempton
mengenai
daya
dukung
ultimit
pondasi
memanjang
q
u
dan
daya dukung ultimit neto q
un
dinyatakan dalam persamaan-persamaan berikut.
q
u
=
c
u
N
c
+
D
f
?
(2.21)
q
un
=
c
u
N
c
dimana:
q
u
=
daya dukung ultimit (kN/m2
)
q
un
=
daya dukung ultimit neto (kN/m²
)
D
f
=
kedalaman pondasi yang tertanam di dalam tanah (m)
?
=
berat volume tanah (kN/m³)
c
u
=
kohesi tak terdrainase (kN/m²
)
Nc
=
faktor daya dukung Skempton
|
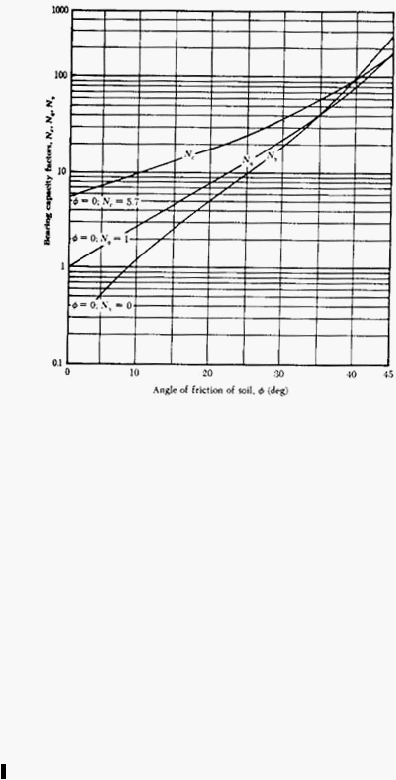
 20
Gambar 2.5. Grafik Faktor Daya Dukung Nc Menurut Skempton
(Sumber : Hary C.H., 2002)
Faktor daya
dukung
Skempton
merupakan
fungsi dari
D
f
B
dan
bentuk
pondasi.
Untuk
pondasi
empat persegi
panjang
dengan
panjang
L
dan
lebar
B, daya
dukung ultimit diperoleh dari nilai faktor daya dukung Nc yang dikalikan dengan
0,84
+
0,16 B
L
sehingga persamaan daya dukung ultimit menjadi:
q
u
=
(0,84
+
0,16 B
L)c
u
N
c untuk pondasi bujursangkar )
(untuk pondasi bujursangkar )
(2.22)
2.1.4
Analisa Meyerhof
Analisa daya dukung Meyerhof
mengasumsikan sudut baji
ß
antara bidang AD
atau BD terhadap normal horisontal lebih besar dari sudut geser dalam tanah
f
.
Hal ini
menyebabkan faktor daya dukung Meyerhof lebih rendah daripada yang disarankan oleh
Terzaghi.
Akan
tetapi
Meyerhof
mempertimbangkan
faktor
pengaruh
kedalaman
pondasi, sehingga nilai daya dukung menjadi lebih besar.
|
|
21
Meyerhof menganalisa daya dukung dengan mempertimbangkan bentuk pondasi,
kemiringan beban,
dan
kuat
geser
tanah
di
atas
pondasinya
yang
dinyatakan
dengan
persamaan berikut.
q
u
=
s
c
d i
c
c
cN
c
+
s
q
d i
q
q
p
o
N
q
+
s
?
d
?
i
?
0,5B'
?
N
?
(2.23)
dimana:
q
u
=
kapasitas dukung ultimit (kN/m²)
Nc, Nq, N
?
=
faktor kapasitas daya dukung Meyerhof untuk pondasi memanjang
sc
,
s
q
,
s
?
=
faktor bentuk pondasi
dc, d
q
,
d
?
=
faktor kedalaman pondasi
ic
,
i
q
,
i
?
=
faktor kemiringan beban
B’
=
lebar pondasi efektif (m)
p
o
=
D .
f
?
=
tekanan overburden pada dasar pondasi (kN/m²)
D
f
=
kedalaman pondasi yang tertanam di dalam tanah (m)
?
=
berat volume tanah (kN/m³
)
|
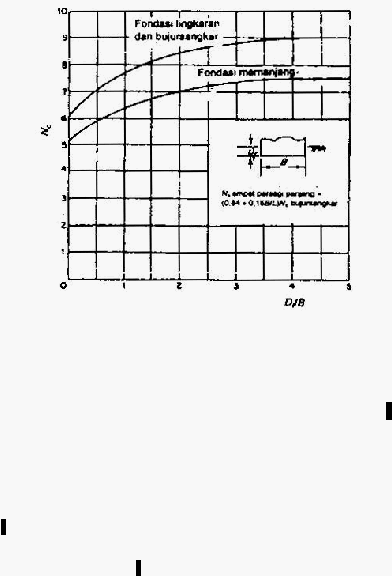
 22
q
Gambar 2.6. Faktor-faktor Daya Dukung Meyerhof (1963)
(Sumber : Hary C.H., 2002)
Faktor kapasitas dukung tanah yang diusulkan Meyerhof (1963) adalah :
N
c
=
(
N
q
-
1) cot
f
N =
tan
2
(45
o
+
f
2)e
(p tan f )
N
?
=
(
N
q
-
1) tan(1,4
f
)
Nilai-nilai faktor daya dukung Meyerhof untuk dasar pondasi kasar dengan
bentuk memanjang dan bujursangkar ditunjukkan dalam
gambar 2.6. sedangkan untuk
pondasi
memanjang,
nilai-nilai
faktor
daya dukung tanah
ditunjukkan
pada
tabel
2.1.
Berdasarkan gambar 2.6., nilai faktor daya dukung pondasi bujursangkar lebih besar
daripada pondasi
memanjang.
Dalam tabel 2.2. diperlihatkan
faktor-faktor bentuk
pondasi, f
dan
pada
tabel 2.3.
ditunjukkan
faktor-faktor
kedalaman
pondasi. Nilai
tan(45° + f
2) merupakan nilai K
p
.
Untuk pondasi berbentuk lingkaran, nilai
B
L
=
1
.
|
 23
Tabel 2.1. Faktor Daya Dukung Meyerhof
f
(°)
Nc
N
q
N
?
f
(°)
Nc
N
q
N
?
0
5,14
1,00
0,00
26
22,25
11,85
8,00
1
5,38
1,09
0,00
27
23,94
13,20
9,46
2
5,63
1,20
0,01
28
25,80
14,72
11,19
3
5,90
1,31
0,02
29
27,86
16,44
13,24
4
6,19
1,43
0,04
30
30,14
18,40
15,67
5
6,49
1,57
0,07
31
32,67
20,63
18,56
6
6,81
1,72
0,11
32
35,49
23,18
22,02
7
7,16
1,88
0,15
33
38,64
26,09
26,17
8
7,53
2,06
0,21
34
42,16
29,44
31,15
9
7,92
2,25
0,28
35
46,12
33,30
37,15
10
8,34
2,47
0,37
36
50,59
37,75
44,43
11
8,80
2,71
0,47
37
55,63
42,92
53,27
12
9,28
2,97
0,60
38
61,35
48,93
64,07
13
9,81
3,26
0,74
39
67,87
55,96
77,33
14
10,37
3,59
0,92
40
75,31
64,20
93,69
15
10,98
3,94
1,13
41
83,86
73,90
113,99
16
11,63
4,34
1,37
42
93,71
85,37
139,32
17
12,34
4,77
1,66
43
105,11
99,01
171,14
18
13,10
5,26
2,00
44
118,37
115,31
211,41
19
13,93
5,80
2,40
45
133,87
134,87
262,74
20
14,83
6,40
2,87
46
152,10
158,50
328,73
21
15,81
7,07
3,42
47
173,64
187,21
414,33
22
16,88
7,82
4,07
48
199,26
222,30
526,45
23
18,05
8,66
4,82
49
229,92
265,50
674,92
24
19,32
9,60
5,72
50
266.88
319,06
873,86
25
20,72
10,66
6,77
(Sumber : Hary C.H., 2002)
|
 24
Tabel 2.2. Faktor Bentuk Pondasi Meyerhof
Faktor
Bentuk
Nilai
Keterangan
s
c
1+ 0,2 (B/L) tan
2
(45 + f/2)°
untuk sembarang f
s
q
= s
?
1+ 0,1 (B/L) tan 2 (45 + f
/2)°
1
untuk
f
=
10°
untuk f = 0
(Sumber : Hary C.H., 2002)
Tabel 2.3. Faktor Kedalaman Pondasi
Faktor
Kedalaman
Nilai
Keterangan
dc
1+ 0,2 (D/B) tan (45 +
f/2)°
untuk sembarang f
d
q
=d
?
1+ 0,1 (D/B) tan (45 + f/2)°
1
untuk
f
=
10°
untuk
f
=
0
(Sumber : Hary C.H., 2002)
2.1.5
Analisa Brinch Hansen
Teori Brinch Hansen mengenai persamaan daya dukung pada dasarnya sama
dengan
Terzaghi.
Yang
membedakan
adalah
Brinch
Hansen
memperhatikan pengaruh
bentuk pondasi, kedalaman pondasi, inklinasi beban,
inklinasi
dasar dan inklinasi
permukaan tanah.
Untuk
tanah
dengan
sudut
geser
dalam
f
>
0,
Brinch
Hansen
menyarankan
persamaan daya dukung ultimit sebagai berikut.
q
u
=
Q
u
B'.L'
=
s
c
d
c
i
c
b
c
g
c
cN
c
+
s
q
d
q
i
q
b
q
g
q
p
o
N
q
+
s
?
d i
? i
?
b
?
g
?
0,5B'
?N
?
(2.24)
dimana:
Q
u
=
beban vertikal ultimit (kN)
L’
=
panjang efektif pondasi (m)
|
|
25
q
B’
=
lebar efektif pondasi (m)
?
=
berat volume tanah (kN/m3
)
c
=
kohesi tanah (kN/m²)
p
o
=
D
f
.?
=
tekanan overburden pada dasar pondasi (kN/m²)
sc
,
s
q
,
s
?
=
faktor-faktor bentuk pondasi
dc, d
q
,
d
?
=
faktor-faktor kedalaman pondasi
ic
,
i
q
,
i
?
=
faktor-faktor kemiringan beban
bc, b
q
,
b
?
=
faktor-faktor kemiringan dasar
gc
,
g
q
,
g
?
=
faktor-faktor kemiringan permukaan
Nc, Nq, N
?
=
faktor-faktor kapasitas daya dukung Hansen
Untuk
lempung
jenuh (
f
=
0),
Brinch
Hansen
menyarankan
persamaan daya
dukung ultimit sebagai berikut.
q
u
=
5,14
c
u
(1
+
s
c
'
+
d '
c
-
i
c
'
-
b
c
'
-
g
c
'
)
+
p
0
(2.25)
Pada persamaan Brinch Hansen nilai faktor-faktor kapasitas dukung adalah:
N
=
e
(p tan f )
tan (45
2 (45
°
+
f
2)
N
c
=
(
N
q
-
1) cot
f
N
?
=
1,5
(
N
q
-
1) tan
f
Nilai
faktor
daya
dukung
lainnya
terdapat
pada
tabel
2.4.
Dalam perhitungan
faktor
kemiringan beban
nilai
kohesi
c
diganti dengan
nilai
c
a
(adhesi)
apabila
dasar
pondasi
tidak
terlalu kasar. Nilai adhesi c
a
ini diperoleh dari
mengalikan
faktor adhesi dengan
nilai kohesi.
|
 26
Tabel 2.4. Faktor Daya Dukung Hansen
f
(°)
Nc
N
q
N
?
f
(°)
Nc
N
q
N
?
0
5,14
1,00
0,00
26
22,25
11,85
7,94
1
5,38
1,09
0,00
27
23,94
13,20
9,32
2
5,63
1,20
0,01
28
25,80
14,72
10,94
3
5,90
1,31
0,02
29
27,86
16,44
12,84
4
6,19
1,43
0,05
30
30,14
18,40
15,07
5
6,49
1,57
0,07
31
32,67
20,63
17,69
6
6,81
1,72
0,11
32
35,49
23,18
20,79
7
7,16
1,88
0,16
33
38,64
26,09
24,44
8
7,53
2,06
0,22
34
42,16
29,44
28,77
9
7,92
2,25
0,30
35
46,12
33,30
33,92
10
8,34
2,47
0,39
36
50,59
37,75
40,05
11
8,80
2,71
0,50
37
55,63
42,92
47,38
12
9,28
2,97
0,63
38
61,35
48,93
56,17
13
9,81
3,26
0,78
39
67,87
55,96
66,76
14
10,37
3,59
0,97
40
75,31
64,20
79,54
15
10,98
3,94
1,18
41
83,86
73,90
95,05
16
11,63
4,34
1,43
42
93,71
85,37
113,96
17
12,34
4,77
1,73
43
105,11
99,01
137,10
18
13,10
5,26
2,08
44
118,37
115,31
165,58
19
13,93
5,80
2,48
45
133,87
134,87
200,81
20
14,83
6,40
2,95
46
152,10
158,50
244,65
21
15,81
7,07
3,50
47
173,64
187,21
299,52
22
16,88
7,82
4,13
48
199,26
222,30
368,67
23
18,05
8,66
4,88
49
229,92
265,50
456,40
24
19,32
9,60
5,75
50
266,88
319,06
568,57
25
20,72
10,66
6,76
(Sumber : Hary C.H., 2002)
Hansen
menganalisa
daya
dukung
dalam kondisi
plane
strain seperti
yang
dilakukan
Meyerhof dimana analisa
ini
hanya
dapat
digunakan
apabila pondasi
berbentuk
memanjang
tak
berhingga.
Oleh
karena
itu,
Hansen
menyarankan
adanya
|
 27
dimana:
Q
u
B
=
=
beban vertikal ultimit, dapat miring dan eksentris (kN)
lebar pondasi (m)
L’
=
panjang efektif pondasi (m)
B’
=
lebar efektif pondasi (m)
koreksi
sudut
geser
dalam sehingga
nilai sudut
geser
dalam
f
ps
=
1,1
f
tr
dengan
f
ps
adalah sudut geser dalam yang digunakan dalam perhitungan daya dukung tanah dan
f
tr
adalah sudut geser dalam dari uji triaksial.
2.1.6
Analisa Vesic
Vesic menganalisa daya dukung tanah berdasarkan prinsip superposisi yang
diperoleh dari beberapa peneliti, yaitu:
•
Usulan Reissner (1924) :
q
q
=
p
0
.N
q
dengan nilai
N
q
=
e
(
p
tan
f
)
tan
2
(45
°
+
f
2)
•
Analisa Prandtl (1924) :
q
c
=
c.N
c
dengan nilai
N
c
=
(
N
q
-
1) cot
f
•
Usulan Caquot - Kerisel (1953) :
q
?
= 0,5
B
?
N
?
dengan nilai
N
?
=
2(
N
q
+
1) tan
f
Superposisi
dari
ketiga
persamaan
tersebut
adalah
q
u
=
q
c
+
q
q
+
q
?
.
Dengan
mensubstitusikan nilai dari tiga persamaan di atas maka diperoleh nilai daya dukung:
q
u
=
cN
c
+
p
0
N
q
+
0,5
B
?
N
?
(2.26)
Analisa
daya
dukung
Vesic
memperhitungkan
faktor
kedalaman
pondasi,
kemiringan dan eksentrisitas beban, kemiringan dasar dan kemiringan permukaan seperti
halnya Brinch Hansen. Analisa ini dinyatakan selengkapnya sebagai berikut.
q
u
=
Q
u
B'.L' =
s
c
d i
c
c
b
c
g cN
c
c
+
s
q
d i
q
q
b
q
g
q
p
0
N
q
+
s
?
d
?
i
?
b
?
g
?
0,5
B.?
.N
?
(2.27)
|
|
28
?
=
berat volume tanah (kN/m3
)
c
=
kohesi tanah (kN/m²)
p
o
=
D
f
.
?
=
tekanan overburden pada dasar pondasi (kN/m²)
sc
,
s
q
,
s
?
=
faktor-faktor bentuk pondasi
dc, d
q
,
d
?
=
faktor-faktor kedalaman pondasi
ic
,
i
q
,
i
?
=
faktor-faktor kemiringan beban
bc, b
q
,
b
?
=
faktor-faktor kemiringan dasar
gc
,
g
q
,
g
?
=
faktor-faktor kemiringan permukaan
Nc, Nq, N
?
=
faktor-faktor kapasitas daya dukung Vesic
Untuk faktor-faktor bentuk pondasi,
Vesic menyarankan pemakaian faktor
bentuk pondasi dari De Beer (1970) sedangkan untuk faktor-faktor kedalaman, Vesic
mengadopsi faktor kedalaman dari Hansen (1970).
2.2. Pondasi Dangkal
Pondasi
adalah bagian
terendah
dalam suatu konstruksi
yang
meneruskan
beban
konstruksi ke tanah atau batuan di bawahnya. Berdasarkan jenisnya, pondasi dibedakan
menjadi
dua
macam
yaitu
pondasi
dangkal dan
pondasi
dalam.
Pondasi
dangkal
didefinisikan sebagai pondasi yang mendukung beban konstruksi secara
langsung.
Contoh
pondasi dangkal
antara
lain
pondasi telapak,
pondasi
memanjang
dan
pondasi
rakit. Sedangkan pondasi dalam didefinisikan sebagai pondasi
yang
meneruskan beban
struktur di atasnya ke tanah keras atau batuan yang terletak jauh dari permukaan. Contoh
pondasi dalam antara lain pondasi tiang dan pondasi sumuran.
|
|
29
Pemilihan jenis pondasi bergantung pada beban yang akan didukung, kondisi tanah
dasar,
dan
biaya
pembuatan
pondasi
yang dibandingkan
terhadap
biaya struktur atas.
Pondasi dalam
digunakan pada bangunan struktur tinggi dan pada struktur yang tanah
kerasnya terletak
pada kedalaman yang
sangat
dalam.
Pondasi
dangkal
biasanya
digunakan
pada
bangunan
tinggal
sederhana,
bangunan
dengan
kolom yang
berjarak
sangat dekat, dan untuk bangunan yang terletak pada tanah lunak.
Beberapa definisi yang perlu diketahui dalam perancangan pondasi antara lain :
a. Tekanan
overburden
total
p
adalah
intensitas
tekanan total
yang
terdiri dari
berat
material
di atas dasar pondasi total yaitu berat tanah dan air sebelum
pondasi dibangun.
b. Daya dukung
ultimit
neto q
un
adalah nilai
intensitas beban pondasi saat tanah
akan mengalami keruntuhan geser.
c.
Tekanan
pondasi total q
adalah
intensitas
tekanan total
pada
tanah
di
dasar
pondasi. Beban ini termasuk berat pondasi, berat struktur atas, berat tanah
urugan dan berat air di atas dasar pondasi.
d. Tekanan pondasi neto q
n
adalah tambahan tekanan pada dasar pondasi akibat
beban hidup dan mati dari strukturnya.
e. Daya
dukung
batas
q
u
adalah
tekanan
pondasi
maksimum
yang
dapat
dibebankan pada tanah.
f.
Faktor keamanan SF diperoleh dari
hasil pembagian nilai daya dukung ultimit
neto dengan tekanan pondasi neto.
g. Daya
dukung
aman
q
s
didefinisikan
tekanan
pondasi
total
ke
dalam tanah
maksimum yang tidak mengakibatkan resiko keruntuhan daya dukung.
|
 30
Perencanaan pondasi sangat memperhatikan faktor kapasitas dukung tanah.
Kurangnya daya dukung pada pondasi dapat menyebabkan keruntuhan pondasi.
Berdasarkan hasil uji model, Vesic (1963) membagi mekanisme keruntuhan pondasi
menjadi tiga macam, yaitu:
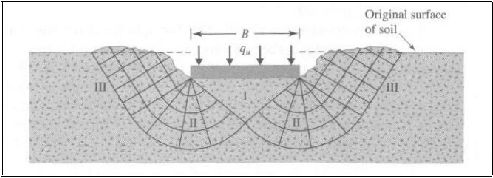
a. Keruntuhan geser umum
Keruntuhan
geser umum
merupakan keruntuhan pondasi yang terjadi
menurut
bidang runtuh yang dapat diidentifikasi dengan jelas karena bidang longsor, berupa
lengkung dan garis lurus, yang terbentuk berkembang hingga mencapai permukaan
tanah. Keruntuhan ini terjadi dalam waktu yang relatif mendadak yang kemudian
diikuti dengan penggulingan pondasi.
Gambar 2.7. Keruntuhan Geser Umum
(Sumber : Braja M. Das, 2005)
b. Keruntuhan geser lokal
Tipe keruntuhannya hampir sama dengan keruntuhan geser umum. Akan tetapi
bidang runtuh yang terbentuk tidak berkembang sehingga tidak mencapai
permukaan tanah. Pada keruntuhan geser lokal ini terjadi sedikit penggembungan
tanah di sekitar pondasi tetapi tidak sampai terjadi penggulingan pondasi.
|
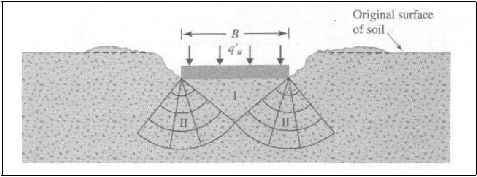 31
Gambar 2.8. Keruntuhan Geser Lokal
(Sumber : Braja M. Das, 2005)
c. Keruntuhan penetrasi
Keruntuhan
penetrasi
merupakan
kondisi
dimana
pondasi
hanya
menembus
dan menekan tanah ke samping yang menyebabkan pemampatan tanah di dekat
pondasi. Penurunan pondasi bertambah secara linier dengan penambahan
bebannya.
Penurunan
yang terjadi
tidak
menghasilkan
cukup
getaran
arah
lateral
yang menuju kedudukan kritis keruntuhan tanah sehingga kuat geser ultimit tanah
tidak dapat berkembang. Pada saat terjadi keruntuhan, bidang runtuh tidak terlihat
sama sekali.
Langkah
pertama
dalam perancangan
pondasi
adalah
menghitung
jumlah
beban
efektif
yang
akan
ditransfer ke
tanah
di
bawah pondasi. Selanjutnya
menentukan
nilai
daya dukung izin q
a
. Luas dasar pondasi dapat diketahui dengan membagi jumlah beban
efektif dengan daya dukung izin. Berdasarkan
pada tekanan yang terjadi pada dasar
pondasi dilakukan perancangan struktural
pondasi yaitu dengan menghitung momen-
momen lentur dan gaya-gaya geser yang terjadi pada pelat pondasi.
Perancangan pondasi harus mempertimbangkan adanya keruntuhan geser dan
penurunan
yang
berlebihan, oleh
karena
itu kriteria
stabilitas dan kriteria
penurunan
|
|
32
harus dipenuhi. Dalam perencanaan pondasi dangkal perlu diperhatikan hal-hal sebagai
berikut.
•
Faktor keamanan terhadap keruntuhan akibat terlampauinya kapasitas dukung
tanah harus dipenuhi.
•
Penurunan pondasi harus berada dalam batas-batas
nilai
yang ditoleransikan.
Untuk penurunan yang tidak seragam, tidak boleh terjadi kerusakan pada
struktur.
Untuk
memenuhi
stabilitas
jangka
panjang, perletakan dasar pondasi perlu
diperhatikan. Pondasi harus diletakkan pada kedalaman yang cukup untuk
menanggulangi
resiko erosi permukaan,
gerusan, kembang susut tanah dan gangguan
lainnya
pada
tanah
di
sekitar
pondasi.
Keterangan
umum mengenai
beberapa
jenis
pondasi dangkal akan dijelaskan berikut ini.
2.2.1. Pondasi memanjang
Pondasi
memanjang digunakan
untuk
mendukung beban segaris seperti dinding
memanjang. Perancangan pondasi memanjang menganggap beban dinding sebagai
beban garis per satuan panjang. Perancangan struktur pondasi didasarkan pada momen-
momen dan tegangan geser yang terjadi akibat tekanan sentuh antara dasar pondasi dan
tanah. Oleh karena itu besar distribusi tekanan sentuh pada dasar pondasi harus
diketahui.
Dalam
analisa
perancangan
dapat
diasumsikan
bahwa
pondasi
sangat
kaku
dan
tekanan
pondasi didistribusikan
secara
linier pada
dasar
pondasi.
Apabila
resultan
beban berhimpit dengan pusat berat luasan
pondasi maka tekanan pada dasar pondasi
dapat dianggap disebarkan merata ke seluruh luasan pondasi.
|
|
33
2.2.2. Pondasi telapak
Berdasarkan bentuknya, pondasi telapak terbagi lagi atas tiga jenis pondasi yaitu
pondasi telapak terpisah, telapak gabungan dan telapak kantilever.
a . Pondasi telapak terpisah
Pondasi telapak terpisah umumnya digunakan untuk mendukung sebuah
kolom. Perancangan pondasi telapak terpisah menganggap beban kolom sebagai
beban
titik.
Secara
umum perhitungan
perancangan
struktural
pondasi
telapak
terpisah sama dengan perhitungan perancangan struktural pondasi secara umum.
b. Pondasi telapak gabungan
Pondasi telapak gabungan digunakan apabila terdapat dua atau lebih kolom
berdekatan. Pondasi ini menggabungkan kolom-kolom tersebut sehingga menjadi
satu pondasi tunggal. Pondasi ini juga digunakan untuk mendukung beban-beban
struktur yang tidak begitu besar dengan kondisi tanah yang mudah dimampatkan.
Perancangan pondasi telapak gabungan dilakukan dengan asumsi bahwa pelat
pondasi maupun pondasi sangat kaku sehingga pelengkungan pondasi tidak
mempengaruhi
penyebaran
tekanan.
Asumsi lainnya
adalah
distribusi
tekanan
sentuh pada dasar pondasi disebarkan secara linier.
c. Pondasi telapak kantilever
Pondasi telapak kantilever merupakan dua atau lebih pondasi telapak yang
digabungkan oleh suatu balok. Pondasi telapak kantilever digunakan untuk
menyeragamkan distribusi
tekanan pada dasar pondasi. Penentuan daya dukung
izin pada pondasi ini sama dengan penentuan daya dukung izin pondasi secara
umum.
|
|
34
Dalam
perancangan,
hasil akhir tekanan pada dasar pondasi kolom
harus
lebih
kecil
daripada daya
dukung
izin
q
a
. Setelah
memperoleh tekanan
pada
dasar
pondasi
dapat
dihitung
besarnya
momen
dan
gaya
lintang
yang
terjadi
pada
balok
ikat
dan
telapak pondasinya. Setelah itu dapat dilakukan perhitungan penulangan beton.
2.3. Geotextile
Geotextile merupakan
bagian
dari
material
geosintetik
yang
berbentuk
lembaran
dan
mempunyai
sifat
yang
permeabel
(tembus
air).
Geosintetik
adalah
suatu
produk
yang dibentuk oleh bahan polimer dan penggunaannya terkait dengan tanah, batuan, dan
rekayasa geoteknik lainnya sebagai bagian dari proyek konstruksi. Jenis geosintetik ada
bermacam-macam yaitu:
•
Geotextile
•
Geogrid
•
Geonet
•
Geomembrane
•
Geopipe
•
Geofoam
•
Geosynthetic Clay Linier
•
Geocomposite
•
Geo-others
Geotextile (dalam Bahasa Indonesia Geotekstil) memiliki ketahanan terhadap daya
tarik
yang
relatif
cukup
tinggi
sehingga
dapat
diaplikasikan
antara lain
sebagai
bahan
lapis perkuatan, lapis
filtrasi,
lapis separasi dan lapis proteksi. Secara umum ada enam
fungsi utama
geotekstil
yang dapat
bekerja sendiri-sendiri
ataupun secara bersamaan,
yaitu:
1. Separasi, yaitu untuk memisahkan dua jenis material/agregat yang berbeda
karakteristik dan ukuran.
|
|
35
2. Perkuatan; Penggunaan material geotekstil yang mempunyai properti kuat tarik
yang baik dapat digunakan untuk menstabilkan konstruksi dengan bahan tanah.
Geotekstil akan mengambil alih gaya tarik yang harus dipikul oleh tanah.
3. Filtrasi; Fungsi
ini memungkinkan
mobilisasi air/cairan pada arah tegak
lurus
bidang geotekstil dan pada saat bersamaan menahan butiran tanah.
4. Drainasi, yaitu fungsi geotekstil sebagai sarana untuk mengalirkan air searah
bidang geotekstil.
5. Proteksi, dimana
geotekstil digunakan untuk melindungi material atau lapisan
dari kerusakan akibat tusukan benda-benda tajam.
6. Lapis kedap air;
fungsi
ini berlaku apabila
geotekstil dikombinasikan dengan
cairan bitumen atau semen karena geotekstil merupakan material yang porous.
Geotekstil diklasifikasikan menjadi dua macam yaitu:
a. Geotekstil woven
Geotekstil woven
merupakan
geotekstil
yang
berbentuk
anyaman.
Yang
termasuk dalam geotekstil
woven
adalah
slit
filament,
mono filament
dan
multi
filament.
b. Geotekstil non woven
Sebaliknya
dari geotekstil woven,
geotekstil
non
woven
tidak
berbentuk
anyaman. Beberapa jenis geotekstil non woven dibedakan dari panjang serat
pembentuk
dan
cara
penyatuan serat-serat
pembentuk tersebut.
Berdasarkan
panjang
serat
pembentuk
dikenal
jenis continuous
filament
dan
staple
fiber
Berdasarkan
cara
penyatuannya,
geotekstil
non woven
dibedakan
menjadi needle
punch dan heat bonded.
|
 36
2
?
2.3.1. Aplikasi Geotekstil Sebagai Lapis Perkuatan
Geotekstil
sebagai
lapis
perkuatan dapat digunakan untuk meningkatkan daya
dukung tanah. Prinsip kerja geotekstil sebagai lapis perkuatan adalah dengan memikul
beban
tarik
yang
terjadi
pada
lapisan
tanah
atau
material
yang
mempunyai ketahanan
yang
baik
terhadap
gaya
tekan
akan
tetapi
lemah
menahan
gaya
tarik.
Gambar
2.9.
berikut menjelaskan bagaimana geotekstil digunakan sebagai lapis perkuatan.
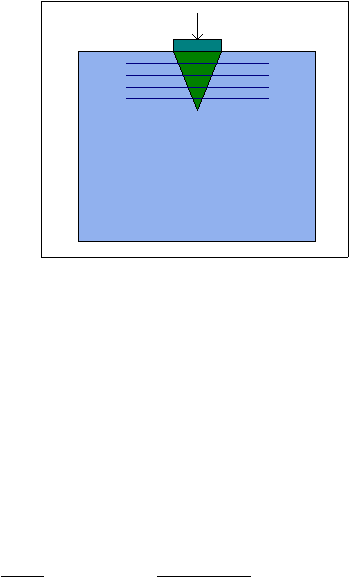
Gambar 2.9. Lapis Perkuatan dengan Geotekstil Memotong Garis Keruntuhan
Tiga mekanisme perkuatan geotekstil yaitu:
•
Tipe Membran
Perkuatan
membran
terjadi
pada
saat
terdapat
gaya
vertikal
yang
bekerja
pada geotekstil
yang diletakkan pada lapisan tanah yang
deformable.
Berdasarkan posisi diletakkannya geotekstil dari aplikasi beban kerja,
ditetapkan bahwa:
s
h
=
P
2p
z
?
2
?
3sin
?
2
?
cos
3
?
-
(1 -
2
µ
)
cos
?
?
1
+
cos
?
?
(2.28)
|
|
37
dimana:
s
h
= Tegangan horisontal pada kedalaman z dan sudut
?
P = Gaya vertikal yang terjadi
z = kedalaman di bawah permukaan dimana
s
h
dihitung
µ
= Poisson ratio
?
= sudut vertikal dari bawah tekanan permukaan P
•
Tipe Geser
Perkuatan
geser
dapat
digambarkan
melalui percobaan
triaxial
akan
tetapi
lebih jelas
melalui uji direct shear. Geotekstil ditempatkan pada tanah
yang
diberi beban pada arah yang normal, kemudian dua material digeserkan pada
interface-nya. Parameter geotekstil terhadap kuat geser tanah yang dihasilkan
(adhesi dan sudut gesek) dapat diperoleh melalui rumus kriteria keruntuhan
Mohr-Coulomb berikut.
t
=
c
a
+
s
'
n
tan
d
(2.29)
dengan:
t
=
Kuat geser (antara geotekstil dengan tanah)
s
’n
=
Tegangan efektif normal pada bidang geser
c
a
=
adhesi (antara geotekstil dengan tanah)
d
=
sudut gesek (antara geotekstil dengan tanah)
Parameter
kuat
geser
c
a
dan d
dapat
dibandingkan
dengan
parameter
kuat
geser tanah secara umum sebagai berikut.
t
=
c
+
s
'
n
tan
f
(2.30)
|
|
38
dengan:
c = kohesi (antara tanah dengan tanah)
f
= sudut gesek (antara tanah dengan tanah)
•
Tipe Pengangkuran/Penjangkaran
Tipe ini menyerupai tipe geser hanya pada tipe ini tanah diaplikasikan pada
kedua sisi horisontal geotekstil sehingga terjadi kecenderungan gaya tarik
yang menarik geotekstil keluar dari tanah. Kondisi perkuatan ini menyerupai
percobaan direct shear kecuali tanah di kedua sisi geotekstil bergerak pada
kedua bagian alat penguji dan geotekstil ditarik keluar dari alat penguji. Tipe
pengangkuran ini juga memberikan gambaran mengenai efisiensi fungsi
kekuatan geotekstil yang bergerak.
Dengan pertimbangan bahwa
beberapa
lapis
geotekstil dan/atau
geotekstil
dengan kekuatan yang tinggi dapat memperkuat dinding fleksibel, lereng dan pondasi,
dapat dikatakan bahwa tanah di bawah dinding kaku, perletakan/tumpuan, dermaga dan
lain-lain
yang
memiliki
daya
dukung
rendah dapat
pula
menjadi
sasaran
dalam
peningkatan kinerja dengan pengaplikasian geotekstil. Binquet dan Lee (1985)
melakukan
percobaan
untuk
meningkatkan daya
dukung
pasir
yang
telah
dikompres
menggunakan batangan
logam.
Mereka
menemukan
bahwa
peningkatan tertentu
yang
kemudian dibuktikan melalui analisa ekonomi
yang menunjukkan penghematan biaya.
Akan tetapi ketika korosi dipertimbangkan, tidak ada lagi keuntungan secara ekonomi.
Dengan
menggunakan
geotekstil
yang
tidak
akan berkarat
sebagai
lapis
perkuatan,
masalah korosi/karatan dapat dihilangkan dan memenuhi kebutuhan penelitian dalam
mengukur peningkatan yang mungkin terjadi.
|
|
39
Beberapa penelitian
untuk melihat bagaimana
geotekstil sebagai
lapis perkuatan
dapat
meningkatkan
daya
dukung
dan
perkuatan
dasar.
Penelitian
laboratorium yang
dilakukan oleh Guido (1985)
menggunakan beberapa
lapis
geotekstil dalam pasir
yang
tidak dipadatkan menghasilkan bahwa beberapa lapis geotekstil (di atas tiga lapis)
memberikan hasil yang menguntungkan setelah terjadi penurunan tertentu. Penelitian ini
menggunakan geotekstil
heat bonded non woven dan diberikan variasi sejumlah
parameter, termasuk jarak ke geotekstil yang berada di posisi teratas, jarak antar lapisan
dan perpanjangan geotekstil ke arah luar diukur dari salah satu sudut pondasi. Hasil ini
diperlihatkan melalui gambar 2.10(a).
Riset
yang
dilakukan
oleh
Geosynthetic
Research
Institute
(GRI)
pada
tanah
lunak
yang
bergradasi
baik
dan
terkompres
pada
kondisi
jenuh
di
atas
batas
plastisitasnya
menghasilkan hasil yang menyerupai percobaan Guido dimana percobaan
menunjukkan bahwa terjadi peningkatan pada tekanan dukung pada kondisi deformasi
tanah yang besar. GRI menggunakan geotekstil woven-slit film. Hasil
ini diplot
pada
kurva pada gambar 2.10 (b). Dari kedua percobaan di atas dapat dilihat bahwa metode
prategang geotekstil
dapat
menjadi
keuntungan sama
halnya
untuk
menghilangkan
deformasi yang dibutuhkan
untuk menciptakan peningkatan
yang signifikan. Sebagai
pengganti prategang
geotekstil, perencanaan dalam penggunaan geotekstil sebagai lapis
perkuatan harus mempertimbangkan bahwa peningkatan daya dukung hanya terjadi
setelah penurunan yang relatif besar.
|
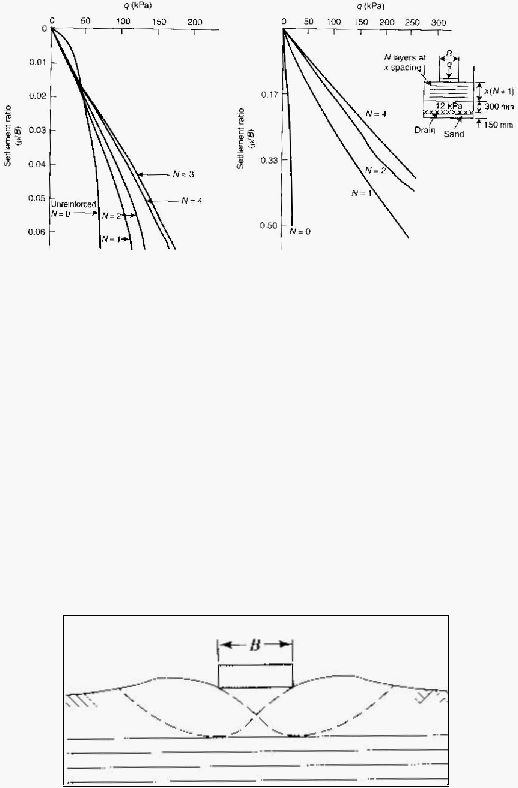 40
Gambar 2.10. Hasil Percobaan Laboratorium yang Menunjukkan Kenaikan
Daya Dukung Dengan Beberapa Lapis Geotekstil
(a) Percobaan oleh Guido (b) Percobaan oleh GRI
(Sumber : Robert M. Koerner, 2005)
Di dalam
perancangan, empat
jenis
keruntuhan
yang ditunjukkan
pula
secara
skematis berikut harus dipertimbangkan:
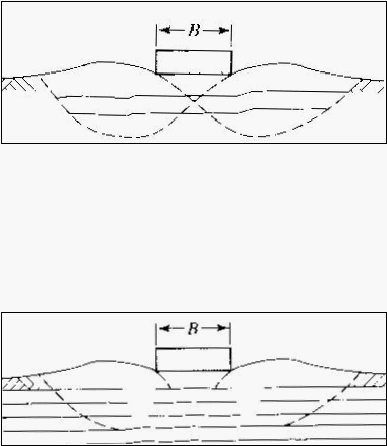
1.
Keruntuhan daya dukung di atas
lapisan geotekstil
paling atas; Hal ini
mungkin
dapat dihindari apabila jarak lapisan teratas geotekstil berkisar antara 300 mm dari
permukaan tanah.
Gambar 2.11. Keruntuhan Daya Dukung di Atas Lapisan Geotekstil Pertama
(Sumber : Robert M. Koerner, 2005)
|
 41
2.
Geotekstil yang tertarik keluar dari tanah karena kurangnya panjang penjangkaran
yang tertanam. Kasus ini dapat dihindari jika panjang penjangkaran melebihi zona
keruntuhan aktif.
Gambar 2.12. Geotekstil Tertarik Keluar Dari Tanah
(Sumber : Robert M. Koerner, 2005)
3.
Keruntuhan yang menyebabkan rusak/putusnya geotekstil, yang merupakan
elemen utama yang diperhatikan dalam perancangan.
Gambar 2.13. Keruntuhan yang Menyebabkan Rusak/Putusnya Geotekstil
(Sumber : Robert M. Koerner, 2005)
4.
Deformasi jangka panjang yang berkelanjutan (rangkak) yang berhubungan dengan
beban
permukaan
yang menahan
dan
relaksasi
tegangan
geotekstil, yang
dapat
dihindari apabila digunakan geotekstil dengan tegangan ijin yang cukup rendah.
|
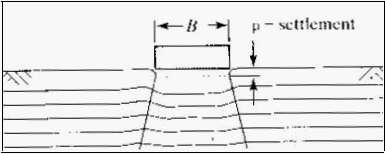 42
Gambar 2.14. Deformasi Jangka Panjang yang Berkelanjutan (Rangkak)
(Sumber : Robert M. Koerner, 2005)
Sakti
dan
Das (1987) melakukan beberapa
percobaan
untuk
melihat
pengaruh
pemasangan geotekstil untuk meningkatkan daya dukung. Geotekstil yang digunakan
mempunyai kuat
tarik batas 534 N dan
merupakan
jenis heat bonded non woven yang
dipasang berlapis-lapis. Geotekstil tersebut dipasang untuk meningkatkan daya dukung
pondasi memanjang dengan beban yang bervariasi yang diletakkan pada tanah lempung
yang jenuh. Berdasarkan percobaan tersebut, Sakti dan Das menyimpulkan bahwa:
•
Dampak yang menguntungkan dari perkuatan geotekstil baru ditemukan
ketika perkuatan dipasang pada jarak yang sama dengan lebar pondasi.
•
Lapisan pertama perkuatan geotekstil harus diletakkan pada jarak d = 0,35 B
(B = lebar pondasi) untuk memperoleh hasil yang maksimum.
•
Nilai L
0
/B
yang paling ekonomis adalah sekitar 2 (L
0
adalah jarak dari titik
tengah pondasi ke ujung batas perkuatan geotekstil).
2.4. Metode Elemen Hingga
Metode elemen hingga
menggunakan prinsip diskretisasi atau pembagian suatu
kontinum,
dimana
kontinum tersebut
dapat
berupa
sistem struktur,
massa
atau
benda
padat
lain
yang akan dianalisa, menjadi suatu elemen yang lebih kecil sehingga
|
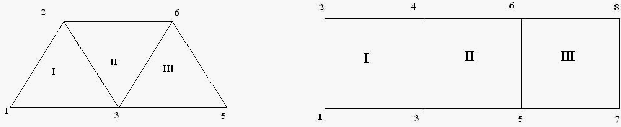 43
mempermudah
analisa.
Pembagian tersebut
memungkinkan
sistem
yang
memiliki
derajat
kebebasan
tak
terhingga
dapat
didekati
menjadi
suatu
sistem yang
memiliki
derajat kebebasan berhingga. Semakin kecil elemen terbagi yang digunakan dalam
analisa maka semakin akurat hasil yang diperoleh melalui analisa tersebut, selama
elemen kecil ini tidak mengalami putus di suatu tempat.
Dalam metode
elemen
hingga,
wilayah
model
didiskretisasi
menjadi
elemen-
elemen, baik dengan jarak teratur maupun yang tidak teratur. Dalam diskretisasi, benda
dibagi menjadi beberapa elemen
dengan bentuk yang teratur pada bagian dalam. Jenis
elemen
yang
akan
digunakan
tergantung
pada karakteristik rangkaian kesatuan dan
idealisasi.
Sebagai
contoh,
jika
suatu
struktur diidealisasi
sebagai
suatu
garis
satu
dimensi, elemen yang digunakan adalah suatu elemen garis. Untuk benda dua dimensi,
digunakan jenis elemen segitiga dengan tiga atau enam titik nodal atau segiempat
dengan empat atau lebih titik nodal dan untuk obyek idealisasi tiga dimensi digunakan
jenis elemen segienam (heksahedron) dengan kekhususan
yang berbeda. Secara umum
bentuk aplikasi dari elemen tersebut dapat dilihat pada gambar 2.16.
Gambar 2.15. Aplikasi Elemen Segitiga dan Elemen Segiempat
(Sumber : C.S. Desai, 1988)
|
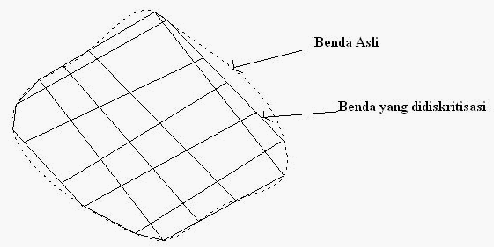 44
Untuk
benda
dengan
batas
tidak
teratur,
dapat
dibuatkan
suatu
provisi
khusus
yang
mendekati
suatu
batas
teratur
dalam garis
lurus.
Dalam beberapa
persoalan,
dibutuhkan fungsi matematis dengan orde secukupnya untuk mendeteksi batas yang ada.
Contohnya
jika
bentuk
batas
serupa
kurva
parabola
maka
fungsi
kuadratis
orde
dua
dapat digunakan untuk mendekati batas tersebut.
Gambar 2.16. Diskritisasi untuk Batas Tak Teratur
(Sumber : C.S. Desai, 1988)
2.4.1. Sistem Koordinat
Untuk
menentukan
lokasi
titik
nodal
pada
elemen
diperlukan
suatu sistem
koordinat yang terdiri dari koordinat global (x, y) dan koordinat lokal (s, t).
2.4.2. Fungsi Bentuk (Shape Function)
Sistem koordinat global dan lokal dapat dihubungkan dengan suatu fungsi
yang
dikenal sebagai fungsi bentuk (shape function). Fungsi bentuk bernilai satu (1) pada titik
nodal
yang ditinjau
dan
bernilai
nol
(0)
pada titik
lainnya. Fungsi bentuk diturunkan
|
|
45
dalam sistem koordinat lokal sehingga titik (x,
y) dalam koordinat
global dapat
diselesaikan apabila titik nodal dalam koordinat lokal (s, t) diketahui.
Koordinat
x
dan
y
dalam
elemen
dapat
dihubungkan
dengan koordinat
lokal
menggunakan hubungan sebagai berikut.
x
=
[
N
]{
X
}
y
=
[N
]{Y
}
(2.28)
(2.29)
dimana:
[N]
=
Fungsi Bentuk
{X}, {Y} =
Koordinat global x-y dari titik nodal
Fungsi bentuk dari elemen segiempat dengan empat titik nodal adalah sebagai berikut.
N
=
1
(1 - s
)(1 - t
)
1
4
N =
1
(1 + s
)(1 - t
)
2
4
N
=
1
(1 + s
)(1 + t
)
3
4
N =
1
(1 - s
)(1 + t
)
4
4
(2.30)
(2.31)
(2.32)
(2.33)
Sedangkan fungsi bentuk untuk elemen segitiga dengan tiga titik nodal adalah sebagai
berikut.
N
1
=
1
-
s
-
t
N
2
=
s
N
3
=
t
(2.34)
|
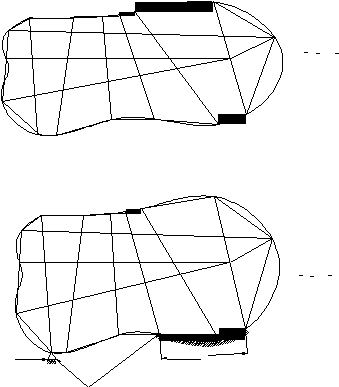 46
S¹
2.4.3. Syarat Batas (Boundary Condition)
Syarat batas
merupakan batasan atau penyangga fisik
yang membatasi struktur
sehingga
sistem
tersebut
dapat
berdiri
sendiri
dalam
suatu
ruang.
Syarat-syarat ini
umumnya
diperinci
dan
dinyatakan sebagai
nilai-nilai
yang
diketahui
dari
besaran-
besaran
yang
tidak
diketahui
pada
suatu
bagian
permukaan
atau
batas
S1 dan
atau
gradien atau
turunan dari besaran
yang tidak diketahui pada S2 (Gambar 2.19). Syarat
batas
ini
harus
ditetapkan
untuk
menghindari
matriks
singular
sehingga
perhitungan
dapat dilakukan dan besaran-besaran yang dicari dapat dihitung dan diselesaikan.
[K ] r} = { R }
{ r} = { R }
(a)
[K ]{r} = {R }
S2
Batasan
(b)
Gambar 2.17. Syarat Batas atau Batasan
(a) Benda tanpa batasan (b) Benda dengan batasan
(Sumber : C.S. Desai, 1988)
|
|
47
Syarat batas secara umum dibedakan menjadi:
a.
Syarat batas paksa atau syarat batas geometri (forced on geometric boundary
condition); Merupakan syarat batas yang dinyatakan oleh besarnya peralihan.
b.
Syarat batas alamiah (natural boundary condition); terjadi jika turunan kedua
dari peralihan adalah nol.
Untuk menggambarkan syarat batas dalam pendekatan metode elemen hingga perlu
dilakukan modifikasi pada sistem persamaan yang telah diperoleh. Persamaan gabungan
yang telah dimodifikasi dapat dinyatakan sebagai berikut.
[K]{r}={R} (2.35)
dimana
matriks-matriks tersebut
merupakan persamaan yang telah dimodifikasi dengan
syarat batas. Persamaan 2.36. merupakan sekumpulan persamaan aljabar simultan linier
(atau non linier) yang dapat dituliskan dalam bentuk baku dan umum sebagai berikut.
K
11 1
r
+
K
12
r
2
+
...
+
K
1n
r
n
=
R
1
K
21
r
1
+
K
22
r
2
+
...
+
K
2
n
r
n
=
R
2
(2.36)
...
K
n1 1
r
+
K
n
2
r
2
+
...
+
K
nn
r
n
=
R
n
2.4.4. Penyelesaian Persamaan Elemen Hingga
Dasar
dari
penyelesaian persamaan
elemen
hingga
adalah
dengan
menggunakan
hubungan antara regangan, perpindahan dan tegangan dari tiap titik serta faktor bentuk
dari setiap elemen.
Hubungan antara matriks regangan dan perpindahan adalah:
|
 48
?
?
?u?
{
e
}
=
[B]
?
?
(2.37)
?
v
?
dimana:
{e}
=
Vektor regangan
?
e
x
?
?
?
?
e
y
?
=
?
?
?
e
z
?
?
?
?
xy
?
?
[B]
=
Matriks regangan
?
?
N
1
?
?
x
0
?
?N
...
?
N
8
?
x
?
0
?
?N
?
?
0
1
...
0
8
?
=
?
?
y
?
0
0
...
0
?
y
?
;
Kondisi Plane Strain
0
?
?
?N
1
?
?N
1
...
?N
8
?N
8
?
?
?
?x
?y
?x
?y
?
?u ?
?
?
=
Perpindahan titik nodal arah x dan y
?
v
?
Hubungan antara tegangan dan regangan adalah sebagai berikut.
{
s
}
=
[C ]{
e
}
(2.38)
dimana:
[C]
=
Matriks Konstitutif (properti material)
?
1
-
?
?
?
0
?
E
?
?
1
-
?
?
0
?
=
(1
+
?
)(1
-
2
?
)
?
?
?
1
-
?
0
?
?
0
0
0
1
-
2
?
?
?
?
2
?
?
E
=
Modulus Young
?
=
Poisson ratio
|
|
49
2.5. Program Plaxis
Program Plaxis adalah suatu program khusus
yang dikembangkan oleh
Departemen Pekerjaan
Umum
dan
Pengendalian Air
Negara Belanda pada
tahun
1987
untuk
mempermudah
insinyur
dalam analisa
tanggul
sungai
pada
tanah
lunak dengan
menggunakan metode elemen hingga. Pada awal pembuatan program ini, elemen hingga
harus ditentukan dan dimodelkan secara manual.
Program Plaxis
dimaksudkan
sebagai
alat
bantu
para
insinyur
geoteknik
dalam
mengerjakan perhitungan manual
menggunakan metode elemen
hingga
yang rumit dan
membutuhkan waktu
yang
lama.
Program
Plaxis
dapat
digunakan
antara
lain
dalam
analisa kestabilan konstruksi, deformasi, dan perhitungan faktor keamanan.
Prosedur
input
program
Plaxis
secara
grafik
yang
sederhana memungkinkan
generasi yang lebih cepat dari
metode elemen hingga yang rumit. Peningkatan fasilitas
output
program memberikan gambaran
yang
lebih
terperinci
dari
hasil
perhitungan.
Proses
kalkulasinya
sendiri
berjalan
secara
otomatis
dan
berdasarkan pada
prosedur
numerikal yang mantap. Konsep ini memungkinkan program ini digunakan oleh pemula
setelah melalui pelatihan selama beberapa jam.
2.5.1. Material Data Geogrid atau Geotekstil Dalam Program Plaxis
Properti
yang
tersedia
pada
program Plaxis
untuk
input
data
geogrid
atau
geotekstil adalah
properti
kekakuan elastis
aksial,
EA,
dengan
satuan
unit
kN/m.
Kekakuan elastis aksial merupakan rasio dari kekuatan aksial per unit lebar dan
tegangan aksial. Nilai kekakuan elastis aksial tersebut biasanya disediakan oleh pembuat
geogrid atau geotekstil dan dapat pula ditetapkan melalui suatu diagram dimana elongasi
|
|
50
geogrid/geotekstil diplot berbanding dengan beban
yang diaplikasikan membujur pada
geogrid/geotekstil tersebut.
EA
=
F
?
l
(2.39)
l
|