|
7
BAB II
TINJAUAN KEPUSTAKAAN
2.1.
Gambut
Gambut (Peat) merupakan campuran dari fragmen material organik yang berasal
dari tumbuh –tumbuhan yang telah berubah sifatnya secara kimiawi dan
menjadi
fosil.
Material gambut yang berada dibawah permukaan mempunyai daya mampat yang tinggi
dibandingkan dengan material tanah yang umumnya (Mac Farlane, 1958). Sub komisi 6
pada
kongres
Ilmu Tanah
Internasional
di
Rusia pada
Tahun
1930
telah
merumuskan
pengertian Peat atau gambut sebagai ”Bahan organik tanah dengan kedalaman 0,5 meter
dan
luasnya
1
Hektar”.
Pengertian
ini
bertahan
cukup
lama
hingga
Anderson
(1964)
pada
tahun 1960
menambah
pengertian
ini
dengan
”jumlah
mineral
maksimun
35%”.
Apabila mineral di antara 35% - 65% maka tanah tersebut disebut Muck (gambul).
Gambut
hanya
mungkin
terbentuk apabila
terdapat
limpahan
biomass
atau
vegetasi pada suatu kawasan yang mengalami hambatan dalam proses dekomposisinya.
Faktor
penghambat utama
tersebut
adalah
genangan
air
sepanjang tahun
atau kondisi
rawa.
Dalam
konteks
yang
demikian, hutan
sebagai
penghasil limpahan
biomass,
khususnya
pada
areal-areal
yang
selalu
tergenang
air
adalah
merupakan kawasan
potensial terbentuknya gambut.
|
 8
Menurut
(Maltby,
1992) akumulasi
bahan
organik
sebagai
hasil
perombakan
tidak sempurna sisa jaringan tanaman yang mati pada suatu kondisi air yang berlimpah
yang
mengakibatkan kekurangan
oksigen.
Akumulasi
dipacu
oleh
faktor
–
faktor
lingkungan
antara
lain
suhu
rendah,
pH
rendah
dan
pasokan
hara
sedikit.
Pada
saat
proses
perombakan bahan organik berjalan lambat dan sisa tumbuhan terus
menimbun
tahun demi tahun maka terjadilah deposit gambut.
Gambar 2.1 Lahan Gambut.
2.1.1. Sifat dan Jenis tanah Gambut
Tanah
gambut
pada
umumnya berwarna coklat
tua
sampai
kehitaman,
akibat
mengalami
proses
dekomposisi sehingga
muncul
senyawa
–
senyawa
humus yang berwarna gelap. Selain itu gambut juga memiliki sifat menyerap air
yang
tinggi
serta
dapat
menahan
air
2
–
4
kali
dari
beratnya,
terlebih
pada
gambut lumut (moss peat) yang belum terdekomposisi dapat menahan air 12 – 15
kali bahkan sampai 20 kali beratnya.
|
|
9
Salah satu sifat tanah gambut yang penting untuk diketahui adalah tanah
gambut
mempunyai sifat
menyusut
(subsidience),
hal
ini
disebabkan
karena
proses dehidrasi
(kehilangan air)
maupun
proses dekomposisi bahan
organik
yang
terus
berjalan
sehingga
ketebalan
gambut akan
terus
menyusut
(Setiadi,
1990).
Selain
itu
tanah
gambut
juga
cenderung bersifat
lebih
asam
apabila
dibandingkan dengan tanah mineral pada kejenuhan basa yang sama.
Komponen
pembentuk tanah
gambut
terdiri
dari
zat
organik
dan
zat
anorganik dalam
jumlah
yang
kecil.
Zat
organik
tersebut terdiri
dari selulosa,
lignin,
bitumen
(wax
dan
resin), humus,
dan
yang
lainnya. Selulosa (C
6
H1
0
O
5
)
merupakan senyawa
organik
yang
paling
utama
terdapat
pada
tanah:
dimana
komposisi dari
zat
organik
ini
tidak
stabil,
tergantung pada
proses
pembusukannya, misalnya
selulosa
pada
tingkat
pembusukan
dini
(H1-H2)
sebanyak 15-20% tetapi pada tingkat pembusukan lanjut (H9-H10)
mencapai
50-60%.
Unsur
–
unsur
pembentukgambut
sebagian
besar
terdiri
dari
karbon,
hidrogen, nitrogen
dan
unsur
lainnya
seperti
Al,
Si,
Na,
S,
P,
Ca.
Tingkat
pembusukan pada tanah gambut akan menaikkan kadar karbon dan menurunkan
oksigen (Setiadi, 1990). Partikel organik berukuran kurang dari 0,1µm, dimana
sifat spesifik dari partikel koloidal ini sangat tergantung dari mineral pembentuk
iklim dan tingkat dekomposisi tanah.
|
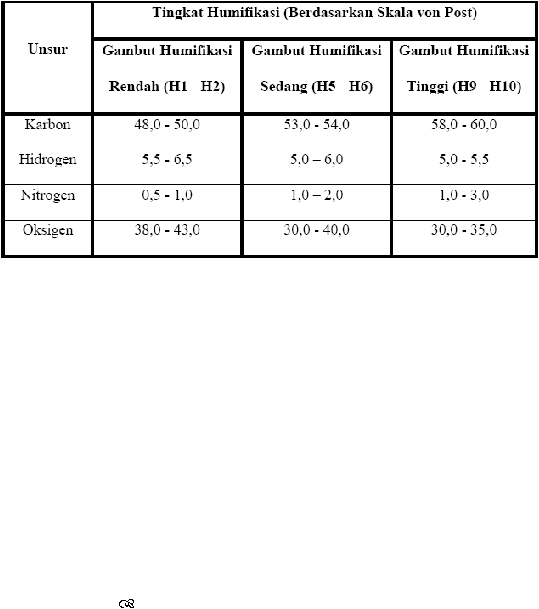 10
Tabel 2. 1 Unsur utama Gambut Berdasarkan perbedaan tingkat Humifikasi.
(Sumber. Setiadi, 1990)
2.1.2. Klasifikasi Tanah Gambut
Pengklasifikasian mengenai
tanah
gambut telah
banyak dilakukan tetapi
sampai saat
ini
belum
ditemukan sistem klasifikasi yang berlaku
baku
secara
universal,
karena
banyak
peneliti
yang
mengklasifikasikan tanah
gambut
berdasarkan hal
yang
berbeda
dan
untuk
kepentingan yang
berbeda
pula.
Beberapa klasifikasi yang ada antara lain :
A. Menurut Mac Farlane (1969), berdasarkan kadar serat tanah gambut
dapat digolongkan menjadi :
Fibrous
Peat,
merupakan
tanah
gambut
yan
mempunyai
kandungan serat
sebesar
20%
atau
lebih,
dan
gambut
ini
mempunyai
dua jenis pori yaitu
makropori
(pori diantara
serat) dan mikropori (pori yang ada didalam serat – serat yang
bersangkutan).
|
|
11
Amorphous
Granular
Peat,
merupakan
gambut
yang
mempunyai kandungan serat kurang dari 20% dan
terdiri dari
butiran dengan
ukuran koloidal
(2µ), serta sebagian besar air
porinya terserap di sekeliling permukaan butiran gambut.
B.
Menurut Van
De
Meene
(1982),
berdasarkan perbedaan
bentuk
dan kondisi geografisnya, tanah gambut dibedakan menjadi :
Topogenous Peat atau Marsh Peat
merupakan gambut
yang
diendapkan dibawah
muka
air
tanah.
Endapan
gambut
ini
dibentuk
oleh
tumbuhan
yang
menyerap
sisa
makanan
yang
terbawa
air
limpahan
sungai
akibat
pasang
surut
sungai
dan
hasil
dekomposisi
tumbuhan
di
daerah
lembah
antar
pegunungan. Endapan gambut
ini
disebut juga Eutropic Peat
atau
gambut
yang
terbentuk
oleh
tumbuhan
yang
kaya
akan
nutrisi.
Ombrogeneus
Peat, merupakan
gambut
yang diendapkan
diatas
muka
air
tanah.
Endapan
gambut
ini
dibentuk oleh
tumbuhan yang
menyerap zat
makanan
hasil
dekomposisi
material
organik
/
gambut
itu
sendiri
dan
tergantung pada
daerah
genangan air.
Endapan
gambut
ini
disebut
juga
Oligotropic peat
atau
gambut
yang
terbentuk dari
tumbuhan
yang
kekurangan zat
makanan
atau
kandungan
nutrisinya
rendah.
|
|
12
C. Rigg dan Gessel (1956), membagi gambut menjadi 4 jenis yaitu :
Tanah gambut yang berasal dari lumut.
Tanah gambut berserat.
Tanah gambut yang berasal dari kayu, seperti batang, daun,
dan ranting.
Tanah gambut sedimen yang berasal dari tumbuhan
mikroskopik.
D. Menurut ASTM
D2607-69 (1989), berdasarkan kandungan organik dan
kadar seratnya tanah gambut dibagi menjadi :
Spahagnum Moss Peat, yang memiliki kandungan
serat
minimum sebesar 66,6% dari berat kering.
Hypnum Moss Peat,
yang
memiliki
kandungan serat
minimum sebesar 33,3% dari berat kering.
Reed Sedge Peat, yang memiliki kandungan serat minimum
sebesar 33,3% dan serat – serat selain lumut (Moss).
Peat Hummus yang
memiliki kandungan serat
lebih kecil
dari 33,3% dari berat kering.
Gambut
lainnya yaitu semua bentuk selain klasifikasi
diatas.
|
|
13
E. Menurut ASTM D4427-84 (1989) dan Organic Sediments Research
Center (OSRC) dari The University of South Carolina (A.O. Landva, E.O
Korpijaako, dan
P.E. Pheeney, 1982) berdasarkan kadar abunya
gambut
digolongkan menjadi :
Low Ash Peat yang memiliki kadar abu kurang dari 5% berat kering.
Medium Ash Peat yang memiliki kadar abu 5% - 15% berat kering.
High Ash Peat yang memiliki kadar abu 15% - 25% berat kering.
F.
Selain
menurut
OSRC,
LGS
(Lousiana
Geological
Survey) dan
Jarrett
System
(1982)
juga
mendefinisikan bahwa
suatu
tanah
disebut
sebagai
tanah
gambut bila kandungan abunya kurang atau sebesar 25%. Sedang
menurut Davis (1946)
suatu tanah disebut sebagai tanah
gambut apabila
kandungan abunya sebesar 35% atau kurang . Berdasarkan USSR System
suatu
tanah
disebut
sebagai
tanah
gambut
apabila
kandungan abunya
sebesar 50% atau kurang.
|
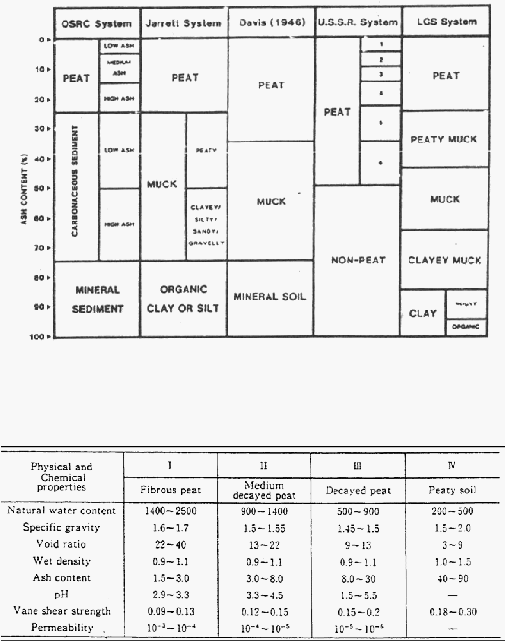 14
Kelima
sistem
klasifikasi
tanah
gambut
berdasarkan
kandungan
abunya dapat ditunjukkan sebagai berikut :
Tabel 2. 2 Klasifikasi Tanah berdasarkan OSRC System, Jarrett System, Davis,
USSR System dan LGS System.
(Sumber. ASTM, 1983)
G. Klasifikasi tanah yang dibuat oleh Amaryan, dkk.adalah :
Tabel 2. 3 Klasifikasi tanah Gambut menurut Amaryan, dkk.
(
Peat Engineering Hanbook, 1991)
|
|
15
2.1.3. Sejarah Tanah Gambut di Indonesia
Menurut
Anderson
(1964),
orang
pertama
yang
menemukan gambut
di
daerah tropika adalah Beecari pada tahun 1904, tetapi penemuan itu baru berarti
setelah
dilaporkan oleh
Potonie
dan
Koordes
pada
tahun
1909
mengenai
pentingnya gambut
di
pedalaman
Sumatera
sebagai
bahan
asal
Batubara.
Penelitian
mengenai
hutan
gambut di
Sumatera Selatan dan
Riau pernah
dilakukan oleh Endert (1920) dan Sewandodo ( 1938).
Sedangkan
penelitian
pertama
yang
dilakukan
mengenai asal
dan
perkembangan
gambut
di
Indonesia
dilakukan
oleh
Polak
pada
tahun
1930-an
(Diemont,
1986).
Proses
pembentukan gambut
di
daerah
tropika
seperti
di
Indonesia terutama dipengaruhi oleh kelebihan kadar air dan kekurangan oksigen
serta pH yang rendah. Sieffermann et al (1987) memberikan pemikiran tambahan
mengenai terjadinya gambut di wilayah tropika yaitu disebabkan oleh
kemampuan faktor organik untuk bereaksi dengan
tanah
mineral dan
desaturasi
basa yang sangat kuat.
Diemont
(1986)
merangkum pemikiran Polak
(1933),
Anderson (1964),
Adriesse (1974) dan
Driessen (1978) tentang pembentukan gambut di
Indonesia
yaitu sebagai berikut :
Permukaan laut berada dalam kondisi stabil 5000 tahun yang lalu.
Beberapa
abad
kemudian
terjadi dengan
cepat
deposisi
sedimen
pantai
yang
menyebabkan terbentuknya
daratan
pantai
yang
luas
dibeberapa
daerah
pantai
timur
Sumatera,
Kalimantan, dan
Irian
Jaya.
Beberapa
daratan tersebut tertutupi oleh komunitas Hutan Mangrove.
|
|
16
Komunitas
Mangrove
itu
membuat
daerah
menjadi
stabil dan
mengakibatkan terjadinya
perluasan
tanah
–tanah
yang
akhirnya
membentuk daerah mangrove dan Lagoon yang mampu mengurangi
kadar
garam
serta
meningkatkan
daerah
air
yang
segar
(Fresh
water)
yang mengakibatkan terjadinya hutan tropika atau danau berair segar.
Danau berair segar
itu secara bertahap menampung bahan organik
yang
dihasilkan oleh
tumbuhan, dan
berkembang
menjadi
hutan gambut
tropika
yang
dipengaruhi oleh
air
tanah
gambut
(Groundwater
peat).
Pembentukan gambut
seperti
ini
disebut
sebagai
gambut
topogen
yaitu
terbentuk berdasarkan kondisi topografi dan geomorphologi.
Diatas
gambut
topogen
tersebut
terbentuklah
hutan
gambut
Ombrotrophic.
2.1.4. Tanah Gambut di Indonesia
Secara
geologis
gambut
terbentuk
pada
lingkungan
pengendapan yang
berbeda-beda yaitu dapat
terjadi pada daerah dataran rendah, dataran tinggi dan
pegunungan,
sedangkan kondisi
pembentukannya terjadi
pada
daerah
beriklim
tropis,
sedang
dan
dingin.
Serta
tumbuhan pembentuk gambut
juga
sangat
bervariasi
di
setiap
daerah
mulai
dari
tumbuhan tropis
hingga
padang
rumput
atau lumut pada daerah yang tinggi. Karena beragamnya tipe tumbuhan tersebut
maka
sumber
formasi
pembentuk
endapan
gambut
juga
akan
berbeda.
Dengan
demikian, karena bervariasinya kondisi iklim dan tumbuhan sisa di suatu daerah
pembentukan
maka
tipe
gambut
di
suatu
daerah
akan
berbeda
dengan
daerah
yang lain.
|
 17
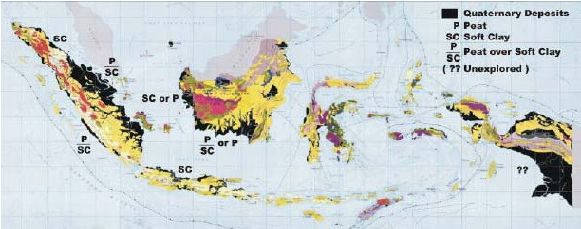
Luas lahan gambut diperkirakan sekitar 384 juta
hektar yang tersebar di
seluruh
negara
di
dunia.
Diantaranya sekitar
31
juta
hektar
terdapat
didaerah
tropika,
yaitu 21
juta
hektar di
Asia
Tenggara, 4,5 juta hektar di
Amazone dan
Caribean,
3
juta
hektar
di
USA, 1,5 juta
hektar
di
Afrika dan
1
juta
hektar
di
Cina.
Di Asia Tenggara sendiri
lahan
gambut sebagian besar terpusat di
Indonesia dan Malaysia, dan sedikit di beberapa negara lainnya seperti Filipina,
Thailand, Vietnam, dan Papua (Andriesse, 1986).
Sedangkan menurut
Soekardi
dan
Hidayat
(1988)
lahan
gambut
di
Indonesia
diperkirakan
seluas
18,4
juta
hektar
yang terbagi atas
4,5 juta
ha
di
pulau Sumatera, 9,3 juta ha di pulau Kalimantan, dan sekitar 4,6 juta ha di pulau
Irian
Jaya,
dan
di
pulau-pulau lainnya
hanya
menempati
lembah
pedalaman
dengan
luas
yang
sedikit.
Lahan
gambut tersebut tersebar di
pantai
timur
Sumatera, pantai selatan dan barat Kalimantan, pantai selatan Irian, dan sedikit di
Sulawesi, Maluku dan Jawa.
Peta penyebaran lahan gambut di Indonesia dapat dilihat di bawah ini :
Gambar 2.2 Peta penyebaran Gambut di Indonesia.
(Sumber. GEOguide)
|
|
18
2.1.5. Pengujian pada Tanah Gambut
Penyelidikan tanah merupakan suatu upaya memperoleh informasi bawah
tanah
untuk perencanaan pondasi bangunan sipil. Penyelidikan tanah mencakup
antara
lain,
pengeboran
tanah,
pengambilan
contoh
tanah,
pengujian
lapangan,
pengujian
laboratorium dan
observasi air
tanah.
Penyelidikan
tanah
merupakan
bagian
yang penting dalam perencanaan pondasi sehingga
harus dilakukan oleh
personal
yang
terampil
dalam
melakukan eksplorasi
dan
diawasi
oleh
ahli
geoteknik.
Uji
baling-baling lapangan
merupakan
uji
coba
untuk
mendapatkan
kekuatan
geser
tanah
liat
secara
langsung.
Kekuatan geser
yang
didapat
berhubungan dengan kondisi tidak alir (undrained). Alat uji berupa baling-baling
yang ditekan kedalam tanah. Baling-baling yang umum dipakai berbentuk
persegi dengan perbandingan tinggi sebesar dua kali lebar. Baling-baling tersebut
diputar sehingga terjadi gesekan antara tanah berbentuk silinder disela-sela
baling-baling dengan tanah
disekitarnya. Momen puntir
yang dibutuhkan untuk
memutar silinder
tanah
tersebut
diukur
dan
dapat
dicari
kekuatan
geser
tanah
yang dianggap bekerja secara homogen diselimut silinder tanah serta sisi atas dan
bawahnya.
Uji baling-baling
sangat
sesuai
untuk dilakukan
pada tanah
jenis liat
sangat lunak hingga sedang. Pada tanah lunak, uji baling-baling dapat dilakukan
dengan
menekan
baling-baling secara
menerus
pada
beberapa
kedalaman.
Sedangkan
pada
tanah
liat
sedang,
uji
baling-baling harus
dilakukan
dengan
bantuan membuat lubang bor terlebih dahulu kemudian disusul dengan uji
baling-baling.
Uji baling-baling
tidak dapat dilakukan pada tanah liat keras
|
|
19
karena baling-baling tidak dapat ditekan masuk kedalam tanah. Uji baling-baling
juga tidak sesuai untuk pasir.
Untuk
tanah
liat
sangat
lunak
hingga
lunak,
sangat
dianjurkan untuk
menggunakan alat
uji
baling-baling buatan
Swiss
yaitu
SGI
(Swedish
Geotechnical
Institute)
Vane
atau
buatan
Norwegia
yaitu
Geonor
Vane
yang
mana
stang
putar
terlindung dengan
selubung
luar
dan
putaran
torsi
dapat
dilakukan dengan
kecepatan
rendah
yang
standard.
Alat
uji
baling-baling
sederhana dengan stang putar tunggal hanya boleh dipakai pada tanah liat sedang
yang tidak terlalu sensitif terhadap gangguan. Banyak faktor mempengaruhi hasil
uji baling-baling antara
lain
gesekan stang putar dengan selubung, pelat baling-
baling
yang
lebih
tebal
dari
standar
yaitu
5%
lebar
baling-baling, aus
serta
rusaknya plat baling-baling. Alat uji coba sebaiknya dilakukan perawatan berkala
dan dikalibrasi ulang. Kecepatan putar uji coba juga harus dijaga konstan yaitu
0,1 derajat per detik.
|
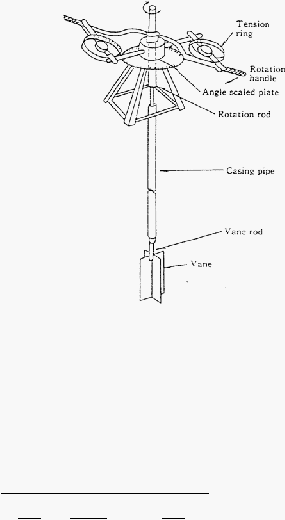 20
Gambar 2. 3 Uji Baling – baling
(Sumber. Peat Engineering Handbook)
Perhitungan kekuatan
geser
untuk
baling-baling persegi adalah sebagai
berikut :
Sfv =
?
?
P ?
T
?
D2H ?
?
?
D
?
?
?
?
?
?
×
?
?
×
?
1
+
?
?
?
?
?
?
106
?
?
2
?
?
?
3H
?
?
?
dimana: Sfv = kekuatan geser uji baling-baling (KPa)
T
=
torsi atau momen puntir (N.m)
D = lebar baling-baling (cm)
H = tinggi baling-baling (cm)
|
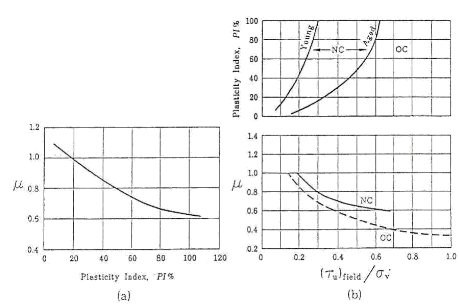 21
Perlu
diperhatikan
bahwa
kekuatan
geser
uji
baling-baling (field
vane
shear
strength)
yang
diukur
serta dihitung dengan
formula diatas
belum tentu
merupakan kekuatan geser tidak alir (undrained shear strength) dari tanah yang
diukur.
Banyak
faktor
mempengaruhi
hasil
uji
antara
lain
kecepatan
uji,
pengaruh isotropi
tanah
liat
sendiri,
sejarah
tegangan tanah
dan
lain-lain.
Berdasarkan hasil pengamatan lapangan, Bjerrum (1972) memperkenalkan faktor
koreksi untuk
mendapatkan kekuatan geser tanah tidak alir
dari kekuatan
geser
uji Baling-baling.
Dengan mendapatkan faktor koreksi (m), kekuatan tanah dapat diperoleh
dengan perkalian dibawah ini:
Su = m × Sfv
dimana: Su = kekuatan geser tanah tidak alir (undrained shear strength )
m
=
faktor koreksi
Gambar. 2. 4 Grafik Korelasi Uji baling – baling.
(Sumber. Paper HATTI)
|
|
22
2.2
Timbunan pada Lahan Gambut
Permasalahan yang
timbul
bilamana
akan
membangun diatas
lapisan
tanah
gambut
adalah:
terbatasnya
informasi perilaku
dan cara
memperkirakan pemampatan
serta
metode perubahan lapisan
tanah
gambut yang akan dijadikan sebagai
tanah dasar
suatu konstruksi.
Dalam studi
ini
dibahas
studi analisis dan eksperimen penggunaan
material geosintetik dan bambu pada tanah gambut Sumatera.
2.2.1. Kasus – Kasus dalam Timbunan Tanah Gambut
Kasus – kasus yang mungkin timbul pada lahan gambut
adalah :
A. Penurunan Konsolidasi tanah yang cukup lama
B. Perilaku pemampatan tanah gambut yang cenderung berbeda dengan
jenis tanah lainnya.
C. Pemilihan sistem drainasi air tanah.
D. Akibat – akibat yang muncul karena daya dukung tanah yang cukup
rendah.
E. Kesulitan jalannya konstruksi akibat sulitnya bahan baku.
F.
Keruntuhan tanah dasar di bawah timbunan.
2.2.2. Alternatif Penanggulangan pada Tanah Gambut
Beberapa Metode
yang sering digunakan untuk
menanggulangi ataupun
menangani permasalahan pada tanah gambut adalah :
A. Metode perbaikan Permukaan :
•
Trench Method
•
Sand Mat Method
•
Material Placement Method
|
 23
B. Metode Pengurangan Beban
mengganti material perkuatan dengan:
•
Serbuk Gergaji
•
Potongan – potongan kayu
•
EPS Block
C. Metode Penggantian (Replacement Method) :
•
Penggantian dengan Penggalian
•
Penggantian dengan Timbunan
•
Perpindahan dengan Peledakan
D. Metode Vertical Drain.
E. Konstruksi dengan Corduroy.
F.
Perkuatan dengan Geosintetik
(a).Penggalian dan penggantian
(b). Cerucuk kayu
dengan potongan kayu
(c). Sand Mat Method
(d). Matras bambu
|
 24
(f)
(e). Penggantian material
(f).Timbunan ulang
(g).Vertical drain
Gambar 2. 5 Alternatif Penanggulangan pada Tanah Gambut
( Sumber. Banlitbang dan Brosur geosintetik)
2.3.
Geosintetik
Geosintetik
adalah
suatu
produk
yang
dibentuk
oleh
bahan
polimer
dan
digunakan terkait dengan tanah, batuan dan
rekayasa
geoteknik
lainnya sebagai bagian
dari proyek konstruksi.
2.3.1. Sejarah Geosintetik
Awalnya
perkembangan geosintetik
dari
usaha
perkuatan
tanah
rawa
dengan cara
menambah material
sehingga memperkuat dan
menstabilkan tanah.
Bahan yang dipakai mula-mula adalah batang pohon dan semak – semak. Tanah
lunak
akan
menerima
material
berserat
sampai
terbentuk suatu
massa
yang
mempunyai sifat memadai sesuai kegunaan yang diinginkan.
Namun
diperoleh bahwa perkuatan
material tesebut
tidak
cukup
kuat
akibat dari beban yang dipikul dan kondisi waktu. Kemudian percobaan
terus
|
|
25
dikembangkan secara sistematis
dimana kayu
yang
dipakai mempunyai
bentuk
dan
ukuran
yang
seragam
disusun
seperti
lapisan
matras.
Terus
dikembangkan
samapai
mengisi
bagian
atas
dengan
tanah
lunak,
beberapa dengan
campuran
berpasir bahkan dengan perkerasan blok batu. Namun kekurangan terhadap
waktu dan ikatan tetap ditemukan.
Tahun
1926,
pertama
kali
digunakan produk
pabrik
yang berupa katun
tebal
oleh South
Carolina
Highway
Department. Hingga
tahun
1935
hasil dari
proyek
ditemukan bahwa
jalan
dalam
kondisi
bagus,
patahan/
retakan
dan
keruntuhan berkurang. Dari proyek inilah penggunaan geosintetik dalam separasi
dan perkuatan mulai digunakan.
2.3.2. Sifat dan jenis Geosintetik pada Perkuatan Tanah
Beberapa fungsi
umum dari
geosintetik adalah sebagai Penyaring/ Filter,
Pemisah/
Separator,
Drainasi/
Drainage,
Perkuatan/ Reinforcement,
Pengontrol
Erosi/
Erosion
Control,
Pelindung/ Protection,
Pelapis
kedap/
Sealing,
Pembungkus/ Container.
Klasifikasi Jenis – jenis Geosintetik antara lain:
1. Geotekstil (Woven dan Non Woven)
2. Geogrid.
3. Geonet.
4. Geomembrane.
5. Geosynthetic Clay Liners
6. Geopipes.
7. Geocomposite
8. Geofoam.
|
 26
Gambar 2.6 Contoh Geosintetik
(Sumber . Brosur Geosintetik)
2.3.3. Aplikasi Geosintetik untuk Perkuatan Tanah
Pengunaan geosintetik telah banyak berkembang, berbagai jenis dan
ragam
dari
geosintetik
telah
dikembangkan, salah
satunya
untuk
pengunaan
perkuatan tanah.
Tipe
geosintetik
yang
umum
digunakan
untuk
perkuatan
tanah
dalam
dilihat pada Gambar 2.8
Geotekstil
woven (teranyam)
non woven (tidak dianyam)
Geosintetik
Geogrid
biaksial (dua arah)
uniaksial (satu arah)
Geocomposite
non woven dengan benang-
benang perkuatan
Gambar 2.7. Bagan tipe geosintetik untuk perkuatan tanah
|
 27
(a)
(b)
Gambar 2.8 (a) Geosintetik woven dan (b) non woven
(Sumber Koerner, 2005)
(a)
(b)
Gambar 2.9 (a) Biaksial geogrid dan (b) Uniaksial geogrid
(Sumber Koerner, 2005)
2.4.
Bambu
Menurut Siopongco dan Munandar (1987) bambu adalah tanaman yang termasuk
Bamboodiae,
salah
satu
anggota
sub
familia
rumput,
yang
pertumbuhannya
sangat
cepat.
Gambar 2.10 Hutan Bambu
|
|
28
2.4.1. Keunggulan Bambu
Pada masa pertumbuhan, bambu tertentu dapat tumbuh vertikal 5 cm per
jam, atau 120 cm per hari. Bambu dapat dimamfaatkan
dalam banyak hal.
Sebagai komponen bangunan, bambu dapat dijumpai dalam bentuk tiang, balok,
lantai,
dinding atau
sekat,
struktur atap,
serta atap,
pintu
dan
jendela, langit
–
langit tangga, dinding penahan tanah, perancah pada saat pelaksanaan bangunan
berlantai banyak,
tirai
gulung,
peralatan dapur,
penyalur
air
minum,
jembatan
ringan,
bahan
makanan,
bahan
kerajinan tangan,
alat
musik.
Bahkan
ketika
Thomas
Alva
Edison
memerlukan kawat
halus
yang
dapat
dipakai
untuk
menghasilkan cahaya dalam bola lampunya yang pertama, Edison berpaling pada
bambu
sebagai
bahannya.
Waktu
Graham
Bell
mengembangkan kotak
musik
piringan
hitam,
maka bambulah
yang dijadikan
bahan
baku untuk
membuat
jarum kotak musik yang pertama.
Tanaman bambu mempunyai ketahanan yang luar biasa, Rumpun bambu
yang telah dibakar, masih dapat tumbuh lagi, bahkan pada saat Hiroshima
dijatuhi bom atom sampai
rata dengan tanah, bambu
adalah
satu- satunya jenis
tanaman
yang
masih dapat bertahan hidup. Bambu bahkan dapat tumbuh
diladang yang sangat kering seperti kepulauan Nusa
Tenggara atau dilahan yang
banyak disirami air hujan seperti di Parahiyangan (Salim,1994).
|
|
29
2.4.2. Jenis Bambu
Menurut Sharma (1987) didunia tercatat lebih dari 75 genus dan 1250 species
bambu,
sedang
Uchimura
(1980)
menyatakan bahwa
bambu
yang
ada
di
Asia
Selatan dan Asia Tenggara kira – kira 80% dari keseluruhan bambu yang ada di
dunia. Genus Bambussa mempunyai jumlah spesies paling banyak dan terutama
tersebar di daerah tropis, termasuk di Indonesia.
Adapun
jenis
bambu
yang
akan
di
bahas terbatas pada
jenis
bambu
yang
banyak terdapat di Indonesia, yang antara lain
:
A. Bambusa vulgaris Schrad
Beberapa jenis
bambu
yang
mempunyai
nama botani
bambusa
vulgaris Schrad antara lain bambu kuning, bambu tutul, dan bambu
ampel.
Bebrapa nama daerah dari bambu
yang termasuk jenis
ini yaitu:
Hao adulo,
Aur
gading, Bambu
kuring,
Buluh
swanggi,
Bulog
gading,
Haur bahenda dan yang lainnya.
Bambusa vulgaris Schrad
mempunyai
rumpun
tidak
rapat
dan
tidak
teratur,
warna
kulit
kuning,
hijau,
hijau
bertutul cokelat, hijau
bergaris teratur,atau kuning bergaris hijau. Tinggi bambu bervariasi 10-
20 m, dengan diameter 7-13 cm,
dan tebal dinding 6-15mm.
Bambusa
vulgaris
Schrad banyak dipakai untuk
tanaman hias,
peralatan rumah tangga, bahan kerajinan serta bahan kertas.
|
|
30
B. Dendrocalamus asper (Schult.F) Backer ex Heyne
Bambu
dengan nama
botani Dendrocalamus
asper
(Schult.F)
Backer
ex Heyne
di
Indonesia dikenal
dengan
nama
Bambu
petung. Di
berbagai daerah, bambu yang termasuk jenis
ini di kenal dengan
nama
:
Buluh petong,
Buluh
swanggi,
Bambu batueng,
Pering betung,
Betong,
Bulo
lotung, Awi bitung, Jajang betung, Pring betung, Pereng petong,
Tiing petung, Au petung, Bulo patung dan Awo petung.
Bambu jenis ini
mempunyai rumpun agak rapat, dapat tumbuh di
dataran rendah sampai
pegunungan dengan
ketinggian 2000
m
di
atas
permukaan
air
laut.
Pertumbuhan cukup
baik
khususnya
untuk
daerah
yang tidak
terlalu kering. Warna kulit batang
hijau kekuningan. Batang
dapat mencapai panjang 10-14 m, panjang ruas berkisar antara 40-60 cm,
dengan diameter 6-15 cm, tebal dinding 10-15 mm.
Bambu
betung
banyak dipakai
sebagai bahan
bangunan, perahu,
kursi, saluran air, dinding (Gedeg), dan kerajinan tangan.
C. Gigantochloa atroviolacea Widjaja
Bambu
dengan nama
botani Gigantochola
atroviolacea
Widjaja
lebih
dikenal
dengan
nama
bambu
hitam. Jenis bambu
ini
juga dikenal
dengan nama Awi hideung, Pring wulung, dan Pring ireng.
Bambu
hitam
mempunyai rumpun
jarang, tumbuh
di
dataran
rendah
sampai
ketinggian
650
m
diatas
permukaan
air
laut.Warna
kulit
batang hitam, hijau kehitam – hitaman atau ungu tua. Tinggi batang dapat
mencapai 20
m, panjang
ruas 40-60
cm, dengan diameter 6-8
cm, tebal
dinding buluh 6-8 mm.
|
|
31
D. Gigantochloa atter (Hassk) Kurz ex. Munro
Bambu dengan nama botani Gigantochloa atter (Hassk) Kurz ex.
Munro di Indonesia
dikenal dengan nama Bambu Atter, sedang
diberbagai
daerah
lebih
dikenal
dengan
nama
Awi
Ater,
Pring
Jawa,
Pring Legi, Pereng Keles, Tereng Galah, Auloto, dan Tabadiketul.
Bambu
Atter
dapat
tumbuh di
dataran rendah
sampai
dataran
rendah sampai dataran ketinggian 750 m diatas permukaan air laut. Kulit
batang berwarna hijau sampai hijau gelap. Tinggi batang dapat mencapai
22 m, panjang ruas 40-50 cm, diameter 5-10 cm, tebal dinding 8 mm.
E. Gigantochloa verticillata (Wild) Munro
Bambu
dengan nama
botani
Gigantochloa
verticillata
(Wild)
Munro
dikenal dengan
nama
Bambu Andong,
sedang diberbagai daerah
dikenal dengan
nama
Awi
gombong, Awi
surat,
Awi
temen, dan Pring
surat.
Bambu
andong
mempunyai
rumpun
tidak
terlalu
rapat.
Warna
kulit batang hijau kekuningan dengan garis kuning sejajar batang. Tinggi
batang berkisar antara 10 -12 m, panjang ruas 40-60 cm, diameter 8-12
cm, dan tebal dinding sampai 20 mm.
Bambu andong dapat dipakai
untuk bahan bangunan,
chopstick
dan kerajinan tangan.
|
|
32
F.
Gigantochloa apus BI Ex. (Schult.f) Kurz
Bambu dengan nama botani Gigantochloa apus
BI Ex. (Schult.f)
Kurz di Indonesia dikenal dengan nama Bambu Apus atau Bambu Tali,
sedang di berbagai daerah dikenal dengan nama Awi tali, Pring tali, Pring
apus, Pereng tali, Tiing tali, dan Tiing telantan.
Bambu Apus dapat tumbuh di dataran rendah sampai pegunungan
dengan tinggi 1000 m di atas permukaan laut. Tinggi batang 8-11 m, ruas
45 – 65 cm, diameter 5-8 cm, tebal 3-15 mm.
Jenis
bambu
ini
kuat,
liat,
baik untuk
kerajinan anyaman
karena
seratnya
kuat dan lentur. Menurut
Sulthoni (1988) bambu ini tidak
mudah terserang hama bubuk sekalipun tidak diawetkan. Oleh karena itu
bambu jenis ini banyak dipakai sebagai bahan bangunan.
2.4.3.
Sifat Mekanik Bambu
Pemakaian Bambu seringkali didasarkan pada pengalaman nenek
moyang
saja.
Perangkaian batang
–
batang
struktur
bambu
dilakukan
secara
konvensional menggunakan tali atau pasak, sehingga rangkaian itu kurang
kokoh.
Sebagai
akibat
penyusutan bahan,
ikatan
tali/pasak
menjadi
kendor,
sehingga
struktur
akan
mengalami perubahan bentuk
yang
cukup
besar,
dan
kekuatannya pun
merosot.
Oleh
karena
itu
tidak
mengherankan jika
pemakaian
bambu selama ini hanya terbatas pada pemakaian struktur yang ringan saja.
Agar suatu bahan dapat di pakai secara optimum,
maka
sifat mekanik
bahan
itu
harus
dipahami
betul.
Tanpa pemahaman sifat
mekanik,
pemakaian
bahan
dapat
berlebihan, sehingga
dari
segi
ekonomis
akan
boros,
sedang
pemakaian
dengan
ukuran
yang
kecil
dapat
membahayakan pemakainya. Jika
|
 33
sifat
mekanik dapat
dikuasai,
maka
dapat dipikirkan cara
mengatasi
kelemahannya, serta
memamfaatkan sifat
–
sifat
unggulannya.
Lebih
lanjut
pemakaian bahan
dapat
diusahakan lebih
optimum.
Selain
itu
dapat
juga
dipikirkan kemungkinan diversifikasi produk.
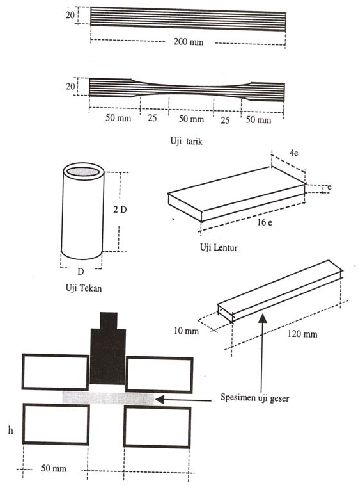
Untuk mengetahui sifat mekanik bambu, Ghavani (1990) melakukan
pengujian
dengan bentuk spesimen seperti terlihat pada gambar 2.11.
Gambar 2. 11. Uji Spesimen Bambu
(
Sumber: Rekayasa Bambu, Morisco. 1999 )
|
 34
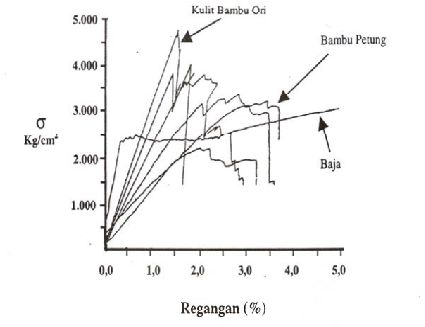
Menurut Morisco
(1999) dan
Ananda (1996), bambu
mempunyai
kekuatan tarik dua kali lebih besar dibandingkan kayu, sedangkan kuat tekannya
10% lebih tinggi dibandingkan dengan kekuatan tarik kayu.
Apabila dibandingkan dengan baja
yang
mempunyai berat
jenis antara
6.0 – 8.0
(Sementara
BJ bambu 0.6 – 0.8), kuat tarik (Tensile Strength) baja
hanya sebesar 2.3 – 3.0 lebih besar dibandingkan dengan kekuatan tarik bambu.
Dengan
demikian
bambu
mempunyai kekuatan
tarik
per
unit
berat
jenisnya
sebesar 3 - 4 kali lebih besar dibandingkan dengan baja (Gambar 2.12)
Gambar 2.12. Diagram Tegangan dan Regangan Bambu dan Baja.
(
Sumber: Morisco, 1999 )
|
 35
Gambar 2. 13. Pengambilan Spesimen Bambu
(Sumber: Morisco, 1999).
2.4.4.
Aplikasi Bambu Untuk Perkuatan Tanah
Konstruksi
timbunan di
atas
tanah
lunak disebut
reklamasi. Reklamasi
adalah suatu pekerjaan penimbunan tanah (pasir berlanau) dengan skala volume
dan
luasan yang sangat besar pada suatu kawasan atau
lahan
yang relatif
masih
kosong
dan
berair,
misalnya pantai,
daerah rawa
suatu
lokasi
di
laut,
tengah
sungai yang lebar ataupun di danau.
Oleh karena
itu dilaksanakan pada kawasan tersebut di atas
maka
problem
utama
tersebut
umumnya
berkisar
pada
permasalahan rekayasa
geoteknik,
yaitu
terkendala dengan
kuat
dukung
tanah
yang
rendah
dan
penurunan yang besar akibat konsolidasi maka stabilitas timbunan di atas tanah
tersebut
perlu
perhatikan. Salah
satu
perkuatan
yang
dapat
digunakan
adalah
dengan penggunaan matras dan tiang bambu sebagai soil reinforcement.
|
|
36
Untuk
memilih
metoda
perbaikan tanah
yang
tepat
dan
juga
ekonomis
harus mempertimbangkan juga faktor – faktor lainnya seperti : (Rahardjo (1998)
1. Kualifikasi Pelaksana
/
Kontraktor.
2. Waktu Pelaksanaan.
3. Pengaruh terhadap lingkungan sekitarnya.
4. Biaya.
Melihat
faktor
di
atas
maka
penggunaan bambu
yang telah dilaminasi
cukup
baik
untuk
bahan
perbaikan
tanah.
Bambu
memiliki
banyak
sifat
yang
baik
untuk
konstruksi, karena
bambu
kuat,
ulet,
lurus,
ringan
dan
mudah
pengerjaannya. Selain itu bambu mudah didapat dengan harga yang relaif murah.
Bambu
dalam
bentuk
bulat
biasa
dipakai
untuk
konstruksi lainnya
sebagai
perancah (Scafollding) [ASTM (1989), Ananda et al (1996) dan CNBRC (001)].
Selain
keunggulan – keunggulan bambu seperti yang dipaparkan tersebut
diatas,
maka
bambu
dalam
penggunaannya menemui
beberapa
keterbatasan.
Dalam
pemakaian sebagai
bahan
bangunan
(konstruksi),
faktor
yang
sangat
mempengaruhi adalah
sifat
fisik
bambu
yang
membuat sukar
dikerjakan secara
mekanis, variasi dimensi dan ketidakseragaman
panjang ruas [ Bodiq et al
(1982), Fangchun (2000) ].
|
|
37
2.5.1.
Perkuatan Timbunan jalan dengan Bambu
Permasalahan longsoran
timbunan jalan
yang
banyak
terjadi
selama
ini
dapat
ditanggulangi dengan
membuat
sistem
perkuatan
timbunan.
Salah
satu
alternatif
perkuatan
timbunan
adalah
dengan
mengembangkan teknologi
sederhana dengan sistem perkuatan (penulangan) timbunan menggunakan matras
bambu (Corduroy) atau cerucuk bambu.
Yang
dimaksud
dengan
penulangan tanah
(Corduroy)
adalah
tanah
timbunan
dibuat
berlapis
bambu
untuk
memperoleh suatu
konstruksi
yang
komposit. Ataupun menggunakan bambu sebagai pondasi dasar
(cerucuk) untuk
memperkuat stabilisasi tanah.
Mempertimbangkan
ketersediaan bambu
sangat
banyak
dan
tidak
sulit
didapat di Indonesia serta jenis bambu ini memiliki kuat tarik yang cukup besar,
maka bambu tali dapat digunakan sebagai bahan lokal untuk penulangan tanah.
Keuntungan dari penggunaan perkuatan dengan Bambu adalah :
1. Ketersediaan bambu yang cukup banyak di Indonesia .
2. Pelaksanaan lapangan sangat mudah dikerjakan .
3. Teknologi sederhana
ini
dengan
menggunakan bahan
lokal sebagai
substitusi produk import sangat dapat diandalkan.
|
 38
Gambar 2.15. Konstruksi Perkuatan Bambu.
(Sumber : Pusat Penelitian Antar Universitas, Institut Teknologi Bandung)
|
|
39
2.5.
Metode Elemen Hingga / The Finite Element Method
Banyak
program
komputer
yang
menggunakan metode
ini,
sehingga
dalam
menggunakannya perlu
memahami konsep dasar,
struktur,
sistem operasi
program
itu.
Program Plaxis menggunakan konsep metode elemen hingga.
Metode
elemen
hingga
didasari
prinsip
membagi
atau
diskretisasi dari
suatu
kontinum, di mana kontinum tersebut dapat berupa sistem struktur, massa ataupun benda
padat lainnya yang akan dianalisis. Pembagian dalam metode
ini
untuk membagi
suatu
benda menjadi elemen yang lebih kecil, sehingga
mudah untuk dianalisis.
Dengan
adanya
pembagian
tersebut
maka
suatu
sistem
yang
memiliki
derajat
kebebasan tak
terhingga dapat
didekati
menjadi
suatu
sistem
yang
memiliki derajat
kebebasan
berhingga.
Semakin kecil
elemen
yang dibagi
yang
akan
ditinjau,
maka
hasil
analisisnya
akan semakin
akurat.
Dalam
syarat pembagian
menjadi
elemen
kecil
ini
tidak
mengalami putus di suatu tempat.
2.5.1.
Langkah-langkah dalam Metode Elemen Hingga
Langkah – Langkah perumusan dan penerapan dari metode elemen
hingga terdiri atas 8 langkah, yaitu:
|
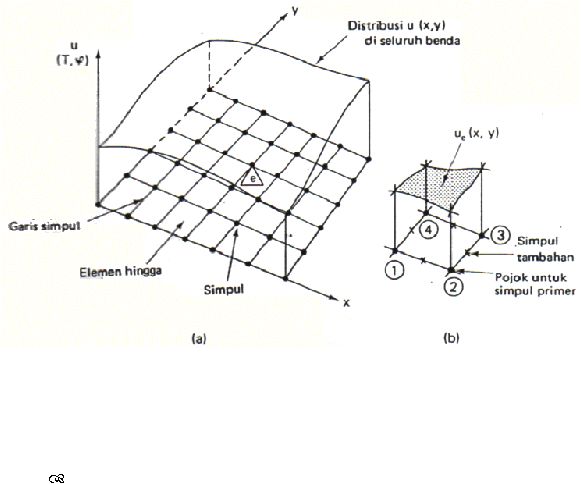 40
Gambar 2.16. (a) Diskritisasi benda dua dimensi
(b) Distribusi u
e
pada suatu elemen umum e.
(Sumber: Desai, 1979)
Langkah 1. Diskritisasi dan Memilih Konfigurasi Elemen.
Langkah
ini
menyangkut pembagian
benda
menjadi
sejumlah
benda
“kecil” yang sesuai. Yang dinamakan elemen-elemen hingga. Perpotongan antara
sisi
elemen dinamakan simpul atau titik simpul dan permukaan antara
elemen-
elemen disebut garis simpul dan bidang simpul. Seringkali kita perlu
memasukkan titik simpul tambahan di sepanjang garis-garis dan bidang simpul.
(Gambar 2.16 b).
|
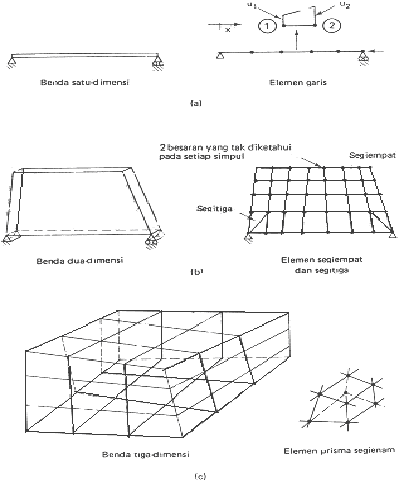 41
Gambar 2.17. Berbagai jenis elemen (a) Elemen satu-dimensi (b) Elemen
dua-dimensi (c) Elemen tiga-dimensi
(Sumber: Desai, 1979)
Jenis elemen yang akan digunakan tergantung pada karakteristik
rangkaian
kesatuan
dan
idealisasi
yang
kita
pilih
untuk
digunakan. Sebagai
contoh, jika suatu struktur atau suatu benda diidealisasi sebagai suatu garis satu-
dimensi, elemen yang akan kita gunakan adalah suatu elemen “garis” (Gambar
2.17.a). Untuk benda-benda dua-dimensi, kita gunakan segitiga dan segiempat
(Gambar 2.17.b),
sedangkan
untuk
idealisasi tiga-dimensi, dapat dipakai
suatu
|
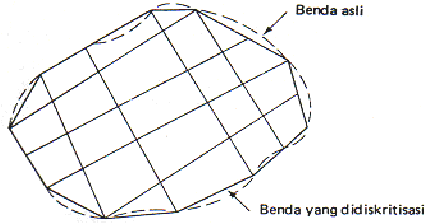 42
prisma segi enam (Hexahedron) dengan kekhususan yang berbeda (Gambar
2.17.c).
Gambar 2.18. Diskritisasi untuk batas tak teratur
(Sumber: Desai, 1979)
Walaupun kita dapat
membagi-bagi benda itu ke dalam beberapa bagian
elemen dengan bentuk yang teratur pada bagian dalam (Gambar 2.18), kita bisa
membentuk provisi khusus jika batas yang ada ternyata tak teratur. Dalam
banyak hal, batas tak teratur dapat didekati dengan sejumlah garis lurus (Gambar
2.18).
Sebaliknya, dalam
banyak
persoalan
lainnya,
mungkin
perlu
memakai
fungsi
matematis
dengan orde
yang
secukupnya
untuk
mendeteksi
batas
yang
ada. Sebagai contoh, jika bentuk batas adalah serupa dengan suatu kurva
parabola,
maka
kita
dapat
memakai suatu
fungsi
kaudratis
orde-dua
untuk
mendekati batas tersebut.
|
|
43
Langkah 2. Memilih Model atau Fungsi Pendekatan.
Dalam langkah ini, dipilih suatu pola atau bentuk untuk distribusi besaran
yang tak diketahui (Gambar 2.18.) yang dapat berupa suatu perpindahan dan atau
tegangan
untuk
persoalan
tegangan-deformasi, maupun
perpindahan
untuk
persoalan gabungan yang menyangkut efek-efek aliran maupun deformasi.
Titik-titik simpul elemen memberikan titik-titik strategis untuk penulisan
fungsi-fungsi
matematis
yang
menggambarkan
bentuk
distribusi
dari
besaran
yang
tak
diketahui pada
wilayah
elemen.
Sejumlah
fungsi
matematis seperti
polinomial
dan
deret
trigonometri dapat
dipakai
untuk
maksud
ini,
terutama
polinomial karena
mereka
memberikan perumusan elemen
hingga
yang
mudah
dan sederhana. Jika kita menyatakan u sebagai besaran yang tak diketahui, maka
fungsi interpolasi dapat dinyatakan sebagai
u = N1 u1 + N2 u2 + N3 u3 + . . . + N
m
u
m
(2.1.)
di
sini u1,
u2
,
u3,
.
.
.
u
m
adalah
nilai
dari
besaran-besaran yang
tak
diketahui pada
titik-titik simpul
dan
N1
,
N2
,
.
.
.
N
m
adalah
fungsi-fungsi
interpolasi. Misalnya dalam hal elemen garis dengan dua simpul ujung (Gambar
2.17.a) kita bisa mempunyai u
1
dan
u2
sebagai besaran yang
tak
diketahui atau
sebagai derajat kebebasan dan
untuk
segitiga
(Gambar
2.17.b) kita
mempunyai
u1, u2, . . . u
6
sebagai besaran yang tak diketahui atau derajat kebebasan jika kita
berhubungan dengan
suatu
persoalan
deformasi
dengan
dua
perpindahan
pada
setiap simpul.
Derajat kebebasan
dapat
didefinisikan
sebagai
suatu
perpindahan bebas
(tak diketahui) yang dapat terjadi di suatu titik. Sebagai contoh, untuk persoalan
deformasi satu-dimensi dalam suatu kolom (Gambar 2.17.a) hanya ada satu arah
|
|
44
dengan suatu titik bebas bergerak, yaitu dalam arah sumbu tunggal. Jadi sebuah
titik mempunyai satu derajat kebebasan. Untuk persoalan dua-dimensi (Gambar
2.17.b),
jika
deformasi hanya
dapat
terjadi
dalam
bidang
benda
(dan
akibat
lenturan
diabaikan), maka
suatu
titik
hanya
bebas
bergerak
dalam
dua
arah
koordinat yang bebas, jadi di sini suatu titik mempunyai dua derajat kebebasan.
Setelah semua
langkah
metode
elemen-hingga
dilaksanakan,
maka
kita
bisa
menemukan
jawaban
sebagai
nilai
dari
besaran
u
yang
tak
diketahui
di
semua
simpul, yaitu u1
,
u
2
, . . .
u
m
.
Tetapi dalam mengawali
tindakan untuk
memperoleh
jawaban,
kita
telah
mengasumsikan secara
teoritis
atau
terlebih
dahulu bahwa bentuk atau pola yang kita harapkan akan memenuhi
syarat,
hukum dan prinsip persoalan yang ada.
Jawaban
yang
diperoleh akan dinyatakan dalam
besaran
yang
tak
diketahui hanya di titik-titik simpul. Ini adalah salah satu hasil proses diskritisasi.
Gambar
2.19.
menunjukkan bahwa
jawaban
akhir
adalah
suatu
kombinasi
jawaban
setiap
elemen
yang
dihubungkan
menjadi
satu
pada
batas-batas
yang
sekutu
(bersama). Selanjutnya
hal
ini
dilukiskan
dengan
memberi
sketsa
suatu
penampang lintang di sepanjang A-A. Dapat dilihat bahwa jawaban yang dihitung
tidak
perlu
sama
seperti
jawaban
kontinu
yang
digambarkan dengan
kurva
bergaris
tebal.
Jelaslah,
kita
ingin
mendiskritisasi sedemikian
rupa
sehingga
jawaban
hasil
perhitungan akan
sedekat
mungkin
pada
jawaban
eksak,
yaitu
kesalahan minimum.
|
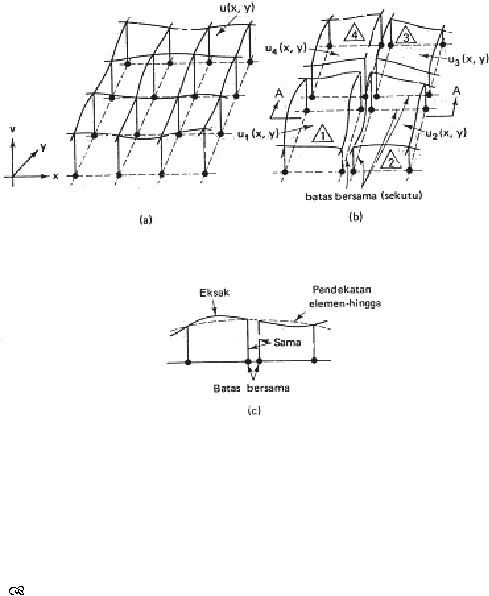 45
Gambar 2.19 Pendekatan potongan-potongan kecil jawaban pada elemen
(a) Rakitan (b) Elemen-elemen yang bersebelahan
(c) Bagian di sepanjang penampang A-A (Sumbe®:
Desai, 1979)
Langkah
3.
Menentukan
Hubungan
Regangan
(Gradien)-
Perpindahan (yang tak Diketahui) dan Tegangan-Regangan.
Untuk
maju ke
langkah berikutnya, yang
mempergunakan suatu
prinsip
(katakanlah, prinsip
energi
potensial
minimum)
untuk
penurunan
persamaan-
persamaan
elemen,
kita
harus
menentukan
besaran-besaran yang
tepat
yang
muncul dalam prinsip
tersebut. Untuk persoalan tegangan-deformasi, salah satu
dari besaran semacam ini adalah regangan (atau gradien) perpindahan. Misalnya,
|
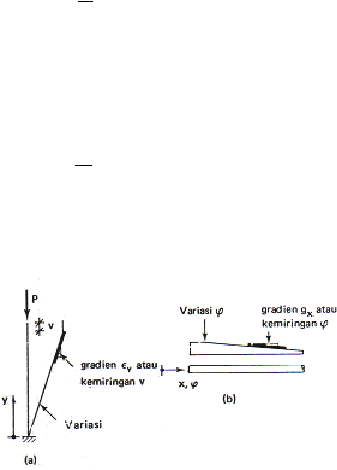 46
dalam
hal
deformasi
yang
hanya
terjadi
dalam satu
arah y
(Gambar 2.17.a),
diasumsikan bahwa regangan €
y
,
yang bernilai kecil dinyatakan oleh :
€
y
=
dv
(2.2.)
dy
di
sini
v
adalah
deformasi
dalam
arah
y. Untuk
hal aliran
fluida
dalam
satu
arah,
hubungan semacam ini
adalah
gradien
g
x
dari
tinggi
tekan
fluida
(Gambar 2.19.b):
g
x
=
df
(2.3.)
dx
di sini f adalah tinggi tekan
fluida atau potensial dan g
x
adalah gradien
dari f, yaitu laju perubahan f terhadap koordinat x.
Gambar 2.20. Persoalan-persoalan yang di idealisasi menjadi satu-dimensi.
(a)Tegangan-deformasi satu-dimensi.
(b) Aliran satu-dimensi.
(Sumber: Desai, 1979)
Selain regangan atau gradien, kita
juga
harus
menentukan suatu besaran
tambahan,
tegangan
atau
kecepatan; umumnya
hal
ini
dilakukan dengan
menyatakan hubungannya dengan regangan. Hubungan semacam ini adalah
suatu hukum konstitutif dan menyatakan tanggapan atau pengaruh (perpindahan,
regangan) dalam suatu sistem karena bekerjanya suatu penyebab (gaya). Hukum
|
|
47
tegangan-regangan adalah salah satu bagian
yang paling penting
dalam analisis
elemen-hingga. Kecuali
kalau
ditentukan
untuk
mencerminkan
secara
tepat
perilaku dari bahan atau sistem, maka hasil-hasil dari analisis dapat mempunyai
arti
yang
sangat
kecil.
Sebagai
suatu
contoh
yang
sederhana, tinjauan hukum
Hooke, yang mendefinisikan hubungan tegangan terhadap regangan dalam suatu
benda pejal:
s
y
=
E
y
€
y
(2.4.a)
Di sini
s
y
=
tegangan
dalam
arah
vertikal
dan
E
y
=
modulus
elastisitas
Young.
Jika
kita
mensubstitusi €
y
dari
Persamaan
(2.3)
ke
dalam
Persamaan
(2.4a), kita akan memperoleh pernyataan untuk tegangan yang dinyatakan dalam
suku-suku perpindahan sebagai
s
y
=
E
y
dv
(2.4.b)
dy
Salah satu
dari
hukum
kontitutif
yang
linear
sederhana
adalah
hukum
Darcy untuk aliran fluida melalui media berpori:
v
x
=
-
k
x
g
x
(2.4.c)
di sini k
x
=
koefisien permeabilitas, v
x
=
kecepatan, dan g
x
=
gradien.
|
|
48
Langkah 4. Menurunkan Persamaan-persamaan Elemen.
Dengan memakai hukum atau prinsip yang tersedia, kita akan
memperoleh persamaan-persamaan
yang mengatur perilaku elemen. Persamaan-
persamaan
ini
dinyatakan
dalam
bentuk
yang
umum,
sehingga
dapat
dipakai
untuk semua elemen dalam benda yang didiskritisasi.
Ada sejumlah cara yang berbeda yang mungkin dipakai untuk
menurunkan persamaan-persamaan elemen. Dua cara yang paling umum dipakai
adalah metode energi dan metode residu.
Dari
kedua
metode
itu
akan
menghasilkan
persamaan-persamaan
yang
menggambarkan perilaku suatu elemen, yang umumnya dinyatakan sebagai
[k] {q} = {Q}
(2.5)
Di sini [k] = matriks sifat elemen, {q} = vektor besaran yang tak
diketahui di simpul-simpul elemen, dan {Q} = vektor parameter pemaksa simpul
elemen.
Persamaan (2.5)
dinyatakan dalam
pengertian yang
umum;
untuk
persoalan yang khusus mengenai analisis tegangan, [k] = matriks kekakuan, {q}
=
vektor perpindahan simpul dan {Q} = vektor gaya simpul.
Langkah
5.
Perakitan
Persamaan
Elemen
untuk
Mendapatkan
Persamaan Global
atau
Persamaan
Rakitan
dan
Mengenal
Syarat
Batas.
Tujuan
akhir
adalah
memperoleh
persamaan-persamaan untuk
benda
secara keseluruhan
yang akan menentukan kira-kira perilaku keseluruhan benda
atau struktur. Kenyataannya, penggunaan cara-cara
variasi atau
residu
memang
bersangkut paut dengan benda keseluruhan; adalah untuk tujuan penyederhanaan
|
|
49
bahwa kita
meninjau tata cara dalam Langkah 4
seolah diterapkan pada suatu
elemen tunggal.
Sekali
persamaan-persamaan elemen,
Persamaan
(2.5),
ditetapkan untuk
suatu
elemen
umum,
maka
kita
akan
soap
menghasilkan Persamaan
secara
berulang-ulang untuk
elemen-elemen
lainya
dengan
berkali-kali
memakai
Persamaan
(2.5).
Kemudian
kita
menjumlahkannya untuk
mendapatkan
persamaan-persamaan global.
Proses
perakitan
ini
didasarkan
pada
hukum
kecocokan
atau
kekontinuan. Hal
ini
memerlukan
bahwa
benda
harus
tetap
kontinu
yang
artinya
bahwa,
titik-titik
yang bersebelahan
harus tetap
bersebelahan
satu
sama
lain
setelah
diberikan
beban
(Gambar
2.20.).
Dengan
kata
lain,
perpindahan dua
titik
yang
berbatasan
atau
yang
berurutan
harus
mempunyai nilai-nilai identik (Gambar 2.20.a).
Tergantung
pada
jenis dan sifat
persoalan,
kita
dapat saja
memaksakan
syarat-syarat kekontinuan yang
lebih
berat.
Misalnya,
untuk
deformasi
yang
terjadi
dalam
suatu
bidang
datar, maka
mungkin
cukup memaksakan
kekontinuan dari
perpindahan saja.
Sebaliknya,
untuk
persoalan-persoalan
pelenturan, sifat-sifat fisis benda yang mengalami deformasi karena beban selain
memerlukan kekontinuan dari perpindahan,
juga
kita
harus
memastikan bahwa
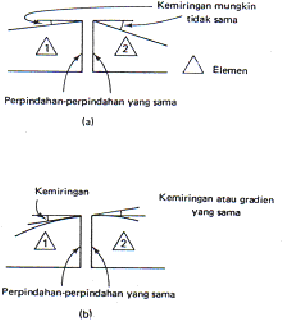
kemiringan atau turunan pertama dari perpindahan juga kontinu atau cocok pada
simpul-simpul yang berbatasan (Gambar 2.19.b). Seringkali hal ini menjadi perlu
untuk memenuhi kecocokan dari lengkungan-lengkungan atau turunan kedua.
|
 50
Akhirnya,
kita
memperoleh persamaan
rakitan
yang
dinyatakan dalam
notasi matriks sebagai :
[K] {r} = {R}
(2.6)
Di sini [K] = matriks sifat rakitan, {r} = vektor rakitan dari simpul yang
tak diketahui dan {Q} = vektor rakitan dari parameter pemaksa simpul.
Untuk
persoalan
tegangan-deformasi, besaran-besaran
tersebut
masing-
masing adalah
matriks kekakuan rakitan,
vektor perpindahan simpul dan
vektor
beban simpul.
Gambar 2.21. Kecocokan antar elemen.
(a) Kecocokan untuk persoalan dalam bidang datar.
(b) Kecocokan untuk persoalan jenis-pelenturan.
(Sumber: Desai, 1979)
|
|
51
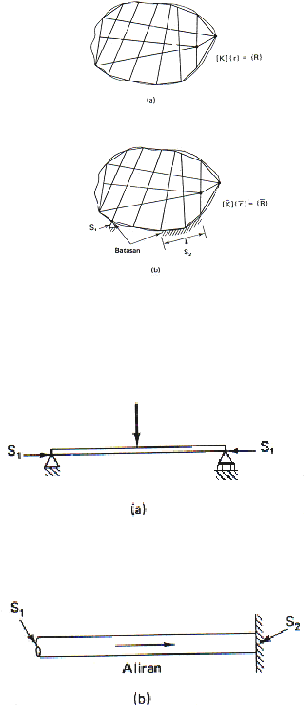
Syarat-syarat Batas
Syarat
batas
adalah batasan
atau penyangga
fisis (Gambar
2.21.b)
yang
harus ada
sehingga suatu
struktur
atau
benda
dapat
berdiri
sendiri
di
dalam
ruang.
Syarat-syarat ini
umumnya
diperinci
dan
dinyatakan
sebagai
nilai-nilai
yang
diketahui
dari
besaran-besarn yang
tak
diketahui
pada
suatu
bagian
permukaan atau batas S1
dan
atau
gradien atau
turunan dari
besaran
yang
tak
diketahui
pada
S
2
.
Gambar
2.22.a
menggambarkan suatu
balok.
Dalam
kasus
balok yang disangga secara sederhana, batas S1 adalah dua
titik ujung di
mana
perpindahan diberikan.
Batasan semacam
ini seringkali dinamakan syarat batas
balok, dipaksakan atau geometris.
Pada
tumpuan-timpuan sederhana dari
balok,
momen
lentur
adalah
nol;
yaitu
turunan
kedua
dari perpindahan
menghilang.
Batasan semacam
ini
seringkali dinamakan syarat batas alamiah.
Gambar 2.23.b menunjukkan
suatu silinder di mana fluida atau
temperatur mengalir. Pada batas S1, temperatur atau tinggi tekan fluida diketahui;
hal ini adalah syarat batas pokok. Ujung kanan kedap terhadap air, atau diisolasi
terhadap kalor;
selanjutnya
syarat batas diperincikan sebagai
fluks
fluida atau
kalor
yang
sebanding dengan
turunan
pertaman
dari
tinggi
tekan
fluida
atau
temperatur. Syarat batas ini adalah syarat batas almiah.
|
 52
Gambar 2.22. Syarat batas atau batasan
(a) Benda tanpa batasan
(b) Benda dengan batasan
(Sumber: Desai, 1979)
Gambar 2.23. Contoh syarat batas.
(a) Balok dengan syarat-syarat batas.
(b) Aliran pipa dengan syarat-syarat batas.
(Sumber: Desai, 1979)
|
 53
Untuk
mengambarkan syarat-syarat
batas
dalam
pendekatan
elemen-
hingga,
benda
dinyatakan oleh
Persamaan 2.6,
dan
biasanya
perlu
mengubah
persamaan
ini hanya untuk syarat-syarat
batas geometris.
Persamaan
rakitan
akhir yang telah dimodifikasi dinyatakan dengan menambahkan garis di sebelah
atas sebagai berikut:
[K] {r} =
{R}
(2.7)
Langkah
6.
Memecahkan
Besaran-besaran
Primer
yang
tak
Diketahui
Persamaan
(2.8)
adalah
sekumpulan
persamaan
aljabar
simultan
linier
(atau tak linear), yang dapat dituliskan dalam bentuk baku dan umum sebagai
K1
1
r1 +
K1
2
r2
+
. . . + K1
n
r
n
=
R1
K2
1
r1 +
K2
2
r2
+
. . . + K2
n
r
n
=
R2..
(2.8)
K
n1
r1 +
K
n2
r2
+
. . . + K
nn
r
n
=
R
n
Persamaan-persamaan ini
dapat
dipecahkan
dengan
memakai
metode
eliminasi
Gauss
atau
metode
iterasi
yang sudah
dikenal.
Di
akhir
langkah
ini,
kita telah memecahkan besaran-besaran yang tak diketahui (perpindahan) r1
, r
2
,
. . . r
n
. Besaran-besaran ini dinamakan besaran-besaran primer yang tak
diketahui,
karena
mereka
muncul
sebagai
besaran-besaran pertama
yang dicari
dalam Persamaan dasar (2.8). Pemberian
nama primer akan berubah
tergantung
pada besaran yang tak diketahui yang muncul dalam Persamaan (2.8). Misalnya,
jika persoalan dirumuskan dengan memakai tegangan sebagai besaran yang
tak
diketahui, maka tegangan tersebut dinamakan besaran primer.
|
|
54
Langkah
7.
Memecahkan
Besaran-besaran
Penurunan
atau
Sekunder.
Seringkali
besaran-besaran
tambahan
atau
sekunder
harus
dihitung dari
besaran-besaran
primer.
Dalam
hal
persoalan
tegangan-deformasi, besaran-
besaran semacam ini dapat berupa regangan, tegangan, momen dan
gaya geser,
untuk
persoalan
aliran
besaran-besaran itu
dapat
berupa
kecepatan
dan
debit.
Adalah
relatif
langsung
untuk
mencari
besaran-besaran
sekunder
jika
besaran-
besaran primer diketahui, karena kita dapat memakai
hubungan antara regangan
dengan perpindahan dan hubungan antara tegangan dengan regangan yang sudah
ditentukan dalama langkah 3.
Langkah 8. Interpretasi Hasil-hasil.
Tujuan akhir dan penting adalah mengurangi hasil-hasil penggunaan cara
elemen-hingga menjadi
suatu
bentuk
yang
siap
dipakai
dalam
analisis
dan
perancangan.
Umumnya
hasil-hasil diperoleh dalam bentuk keluaran
yang
dicetak dari
komputer.
Kemudian kita
memilih
potongan-potongan
yang
kritis
dari benda
dan
memplotkan
nilai-nilai perpindahan
dan
tegangan
di
sepanjang
benda atau kita dapat
membuat tabal dari hasil-hasil tersebut. Seringkali sangat
menguntungkan
dan tidak membuang waktu dengan menggunakan
‘routine’
yang tersedia dan memerintahkan komputer untuk memplot atau mentabulasikan
hasil-hasilnya.
|
|
55
2.6.
Program Plaxis
Dalam menganalisis timbunan pada kasus di Perkebunan Kelapa Sawit –
Rantau - Sumatera Utara digunakan program Plaxis 7.11 yang sudah dilengkapi
dengan kemampuan untuk melakukan permodelan elemen hingga.
2.6.1
Sejarah Program Plaxis
Program Plaxis
pertama kali
dikembangkan oleh
Departemen Pekerjaan
Umum
dan
Pengendalian Air
di
negara
Belanda
pada tahun
1987.
Pada
awal
pembuatannya
elemen
hingga,
yang
merupakan
dasar
dari
program
ini,
masih
harus ditentukan atau dimodelkan secara
manual.
Tujuan
utama pengembangan
program Plaxis pada waktu itu adalah untuk dapat menggunakan metode elemen
hingga agar lebih mudah dalam pengaplikasiannya untuk analisis tanggul sungai
pada tanah lunak. Di sini dapat ditentukan tingkat ‘kehalusan’ elemen tersebut, di
mana semakin halus elemen yang dipakai maka hasil perhitungan akan semakin
akurat.
Penggunaan Program
Plaxis
dikhususkan
sebagai
alat
bantu
untuk
memudahkan pekerjaan
yang
dikerjakan
oleh
Insinyur
Geoteknik
dalam
mengerjakan perhitungan
manual
menggunakan metode
elemen
hingga
yang
cukup rumit serta membutuhkan waktu yang cukup lama dalam pengerjaannya.
Program
Plaxis
mempunyai
banyak
kemampuan
menganalisa seperti:
kestabilan
konstruksi, faktor
keamanan, deformasi, analisa
konstruksi. Yang
digunakan dalam
aplikasi
konstruksi timbunan, dinding
penahan
tanah
dan
terowongan.
|