|
24
Aminudin (2005, p169) juga menyatakan terdapat beberapa ukuran kinerja
dari sistem antrian. Ukuran-ukuran kinerja tersebut antara lain:
BAB 2
LANDASAN TEORI
2.1
Pendahuluan
Ilmu pengetahuan tentang bentuk antrian,
yang sering disebut sebagai
teori antrian (queueing theory)
merupakan sebuah bagian penting operasi dan
juga
alat
yang
sangat
berharga bagi
manajer
operasi. Menurut
Render
dkk.
(2005, p418) antrian (waiting line / queue) diartikan sebagai orang-orang atau
barang dalam barisan
yang sedang
menunggu untuk dilayani, sebagai contoh
pasien yang sedang menunggu di ruang praktik dokter, mesin bor yang sedang
menunggu di bengkel untuk diperbaiki, dll.
Antrian
merupakan aktivitas
yang
tidak
lepas
dari
kehidupan
manusia
sehari-hari. Suka
atau
tidak
suka,
manusia
tetap
harus
melakukan aktivitas
antrian
tersebut.
Menurut
Taha (1997,
p176),
fenomena
menunggu
atau
mengantri
merupakan
hasil langsung
dari
keacakan
dalam
operasional
pelayanan fasilitas. Secara umum, kedatangan pelanggan ke dalam suatu
sistem dan waktu pelayanan untuk pelanggan tersebut tidak dapat diatur dan
diketahui waktunya secara tepat, namun sebaliknya, fasilitas operasional dapat
diatur sehingga dapat mengurangi antrian.
|
|
25
Lama waktu pelanggan harus menunggu sebelum dilayani.
Persentase waktu fasilitas pelayanan yang tidak digunakan atau
menganggur karena tidak ada pelanggan.
Ukuran-ukuran kinerja
tersebut
merupakan parameter
yang
menentukan
kinerja
dari
suatu
fasilitas.
Semakin
singkat
waktu
bagi
pelanggan untuk
menunggu dan semakin sedikit waktu
menganggur fasilitas pelayanan berarti
kondisi sistem akan semakin optimal.
Penyusunan teori antrian dipelopori oleh
A. K.
Erlang,
seorang
insinyur
berkebangsaan Denmark, pada
tahun
1909. Ia bekerja di
sebuah
perusahaan
telepon
dan
melakukan
percobaan yang
melibatkan
fluktuasi
permintaan
sambungan
telepon
serta
pengaruhnya pada
peralatan switching
telepon.
Sebelum
Perang
Dunia
II,
studi
awal
antrian
ini
telah
berkembang di
lingkungan antrian yang lebih umum.
2.2
Elemen Dasar Model Antrian
Faktor penting dalam sistem antrian
ini adalah pelanggan dan pelayan, di
mana
ada
periode
waktu
yang
dibutuhkan oleh
seorang
pelanggan
untuk
mendapatkan pelayanan. Pelanggan akan segera mendapatkan pelayanan bila
ia
dapat
datang
tepat
pada
waktu
di
antara
waktu tunggu
dengan
waktu
pelayanan
berikutnya. Menurut
Kakiay
(2004,
p4)
yang
harus
diingat
dan
diperhitungkan adalah
bahwa
baik pelayan
maupun pelanggan
yang
ada
di
|
|
26
dan
lain-lain. Populasi
terbatas
(finite)
biasanya
memiliki
ukuran populasi
yang kecil dan
memiliki probabilitas kedatangan yang berubah secara drastis
dalam
sistem
antrian
tersebut
adalah
manusia
yang
berprilaku (human
behaviour). Sebagai manusia pelayan (human server), pelayan dapat melayani
dengan
kecepatan
tinggi
sehingga
mengurangi
waktu
menunggu, atau
juga
melayani dengan lambat sehingga akan memperlama waktu tunggu.
2.2.1
Sifat Pemanggilan Populasi
Populasi
yang dimaksud di dalam
teori antrian merupakan seluruh target
pelanggan yang sedang dan akan menggunakan fasilitas pelayanan, sedangkan
yang
dimaksud
dengan
pelanggan tidak
selalu
berupa
manusia,
melainkan
dapat berupa produk dan benda
lainnya
yang
melakukan aktivitas mengantri
untuk dilayani atau diproses oleh satu atau lebih fasilitas pelayanan.
2.2.2
Ukuran Pemanggilan Populasi
Aminudin (2005,
p173)
mengemukakan bahwa
terdapat
dua
ukuran
pemanggilan populasi,
yaitu terbatas (finite) dan tidak terbatas (infinite). Bila
populasi
relatif
besar
dan
probabilitas seorang
pelanggan
tidak
dipengaruhi
oleh jumlah pelanggan yang telah berada pada suatu fasilitas pelayanan, maka
dapat diasumsikan bahwa populasi tersebut tidak terbatas. Populasi yang tidak
terbatas (infinite) misalnya mobil yang tiba di gerbang tol, pasien yang datang
ke rumah sakit, calon mahasiswa yang mendaftar ke sebuah perguruan tinggi,
|
|
27
ketika
ada
angota
populasi
yang
sedang
menerima pelayanan. Contohnya
antara
lain tiga buah
mesin pada sebuah pabrik
yang
memerlukan pelayanan
operator secara terus menerus, lima buah mobil milik sebuah perusahaan yang
secara
berkala
mengunjungi
fasilitas
reparasi
kendaraan, permainan-
permainan dalam
sebuah
arena
bermain
yang
memerlukan
inspeksi
secara
berkala, dan lain-lain.
2.2.3
Pola Kedatangan dari Pemanggilan Populasi
Subjek
pemangilan populasi
bisa
tiba
pada
sebuah
fasilitas
pelayanan
dalam beberapa pola
tertentu, bisa juga
secara acak. Aminudin (2005, p173)
menyatakan
bahwa analisis
riset
operasi telah
mendapati
bahwa
tingkat
kedatangan
acak
paling
cocok
diuraikan
menurut
distribusi
Poisson.
Tentu
saja tidak semua kedatangan memiliki pola distribusi Poisson, oleh karena itu,
sebelumya perlu dipastikan terlebih dahulu pola distribusi kedatangan tersebut
sebelum
diolah.
Untuk
menentukan apakah
suatu
pola
distribusi
tertentu
Beberapa pola distribusi lainnya akan dibahas kemudian.
2.2.4
Tingkah Laku Pemanggilan Populasi
Terdapat tiga
istilah
yang
biasa
digunakan
dalam
antrian
untuk
menggambarkan tingkah laku pemanggilan populasi (Aminudin, 2005, p174).
Ketiga istilah tersebut antara lain:
|
|
28
1.
Renege
Merupakan
tingkah
laku
pemanggilan populasi
dimana
seseorang
bergabung dalam antrian dan kemudian meninggalkannya.
2.
Balking
Merupakan tingkah
laku pemangilan populasi dimana
seseorang
tidak
mau bergabung dalam antrian.
3.
Bulk
Merupakan tingkah
laku
pemanggilan populasi
dimana
kedatangan
terjadi bersama-sama (berkelompok) ketika memasuki sistem.
2.3
Sifat Fasilitas Pelayanan
2.3.1
Perilaku Sistem Antrian
Terdapat tiga macam perilaku sistem antrian yang mungkin dapat terjadi
dalam suatu sistem antrian (White et al., 1975, p90), yaitu:
1.
Single waiting line
Merupakan
perilaku
sistem
antrian
dimana terdapat
satu
buah
jalur
antrian.
Pelanggan
yang
ingin
menggunakan fasilitas pelayanan
menunggu dalam sebuah antrian sampai gilirannya untuk dilayani oleh
salah satu server.
2.
Multiple waiting line without jockeying
Merupakan perilaku
sistem antrian dimana masing-masing server
memiliki
jalur antriannya
masing-masing dan setiap pelanggan
yang
|
 29
menunggu di
masing-masing jalur
antriannya
tersebut
tidak
dapat
pindah jalur ke jalur lainnya.
3.
Multiple waiting line with jockeying
Merupakan
perilaku
sistem
antrian
dimana
masing-masing server
memiliki
jalur
antriannya
masing-masing
dan
setiap pelanggan
yang
menunggu
di
masing-masing
jalur
antriannya
dapat
pindah
jalur
ke
jalur lainnya jika terdapat jalur lain yang antriannya lebih sedikit.
Gambar 2.1-2.3 berikut ini menunjukkan ketiga perilaku sistem antrian
yang telah dibahas diatas.
Gambar 2.1 Single Waiting Line
|
 30
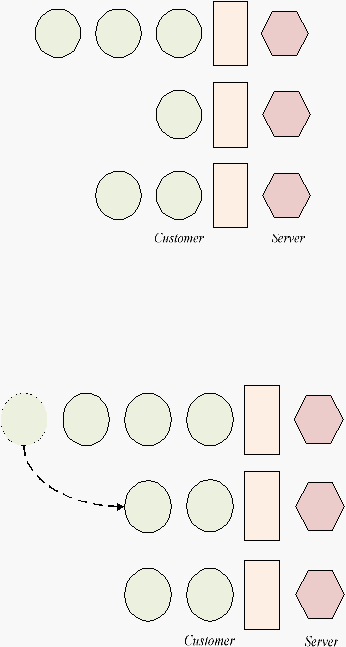
Gambar 2.2 Multiple Waiting Line without Jockeying
Gambar 2.3 Multiple Waiting Line with Jockeying
|
|
31
2.3.2
Disiplin Antrian
Disiplin antrian
merupakan urutan
bagaimana suatu
subjek pemanggilan
populasi akan dilayani. White et al. (1975, p9) mengemukakan bahwa terdapat
lima jenis disiplin antrian yang sering digunakan dalam teori antrian, yaitu:
1.
First Come First Served (FCFS)
FCFS
merupakan
salah
satu disiplin
antrian
dimana pelanggan
yang
dilayani terlebih dahulu adalah pelanggan yang datang lebih awal.
2.
Last Come First Served (LCFS)
LCFS
merupakan
salah
satu disiplin
antrian
dimana pelanggan
yang
datang paling akhirlah yang akan dilayani terlebih dahulu.
3.
Service in Random Order (SIRO)
SIRO
merupakan salah
satu
disiplin
antrian
dimana
pelayanan
dilakukan dengan urutan acak.
4.
Shortest Processing Time (SPT)
SPT
merupakan salah
satu
disiplin
antrian
dimana
pelanggan
yang
memiliki waktu
pelayanan
atau
pemrosesan
yang
paling
singkatlah
yang akan dilayani atau diproses terlebih dahulu.
5.
General Service Discipline (GD)
GD
digunakan
jika disiplin
antrian
tidak
ditentukan dan
hasil
yang
diperoleh akan sama dengan disiplin antrian yang lain, misalnya FCFS
dan LCFS.
|
|
32
2.3.3
Pola Distribusi Waktu Pelayanan
Waktu pelayanan bisa konstan, bisa pula acak.
Apabila waktu pelayanan
didistribusikan secara acak, maka harus ditentukan distribusi probabilitas yang
paling
sesuai
untuk
menggambarkan perilakunya.
Aminudin
(2005,
p175)
menyatakan bahwa
biasanya jika
waktu pelayanannya
acak,
analisis antrian
menggunakan distribusi probabilitas Eksponensial. Pola distribusi lainnya
juga akan dibahas kemudian.
2.4
Struktur Antrian Dasar
Proses antrian secara
umum
dikategorikan
menjadi
empat
struktur dasar
menurut
fasilitas
pelayanan (Kakiay, 2004,
p13).
Keempat struktur
antrian
dasar tersebut adalah:
1.
Single Channel Single Phase
Pada struktur antrian
ini, subjek pemanggilan populasi
yang
dilayani
akan
datang,
masuk
dan
membentuk antrian
pada
satu
baris/aliran
pelayanan
dan
selanjutnya
akan
berhadapan dengan
satu
fasilitas
pelayanan. Contoh dari
struktur antrian
ini adalah
sebuah
kantor pos
yang hanya mempunyai satu loket pelayanan dengan satu jalur antrian.
Gambar
2.4
berikut
ini
akan
menunjukkan
struktur
antrian single
channel single phase.
|
 33
Gambar 2.4 Antrian Single Channel Single Phase
2.
Single Channel Multiple Phase
Pada struktur antrian
ini, subjek pemanggilan populasi
yang
dilayani
akan
datang,
masuk
dan
membentuk antrian
pada
beberapa
aliran
pelayanan
dan
selanjutnya
akan
berhadapan dengan
satu
fasilitas
pelayanan
sampai
pelayanan selesai.
Contoh
dari
struktur
antrian
ini
adalah seorang pasien yang berobat ke rumah sakit, mereka harus antri
untuk
mendaftar
di
loket
pendaftaran terlebih
dahulu, setelah
selesai
mendaftar,
pasien
masuk
ke
ruangan
pemeriksaan awal, dan
setelah
menerima catatan
diagnosa
dari
perawat
maka
pasien
akan
antri
kembali
untuk
diperiksa olah
dokter.
Gambar
2.5
berikut
ini
akan
menunjukkan struktur antrian single channel multiple phase.
Gambar 2.5 Antrian Single Channel Multiple Phase
|
 34
3.
Mulitple Channel Single Phase
Pada struktur antrian
ini, subjek pemanggilan populasi
yang
dilayani
akan
datang,
masuk
dan
membentuk antrian
pada
satu
baris/aliran
pelayanan dan selanjutnya akan berhadapan dengan beberapa
fasilitas
pelayanan identik yang paralel. Contoh dari struktur antrian ini adalah
sebuah kantor pos
yang
mempunyai beberapa loket pelayanan dengan
satu
jalur antrian.
Gambar 2.6 berikut
ini akan
menunjukkan struktur
antrian multiple channel single phase.
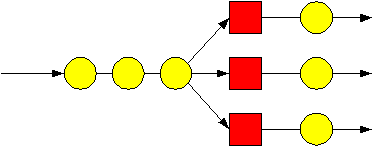
Gambar 2.6 Antrian Multiple Channel Single Phase
4.
Multiple Channel Multiple Phase
Pada struktur antrian
ini,
subjek pemanggilan populasi
yang
dilayani
akan datang dan
masuk ke dalam sistem pelayanan yang dioperasikan
oleh
beberapa
fasilitas
pelayanan paralel
yang
identik
menuju
ke
fasilitas pelayanan setelahnya
sampai
pelayanan
selesai.
Contoh dari
struktur antrian ini adalah seorang pasien yang berobat ke rumah sakit,
|
 35
dimana
terdapat beberapa perawat dan beberapa dokter. Gambar 2.7
berikut
ini
akan
menunjukkan
struktur
antrian multiple
channel
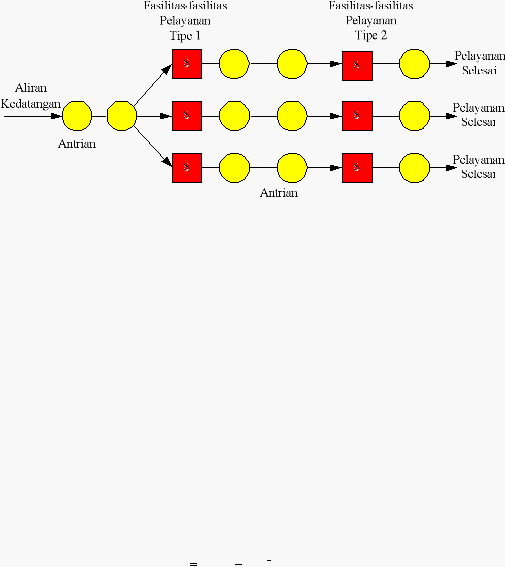
multiple phase.
Gambar 2.7 Antrian Multiple Channel Multiple Phase
2.5
Pola Distribusi Antrian
White et al.
(1975, pp26-30) menyatakan bahwa terdapat beberapa pola
distribusi diskret yang terdapat dalam teori antrian antara lain:
1.
Distribusi Bernoulli
Distribusi Bernoulli
digunakan
jika
percobaan
hanya
menghasilkan
salah
satu
dari
dua
kemungkinan hasil.
Berikut
ini
merupakan
probability mass function dari distribusi Bernoulli:
P( x)
p
x
(1
p)
1
x
, x = 0,1,
0
<
p
<
1
2.
Distribusi Binomial
Distribusi Binomial digunakan jika sebuah percobaan terdiri dari
|
|
36
beberapa
sub-percobaan Bernoulli
yang
independen, dan
setiap
sub-
percobaan
juga
menghasilkan salah
satu
dari
dua
kemungkinan hasil.
Setelah
melakukan beberapa
sub-percobaan tersebut, dihitung
jumlah
terjadinya
kejadian
yang
diteliti.
Berikut
ini
merupakan probability
mass function dari distribusi Binomial:
P( x)
n!
x!(n
x)!
p
x
(1
p)
n
x
, x = 0,1,2,…,n,
0
<
p
< 1
3.
Distribusi Poisson
Suatu distribusi
mengikuti pola distribusi Poisson jika
mengikuti
aturan berikut ini:
a.
Tidak terdapat dua kejadian yang terjadi bersamaan.
b.
Proses kedatangan bersifat acak.
c.
Rata-rata jumlah kedatangan per interval waktu sudah
diketahui dari pengamatan sebelumnya.
d.
Bila interval waktu dibagi ke dalam interval yang lebih kecil,
maka pernyataan-pernyataan berikut ini harus dipenuhi:
-
Probabilitas tepat satu kedatangan adalah sangat kecil dan
konstan.
-
Probabilitas
dua
kedatangan
atau
lebih
selama
interval
waktu tersebut angkanya sangat kecil sehingga mendekati
nol.
|
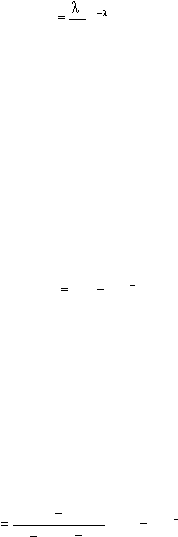 37
x
-
Jumlah kedatangan
pada interval waktu
tersebut
tidak
tergantung
pada
kedatangan
di
interval
waktu
sebelum
dan sesudahnya.
Berikut
ini
merupakan probability
mass
function dari
distribusi
Poisson:
P( x)
e
, x = 0,1,2,…. , ? > 0
x!
4.
Distribusi Geometric
Sama
seperti
distribusi
Binomial,
variabel
acak
distribusi Geometric
juga
terkait
dengan
variabel
acak Bernoulli.
Perbedaannya,
probabilitas
pada
distribusi Geometric
hanya
menentukan
peluang
terjadinya kejadian
pertama
setelah
beberapa kali percobaan.
Berikut
ini merupakan probability mass function dari distribusi Geometric:
P( x)
p(1
p)
x
1
,
x = 0,1,2,… , 0 < p < 1
5.
Distribusi Negative Binomial
Variabel acak Negative Binomial dapat
diinterpretasikan sebagai
jumlah percobaan Bernoulli
yang diperlukan
untuk
memperoleh
hasil
dengan
jumlah
tertentu.
Berikut
ini
merupakan probability
mass
function dari distribusi Negative Binomial:
P( x)
(
x
1)!
(n
1)!( x
n)!
p
n
(1
p)
x
n
, x = n, n+1, … n = 1,2,…
|
|
38
Selain
mengikuti pola distribusi diskret, teori antrian
juga menggunakan
beberapa
pola distribusi
kontinyu
untuk
data-data
kontinyu
(White
et al.,
1975, pp33-39). Pola distribusi kontinyu yang lazim digunakan antara lain:
1.
Distribusi Normal
Distribusi normal merupakan
distribusi yang paling dikenal dalam
teori
probabilitas
karena
kemampuannya untuk
mendeskripsikan
fenomena
kejadian acak. Kurva normal berbentuk lonceng dengan
nilai rata-ratanya berada pada titik tengah kurva yang berarti
jumlahnya
paling
banyak.
Berikut
ini
merupakan probability density
function dari distribusi Normal:
P( x)
1
(2
)¹ ²
/ ²
exp
(
x
)
2
2
2
2.
Distribusi Exponential
Distribusi
eksponensial
biasanya
berguna
untuk
mendeskripsikan
waktu
antar
kedatangan dan
waktu
pelayanan
dalam
teori
antrian.
Distribusi eksponensial memiliki ciri-ciri sebagai berikut:
a.
Waktu antar kejadian bersifat acak.
b.
Waktu antar kejadian berikutnya independen terhadap waktu
antar kejadian sebelumnya.
c.
Waktu pelayanan
dalam antrian tergantung
dari unit yang
dilayani.
|
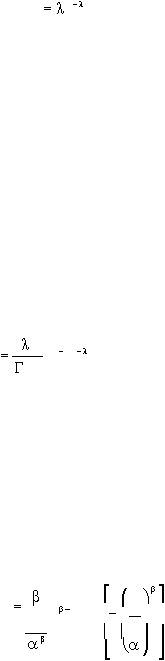 39
n
Berikut ini
merupakan probability density function dari distribusi
Exponential:
P( x)
e
x
, ? > 0
3.
Distribusi Gamma
Distribusi Gamma hanya digunakan jika jumlah jumlah kejadian yang
berhasil berupa
integer.
Jika
jumlah kejadian
berhasil bukan
integer,
maka
variabel
acak
Gamma
tidak
dapat
direpresentasikan dengan
menggunakan jumlah
variabel
acak
eksponensial
yang
identik.
Distribusi
Gamma biasanya
memiliki kurva
berbentuk
kurva
normal
yang
menjulur
positif.
Berikut
ini
merupakan probability
density
function dari distribusi Gamma:
P( x)
x
n
1
e
x
,
?
>
0
,
n
> 0
(n)
4.
Distribusi Weibull
Distribusi Weibull
merupakan salah
satu distribusi data kontinyu yang
paling
berguna
untuk
memodelkan kegagalan
(failure)
dari
sebuah
produk.
Berikut
ini
merupakan probability
density
function
dari
distribusi Weibull:
P( x)
x
x
1
exp
|
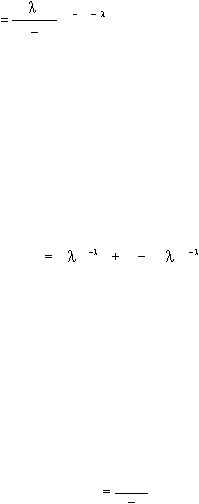 40
5.
Distribusi Erlang
Distribusi Erlang berkaitan erat dengan variabel acak eksponensial dan
Gamma. Distribusi Erlang digunakan jika pelayanan dalam suatu
sistem antrian
sifatnya sama
dan
rutin
serta
waktu
pelayanannya
cenderung menurun. Berikut ini merupakan
probability density
function dari distribusi Erlang:
P( x)
(k
)
k
x
k
1
e
k
x
, ? > 0 , integer k > 0
(k
1)!
6.
Distribusi Hyperexponential
Distribusi
Hyperexponential
terjadi
dalam teori
antrian
ketika
waktu
pelayanan
untuk
satu
unit
berdistribusi eksponensial dengan
jumlah
parameter
lebih
dari
satu.
Berikut
ini
merupakan probability density
function dari distribusi Hyperexponential:
P( x)
p
e
1
x
(1
p)
e
2
x
1
2
7.
Distribusi Uniform
Distribusi Uniform
memiliki nilai variabel acak
yang berada di antara
dua
buah
nilai. Distribusi
ini
penting dalam
simulasi
karena
mampu
menghasilkan banyak
variabel
acak
lainnya.
Berikut
ini
merupakan
probability density function dari distribusi Uniform:
P( x)
1
b
a
|
|
41
2.6
Notasi Model Sistem Antrian
Karakteristik dan
asumsi
dari
model
antrian
dirangkum
dalam
bentuk
notasi. Notasi standar yang digunakan menurut White et al. (1975, p8) adalah
sebagai berikut:
(
x | y | z ) : ( u | v | w )
Berikut ini adalah keterangan dari setiap simbol notasi standar di atas:
x, menyatakan distribusi kedatangan (atau antar kedatangan).
y, menyatakan distribusi waktu pelayanan.
z, menyatakan jumlah fasilitas pelayanan paralel dalam sistem.
u, menyatakan disiplin antrian yang digunakan.
v,
menyatakan
jumlah
maksimum
unit
dalam
sistem (yang
dilayani
dan yang menunggu)
w, menyatakan ukuran pemanggilan populasi
Notasi standar
untuk
simbol x
dan
y
sebagai
distribusi kedatangan dan
waktu
pelayanan
dapat
digantikan
dengan
simbol-simbol dalam
Tabel
2.1
berikut ini:
|
 42
Tabel 2.1 Tabel Simbol Distribusi Kedatangan dan Waktu Pelayanan
Simbol
Keterangan
M
Distribusi
kedatangan Poisson
atau
sama
dengan
distribusi
eksponensial untuk
waktu
antar
kedatangan dan
waktu
pelayanan.
M
menunjukkan properti Markov pada distribusi
eksponensial.
GI
Tingkat
kedatangan
atau
waktu
antar
kedatangan berdistribusi General Independent.
G
Tingkat
pelayanan
atau
waktu
pelayanan
berdistribusi General.
D
Waktu antar kedatangan atau waktu pelayanan
berdistribusi deterministik (konstan).
E
k
Waktu antar kedatangan atau waktu pelayanan
berdistribusi Erlang atau Gamma dengan
fase
k.
K
n
Waktu antar kedatangan atau waktu pelayanan
berdistribusi Chi-Square dengan n
derajat
bebas.
HE
k
Waktu antar kedatangan atau waktu pelayanan
berdistribusi Hyperexponential dengan fase k.
Simbol z, v, dan w digantikan dengan angka nominal yang sesuai dengan
sistem antrian.
Jika jumlah
maksimum unit dalam
sistem dan
populasi
tidak
terbatas (infinite), maka simbol v dan w dapat digantikan dengan simbol 8.
Notasi
standar
untuk simbol u
sebagai
jenis disiplin antrian
yang
digunakan dapat
digantikan
dengan simbol-simbol dalam
Tabel
2.2
berikut
ini:
|
 43
Tabel 2.2 Tabel Simbol Disiplin Antrian
Simbol
Keterangan
FCFS
First Come First Served
LCFS
Last Come First Served
SIRO
Service in Random Order
SPT
Shortest Processing (Service) Time
GD
General Service Discipline
2.7
Identifikasi Distribusi
Identifikasi
distribusi
data
kedatangan
dilakukan
untuk mengetahui
apakah
data
kedatangan tersebut
mengikuti
suatu
pola
distribusi
teoritik
tertentu
sehingga
formula
untuk
mengestimasikan parameter
dapat
disesuaikan
dengan
distribusinya. Menurut
White
et
al.
(1975,
p298),
pengujian ini terdiri dari tiga tahap, yaitu:
1.
Data Collection
Merangkum data dan
menyimpulkan secara kasar pola distribusi data
tersebut berdasarkan bentuk grafiknya.
2.
Parameter Estimation
Mengestimasikan
berbagai
parameter
dari
distribusi
yang
dihipotesiskan.
3.
Goodness of Fit Test
Menentukan apakah data yang dikumpulkan mengikuti pola distribusi
yang dihipotesiskan dengan menggunakan Uji Kebaikan Suai.
|
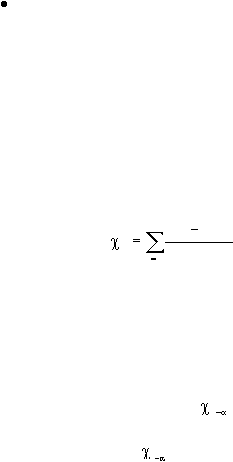 44
i
i
1
2.8
Uji Kebaikan Suai (Goodness of Fit)
Menurut
Walpole
(1995,
p325),
Uji
Kebaikan
Suai
digunakan untuk
mengetahui apakah suatu populasi memiliki suatu distribusi teoritik tertentu.
Uji
ini
didasarkan pada
seberapa
baik
kesesuaian antara
frekuensi
yang
teramati dalam
sampel
dengan
frekuensi
harapan pada
distribusi
yang
dihipotesiskan.
Chi-Square Test
Pengujian
yang
biasa
dilakukan
pada
Chi-Square Test antara
lain
distribusi
Binomial, distribusi
Poisson,
dan
distribusi
Normal.
Adapun
langkah-langkah dalam pengujian tersebut yaitu:
1.
Tentukan interval kelas k.
2.
Tentukan nilai ?²
dengan rumus:
k
(O
E )
2
²
E
i
1
i
3.
Tentukan taraf nyata (a).
4.
Tentukan nilai derajat bebas (d).
d
= ( k – 1 ) – [jumlah parameter pada distribusi yang dihipotesiskan]
5.
Tentukan nilai kritis
²
pada tabel distribusi Chi-Square.
6.
Jika ?
2
>
2
1
,
tolak hipotesis bahwa data
mengikuti pola distribusi
yang dihipotesiskan.
|
 45
D
D
Kolmogorov-Smirnov Test
Uji
Kolmogorov-Smirnov digunakan
untuk
menentukan
seberapa
baik
sebuah
sampel
data
acak
mengikuti pola
distribusi
teoritis
tertentu (normal,
uniform,
poisson,
atau eksponensial). Uji
ini
didasarkan pada
perbandingan
fungsi distribusi kumulatif sampel dengan fungsi distribusi kumulatif
hipotesis. Langkah-langkah dalam uji Kolmogorov-Smirnov adalah:
1.
Tentukan
frekuensi
distribusi
kumulatif
sampel
S
n
(x)
dan
distribusi
kumulatif hipotesis F(x).
2.
Hitung | F(x
i
)
–
S
n
(x
i
)
|
dan | F(x
i
)
–
S
n
(x
i-1
)
|
jika F(x) kontinyu. Jika
F(x) diskret, hanya perlu menghitung F(x
| F(x
i
)
–
S
n
(x
i
)
|.
3.
Tentukan nilai maksimum D
max
dari perhitungan nomor 2.
4.
Tentukan taraf nyata (a).
5.
Tentukan
nilai kritis
n
n
dari tabel nilai kritis perbedaan
absolut
maksimum antara distribusi kumulatif sampel dan populasi.
6.
Jika D
max
n
,
tolak hipotesis bahwa data mengikuti pola distribusi
n
yang dihipotesiskan.
Pada
prakteknya,
hanya
satu
jenis
uji
kebaikan
suai
yang
perlu
dilakukan.
White
et
al.
(1975,
p338)
mengemukakan bahwa
sebaiknya
menggunakan
Kolmogorov-Smirnov
Test karena secara statistik terbukti
lebih baik daripada Chi-Square Test.
|
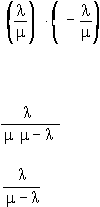 46
2.9
Model M/M/1/FCFS/8/8
Model
M/M/1/GD/8/8
ini
adalah
model
yang paling
umum
dan
sering
dibahas dalam
masalah antrian. Model ini adalah model antrian
yang paling
sederhana
dengan
mengasumsikan
bahwa input
kedatangan
mengikuti
distribusi Poisson dan pelayanan mengikuti distribusi Eksponensial.
Menurut Harris et
al.
(1998,
p53),
fungsi densitas
untuk
waktu
antar
kedatangan dan waktu pelayanan untuk model M/M/1 adalah :
a(t) = ?e-
?t
,
b(t) = µe
-µt
Dimana 1/? adalah rata-rata waktu antar kedatangan dan 1/µ adalah waktu
pelayanan, sebaiknya
waktu
pelayanan
diasumsikan secara
statistik
berdiri
sendiri.
Berikut
adalah
rumus-rumus
penghitungan
karakteristik operasional
dalam model antrian M/M/1 :
n
1.
Po
=
1
,
Po
adalah
probabilitas tidak
ada
individu dalam
sistem.
2.
Lq =
2
(
)
,
Lq adalah rata-rata jumlah individu dalam antrian (unit).
3.
Ls =
,
Ls adalah rata-rata jumlah
individu dalam sistem (antrian
dan pelayanan) (unit).
|
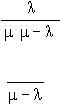 47
4.
Wq =
(
)
, Wq adalah rata-rata waktu tunggu dalam antrian (jam).
5.
Ws
=
1
,
Ws
adalah
rata-rata
waktu dalam
sistem
(antrian
dan
pelayanan) (jam).
6.
?
adalah tingkat rata-rata kedatangan per satuan waktu (unit/waktu).
7.
µ
adalah tingkat rata-rata pelayanan per satuan waktu (unit/waktu).
2.10
Model M/E
k
/1/FCFS/8/8
Distribusi Erlang
adalah
merupakan
satu
keluarga
dengan
distribusi
Gamma dan distribusi Eksponensial. Menurut
Harris et al. (1998, p128-129)
eksponensial
itu adalah kasus
khusus
dari
Erlang
yang
dinamakan
tipe
1
(k
=
1),
sedangkan
untuk
Erlang
(k
>
1).
Hubungan antara
Erlang
dengan
Eksponensial dapat dijelaskan dengan model antrian dimana bentuk pelayanan
suatu sistem memiliki bentuk seri fase-fase yang identik.
Dengan
mempertimbangkan jika
sebuah
model
dengan
waktu
pelayanannya
memiliki
distribusi Erlang
tipe-k,
itu
lebih
mudah
untuk
di
analisa
model
seperti
ini
dengan
melihat
bahwa Erlang
dipecah dari k
fase-
fase untuk Eksponensial dengan rata-rata menjadi 1/kµ.
Menurut
Budihardjo
et
al.
(1999,
p866)
suatu
skema
dari
bentuk
pola
yang digambarkan di jurnal tersebut menjelaskan suatu
model
hipotesa
|
 48
dimana jika terdapat fase yang berbentuk
Erlang waktu menunggu akan
terjadi peningkatan dimana k > q, dan menurun jika k < q.
Gambar 2.8 Skema One Maverick Stage
Dimana ? A : Erlang (k) fase = 1, Bi : Erlang (q) fase > 1.
Berikut
adalah
rumus-rumus
penghitungan karakteristik
operasional
dalam model antrian M/E
k
/1 :
1.
,
adalah tingkat kegunaan fasilitas sistem atau utilitas (rasio)
2.
Lq =
Wq, Lq adalah rata-rata jumlah individu dalam antrian (unit).
3.
Ls = Lq +
,
Ls adalah rata-rata jumlah individu dalam sistem (antrian
dan pelayanan) (unit).
4.
Wq =
k
1
2k
1
(1
)
, Wq adalah rata-rata waktu tunggu dalam antrian
(jam).
5.
Ws = Wq +
1
, Ws adalah rata-rata waktu tunggu sistem (antrian dan
pelayanan) (jam).
6.
?
adalah tingkat rata-rata kedatangan per satuan waktu (unit/waktu).
7.
µ
adalah tingkat rata-rata pelayanan per satuan waktu (unit/waktu).
|