|
BAB II LANDASAN
TEORI
Perancangan program aplikasi yang akan dibuat menggabungkan algoritma Brute
Force dan algoritma Greedy yang digunakan secara bergantian pada tahap-tahap
tertentu. Karena itu, pada bagian ini akan dibahas juga algoritma Brute
Force
dan
Greedy terlebih
dahulu
sebelum
masuk
ke
dalam
pembahasan
algoritma
kombinasi
keduanya yaitu algoritma Brudy.
2.1. Algoritma Brute Force
Brute
Force (Rinaldi
Munir,
2004,
p.
2)
adalah
sebuah
pendekatan
langsung
(straight forward)
untuk
memecahkan
suatu
masalah,
yang
biasanya didasarkan
pada
pernyataan
masalah
(problem
statement) dan
definisi
konsep
yang
dilibatkan.
Pada
dasarnya
algoritma
Brute
Force adalah
alur
penyelesaian
suatu
permasalahan
dengan
cara berpikir yang sederhana dan tidak membutuhkan suatu permikiran yang lama.
Sebenarnya, algoritma Brute Force merupakan algoritma yang muncul karena pada
dasarnya alur pikir manusia adalah Brute Force (langsung/to the point).
Beberapa karakteristik dari algoritma Brute Force dapat dijelaskan sebagai berikut.
a. Membutuhkan
jumlah
langkah
yang
banyak
dalam
menyelesaikan suatu
permasalahan sehingga jika
diterapkan menjadi suatu algoritma program
aplikasi akan membutuhkan banyak memori.
b. Digunakan sebagai dasar dalam menemukan suatu solusi yang lebih efektif.
c. Banyak dipilih dalam penyelesaian
sebuah permasalahan
yang sederhana
karena kemudahan cara berpikirnya.
|
|
8
d. Pada
banyak
kasus,
algoritma
ini
banyak
dipilih
karena
hampir
dapat
dipastikan dapat menyelesaikan banyak persoalan yang ada.
e. Digunakan sebagai dasar bagi perbandingan keefektifan sebuah algoritma.
Dalam beberapa kasus tertentu algoritma
Brute Force hampir sama dengan
Exhaustive Search.
Exhausitve Search yang
merupakan
teknik
pencarian
solusi
secara
Brute
Force pada
masalah
yang
melibatkan
pencarian
elemen
dengan
sifat
khusus.
Biasanya elemen tersebut berada di antara objek-objek kombinatorik seperti permutasi,
kombinasi, atau himpunan bagian dari sebuah himpunan. Berdasarkan definisi ini, maka
dapat ditarik kesimpulan bahwa Exhaustive
Search adalah Brute Force juga. Oleh
karena
itu
Exhaustive Search
adalah
salah
satu
implementasi
dari
Brute
Force
dalam
kasus pencarian. Masalah–masalah dalam Exhaustive
Search dengan penerapan
algoritma Brute Force dapat dijelaskan sebagai berikut.
a. Enumerasi setiap solusi yang mungkin dengan cara yang sistematis.
b.
Evaluasi
setiap
kemungkinan
solusi yang
ditemukan
satu per
satu,
meskipun
terdapat beberapa kemungkinan ditemukannya solusi yang tidak layak atau
bahkan
terdapat kemungkinan–kemungkinan solusi terbaik yang telah
ditemukan dan dievaluasi.
c. Bila pencarian sudah sampai pada tujuan, maka pilih solusi yang terbaik.
Berikut ini adalah contoh-contoh penerapan algoritma Brute Force pada
perhitungan matematika biasa.
1.
Menghitung an (a > 0, n adalah bilangan bulat tak-negatif)
a
n
= a x a x … x a (n kali) , jika n > 0
= 1
, jika n = 0
Algoritma: kalikan 1 dengan a sebanyak n kali.
|
|
9
2.
Menghitung n! (n bilangan bulat tak-negatif)
n! = 1 × 2 × 3 × … × n , jika n > 0
= 1
, jika n = 0
Algoritma: kalikan n buah bilangan, yaitu 1, 2, 3, …, n, sekaligus.
3.
Mengalikan dua buah matrik yang berukuran n × n.
Misalkan C = A × B dan elemen-elemen matrik dinyatakan sebagai c
ij
,
a
ij
,
dan b
ij
.
Algoritma: hitung setiap elemen hasil perkalian satu per satu, dengan cara
mengalikan dua vektor baris dan kolom yang panjangnya n.
4.
Menemukan semua faktor dari bilangan bulat n selain dari 1 dan n
itu sendiri.
Definisi: Bilangan bulat a adalah faktor dari bilangan bulat b jika a habis
membagi b.
5.
Mencari elemen terbesar (atau terkecil)
Diberikan sebuah himpunan yang beranggotakan n buah bilangan bulat.
Bilangan-bilangan bulat tersebut dinyatakan sebagai a1, a
2
,
…, a
n
.
Carilah
elemen terbesar di dalam himpunan tersebut.
6.
Sequential Search
Diberikan n buah bilangan bulat
yang dinyatakan sebagai a1
,
a2, …, a
n
.
Carilah apakah
x
terdapat di dalam
himpunan
bilangan bulat tersebut.
Jika x ditemukan, maka lokasi (indeks) elemen yang bernilai x disimpan
di dalam peubah
idx.
Jika x tidak
terdapat di dalam
himpunan
tersebut,
maka idx diisi dengan nilai 0.
|
|
10
7.
Bubble Sort
Algoritma Bubble Sort mengimplementasikan teknik Brute Force dengan
jelas sekali.
8.
Menghitung nilai polinom secara Brute Force
Kelebihan dari algoritma Brute Force adalah sebagai berikut.
1.
Metode Brute Force dapat digunakan untuk memecahkan hampir
sebagian besar masalah (wide applicability).
2.
Metode Brute Force sederhana dan mudah dimengerti.
3.
Metode
Brute
Force
menghasilkan
algoritma
yang
layak
untuk
beberapa
masalah
penting,
seperti
pencarian,
pengurutan,
pencocokan string, perkalian matriks.
4.
Metode Brute Force menghasilkan algoritma baku (standard)
untuk
tugas-tugas
komputasi
seperti penjumlahan/perkalian n
buah bilangan, menentukan elemen minimum atau maksimum di
dalam tabel (list).
Selain itu, terdapat beberapa kelemahan dari algoritma Brute Force:
1.
Metode Brute Force jarang menghasilkan algoritma yang efektif.
2.
Beberapa algoritma Brute Force lambat sehingga tidak dapat
diterima.
3.
Tidak sekontruktif/sekreatif teknik pemecahan masalah lainnya.
Algoritma
Brute Force
pada
penyelesaian
masalah
Knapsack
dilakukan
dengan
menghitung
satu
per satu
keuntungan
yang diperoleh
dari semua
kemungkinan
pemilihan barang yang ada. Banyaknya kemungkinan pemilihan barang tersebut dapat
dirumuskan sebagai: 2
n
.
|
|
11
Adapun n adalah jumlah dari barang yang akan dikirim. Jadi, seandainya banyak barang
yang
akan
dikirm 5
buah,
maka
untuk
mencari
solusi
optimal
diperlukan
2
5
=
32
kemungkinan. Memang, akan didapatkan hasil yang sangat optimal mengingat akan
ditelusuri satu per satu kemungkinan yang ada, tetapi akan sangat membutuhkan waktu
yang sangat lama (perhitungan manual) dan memori yang besar (jika menggunakan
program komputer) untuk jumlah barang yang ada sangat banyak.
2.2 Algoritma Greedy
Algoritma Greedy merupakan algoritma yang lazim untuk memecahkan persoalan
optimasi meskipun hasilnya tidak selalu merupakan solusi yang optimum. Sesuai arti
harafiah,
Greedy berarti
tamak.
Prinsip
utama
dari
algoritma
ini
adalah
mengambil
sebanyak mungkin apa yang dapat diperoleh sekarang. Untuk memecahkan persoalan
dengan algoritma Greedy, kita memerlukan elemen-elemen sebagai berikut.
a. Himpunan Kandidat (C)
Himpunan ini berisi elemen-elemen pembentuk solusi.
b. Himpunan Solusi, (S)
Himpunan
ini berisi kandidat
yang terpilih sebagai solusi persoalan.
Dengan kata lain, himpunan solusi adalah himpunan bagian dari
himpunan kandidat.
c. Fungsi Seleksi
Fungsi seleksi merupakan fungsi yang ada pada setiap langkah
memilih kandidat yang paling
memungkinkan
guna
mencapai
solusi
optimal.
|
|
12
d. Fungsi Kelayakan (Feasible)
Fungsi
kelayakan
adalah
fungsi yang
memeriksa
apakah
suatu
kandidat yang telah dipilih dapat memberikan solusi yang layak dan
tidak melanggar batasan atau constraints yang ada.
e. Fungsi Objektif
Fungsi objektif adalah fungsi yang memaksimumkan atau
meminimumkan nilai solusi.
Skema umum algoritma Greedy adalah sebagai berikut.
a. Inisialisasi S dengan kosong.
b. Pilih sebuah kandidat C dengan fungsi seleksi.
c. Kurangi C dengan kandidat yang sudah dipilih dari langkah (b) di
atas.
d. Periksa apakah kandidat yang dipilih
tersebut bersama-sama dengan
himpunan solusi membentuk solusi yang layak atau feasible (dengan
fungsi kelayakan).
e.
Periksa apakah himpunan solusi sudah
memberikan solusi
yang
lengkap serta optimal (dengan fungsi objektif).
Contoh permasalahan
yang
dapat diselesaikan
dengan algoritma Greedy adalah
masalah penukaran uang koin. Strategi Greedy adalah pada setiap langkah, pilihlah koin
dengan nilai
terbesar dari himpunan koin yang tersisa.
•
Misal: A = 32, koin yang tersedia: 1, 5, 10, dan 25.
•
Himpunan Kandidat: himpunan koin yang merepresentasikan nilai 1,
5, 10, 25, paling sedikit mengandung satu koin untuk setiap nilai.
|
|
13
•
Himpunan Solusi: total
nilai koin
yang dipilih
tepat sama jumlahnya
dengan nilai uang yang ditukarkan.
•
Fungsi
Seleksi:
pilihlah
koin
yang
bernilai
tertinggi
dari
himpunan
kandidat yang tersisa.
•
Fungsi
Layak:
memeriksa apakah nilai total dari
himpunan koin yang
dipilih tidak melebihi jumlah uang yang harus dibayar.
•
Fungsi Objektif: jumlah koin yang digunakan minimum.
•
Langkah 1: pilih 1 buah koin 25 (Total = 25)
Langkah 2: pilih 1 buah koin 5
(Total = 25 + 5 = 30)
Langkah 3: pilih 2 buah koin 1
(Total = 25+5+1+1= 32)
Solusi: Jumlah koin minimum = 4
(solusi optimal!)
Optimum global dengan
menggunakan
algoritma
Greedy belum
tentu
merupakan
solusi
optimum (terbaik),
tetapi sub-optimum
atau pseudo-optimum. Alasannya
adalah
sebagai berikut.
1. Algoritma Greedy tidak
beroperasi
secara
menyeluruh
terhadap
semua alternatif solusi yang ada (sebagaimana pada metode
Exhaustive Search).
2. Terdapat beberapa fungsi seleksi yang berbeda, sehingga harus dipilih
fungsi yang tepat agar algoritma yang digunakan menghasilkan solusi
optimal.
Secara umum rumus dari algoritma Greedy adalah:
Berat barang total =
?
WjXj
=
K
j?N
Volume barang total =
?
V
j
X
j
=
K
j?N
di mana X
j
€ {0,1}
di mana X
j
€ {0,1}
|
|
14
Keuntungan total =
?
P
j
X
j
j?N
di mana X
j
€ {0,1}
W
j
adalah berat barang, V
j
adalah volume barang, P
j
adalah keuntungan barang, X
j
adalah
bernilai
0
jika
barang
tersebut
tidak
dipilih
untuk
dimasukkan
ke
dalam kapasitas
Knapsack dan
1
jika
barang
tersebut
terpilih
untuk
dimasukkan
ke
dalam
kapasitas
Knapsack, dan K adalah kapasitas media pengiriman.
Pada penyelesaian masalah Knapsack
dengan menggunakan algoritma Greedy
dapat dipilih 3 cara sebagai berikut.
1. Greedy by Profit, pilih benda-benda dengan keuntungan maksimum dan benda-
benda tersebut memiliki berat yang masih dapat ditampung oleh sisa kapasitas
Knapsack.
2. Greedy by Weight, pilih benda-benda dengan berat minimum dan benda-benda
tersebut memiliki volume yang masih dapat ditampung oleh sisa kapasitas Knapsack.
3. Greedy by Volume, pilih
benda-benda
dengan
volume
minimum
dan benda-benda
tersebut memiliki berat yang masih dapat ditampung oleh sisa kapasitas Knapsack.
4. Greedy
by Weight
Density, pilih
benda-benda
dengan keuntungan
per berat
yang
nilainya maksimum dan benda-benda tersebut memiliki berat dan volume yang
masih dapat ditampung
oleh sisa kapasitas
Knapsack. Rumus
untuk
mendapatkan
density adalah:
D
j =
Pj
W
j
5. Greedy by Volume Density, pilih benda-benda dengan keuntungan per volume yang
nilainya maksimum dan benda-benda tersebut memiliki berat dan volume yang
|
|
15
masih
dapat ditampung
oleh sisa kapasitas
Knapsack. Rumus
untuk
mendapatkan
density adalah:
D
j =
Pj
Vj
Pada sebagian masalah, algoritma Greedy tidak selalu berhasil memberikan solusi
yang
optimal.
Jika
jawaban
terbaik
mutlak
tidak
diperlukan,
maka algoritma Greedy
sering
berguna
untuk
menghasilkan
solusi
hampiran
(approximation), dibandingkan
dengan menggunakan algoritma yang lebih rumit untuk menghasilkan solusi yang eksak.
Bila
algoritma
Greedy optimum,
maka
keoptimalannya
itu
dapat
dibuktikan
secara
matematis.
2.3
Algoritma Brudy (Brute Force-Greedy)
Ide awal dari penggabungan kedua algoritma tersebut adalah membentuk sebuah
algoritma baru yang di tengah-tengah. Misalkan diperlukan algoritma dengan kecepatan
yang
cukup
tinggi
(lebih
tinggi
dari
kecepatan
Brute Force), algoritma
yang
cukup
sederhana, serta ketepatan penemuan solusi yang cukup baik (lebih baik dari Greedy).
Algoritma
ini
(untuk
selanjutnya,
dinamakan sebagai
algoritma
Brudy (Brute
Force-
Greedy)) lebih
mengacu
pada
algoritma
Greedy. Bedanya, algoritma Greedy mencari
optimum
lokal
pada
tiap
langkahnya,
sedangkan
algoritma
Brudy
mencari
optimum
lokal
pada
tiap
b-langkah (untuk
selanjutnya
b
dinamakan
sebagai nilai batas, dengan
catatan b > 1 dan b < jumlah_tahap), sehingga dapat dikatakan algoritma Brudy ini sama
dengan algoritma B-Greedy. Jadi, pada suatu keadaan, misalkan pada suatu
permasalahan
yang
pengerjaannya
bertahap (anggap
saja
14 tahap dengan
tahap
ke-0
adalah kondisi awal), algoritma Brute Force akan
mencari semua cara mencapai
tahap
|
|
16
ke-13 tersebut. Algoritma Greedy akan mencari optimum dari tahap ke-i menuju tahap
ke-(i+1),
sedangkan
algoritma
Brudy
akan
mencari
optimum
dari
tahap
ke-i
menuju
tahap ke-(i+b)
dan
b
bebas
ditentukan oleh
pengguna. Misalkan
dipilih
b
adalah
3,
berarti akan dicari optimum tahap ke-1 menuju tahap ke-4, setelah itu dicari optimum
tahap ke-4 menuju tahap ke-7, dan seterusnya. Begitu diperoleh optimum dari tahap ke-1
menuju ke tahap ke-4, status di tahap ke-4 tersebut itulah yang akan diperluas untuk
dicari optimumnya menuju tahap ke-7 dan seterusnya. Hal inilah yang merupakan letak
kemiripan
algoritma
Brudy dengan algoritma
Greedy.
Sedangkan
untuk
mencari
optimum dari tahap ke-1 sampai tahap ke-4, akan dicoba semua cara yang mungkin dari
tahap
ke-1
sampai
tahap
ke-4,
begitu
seterusnya.
Inilah
kemiripan
algoritma Brudy
dengan
algoritma
Brute
Force.
Sedikit
perbedaan
dengan
algoritma
Greedy, yang
sekaligus
berguna
menutupi
kelemahan
algoritma ini, adalah apabila tahap ke-(i+b)
melebihi
solusi
akhir,
kurangilah
b
dengan
1
dan
lakukan
lagi
untuk
langkah
selanjutnya.
Berikut
ini
contoh
perbandingan
hasil
penyelesaian permasalahan
Knapsack
menggunakan metode Brute Force, Greedy, dan Brudy.
Persoalan: Misalkan diberikan beberapa buah barang dengan keuntungan serta beratnya
masing-masing, akan tetapi container yang dimiliki hanya dapat memuat sejumlah berat
tertentu.
Pilih
barang-barang
yang
akan dibawa
agar
keuntungan yang diperoleh
maksimum.
Contoh: Terdapat 6 benda (label 1 sampai 6), dengan w
i
adalah berat benda ke-i dan p
i
adalah keuntungan benda ke-i.
w1 = 100
p1
=
40
v1
=
50
w2 = 50
p2
=
35
v2
=
70
|
|
17
w3 = 45
p3
=
18
v3
=
30
w
4
=
20
p
4
=
4
v
4
=
25
w
5
=
10
p
5
=
10
v
5
=
10
w
6
=
5
p
6
=
2
v
6
=
18
Kapasitas Knapsack K = 100, volume = 200
Tuliskan solusi sebagai X = (x1
,
x2
,
…, x
6
)
dengan x
i
= 0 jika benda ke-i dibawa atau x
i
=
1 jika benda ke-i tidak dibawa.
Penyelesaian dengan Brute Force.
Dicoba semua kemungkinan X, mulai X = (0, 0, 0, 0, 0,0), sampai dengan X = (1,
1, 1, 1, 1, 1). Jumlah kemungkinan yang harus dicoba ada 2
6
=
64 kemungkinan. Tiap
kemungkinan harus dihitung berat totalnya, dan dari semua kemungkinan yang berat
totalnya tidak melebihi kapasitas Knapsack, pilih satu yang keuntungannya paling besar.
Pada akhirnya akan diperoleh solusi optimum X = (0, 1, 1, 0, 0, 1), dengan berat total
100, volume total 118, dan keuntungan
total 55. Hal
ini
memang sangat optimal tetapi
untuk memperoleh hasil tersebut membutuhkan proses yang sangat panjang dan lama
(perhitungan manual). Apabila metode ini
diterapkan
menjadi
algoritma
pembuatan
program aplikasi akan menggunakan memori yang sangat besar.
Penyelesaian dengan Greedy.
Dengan Greedy, bisa dipilih 3 cara sebagai berikut.
1. Greedy by Profit, pilih benda-benda dengan keuntungan maksimum dan benda-
benda tersebut memiliki berat yang masih dapat ditampung oleh sisa kapasitas
Knapsack.
|
|
18
2. Greedy by Weight, pilih benda-benda dengan berat minimum dan benda-benda
tersebut memiliki volume yang masih dapat ditampung oleh sisa kapasitas Knapsack.
3. Greedy by Volume, pilih
benda-benda
dengan
volume
minimum
dan benda-benda
tersebut memiliki berat yang masih dapat ditampung oleh sisa kapasitas Knapsack.
4. Greedy
by Weight
Density, pilih
benda-benda
dengan keuntungan
per berat
yang
nilainya maksimum dan benda-benda tersebut memiliki berat dan volume yang
masih
dapat ditampung
oleh sisa kapasitas
Knapsack. Rumus
untuk
mendapatkan
density adalah:
D
j =
Pj
W
j
4.
Greedy by Volume Density, pilih benda-benda dengan keuntungan per volume yang
nilainya maksimum dan benda-benda tersebut memiliki berat dan volume yang
masih
dapat ditampung
oleh sisa kapasitas
Knapsack. Rumus
untuk
mendapatkan
density adalah:
D
j =
Pj
Vj
|
 19
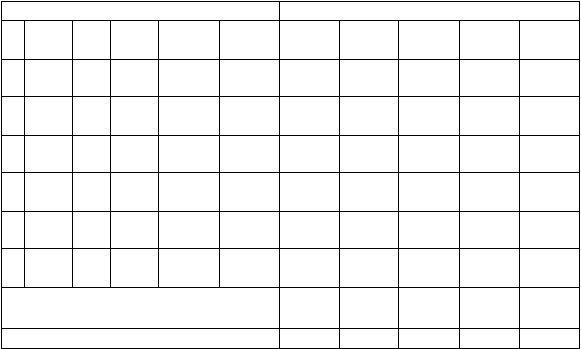
Sehingga bisa dibuat tabelnya sebagai berikut.
Tabel 2.1 Data Permasalahan Knapsack dengan solusi Greedy
Sumber : (Rinaldi Munir, 2004, p31)
Sifat objek
Greedy by
i
W
i
V
i
P
i
D
i
volume
D
i
weight
profit
weight
volume
weight
density
volume
density
1
100
50
40
0,8
0,4
1
0
0
0
0
2
50
70
35
0,5
0,7
0
0
0
1
0
3
45
30
18
0,6
0,4
0
1
1
0
1
4
20
25
4
0,16
0.2
0
1
1
1
1
5
10
10
10
1,0
1,0
0
1
1
1
1
6
5
18
2
0,11
0,4
0
1
1
1
1
Total bobot
Total volume
100
50
80
83
80
83
85
123
80
83
Total keuntungan
40
34
34
51
34
Sehingga diperolehlah solusi sebagai berikut.
•
Greedy by Profit: X = (1, 0, 0, 0, 0, 0), dengan keuntungan total = 40.
•
Greedy by Weight: X = (0, 0, 1, 1, 1, 1), dengan keuntungan total = 34.
•
Greedy by Volume: X = (0, 0, 1, 1, 1, 1), dengan keuntungan total = 34.
•
Greedy by Weight Density: X = (0, 1, 0, 1, 1, 1), dengan keuntungan total = 51.
•
Greedy by Weight Density: X = (0, 0, 1, 1, 1, 1), dengan keuntungan total = 34.
Dari
hal-hal
di atas
diperoleh kenyataan,
bahwa
langkah
Greedy
mengutamakan
kecepatan dan hanya
optimum pada setiap
langkah,
dan
tidak ada
yang menghasilkan
keuntungan optimum pada
langkah akhir. Secara
umum,
jika banyak barang adalah n,
kompleksitas algoritma untuk Brute Force adalah: O(2
n
).
|
|
20
Sedangkan untuk algoritma greedy, kompleksitas pada greedy by profit dan greedy
by weight adalah sama, yaitu: O(n²),
yang artinya pemilihan k barang yang diambil, dengan maksimal n buah iterasi, karena
jumlah
barang
yang
diambil
tidak
mungkin
lebih
dari
n.
Pada
greedy by
density,
kompleksitasnya berbeda sedikit karena harus ada perhitungan p
i
/w
i
untuk setiap i
barang-barang yang ada, yaitu: T(n) = n² + n, sehingga kompleksitasnya adalah: O(n²
).
Dengan menggunakan algoritma Brudy maka akan memperoleh hasil sebagai
berikut.
Pertama, pilih nilai batas secara bebas (penjelasan mengenai nilai batas). Misalkan saja
nilai batasnya dipilih yaitu b = 2.
Langkah-langkah penyelesaian algoritma adalah sebagai berikut.
1. Karena dipilih b = 2, berikutnya tentukan semua himpunan bagian dari 6 benda
tersebut ({1, 2, 3, 4, 5, 6}) yang banyak anggotanya adalah 2. Banyaknya
himpunan bagian tersebut didapat dengan menggunakan rumus kombinasi
yaitu:
C(n,r) =
n!
(n - r
)!r!
2. Cari profit, berat, dan profit/berat untuk tiap 2 benda tersebut. Untuk
memudahkan, dapat dibuat tabel.
|
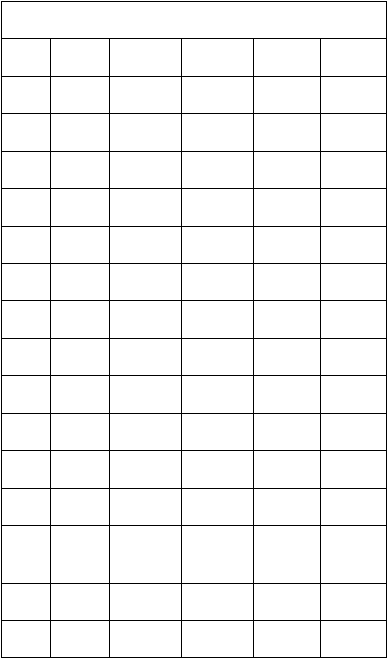 21
Tabel 2.2 Data Permasalahan Knapsack dengan solusi Brudy
Sumber : (Anggriawan Sugianto, 2005, p4)
Properti objek
i
w
i
v
i
p
i
p
i
/w
i
p
i
/v
i
{1,2}
150
120
75
0,5
0,63
{1,3}
145
80
58
0,4
0,73
{1,4}
140
75
44
0,37
0,59
{1,5}
110
60
50
0,45
0,83
{1,6}
105
68
42
0,4
0,62
{2,3}
95
100
53
0,56
0,53
{2,4}
70
95
39
0,56
0,41
{2,5}
60
80
45
0,75
0,56
{2,6}
55
88
37
0,67
0,42
{3,4}
65
55
22
0,34
0,4
{3,5}
55
40
28
0,51
0,7
{3,6}
50
48
20
0,4
0,42
{4,5}
30
35
14
0,47
0,4
{4,6}
25
43
6
0,24
0,14
{5,6}
15
28
12
0,8
0,43
Untuk
memperoleh
solusi
optimal
masalah
Knapsack di
atas
dengan
menggunakan
algoritma Brudy adalah dengan cara menganalisis data-data di atas ke dalam 5 cara yang
berbeda, yaitu Brudy
by
Weight
(dengan memprioritaskan berat yang paling kecil),
|
|
22
Brudy by Weight (dengan memprioritaskan volume
yang paling kecil), Brudy by Profit
(dengan
memprioritaskan
keuntungan
yang
paling
besar
terlebih
dahulu),
Brudy by
Weight Density (dengan memprioritaskan keuntungan per berat yang paling besar
terlebih
dahulu),
dan
Brudy by
Volume Density
(dengan
memprioritaskan
keuntungan
per volume yang paling besar terlebih dahulu). Kemudian setelah mendapatkan solusi-
solusi dari ketiga cara tersebut digunakan
suatu
rumusan
untuk
memperoleh
solusi
optimal yaitu:
P
opt
=
maks (P
p
,
P
w
,
P
v
,
P
dw
,P
dv
), W
opt
=
W
(
Popt)
,
dan V
opt
=
V
(Popt)
P
opt
adalah keuntungan optimal yang dicari, W
opt
adalah berat total dari barang-barang
yang diprioritaskan sehingga memperoleh keuntungan
yang maksimal, V
opt
adalah
volume total dari barang-barang yang diprioritaskan sehingga
memperoleh keuntungan
yang
maksimal,
P
p
adalah
keuntungan
yang
diperoleh
dalam
perhitungan
dengan
menggunakan
cara
Brudy by
Profit, P
w
adalah
keuntungan
yang
diperoleh
dalam
perhitungan
dengan
menggunakan
cara
Brudy
by
Weight, P
v
adalah
keuntungan
yang
diperoleh
dalam perhitungan
dengan
menggunakan
cara
Brudy by Volume, P
dw
adalah
keuntungan
yang
diperoleh
dalam
perhitungan
dengan
menggunakan
cara
Brudy by
Weight
Density, sedangkan P
dv
adalah keuntungan yang diperoleh dalam perhitungan
dengan menggunakan cara Brudy by Volume Density.
Brudy by Weight:
1. Pilih i dengan berat terkecil dan tidak
lebih dari 100,
volume tidak lebih dari
200, dipilih {5,6}, berat sisa = 85, volume sisa = 172.
2. Pilih i berikutnya dengan berat terkecil, tidak lebih dari 85, volume tidak lebih
dari 172, dan i n {5,6} = {}, dipilih {3,4}, berat sisa = 20, volume sisa = 117.
|
|
23
3. Pilih i berikutnya dengan berat terkecil, tidak lebih dari 20, volume tidak lebih
dari 117 dan i n {3,4,5,6} = {}. Tidak ada yang dipilih.
4. Decrement
b, b = 1, gunakan tabel 2.1 pada pembahasan dengan metode
Greedy,
pilih
i
berikutnya dengan berat terkecil, tidak lebih dari 20, volume
tidak lebih dari 117, dan i n {3,4,5,6} = {}. Tidak ada yang dipilih.
5. Decrement b, b = 0. Ketika b = 0 proses berhenti.
Solusi = (0, 0, 1, 1, 1, 1). Berat = 80, volume = 83, keuntungan = 34.
Brudy by Volume:
1. Pilih i dengan
volume terkecil dan tidak
lebih dari 200, berat tidak lebih dari
100, dipilih {5, 6), berat sisa = 85, volume sisa = 172.
2. Pilih i berikutnya dengan volume terkecil, tidak lebih dari 172, berat tidak lebih
dari 85, dan i n {5, 6} = {}, dipilih {3,4}, berat sisa = 20, volume sisa = 117.
3. Pilih i berikutnya dengan volume terkecil, tidak lebih dari 117, berat tidak lebih
dari 20 dan i n {3, 4, 5, 6} = {}. Tidak ada yang dipilih.
4. Decrement
b, b = 1, gunakan tabel 2.1 pada pembahasan dengan metode
Greedy, pilih
i
berikutnya dengan volume
terkecil, tidak lebih dari 117, berat
tidak lebih dari 20, dan i n {3, 4, 5, 6} = {}. Tidak ada yang dipilih.
5. Decrement b, b = 0. Ketika b = 0 proses berhenti.
Solusi = (0, 0, 1, 1, 1, 1). Berat = 80, volume = 83, keuntungan = 34.
|
|
24
Brudy by Profit:
1. Pilih i dengan keuntungan terbesar dengan berat tidak lebih dari 100 dan
volume tidak
lebih dari 200, dipilih {2, 3), berat sisa = 5 dan volume sisa =
100.
2. Pilih i berikutnya dengan keuntungan terbesar, berat tidak lebih dari 5, volume
tidak lebih dari 100, dan i n {2, 3} = {}.
3.. Decrement
b, b = 1, gunakan tabel 2.1 pada pembahasan dengan metode
Greedy, pilih i berikutnya dengan keuntungan terbesar, berat tidak lebih dari 5,
volume tidak lebih dari 100, dan i n {2,3} = {6}, berat sisa = 0, sisa volume =
95.
4. Pilih i berikutnya dengan keuntungan terbesar, berat tidak lebih dari 0, volume
tidak lebih dari 82 dan i n {2, 3, 6} = {}. Tidak ada yang dipilih.
5. Decrement b, b = 0. Ketika b = 0 proses berhenti.
Solusi = (0, 1, 1, 0, 0, 1). Berat = 100, volume = 118, keuntungan = 55.
Brudy by Weight Density:
1. Pilih i dengan keuntungan per berat terbesar dengan berat tidak lebih dari 100
dan volume tidak lebih dari 200, dipilih {5, 6}, berat sisa = 85, volume sisa =
172.
2. Pilih i berikutnya dengan keuntungan per berat terbesar, berat tidak lebih dari
85, volume tidak lebih dari 172, dan i n {5, 6} = {2, 4}, berat sisa = 15, volume
sisa = 77.
|
|
25
3. Pilih i berikutnya dengan keuntungan per berat
terbesar dan berat tidak
lebih
dari 15, volume tidak
lebih dari 77 dan i n {2, 4, 5, 6} = {}. Tidak ada yang
dipilih.
4. Decrement
b, b = 1, gunakan tabel 2.1 pada pembahasan dengan metode
Greedy, pilih i berikutnya dengan keuntungan per berat terbesar dan berat tidak
lebih dari 15, volume tidak lebih dari 77 dan i n {2, 4, 5, 6} = {}. Tidak ada
yang dipilih.
5. Decrement b, b = 0. Ketika b = 0 proses berhenti.
Solusi = (0, 1, 0, 1, 1, 1). Berat = 85, volume = 123, keuntungan = 51.
Brudy by Volume Density:
1. Pilih
i
dengan keuntungan per
volume
terbesar dengan berat tidak lebih dari
100 dan volume tidak lebih dari 200, dipilih {3, 5}, berat sisa = 45, volume sisa
= 160.
2. Pilih
i
berikutnya
dengan keuntungan
per
volume
terbesar,
berat
tidak
lebih
dari 45, volume tidak lebih dari 160, dan i n {3, 5} = {4, 6}, berat sisa = 20,
volume sisa = 117.
3. Pilih i berikutnya dengan keuntungan per volume terbesar dan berat tidak lebih
dari 20, volume tidak lebih dari 117,dan i n {3, 4, 5, 6} = {}. Tidak ada yang
dipilih.
4. Decrement
b, b = 1, gunakan tabel 2.1 pada pembahasan dengan metode
Greedy, pilih i berikutnya dengan keuntungan per berat terbesar dan berat tidak
lebih dari 20, volume tidak lebih dari 117 dan i n {3, 4, 5, 6} = {}. Tidak ada
yang dipilih.
|
|
26
5. Decrement b, b = 0. Ketika b = 0 proses berhenti.
Solusi = (0, 0, 1, 1, 1, 1). Berat = 80, volume = 83, keuntungan = 34.
Dari
kelima
solusi
di
atas
selanjutnya
dicari
solusi
yang
memberi
keuntungan
paling besar yaitu solusi yang diperoleh dengan menggunakan cara Brudy by Profit yaitu
keuntungan sebesar 55, volume sebesar 118, dan berat sebesar 100. Sedangkan solusi =
(0, 1, 1, 0, 0, 1) artinya barang yang akan dipriopritaskan untuk dikirim adalah:
•
barang dengan i = 2, yaitu berat = 50, volume = 70, dan keuntungan = 35.
•
barang dengan i = 3, yaitu berat = 45, volume = 30, dan keuntungan = 18.
•
barang dengan i = 6, yaitu berat = 5, volume = 18 dan keuntungan = 2.
Jika
hasil
yang
diperoleh
dengan
menggunakan
algoritma
Brudy dibandingkan
dengan
hasil
yang
diperoleh
dengan
2
algoritma
lain,
yaitu
Brute Force dan
Greedy,
maka hasil yang diperoleh sama dengan yang diperoleh dengan menggunakan algoritma
Brute Force namun
dengan
proses
yang jauh
lebih
cepat. Pada
hasil
yang
diperoleh
dengan
menggunakan
algoritma
Greedy hasil
yang
diperoleh
tidak
optimal
yaitu
keuntungan = 51 dan berat = 85 walaupun untuk memperoleh hasilnya jauh lebih cepat
dibanding dengan menggunakan algoritma Brute Force.
Dari
contoh
penyelesaian
masalah
Knapsack di
atas
dapat
dilihat
dengan
jelas
penggabungan dua buah algoritma
yang
sangat
sederhana
(Brute
Force
dan
Greedy)
yang saling memiliki kekurangan masing-masing ternyata menghasilkan suatu algoritma
baru
(Brudy) yang bukan
hanya
memberikan solusi
yang
optimal tetapi
juga dengan
proses yang cukup cepat. Untuk pencarian solusi dengan perhitungan manual saja lebih
mudah dan singkat apalagi jika algoritma Brudy ini diterapkan dalam pembuatan
|
|
27
program aplikasi. Memori
yang
digunakan
untuk
menjalankan
program aplikasi
lebih
hemat (walaupun tidak sehemat menggunakan algoritma Greedy) tapi tetap memberikan
solusi yang optimal.
Secara kasarnya, kompleksitas untuk algoritma ini adalah: O(2
b
n
2
/b²). Jadi, jika b
=
n,
maka kompleksitasnya menjadi O(2
n
),
yang sama dengan algoritma
Brute Force.
Sebaliknya, jika
b
= 1,
maka
kompleksitasnya pun akan
sama
pula
dengan
algoritma
Greedy, yaitu: O(2n²) = O(n
2
).
2.4 Dasar Perancangan Piranti Lunak
Menurut
IEEE
(Institute
of
Electrical
and
Electonics
Engineers), perancangan
piranti lunak didefinisikan sebagai penggunaan pendekatan yang sistematik, disiplin, dan
dapat dikualifikasi dalam pengembangan, pengoperasian, dan pemeliharaan piranti
lunak; atau juga berarti studi mengenai hal-hal tersebut (Pressman, 2001, p20).
2.5 Daur Hidup Perangkat Lunak
Salah satu model perancangan piranti lunak adalah dengan menggunakan model air
terjun
(Waterfall model).
Perancangan
program
aplikasi
dengan
model
Waterfall
dilakukan dalam 5 tahap. Tahap-tahap tersebut adalah sebagai berikut.
a. Analisis
Analisis
adalah
suatu
kegiatan
untuk
memnentukan topik dari
masalah
yang
sedang duhadapi dan bagaimana cara pemecahan masalah tersebut.
|
|
28
b. Desain
Dalam
tahap
ini
ditentukan
konsep
dasara
rancangan
dari
program
aplikasi
yang akan dibuat sehingga diharapakan dengan desain yang baik, maka para
pengguna
(user)
akan
merasa
nyaman dalam menggunakan
program aplikasi
yang dirancang tersebut.
c. Pengkodean (coding)
Pada tahap ini dilakukan penulisan kode program sebagai penterjemahan hasil
perancangan menjadi suatu bentuk yang dapat dimengert oleh mesin.
d. Pengujian (testing)
Pengujian dilakukan untuk mencari kelemahan dan kesalahan (error) yang
terjadi
pada
program aplikasi.
Kelemahan
dan
kesalahan
tersebut
diperbaiki
sehingga dihasilkan suatu program aplikasi sesuai dengan yang diharapkan.
e. Pemeliharaan (maintenance)
Perangkat lunak akan mengalamai perubahan setelah disampaikan kepada
pelanggan. Pemeliharaan perangkat lunak mengaplikasikan lagi setiap fase
program sebelumnya dan tidak membuat yang baru lagi.
2.6
Teori Interaksi Manusia dan Komputer
Selain
memiliki
tampilan
yang
menarik, suatu program aplikasi
yang baik tenetu
harus
user
friendly. Yang
dimaksud
dengan
user
friendly (Shneiderman,
1998,
p15)
adalah sebagai berikut.
1)
Waktu untuk balajar tidak lama.
2)
Kecepatan dan ketepatan dalam penyajian informasi.
3)
Tingkat kesalahan user rendah.
|
|
29
4)
Cara penggunaan oleh user tidak gampang dilupakan.
5)
Kepuasan pribadi.
Selain itu, terdapat 8 hal penting yang harus diperhatikan dalam merancang
program aplikasi (Shneiderman, 1998, p74-75), yaitu:
1)
Konsistensi.
2)
User dapat menggunakan fasilitas shortcut.
3)
Memberi umpan balik yang informatif.
4)
Merancang dialog yang memberikan penutup.
5)
Mempunyai pencegahan kesalahan.
6)
Adanya pilihan redo dan undo.
7)
User sebagai pemegang kendali.
8)
Mengurangi beban ingatan jangka pendek.
2.7
Pseudocode
Pseudocode (Pressman,
1999,
p411)
adalah
suatu
bahasa
umum
yang
menggunakan kosa kata dari suatu bahasa (seperti bahasa Inggris) dan perintah (syntax)
dari
bahahas
lain
(seperti
bahasa
pemrograman
terstruktur).
Pseudocode biasanya
dijadikan
alternatif
pilihan
dalam perancangan piranti
lunak
selain
alat bantu
berupa
diagram. Tidak ada standarisasi dalam hal penulisan pseudocode.
2.8
State Transititon Diagram
State
Transititon
Diagram
(STD)
adalah
suatu
alat
bantu
yang
digunakan
untuk
memodelkan suatu sistem yang memiliki ketergantungan terhadap waktu. STD memiliki
suatu tingkah laku suatu sistem dengan menggambarkan state dan kejadian yang
|
 30
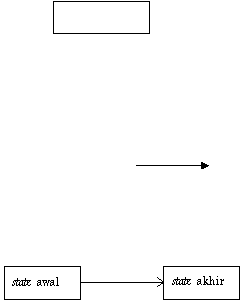
menyebabkan suatu state berubah ke state lain. Komponen-komponen pada STD adalah
sebagai berikut.
1)
State,disimbolkan dengan
State mempresentasikan
reaksi
yang
muncul
setelah
suatu
kejadian dilakukan.
Ada 2 jenis state yaitu state awal dan state akhir. State akhir dapat terdiri dari
beberapa state tapi state awal hanya boleh berupa satu state.
2)
State Transititon, disimbolkan dengan
Label tersebut menunjukan kejadian yang menyebabkan transisi tersebut terjadi.
3)
Kondisi dan aksi, disimbolkan dengan
Kondisi berfungsi mengubah state
dan aksi adalah tindakan yang dilakukan
sistem ketika state berubah. Kondisi dan aksi digambarkan dengan anak panah
yang menghubungkan 2 state yang berkaitan.
|