|
7
BAB 2
LANDASAN TEORI
Suspensi
adalah
suatu
sistem
yang
berfungsi
meredam kejutan,
getaran
yang
terjadi
pada
kendaraan
akibat
permukaan jalan
yang
tidak
rata.
Suspensi
dapat
meningkatkan kenyamanan berkendaraan dan mengendalikan kendaraan. Suspensi pada
kendaraan
berawal
pada abad
XVI
(sumber
/2006/042006/07/otokir/utama01.htm, 2007),
pada saat
itu suspensi dipergunakan pada
kereta
kuda agar nyaman.
Dimana
jalan-jalan
saat itu banyak
yang bergelombang.
Sistem suspensi pada kendaraan digantung pada keempat tiang yang terkait ke sasis atau
rangka. Suspensi
pada dasarnya
merupakan bagian dari sasis.
Sasis
terdiri atas rangka
kendaraan, sistem suspensi, sistem kemudi, dan roda. Sistem suspensi terdiri atas pegas,
peredam (shock absorber), dan komponen lain seperti lengan ayun, sambungan (joints),
batang pengkaku (anti-roll bar atau stabilizer), dan karet-karet.
Berkenaan
dengan
konfigurasi, terdapat
dua
jenis
sistem
suspensi,
yakni
dependent dan independent. Suspensi dependent dapat dicirikan dari poros penghubung
roda
kiri
dan
kanan
yang
merupakan satu
kesatuan
utuh
serta kaku
(rigid). Biasanya,
suspensi dependent dipakai di kendaran angkutan barang (truk). Pegas yang digunakan
untuk menumpu beban kendaraan biasanya dari jenis pegas daun (leaf spring).
Suspensi independen, seperti jenis MacPherson atau double wishbone umumnya
digunakan
di
roda
depan
pada
kendaraan jenis
sedan
atau
kendaraan
penumpang
(minibus) keluaran terbaru. Dari konstruksinya, dapat dilihat pada gambar (2.1) bahwa
suspensi independent memungkinkan
roda
kiri
untuk
bergerak
bebas
terhadap
roda
|
 8
kanan,
meski
hanya
untuk
kisaran
gerak
yang
terbatas
(sumber,
rakyat.com /cetak/2007/022007/16/otokir/utama01.htm, 2007).
Gambar 2.1 Suspensi independent jenis MacPherson
Berdasarkan
sistem
pengontrolannya, terdapat dua jenis
sistem
suspensi
yakni
suspensi pasif
dan
suspensi aktif. Pada
suspensi pasif
(sistem
yang
umum
diterapkan
pada kendaraan saat
ini) kekakuan pegas dan konstanta redamannya bernilai konstan.
Namun
pada suspensi
aktif,
pengontrolan
kekakuan
pegas
dan
redaman dapat
diatur,
sehingga dapat menambah kenyamanan penumpangnya.
Konstanta suspensi atau yang biasa disebut dengan konstanta spring didapatkan
dari besarnya gaya per satuan jarak. Dengan rumusan sebagai berikut.
F
=
-
kx
•
F = gaya
•
k
=
konstanta spring
•
x
=
perpindahan jarak
2.1
Suspensi Aktif
Pada
penelitian
tugas
akhir
ini
hanya
akan
meninjau
suspensi
aktif.
Suspensi
aktif
merupakan
teknologi
otomotif
yang
mengontrol
pergerakan
vertikal
pada
roda.
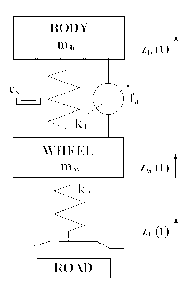
Pada model suspensi aktif dijelaskan dengan gambar(2.2) dibawah ini.
|
 9
Gambar 2.2 Sistem suspensi aktif
Dalam
hal
Ini
diasumsikan bahwa
roda
kendaraan
menempel
pada
jalan.
Persamaan pergerakan pada sistem aktif, berdasarkan hukum Newton 2, akan diberikan
sebagai berikut:
m
b
&
z
&
b
=
f
a
-
k
1
(
z
b
-
z
w
)
-
c
s
(
z
&
b
-
z
&
w
)
m
w
&
z
&
w
=
-
f
a
+
k
1
(
z
b
-
z
w
)
-
k
2
(
z
w
-
z
r
)
+
c
s
(
z
&
b
-
z
&
w
)
•
m
b
=
berat body
•
m
w
=
berat roda
•
k
1
=
konstanta spring
•
k
2
=
konstanta roda
•
f
a
=
actuator force (besaran gaya pada hidrolik)
•
c
s
=
damping rasio (peredam kejut)
•
z
r
=
pemindahan jalan (perpindahan vertikal pada jalan)
|
|
10
•
z
b
=
pemindahan body
•
z
w
=
pemindahan roda
Pada hukum Newton 2, jumlah gaya yang bekerja sama dengan massa dikalikan
dengan percepatan. Dengan rumusan sebagai berikut.
F
=
ma
•
F = gaya
•
m
=
massa
•
a
=
percepatan
Damping adalah kontrol dari
osilasi.
Damping
tersebut
mengontrol kecepatan
gerak suspensi. Arah gaya yang bekerja berlawanan dengan arah gerak suspensi.
Kendaraan
yang
tidak
memiliki
damping akan
terus
berosilasi
naik
turun.
Rumusan
damping adalah sebagai berikut.
F
=
-cv
•
F = gaya
•
c
=
koefisien damping
•
v
=
kecepatan
2.2
Logika Fuzzy
Logika fuzzy dikatakan sebagai logika baru yang lama, sebab ilmu tentang logika
fuzzy
baru
ditemukan
beberapa
tahun
yang
lalu,
padahal
sebenarnya konsep
tentang
logika fuzzy
itu sendiri sudah ada pada diri kita sejak
lama. Logika fuzzy adalah suatu
cara yang tepat untuk memetakan suatu ruang masukan ke dalam suatu ruang keluaran
(Sri Kusumadewi, 2003,p163).
|
|
11
Logika
fuzzy
pertama
kali
diperkenalkan oleh
profesor
Lotfi
Zadeh
dari
universitas california di Berkeley pada tahun 1965. Logika fuzzy merupakan suatu teori
himpunan
logika
yang
dikembangkan untuk
mengatasi
konsep
nilai
yang
terdapat
diantara
kebenaran
(truth)
dan
kesalahan
(false).
Dengan
menggunakan
logika
fuzzy
nilai
yang
dihasilkan bukan
hanya
ya
(1)
atau
tidak
(0)
tetapi
seluruh
kemungkinan
diantara 0 dan 1. (sumber, http://en.wikipedia.org/wiki/Fuzzy_logic)
2.2.1 Himpunan Crisp dan Himpunan Fuzzy
Himpunan nilai keanggotaan dari a adalah 1. Namun, jika a ? A,
Crisp
A
didefinisikan
oleh
item-item
yang
ada
pada
himpunan
itu.
Jika a ?
A,
maka nilai keanggotaan dari a adalah 1. Namun, jika a ? A,
maka nilai
keanggotaan dari a adalah 0. Notasi A = {x | P(x)} menunjukkan bahwa A berisi item x
dengan
P
(x)
benar. Jika
X
A
merupakan
fungsi
karakteristik
A
dan properti
P,
dapat
dikatakan bahwa P(x) benar, jika dan hanya jika X
A
(x) = 1.
Himpunan fuzzy didasarkan pada gagasan
untuk memperluas jangkauan fungsi
karakteristik sedemikian
hingga
fungsi
tersebut
akan
mencakup
bilangan
real
pada
interval [0,1]. Nilai keanggotaannya menunjukkan bahwa suatu item tidak
hanya
bernilai benar
atau salah.
Nilai 0
menunjukkan salah,
nilai
1
menunjukkan benar, dan
masih ada nilai-nilai yang terletak antara benar dan salah.
Sebagai contoh, kecepatan kendaraan dapat masuk dalam 2
himpunan berbeda,
lambat dan sedang,
sedang
dan
cepat.
Seberapa besar eksistensinya
dalam
himpunan
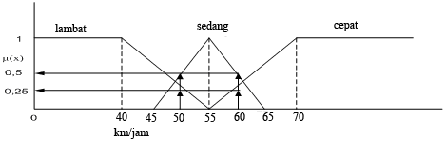
tersebut dapat dilihat pada nilai keanggotaannya. Gambar (2.3) menunjukkan himpunan
fuzzy untuk peubah kecepatan kendaraan.
|
 12
Gambar 2.3 Grafik pengelompokan kecepatan kendaraan dengan logika fuzzy
Pada Gambar (2.3) dapat dilihat bahwa:
•
Kendaraan
yang berkecepatan
40
km/jam,
termasuk
dalam
himpunan
lambat
dengan
µ
lambat
[50] = 0,25; namun kecepatan
tersebut
juga termasuk dalam
himpunan sedang dengan µ
sedang
[50] = 0,5.
•
Kendaraan yang berkecepatan
50 km/jam, termasuk dalam himpunan cepat
dengan µ
cepat
[60] = 0,25, namun kecepatan tersebut juga termasuk dalam
himpunan sedang dengan µ
sedang
[60] = 0,5.
Pada himpunan crisp,
nilai keanggotaannya hanya ada dua kemungkinan,
yaitu
antara
0
atau
1,
sedangkan pada
himpunan fuzzy
nilai
keanggotaannya pada
rentang
antara 0 sampai 1. Apabila x memiliki nilai keanggotaan fuzzy µ
A
[x] = 0, berarti x tidak
menjadi
anggota
himpunan A,
dan
juga
apabila
x
memiliki
nilai keanggotaan fuzzy
µ
A
[x] = 1 berarti x menjadi anggota penuh pada himpunan A.
Istilah
fuzzy
logic
memiliki berbagai arti.
Salah
satu
arti
fuzzy
logic
adalah
perluasan crisp
logic,
sehingga dapat
mempunyai
nilai antara
0
sampai
1.
Pertanyaan
yang
akan
timbul
adalah,
bagaimana dengan operasi
NOT,
AND
dan OR-nya?
Ada
banyak solusi untuk masalah tersebut. Salah satunya adalah:
•
operasi NOT x diperluas menjadi 1 - µ
x,
•
x OR y diperluas menjadi max(µ
x,
µ
y
)
|
|
13
•
x AND y diperluas menjadi min(µ
x,
µ
y
).
Dengan cara ini, operasi dasar untuk crisp logic tetap sama. Sebagai contoh :
•
NOT 1 = 1 – 1 = 0
•
1 OR 0 = max (1,0) = 1
•
1 AND 0 = min (1,0) = 0
dan ini diperluas untuk logika fuzzy. Sebagai contoh :
•
NOT 0,7 = 1 – 0,7 = 0,3
•
0,3 OR 0,1 = max (0,3, 0,1) = 0,3
•
0,8 AND 0,4 = min (0,8, 0,4) = 0,4
2.2.2
Fungsi Keanggotaan
Fungsi
keanggotaan (membership
function)
adalah
suatu
kurva
yang
menunjukkan pemetaan titik-titik input data kedalam nilai keanggotaannya (sering juga
disebut
dengan
derajat
keanggotaan)
yang
memiliki
interval
antara 0
sampai 1.
Salah
satu cara
yang
dapat
digunakan
untuk
mendapatkan
nilai keanggotaan adalah
dengan
melalui pendekatan fungsi.
Ada beberapa
fungsi
representasi
yang
bisa
digunakan dalam
logika
fuzzy.
Di
antaranya adalah sebagai berikut (Sri Kusumadewi, 2003,p160).
•
Representasi linear, permukaan digambarkan sebagai suatu garis lurus. Bentuk
ini paling
sederhana
dan menjadi
pilihan
yang baik untuk mendekati
suatu
konsep
yang
kurang jelas.
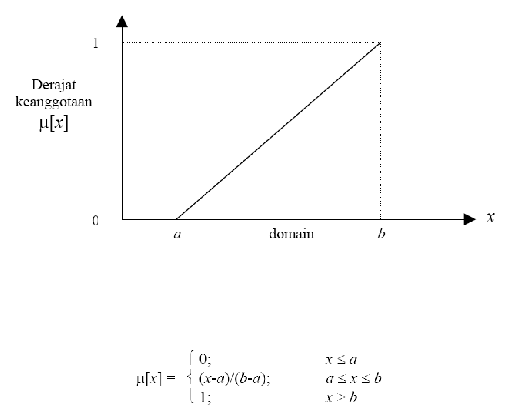
Ada
dua
keadaan
himpunan fuzzy linear. Pertama,
kenaikan himpunan dimulai dari domain yang memiliki derajat keanggotaan nol
|
 14
(0) bergerak
ke
kanan
menuju
ke
nilai
domain
yang
memiliki
derajat
keanggotaan lebih tinggi. Perhatikan gambar (2.4) dibawah ini.
Gambar 2.4 Representasi linear naik
Fungsi keanggotaan pada linear naik:
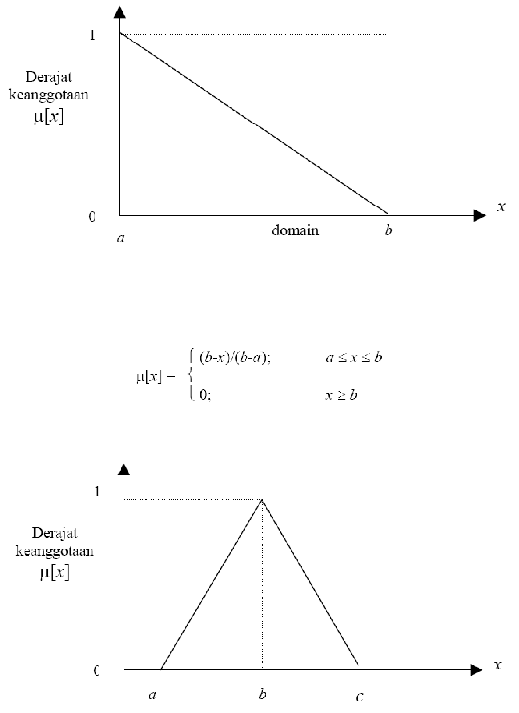
Kedua, merupakan kebalikan yang pertama. Garis lurus dimulai dari nilai
dominan dengan derajat keanggotaan tertinggi pada sisi kiri, kemudian bergerak
menurun ke nilai dominan yang memiliki derajat keanggotaan lebih rendah.
|
 15
Gambar 2.5 Representasi linear turun
Fungsi keanggotaan pada linear turun:
•
Representasi
kurva
segitiga,
pada
dasarnya
merupakan
gabungan
antara
dua
garis linear. Perhatikan gambar (2.6)
Gambar 2.6 Representasi kurva segitiga
|
 16
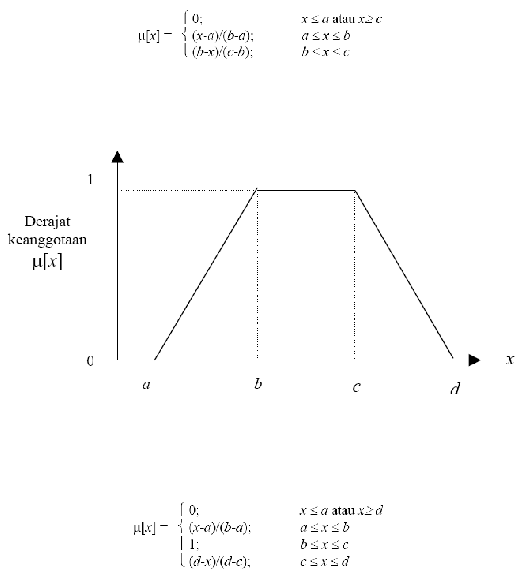
Fungsi keanggotaan pada kurva segitiga:
•
Representasi kurva trapesium, kurva segitiga pada dasarnya seperti bentuk
segitiga, hanya saja ada beberapa titik yang memiliki nilai keanggotaan
1.
Perhatikan gambar (2.7)
Gambar 2.7 Representasi kurva trapesium
Fungsi keanggotaan pada kurva trapesium:
•
Representasi kurva
bentuk
bahu, daerah
yang
terletak
di
tengah-tengah suatu
variabel
yang direpresentasikan
dalam
bentuk
segitiga,
pada sisi kanan dan
dirinya akan naik turun (misalkan: dingin bergerak ke sejuk bergerak ke hangat
dan
bergerak ke
panas).
Tetapi
terkadang
salah satu
sisi
dari
variabel
tersebut
tidak
mengalami
perubahan.
Sebagai contoh,
apabila telah
mencapai
puncak
|
 17
panas.
Himpunan fuzzy
bahu,
bukan
segitiga,
digunakan untuk
mengakhiri
variabel
suatu
daerah
fuzzy. Bahu kiri bergerak
dari
benar
ke salah,
demikian
juga
bahu kanan
bergerak dari
salah
ke
benar.
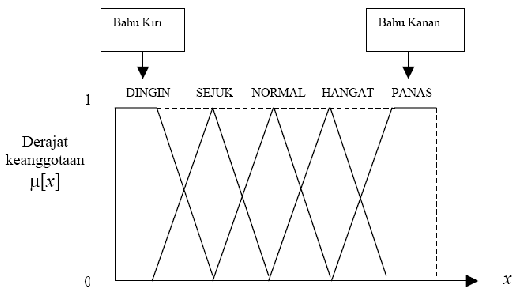
Gambar (2.8)
memperlihatkan
variabel temperatur dengan daerah bahunya.
Gambar 2.8 Representasi bentuk bahu pada variabel temperatur
•
Representasi kurva-S, kurva pertumbuhan dan penyusutan
merupakan kurva-S
atau sigmoid
yang
berhubungan dengan
kenaikan
dan
penurunan
permukaan
secara tak linear. Kurva-S untuk pertumbuhan akan bergerak dari sisi paling kiri
dengan nilai keanggotaan = 0 ke sisi paling kanan dengan nilai keanggotaan =1.
|
 18
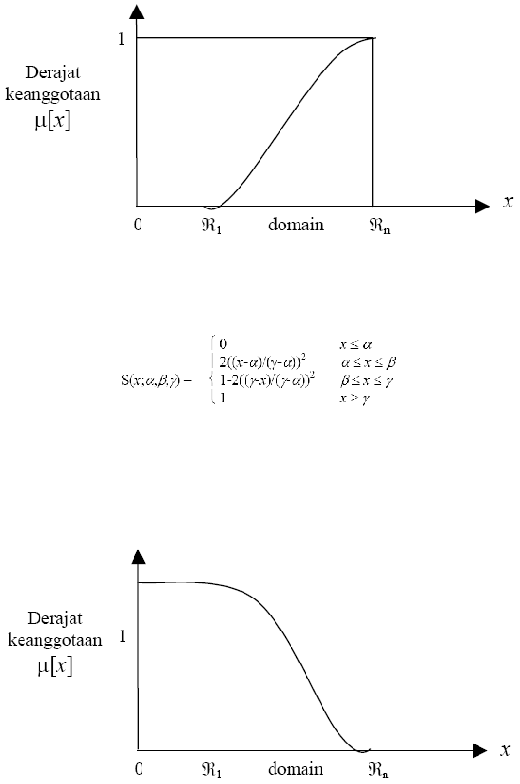
Gambar 2.9 Representasi kurva-S pertumbuhan
Fungsi keanggotaan pada kurva-S pertumbuhan:
Kurva-s
untuk penyusutan akan bergerak
dari
sisi
paling
kanan dengan
nilai
keanggotaan = 1 ke sisi paling kiri dengan nilai keanggotaan = 0 seperti terlihat
pada gambar (2.10) dibawah ini.
Gambar 2.10 Representasi kurva-S menurun
|
 19
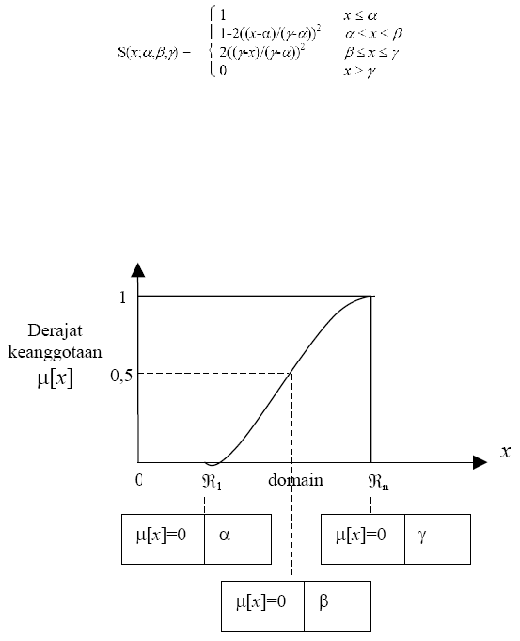
Fungsi keanggotaan pada kurva-S menurun:
Kurva-S
didefinisikan
dengan
menggunakan
3
parameter,
yaitu:
nilai
keanggotaan
nol
(
a
),
nilai
keanggotaan
lengkap
(
?
),
dan
titik
infleksi
atau
crossover
(
ß
)
yaitu
titik
yang
memiliki
domain
50%
benar.
Gambar
(2.11)
dibawah ini menunjukkan karakteristik kurva-S dalam bentuk skema.
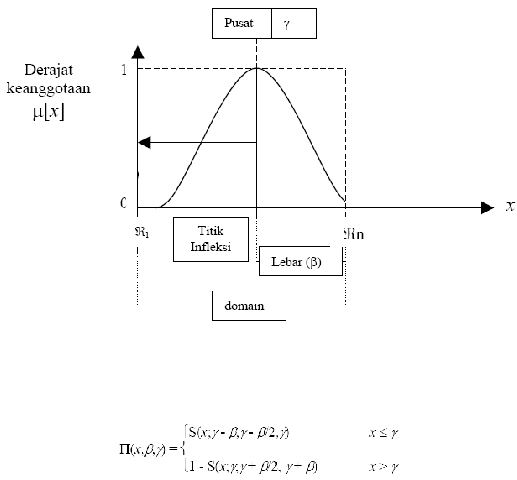
Gambar 2.11 Karakteristik fungsi kurva-S
•
Representasi
kurva
bentuk
lonceng
(bell
curve), pada
kurva
bentuk
lonceng
dibagi menjadi tiga kelas, yaitu kurva PI, beta, dan Gauss.
|
 20
i.
Kurva PI, berderajat keanggotaan 1 terletak pada pusat dengan domain (
?
), dan
lebar kurva (
ß
) seperti terlihat pada gambar (2.12)
Gambar 2.12 Karakteristik fungsi kurva PI
Fungsi keanggotaan pada kurva PI:
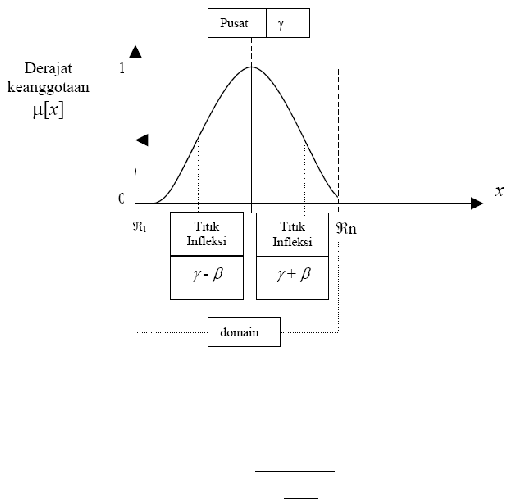
ii.
Pada kurva
beta
juga berbentuk
lonceng
namun
lebih rapat.
Kurva
ini
juga
didefinisikan dengan dua parameter, yaitu nilai pada domain yang menunjukan
pusat
kurva
(
?
), dan
setengah
lebar
kurva
(
ß
)
seperti
terlihat pada
gambar
(2.13) dibawah ini.
|
 21
Gambar 2.13 Karakteristik fungsi kurva Beta
Fungsi keanggotaan pada kurva Beta:
B
(
x,
?
,
ß
)
=
1
2
?
x -
?
?
1
+
?
?
?
ß
?
Salah satu perbedaan
mencolok kurva Beta dari kurva PI
adalah
fungsi
keanggotaan Beta akan mendekati nol hanya jika nilai (
ß
) sangat besar
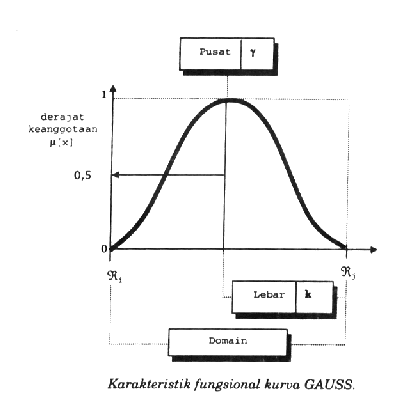
iii.
Pada
kurva
Gauss, menggunakan
(
?
) untuk
menunjukan
nilai
domain
pada
pusat
kurva,
dan
(k).
Seperti terlihat
pada
gambar
(2.14)
dibawah
ini.
Pada
|
 22
2
makalah
ini,
akan
menggunakan
model
fuzzy representasi
kurva
Gauss.
Gambar 2.4 Karakteristik fungsi kurva Gauss
Fungsi keanggotaan pada kurva Gauss:
G( x, k,
?
)
=
e
-
k
(? - x )
2.3
Blok Diagram
Sebuah
blok
diagram
pada
sistem
adalah
gambaran
representasi dari
fungsi
masing-masing komponen dan
menurunkan beberapa sinyal. Pada blok diagram semua
sistem variabel dihubungkan ke masing-masing fungsional blok. Fungsional blok adalah
sebuah simbol untuk operasi
matematik pada sinyal input ke blok
yang
mengeluarkan
output. Blok yang berhubungan ditandai dengan sebuah panah sebagai arah sinyal.
|
 23
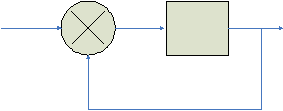
Gambar 2.15 Elemen dari blok diagram
Arah panah yang menuju ke blok menandakan sinyal input dan arah panah yang
meninggalkan blok menandakan sinyal output.
2.3.1
Node Penjumlahan (summing point) dan Node Pencabangan (branch point)
Gambar 2.16 Node penjumlah (Summing point)
Pada gambar di atas, lingkaran dengan di dalamnya ada tanda silang merupakan
sebuah simbol dari operasi penjumlahan atau pengurangan. Tanda tambah atau kurang
pada
arah panah
menandakan
sinyal tersebut
ditambah
atau dikurang.
Hal
ini
sangat
penting bahwa kuantitas ditambah atau dikurang memiliki dimensi dan unit yang sama.
Node pencabangan
(branch point) adalah sebuah node di mana sinyal dari
sebuah blok pergi menuju ke blok yang lain atau ke node penjumlahan.
|
 24
2.3.2
Blok Diagram Pada Sistem Perulangan Tertutup
R(s)
E(s)
C(s)
+
-
G(s)
Gambar 2.17 Sistem perulangan tertutup (Closed-loop system)
Gambar
di
atas
adalah
contoh
dari
blok
diagram
sistem
perulangan tertutup.
Perulangan tertutup pada sistem hanya dapat diindikasi dengan gambar diagram
tersebut. Nilai keluaran C(s) akan kembali ke
node penjumlahan di
mana nilai
tersebut
akan dibandingkan dengan nilai masukan R(s). Masukan dari E(s) akan menuju ke blok
fungsi transfer (transfer function) G(s), setelah itu akan memperoleh nilai keluaran C(s).
Beberapa
sistem
control
linier
mungkin
dipresentasikan
dengan
blok
diagram
yang
terdiri dari blok, node penjumlah dan node pencabangan.
Ketika
nilai output kembali
ke
node
penjumlah untuk
membandingkan dengan
nilai
masukan,
nilai
tersebut perlu dikonversi dari sinyal keluaran ke
sinyal
masukan.
Untuk contohnya, pada kontrol sistem suhu, sinyal keluaran biasanya yang mengontrol
suhu.
Sinyal keluaran, di
mana
yang
memiliki dimensi dari
suhu,
harus
sebelumnya
dikonversi
ke
gaya
atau
pasisi
atau
voltase
sebelum
dibandingkan dengan
sinyal
masukan. Konversi ini
akan diselesaikan oleh sebuah fungsi transfer (transfer function)
H(s). Terlihat gambar dibawah ini.
|
 25
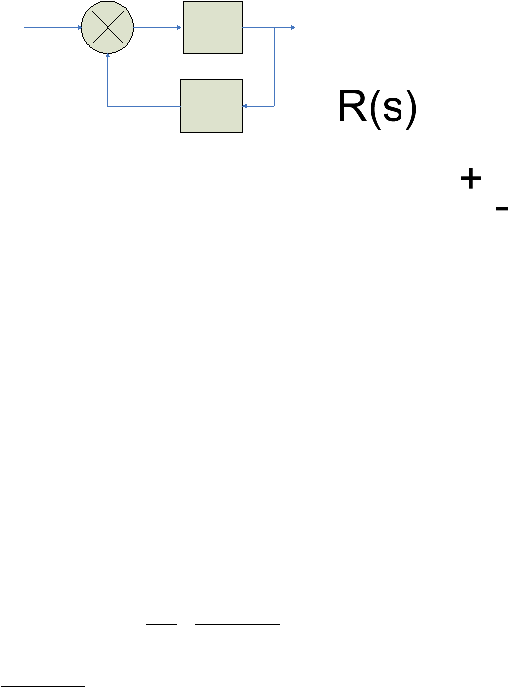
Gambar 2.18 Sistem perulangan tertutup 2
Pengaturan pada
elemen
umpan balik (feedback
element)
harus
memodifikasi
nilai
keluaran
sebelum
nilai
tersebut
dibandingkan dengan
nilai
masukan.
Pada
kebanyakan masalah, umpan balik adalah sebuah sensor
yang mengukur
nilai keluaran
dari rencana. Nilai dari keluaran tersebut akan dibandingkan dengan nilai masukan dan
gerakan sinyal kesalahan dapat dihasilkan. Sinyal umpan balik yang mengarah ke
node
penjumlahan untuk dibandingkan dengan masukan adalah B(s)=G(s)H(s).
Nilai keluaran dan masukan pada gambar (2.8) di atas dapat dijabarkan seperti di
bawah ini.
C
(s) =
G(s)E(s)
E
(s) =
R(s) -
B(s) ?
E s) =
(s) =
R(s) -
H
(s)C
(s)
Dengan mengeliminasi E(s)
maka
C
(s) =
G(s)[R(s) -
H
(s)C
(s)] atau
C
(s)
=
R(s)
G(s)
1
+
G(s)H (s)
Maka C (s) =
G(s)
1
+
G(s)H (s)
R(s)
|
|
26
2.4
Transformasi Laplace
Transformasi Laplace adalah suatu teknik untuk menyederhanakan
permasalahan
dalam suatu
sistem yang
mengandung
masukan
dan
keluaran,
dengan
melakukan
transformasi
dari
suatu
domain
pengamatan
ke
domain
pengamatan
yang
Dalam matematika jenis transformasi ini merupakan suatu konsep yang penting
sebagai bagian dari analisa fungsional, yang dapat membantu dalam melakukan analisa
sistem
invarian-waktu
linier,
seperti
rangkaian
elektronik,
osilator
harmonik,
devais
optik
dan
sistem-sistem mekanik.
Dengan
mengetahui
deksripsi
matematika
atau
fungsional sederhana dari masukan atau keluaran suatu sistem, transformasi Laplace
dapat
memberikan
deskripsi
funsional
alternatif yang kadang dapat menyederhanakan
proses analisa kelakukan dari sistem atau membuat suatu sistem baru yang berdasarkan
suatu kumpulan spesifikasi.
Dalam sistem
fisik
sebenarnya
transformasi
Laplace
sering
dianggap
sebagai
suatu transformasi dari cara pandang domain-waktu, di mana masukan dan keluaran
dimengerti sebagai fungsi dari waktu, ke cara pandang domain-frekuensi, di mana
masukan dan keluaran yang sama dipandang sebagai fungsi dari frekuensi angular
kompleks, atau radian per satuan waktu. Transformasi ini tidak hanya menyediakan cara
mendasar lain untuk mengerti kelakukan suatu sistem, tetapi juga secara drastis
mengurangi
kerumitan
perhitungan
matematika yang dibutuhkan dalam menganalisa
suatu sistem.
|
 27
Transformasi
Laplace
memiliki
peran
penting
dalam aplikasi-aplikasi
dalam
bidang fisika, optik, rekayasa listrik, rekayasa kendali, pemrosesan sinyal dan teori
kemungkinan.
Nama
transformasi
ini
diberikan
untuk
menghormati
seorang
ahli
matematika
dan astronomi, Pierre-Simon
Laplace, yang
menggunakan teknik transformasi ini pada
hasil karyanya dalam teori kemungkinan. Sebenarnya teknik ini ditemukan sebelumnya
oleh Leonhard Euler, seorang ahli matematika prolific Swiss abad kedelapanbelas.
Transformasi Laplace dari suatu fungsi f(t), yang terdefinisi untuk semua nilai t
riil dengan t = 0, adalah fungsi F(s), yang didefinisikan sebagai:
F
(s)
=
L{ f (t )}
=
?
8
e
-
st
f
(t )dt
Transformasi Laplace ini memiliki sejumlah sifat yang membuatnya amat
berguna
bagi
analisa
sistem dinamik
linier.
Keunggulan
utama
dari
cara
ini
adalah
mengubah
proses diferensiasi
menjadi
perkalian dan integrasi menjadi pembagian,
dengan adanya s (Hal ini mirip dengan fungsi logaritma
yang mengubah operasi
perkalian dan pembagian menjadi penjumlahan dan pengurangan). Perubahan
persamaan integral dan diferensial menjadi bentuk polinomial menyederhanakan proses
penyelesaian.
Beberapa fungsi dasar Trasformasi Laplace:
•
L{1}
=
f
(s)
=
1
s
•
L{t
n
}
=
•
L{e
at
}
=
f
(s)
=
f
(s)
=
n!
s
n 1
+1
1
s
-
a
|
 28
•
L{cos
?
t}
=
•
L{sin
?t}
=
f
(s) =
f
(s) =
s
s
2
+
?
2
?
s
2
+
?
2
•
L{cosh at} =
•
L{sinh at} =
f
(s) =
f
(s) =
s
s
2
-
a
2
a
s
2
-
a
2
2.5
Simulasi
Simulasi
adalah
sesuatu
bentuk
imitasi
yang
menyerupai aslinya
Pada proses kerja,
simulasi mempresentasikan
karakteristik dan bentuk fisik seperti pada aslinya. Dengan menggunakan simulasi maka
kita dapat memperoleh berbagai kelebihan, seperti:
•
Efisiensi biaya.
Didalam
simulasi sangatlah dipertimbangkan, karena sebagian
inti dari simulasi adalah untuk memperoleh efisiensi pengeluaran biaya.
•
Menghemat waktu. Simulasi dapat dengan signifikan menghemat waktu
untuk
memproses suatu pemecahan masalah dengan akurat.
•
Tidak mempengaruhi keadaan sistem aslinya sehingga dapat dilakukan metode
Trial and Error.
•
Mudah
untuk diperbanyak. Dengan
menggunakan bantuan komputer, simulasi
sangatlah mudah untuk dilakukan perubahan baik penambahan maupun
pengurangan.
|
 29
Adapun kekurangan yang terdapat pada simulasi, sebagai berikut:
•
Perlu belajar terlebih dahulu untuk dapat melakukan suatu proses simulasi
•
Diperlukan data yang cukup akurat untuk dapat memperoleh hasil yang akurat.
•
Diperlukan ketelitian yang tinggi sehingga tidak terjadi kesalahan dalam
menurunkan persamaan.
2.6
Alat Bantu Perancangan
2.6.1
State Transition Diagram (STD)
State
Transition
Diagram
merupakan salah
satu
cara
untuk
menggambarkan
jalannya suatu proses. STD ini terdiri dari input/kondisi, state proses, output/aksi
yang
terjadi dan perubahan statenya. Komponen dasar State Transition Diagram dapat dilihat
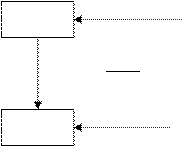
pada gambar 2.9 dibawah ini.
State X
State Sekarang
Input
Output
State Y
State Selanjutnya
Gambar 2.19 Komponen dasar State Transition Diagram
State
menunjukkan satu
atau
lebih
kegiatan
atau
keadaan
atau
atribut
yang
menjelaskan bagian tertentu dari proses.
Anak
panah berarah
menunjukkan perubahan
state
yang
disebabkan oleh
input
tertentu
(state
X
ke
state
Y).
Input
atau
kondisi
merupakan suatu kejadian pada
lingkungan eksternal
yang dapat dideteksi oleh sistem
misal sinyal, interupsi atau data. Hal ini menyebabkan perubahan dari satu state ke state
|
|
30
yang
lainnya atau dari
satu aktivitas ke aktivitas lainnya. Output
atau aksi
merupakan
hal
yang
dilakukan
oleh
sistem
jika
terjadi
perubahan state
atau
merupakan
reaksi
terhadap
kondisi.
Aksi
dapat
menghasilkan output,
tampilan
pesanan
pada
layar,
kalkulasi atau kegiatan lainnya.
2.6.2 Pseudocode
Pseudocode berasal dari kata pseudo dan
code, adalah deskripsi
yang informal
dan
padat
dari
sebuah
algoritma
pemrograman
komputer
yang
menggunakan aturan
struktural dari bahasa pemrograman, tetapi menghilangkan detail-detail seperti subrutin,
deklarasi variabel
atau
syntax
bahasa
pemrograman tertentu
Bahasa pemrograman dalam hal ini digabungkan dengan penjelasan detail dalam
bahasa natural agar
terlihat
lebih
umum. Pseudocode bukanlah skeleton
program
atau
dummy code yang
masih dapat di-compile
tanpa error. Flowchart dapat juga dianggap
sebagai salah satu bentuk pseudocode.
2.7 Teori Perancangan Program
2.7.1 Waterfall Method
Metode Waterfall adalah sebuah model perancangan program secara sekuensial,
dimana proses perancangan tersebut
mengalir secara teratur kebawah sehingga terlihat
seperti air terjun (sumber, http://en.wikipedia.org/wiki/waterfall_method, 2007).
Proses
ini
melalui
fase-fase seperti,
analisis
kebutuhan, desain,
implementasi,
pengetesan atau validasi, integrasi dan perawatan. Asal kata waterfall sering dikutip dari
|
 31
artikel yang dipublikasikan pada tahun 1970 oleh W. W. Royce, ironisnya, Royce sendiri
tidak
menggunakan kata
tersebut, sebaliknya
memakai kata
pendekatan
iteratif
dalam
perancangan software.
Pada awalnya Royce
menggambarkan metode
Waterfall adalah
contoh
metode
yang
beresiko
dan
rawan terhadap
kegagalan. Tetapi
walapun begitu,
penggunaan metode ini tetap populer di dalam perancangan program.
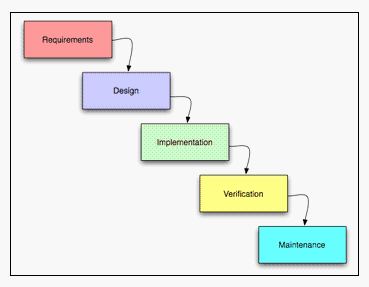
Gambar 2.20 Metode Waterfall
Seperti yang terlihat pada Gambar (2.20), proses perancangan program bergerak
dari atas ke bawah seperti air terjun. Di dalam model Waterfall yang dinyatakan oleh
Royce, fase-fasenya adalah sebagai berikut :
•
Spesifikasi Kebutuhan
•
Desain
•
Konstruksi atau Implementasi
•
Pengetesan dan Debugging (verifikasi)
•
Perawatan
|