|
BAB 2
LANDASAN TEORI
2.1 Software Defined Radio
2.1.1
Pengertian SDR
Software Defined Radio (SDR)
adalah sebuah sistem
komunikasi radio
yang
dapat
disesuaikan
pada
frekuensi apapun
dan
menerima
modulasi
apapun
melalui sebuah spektrum frekuensi yang besar.
Pada umumnya SDR melakukan beberapa signal processing sebagian besar
menggunakan software yang berjalan pada Personal Computer (PC) biasa yang
dilengkapi dengan soundcard, atau komponen elektronik digital buatan sendiri.
Tujuan dari rancangan
tersebut adalah agar membuat SDR dapat
menerima dan
mengirim bentuk
lain
dari protokol radio
hanya
dengan
menjalankan software
yang berbeda.
SDR mempunyai peran yang penting untuk radio militer dan service-
service pada ponsel, karena baik radio militer maupun service pada ponsel harus
memungkinan untuk disetel pada berbagai jenis protokol yang berubah-ubah.
2.1.2
Cara Kerja SDR
Pada
SDR,
sinyal analog diubah
menjadi
sinyal digital dengan
menggunakan
komponen Analog-to-Digital
Converter (ADC),
yang
kemudian
akan
sinyal
tersebut
akan
diolah
agar
dapat
masuk
kedalam tahap pemrosesan
software pada SDR.
|
|
9
Sinyal
analog
yang
diterima oleh sebuah
SDR, dapat
diolah secara
langsung
apabila
frekuensi
sinyal
tersebut dibawah 40MHz. Tetapi untuk
frekuensi
diatas
40MHz
konversi
langsung akan mengakibatkan pelambatan.
Sehingga untuk menangani frekuensi diatas 40MHz, digunakan arsitektur
superheterodyne
RF
front-end. Arsitektur ini akan
mengolah
frekuensi
tinggi
menjadi
frekuensi
menengah
(Intermediate
Frequency /
IF)
terlebih
dahulu
sebelum dikonversi.
SDR harus mengolah modulasi dengan jarak yang luas, sehingga dapat
disesuaikan
dengan
bermacam-macam protokol.
Oleh
karena
itu,
pengaturan
secara adaptif sangat penting. Pengaturan adaptif dapat diimplementasikan pada
hardware atau software.
2.2 Field Programmable Gate Array
2.2.1
Pengertian FPGA
FPGA adalah komponen semikonduktor
yang
mengandung
komponen
programmable-logic yang disebut dengan Logic Blocks, dan komponen-
komponen programmable interconnects. Logic Blocks
dapat deprogram untuk
melaksanakan fungsi-fungsi aritmatika dasar seperti AND, dan XOR, ataupun
fungsi kombinasi
lainnya yang
lebih kompleks
misalnya
membaca sandi atapun
fungsi-fungsi matematika sederhana.
Pada sebagian besar FPGA, Logic Blocks juga mengandung unsur memori,
yang
mungkin
merupakan
flip-flop
sederhana
atau block memory
yang
lebih
lengkap.
|
 10
Komponen-komponen
programmable
interconnects
pada
FPGA
memungkinkan
Logic
Blocks
untuk saling.
Komponen-komponen Logic
Block
dan Interconnect
dapat diprogram oleh pengguna setelah FPGA diproduksi,
untuk
mengimplementasikan
beberapa
fungsi
logika,
sesuai
dengan
namanya
Field-Programmable.
2.2.2
Aplikasi FPGA
Aplikasi-aplikasi pada
FPGA termasuk
Digital
Signal
Processor
(DSP),
Software
Defined Radio
(SDR),
prototype
ASIC,
Medical Imaging,
Computer
Vision,
pengenalan
suara,
kriptografi, biometrics dan
computer
hardware
emulation ataupun perkembangan pada hal-hal lain.
2.2.3
Arsitektur FPGA
Arsitektur FPGA tersusun dari kumpulan Configurable Logic Blocks (CLB)
dan saluran routing yang memiliki jumlah kabel yang sama. Sebuah logic blocks
FPGA klasik terdiri dari empat atau enam buah input Look-Up Table (LUT) dan
sebuah flip-flop, seperti yang ditunjukkan dibawah.
.
Gambar 2.1 Logic Block Pada Umumnya
|
 11
Input pada logic blocks terdiri dari empat sinyal LUT dan sinyal
waktu.
Output pada
logic
blocks
hanya
terdiri
dari
satu
sinyal
LUT. Sebagai
contoh
arsitektur ini, lokasi dari pin logic blocks FPGA ditunjukkan sebagai berikut.
Gambar 2.2 Input Output Pad
Setiap pin input dapat diakses melalui satu sisi dari logic blocks, sementara
pin output
dapat
dihubungkan
dengan
kabel
routing
dalam
kedua
saluran
ke
kanan dan saluran ke bawah logic blocks.
Gambar 2.3 Topologi Kotak Switch
|
|
12
Pin output pada logic blocks dan I/O Pads dapat saling berhubungan untuk
membentuk kotak switch. Setiap terjadi perpotongan antara saluran mendatar dan
menurun, dimana didalamnya terdapat sebuah kotak switch, terdapat tiga switch
yang
dapat
diprogram yang
memungkinkan
untuk
menghubungkan
tiga
kabel
lainnya dalam saluran yang bersebelahan.
2.3 Serpent Advanced Encryption Standard
2.3.1
Algoritma
2.3.1.1 Pengertian Algoritma
Dalam
ilmu Matematika
dan
ilmu Komputer,
algoritma
adalah
kumpulan
instruksi yang terdeskripsi dengan jelas isi dan urutan pengerjaannya, yang
bertujuan untuk menyelesakan suatu tugas, dengan mendefenisikan kondisi awal
dan akan berakhir pada kondisi akhir yang telah ditentukan pula. Konsep dari
algoritma, secara informal dapat digambarkan sebagai sebuah resep.
2.3.1.2 Sejarah Algoritma
Konsep
algoritma
berawal dari penggabungan
urutan-urutan
prosedur
untuk
menyelesaikan
masalah matematika,
seperti
mencari
Greater
Common
Divisor
(Faktor
Persekutuan
Terbesar) dari
dua
buah bilangan.
Sebagian
besar
algoritma
dapat
diimplementasikan
pada bahasa
pemrograman
atau
setidaknya
dapat disimulasikan secara teoritis oleh program komputer.
|
 13
2.3.1.3 Notasi Big O
Dalam teori
perhitungan
kompleksitas,
notasi
Big
O
digunakan
untuk
menggambarkan bagaimana ukuran data input
mempengaruhi kecepatan dan
penggunaan memori. Notasi Big O juga disebut sebagai notasi Bachman-Landau,
atau
notasi
asimtotis.
Notasi
Big
O juga
digunakan
pada
matematika
untuk
menghasilkan estimasi yang mirip.
Berikut adalah contoh dari notasi Big O:
Tabel 2.1 Notasi Big O
Notasi
Nama
Contoh
?1
Konstan
Menentukan genap-ganjil suatu angka
???
??
Ackermann invers
?log?
?
Logaritmik beriterasi
Hopcroft and Ullman search dengan
menggunakan disjoint set
?log
?
Logaritmik
Binary search
??log
?
Polilogaritmik
Tes Primalitas AKS
?
?
Akar
Pencarian pada KD-Tree
?
?
Linear
Sequencial search
?
log
?
Linearitmik, Loglinear
Heapsort, Fast Fourier Transform
?
?
?
Kuardratik
Insertion Sort
?
?
Polinomial
Algoritma Floyd-Warshall
?
?
?
Eksponensial
Travelling Sales Problem
?
!?
Faktorial
Brute Force
?
?
?
Eksponensial n
?
1
?
?
?
Eksponensial ganda
Notasi
Big O sangat berguna dalam analisa algoritma dalam hal efisiensi.
Contohnya, waktu atau jumlah langkah yang dibutuhkan untuk menyelesaikan
suatu persoalan dengan ukuran data n dapat dihitung sebagai berikut
?
?
4
?
2
2
|
|
14
2.3.1.4 Pseudocode
Pseudocode adalah
gambaran
singkat dan
informal dari
sebuah
algoritma
pemrograman komputer yang menggunakan bentuk pemrograman struktural.
Pseudocode
mengabaikan
detil-detil
seperti subrutin,
deklarasi
variabel
dan
sintaks yang spesifik dari
suatu bahasa pemrograman. Pseudocode dapat ditulis
dalam bahasa-bahasa
pemrograman
dengan
sintaks
yang
disederhanakan,
misalnya bahasa pemrograman PASCAL, C atau BASIC.
Tujuan penggunaan pseudocode
adalah
untuk
menyederhanakan
bahasa
pemrograman menjadi bahasa manusia,
sehingga memudahkan manusia
untuk
membaca alur dari suatu algoritma.
Berikut
adalah
contoh
dari
sebuah pseudocode
untuk
pengenalan
angka
genap atau angka ganjil:
JIKA Angka = 0 MAKA Tulis “NOL”
SELAIN ITU JIKA Angka MODULUS 2 = 0 MAKA Tulis “Genap”
SELAIN ITU Tulis “Ganjil”
2.3.2
Kriptografi
2.3.2.1 Pengertian Kriptografi
Dalam konteks
Matematika
dan
ilmu
Komputer, kriptografi
adalah
ilmu
yang mempelajari tentang kerahasiaan data. Pada zaman modern ini, kriptografi
adalah
salah
satu
cabang
dari
Information
Theory
(mata
pelajaran Applied
Mathematics), yang bertujuan untuk membuat data menjadi rahasia dan
memastikan autentikasi sebelum akses data tersebut.
|
|
15
Kriptografi
mencakup
ilmu
matematika
dari berbagai cabang
seperti
Aljabar Linear, Aljabar Modern maupun Analisis Real. Kriptografi mengandung
istilah-istilah penting yang mendasar sebagai berikut:
•
Plaintext (Cleartext) merupakan data yang dapat dimengerti.
•
Ciphertext, merupakan data yang tidak dapat dimengerti.
•
Encryption (Encoding),
merupakan proses
penyamaran
data,
dari
plaintext
menjadi ciphertext.
•
Decryption (Decoding),
merupakan proses
untuk mengembalikan ciphertext
menjadi plaintext agar dapat dimengerti.
•
Key,
merupakan angka atau
metode
yang digunakan dalam proses enkripsi
dan dekripsi.
2.3.2.2 Sejarah Kriptografi
Sejarah kriptografi dimulai ribuan tahun yang lalu. Sampai beberapa
dekade terakhir ini, sejarah kriptografi merupakan sebuah cerita yang disebut
Classic Cryptography, yang merupakan metode kriptografi yang masih
menggunakan pensil dan kertas atau mungkin bantuan mekanik sederhana.
Pada zaman romawi kuno, Julius Caesar menggunakan kriptografi untuk
mengirim pesan rahasia
yang
masih
menggunakan
algoritma
kriptografi
klasik
yaitu
algoritma
penggeseran
atau
disebut
juga
Shift
Cipher atau Caesar
Cryptography.
Pada abad ke-20, ditemukan mesin elektronik untuk kriptografi yang lebih
kompleks, seperti Enigma
Rotor Machine,
dilengkapi
dengan
metode enkripsi
|
|
16
yang
lebih
cerdas
dan
berarti.
Kemudian
menjadi
awal
dari
enkripsi-enkripsi
baru yang memiliki kompleksitas yang lebih besar.
2.3.2.3 Algoritma Kriptografi
Algoritma
kriptografi
adalah
metode
yang
digunakan
dalam kriptografi
untuk mengubah data berupa plaintext menjadi ciphertext sehingga dapat
membuat
data
yang
ingin
dikirimkan
menjadi rahasia dan hanya dapat diakses
oleh user-user yang mengetahui key untuk mendekripsi ciphertext tersebut.
2.3.2.4 Pembagian Algoritma Kriptografi
Algoritma kriptografi sering juga disebut sebagai kriptosistem, dapat dibagi
dalam tiga karakteristik:
•
Berdasarkan jenis operasi yang digunakan
Berdasarkan
jenis
operasi
yang
digunakan
untuk
mengubah plaintext
menjadi ciphertext, algoritma kriptografi dibagi menjadi dua jenis umum
antara
lain substitution cipher
dan
transposition
cipher.
Semua
algoritma
kriptografi selalu berlandaskan pada dua prinsip umum tersebut, proses
substitusi dan proses transposisi. Tetapi ada juga algoritma kriptografi yang
menggabungkan kedua konsep tersebut sekaligus.
Substitution cipher
adalah
algoritma
kriptografi
yang
bertujuan
untuk
mengubah plaintext tertentu menjadi ciphertext tertentu. Inti dari substitution
cipher adalah mengubah isi plaintext.
|
|
17
Transposition cipher adalah algoritma kriptografi yang bertujuan untuk
menggeser posisi-posisi plaintext menjadi acak. Inti dari transposition cipher
adalah mengubah posisi plaintext.
•
Berdasarkan jumlah key yang digunakan
Berdasarkan jumlah
key
yang
digunakan,
algoritma
kriptografi
dibagi
menjadi symmetric cryptography dan asymmetric cryptography.
Symmetric cryptography adalah algoritma kriptografi yang hanya
menggunakan satu jenis key, dimana untuk proses enkripsi dan dekripsi pada
algoritma kriptografi tersebut akan menggunakan key yang sama. Oleh
karena itu pada symmetric
cryptography key tersebut
bersifat rahasia yang
hanya boleh diketahui oleh orang yang membuat pesan dan orang yang akan
mendapatkan pesan.
Asymmetric
cryptography adalah algoritma kriptografi yang
menggunakan dua jenis key, yaitu public key dan private key. Public key pada
asymmetric cryptography
adalah
key
pribadi
yang
dibagikan
kepada
semua
orang sehingga keberadaan public key tidak bersifat rahasia. Private key pada
asymmetric
cryptography
adalah key
pribadi
yang
hanya
diketahui
oleh
pemilik key sendiri.
•
Berdasarkan cara plaintext diproses
Berdasarkan cara plaintext diproses, algoritma kriptografi dibagi
menjadi stream cipher dan block cipher.
|
 18
Stream cipher
adalah algoritma kriptografi
yang
memproses plaintext
dari awal hingga akhir sekaligus tanpa
mempedulikan panjang plaintext itu
sendiri.
Block
cipher adalah algoritma kriptografi
yang
hanya
memproses
plaintext dengan panjang tertentu.
2.3.3
Symmetric Cryptography
2.3.3.1
Pengertian Symmetric Cryptography
Symmetric
cryptography
atau
disebut
juga
single
key
Encryption
merupakan
asal
mula
dari asymmetric cryptography. Symmetric
cryptography
menggunakan key yang sama dalam proses enkripsi dan dekripsi sehingga dapat
digambarkan bahwa proses dekripsi adalah kebalikan dari proses enkripsi dengan
menggunakan key yang sama.
Symmetric Cryptography
Gambar 2.4 Symmetric Cryptography
|
 19
Symmetric cryptography
merupakan
algoritma
kriptografi
yang
lebih
sederhana dibandingkan dengan asymmetric cryptography, sehingga ada banyak
symmetric cryptography
yang
digunakan
saat
ini.
Contoh-contoh
symmetric
cryptography antara lain:
Tabel 2.2 Contoh-Contoh Symmetric Cryptography
Algoritma
Block
Proses
Key
Rumus
Shift Cipher
Stream
Cipher
Monoalphabetic
Substitution
Key: Integer
?
?
= (
?
+ key)
mod 26
Affine Cipher
Stream
Cipher
Monoalphabetic
Substitution
Key1:Integer
Key2:Integer
?
?
=(key1.
?
+key2)
mod 26
Vigenere
Block
Cipher
Polyalphabetic
Key: String
?
?
= (
?
+
?
?
)
mod 26
Transposition
Stream
Cipher
Transposition
Key: Integer
?
?
=
?
?/???
?
?
?
Palindrome
Stream
Transposition
Tidak ada
?
?
=
??????
?
?
?
DES
Block
Kompleks
Key: 56 bit
Kompleks
TDES
Block
Cipher
Kompleks
Key1: 56 bit
Key2: 56 bit
Key3: 56 bit
Implementasi dari
DES tiga kali
dengan tiga key
AES
Block
Cipher
Kompleks
Key: 128 bit
–
256 bit
Kompleks
2.3.3.2 Advanced Encryption Standard (AES)
Advanced
Encryption
Standard (AES)
atau
dikenal
juga
dengan
sebutan
Rijndael, adalah block cipher yang dianggap sebagai standard enkripsi oleh
pemerintah Amerika Serikat.
AES tidak sepenuhnya merupakan Rijndael, karena AES hanya mendukung
ukuran block 128 bit dan ukuran key 128, 192 dan 256 bit, sedangkan
Rijndael
dapat menggunakan ukuran key dan block kelipatan 32 bit, dimulai dari 128 bit
hingga 256 bit.
|
 20
Secara umum AES terdiri dari 4 langkah:
1.
SubBytes,
merupakan
langkah substitusi non-linear dimana setiap
byte
diganti sesuai dengan tabel tertentu. Pada langkah subbytes, setiap byte pada
array akan
diubah dengan menggunakan S-Box Rijndael. S-Box
yang
digunakan,
diturunkan
dari invers multiplikatif terhadap
GF (2
8
),
yang
diketahui mempunyai sifat non-linear.
Gambar 2.5 Langkah SubBytes Pada AES
2.
ShiftRows, merupakan langkah transposisi bytet dimana masing-masing
baris byte dirotasi dengan jumlah pergeseran tertentu. Jumlah pergeseran
baris adalah 0, 1, 2 dan 3 byte untuk masing-masing baris pertama, kedua
ketiga dan keempat.
Gambar 2.6 Langkah ShiftRows Pada AES
|
 21
3.
MixColumns, merupakan operasi pencampuran empat byte pada masing-
masing kolom
untuk
menghasilkan
empat
byte
output. Masing-masing
kolom dibuat menjadi polinom GF (2
8
)
dan kemudian dikalikan dengan
modulo
dengan polinomial konstan
.
Gambar 2.7 Langkah MixColumns Pada AES
4.
AddRoundKey, mengoperasikan byte-byte
input
dengan
round
key.
Round
key
didapat
melalui
algoritma
key
schedule.
Proses
kombinasi
dilakukan dengan menggunakan operasi
Gambar 2.8 Langkah AddRoundKey Pada AES
|
|
22
2.3.3.3 Peranan Serpent AES Pada Symmetric Cryptography
Serpent AES adalah symmetric cryptography yang memproses ukuran block
128 bit dengan
ukuran key 128 bit. Serpent
merupakan
finalis dari
lomba AES
yang dimenangkan oleh Rijndael. Serpent mempunyai kompleksitas yang lebih
rumit
sehingga Serpent lebih
lambat
dibandingkan
dengan Rijndael. Meskipun
demikian
keamanan Serpent lebih
kompleks
dibandingkan
dengan
kriptografi
Rijndael sendiri.
Keamanan Serpent telah terbukti, hingga hanya
dapat
diserang
dengan
pencarian brute-force. Berdasarkan analisis yang ada, untuk mendapatkan sebuah
key
berukuran
256
bit,
sebuah
supercomputer membutuhkan
waktu
256
bit.
Hingga
saat
ini algoritma Serpent belum dipatenkan
sebagai sebuah AES
sehingga semua orang
dapat
menggunakan Serpent
untuk
mengamankan
data-
data
mereka
ataupun
mempelajari Serpent
untuk
mengembangkan
ilmu
kriptografi.
2.3.3.4 Substitution Permutation Network (SP-Network)
Pada kriptografi, SP-Network adalah sekumpulan operasi matematika yang
digunakan dalam algoritma kriptografi block cipher seperti AES. SP-Network ini
terdiri dari S-Box dan P-Box yang mengubah block input menjadi block output.
Operasi-operasi pada SP-Network merupakan operasi yang dapat dilakukan
secara langsung oleh hardware, seperti operasi AND dan XOR.
S-Box mengubah bit-bit input menjadi bit-bit output. Pada S-Box yang
ideal, perubahan satu bit input dapat berakibat perubahan untuk setengah dari bit-
bit output, dan masing-masing bit output bergantung pada setiap bit input.
|
 23
Pada kriptografi, S-Box adalah komponen dasar dari symmetric
cryptography. Pada block cipher, S-Box digunakan untuk membuat hubungan
antara plaintext dan ciphertext menjadi tidak jelas. S-Box biasanya dibuat dengan
teliti sehingga dapat bertahan dari cryptanalysis.
Pada umumnya, S-Box menggunakan
beberapa input m,
kemudian
mengubahnya menjadi beberapa bit output n (S-Box
). S-Box
tersebut diimplementasikan
sebagai
suatu
tabel.
Tabel
S-Box
pada
kriptografi
biasanya telah
ditentukan,
misalnya
S-Box
Data
Encryption
Standard
(DES),
tetapi
pada beberapa
algoritma
kriptografi,
S-Box
dibuat
secara
dinamis
tergantung pada key, misalnya kriptografi Blowfish atau kriptografi Twofish.
Berikut adalah contoh S-Box dari DES (S5):
Tabel 2.3 Contoh S-Box Pada DES (S5)
S
5
Bit-bit dalam
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
Bit-bit
luar
00
0010
1100
0100
0001
0111
1100
1011
0110
1000
0101
0011
1111
1101
0000
1110
1001
01
1110
1011
0010
1100
0100
0111
1101
0001
0101
0000
1111
1100
0011
1001
1000
0110
10
0100
0010
0001
1011
1100
1101
0111
1000
1111
1001
1100
0101
0110
0011
0000
1110
11
1011
1000
1100
0111
0001
1110
0010
1101
0110
1111
0000
1001
1100
0100
0101
0011
Dengan diketahui 6 bit input 011011 maka akan didapat 4 bit output 1001.
Bit-bit
input
dibagi
menjadi
2
bit
luar
dan
4
bit
dalam (0-1101-1),
sehingga
menghasilkan 01 dan 1101. Output didapat dari hasil kombinasi tabel antara 01
dan 1101, yaitu 1001.
|
 24
2.3.3.5 Key Schedule
Pada
kriptografi, key
schedule
disebut
juga
dengan
product
cipher,
merupakan bagian dalam
symmetric
cryptography
yang
bertujuan
untuk
menghasilkan subkey-subkey dengan
mengoperasikan key
pada tahap-tahap
kriptografi tertentu. Tujuan utama dari pembentukan subkey-subkey adalah untuk
mempersulit kriptoanalis untuk mendapatkan key.
Gambar 2.9 Key Schedule Pada DES
Beberapa algoritma kriptografi
mempunyai key schedule
yang sederhana.
Misalnya key schedule pada block cipher TEA, hanya
memisahkan key 128 bit
menjadi empat buah subkey berukuran 32 bit dan menggunakan masing-masing
subkey tersebut secara bergantian pada masing-masing tahap.
|
|
25
Salah satu key schedule yang banyak digunakan adalah key schedule pada
DES. Key berukuran 56 bit pada DES dipisah menjadi dua bagian berukuran 28
bit.
Masing-masing
bagian
dioperasikan
secara
terpisah,
yaitu dengan
merotasikan satu atau dua bit, kemudian 48 subkey dipilih dengan menggunakan
Permutation Choice 2 (PC2). 48 subkey tersebut dihasilkan oleh masing-masing
24 bit dari 28 bit bagian kiri dan kanan.
Banyak
algoritma
modern
menggunakan key
schedule yang
lebih
rumit,
seperti
penggunaan one-way
function
untuk
memperluas
sebuah
key menjadi
subkey. Algoritma kriptografi Rijndael dan Blowfish kadang-kadang
mengawali
key schedule dengan random angka.
2.3.4
Asymmetric Cryptography
Asymmetric cryptography atau sering disebut sebagai public key encryption
menggunakan dua buah key yang berbeda yaitu public key dan private key.
Public key merupakan key tanda dari user yang diketahui oleh semua orang yang
kemudian akan digunakan
untuk proses enkripsi, sedangkan private key bersifat
rahasia dan merupakan key yang digunakan untuk proses dekripsi.
Pada buku “Golden Bough” karangan
Sir James
George
Frazer,
terdapat
tulisan “Every Egyptians receive two names, which were known respectively as
the true name and the good name, or the great name and the little name; and
while the good name or the little name was made public, the true name or the
great name appears to have been carefully concealed”. Tulisan tersebut adalah
asal mula ilustrasi dari asymmetric cryptography.
|
 26
Pada
asymmetric cryptography,
pengirim mengenkripsi
plaintext
dengan
menyertakan public key
penerima,
dan
apabila
penerima
sudah
menerima
ciphertext, proses dekripsi dilakukan dengan
menginput ciphertext yang disertai
private key penerima,
yang
hanya
diketahui
oleh
penerima.
Dengan
demikian
data tersebut aman.
?
???,
???????
?
?
?
???,
????????
?
?
Asymmetric Cryptography
Gambar 2.10 Asymmetric Cryptography
RSA
adalah sebuah
algoritma kriptografi
untuk
asymmetric cryptography
atau disebut
juga public key
encryption.
RSA
merupakan algoritma
kriptografi
pertama yang menggunakan konsep message-signing seiringan dengan proses
enkripsi, yang merupakan salah satu dari kelebihan besar asymmetric
cryptography. RSA banyak digunakan dalam protokol e-commerce, dan
dipercaya bahwa aman dengan key yang panjang dan menggunakan
implementasi terbaru.
|
|
27
2.3.5
Serpent Advanced Encryption Standard (Serpent AES)
Serpent adalah algoritma kriptografi yang bersifat block cipher symmetric
cryptography
yang
merupakan
AES
finalis
pada
kontes AES,
dimana
kontes
tersebut dimenangkan oleh Rijndael AES. Serpent ditemukan oleh Ross
Anderson, Eli Biham dan Lars Knudsen.
Seperti
halnya
AES yang
lain,
Serpent
mempunyai
ukuran
block
sebesar
128 bit dan dapat mendukung key dengan
ukuran 128 bit, 192 bit ataupun 256
bit.
Serpent
mengimplementasikan
kriptosistem 32
tahap
Substitution-
Permutation Network
(SP
Network),
dimana
tahap-tahap
tersebut
mengoperasikan empat buah variable dengan ukuran 32 bit. Masing-masing
tahap
menggunakan
delapan
buah
4
bit
x
4
bit S-Box
secara
paralel. Serpent
dirancang sehingga semua operasi dapat dijalankan secara paralel, menggunakan
32
buah 1 bitslice. Hal
ini
memaksimalkan
pararelisme,
tetapi juga
memungkinkan adanya kriptoanalisis yang luas.
2.3.5.1 Cara Kerja Serpent AES
Penjelasan Cara Kerja Serpent AES
Serpent
dapat
digambarkan
sebagai Substitution-Permutation
Network
sebanyak 32 tahap, yang mengoperasikan 4 buah variabel 32 bit, sehingga
ukuran block plaintext adalah 128 bit. Nilai-nilai yang ada di dalam algoritma ini
direpresentasikan
sebagai
aliran
bit. Serpent mengenkripsi
plaintext dengan
ukuran 128 bit menjadi ciphertext dengan ukuran 128 bit dalam 32 tahap dengan
bantuan 33 buah key berukuran
128
bit,
192 bit ataupun 256 bit.
Key pendek
dibawah 256 bit akan diperpanjang menjadi 256 bit dengan cara menambahkan
|
 28
bit 1 pada akhir MSB dan menambahkan bit 0 pada sisanya sehingga
lengkap
menjadi 256 bit.
Algoritma Serpent sendiri terdiri dari:
•
Permutasi awal
•
32 tahap Substitution Permutation Network, terdiri dari operasi pencampuran
key, melalui S-Box dan transformasi linear kecuali pada tahap terakhir. Pada
tahap terakhir, transformasi linear diganti menjadi operasi pencampuran key.
•
Permutasi akhir
Gambar 2.11 Substitution Permutation Network Pada Serpent AES
|
 29
Permutasi awal dan permutasi akhir tidak mempunyai guna kriptografi, dan
hanya berguna untuk menyederhanakan dan mengoptimalisasi algoritma
kriptografi tersebut dan untuk meningkatkan efisiensi perhitungan.
Notasi-notasi yang kita gunakan adalah:
• Plaintext P disebut juga ?
?
, yang merupakan inputan untuk tahap pertama.
• Tahap terdiri dari 32 tahap, dinotasi dengan tahap 0 hingga tahap 31.
•
B,
merupakan input dan output dari
masing-masing
tahap. ?
?
, merupakan
input
untuk
tahap
0
adalah
?
?
dan
hasilnya
adalah
?
?
.
?
?
akan
digunakan sebagai
input pada tahap kedua untuk menghasilkan
?
?
dan
seterusnya.
• Ciphertext C.
• Permutasi awal IP.
• Permutasi akhir FP.
• SBox yang terdiri dari 8 bagian yaitu
?
,
?
,
?
,
?
,
?
,
?
,
?
dan
?
.
Untuk
masing-masing
tahap
?
{i=0,
1,
2,
…,
31}
hanya
menggunakan sebaris
S-Box.
Contohnya,
?
menggunakan
?
,
diduplikat
sebanyak 32 buah dan dijalankan bersamaan. Jadi duplikat
?
mengambil bit-bit
dari ?
?
?
?
sebagai masukan dan menghasilkan empat bit pertama dari bit
panjang yang akan
dikembalikan.
Duplikat
selanjutnya
dari
?
akan
dioperasikan
kembali
dengan ?
?
?
?
untuk mendapat 4 bit selanjutnya. Hal ini berlangsung untuk
?
,
?
dan seterusnya untuk menghasilkan ?
?
, ?
?
, ?
?
dan seterusnya hingga ?
??
.
Himpunan dari delapan S-Box tersebut digunakan empat kali. Jadi setelah
menggunakan
?
pada
tahap
7,
kita
kembali
menggunakan
?
pada tahap
8. Tahap 31 terakhir sedikit berbeda dari yang lain, dimana setelah
|
|
30
kita
|
 31
mengoperasikan
?
dengan hasil ?
??
?
?
??
,
tidak dijalankan transformasi linear
melainkan XOR dengan ?
??
. Hasil pada tahap
tersebut berupa ?
??
, akan
dipermutasikankembali dengan FP, untuk mendapatkan tulisan sandi.
Kesimpulannya, ketigapuluhdua tahap menggunakan delapan S-Box yang
berbeda, yang masing-masing menyocokkan empat bit input dan empat bit
output. Masing-masing S-Box digunakan sebanyak empat tahap, dan digunakan
secara
sekaligus.
Bentuk S-Box
akan
dibahas kemudian.
Algoritma
kriptografi
Serpent dapat digambarkan sebagai berikut:
?
?
?????
?
?
?
?
?
??
?
?
?
????
??
?
dimana
?
?
?
?
?
?
?
?? ?
?
?
?
??
Algoritma Serpent AES
S-Box pada Serpent adalah permutasi 4 bit dengan sifat-sifat sebagai
berikut:
•
Masing-masing
karakteristik
diferensial
memiliki
probabilitas paling
besar
1
4
,
dan sebuah perbedaan input 1 bit akan menghasilkan perbedaan
yang besar
•
Masing-masing karakteristik linear memiliki probabilitas diantara
1
2
1
4
,
dan
hubungan
linear
antara
sebuah
bit
input
dan
sebuah
bit
output
|
|
32
mempunyai probabilitas diantara
1
2
1
8
|
|
33
•
Deretan
non-linear
bit
output merupakan
fungsi dari
input
bit adalah
maksimum, bernilai 3.
S-Box
pada Serpent
dibuat
atas
sifat-sifat
tersebut,
dimana
ide
tersebut
berasal dari RC4. Serpent
menggunakan matrix yang
terdiri dari 32 array
yang
masing-masing memiliki 16 nilai. 32 baris pertama matrix tersebut merupakan 32
baris S-Box pada DES dan ditransformasi dengan menukar nilai-nilai pada array
ke-r tergantung pada nilai pada nilai-nilai di dalam array yang ke (r+1) dan pada
string
awal
yang
mewakili
key. Jika
pada array
hasil
terdapat sifat-sifat
diferensial atau linear, maka array tersebut akan disimpan sebagai barisan S-Box
pada Serpent. Hal ini diulang hingga dihasilkan delapan baris S-Box.
Misalkan, serpent[.] adalah array yang mengandung 4 bit terakhir pada
masing-masing karakter dari 16 karakter ASCII sebagai berikut
“sboxesforserpent”. Kemudian sbox[.][.] merupakan array dengan ukuran 32x16,
mengandung 32 baris dari 8 S-Box DES, dimana sbox[r][.]
melambangkan baris
ke-r. Fungsi
swapentries(., .) berguna
untuk
menukar
kedua
nilai
yang
dikirimkannya.
Maka
algoritma
untuk
mendapatkan S-Box pada
Serpent dapat
dijelaskan pada pseudocode sebagai berikut:
MODUL S-BoxGenerator
Index = 0
ULANG
Current_SBox = Index modulo 32
MULAI i BERNILAI 0 HINGGA 15 LAKUKAN
j = SBox[(Current_SBox + 1) modulo 32][i]
|
|
34
Tukar SBox[Current_SBox][i] Dengan SBox[Current_SBox][j]
AKHIR MULAI
JIKA SBox[Current_SBox][.] (Memenuhi Syarat) MAKA
Simpan SBOX[Current_SBOX][.]
AKHIR JIKA
Index = Index + 1
HINGGA 8 S-Box Selesai dibuat
AKHIR MODUL S-BoxGenerator
Pseudocode S-Box Generator Pada Serpent AES
Sumber: A Proposal for the AES (2007, Anderson-Biham-Knudsen)
Pada
Serpent-0,
pencipta
menggunakan S-Box DES
dengan
tujuan
untuk
meningkatkan kepercayaan publik bahwa
pencipta tidak membuat jebakan
apapun pada algoritma
ini. Jaminan yang
sama
terdapat pada Serpent-1 dengan
fakta bahwa S-Box tersebut dibuat dengan syarat sederhana yang jelas tersebut.
Algoritma kriptografi Serpent AES memiliki 32 tahap yang disebut dengan
Substitution-Permutation
Network.
Plaintext
akan
menjadi
data
awal
?
?
dari
data-data
?
?
hingga
?
??
yang
akan
digunakan
untuk
32
tahap, dimana pada
masing-masing tahap terdapat operasi-operasi sebagai berikut:
1. Key Mixing: pada masing-masing tahap, sebuah subkey berukuran 128 bit ?
?
di-XOR dengan data ?
?
.
2. S-Box: mengkombinasikan 128 bit input dengan key, yang terdiri dari empat
buah
variabel dengan masing-masing 32 bit. S-Box tersebut,
diimplementasikan
sebagai
operasi logical, kemudian
mengoperasikan
variabel-variabel tersebut, dan hasilnya adalah empat buah variabel kembali.
|
 35
CPU dimaksudkan untuk mengerjakan 32 S-Box sekaligus, menghasilkan
?
??
?
?
?
?
3. Transformasi linear:
variabel-variabel 32 bit tersebut, dicampurkan secara
linear dengan cara:
?
?
,
?
?
,
?
?
,
?
?
?
??
?
?
?
?
?
?
?
?
?
13
?
?
?
?
?
3
?
?
?
?
?
?
?
?
?
?
?
?
?
?
??
?
?
3?
?
?
?
?
?
1
?
?
?
?
?
7
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
7
?
?
?
?
?
?
5
?
?
?
?
?
22 ?
?
?
?
?
,
?
?
,
?
?
,
?
?
Dimana <<<
melambangkan rotasi dan <<
melambangkan pergeseran bit.
Pada
tahap
terakhir,
transformasi
linear
ini
diganti
dengan
proses
key mixing
tambahan, yaitu ?
??
:=
?
(?
??
?
??
) ?
??
. Harap diingat bahwa pada
masing-masing tahap ke-i, IP(?
?
) = ?
?
dan IP(?
?
) = ?
?
.
Alasan
utama
untuk
memilih
transformasi
linear adalah
untuk
memaksimalkan efek longsor pada S-Box. S-Box mempunyai
sifat dimana
|
|
36
perbedaan sebuah bit input akan
mengakibatkan perubahan dua buah bit output,
sebagai mana deret {0, 1, 3, 5, 7, 13, 22} modulo 32 tidak mempunyai bit yang
sama
kecuali bit
pertama,
ini
mengakibatkan
perubahan
sebuah
bit input
akan
mengubah jumlah perubahan bit yang sangat banyak setelah dua tahap atau lebih.
Efek tersebut adalah setiap bit plaintext mempengaruhi semua bit dari data
setelah tiga
tahap,
sebagaimana
juga
bit
pada key
pada
masing-masing
tahap.
Meskipun seseorang
mencari subkey tertentu dan bekerja secara terbalik, hal ini
tetap terjamin bahwa setiap bit pada key akan mempengaruhi setiap data setelah
enam tahap.
Alasan kedua adalah karena kesederhanaannya, dan dapat digunakan pada
prosesor modern dengan jumlah
pipeline stall yang minimum. Alasan ketiga
adalah bahwa hal ini telah dianalisis dan telah ditemukan hubungan antara sifat-
sifat linear dan diferensial. Hubungan ini menunjukkan bahwa pilihan ini sesuai
dengan kebutuhan kita.
Algoritma kriptografi kita membutuhkan 132 buah variabel berukuran 32
bit. Pada awalnya user
menyediakan key dengan
ukuran 256 bit, kemudian kita
memperluas key tersebut hingga
menjadi 33 buah subkey (?
?
,
?
?
,
?
?
,
…, ?
??
)
dengan ukuran 128 bit. Kita menuliskan key K sebagai delapan buah variabel 32
bit w-8,
w-7,
w-6, …,
w-1
dan
memperluas variabel-variabel tersebut menjadi
deretan
panjang key (dimana
kita
menyebutnya
prekey)
?
?
,
?
?
,
?
?
,
…, ?
??
dengan rekursi dari transformasi affine sebagai berikut:
?
?
?
?
??
?
??
?
??
?
??
? ?
?
?
??
|
 37
dimana PHI adalah bagian fractal dengan perbandingan emas
?
v5
1
?/2
atau 0x9E3779B9 pada hexadecimal. Polinom yang mendasari, ?
?
?
?
?
1
bersifat
primitif,
dimana
bersama
dengan
round key dilakukan
untuk
memastikan distribusi genap dari
key
pada tahap-tahap, dan untuk
menghilangkan key-key lemah dan key yang saling berhubungan.
Round key dikalkulasi dengan prekey dari S-Box. Kita menggunakan S-Box
untuk
mentransformasi
prekey
?
?
menjadi
?
dengan cara sebagai
berikut:
{?
?
, ?
?
, ?
?
, ?
?
} := ?
?
(?
?
, ?
?
, ?
?
, ?
?
)
{?
?
, ?
?
, ?
?
, ?
?
} := ?
?
(?
?
, ?
?
, ?
?
, ?
?
)
{?
?
, ?
, ?
??
, ?
??
} := ?
?
(?
?
, ?
, ?
??
,
?
??
)
{?
??
, ?
??
, ?
??
, ?
??
} := ?
?
(?
??
, ?
??
, ?
??
,
?
??
)
{?
??
, ?
??
, ?
??
, ?
} := ?
?
(?
??
, ?
??
, ?
??
,
?
?
)
…
{?
???
, ?
???
, ?
???
, ?
???
} := ?
?
(?
???
, ?
???
, ?
???
,
?
???
)
{?
???
, ?
, ?
???
, ?
???
} := ?
?
(?
???
, ?
??
, ?
???
,
?
???
)
Kemudian kita menomori angka-angka 32 bit kj sebagai subkey Ki sebagai
berikut:
?
?
:= {?
??
, ?
??
?
, ?
??
?
, ?
??
?
}
Saat kita mengimplementasikan algoritma ini, awalnya sesuai dengan yang
disebutkan diatas, daripada menggunakan operasi bitslice, sekarang kita
menggunakan permutasi awal daripada roundkey untuk dapat menempatkan
posisi bit yang benar pada kolom yang benar. ?
?
= IP(?
?
).
|
 38
2.3.5.2 Keamanan Serpent AES
Serpent AES merupakan salah satu algoritma kriptografi yang bersifat
sangat
ketat
dan
hanya
dapat
dibobol
oleh brute
force attack, yaitu dengan
mencoba
masing-masing
peluang yang
artinya
dengan
komputer
yang
dapat
melakukan
proses
brute
force
sebanyak 2
???
kali
per
detik, dibutuhkan lebih
kurang
2
detik
untuk
mendapatkan
sebuah
key
sebesar
128
bit, sedangkan
untuk
mendapatkan
key
sebesar
192
bit dibutuhkan 2
??
detik
dan dibutuhkan
2
???
detik untuk mendapatkan sebuah key sebesar 256 bit.
Serangan XSL, jika dilakukan dengan efektif, dapat
melemahkan Serpent.
Hanya saja, banyak kriptoanalis beranggapan bahwa implementasi serangan XSL
harus menghabiskan biaya yang lebih mahal dibandingkan dengan Serpent.
Perkiraan angka
untuk mendapatkan plaintext tertentu dengan segala jenis
attack adalah 2
???
dan dengan diperkuat S-Box yang kita dapat dari DES akan
mencapai 2
??
?
.
Dengan
keamanan
mencapai
2
???
,
dimaksudkan
bahwa
serangan
diferensial ataupun linear terhadap key apapun akan menggunakan text sebanyak
itu,
jika
diasumsikan
bahwa
itu
mungkin (karena
pada
kenyataannya
tidak).
Keamanan Serpent dapat digambarkan sebagai berikut:
Tabel 2.4 Keamanan Serpent
Sumber: A Proposal for the AES (2007, Anderson-Biham-Knudsen)
Ukuran
Block
Ukuran Key
Beban
Pencarian
Tipe
Serangan
Text
128
128
2
?
Brute Force
1
128
192
2
?
??
Brute Force
2
128
256
2
???
Brute Force
2
|
|
39
Setelah
dianalisis,
kita
menggunakan hubungan yang konservatif untuk
menyanggupi permintaan untuk bertahan dari attack yang telah berkembang dan
dipelajari. Misalnya analisis diferensial dan
linear
menggunakan 24-tahap dan
28-tahap karakteristik, lebih pendek 8 tahap dan 4 tahap dibandingkan dengan
Serpent, sementara serangan terbaik DES
menggunakan karakteristik
yang
lebih
pendek daripada tiga tahap. Perkiraan
untuk kemungkinan dari karakteristik
terbaik juga bersifat sangat konservatif, dalam praktiknya
hal tersebut
memang
seharusnya lebih rendah. Sehingga, dari segi kompleksitas
Serpent
mengharapkan jauh lebih rendah dibandingkan dengan angka sebenarnya, dan
Serpent mungkin saja lebih aman dibandingkan yang telah dianalisis.
2.4 Teori Simulasi
Menurut Law dan Kelton (1991, p1), simulasi atau juga dapat disebut
pengimitasian adalah meniru atau menggambarkan operasi-operasi yang terjadi
pada berbagai macam fasilitas atau proses yang terjadi pada kehidupan nyata
dengan menggunakan bantuan komputer. Fasilitas-fasilitas atau proses-proses yang
disebutkan di atas itulah yang dikenal
dengan nama sistem. Lebih lengkapnya,
sistem adalah
kumpulan
kesatuan,
yang
bekerja
dan
berinteraksi
bersama-sama
menuju hasil akhir yang logis, yang menjadi tujuan bersama.
Untuk
mempelajari
suatu
sistem secara
ilmiah,
asumsi-asumsi
tentang
bagaimana
sistem
itu bekerja seringkali
harus dilakukan.
Asumsi-asumsi
ini
biasanya dipaparkan dalam relasi matematik atau logik. Dari sanalah dibangun
|
 40
sebuah model yang digunakan untuk mencoba membangun pengertian tentang kerja
atau perilaku dari sistem yang bersangkutan.
Apabila hubungan yang membangun model cukup sederhana, dapat
digunakan metode-metode
matematik seperti aljabar, kalkulus, atau teori
probabilitas untuk mendapatkan jawaban yang pasti. Solusi ini dikenal dengan
solusi analitik.
Sayangnya, seperti
yang telah dipaparkan diatas, banyaknya faktor-faktor tak
terduga
maupun
yang
tidak dapat
diprediksikan
sebelumnya
terlalu banyak,
sehingga
sistem menjadi
sangat
kompleks.
Karena
itu,
sistem ini
tidak
memungkinkan model yang realistik untuk dievaluasi secara analitik.
Dalam simulasi, komputer digunakan sebagai alat bantu untuk mengevaluasi
sebuah model secara numerik, dan data-data dikumpulkan untuk mengestimasi
karakteristik sesungguhnya dari sebuah model.
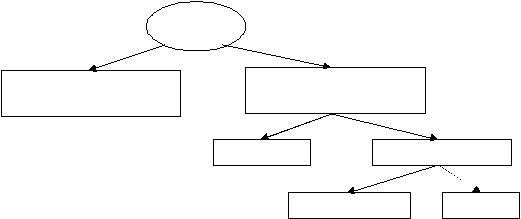
Secara umum, sistem dapat dipelajari perilakunya dengan
menggunakan
beberapa metode yang digambarkan pada diagram berikut.
Sistem
Eksperimen dengan
sistem yang sebenarnya
Eksperimen dengan model
dari suatu sistem
Model fisik
Model matematik
Solusi analitik
Simulasi
Gambar 2.12 Cara Untuk Mempelajari Sistem
Sumber: Law (1991, p4)
|
|
41
Jika
memungkinkan
untuk
bereksperimen
dengan
sistem yang
sebenarnya,
tentunya hasil yang didapatkan mempunyai tingkat ketepatan yang sangat tinggi,
bahkan sempurna. Sayangnya eksperimen ini membutuhkan biaya yang sangat
tinggi dan waktu yang lama serta source yang besar, dan mungkin saja sistem yang
diteliti belum
pernah ada sebelumnya, sehingga eksperimen dengan menggunakan
model merupakan pilihan yang seringkali harus ditempuh.
Model fisik, atau yang pada umumnya dikenal sebagai emulator adalah model
yang
dibuat
sungguh-sungguh
mirip
dengan
aslinya, model tersebut dapat
berperilaku
hampir sama dengan sistem asli. Contohnya simulator pesawat terbang
yang digunakan sekolah penerbangan untuk memberikan gambaran kondisi terbang
sesungguhnya
pada
para
siswa.
Model
ini
dapat
menggambarkan
sistem dengan
akurat, mendekati kondisi aslinya, tetapi biaya dan resource yang diperlukan
sangatlah besar, sehingga seringkali model matematik dipilih untuk membuat model
dari suatu sistem.
Model matematik merepresentasikan sistem dalam relasi logical dan
kuantitatif yang kemudian diubah dan dimanipulasi untuk melihat reaksi dari sistem
yang
dimaksud.
Contoh
sederhana
dari
model
ini
adalah
relasi
?
??,
di
mana
?
adalah
jarak
tempuh,
?
adalah
kecepatan
dan
?
adalah
waktu
tempuhnya.
Relasi matematik
tersebut
diharapkan
dapat
menggambarkan
jalannya
sistem,
yaitu seberapa
panjang
jarak
yang ditempuh
dengan
kecepatan
dan
waktu
tempuh
yang telah diketahui.
Setelah menggambarkan
model matematik,
harus dilihat
apakah sistem yang
digambarkan cukup sederhana. Jika cukup sederhana, maka
model matematik ini
dapat dikembangkan untuk
mencari solusi pasti dari
masalah tersebut,
yaitu yang
|
|
42
dikenal dengan solusi analitik. Sebaliknya, apabila sistem terlalu kompleks,
maka
harus dibuat simulasi.
Pembuatan simulasi tentunya harus disesuaikan dengan data yang didapat,
karena itu simulasi dapat dibagi menjadi 3 dimensi perbedaan.
1.
Simulasi statis dan dinamis, yang menggambarkan suatu sistem pada
waktu tertentu di mana pada saat itu waktu tidak memiliki pengaruh terhadap
perubahan state. Sebaliknya, simulasi dinamis menggambarkan sebuah sistem
yang berubah seiring dengan perubahan waktu.
2.
Simulasi deterministik dan stokastik, adalah simulasi yang tidak
mempunyai komponen berdasarkan probabilitas. Sebaliknya, simulasi
stokastik adalah simulasi yang memiliki komponen berdasarkan probabilitas.
3. Simulasi
kontinu
dan
diskrit,
adalah
simulasi
di
mana
komponen-
komponen di dalamnya berubah secara kontinu, tidak selalu sesuai dengan
perubahan waktu. Sebaliknya
simulasi
diskrit
adalah
simulasi
yang
komponen-komponennya berubah sesuai dengan perubahan waktu.
2.5 Software Development Life Cycle
Menurut Turban, et. al. (2001, p477-486), Software Development Life Cycle
(SDLC) adalah kerangka terstruktur yang terdiri dari beberapa proses yang berurutan
yang
diperlukan
untuk
membangun
suatu
sistem
informasi.
Pendekatan waterfall
digunakan untuk menggambarkan SDLC.
SDLC dirancang dengan tujuan untuk membangun alur pemrograman yang
terstruktur
dan
untuk
membantu
manajemen
proyek
dalam perhitungan
estimasi
waktu dan sumber yang dibutuhkan suatu proyek.
|
 43
Gambar 2.13 Eight Stage SDLC
Sumber: Turban, et. al. (2001, p. 477)
Tahap-tahap SDLC adalah sebagai berikut:
1.
System Investigation
System Investigation
adalah tahap
yang
mengutamakan pembelajaran
terhadap segala kemungkinan yang dapat terjadi. Dengan pembelajaran maka
suatu sistem
dapat
terhindar dari
kesalahan
yang dapat
mengakibatkan
peningkatan usaha, waktu dan jumlah pengeluaran.
2.
System Analysis
System Analysis adalah tahap
yang menganalisis masalah yang
perlu
diselesaikan.
Tahap ini
mendefinisikan
permasalahan,
mengidentifikasikan
penyebab,
menspesifikasikan solusi, serta mengidentifikasikan informasi-
informasi yang diperlukan.
|
|
44
3. System Design
System Design adalah tahap yang menjelaskan
bagaimana
suatu
sistem
akan bekerja. Hasil dari tahap ini adalah output, input dan user interface dari
sistem serta hardware, software, database dan prosedur.
4. Programming
Programming adalah tahap yang menerjemahkan spesifikasi desain sistem
menjadi bahasa pemrograman yang dapat dimengerti oleh komputer.
5. Testing
Testing adalah tahap yang digunakan untuk memeriksa apakah
pemrograman telah menghasilkan
hasil yang diinginkan dan diharapkan atas
situasi tertentu. Testing dirancang untuk mendeteksi adanya kesalahan coding.
6. Implementation
Implementation
adalah
proses
perubahan
dari
penggunaan
sistem lama
menjadi sistem yang baru.
7. Operation and Maintenance
Operation
and
Maintenance
adalah tahap untuk
memelihara sistem baru
yang akan dioperasikan dalam suatu periode waktu.
2.6 Unified Modelling Language
Unified Modelling Language (UML) adalah bahasa grafis yang standar untuk
memodelkan software object oriented (Lethbridge, 2002, p.151). UML mengandung
tipe diagram yang bervariasi, termasuk:
1. Class Diagram
2. Sequence Diagram
|
 45
2.6.1
Class Diagram
Class diagram adalah salah satu diagram struktur statis yang menunjukkan
struktur
dari sistem
dengan
menunjukkan
class-class
yang
ada pada sistem,
attribute dan method class-class tersebut dan
hubungan antar class.
Hubungan
class terdiri dari link, association, aggregation dan composition.
Gambar 2.14 Notasi Class
Sumber: Lethbridge (2002, p.439)
Gambar 2.15 Hubungan Class Pada Class Diagram
Sumber: Website http://en.wikipedia.org/wiki/Class_Diagram
Link adalah
hubungan dasar antar objek
yang
menggambarkan
garis
penghubung antara dua atau lebih class. Link merupakan bagian dari association.
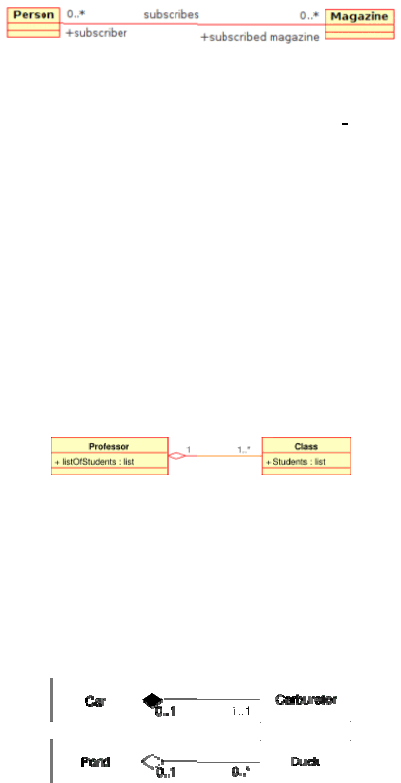
Association menggambarkan kumpulan link yang saling berhubungan.
Binary Association (dengan dua titik
akhir) biasanya digambarkan sebagai
sebuah
garis,
dimana
masing-masing
titik
akhir
dihubungkan dengan
sebuah
class. Association memiliki dua atau lebih titik akhir.
|
 46
Gambar 2.16 Hubungan Association Pada Class Diagram
Aggregation adalah
lambang
dari
“memiliki sebuah”
atau
hubungan
association, tetapi
aggregation
lebih spesifik
daripada association.
Meskipun
aggregation merupakan perluasan association, hubungan aggregation
hanya
dapat melibatkan dua class.
Aggregation terjadi bila suatu class mengandung satu atau lebih objek dari
class
lain,
tetapi
class
yang
dikandung
tidak
memiliki
life
cycle
dependency
dengan class yang mengandung.
Gambar 2.17 Hubungan Aggregation Pada Class Diagram
Sumber: Website http://en.wikipedia.org/wiki/Class_Diagram
Composition
merupakan hubungan
aggregation
di
mana
class
yang
dikandung telah memiliki life cycle dependency dengan class yang mengandung.
Gambar 2.18 Hubungan Composition Pada Class Diagram
Sumber: Website http://en.wikipedia.org/wiki/Class_Diagram
|
 47
2.6.2
Sequence Diagram
Menurut Lethbridge (2002, p270), sequence diagram adalah diagram yang
menunjukkan
urutan proses dan penukaran pesan oleh sejumlah objek
(dan
seorang aktor yang optional) dalam melakukan tugas tertentu. Sequence diagram
menggambarkan skenario runtime sederhana secara grafis.
Gambar 2.19 Notasi Object, Lifetime dan Activation
Sumber: Lethbridge (2002, p.440)
Gambar 2.20 Contoh Sequence Diagram
|
 48
2.7 State Transition Diagram
2.7.1
Pengertian STD
STD
merupakan
suatu
modeling tool
yang
menggambarkan
sifat
ketergantungan sistem. Pada mulanya hanya digunakan untuk menggambarkan
suatu
sistem yang
memiliki
sifat
real
time
seperti
proses
control, telephone
switching system, dan control system.
2.7.2
Simbol dan Sifat STD
State
adalah kumpulan
keadaan
dan
atribut
yang
mencirikan
objek
pada
waktu atau kondisi tertentu. Disimbolkan dengan segi empat.
Gambar 2.21 Notasi State
Transition adalah simbol perpindahan keaktifan dari sebuah objek menjadi
objek lain. Transition disimbolkan dengan anak panah.
Gambar 2.22 Notasi Transition
Condition adalah
suatu
keadaan
pada
lingkungan
eksternal
yang
dapat
dideteksi oleh sitem. Condition menggambarkan syarat yang biasanya digunakan
dalam
hubungan seleksi. Action adalah
yang dilakukan sistem bila terjadi
|
|
49
perubahan
state
atau
merupakan
reaksi
terhadap
kondisi.
Aksi
akan
menghasilkan keluaran atau output. Display adalah hasil yang merupakan STD.
2.8 User Interface Design
User
Interface
(UI) Design
adalah
perancangan
tampilan
antarmuka
yang
bersifat
visual
dari
suatu aplikasi
agar aplikasi
tersebut
dapat berinteraksi dengan
baik dengan user dan dapat digunakan dengan maksimal.
Proses perancangan UI harus mengandung arti dari unsur-unsur visual yang
seimbang, yang dapat
memodelkan
inti dari operasi aplikasi yang akan dijalankan.
Selain
itu perancangan
UI
yang baik
juga
harus
dapat
membuat
aplikasi
hingga
mudah digunakan dan dapat disesuaikan dengan kebutuhan masing-masing user.
Dalam perancangan UI, terdapat delapan aturan emas yang mendukung
sebuah perancangan UI yang baik. Delapan aturan emas, yang dijabarkan oleh Ben
Scneiderman, tersebut antara lain:
1. Usaha untuk konsistensi dalam tampilan.
2. Memungkinkan user yang rutin untuk menggunakan shortcut.
3. Memberikan umpan balik yang informatif.
4. Memunculkan dialog box pada penutupan.
5. Mempunyai error-handling sederhana.
6. Memungkinkan user untuk membatalkan tindakan.
7. Mendukung komponen dan control.
8. Mengurangi penggunaan memori jangka pendek.
|