23
Algoritma 2.2 : Algoritma Euclide (Menezes, Oorschot and Vanstone, 1996)
Input : Bilangan bulat nonnegatif a dan b,
a
=
b
.
Output :
gcd
(a, b)
Langkah :
1. While
b
?
0
do : Set
r
?
a
mod b ,
a
?
b
,
b
?
r
.
2. Output (a).
Contoh 2.1.2.9. (Buchmann, 2000)
Akan dihitung nilai gcd(100,35). Menggunakan algoritma Euclide diperoleh:
Langkah 1 : gcd(100,35) = gcd(35,100 mod 35) = gcd(35,30).
Langkah 2 : gcd(35,30) = gcd(30,35 mod 30) = gcd(30,5).
Langkah 3 : gcd(30,5) = gcd(5,30 mod 5) = gcd(5,0).
Langkah 4 : gcd(5,0) = 5.
Jadi, gcd(100,35) = gcd(35,30) = gcd(30,5) = gcd(5,0) = 5.
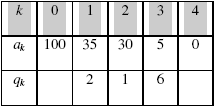
Tabel 2.1. Perhitungan gcd(100,35) menggunakan algoritma Euclide
F.
Algoritma Euclide yang Diperluas
Dengan algoritma Euclide dapat dihitung nilai pembagi persekutuan terbesar dari
bilangan bulat a dan b. Menurut
Akibat 2.1.2.2, terdapat bilangan bulat x dan y dengan
gcd
(a, b)
=
ax + by .
Selanjutnya,
algoritma
Euclide
dapat
diperluas
sedemikian
hingga
dapat
digunakan
untuk
menghitung
nilai
x
dan
y
tersebut.
Pada
pembahasan
tentang