 BAB 2
TINJAUAN
PUSTAKA
2.1
TANAH
LUNAK
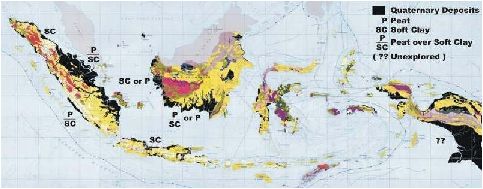
Sebagian besar deposit tanah yang ada di Indonesia merupakan tanah lunak. Tanah
jenis ini umumnya dapat ditemui di wilayah Sumatera, Kalimantan, dan Irian Jaya.
Ketebalan tanah lunak pada ketiga wilayah di atas dapat mencapai lebih dari 30 m.
Selain ketiga wilayah
yang telah disebutkan di
atas, tanah lunak juga
tersebar di
kawasan Indonesia lainnya walaupun dalam jumlah yang relatif lebih sedikit.
Gambar 2.1
Peta Penyebaran Tanah Lunak di Indonesia
(Sumber: Panduan Geoteknik 1, Departemen Pemukiman dan Prasarana Wilayah)
Tanah
lunak
merupakan
tanah
yang
berkarakteristik buruk.
Hal
ini
karena
tanah
lunak
memiliki
sifat
kompresibilitas yang
sangat
tinggi.
Salah
satu
faktor
yang
menyebabkan
tingginya tingkat
kompresibilitas pada
tanah
lunak
adalah
karena
tanah
jenis
ini
memiliki angka pori
yang
tinggi. Selain
itu
tanah
jenis
ini
juga
memiliki kadar air yang tinggi sehingga menyebabkan tanah lunak memiliki daya
8
|
|
9
dukung
yang
sangat
rendah
dan
memiliki masalah penurunan
yang besar
selama
dan
setelah
konstruksi dibangun. Untuk
menangani
permasalahan yang
ada
pada
tanah
lunak,
maka
sebelum dilakukan pekerjaan konstruksi, terlebih dahulu perlu
dilakukan upaya perbaikan pada tanah jenis ini, diantaranya dengan menggunakan
material
geosintetik
untuk
perkuatan
pada
dasar
timbunan
yang
berada
di
atas
tanah lunak.
Tanah
lempung
jenuh
air
merupakan salah
satu
jenis
tanah
lunak
yang
umum
ditemui. Sebagaimana yang telah dijelaskan di atas, jika tanah lunak (dalam hal ini
tanah
lempung
jenuh
air)
menerima
beban,
maka
akan
terjadi
penurunan
yang
relatif besar dalam suatu jangka waktu tertentu. Proses penurunan yang sebenarnya
sangat kompleks tersebut dapat disederhanakan dengan membaginya ke dalam tiga
kelompok, yaitu:
1. Penurunan segera (penurunan elastis)
Penurunan segera (penurunan elastis) terjadi pada saat beban diberikan. Pada
saat ini, beban pertama kali diterima oleh air pori sehingga timbul tegangan air
pori. Pada
tanah
yang berpermeabilitas rendah,
untuk sementara
tidak ada air
pori
yang terdisipasi dan tanah disebut dalam keadaan
undrained. Tanah akan
berdeformasi tanpa
mengalami
perubahan
volume
sedemikian
sehingga
deformasi
vertikal
(penurunan) yang
dialami
oleh
tanah
diikuti
dengan
pengembangan ke arah
lateral. Menurut Janbu, Bjerrum, dan Kjaernsli (1956),
besarnya penurunan segera dapat dihitung dengan persamaan:
S
i
1
0
qB
............................................................................................
(2.1) E
|
 10
Dimana:
S
i
=
Penurunan segera
1
=
Koefisien (terkait perbandingan antara H dan B)
0
=
Koefisien (terkait perbandingan antara D dan B)
q
=
Tegangan pada bidang kontak antara beban dengan tanah dasar
B
=
Lebar timbunan ekivalen
E
=
Modulus Young
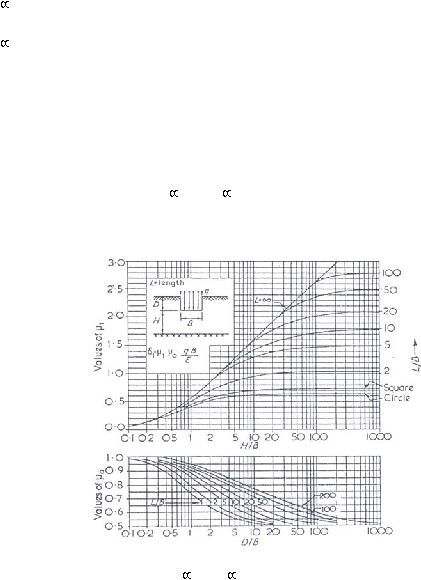
Besarnya
nilai
koefisien
1
dan
0
dapat
ditentukan
dengan
menggunakan
grafik sebagaimana yang diberikan pada Gambar 2.2.
Gambar 2.2
Koefisien
0
dan
1
(Janbu, Bjerrum, dan Kjaernsli; 1956)
(Sumber: Short Course on Geotechnical Engineering by GOUW Tjie Liong)
|
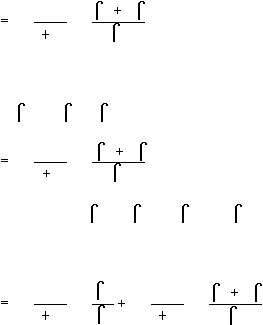 11
2. Penurunan konsolidasi (penurunan primer)
Penurunan konsolidasi terjadi bersama dengan berlalunya
waktu,
yaitu terjadi
bersama-sama dengan terdisipasinya tegangan air
pori. Akibatnya, penurunan
yang
terjadi disertai dengan perubahan
volume tanah. Tegangan air pori
yang
timbul akan dipindahkan ke partikel tanah dalam suatu jangka waktu tertentu
menjadi
tegangan
efektif tanah.
Kecepatan terjadinya
konsolidasi bergantung
pada
kecepatan
keluarnya
air pori
yang
merupakan
fungsi
dari permeabilitas
tanah dan batas-batas drainase. Besarnya penurunan konsolidasi dapat dihitung
dengan menggunakan persamaan berikut:
a. Untuk tanah terkonsolidasi normal
S
c
H
0
C
c
1
e
0
log
0
'
'
...................................................................... (2.2)
0
'
b. Untuk tanah terkonsolidasi berlebih
Jika (
0
'
+
') =
0
', maka besarnya penurunan konsolidasi adalah:
S
c
H
0
C
s
1
e
0
log
0
'
'
...................................................................... (2.3)
0
'
Sedangkan
jika
0
'
<
p
'
<
(
0
'
+
'),
besarnya
penurunan konsolidasi
adalah sebagai berikut:
S
c
H
0
C
s
1
e
0
p
'
log
H
0
0
'
C
c
1
e
0
log
0
'
'
......................................... (2.4)
p
'
|
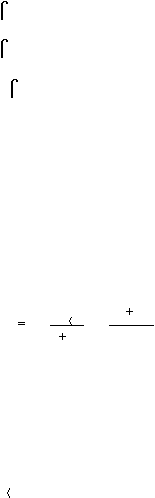 12
p
Dimana:
Sc
=
Penurunan konsolidasi
H
0
=
Tebal lapisan tanah
Cc
=
Indeks kompresi
C
s
=
Indeks swelling
e
0
=
Angka pori awal
0
'
=
Tegangan efektif awal
p
'
=
Tegangan prakonsolidasi efektif awal
'
=
Perubahan tegangan efektif
3. Penurunan rangkak (penurunan sekunder)
Penurunan sekunder merupakan penurunan jangka panjang yang terjadi setelah
seluruh tegangan air pori terdisipasi dan
tegangan efektif
tanah telah konstan.
Deformasi ini terjadi akibat efek rangkak yang disebut drained creep. Besarnya
penurunan sekunder dapat dihitung dengan menggunakan Persamaan (2.5).
S
s
H
C
0
1
e
t
p
t
log
t
p
.............................................................................. (2.5)
Dimana:
S
s
=
Penurunan rangkak (sekunder)
H
0
=
Tebal lapisan tanah
C
=
Indeks kompresi penurunan sekunder
e
p
=
Angka pori pada akhir konsolidasi
t
p
=
Waktu ketika konsolidasi selesai
t
=
Selang waktu terjadinya penurunan sekunder
|
 13
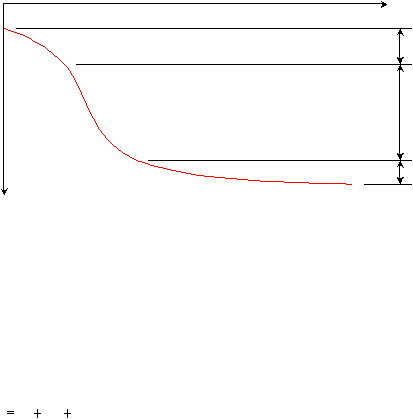
Waktu
Penurunan segera
Penurunan konsolidasi
Penurunan
Penurunan sekunder
Gambar 2.3
Hubungan Antara Penurunan dan Waktu
(Sumber: Short Course on Geotechnical Engineering by GOUW Tjie Liong)
Dengan
demikian,
maka
penurunan total
yang
terjadi pada
tanah setelah beban
kerja diberikan adalah sebagai berikut:
S
S
i
S
c
S
s
.................................................................................................... (2.6)
Dimana:
S
=
Penurunan total
S
i
=
Penurunan segera
Sc
=
Penurunan konsolidasi
S
s
=
Penurunan rangkak (sekunder)
|
 14
Besarnya ketiga macam penurunan ini sangat bergantung kepada tipe tanah, sifat-
sifat
kompresibilitas, riwayat
tegangan
(stress
history),
besar
dan
kecepatan
pembebanan,
dan
berkaitan
juga
dengan
perbandingan luas
bidang
pembebanan
terhadap ketebalan tanah kompresif tersebut. Tanah inorganik umumnya
mengalami
penurunan
seketika
dan
penurunan
sekunder
yang
jauh
relatif
lebih
kecil dibandingkan dengan penurunan konsolidasi. Karena itu penurunan
konsolidasi disebut juga penurunan primer.
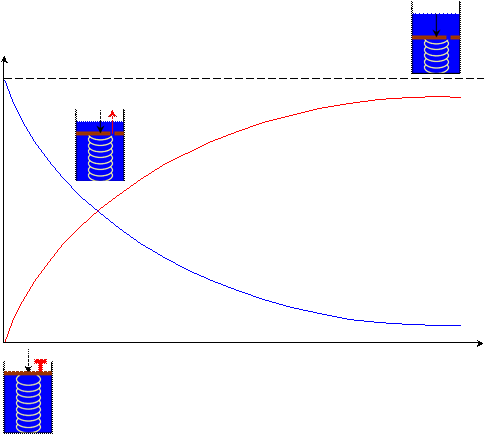
P
Gaya
P
P
Pegas
Air pori
P
Waktu
Gambar 2.4
Hubungan Gaya Terhadap Waktu Penurunan Total
(Sumber: Short Course on Geotechnical Engineering by GOUW Tjie Liong)
|
 15
Berlangsungnya konsolidasi
yang
terjadi
pada
tanah
lunak
akibat
beban
kerja,
seperti timbunan, akan menurunkan tegangan air pori berlebih dan angka pori pada
tanah
lunak
sehingga
kepadatan
dan
tegangan
vertikal
efektif
tanah
lunak
akan
naik.
Akibatnya, kuat
geser tak
terdrainase (undrained)
tanah
lunak
dan
faktor
keamanan akan
naik. Peningkatan kuat geser pada tanah dasar merupakan fungsi
dari
derajat konsolidasi, seperti ditunjukkan pada Persamaan 2.7. Oleh karena itu
kecepatan
penimbunan harus
dikontrol
supaya
terjadi
konsolidasi
yang
cukup,
sehingga
kuat
geser
yang
diinginkan dapat
tercapai.
Metode
ini
harus
dipertimbangkan bila
tinggi
desain
timbunan
melebihi
tinggi
kritis
yang
dapat
dengan aman didukung oleh tanah dasar.
a
U .....................................................................................................
(2.7) Dimana:
=
Perubahan kuat geser
a
=
Koefisien
= Perubahan tegangan
U = Derajat konsolidasi
Besarnya perubahan tegangan pada tanah dasar dapat diambil kira-kira sama
dengan
beban
timbunan.
Untuk
lempung
yang
terkonsolidasi normal,
faktor
a
berkisar antara 0,20 – 0,40. Kenaikan kuat geser penuh hanya akan terjadi tepat di
bawah areal timbunan paling tinggi dan menurun ke arah kaki timbunan. Perkiraan
yang
ditunjukkan pada
Gambar
2.5
cukup
memadai
untuk
keperluan
analisa
stabilitas.
|
 16
2
2
Lebar ekivalen
Titik tengah dari
lereng samping
Kuat geser
tidak bertambah
Kuat geser
bertambah
Kuat geser
tidak bertambah
Gambar 2.5
Kenaikan Kuat Geser Tanah Dasar Akibat Konsolidasi
(Sumber: Panduan Geoteknik 4, Departemen Pemukiman dan Prasarana Wilayah)
Peningkatan kuat
geser
pada
tanah
lunak
berlangsung secara
perlahan
sejalan
dengan
proses
konsolidasi
tanah
lunak.
Adapun
waktu
konsolidasi tanah
dapat
dihitung dengan menggunakan Persamaan (2.8).
t
T
v
H
dr
C
v
.......................................................................................................... (2.8)
Dimana:
U
Untuk U < 60 %, T
v
4 100
........................................................................ (2.9)
Untuk U = 60 %, T
v
1,781
0,933log
100
U
............................................. (2.10)
|
 17
Keterangan:
t
=
Waktu konsolidasi
T
v
=
Faktor waktu
H
dr
=
Panjang lintasan drainase air
C
v
=
Koefisien konsolidasi
U = Derajat konsolidasi
Nilai
koefisien
konsolidasi umumnya
dapat
diperoleh
melalui
pengujian
di
laboratorium. Apabila pengujian tidak dilakukan, maka koefisien konsolidasi tanah
dapat didekati dengan menggunakan persamaan (Terzaghi; 1996):
C
v
k
w
m
v
....................................................................................................... (2.11)
Dimana:
C
v
=
Koefisien konsolidasi
k
=
Koefisien permeabilitas
w
=
Berat isi air
m
v
=
Koefisien kompresibilitas
|
|
18
2.2
GEOSINTETIK
Menurut Etimologi, kata “GEOSINTETIK” terdiri dari dua suku kata, yaitu
“GEO”
yang
berarti
bumi/tanah dan
“SINTETIK” yang
berarti
bahan
sintetik/buatan. Dengan
demikian,
maka
geosintetik
dapat
didefinisikan
sebagai
material
yang
terbuat
dari
bahan
polimer
yang
digunakan pada
konstruksi-
konstruksi yang
berkaitan
dengan
bidang
Geoteknik.
Secara
umum,
geosintetik
dapat diklasifikasikan ke dalam sembilan kelompok, yaitu:
1. Geotextile
2. Geogrid
3. Geonet
4. Geomembrane
5. Geosynthetics clay liners
6. Geopipes
7. Geocomposites
8. Geofoam
9. Geo-others
|
 19
Secara umum ada enam fungsi utama geosintetik yang dapat bekerja secara
mandiri ataupun berkolaborasi satu sama lain, yaitu:
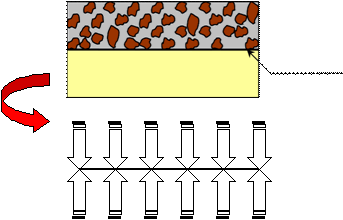
1. Sebagai lapis pemisah (separation)
Geosintetik berfungsi untuk memisahkan dua jenis material yang berbeda
dalam karakteristik dan ukurannya, misalnya antara material timbunan dengan
tanah dasar
yang
lunak.
Melalui
fungsi separasi
ini,
diharapkan
properti
dan
karakteristik material timbunan akan tetap terjaga.
Geosintetik
Gambar 2.6
Material Geosintetik Sebagai Lapis Pemisah
|
 20
+
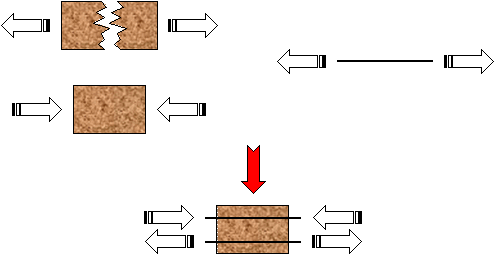
2. Sebagai lapis perkuatan (reinforcement)
TARIK = LEMAH
TEKAN = KUAT
TARIK =
KUAT
GEOSINTETIK
TANAH
TARIK = KUAT
TEKAN = KUAT
TANAH DENGAN PERKUATAN GEOSINTETIK
Gambar 2.7
Material Geosintetik Sebagai Lapis Perkuatan
Penggunaan material geosintetik yang mempunyai properti kuat tarik yang baik
dapat
menstabilkan suatu
konstruksi berbahan tanah.
Tanah
dikenal
mempunyai kemampuan yang baik terhadap pengaruh gaya tekan namun
lemah
terhadap
gaya
tarik,
dan
geosintetik
akan
mengambil
alih
gaya
tarik
yang harus dipikul oleh tanah.
3. Sebagai lapis filtrasi (filtration)
Melalui
fungsi
ini,
air
atau
cairan
dapat
dengan
mudah
melewati material
geosintetik
pada
arah
tegak
lurus dengan
bidang
geosintetik,
namun
butiran-
butiran
tanah
akan
tertahan.
Oleh
karena
itu
geosintetik harus
mempunyai
ukuran bukaan pori yang cukup besar (sehingga air dapat lewat dengan mudah)
dan juga cukup kecil (sehingga butiran tanah akan tertahan).
|
|
21
4. Sebagai lapis drainase (drainage)
Pada
fungsi
drainase
ini,
geosintetik digunakan
sebagai
media
untuk
mengalirkan air searah dengan bidang geosintetik. Untuk
itu, geosintetik yang
digunakan
harus mempunyai
koefisien transmissivity (pengaliran
searah
bidang) yang cukup besar.
5. Sebagai lapis kedap (impermeable liner)
Geotekstil
merupakan material
yang porous,
namun jika dikombinasikan
dengan cairan bitumen atau semen pada geotekstil
nonwoven akan didapatkan
suatu lapisan yang cukup kedap air. Alternatif lain yang lebih umum digunakan
adalah menggunakan material geomembran.
6. Sebagai lapis pelindung (protection)
Umumnya
fungsi
ini
diperlukan
untuk melindungi suatu material
atau lapisan
dari
kerusakan
akibat
pengaruh
benda-benda tajam.
Jenis
lapisan
yang
umumnya perlu dilindungi adalah geomembran yang merupakan material
kedap air.
Stabilitas tanah disebabkan oleh adanya kuat geser tanah yang berasal dari gesekan
antara
partikel
tanah
dan
tegangan
tekan
pada
tanah.
Gaya
penggerak yang
menyebabkan
keruntuhan pada
tanah
harus
dapat
ditanggulangi
oleh
gaya
resistansi akibat kuat geser pada
tanah di
sepanjang bidang keruntuhan. Sebelum
terjadi kegagalan
(failure)
pada
massa
tanah,
partikel-partikel tanah
di
sepanjang
bidang
kelongsoran akan saling
bergeser
satu
sama
lain.
Hal
ini
menyebabkan
terjadinya
regangan
tarik dan regangan
tekan pada massa tanah di sepanjang
bidang kelongsoran yang terjadi.
|
|
22
Pemanfaatan
material perkuatan seperti geosintetik
harus
memperhatikan perilaku
tanah
sebagaimana yang
dijelaskan
sebelumnya
agar
material
perkuatan
yang
digunakan
dapat
bekerja
bersama-sama dengan
massa
tanah
dalam
mencegah
kegagalan pada
tanah. Karena
sifat tanah yang
lemah terhadap
gaya
tarik,
maka
material
perkuatan
harus
diletakkan pada
arah
dimana
terjadi
regangan
tarik
sehingga timbul
gaya tarik pada
material perkuatan akibat deformasi yang terjadi
pada
tanah.
Gaya
tarik
yang
timbul pada
material
perkuatan
akan
meningkatkan
stabilitas tanah dengan cara mengurangi gaya penyebab keruntuhan pada tanah dan
meningkatkan
gaya
resistansi
pada
tanah.
Perilaku
dari material
perkuatan
ini
dapat diilustrasikan pada Gambar 2.8.
Pada Gambar 2.8(a), regangan tekan dan regangan tarik akan timbul pada bidang
geser
akibat
bekerjanya
gaya
horizontal (P
h
)
pada
massa
tanah.
Gaya
horizontal
yang
diberikan
tersebut
akan
ditahan oleh
gaya resistansi
pada
tanah
(P
r
)
akibat
gaya gesek antar partikel tanah. Pada Gambar 2.8(b), deformasi geser yang terjadi
pada tanah menyebabkan timbulnya gaya tarik (Pr) pada material perkuatan.
Akibat gaya tarik yang timbul pada material perkuatan tersebut, maka akan timbul
gaya resistansi tambahan di sepanjang bidang geser. Adapun gaya resistansi
tersebut adalah:
1. Komponen
gaya
tarik (Pr) pada
material perkuatan disepanjang bidang
geser
(Prsin
)
Komponen
gaya
resistansi
ini
secara
langsung
akan
mengurangi
gaya
geser
yang disebabkan oleh gaya horizontal (P
h
).
|
 23
2. Komponen
gaya tarik (Pr) pada
material perkuatan
yang bekerja dalam arah
tegak lurus terhadap bidang geser (Prcos
)
Komponen gaya ini
meningkatkan gaya tekan pada tanah disepanjang bidang
geser. Dengan adanya tambahan gaya tekan, maka gaya geser yang bertindak
sebagai gaya penahan juga akan mengalami peningkatan.
(a)
P
v
Soil,
P
h
Shearing soil
Tensile strain
Compressive strain
Shearing resistance:
P
resisting
= P
v
tan
P
v
(b)
Reinforcement
Soil,
P
h
P
r
Prcos
Prsin
Shearing soil
Shearing resistance:
From soil alone: P
v
tan
Reduction in forces causing failure: Prsin
Increase in forces resisting failure: Prcos
tan
Total shearing resistance:
P
resisting
= P
v
tan
+ Pr(sin
+ cos
tan
)
Gambar 2.8 Ilustrasi Perilaku Material Perkuatan pada Pengujian Direct Shear
(a)
Regangan Tekan
dan
Regangan
Tarik
pada
Saat
Terjadi
Pergerakan pada
Massa
Tanah
(b)
Gaya
pada Material
Perkuatan
Meningkatkan Gaya Resistansi pada Saat Terjadi Pergerakan Massa
Tanah
(Sumber: Terram Design Guide)
|
  24
Geotekstil
V
g
V
g
P
H
g
H
g
Gambar 2.9
Konsep Perkuatan Tanah dengan Material Geotekstil
Pada
perkuatan
geotekstil,
deformasi
yang
terjadi
pada
geotekstil
akibat
beban
kerja
menyebabkan geotekstil tertarik. Akibatnya, timbul reaksi berupa gaya tarik
pada
geotekstil. Komponen
vertikal
dari
gaya
tarik
geotekstil (V
g
)
ini
akan
mengeliminasi sebagian dari beban yang bekerja, sehingga gaya yang harus dipikul
oleh tanah dasar menjadi lebih kecil. Mekanisme kerja perkuatan dengan geotekstil
ini
dikenal
dengan
nama
efek
kurva
(curvature
effect). Tanpa
analisa
dengan
menggunakan
metode
elemen
hingga
sangat
sulit
untuk
memperkirakan besarnya
deformasi yang terjadi pada geotekstil.
|
 25
2.3
TEKNIK
PENINGKATAN
STABILITAS
TANAH
DASAR
PADA
KONSTRUKSI
TIMBUNAN
Ada tiga cara
yang
dapat
digunakan
untuk
meningkatkan
stabilitas
tanah
dasar
selama masa konstruksi timbunan berlangsung, yaitu:
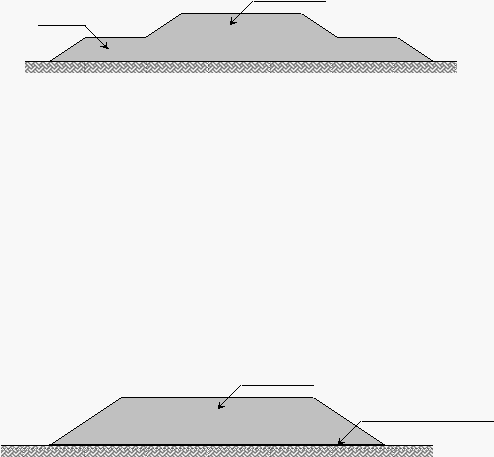
1. Membangun timbunan secara bertahap
Pembangunan konstruksi timbunan
secara
bertahap
dilakukan
dengan
menimbun
tanah
dalam
jangka
waktu
tertentu
secara
bertahap. Metode
ini
bertujuan
untuk
mencegah kegagalan
pada
tanah
dasar
dengan
cara
mengkonsolidasikan tanah
dasar
hingga
timbunan
berikutnya
diberikan
sehingga
stabilitas
tanah
dasar
dapat
ditingkatkan. Akan
tetapi
untuk
tanah
dengan karakteristik drainase yang buruk,
metode ini sangat jarang digunakan
secara
mandiri
karena
metode
ini
memerlukan waktu konstruksi
yang
lama
sehingga seringkali tidak ekonomis jika ditinjau dari sudut pandang ekonomi.
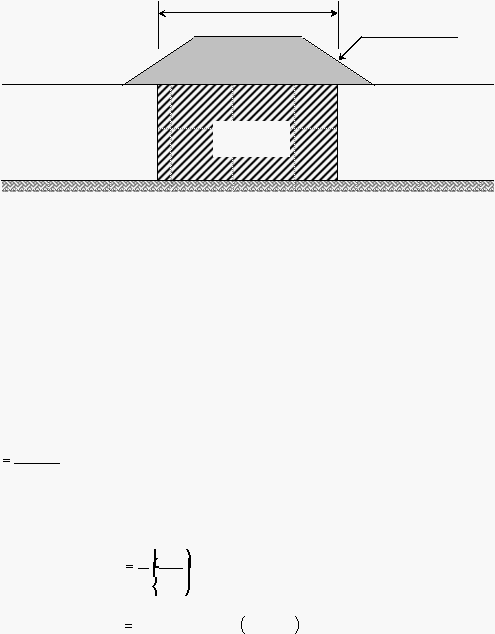
Gambar 2.10
Teknik Penimbunan dengan Metode Penimbunan Bertahap
|
 26
2. Membangun timbunan dengan menggunakan berm
Penggunaan
berm pada timbunan
bertujuan
untuk
mencegah
squeeze
pada
tanah dasar
dan
meningkatkan area
pembebanan
sehingga
dapat
mengurangi
tegangan
yang
terjadi
pada
tanah
dasar.
Dengan
demikian,
maka
stabilitas
tanah dasar dapat tetap terjaga. Akan tetapi metode ini
memerlukan luas lahan
yang besar sehingga metode ini jarang untuk digunakan.
Berm
Timbunan
Gambar 2.11
Teknik Penimbunan dengan Menggunakan Berm
3. Membangun timbunan dengan menggunakan perkuatan pada dasar timbunan
Pemakaian sistem perkuatan pada dasar timbunan seperti geotekstil merupakan
metode
yang paling
ekonomis
dan
paling
banyak digunakan
akhir-akhir
ini
karena
metode
ini
dapat
meminimalkan
geometri
timbunan
(meminimalkan
luas area penimbunan dan memaksimalkan tinggi timbunan) serta mengurangi
masa pelaksanaan konstruksi timbunan.
Timbunan
Perkuatan geosintetik
Gambar 2.12
Teknik Penimbunan dengan Perkuatan Dasar Timbunan
|
|
27
2.4
ANALISA
KESEIMBANGAN
BATAS
PADA
TIMBUNAN
DENGAN
PERKUATAN GEOTEKSTIL
Umumnya
timbunan
di
atas
tanah
lunak
akan
mengalami
penurunan
yang
besar
dan
berpeluang mengalami failure
akibat
kurangnya
daya
dukung
tanah
lunak
terhadap beban timbunan. Salah satu cara yang dapat digunakan untuk
memperbaiki kondisi tanah dasar
yang ada
adalah dengan
menggunakan material
geosintetik seperti geotekstil yang digelar di atas tanah lunak sebelum pelaksanaan
konstruksi
timbunan. Material
geosintetik
dalam
hal
ini
berfungsi sebagai
perkuatan tanah (soil reinforcement). Perkuatan dasar timbunan di atas tanah lunak
hanya
bekerja
sementara hingga
daya
dukung
tanah
lunak
meningkat sehingga
mampu mendukung beban yang ada di atasnya. Umumnya desain perkuatan tanah
sebagaimana
yang
digambarkan
di
atas
dilakukan
dengan
menggunakan
metode
limit
equilibrium
dimana
analisa
stabilitas baru dapat
diterima
jika
faktor
keamanan yang dihasilkan menunjukkan hasil yang memuaskan (lebih besar dari
1). Analisa
dengan
menggunakan
metode
limit
equilibrium
meninjau
tiga
modus
stabilitas konstruksi timbunan di atas tanah lunak, yaitu stabilitas internal (internal
stability), stabilitas tanah
dasar
(foundation
stability), dan
stabilitas konstruksi
secara keseluruhan (overall stability).
|
  28
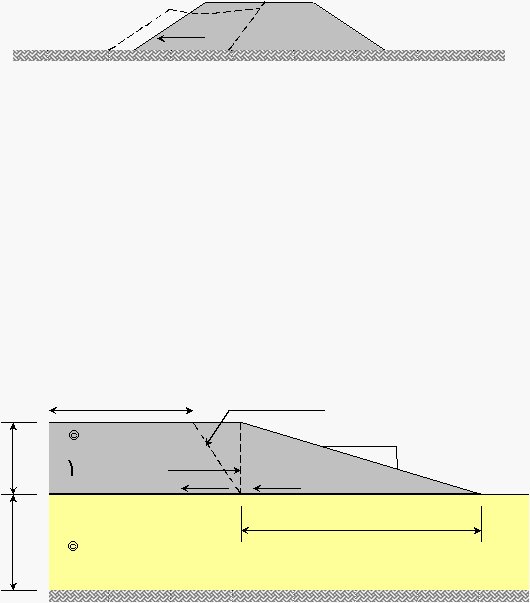
Gambar 2.13
Model Keruntuhan pada Internal Stability (Hird dan Jewel; 1990)
(Sumber: Proceeding of Seminar Road Construction in Indonesia with Special Reference to the
Role of Geosynthetics)
Analisa stabilitas internal (internal
stability) bertujuan untuk mencegah pergerakan
lateral
pada
konstruksi
timbunan.
Gaya
lateral
yang
timbul
harus
dapat
ditahan
oleh kaki
timbunan. Oleh
karena
itu,
stabilitas
internal
(internal
stability)
suatu
timbunan sangat dipengaruhi oleh kemiringan kaki timbunan itu sendiri.
Anchor zone
Sliding plane
n
c
H
E
a
1
T
F
internal
Reinforcing mat
c
u
L = nH
D
s
Soft subsoil
Gambar 2.14
Keseimbangan Batas pada Stabilitas Internal
(Sumber: Stabilenka Design Guide)
Gaya lateral yang timbul pada analisa stabilitas internal diakibatkan oleh tegangan
lateral aktif
akibat
tanah
timbunan. Secara
matematis besarnya
gaya lateral
yang
timbul pada konstruksi timbunan diberikan oleh Persamaan (2.12).
|
 29
E
a
1
2
K
a
H
2
............................................................................................ (2.12)
Dimana:
E
a
=
Tegangan lateral aktif
K
a
=
Koefisien tegangan lateral aktif
= Berat
isi
H = Tinggi timbunan
Untuk
timbunan tanpa perkuatan (unreinforced embankment) yang berada di atas
tanah lunak jenuh air tak terkonsolidasi, pada interface antara timbunan dan tanah
dasar akan timbul sebuah bidang geser. Bidang geser inilah yang akan
mengimbangi gaya lateral yang ada. Besarnya gaya geser yang timbul pada bagian
interface antara material
timbunan
dan tanah dasar ini dipengaruhi
oleh nilai
kohesi tanah dasar yang dapat dihitung dengan menggunakan Persamaan (2.13).
F
internal
c
u
n
H ...............................................................................................
(2.13) Dimana:
F
internal
=
Gaya internal
c
u
=
Kohesi undrained
n
=
Kemiringan kaki timbunan
H
=
Tinggi timbunan
|
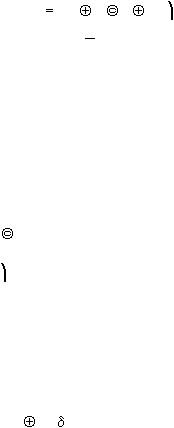 30
Sedangkan untuk timbunan dengan perkuatan (reinforced
embankment), kuat geser
yang
timbul pada area
interface
ditentukan berdasarkan besarnya gesekan
antara
material timbunan dan material perkuatan geotekstil
yang digunakan.
Adapun
besarnya kuat geser yang timbul dapat ditentukan dengan Persamaan (2.14).
F
internal
nH
1
H
tan
....................................................................................
(2.14)
2
Dimana:
F
internal
=
Gaya internal
n
=
Kemiringan kaki timbunan
H
=
Tinggi timbunan
=
Berat isi
=
Sudut geser dalam
Dengan demikian, struktur
timbunan dikatakan aman
terhadap
stabilitas internal
jika:
SF
E
a
F
internal
..................................................................................................
(2.15) Dimana:
SF
=
Faktor keamanan
E
a
=
Tegangan lateral aktif
F
internal
=
Gaya internal
|
  31
Apabila kondisi keseimbangan batas tidak tercapai, maka diperlukan adanya suatu
gaya tambahan untuk menahan gaya lateral yang timbul. Gaya tambahan ini
berasal dari material perkuatan (geotekstil) yang digunakan. Adapun besarnya kuat
tarik material
geotekstil
yang diperlukan
dapat
dihitung
dengan
menggunakan
Persamaan (2.16).
T
SF
E
a
F
internal
............................................................................................
(2.16) Dimana:
T = Kuat tarik perlu geotekstil
SF = Faktor keamanan
E
a
=
Tegangan lateral aktif
F
internal
=
Gaya internal
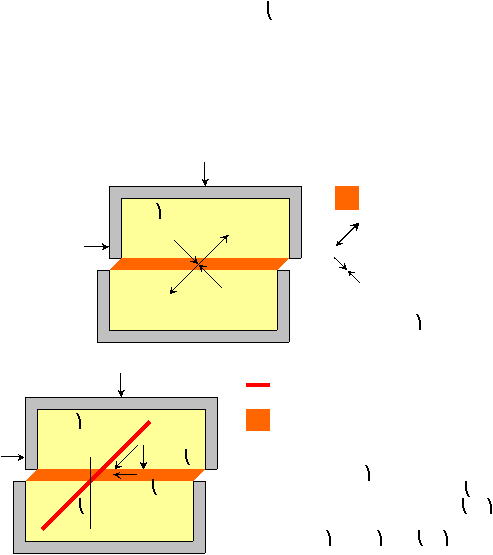
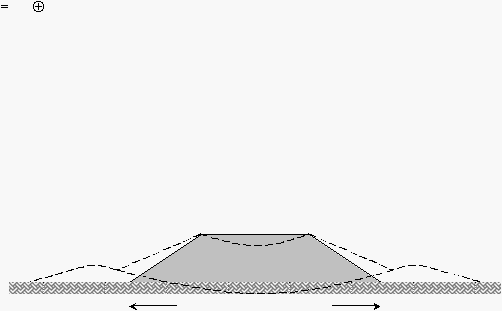
Gambar 2.15 Model
Keruntuhan
pada
Foundation Stability (Hird
dan
Jewel;
1990)
(Sumber: Proceeding of Seminar Road Construction in Indonesia with Special Reference to the
Role of Geosynthetics)
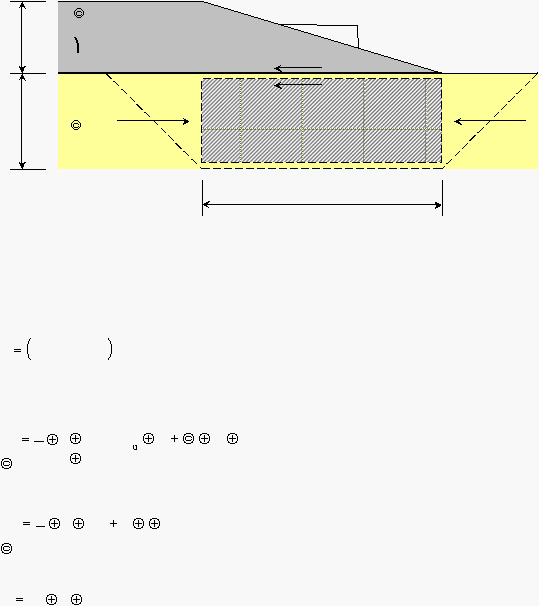
Akibat adanya beban timbunan, maka
tanah dasar
yang berupa tanah
lunak
akan
terdorong keluar. Hal inilah yang menjadi perhatian dalam analisa stabilitas tanah
dasar
pada
metode
keseimbangan
batas. Pada analisa keseimbangan batas
untuk
foundation
stability,
modus
keruntuhan yang
terjadi
adalah
modus
keruntuhan
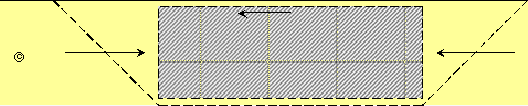
translasi dimana bidang keruntuhan akan terjadi pada bidang WXYZ sebagaimana
|
  32
a
u
yang ditunjukkan oleh Gambar
2.16. Pada
bidang
ini
akan bekerja
tekanan
tanah
aktif
(E
a
)
dan
tekanan
tanah
pasif
(E
p
)
yang
besarnya dapat
dihitung
dengan
menggunakan Teori
Rankine
ataupun
Teori
Coulomb.
Adapun
asumsi
yang
digunakan
dalam
analisa
keseimbangan
batas
untuk
foundation
stability
adalah
pada
bidang
WX
dan
YZ
tidak
bekerja
gaya
geser.
Dengan
demikian, secara
matematis besarnya kuat tarik
material geotekstil yang diperlukan dapat dihitung
dengan menggunakan Persamaan (2.17).
n
H
c
1
Reinforcing mat
T
W
Z
G
c
u
D
s
Soft subsoil
E
a
E
p
X
Y
L = nH
Gambar 2.16
Keseimbangan Batas pada Stabilitas Pondasi
(Sumber: Stabilenka Design Guide)
T
E
E
p
G SF ......................................................................................... (2.17)
Dimana:
E
1
a
2
s
D
2
2
c
D
H
D ..................................................................
(2.18)
E
1
p
2
s
D
2
2
c
D ................................................................................ (2.19)
G
c
u
n
H .....................................................................................................
(2.20)
|
  33
Keterangan:
T = Kuat tarik perlu geotekstil
E
a
=
Tegangan lateral aktif
E
p
=
Tegangan lateral pasif
G
=
Gaya geser
SF = Faktor keamanan
s
,
=
Berat
isi
c
u
=
Kohesi undrained
H = Tinggi timbunan
D = Tebal lapisan tanah dasar dimana terjadi keruntuhan
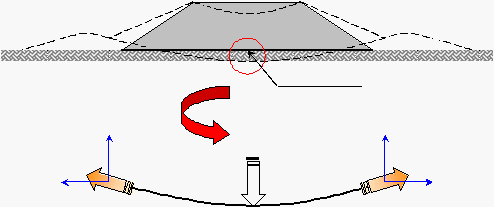
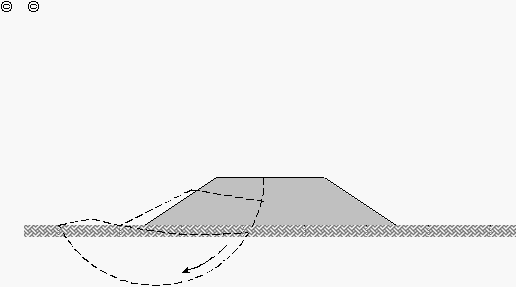
Gambar 2.17 Model Keruntuhan pada Overall Stability (Hird dan Jewel; 1990)
(Sumber: Proceeding of Seminar Road Construction in Indonesia with Special Reference to the
Role of Geosynthetics)
Analisa stabilitas keseluruhan (overall
stability) pada metode keseimbangan batas
memfokuskan
perhatian
pada
mekanisme keruntuhan
struktur
timbunan
secara
keseluruhan, yaitu stabilitas tanah timbunan dan tanah dasar. Untuk kondisi
dimana tanah dasar terdiri dari tanah yang relatif homogen dengan kuat geser yang
rendah, model keruntuhan umumnya diasumsikan sebagai keruntuhan rotasi dan
dianalisa dengan menggunakan Bishop Simplified
Method. Dengan demikian,
|
 34
maka faktor keamanan pada analisa stabilitas keseluruhan suatu struktur timbunan
didefinisikan sebagai perbandingan antara momen penahan yang tersedia dengan
momen pendorong
yang ada. Perhitungan dilakukan secara iterasi
untuk sejumlah
mekanisme keruntuhan rotasi
hingga
diperoleh
faktor
keamanan
terkecil.
Oleh
karena itu perhitungan analisa
stabilitas
keseluruhan pada metode keseimbangan
batas umumnya dilakukan dengan menggunakan bantuan program komputer.
Faktor keamanan untuk timbunan tanpa perkuatan dapat dihitung dengan
menggunakan persamaan:
cb
W
ub
tan
cos
1
tan
tan
SF
SF
W
sin
......................................................................... (2.21)
Dimana:
SF
=
Faktor keamanan
c
=
Kohesi
b
=
Lebar slice
W
=
Berat slice
u
=
Tegangan air pori
=
Sudut geser dalam
=
Kemiringan slice pada bidang keruntuhan
|
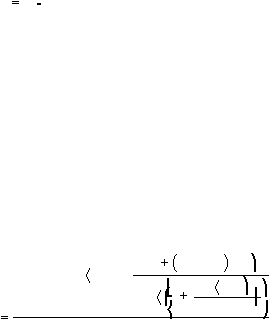 35
Apabila faktor keamanan struktur timbunan tanpa perkuatan tidak mencukupi,
maka faktor keamanan struktur timbunan dapat ditingkatkan dengan menggunakan
perkuatan geotekstil pada dasar timbunan. Gaya yang timbul pada material
geotekstil
akan
meningkatkan
momen penahan
pada
struktur
timbunan sehingga
akan meningkatkan faktor keamanan timbunan secara keseluruhan. Besarnya
momen penahan tambahan yang terjadi pada struktur timbunan akibat adanya
perkuatan geotekstil pada dasar timbunan adalah:
M
r
T
y ........................................................................................................ (2.22)
Dimana:
Mr
=
Momen penahan tambahan akibat material geotekstil
T
=
Kuat tarik perlu geotekstil
y
=
Ordinat pusat kelongsoran
Sehingga besarnya kuat
tarik
geotekstil
yang diperlukan sebagai perkuatan dasar
timbunan adalah:
SF
W
sin
cb
W
ub
tan
cos
1
tan
tan
T
SF
y
.................................................. (2.23)
Dimana:
T
=
Kuat tarik perlu geotekstil
SF
=
Faktor keamanan
c
=
Kohesi
W
=
Berat slice
b
=
Lebar slice
u
=
Tegangan air pori
|
|
36
=
Sudut geser dalam
= Kemiringan slice pada bidang keruntuhan
y
=
Jarak antara resultan gaya tarik pada material geotekstil dengan pusat
kelongsoran
Walaupun perkuatan geotekstil pada dasar timbunan dapat memberikan gaya
penahan
tambahan
dalam arah
horizontal
sehingga
faktor
keamanan
timbunan
meningkat,
beban
vertikal
yang
bekerja pada tanah dasar akibat timbunan tetap
dipikul oleh tanah dasar. Apabila daya dukung tanah dasar tidak mencukupi, maka
akan terjadi deformasi
yang besar pada struktur timbunan. Besarnya daya dukung
timbunan di atas tanah lunak dapat dihitung
dengan menggunakan Persamaan
(2.24).
Q
ult
c
u
N
c
....................................................................................................... (2.24)
Dimana:
Q
ult
=
Daya dukung batas
c
u
=
Kohesi undrained
Nc
= Faktor kapasitas daya dukung
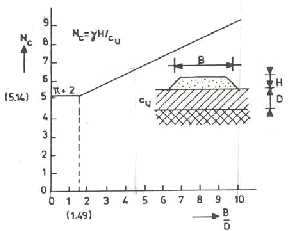
Adapun nilai Nc
diperoleh dari grafik yang dipublikasikan oleh Pilot (1976) seperti
pada Gambar 2.18.
|
 37
Gambar 2.18
Faktor Kapasitas Daya Dukung (Pilot; 1976)
(Sumber: Stabilenka Design Guide)
2.5
METODE ELEMEN
HINGGA
Metode
elemen
hingga
(finite
element method)
merupakan
metode
perhitungan
yang didasarkan pada konsep diskretisasi, yaitu membagi sebuah elemen kontinu
menjadi
elemen-elemen
kecil,
sehingga
suatu
sistem yang
mempunyai
derajat
kebebasan tidak terhingga dapat didekati dengan menggunakan sejumlah elemen
yang mempunyai derajat kebebasan tertentu. Dengan
demikian, metode elemen
hingga merupakan suatu metode penyelesaian yang bersifat pendekatan
(hampiran).
Dengan
membagi
sebuah elemen kontinu
menjadi elemen
yang
sekecil-kecilnya,
maka penyelesaian
yang diperoleh akan semakin akurat selama
elemen-elemen kecil tersebut dapat bekerja secara simultan. Metode elemen
hingga dapat digunakan untuk mencari distribusi beban yang bekerja pada suatu
elemen, seperti deformasi dan tegangan.
|
|
38
2.6
PLAXIS
PLAXIS adalah
sebuah paket program yang disusun berdasarkan
metode elemen
hingga yang telah dikembangkan secara khusus untuk melakukan analisa
deformasi dan stabilitas dalam bidang Geoteknik. Prosedur pembuatan model
secara grafis yang mudah memungkinkan pembuatan suatu model elemen hingga
yang rumit dapat dilakukan dengan cepat, sedangkan berbagai fasilitas yang
tersedia dapat digunakan untuk menampilkan hasil komputasi secara mendetail.
Proses perhitungannya sendiri sepenuhnya berjalan secara otomatis dan didasarkan
pada prosedur numerik.
Pengembangan
PLAXIS
dimulai
pada
tahun 1987
di
Universitas
Teknik
Delft
(Technical
University of
Delft)
atas
inisiatif
Departemen
Tenaga
Kerja
dan
Pengelolaan Sumber Daya Air
Belanda
(Dutch Department
of Public
Works and
Water Management). Tujuan awal dari pembuatan Program PLAXIS adalah untuk
menciptakan
sebuah
program komputer
berdasarkan
metode
elemen
hingga
dua
dimensi yang mudah digunakan untuk menganalisa tanggul-tanggul yang dibangun
di atas tanah lunak di dataran rendah Holland. Pada tahun-tahun berikutnya,
PLAXIS dikembangkan lebih lanjut hingga mencakup hampir seluruh aspek
perencanaan Geoteknik lainnya.
|
|
39
Pada
PLAXIS, struktur
Geoteknik pada
kondisi sesungguhnya
dapat dimodelkan
dalam regangan
bidang
maupun
secara
axi-simetri.
Model
regangan
bidang
digunakan untuk model geometri dengan penampang melintang yang kurang lebih
seragam, dengan kondisi tegangan dan kondisi pembebanan yang cukup panjang
dalam arah
tegak
lurus
terhadap
penampang tersebut. Perpindahan
dan
regangan
dalam arah tegak lurus terhadap penampang diasumsikan tidak terjadi atau bernilai
nol. Walaupun demikian, tegangan normal
pada arah tegak lurus terhadap
penampang diperhitungkan sepenuhnya dalam analisa. Model axi-simetri
digunakan untuk struktur berbentuk lingkaran dengan penampang melintang radial
yang
kurang
lebih
seragam dan
kondisi
pembebanan
mengelilingi
sumbu
aksial,
dimana deformasi dan kondisi tegangan diasumsikan sama pada setiap arah radial.
Dalam
model
axi-simetri
koordinat
x
menyatakan
radius
dan
koordinat
y
merupakan sumbu simetris dalam arah aksial. Koordinat x negatif tidak digunakan.
Penggunaan
regangan
bidang maupun
axi-simetri
akan
menghasilkan
model
elemen
hingga
dua
dimensi
dengan
dua
buah
derajat
kebebasan
translasi
pada
setiap titik nodalnya (arah x dan y).
|
 40
y
x
y
x
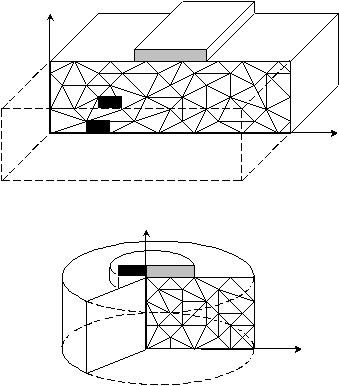
Gambar 2.19
Contoh Permasalahan Regangan Bidang dan Axi-simetri
(Sumber: Manual PLAXIS)
Elemen
tanah
dalam Program PLAXIS
dimodelkan
sebagai
elemen
segitiga.
PLAXIS membagi elemen segitiga ke dalam dua jenis, yaitu elemen segitiga
dengan 6 titik nodal dan elemen segitiga dengan 15 titik nodal. Elemen segitiga
dengan
15 titik nodal menggunakan interpolasi ordo empat untuk menghitung
perpindahan dan integrasi numerik melibatkan 12 titik Gauss (titik tegangan).
Untuk elemen segitiga dengan 6 titik nodal, ordo interpolasi adalah dua dan
integrasi numerik melibatkan tiga buah titik Gauss. Dengan demikian, maka
analisa
elemen
hingga dengan
menggunakan segitiga
dengan 15
titik
nodal
akan
menghasilkan
hasil
yang
lebih
akurat
dibandingkan dengan analisa
dengan
|
 41
menggunakan 6 titik nodal. Akan tetapi proses perhitungan akan lebih lambat jika
analisa dilakukan dengan menggunakan elemen segitiga dengan 15 titik nodal.
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
?
?
?
?
?
?
?
?
?
?
?
?
?
Gambar 2.20
Posisi Titik Nodal dan Titik Tegangan pada Elemen Tanah
(Sumber: Manual PLAXIS)
Dalam model
analisa
regangan
bidang,
gaya
yang
dihasilkan
akibat
adanya
perpindahan
yang diberikan
dinyatakan
dalam
gaya per
satu satuan
lebar
dalam
arah tegak lurus terhadap penampang. Dalam model analisa axi-simetri, gaya-gaya
yang dihasilkan adalah gaya-gaya yang bekerja pada bidang batas yang
membentuk busur lingkaran sebesar 1 radian yang saling berhadapan. Untuk
memperoleh
besarnya
gaya
yang
bekerja pada
model,
maka
gaya-gaya
tersebut
harus
dikalikan
dengan
faktor sebesar
2
.
Seluruh keluaran
lainnya
pada model
axi-simetri diberikan per satu satuan panjang dan bukan per radian.
|
 42
PLAXIS
selalu
menghasilkan
model
elemen hingga dua dimensi dengan
berdasarkan pada
suatu
model geometri. Model
geometri dibuat dalam bidang xy
yang berada dalam sistem koordinat global dimana arah z positif adalah arah yang
tegak lurus keluar dari bidang gambar.
Walaupun
PLAXIS
merupakan program dua
dimensi,
namun
tegangan-tegangan
tetap diperhitungkan berdasarkan sistem koordinat Cartesius
tiga
dimensi.
Dalam
suatu analisa regangan bidang,
zz
adalah tegangan yang bekerja tegak lurus keluar
dari
bidang
gambar.
Dalam
analisa
axi-simetri,
x
menyatakan koordinat
radial, y
menyatakan koordinat aksial dan z
menyatakan
arah tangensial. Dalam kasus
ini,
xx
menyatakan
tegangan
radial
dan
zz
menyatakan tegangan melingkar
(hoop
stress).
y
yz
yy
zy
yx
xz
xy
xx
x
zz
z
zx
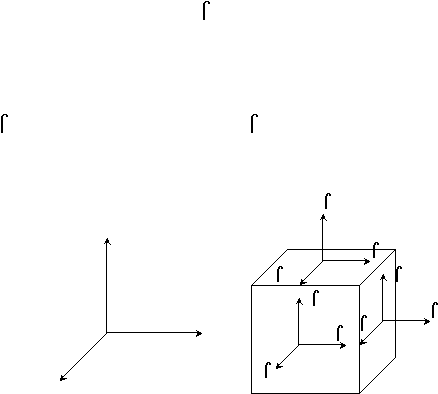
Gambar 2.21
Sistem Koordinat dan Perjanjian Tanda Positif untuk Tegangan
(Sumber: Manual PLAXIS)
|
 43
Dalam seluruh data keluaran, gaya dan tegangan tekan, termasuk tegangan air pori
ditetapkan bernilai
negatif, dan sebaliknya
gaya dan tegangan tarik akan bernilai
positif. Gambar 2.21 menunjukkan arah-arah tegangan yang bernilai positif.
Faktor keamanan
umumnya didefinisikan
sebagai
rasio antara beban runtuh
dengan beban kerja. Namun demikian, untuk
struktur tanah definisi di atas tidak
selalu dapat diaplikasikan. Sebagai contoh, pada struktur timbunan sebagian besar
beban
yang bekerja
diakibatkan
oleh
berat
sendiri
tanah
dan
peningkatan
berat
tanah umumnya tidak mengakibatkan keruntuhan. Dengan demikian, definisi yang
lebih tepat untuk faktor keamanan adalah:
SF
ult
all
........................................................................................................... (2.25)
Dimana:
SF = Faktor keamanan
ult
=
Kuat geser batas
all
=
Kuat geser ijin
Rasio dari kekuatan tanah yang tersedia terhadap kekuatan minimum yang dihitung
untuk mencapai keseimbangan adalah
faktor keamanan
yang
secara konvensional
digunakan
dalam Mekanika
Tanah.
Dengan
menerapkan
kondisi
standar
dari
Coulomb, faktor keamanan dapat diperoleh dengan persamaan:
SF
c
ult
n
tan
ult
c
all
n
tan
all
........................................................................................ (2.26)
|
 44
Dimana:
SF = Faktor keamanan
n
=
Tegangan normal
c
all
=
Kohesi yang diijinkan
c
ult
=
Kohesi yang tersedia
all
=
Sudut geser dalam yang diijinkan
ult
=
Sudut geser dalam yang tersedia
Prinsip
di
atas adalah
dasar dari
metode
phi/c reduction
yang
digunakan
dalam
PLAXIS untuk menghitung faktor keamanan global. Dengan pendekatan ini,
parameter tanah c dan tan
direduksi dengan proporsi yang sama. Reduksi
parameter kekuatan diatur oleh faktor pengali total
Msf. Parameter ini akan
ditingkatkan secara bertahap hingga keruntuhan terjadi. Faktor keamanan
kemudian didefinisikan sebagai nilai
Msf saat keruntuhan terjadi, hanya jika saat
keruntuhan
terjadi
suatu
nilai
yang kurang
lebih konstan
telah diperoleh
untuk
beberapa langkah pembebanan secara berturut-turut. Adapun penentuan faktor
keamanan dalam PLAXIS secara matematis dapat dinyatakan dengan:
Msf
c
ult
c
r
tan
ult
tan
r
.................................................................................... (2.27)
|
|
45
Dimana:
Msf = Faktor keamanan pada PLAXIS
c
ult
=
Kohesi yang tersedia
ult
=
Sudut geser dalam yang tersedia
cr
=
Kohesi tereduksi
r
=
Sudut geser dalam tereduksi
2.7
MATERIAL GEOSINTETIK
DALAM PROGRAM PLAXIS
Dalam Program PLAXIS,
material
geosintetik
yang
berbentuk
lembaran
dan
fleksibel
seperti
geotekstil
dan
geogrid
dimodelkan
sebagai
elemen geogrid.
Kekakuan aksial (EA)
merupakan data
input yang
tersedia dalam Program
PLAXIS untuk mendefinisikan
properti dari geotekstil atau geogrid yang akan
digunakan. Kekakuan aksial
yang dimasukkan sebagai data
input di dalam
Program PLAXIS dinyatakan dalam satuan
gaya per satu satuan lebar. Kekakuan
aksial material
geotekstil atau
geogrid umumnya diketahui karena telah diberikan
oleh pihak manufaktur geosintetik.
Jika
kekakuan
aksial
tidak
diketahui,
maka
besarnya kekakuan aksial dapat ditentukan melalui grafik yang menggambarkan
korelasi
antara perpanjangan
yang
dialami
oleh
material geotekstil
atau
geogrid
terhadap gaya yang diberikan dalam arah longitudinal. Kekakuan aksial merupakan
rasio antara
gaya per satu satuan lebar dengan regangan aksial. Secara matematis
kekakuan aksial dinyatakan dalam Persamaan (2.28).
|
 46
EA
F
............................................................................................................. (2.28)
Dimana:
l
l
............................................................................................................... (2.29)
Keterangan:
EA
=
Kekakuan aksial material geotekstil/geogrid
F
=
Kuat tarik material geotekstil/geogrid
=
Regangan aksial material
geotekstil/geogrid
l = Pertambahan panjang material geosintetik/geogrid akibat F
l
=
Panjang awal material geosintetik/geogrid
Elemen
geogrid
merupakan
elemen garis dengan dua buah
derajat kebebasan
translasi pada setiap titik nodalnya (u
x
, u
y
). Jika elemen tanah dimodelkan dengan
menggunakan elemen segitiga dengan 15 titik
nodal, maka setiap elemen
geogrid
didefinisikan dengan lima buah titik nodal, sedangkan elemen geogrid dengan tiga
titik nodal digunakan untuk elemen tanah dengan 6 titik nodal. Gaya aksial
dihitung pada setiap titik tegangan Newton-Cotes dan titik-titik tegangan ini
mempunyai
lokasi
yang sama dengan titik
nodal. Posisi
titik nodal dan titik-titik
tegangan dalam elemen geogrid ditunjukkan pada Gambar 2.22.
|
 47
?
Titik nodal
×
Titik tegangan
×
?
×
?
×
?
×
?
×
?
×
?
×
?
×
?
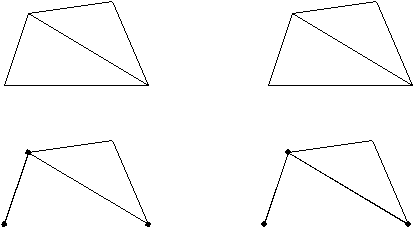
Gambar 2.22
Posisi
Titik
Nodal
dan
Titik
Tegangan
dalam
Elemen
Geogrid
dengan 3 dan 5 Buah Titik Nodal
(Sumber: Manual PLAXIS)
2.8
KORELASI EMPIRIS ANTAR PARAMETER
UNTUK TANAH LEMPUNG
Untuk
memperoleh parameter
tanah yang diperlukan dalam desain
struktur tanah,
ada
tiga
cara
yang
dapat
ditempuh, yaitu
melakukan
pengujian
langsung
di
lapangan, melakukan
pengujian laboratorium,
ataupun
dengan
menggunakan
korelasi empiris antar parameter yang telah dipublikasikan oleh para ahli.
Umumnya
parameter
tanah
diperoleh
dari
hasil
pengujian
laboratorium
ataupun
dari hasil pengujian langsung di lapangan. Pemakaian korelasi empiris antar
parameter
umumnya hanya
digunakan
apabila data tanah hasil pengujian di
laboratorium ataupun pengujian langsung di lapangan tidak tersedia ataupun untuk
melakukan
verifikasi
terhadap
hasil pengujian yang telah dilakukan. Berikut ini
adalah
beberapa
korelasi
empiris untuk tanah lempung yang diberikan oleh para
ahli:
|
 48
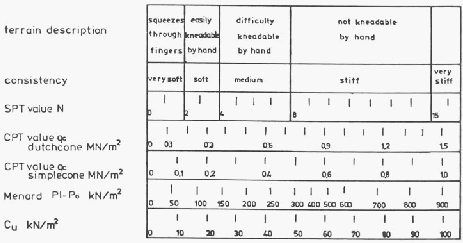
1. Hubungan antara konsistensi tanah dengan kohesi tanah undrained (c
u
)
Hamilton
(1987)
memberikan
interval
nilai
kohesi
tanah
dalam
kondisi
undrained berdasarkan konsistensi tanah. Adapun hubungan tersebut disajikan
pada Gambar 2.23.
Gambar 2.23 Interval Nilai Kohesi Tanah dalam Kondisi Undrained
Berdasarkan Konsistensi Tanah (Hamilton; 1987)
(Sumber: Stabilenka Design Guide)
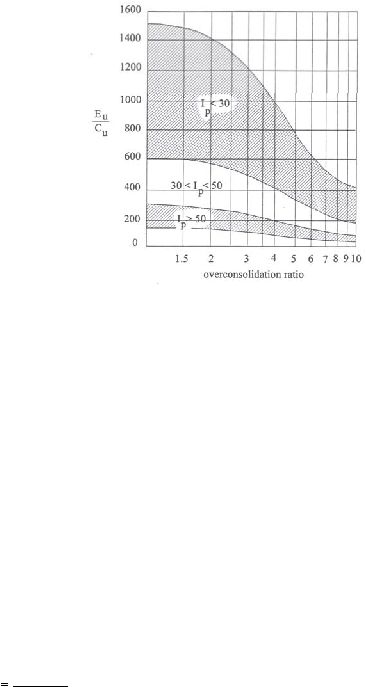
2. Korelasi antara modulus Young (E
u
)
dengan kohesi (c
u
)
tanah
Ducan
dan
Buchignani
(1976)
memberikan
hubungan
antara
modulus
Young
dengan
kohesi
tanah
pada
kondisi undrained
sebagai
fungsi
dari
indeks
plastisitas tanah dan overconsolidation ratio. Adapun
hubungan tersebut dapat
dilihat pada Gambar 2.24.
|
 49
Gambar 2.24 Korelasi
Antara
Kohesi
Tanah
dan
Modulus
Young
Tanah
dalam Kondisi Undrained
Berdasarkan Nilai OCR dan Indeks
Plastisitas (Ducan dan Buchignani; 1976)
(Sumber: PLAXIS Standard Course)
Korelasi
antara
modulus
elastisitas
dengan
kohesi
tanah
dalam kondisi
undrained juga diberikan oleh
Termaat,
Vermeer, dan Vergeer (1985). Secara
grafis, korelasi kedua parameter tersebut dapat dilihat
pada Gambar 2.25.
Adapun persamaan garis yang ada pada Gambar 2.25 diberikan oleh
Persamaan (2.31)
E
50
15000c
u
u
............................................................................................ (2.30)
I
p
%
Dimana:
E
u
50
=
Modulus Young undrained
c
u
=
Kohesi undrained
I
p
=
Indeks plastisitas
|
 50
Gambar 2.25 Korelasi
Antara
Kohesi
Tanah
dan
Modulus
Young
Tanah
dalam Kondisi Undrained Berdasarkan Nilai Indeks Plastisitas
(Termaat, Vermeer, dan Vergeer; 1985)
(Sumber: PLAXIS Standard Course)
3. Korelasi antara Poisson rasio (
)
dengan indeks plastisitas (I
P
)
tanah
Untuk tanah yang terkonsolidasi
normal,
Wroth
(1975) menyatakan
bahwa
Poisson
rasio
tanah
merupakan
fungsi
dari indeks plastisitas
tanah.
Adapun
hubungan antara
kedua parameter
tanah
tersebut
dapat
dilihat
pada Gambar
2.26.
Gambar 2.26
Hubungan Antara Indeks Plastisitas dengan Poisson Rasio
(Wroth; 1975)
(Sumber: PLAXIS Standard Course)
|
 51
4. Nilai kisaran parameter pada tanah lunak
Departemen
Pemukiman
dan
Prasarana
Wilayah
dalam
Pedoman Kimpraswil
No: Pt T-10-2002-B memberikan kisaran nilai parameter pada tanah lunak.
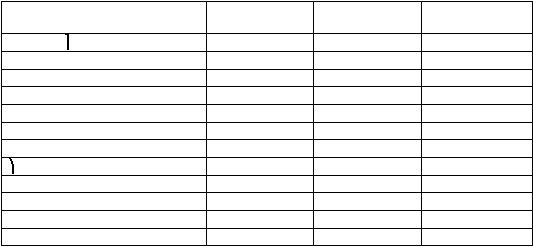
Adapun kisaran nilai yang diberikan dapat dilihat pada Tabel 2.1.
Tabel 2.1
Nilai Kisaran Parameter pada
Tanah Lunak (Departemen
Pemukiman dan Prasarana Wilayah; 2002)
Parameter
Tanah
Lempung
Lempung
Organik
Gambut
Berserat
Kadar air,
%
20 – 150
100 – 500
100 – 4000
Berat isi total, ã
b
kN/m
3
14 – 17
12 – 15
10 – 12
Kadar organik
%
<
25
25 – 75
>
75
Kohesi tak terdrainase, c
u
kPa
5 – 50
5 – 50
10 – 50
Batas cair, LL
%
60 – 120
–
–
Indeks plastis, PI
%
40 – 80
–
–
c'
kPa
0
0
0
'
21 – 27
25 – 35
30 – 40
Cc
–
–
1 – 20
Cc/(1 + C
0
)
0,1 – 0,3
0,3 – 1,0
–
C
v
m²
/th
1 – 10
5 – 50
10 – 100
C
á
cm/dt
(0,03 – 0,05)Cc
(0,04 – 0,06)Cc
1 – 4
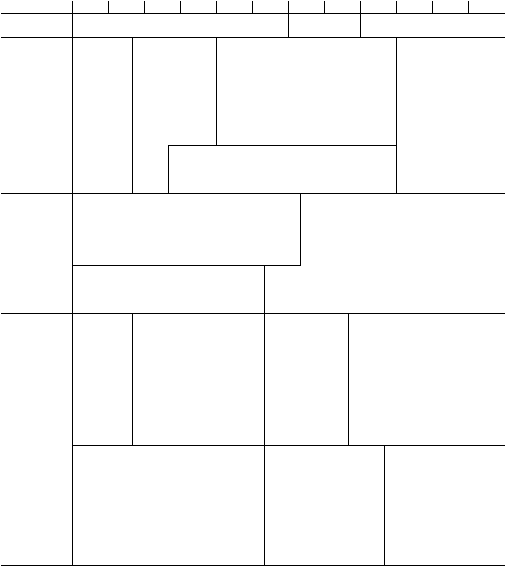
5. Hubungan antara perilaku drainase dengan koefisien permeabilitas (k) tanah
Menurut
Casagrande
dan
Fedum
(1940),hubungan
antara
koefisien
permeabilitas dan karakteristik pengaliran tanah diberikan pada Gambar 2.27.
Gambar
2.27
juga
memberikan
metode
pengujian
yang
tepat
dalam
menentukan koefisien permeabilitas tanah.
|
 52
Coefficient of Permeability k (cm/s) (log scale)
10²
101
10
0
10
–1
10
–2
10
–3
10
–4
10
–5
10
–
6
10
–
7
10
–
8
10
–9
Drainage
Good
Poor
Practically impervious
Soil type
Clean
gravel
Clean sands,
clean sand
and gravel
mixtures
Very fine sands, organic and
inorganic silts, mixtures of
sand silt and clay, glacial till,
stratified clay deposits, etc.
“Impervious”
soils (e.g.,
homogeneous
clays below
zone of
weathering)
“Impervious” soils modified by effects
of vegetation and weathering
Direct
determi-
nation of
k
Direct testing of soil in its original
position – pumping test; reliable if
properly conducted; considerable
experience required
Constant-head permeameter;
little experience required
Indirect
determi-
nation of
k
Falling-head
permeameter;
reliable; little
experience required
Falling-
head
permeame-
ter
unreliable;
much
experience
required
Falling-head
permeameter; fairly
reliable; considerable
experience necessary
Computation from grain-size
distribution; applicable only to
clean cohesionless sands and
gravels
Computation
based on results of
consolidation
tests; reliable;
considerable
experience
required
Gambar 2.27 Interval Nilai Koefisien Permeabilitas Tanah Berdasarkan Jenis
Tanah (Casagrande dan Fadum; 1940)
(Sumber: Soils and Foundations, Prentice Hall)
|