|
BAB 2
LANDASAN TEORI
2.1
Rekayasa Piranti Lunak
Menurut Pressman (2001,p20), rekayasa piranti lunak adalah pembangunan
dengan penggunaan prinsip-prinsip rancang bangun (engineering)
untuk
mendapatkan
piranti lunak ekonomis yang dapat
dipercaya
dan
bekerja
efisien
pada
mesin
yang
sesungguhnya.
Menurut
Lethbridge
dan
Laganiere
(2002,p5),
rekayasa
piranti lunak adalah
proses menyelesaikan masalah konsumen dengan pengembangan sistematik dari sistem
piranti lunak yang besar dan berkualitas dengan biaya, waktu, dan batasan-batasan yang
lainnya.
Menurut Pressman (2001,p26), untuk menyelesaikan masalah dalam suatu
industri, teknisi piranti lunak harus menggabungkan suatu strategi pembangunan yang
disebut
sebagai process model atau paradigma rekayasa piranti
lunak. Strategi tersebut
mencakup tiga elemen yaitu :
1.
Metode-metode (methods), yaitu menyediakan cara-cara teknis membangun piranti
lunak.
2.
Alat-alat bantu (Tools), yaitu
menyediakan dukungan otomatis atau semi otomatis
untuk metode-metode seperti Computer Aided Software Engineering (CASE) yang
mengkombinasikan software, hardware dan software engineering database.
3.
Prosedur-prosedur (procedures),
yaitu
merupakan penggabungan metode dan alat
bantu.
|
|
9
Menurut Pressman (2001,p28), Linear sequential model. Linear sequential model
menyarankan pendekatan yang sistematik dan berurutan untuk pengembangan piranti
lunak yang dimulai dari tingkat sitem dan bergerak ke tingkat analysis, design, coding,
testing, dan support.
Ada
lima
tahap
pengembangan pada
pengembangan
piranti
lunak
berdasarkan
linear sequential model :
-
Analisis kebutuhan piranti lunak
Proses mendapatkan kebutuhan yang dikerjakan secara intensif dan terfokus secara
spesifik pada piranti lunak. Untuk mengerti bagaimana aplikasi dirancang, seorang
teknisi piranti lunak harus mengetahui
informasi yang dibutuhkan dari piranti
lunak tersebut,
juga kebutuhan fungsi, perilaku, performance, dan tatap muka.
Kebutuhan
untuk sistem dan piranti
lunak harus didokumentasikan dan
dikomunikasikan dengan konsumen.
-
Design
Design perangkat lunak sebenarnya proses yang terdiri dari beberapa langkah yang
tertuju
pada
empat
attribute yang berbeda
pada
sebuah
program :
struktur
data,
arsitektur
perangkat
lunak,
representasi
tatap muka,
dan
detil
prosedural
(algoritmik).Proses Design ini mengubah kebutuhan menjadi representasi dari
piranti
lunak
yang dapat diuji kualitasnya sebelum memulai coding. Desain
juga
didokumentasikan dan menjadi bagian dari konfigurasi piranti lunak.
-
Coding
Desain harus ditranslasikan ke bentuk yang dapat dibaca oleh mesin. Proses
coding melakukan tugas ini. Apabila desain dilakukan dengan cara yang detil,
coding dapat diselesaikan secara sistematis.
|
|
10
-
Testing
Setelah
code
telah
dihasilkan,
pegujian
program dilakukan.
Proses
pengujian
difokuskan pada logika internal dari piranti lunak, menjamin bahwa seluruh bagian
telah diuji, juga pada bagian fungsi eksternal, melakukan pengujian untuk mencari
kesalahan
dan
menjamin
bahwa
input
yang diberikan
dapat
mendapatkan
hasil
yang sesuai dan benar.
-
Support
Perangkat lunak akan dilakukan perubahan setelah diberikan kepada pelanggan
(pengecualian pada embedded software). Perubahan akan terjadi karena error yang
ditemukan karena piranti lunak harus beradaptasi untuk mengakomodasi
perubahan
di
dalam lingkungan
eksternal
(contoh,
pada
suatu
perubahaan
diperlukan karena adanya system operasi yang baru atau device baru), atau karena
pelanggan
membutuhkan
fungsi
tambahan
atau
perbaikan
performance.Support /
maintenance menjalankan setiap fase sebelumnya dalam melakukan perubahan.
Menurut Lethbridge
dan
Laganiere
(2002,p402), waterfall model
adalah
suatu
cara klasik melihat rekayasa piranti
lunak
yang
menjelaskan
kebutuhan, design
dan
quality assurance. Waterfall model menyarankan agar teknisi piranti lunak bekerja
dalam tahapan yang terbagi dan berurutan. Sebelum menyelesaikan suatu tahap, teknisi
harus melakukan quality assurance sehingga pada tahap selanjutnya dibangun dari dasar
yang baik dan kuat.
|
|
11
2.2
Interaksi Manusia dan Komputer
Sebuah program yang memiliki interaksi dengan user haruslah bersifat interaktf .
Suatu program yang
interaktif dan baik harus bersifat user friendly, dengan
lima
kriteria (Shneiderman 2005, p15) sebagai berikut.
1.
Waktu belajar yang tidak lama.
2.
Kecepatan penyajian informasi yang tepat.
3.
Tingkat kesalahan pemakaian rendah.
4.
Penghafalan sesudah melampaui jangka waktu.
5.
Kepuasan pribadi.
Sebuah aplikasi yang sudah memenuhi kelima kriteria diatas maka aplikasi
tersebut benar-benar dapat dikatakan user-friendly.
Menurut (Shneiderman
2005, p74), dalam merancang
sistem
interaksi
manusia
dan komputer yang baik juga harus memperhatikan delapan aturan utama (eight golden
rules), yaitu:
1.
Strive for consistency (berusaha untuk konsisten).
2.
Enable frequent user to use shortcuts (memungkinkan pengguna untuk
menggunakan jalan pintas).
3.
Offer informative feedback (memberikan umpan balik yang informatif).
4.
Design dialogs to yield closure (pengorganisasian yang baik sehingga pengguna
mengetahui kapan awal dan akhir dari suatu aksi).
5.
Offer simple error handling (memberikan pencegahan kesalahan dan penanganan
kesalahan yang sederhana).
6.
Permit
easy
reversal
of
actions
(memungkinkan
kembali
ke
aksi
sebelumnya
dengan mudah).
|
|
12
7.
Support
internal locus
of
control
(memungkinkan
pengguna
untuk
menguasai
dan mengontrol sistem).
8.
Reduce short term memory load (mengurangi beban ingatan jangka pendek,
sehingga pengguna tidak perlu banyak menghafal).
Delapan
aturan
emas
inilah
yang
menjadi
pedoman
dalam menentukan
kehandalan sebuah program dalam melakukan
interaksi dengan
user, karena
hal inilah
yang secara tidak langsung mempengaruhi hidup dari program tersebut.
2.3
Pemrograman Berorientasi Objek
Object-oriented mencakup bidang aplikasi yang sangat luas. Para pengguna
sistem
komputer dan sistem
lain
yang didasarkan atas teknologi komputer
merasakan
efek
object-oriented
dalam bentuk
meningkatnya
aplikasi
software
yang
mudah
digunakan dan servis yang lebih fleksibel, yang muncul dalam berbagai bidang industri,
seperti
dalam perbankan,
telekomunikasi,
dan
sebagainya.
Sedangkan
bagi
software
engineer,
object-oriented berpengaruh dalam bahasa pemrograman, metodologi
rekayasa, manajemen proyek, hardware dan sebagainya.
Analisis dan perancangan berorientasi objek amat sangat perlu dilakukan dalam
pengembangan
sistem berorientasi
objek.
Hanya
dengan
kemampuan
menggunakan
bahasa pemrograman berorientasi objek yang andal, kita dapat membangun suatu sistem
berorientasi objek,
namun sistem
aplikasi
yang dibangun akan
menjadi lebih baik
lagi
bila langkah awalnya didahului dengan
proses analisis dan perancangan berorientasi
objek, terutama untuk membangun sistem yang mudah dipelihara.
Analisis berorientasi objek adalah metode analisis yang memeriksa requirements
(syarat/keperluan yang harus dipenuhi suatu sistem) dari sudut pandang kelas-kelas dan
|
|
13
objek-objek
yang ditemui
dalam ruang
lingkup permasalahan. Sedangkan perancangan
berorientasi objek adalah metode untuk mengarahkan arsitektur software yang
didasarkan pada manipulasi objek-objek sistem atau subsistem.
Pemrograman berorientasi objek
merupakan kelanjutan dari proses analisis dan
desain berorientasi objek.
Dalam pemrograman berorientasi objek
ini, komponen
yang
didesain
dalam
proses
desain kemudian
diimplementasikan dengan
menggunakan
bahasa
pemrograman
berorientasi
objek. Syarat sebuah bahasa pemrograman
berorientasi objek adalah bila bahasa pemrograman tersebut memiliki fitur untuk
mengimplementasikan keempat konsep berorientasi objek, yaitu abstraksi,
encapsulation, polymorphism dan inheritance.
Dikenal beberapa bahasa pemrograman berorientasi objek, seperti C++, Java,
Visual Basic, dan sebagainya.
2.4 Keunggulan Object-Oriented dalam Banyak Kasus
Sekarang
ini
terdapat
beberapa
paradigma
yang
digunakan
dalam rekayasa
software, diantaranya procedure-oriented, object-oriented, data structure-oriented, data
flow-oriented
dan
constraint oriented. Tiap-tiap paradigma
tersebut
cocok
untuk
beberapa kasus dan bagian dari seluruh kemungkinan ruang lingkup aplikasi, tetapi
menurut Booch berdasarkan pengalamannya, object-oriented dapat diaplikasikan dalam
seluruh ruang lingkup.
Untuk
memahami
mengapa
object-oriented
unggul
dalam banyak
kasus,
harus
memahami
masalah
yang
dihadapi
perusahaan
rekayasa
software.
Pertama,
software
sulit untuk dimodifikasi bila memerlukan pengembangan. Kedua,
proses pembuatan
software memerlukan waktu yang cukup lama sehingga kadang kala melebihi anggaran
|
|
14
dalam
pembuatannya.
Ketiga,
para
programmer
selalu
membuat
software
dari
dasar
karena tidak adanya kode yang bisa digunakan ulang (reuse).
Kebanyakan perusahaan tersebut sebelumnya telah
menggunakan pemrogramam
structural. Metode structural
menggunakan
pendekatan
dengan pendekatan top-down,
yang mana pendekatan ini memecahkan masalah dengan menbagi masalah kedalam
komponen-komponen
hingga
didapatkan
komponen yang tidak dapat dibagi-bagi lagi.
Pendekatan
dengan
cara
top-down
ini
telah
membuat
peningkatan
dalam kualitas
software, tetapi dalam sistem yang berskala besar, pendekatan ini sering menemui
banyak
masalah.
Pemrograman
structural
seringkali
tidak
dapat
mendesain
apa
yang
akan terjadi dalam sistem yang telah selesai tanpa mengimplementasikan sistem terlebih
dahulu. Jika ditemui
kesalahan
dalam sistem,
maka
desain
harus
disusun ulang
dari
awal
sampai akhir. Hal ini akan terjadi pemborosan biaya dan waktu.
Perbedaan
antara
metode
structural
dan
object-oriented
terletak
pada
bagaimana
data
dan
fungsi
disimpan.
Dalam metode
structural,
data
dan
fungsi
disimpan
terpisah.
Biasanya semua data ditempatkan sebelum
fungsi ditulis.
Seringkali tidak terpikirkan
sebelumnya untuk
mengetahui data mana yang digunakan dalam suatu fungsi tertentu.
Tetapi
dalam
object-oriented,
data
dan
fungsi
yang
berhubungan
dalam
suatu
objek
disimpan bersama-sama dalam satu kesatuan.
Orang akan
lebih mudah
memahami sistem sebagai
objek
daripada
prosedur,
karena
biasanya
orang
berpikir
dalam
bentuk
objek.
Karena
secara
alamiah
lebih
mudah
memikirkan
suatu sistem dalam bentuk
objek-objek,
tidak
heran
kalau object-oriented
menjadi
lebih terkenal.
Satu alasan mengapa object-oriented menguntungkan bagi programmer
adalah
karena
programmer
dapat
mendesain
program
dalam
bentuk
objek-objek
dan
hubungan
|
|
15
antar
objek
tersebut untuk
kemudian
dimodelkan dalam
sistem
nyata. Keuntungan
yang lain
adalah proses pembuatan
software dapat dilakukan dengan lebih cepat karena software
dibangun dari objek-objek standar, dapat menggunakan ulang model yang ada, dan dapat
membuat
model
yang
cepat
melalui
metodologi.
Kualitas
yang
tinggi
dari software
dapat
dicapai karena
adanya tested
component. Lebih mudah
dalam maintenance karena perbaikan
kode
hanya
diperlukan
pada
satu
tempat
(bukan
diurut
dari
awal).
Mudah
dalam
membangun
sistem yang
besar
karena
subsistem dapat
dibuat
dan
diuji
secara
terpisah.
Mengubah sistem
yang sudah ada tidak memerlukan membangun ulang keseluruhan sistem.
2.5 Penjadwalan
2.5.1 Teori Penjadwalan (Timetabling)
Dalam salah satu paper-nya “A Hybrid Genetic Algorithm for Highly
Constrained Timetabling Problems”, Edmund K.Burke, et all mendefinisikan
penjadwalan (timetabling) sebagai berikut :
Timetabling is the problem of scheduling a set of events (for example : exams, lectures,
tutorials) to specific time slots such that no person or resource is expected to be in more
than
one
location
at
the same time
and that there
is
enough
space available in each
location for the number of people expected to be there.
Menurut Burke,E,Petrovic,S (2002) dan Wren, penjadwalan didefinisikan
sebagai berikut :
Timetabling is the allocation, subject of constraints, of given resources to objects being
placed in
space time, in such a way to satisfy as nearly as possible a set of desirable
objectives.
|
|
16
Berdasarkan definisi di atas, penjadwalan adalah pengalokasian sumber daya pada
objek-objek yang ada pada ruang waktu
dan bergantung pada kendala-kendala
sedemikian sehingga sedapat mungkin memenuhi sekumpulan sasaran yang diinginkan.
Secara
sederhana,
penjadwalan
dapat
diartikan sebagai
pengalokasian sumber-sumber
daya yang tersedia pada ruang waktu yang ada sehingga memenuhi kondisi-kondisi
tertentu.
Dalam proses
penjadwalan,
sumber
daya
yang
ada
harus
dialokasikan
secara
optimal, efektif dan efisien, serta sedapat mungkin memenuhi kebutuhan yang ada
namun
biaya
yang
harus
dikeluarkan
harus
pantas.
Penjadwalan
merupakan
masalah
yang sangat sulit dan telah menjadi bahan penelitian di bidang Teknik Riset Operasional
(TRO) dan Inteligensia Semu (IS). Menurut Fang, sulitnya penjadwalan disebabkan oleh
beberapa hal antara lain :
-
Penjadwalan merupakan masalah NP-Complete (Non-deterministic Polynomial-
Complete), yaitu suatu permasalahan dimana dengan bertambahnya variable secara
linier maka waktu yang diperlukan untuk memecahkan masalah itu bertambah
secara
eksponensial.
Hal
ini
sering
disebut
juga
Combinatorial
Explosion, selain
itu
ruang
solusi
yang
mungkin
(space
of
possible
solutions) untuk kebanyakan
masalah riil terlalu besar untuk dilakukan brute-force search atau pencarian
yang
tidak terarah (undirected search).
-
Teknik
pencarian
tingkat
tinggi
dengan
menggunakan
berbagai
heuristcic
untuk
memangkas search space tidak menjamin dihasilkannya suatu solusi yang optimal
dan sangat sulit untuk mendesain suatu heuristic yang efektif.
-
Masalah penjadwalan sering menjadi rumit karena adanya special constraints.
|
|
17
-
Penjadwalan di dunia nyata sering melibatkan constraints yang tidak dapat dengan
tepat direpresentasikan atau bahkan tidak dapat dengan tepat dinyatakan.
2.5.2
Constraints Penjadwalan
Secara umum, masalah penjadwalan terdiri dari pengalokasian sejumlah event ke
dalam periode waktu dan tempat
terbatas dengan
meminimalkan pelanggaran terhadap
serangkaian
constraint. Masalah penjadwalan
yang berbeda
memiliki
constraint
yang
berbeda pula. Di dalam penjadwalan dikenal dua macam constraints (persyaratan), yaitu
-
Hard Constraint
Hard Constraint harus dipertimbangkan karena jadwal yang melanggar hanya satu
dari
constraint ini menjadi tidak berguna. Misalnya, tidak ada orang yang
dialokasikan
untuk
mengajar
dua
atau
lebih
mata
kuliah
pada waktu yang
bersamaan.
-
Soft Constraint
Soft Constraint tidak esensi untuk dipenuhi. Jadwal yang melanggar constraint ini
masih dapat digunakan, meskipun hasilnya kurang memuaskan. Misalnya, asisten
tidak mengajar 3 shift berturut-turut.
Berikut ini adalah beberapa contoh hard constraint dan soft constraint di dalam
course timetabling untuk institusi pendidikan :
Contoh hard constraint :
-
Dosen
hanya
dapat
mengajar
pada
hari, waktu
dan
mata
kuliah
tertentu
sesuai dengan pilihannya (teacher’s availability).
-
Mahasiswa dan dosen hanya bisa berada pada satu tempat pada satu waktu.
|
|
18
-
Satu
ruangan
hanya
bisa
dipakai oleh
satu
mata
kuliah
saja
pada
waktu
tertentu.
-
Kapasitas ruangan harus lebih besar atau sama dengan jumlah mahasiswa
yang mengambil kelas tersebut.
Contoh soft constraint :
-
Jumlah maksimum dan minimum
shift dosen mengajar dan mahasiswa
mengikut mata kuliah dalam satu hari.
-
Shift yang diikuti oleh mahasiswa dalam satu hari sebaiknya berurutan dan
berada dalam satu gedung atau satu ruangan.
-
Mata kuliah tertentu sebaiknya
memakai ruangan yang
memiliki fasilitas
tertentu.
2.5.3
Metode Penyelesaian Masalah penjadwalan
Berbagai metode atau pendekatan untuk menyelesaikan masalah penjadwalan
telah digunakan, berikut ini dipaparkan secara singkat mengenai pendekatan yang
pernah digunakan untuk menyelesaikan masalah penjadwalan :
1.
Pendekatan random search / exhaustive search
Random search merupakan teknik pencarian solusi secara acak. Semakin
besar
ruang
solusi
(solution space)
dan
semakin
banyak
constraint
akan
memperkecil kemungkinan untuk mendapatkan solusi yang baik , oleh karena itu
mencari secara acak suatu solusi yang baik adalah seperti mencari jarum di dalam
tumpukan
jerami. Exhaustive search tidak
dapat digunakan
untuk
masalah NP-
Complete karena search space-nya yang sangat besar.
|
|
19
2.
Pendekatan riset operasional
a.
Enumerative search
-
Mathematical programming
Mathematical programming adalah salah satu teknik yang
digunakan untuk mengoptimasi suatu fungsi yang dibatasi oleh
variable bebas, tetapi mathematical programming hanya cocok
untuk
masalah
penjadwalan
yang sederhana. Linear
programming
dan integer programming merupakan dua contoh pendekatan
yang
pernah dipakai.
-
Dynamic programming
Dynamic
programming adalah implicit enumerative search
method yang dapat dilihat sebagai teknik divide and conquer. Untuk
menyelesaikan
suatu
masalah
yang besar,
dilakukan
pemecahan
masalah yang tersebut menjadi bagian-bagian kecil yang
independen.
Untuk
masalah penjadwalan
yang
kompleks,
pendekatan ini tidak efektif.
-
Branch and bound
Metode ini juga merupakan implicit enumerative search
method. Pendekatan ini terdiri dari dua prosedur dasar. Branching
adalah proses mempartisi masalah yang besar menjadi dua atau
lebih masalah kecil (subproblem) dan bounding adalah proses
menghitung batas bawah pada solusi optimal dari subproblem yang
bersangkutan. Untuk masalah penjadwalan yang kompleks
pendekatan ini juga tidak efektif.
|
|
20
b.
Heuristic Search
-
Simulated Annealing (SA)
Simulated Annealing merupakan
single
solution
randomized
heuristic yang
efektif.
SA
bekerja
berdasarkan
proses
annealing.
Annealing adalah suatu proses termal
untuk
memperoleh kondisi
energi
terendah dari suatu benda padat di dalam
suatu
heat bath. Prosesnya
terdiri
dari
dua
langkah:
pertama,
naikkan
suhu heat bath
sampai
maksimum dimana benda padat itu akan mencair, kedua, turunkan suhu
heat bath perlahan-lahan sampai partikel-partikel itu
menyatu kembali di
lantai dalam bentuk padat. SA meng-update satu solusi tunggal pada
setiap iterasi. Pada dasarnya, SA merupakan local search method.
-
Tabu Search (TS)
Tabu search
merupakan
salah
satu evolutionary
heuristic yang
meng-update satu solusi tunggal. Tabu search dimulai dengan membuat
solusi
acak dan
secara
berturut-turut
pindah (move)
ke
salah
satu
tetangganya. Setiap
kali suatu move dilakukan,
solusi
sebelumnya
akan
dimasukkan ke dalam suatu daftar yang disebut tabu list. Dari suatu solusi
yang diberikan, tidak semua neighbour dapat dicapai. Setiap perpindahan
membawanya pada
solusi
terbaik
yang berada di sekitarnya, tetapi jika
perpindahan
itu
ada
di
dalam tabu
list
maka
hanya
diterima jika dapat
menurunkan nilai dari
fungsi objektif sampai di bawah level
yang
telah
dicapai sejauh ini (aspiration level).
|
|
21
3.
Pendekatan Inteligensia Semu
a.
Constraints Satisfaction problem (CSP)
Menurut Anbulagan et al. (2000,p7) :
Permasalahan umum dari CSP adalah untuk menemukan satu atau
lebih solusi yang dapat memuaskan set constraint yang diberikan. Masing-
masing constraint membatasi kombinasi dari nilai-nilai dimana sebuah set
variable dapat mengambil secara simultan (terus-menerus). Sebuah solusi
untuk masalah CSP adalah penetapan sebuah nilai (value) terhadap setiap
variabel
dari
domain
variabel
yang memuaskan
semua
kendala
yang
diberikan. Apabila ada beberapa solusi maka akan dicoba untuk
menemukan
solusi
yang
optimal
berdasarkan sebuah fungsi objektif yang
spesifik. Namun, apabila tidak terdapat solusi maka akan diminta untuk
menemukan
“solusi
terdekat”
yang terbaik berdasarkan sebuah fungsi
objektif yang spesifik.
b.
Rule-based Expert System
Dalam pendekatan ini digunakan suatu
rule-based language untuk
mencoba menspesifikasikan constraint dan heuristic yang digunakan human
expert untuk memecahkan
masalah
yang bersangkutan. Rule-based systems
jarang digunakan untuk permasalahan optimasi.
c.
Neural Networks
Menurut
Rao,
Vailuru
dan
Rao,
Hayagriva,
Jaringan
Syaraf
Tiruan
(Atrificial Neural Network) adalah suatu sistem komputasi yang
mengikuti
|
|
22
mekanisme
kerja
syaraf
biologis
manusia.
Sistem ini
diharapkan
dapat
menghasilkan
fleksibiliti
dan
kekuatan
otak
manusia.
Sistem ini
juga
menggunakan representasi dari sebuah neuron (sel syaraf) manusia dan
interaksi diantara neuron-neuron tersebut sebagai dasar dari prinsip kerjanya.
Pendekatan
ini
kelihatannya
menjanjikan,
tetapi
belum
banyak
hasil
yang
bisa dicapai saat ini.
2.6
Algoritma Genetik
Algoritma
Genetik
adalah
suatu algoritma
pencarian stokastik (bekerja
berdasarkan acak)
yang
didasarkan
pada
mekanisme
seleksi
alami
dan
genetika.
Algoritma
genetik diinspirasikan
dari
teori
evolusi
Darwin.
Sebuah
masalah
akan
dipecahkan oleh Algoritma
Genetik dengan menggunakan proses evolusi, dari proses
evolusi
tersebut
akan
diambil
solusi
yang terbaik. Solusi
terhadap masalah
yang
dihasilkan
oleh
Algoritma
Genetik
dapat
berubah-ubah
(evolusi).
Hal
ini
disebabkan
oleh penggunaan metode acak pada awal Algoritma Genetik. Pemecahan masalah
dengan menggunakan Algoritma Genetik dapat dilihat pada gambar di bawah ini.
|
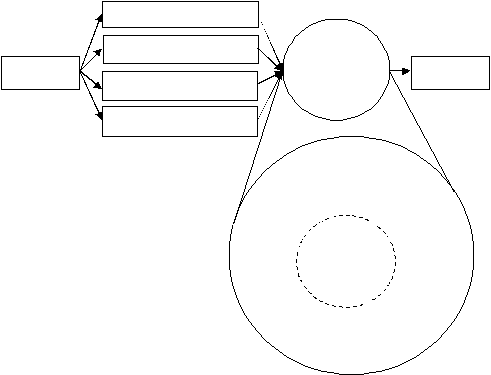 23
coding of solutions
problem
objective function
genetic
operators
genetic
search
solution
specific
fitness
assignment
mutation
genetic
search
selection
replication
recombination
crosssover
Gambar 2.1 Pemecahan Masalah Menggunakan Algoritma Genetik
2.6.1
Sejarah Algoritma Genetik
Algoritma Genetik pertama kali dikembangkan oleh John Holland bersama
rekan-rekan dan mahasiswa-mahasiswanya di University of Michigan pada tahun 1970-
an. Tujuan dari penelitian yang mereka lakukan adalah sebagai berikut :
-
Menggambarkan dan menjelaskan secara
tepat proses-proses adaptif dari
sistem-
sistem alamiah.
-
Merancang
artificial
systems
software
yang
menerapkan
mekanisme-mekanisme
yang penting dari sistem-sistem alamiah.
|
|
24
Sejak saat itu Algoritma Genetik berkembang dengan pesat. Algoritma Genetik
baik
secara
teori
maupun
secara
empiris
terbukti
mempunyai
kemampuan
pencarian
yang tangguh dalam search space yang kompleks.
2.6.2
Latar Belakang Biologi
Setiap
organism terdiri
dari
sel-sel.
Masing-masing
sel
memiliki
serangkaian
kromosom yang sama. Kromosom adalah kumpulan dari DNA yang membentuk sebuah
model untuk organism. Sebuah kromosom terdiri dari gen-gen rangkaian DNA. Masing-
masing gen membentuk protein tertentu. Dengan kata lain gen-gen tersebut membentuk
sebuah cirri khusus, misalnya warna mata. Beberapa kemungkinan warna mata tersebut
adalah
warna
mata
hitam, biru,
hijau, coklat
yang
disebut
Alela. Masing-masing gen
tersebut mempunyai posisi dalam kromosom. Posisi tersebut disebut Lokus.
Semua kromosom disebut Genom. Beberapa rangkaian gen dalam genom disebut
Genotif. Sifat fisik atau mental yang terbentuk dari gentotif disebut sebagai Fenotif,
seperti warna mata, kepandaian.
Kehidupan di dunia dipengaruhi oleh proses seleksi alami, rekombinasi, dan
mutasi. Ketika dua organism bertemu dan melakukan perkawinan maka keturunan yang
terbentuk
adalah
hasil gabungan dari sebagian gen ayahnya dan sebagian
lagi dari
gen
ibunya. Proses ini disebut dengan Rekombinasi. Kadang-kadang beberapa gen dapat
terkena mutasi. Untuk lebih jelasnya, dapat dilihat pada gambar di bawah ini.
|
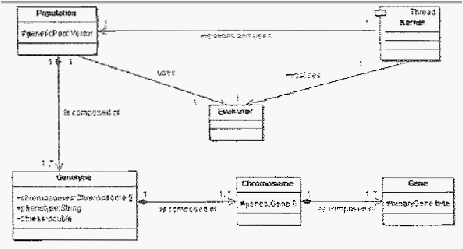 25
Gambar 2.2 Class Diagram Dari Algoritma Genetik
Sumber : Obitko, Marek, 1998
2.6.3
Penjelasan Algoritma Genetik
Algoritma Genetik berbeda dengan teknik pencarian konvensional. Algoritma
Genetik
diawali dengan
inisialisasi
sejumlah
solusi
secara
random yang
disebut
Populasi. Setiap individu dalam populasi tersebut disebut dengan kromosom. Kromosom
menggambarkan sebuah solusi terhadap masalah yang ada. Sebuah kromosom biasanya
berupa kumpulan string,
tetapi
bisa
juga
berupa
kumpulan karakter. Suatu populasi
berada
dalam
satu
generasi.
Setiap
kromosom
yang
ada
dalam
suatu
populasi
yang
berada dalam satu
generasi, akan dievaluasi dengan menggunakan
ukuran fitness value
(nilai kecocokan).
Untuk
menciptakan suatu
generasi
yang baru, kromosom yang baru
(offspring)
dibentuk dari hasil penggabungan duakromosom dari generasi sebelumnya melalui
proses
penyilangan
(crossover)
atau
hasil
dari
modifikasi
sebuah
kromosom melalui
proses
mutasi (mutation). Generasi
baru dibentuk dari
hasil seleksi berdasarkan fitness
value yang terdiri dari beberapa
induk kromosom dan offspring, yang
lainnya dibuang
|
 26
supaya jumlah
kromosom dalam populasi
tersebut
tetap. Kromosom
yang
lebih
baik
mempunyai kemungkinan yang lebih besar untuk dipilih, setelah melewati beberapa
generasi,
Algoritma
Genetik akan
menemukan kromosom yang terbaik dan diharapkan
kromosom tersebut merupakan solusi yang terbaik (optimal) atau yang mendekati solusi
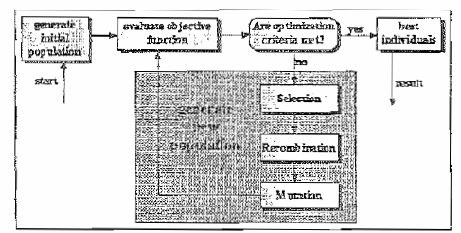
terbaik (suboptimal). Struktur
Algoritma
Genetik dapat dilihat pada gambar di bawah
ini.
Gambar 2.3 Struktur Algoritma Genetik
Sumber : Obitko, Marek, 1998
Bentuk standard Algoritma Genetik dapat ditulis dalam pseudocode sebagai
berikut.
Procedure GeneticAlgorithm
Begin
T=0;
Initialize P(t);
Evaluate P(t);
While not (termination condition) do
Begin
t=t+1;
|
|
27
Select P(t) from P(t-1);
Recombine P(t);
Evaluate P(t);
End
End
Proses inisialisasi P(t) akan menghasilkan populasi awal P(0). Setiap alternative
solusi
yang
terdapat
pada
populasi
awal
kemudian dievaluasi.
Jika solusi yang
diharapkan
terpenuhi
maka
proses
akan
berhenti. Jika
nilai optimal
yang
diharapkan
tidak terpenuhi maka Algoritma Genetik akan masuk ke dalam perulangan yang disebut
generation. Populasi P(t+1) akan dihasilkan dalam 2 tahap, yaitu tahap seleksi dan tahap
rekombinasi. Pada tahap seleksi, populasi sementara dibentuk dengan memilih sejumlah
alternative solusi yang
terdapat dalam
P(t) secara random
(acak). Pada tahap
rekombinasi, akan dihasilkan populasi baru melalui proses penyilangan (crossover) dan
mutasi
(mutation),
kemudian
populasi
baru
tersebut akan dievaluasi lagi. Jika nilai
optimal yang diharapkan masih tidak dipenuhi,
maka
Algoritma
Genetik
melanjutkan
proses perulangan, sedangkan kalau kondisi optimalnya dirasakan sudah terpenuhi maka
Algoritma Genetik akan keluar dari proses perulangan.
Dalam Algoritma
Genetik
terdapat
banyak
kombinasi
operator
dan
parameter
yang dapat digunakan. Untuk kasus/constraint
yang berbeda, operator dan parameter
yang digunakan pun berbeda, maka harus dilakukan uji coba untuk menentukan operator
dan parameter yang terbaik, sedangkan untuk kasus/constraint yang sama, operator dan
parameter yang digunakan sama.
|
 28
2.6.4
Operator-operator dalam Algoritma Genetik
2.6.4.1 Encoding Kromosom
Suatu kromosom
harus dapat
mempresentasikan suatu solusi.
Beberapa
metode
encoding suatu kromosom antara lain :
1.
Binary Encoding
Merupakan tipe encoding yang paling terkenal karena penelitian pertama
dari
algoritma
genetik
menggunakan tipe ini dan juga relatif mudah
penggunaannya. Dalam binary encoding, setiap kromosom hanya terdiri dari bit
0 dan 1. Kelemahan dari tipe ini adalah sering tidak alami untuk beberapa
masalah
dan
beberapa
perbaikan
harus
dilakukan
setelah
crossover
dan atau
mutasi.
Tabel 2.1 Contoh Kromosom Dengan Binary Encoding
Kromosom A
101100101100101011100101
Kromosom B
111111100000110000011111
2.
Permutation Encoding
Suatu kromosom merupakan string angka yang mempresentasikan suatu
posisi
dalam
urutan.
Encoding
semacam ini
biasa
digunakan
untuk
masalah
pengurutan tugas seperti Travelling Salesman problem.
Tabel 2.2 Contoh Kromosom Dengan Permutation Encoding
Kromosom A
1 5 3 2 6 4 7 9 8
Kromosom B
8 5 6 7 2 3 1 4 9
|
 29
3.
Value Encoding
Dalam value encoding suatu kromosom berisi urutan nilai-nilai. Nilai ini
dapat berupa angka, huruf, string, dan lain-lain. Tipe ini sangat bagus untuk
masalah khusus, seperti menemukan weight untuk neural network.
Tabel 2.3 Contoh Kromosom Dengan Value Encoding
Kromosom A
1.2324 5.3243 0.4556 2.3293 2.4545
Kromosom B
ABDJEIFJDHDIERJFDLGLFTGEFT
4.
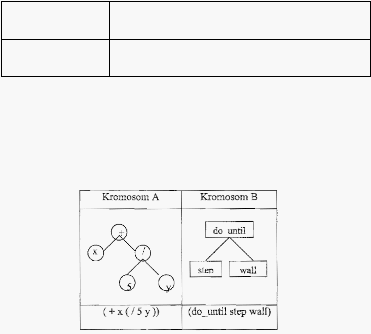
Tree Encoding
Tabel 2.4 Contoh Kromosom Dengan Tree Encoding
Dalam tree
encoding,
suatu
kromosom adalah
suatu
tree
dari
beberapa
objek, seperti function atau command dalam bahasa pemrograman. Encoding tipe
ini digunakan dalam bahasa pemrograman LISP
2.6.4.2 Fungsi Evaluasi
Fungsi evaluasi merupakan dasar untuk proses seleksi. Langkah-langkahnya
yaitu string dikonversi ke parameter fungsi, fungsi objective-nya dievaluasi, kemudian
mengkonvert
fungsi objektif tersebut ke dalam fitness. Dimana
untuk
maksimasi
problem, fitness sama dengan fungsi objective-nya (Gen dan Cheng, 1997). Output dari
|
 30
ma
fungsi fitness dipergunakan sebagai dasar untuk menseleksi individu pada generasi
berikutnya.
Invers dari makespan dapat digunakan untuk menentukan fitness pada tiap
kromosom. Misalnya C
k
menunjukkan makespan untuk kromosom ke-k, fitness
dihitung dengan menggunakan (Gen dan Runwei, 1997) :
2.6.4.3 Selection
Efek
dari
selection adalah
mendapatkan
parent
secara
probabilistic,
meskipun
prosedur selection
bersifat
stokastik,
tidak
berarti
Algoritma
Genetik
melakukan
pencarian
tidak
terarah. Probabilitas
suatu
kromosom untuk
terpilih
menjadi
parent
berhubungan dengan
fitness-nya.
Berikut
ini
dipaparkan secara
singkat beberapa
jenis
selection :
-
Fitness proportionate selection
Metode
yang
umum digunakan
untuk parent
selection
adalah
fitness
proportionate
selection atau
yang
lebih
dikenal
dengan
nama
Roullete
Wheel
Selection. Pada
metode
ini, probabilitas setiap kromosom untuk
terpilih
sebagai
parent
adalah
proporsional
terhadap fitness-nya,
secara matematis dapat
dirumuskan sebagai berikut :
Dimana P adalah ukuran populasi.
|
|
31
-
Rank Selection
Pada metode ini, kromosom-kromosom diurut berdasarkan
fitness-nya.
Probabilitas
suatu
kromosom untuk
terpilih adalah
proporsional
terhadap
posisinya di dalam urutan tersebut.
-
Tournament Selection
Metode tournament selection yang asli memilih K parent secara acak dan
mengembalikan
yang
terbaik. Tournament
selection sering
menghasilkan
suatu
populasi yang lebih beragam daripada fitness proporsionate selection.
-
Steady-State Selection
Ini bukan
merupakan metode
utama dalam memilih parent. Steady–state
selection merupakan metode seleksi dimana setiap generasi dengan kromosom
yang
terbaik (memiliki fitness value tertinggi) akan
terpilih
untuk
menciptakan
keturunan (offspring), sedangkan kromosom yang fitness value-nya rendah akan
tersingkir dan digantikan oleh keturunan baru tadi. Kemudian sisa populasi yang
dapat bertahan akan menjadi generasi yang baru.
-
Elitism
Elitism adalah
metode seleksi dimana satu
atau
lebih kromosom dengan
fitness value tertinggi
langsung disalin ke generasi berikutnya tanpa
mengalami
manipulasi. Hal ini dilakukan untuk mencegah
kromosom-kromosom
terbaik
hilang karena proses crossover dan mutasi, sehingga kualitas generasi berikutnya
dapat membaik.
|
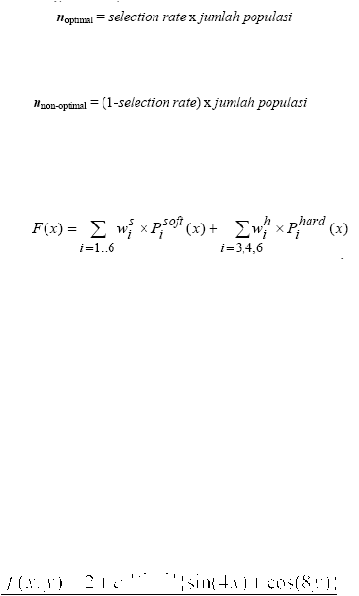 32
Seleksi kromosom ini dilakukan menurut komposisi atau laju seleksi (selection
rate). Komposisi ini berbicara mengenai berapa jumlah kromosom terbesar dalam
populasi
yang
lolos
ke periode
berikutnya.
Jumlah
kromosom
yang
lolos ke
periode
berikutnya didapatkan sebagai berikut :
Sedangkan jumlah kromosom yang tidak lolos adalah :
Fungsi fitness dalam perhitungan Algoritma
Genetik
yang digunakan pada
permasalahan penjadwalan ini adalah :
Keterangan :
x adalah penjadwalan yang dievaluasi
Pi
soft
(x) adalah nilai soft constraint ke-i Pi
hard
(x) adalah nilai hard constraint ke-i W
i
s
adalah faktor bobot soft constraint ke-i W
i
h
adalah faktor bobot hard constraint ke-i
Algoritma Genetik untuk menentukan nilai maksimal fungsi 2 variabel bebas :
•
Penyelesaian berupa
pasangan
nilai
(x,y),
sehingga
individu
didefinisikan
sevagai pasangan (x,y)
|
 33
•
Dalam
hal
ini
digunakan gen float
untuk penyederhanaan system,
karena
gen
biner akan menyebabkan besarnya ukuran kromosom
•
Fungsi fitness adalah fungsi (x,y)
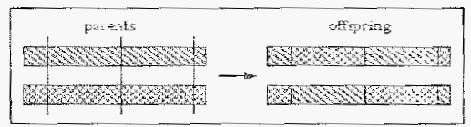
2.6.4.4 Crossover
Crossover
operator
adalah
operator
yang
paling
penting
dalam Algoritma
Genetik. Crossover adalah suatu proses persilangan dua kromosom untuk menghasilkan
dua
kromosom baru.
Proses
crossover
antara
dua
induk
dapat
dilihat
pada
gambar
dibawah ini.
Gambar 2.4 Crossover Antara Dua Induk
Ada
banyak
macam metode crossover.
Berikut
ini
dipaparkan
beberapa
diantaranya.
-
One-Point Crossover
Prosedur
dari
one-point
crossover adalah
secara
acak
membangkitkan
suatu bilangan (lebih besar dari 1 dan lebih kecil dari panjang kromosom)
sebagai
posisi
persilangan
(crossover
position),
kemudian
lakukan
penukaran
|
 34
substring dari kedua parent untuk substring setelah crossover position. Metode
one-point crossover dapat dilihat pada gambar dibawah ini.
Gambar 2.5 One-Point Crossover
Contoh :
A1 = 0 1 1 0 1 1 0 0
A2 = 1 0 1 1 0 1 1 0
Dengan crossover position 4, dihasilkan :
A1’ = 0 1 1 0 0 1 1 0
A2’ = 1 0 1 1 1 1 0 0
-
Two-Point Crossover
Prosedur dari two-point
crossover mirip dengan one-point crossover.
Metode ini menggunakan dua crossover position dan hanya substring yang
berada di antara 2 crossover position itu yang ditukar. Dengan metode ini, bagian
depan dan belakang dari kromosom yang bersangkutan dapat dipertahankan.
Contoh :
A1 = 0 1 1 0 1 1 0 1 1 0 1 1
A2 = 1 0 0 1 0 1 0 0 1 1 0 1
Dengan crossover position 3 dan 8, dihasilkan :
A1’ = 0 1 1 1 0 1 0 1 1 0 1 1
A2’ = 1 0 0 0 1 1 0 0 1 1 0 1
|
 35
-
N-point Crossover
Prosedur dari N-point crossover ini mirip dengan one-point crossover dan
two-point crossover. Pada metode ini harus dipilih n-crossover position dan
hanya substring
yang
berada
di
antara crossover position ganjil
dan
crossover
position genap yang ditukar sedangkan substring yang berada di antara crossover
position genap
dan
crossover
position
ganjil
tidak
berubah.
Metode
N-point
Crossover dapat dilihat pada gambar di bawah ini.
Gambar 2.6 N-Point Crossover
Contoh :
A1 = 1 1 0 1 0 1 0 0 0 1 1 0 1 0 1 1
A2 = 1 0 1 1 1 1 1 1 0 0 0 0 1 0 0 0
Dengan crossover position 3, 7, 11 dan 14 dihasilkan :
A1’= 1 1 0 1 1 1 0 0 0 1 1 0 1 0 1 1
A2’= 1 0 1 1 0 1 1 1 0 0 0 0 1 0 0 0
-
Uniform Crossover
Pada
metode
ini,
untuk
setiap
posisi
(locus)
dalam kromosom
dibangkitkan bilangan acak (random number) yang berkisar 0-1. Jika
bilangan acak tersebut lebih kecil daripada 0,5 maka child1 mendapat gen
dari parent1, child2 mendapat gen dari parent2. Begitu pula sebaliknya.
Misalnya dua parent,
|
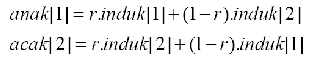 36
A1= 1 1 0 1 0 0 0
A2= 1 0 1 1 1 1 1
Untuk melakukan uniform crossover dibangkitkan 7 bilangan
acak, misalnya 0,3;0,2;0,7;0,8;0,4;0,9;0,5 maka akan dihasilkan
dua child sebagai berikut :
A1’= 1 1 1 1 0 1 1
A2’= 1 0 0 1 1 0 0
-
Arithemetic Crossover
Beberapa
operasi
aritmatik
digunakan
untuk
menciptakan
keturunan (offspring)
Contoh :
A1 = 0 1 0 0 1 0 1 0 0 1
A2 = 1 0 0 0 1 0 1 1 0 0
Dengan operasi AND maka dihasilkan :
A1’= 0 0 0 0 1 0 1 0 0 0
A2’= 0 0 0 0 1 0 1 0 0 0
Crossover secara umum menggunakan arithmetic crossover dengan definisi :
Di mana r adalah bilangan 0 sampai dengan 1
|
 37
2.6.4.5 Mutasi
Mutasi (Mutation)
berfungsi
untuk
memastikan
bahwa
semua
solusi
yang
mungkin
dapat
dicapai,
sebagai
ilustrasi,
posisi
pertama
dalam suatu
kromosom bisa
berisi nilai 1 sampai dengan 15. Mungkin saja terjadi bahwa tidak ada kromosom yang
posisi
pertamanya
berisi
nilai
5. Jika
hanya dengan crossover saja,
tidak
akan
pernah
didapatkan
kromosom yang
posisi
pertamanya
bernilai
5.
Dalam hal
ini,
mutation
operator
bisa
sangat
berguna.
Ada
4
jenis
mutasi
yang
ada,
yaitu
sebagai mutation
operator bisa sangat berguna. Ada 4 jenis mutasi yang ada, yaitu sebagai berikut :
1.
Invertion Mutation
Pilih substring secara acak
1 2 6 4 5 3 7 8 9 10
Ubah urutan substring menjadi terbalik
1 2 3 4 5 6 7 8 9 10
2.
Insertion Mutation
Pilih posisi secara acak
1 2 6 4 5 3 7 8 9 10
Insert pada posisi acak
1 2 3 6 4 5 7 8 9 10
3.
Displacement Mutation
Pilih substring secara acak
1 2 6 4 5 3 7 8 9 10
Insert substring pada posisi acak
1 2 3 7 8 6 4 5 9 10
4.
Raciprocal Exchange Mutation
|
 38
Pilih dua buah posisi secara acak
1 2 6 4 5 3 7 8 9 10
Lakukan pertukaran
1 2 3 4 5 6 7 8 9 10
5.
Mutasi Random
Metode ini memilih secara acak kromosom yang akan dimutasi,
kemudian dari kromosom yang terpilih. Jumlah gen yang akan dimutasikan
diacak
antara
1-n
gen, setelah
itu akan dipilih
gen-gen
yang
akan
dimutasi
sebanyak
jumlah
mutasi
gen,
lalu
gen-gen
tersebut
dimutasi
dengan
cara
menukar
gen
tersebut
dengan
gen
baru.
Mutasi
random dapat
digambarkan
sebagai berikut :
Kromosom awal : 0 0 1 0 1 1 0 0 1 0
Kromosom hasil : 0 0 1 0 0 1 0 0 1 0
6.
Smart Mutation
Smart Mutation dapat
mempercepat evolusi,
karena
mutasi
terjadi
pada
gen
yang
mempunyai
fitness
value
terkecil atau penalty terbesar.
Gen
tersebut
akan diganti dengan gen lain secara acak.
2.6.5
Parameter-parameter dalam Algoritma Genetik
Seperti halnya dengan algoritma lainnya,
Algoritma
Genetik
juga
mempunyai
parameter-parameter
dalam
menjalankan
fungsinya. Parameter-parameter
ini
akan
sangat berpengaruh terhadap kinerja
Algoritma Genetik dalam menyelesaikan
masalah
yang dihadapi.
|
|
39
2.6.5.1 Selection Rate
Selection
rate
menunjukkan
jumlah
kromosom dalam suatu
populasi
yang
mengalami seleksi. Jika selection rate 0% berarti tidak ada kromosom yang mengalami
seleksi.
Jika selection rate
100%
berarti
semua kromosom dalam populasi
mengalami
seleksi.
Selection rate yang rendah akan mengakibatkan proses pencarian berjalan lambat
karena pencarian banyak berulang pada kromosom yang lama, yang jelas bukan solusi
yang
dicari.
Sebaliknya,
jika
selection
rate tinggi
akan
menyebabkan
cepat
hilangnya
kromosom-kromosom yang berpotensi besar menjadi solusi. Ini juga akan
mengakibatkan meningkatnya waktu pencarian.
2.6.5.2 Crossover Rate
Crossover
rate
menunjukkan
seberapa
sering crossover
akan
dilakukan.
Jika
crossover rate 0% maka tidak
terjadi crossover. Jika crossover rate 100%
maka semua
kromosom akan
mengalami
crossover
dan
semua
kromosom anak
merupakan
hasil
crossover.
Crossover rate yang terlalu tinggi akan menyebabkan kromosom-kromosom
yang berpotensi besar menjadi solusi cepat tergantikan oleh kromosom-kromosom baru
yang mungkin saja tidak berguna, sedangkan crossover rate yang terlalu rendah
mengakibatkan
populasi
cenderung
statis sehingga
waktu
pencarian
meningkat
dan
lambat dalam mencapai convergence.
|
|
40
2.6.5.3 Mutation Rate
Mutation rate menunjukkan berapa banyak gen-gen dalam kromosom yang akan
mengalami
mutasi. Jika mutation rate
0% maka
tidak aka
nada
gen
yang
mengalami
perubahan
sehingga
kromosom
anak
murni
merupakan
hasil
crossover.
Jika
mutation
rate 100% maka seluruh gen dalam suatu kromosom akan mengalami perubahan.
Mutation
rate yang terlalu tinggi menyebabkan algoritma
genetic cenderung
bekerja
menyerupai
random search,
karena
algoritma
tersebut
kehilangan
kemampuannya
untuk belajar dari sejarah pencariannya. Sebaliknya, jika mutation rate
terlalu rendah, kromosom-kromosom yang mungkin berpotensi menjadi solusi tidak
pernah dicoba dan algoritma yang digunakan dapat dengan mudah terjebak dalam local
minimum.
2.6.6
Keuntungan dan Kerugian Algoritma Genetik
Menurut Mitsuo ada tiga keuntungan terbesar ketika menerapkan Algoritma
Genetik untuk masalah optimasi :
1.
Algoritma Genetik tidak membutuhkan banyak kebutuhan matematika tentang
masalah optimasi. Algoritma Genetik akan
mencari solusi berdasarkan evolusi
alami
tanpa
memperdulikan
kekhususan
dalam pengerjaan
masalah
tersebut.
Algoritma Genetik dapat menangani beberapa macam fungsi objektif dan beberapa
macam constraint baik linier maupun non linier.
2.
Penggunaan operator evolusi
membuat Algoritma Genetik
menjadi
sangat
efektif
untuk pencarian secara global. Teknik pencarian secara tradisional merupakan
pencarian secara local dengan berdasarkan langkah-langkah prosedur yang
konvergen dan akan membandingkan nilai-nilai dari point-point terdekat kemudian
|
|
41
bergerak kearah point
optimal
yang relatif. Global optima dapat ditemukan
jika
kita ada jaminan bahwa beberapa lokal optima adalah global optima.
3.
Algoritma
Genetik
menyediakan
fleksibilitas dengan
batasan
ketergantungan
heuristik
untuk
membuat
implementasi yang efisien untuk sebuah pencarian
masalah.
Menurut
Nugroho,Anto
Satriyo
(2003,p6) ada
tiga kekurangan
Algoritma
Genetik :
1.
Algoritma
Genetik
tidak
memiliki
rumusan
yang
pasti,
bagaimana
mentransfer
parameter permasalahan ke dalam kode genetik.
2.
Banyak parameter yang perlu diset secara baik agar proses evolusi dalam
Algoritma Genetik berjalan sesuai dengan yang diharapkan.
3.
Penentuan rumus menghitung fitness merupakan hal yang sangat penting dan
mempengaruhi
proses
evolusi
pada Algoritma
Genetik.
Sayangnya,
tidak
ada
prosedur yang baku bagaimana menentukan rumus tersebut.
Menurut Mitchell, kepopuleran Algoritma Genetik
tidak terlepas dari beberapa
faktor :
1.
Evolusi dikenal sebagai metode yang tangguh dan berhasil dalam proses adaptasi
pada sistem-sistem biologi.
2.
Algoritma Genetik dapat melakukan pencarian pada ruang yang terdiri dari
kromosom-kromosom
yang
mengandung
bagian-bagian yang berinteraksi dan
kompleks dimana pengaruh dari setiap bagian pada
fitness dari kromosom yang
bersangkutan sulit untuk dimodelkan.
|
|
42
3.
Algoritma Genetik dapat dengan mudah diparalelkan dan dapat mengambil
keuntungan dari harga perangkat keras komputer yang semakin menurun.
2.6.7
Penerapan Algoritma Genetik dalam Penyelesaian Masalah Penjadwalan
Untuk
menyelesaikan masalah
penjadwalan dengan pendekatan Algoritma
Genetik, pertama-tama harus dipilih suatu representasi dari solusi yang mungkin,
sebagai
suatu
kromosom.
Dalam masalah
penjadwalan,
kromosom adalah representasi
dari suatu jadwal, setelah itu dibuatlah suatu populasi awal dengan ukuran N, setelah
populasi awal terbentuk, setiap kromosom dievaluasi berdasarkan fitness function.
Fitness
score
dari
setiap
kromosom ditentukan
oleh
berapa
banyak constraint
yang
dilanggar dan constraint apa saja
yang dilanggar, selanjutnya kromosom-kromosom itu
akan memasuki tahap selection, crossover dan mutation. Proses ini akan berulang terus
sampai solusi yang diinginkan ditemukan atau sampai pada batas generasi tertentu.
Sejauh
ini
telah
banyak
dilakukan
penelitian
mengenai
masalah
penjadwalan,
dan dapat disimpulan bahwa :
1.
Algoritma
Genetik
mudah
secara
komputasi
meskipun
untuk
masalah
penjadwalan yang begitu rumit, meskipun demikian, penentuan nilai parameter-
parameter
untuk kasus NP-Complete,
khususnya penjadwalan
adalah
hal
yang
sangat sulit karena sangat bergantung pada kasus dan implementasinya.
2.
Algoritma
Genetik
standar
yaitu
Algoritma
Genetik
dengan
operator-operator
standar sangat sulit memecahkan masalah penjadwalan
karena dengan
hanya 6
constraints, pencarian solusi membutuhkan waktu yang cukup lama.
3.
Representasi solusi suatu masalah dalam kromosom sangat menentukan
kecepatan penyelesaian masalah tersebut oleh komputer.
|
|
43
4.
Salah
satu tindakan
yang dapat dilakukan
untuk
mempercepat
proses
pencarian
solusi oleh komputer adalah memangkas search space sebelum masuk pada
proses evaluasi.
5.
Ukuran populasi
yang
sangat
besar akan
meningkatkan
waktu pencarian tetapi
memberikan kemungkinan yang lebih besar untuk mendapatkan solusi.
|