 BAB
2
LANDASAN TEORI
2.1
Teori Graf
2.1.1
Pengenalan Teori Graf
Teori
graf adalah cabang
ilmu
yang
mempelajari
sifat-sifat
graf,
yang
pertama
kali diperkenalkan pada tahun 1736. Baru pada sekitar tahun 1920 teori graf berkembang
pesat terutama di bidang ilmu komputer, kimia, bahasa, ekonomi, dan riset operasi.
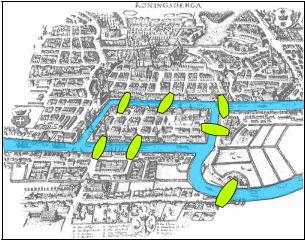
Gambar 2.1 Jembatan utama di Königsberg
(Sumber: Rinardi Munir, 2005, p.355)
Menurut
catatan
sejarah,
masalah
jembatan
Königsberg adalah
masalah
yang
pertama
kali
menggunakan graf
(tahun
1739)
[Rinardi
Munir,
2005,
p.354].
Di
kota
Königsberg (sebelah
timur
negara
bagian
Prussia,
Jerman),
sekarang
bernama
kota
Kaliningrad, terdapat
sungai
Pregal
yang
mengalir
mengitari
Pulau
Kneiphof
lalu
bercabang
menjadi
dua
buah
anak
sungai
yang
diperlihatkan oleh
gambar
2.1.
Permasalahannya ialah
menemukan pejalanan atau rute dari
suatu kota melalui
ketujuh
|
 11
buah
jembatan
masing-masing
tepat
satu
kali,
kemudian
kembali
lagi ke
tempat
awal.
Pulau tersebut tidak
dapat dicapai
oleh rute
apapun selain
melalui jembatan-jembatan
tersebut.
Tahun
1736,
Leonhard
Euler adalah orang
pertama yang
berhasil menemukan
jawaban
masalah tersebut dengan pembuktian yang
sederhana
(melalui karya tulisannya
Seven
Bridges
of
Königsberg).
Daratan
(titik-titik
yang
dihubungkan oleh
jembatan)
dinyatakan sebagai
titik
disebut
verteks
dan
jembatan
dinyatakan
sebagai
edge.
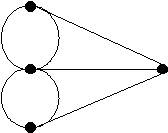
Dari
analisa Euler pada
jembatan Königsberg
menghasilkan sebuah
model
graf, seperti yang
diperlihatkan
pada
gambar
2.2.
Analisis
Euler
mengenai
permasalahan jembatan
di
Königsberg
tidak
menghasilkan solusi.
Karena
orang
tidak
mungkin
melalui
ketujuh
jembatan masing-masing tepat satu kali dan kembali lagi ke tempat awal keberangkatan
jika derajat (banyaknya garis yang bersisian dengan titik) setiap verteks tidak seluruhnya
genap.
Penemuan Euler
adalah kunci
yang
menandai perkembangan topologi,
di
mana
perbedaan antara layout sebenarnya dan
graf scematic adalah contoh yang bagus
untuk
gagasan bahwa topologi tidak dibatasi dengan bentuk kaku dari objek-objek tertentu.
C
A
D
B
Gambar 2.2 Graf yang merepresentasikan jembatan Königsberg
(Sumber: Rinardi Munir, 2005, p.355)
|
|
12
2.1.2
Definisi Graf
Graf adalah kumpulan verteks atau node yang dihubungkan satu sama lain
melalui
sisi/rusuk/busur/edge,
yang
digunakan
untuk
merepresentasikan objek-objek
diskrit dan hubungan antara objek-objek tersebut. Graf G didefinisikan sebagai pasangan
himpunan (V,E), ditulis dengan notasi G(V,E), yang dalam hal ini.
i.
V
adalah himpunan tidak kosong dari simpul-simpul (titik/verteks/node).
ii.
E
adalah himpunan sisi (rusuk/edge) yang menghubungkan sepasang simpul.
Verteks-verteks pada graf dapat merupakan obyek sembarang seperti kota, atom-
atom suatu
zat,
nama anak,
jenis buah, komponen alat
elektronik dan sebagainya. Edge
dapat menunjukkan hubungan sembarang seperti rute penerbangan, jalan raya,
sambungan telepon,
ikatan
kimia,
dan
lain-lain.
Jika
terdapat
sebuah
rusuk
e
yang
menghubungkan verteks v dan w, ditulis edge (v, w).
2.1.3
Jenis Graf
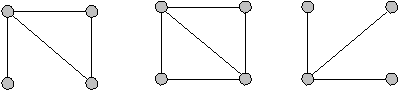
Graf dapat dibagi menjadi 2 jenis berdasarkan arahnya, yaitu sebagai berikut.
1. Graf tidak berarah (undirected graph)
Graf
yang sisinya tidak mempunyai orientasi arah. Edge (v, w) = edge (w, v)
adalah sisi yang sama, di tampilkan pada gambar 2.3 di mana V = {A, B, C,
D} dan e = {e1, e2, e
3
,
e
4
}.
|
 13
e
node
A
e1
D
e
4
e2
B
e3
C
edge
Gambar 2.3 Graf tidak berarah
2. Graf berarah (directed graph)
Graf
yang setiap sisinya diberikan orientasi arah, Edge (v, w) ? edge (w, v),
yang di tampilkan pada gambar 2.4 di mana V = {A, B, C, D} dan e = {e1
,
e2
,
e3, e
4,
e
5
,
e
6
,
e
7
}.
A
D
e1
e3
e2
e
4
e
6
e
5
B
C
7
Gambar 2.4 Graf berarah
(Sumber: Seymour Lipschutz, 1985, p.119)
Sebuah struktur
graf
bisa dikembangkan dengan
memberi bobot atau
nilai pada
tiap edge di mana merupakan
suatu nilai yang dapat berupa
biaya atau jarak, graf
semacam ini
disebut
graf
berbobot
(weighted
graph).
Dalam
pengajaran teori
graf
[Seymour
Lipschutz,
1985,
p.85],
terdapat
graf
khusus
beberapa
diantaranya adalah
sebagai berikut.
|
 14
a)
Complete
graph ialah
graf
di
mana setiap
verteks
berhubungan dengan semua
verteks
yang
lain
(semua
verteks
saling
berhubungan).
Biasanya
direpresentasikan
dengan
simbol
K
n
,
dimana
K
adalah
complete
graph
dan
n
jumlah verteks. Sebuah complete graph dengan n verteks akan mempunyai rusuk
sebanyak n(n-1)/2.
Gambar 2.5 Contoh model complete graph (K
5
)
(Sumber: Seymour Lipschutz, 1985, p.85)
b)
Bipartite graph
adalah graf
dimana satu verteksnya dibagi kedalam dua subset
verteks
m
dan
n,
sedemikian sehingga
tidak
ada
rusuk
yang
menyebabkan
verteks-verteks
dalam
subset
yang
sama.
Biasanya
direpresentasikan dengan
simbol
K
m,n
,
di
mana K
adalah
bipartite graph,
dan m
adalah
jumlah sunset
verteks m, dan n adalah jumlah subset n.
Gambar 2.6 Contoh model bipartite graph (K3
,3
)
(Sumber: Seymour Lipschutz, 1985, p.86)
|
 15
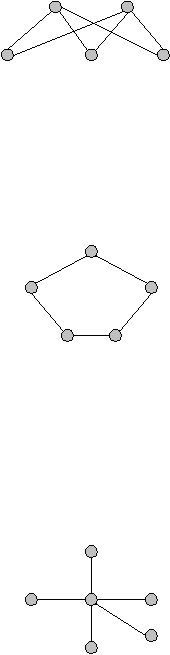
c)
Complete bipartite graph
adalah bipartite graph
di
mana setiap
verteks dari m
harus
memiliki
rusuk
yang
berhubungan ke
semua
verteks
dari
n.
Biasanya
direpresentasikan dengan simbol K
m,n
, sama seperti bipartite graph.
Gambar 2.7 Contoh model bipartite graph (K2
,3
)
(Sumber: Seymour Lipschutz, 1985, p.86)
d)
Regular
graph adalah
graf dimana setiap verteksnya
memiliki
derajat yang
sama.
Gambar 2.8 Contoh model regular graph berderajat 2
(Sumber: Seymour Lipschutz, 1985, p.85)
e)
Tree adalah graf yang tidak memiliki cycle. Jika jumlah verteks pada tree adalah
n, maka jumlah rusuk pada tree adalah n-1.
Gambar 2.9 Contoh model tree graph
(Sumber: Seymour Lipschutz, 1985, p.86)
|
 16
2.1.4
Teori Lintasan dan Siklus
Misalkan
v
o
dan
v
n
adalah
verteks-verteks dalam
sebuah
graf
[Richard
Johnsonbaugh, 2002, p.12]. Sebuah lintasan dari v
o
ke v
n
dengan panjang n adalah sebuah
barisan berselang-seling dari (n+1)
verteks dan n
edge yang berawal dengan
verteks v
o
dan berakhir dengan verteks v
n
,
(v
0
,
e
1
,
v
1
,
e
2
,
v
2
,
…, v
n-1
,
e
n
,
v
n
)
Dengan rusuk e
i
insiden pada verteks v
i-1
dan v
i
( i= 1, 2, …, n).
Sebuah siklus adalah sebuah litasan yang
mempunyai panjang
lintasan tidak nol
dari
kota
pertama
sampai
kota
terakhir
yang
merupakan kota pertama,
di
mana
tidak
terdapat rusuk yang dilalui lebih dari sekali.
Sebuah
siklus
sederhana
adalah
siklus
dari
kota
pertama
sampai
kota
terakhir
yang merupakan kota terakhir juga pada suatu graf, yang kecuali kota pertama dan kota
terakhir yang sama, tidak terdapat verteks yang berulang
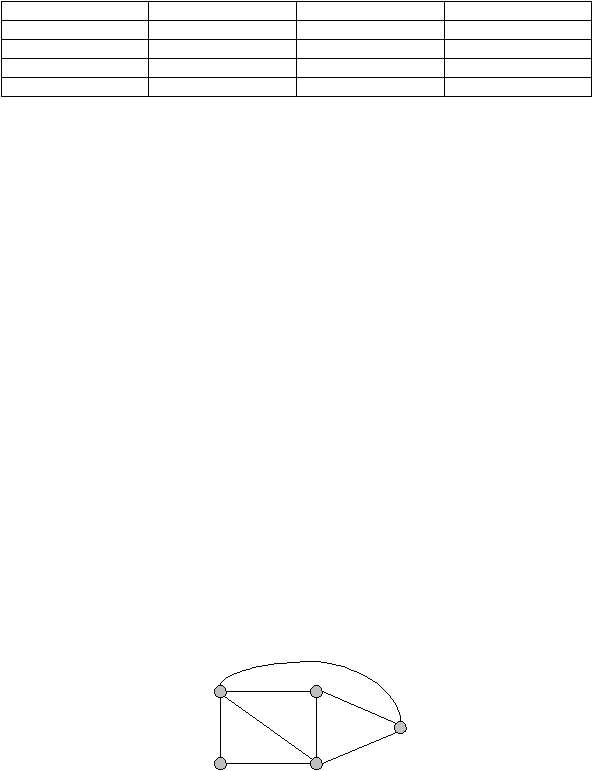
Untuk mengamati
perbedan
anatara
lintasan,
siklus,
siklus
sederhana,
dengan
contoh graf pada gambar 2.10 dapat dilihat yang akan disajikan dalam bentuk tabel.
3
2
1
4
7
5
6
Gambar 2.10 Graf tidak berarah
(Sumber: Richard Johnsonbaugh, 2002, p.12)
|
 17
v
Tabel 2.1 Perbedaan Lintasan, Siklus, dan Siklus Sederhana
(Sumber: Richard Johnsonbaugh, 2002, p.16)
Lintasan
Lintasan Sederhaa
Siklus
Siklus Sederhana
( 5, 6, 2, 5)
Tidak
Ya
Ya
( 2, 6, 5, 2, 4, 3, 2)
Tidak
Ya
Tidak
( 6, 5, 2, 4)
Ya
Tidak
Tidak
( 6, 5, 2, 4, 3, 2, 1)
Tidak
Tidak
Tidak
2.1.5
Representasi Graf
Misalkan G adalah sebuah graf dengan verteks-verteks v1
,
v2
,
…, v
n
dan edge e1,
e2
,
…, e
n
maka didefinisikan dua macam matriks yang berhubungan dengan sebuah graf
G [Seymour Lipschutz, 1985, p.87].
1. Matriks adjacency
Misalkan A=(a
ij
)
adalah matriks m x n yang didefinisikan oleh:
?
1
a
ij
=
?
?
0
jika {u, v} adalah edge, yaitu v
i
adjacent terhadap v
j
lainnya
2. Matriks incident
Misalkan M=(m
ij
)
adalah matriks m x i didefinisikan oleh:
?
1
m
=
?
?
0
verteks v
i
adalah incident pada edge e
i
lainnya
Contoh:
Diketahui graf G:
e
5
v
1
e2
v
5
e
6
e1
e3
e
7
4
e
4
e
8
v
2
v3
|
 18
v
1
0
v
0
0
?
maka:
v1 v
2
v3 v
4
v
5
e1
e
2
e3 e
4
e
5
e
6
e
7
e
8
v
1
?
0
1
1
?
v
2
?
1
0
1
1
1
?
?
0
0
?
v
1
?
1
?
v
2
?
1
1
1
0
1
0
0
0
1
0
0
0
0
?
?
0
0
?
A
=
v
?
1
1
3
?
0
1
1
?
?
m
=
v
?
0
3
?
0
1
1
0
0
1
1
?
?
v
4
?
1
?
5
?
0
1
0
1
?
0
1
1
?
v
4
?
0
0
0
?
5
?
1
0
0
1
1
0
0
1
0
1
?
?
1
?
(a)
(b)
Gambar 2.11 matriks adjecency (a) dan matriks incidence (b)
(Sumber: Seymour Lipschutz, 1985, p.87)
2.1.6
Graf Hamiton
Lintasan Hamilton ialah lintasan yang melalui tiap verteks di dalam graf tepat satu
kali
[Rinardi
Murni,
2005,
p.
408].
Sirkuit
Hamilton
ialah
sirkuit
yang
melalui
tiap
verteks di dalam graf tepat satu kali, kecuali verteks asal (sekaligus verteks akhir) yang
dilalui dua kali.
Graf
yang
memiliki sirkuit
Hamilton dinamakan graf
Hamilton,
sedangkan graf yang hanya memiliki lintasan Hamilton disebut graf semi-Hamilton.
1
2
1
2
1
2
4
3
4
3
4
3
(a)
(b)
(c)
Gambar 2.12 Penggambaran Graf Hamilton
(Sumber: Rinardi Murni, 2005, p. 409)
Keterangan gambar 2.12:
a. Graf yang memiliki lintasan Hamilton (3, 2, 1, 4)
|
|
19
b. Graf yang memiliki lintasan Hamilton (1, 2, 3, 4, 1)
c. Graf yang tidak memiliki lintasan maupun sirkuit Hamilton
2.2
Algoritma
Secara
umum
algoritma
ialah
sejumlah
langkah
komputasi yang
mengubah
masukan (input) menjadi keluaran (output) yang benar [Thompson S. Ngoen, 2004, p.4].
Menurut Donald E. Knuth sebuah algoritma harus memenuhi persyaratan:
•
Finitness: algoritma harus berakhir setelah melakukan sejumlah langkah proses
•
Definitness: setiap langkah algoritma harus didefinisikan dengan tepat dan tidak
menimbulkan makna ganda (ambiguous).
•
Input: setiap algoritma memerlukan data sebagai masukan untuk diolah
•
Output: setiap algoritma memberikan satu atau beberapa hasil keluaran.
•
Effectiveness: langkah-langkah algoritma dikerjakan dalam waktu yang wajar
Terdapat beberapa pengertian algoritma sebagai berikut.
•
Pada
Merriam-Webster’s
Collegiate Dictionary
istilah algorithm diartikan
sebagai
prosedur
langkah
demi
langkah
untuk
memecahkan
masalah
atau
menyeleseikan suatu tugas khususnya dengan menggunakan bantuan komputer.
•
Algoritma [Moh.
Sjukani, 2004,
p.1] adalah alur pikiran dalam
menyelesaikan
suatu
pekerjaan, yang
dituangkan dalam bentuk tertulis
yang dapat
dimengerti
oleh orang lain.
|
|
20
2.3
Optimisasi
2.3.1
Definisi Optimisasi
Optimisasi ialah suatu proses untuk mencapai hasil yang
ideal atau optimal (nilai
efektif yang dapat dicapai) [Ibnu Sina Wardy, 2008, p.2]. Dalam matematika, optimisasi
merujuk
pada
studi
permasalahan yang
mencoba
untuk
mencari
nilai
minimal
atau
maksimal dari
suatu
fungsi
riil.
Untuk dapat
mencapai nilai
optimal baik
minimal atau
maksimal
tersebut,
secara sistematis dilakukan pemilihan
nilai
variabel
integer atau riil
yang akan
memberikan solusi optimal. Nilai optimal adalah
nilai
yang didapat
melalui
suatu
proses
dan
dianggap menjadi suatu solusi
jawaban
yang
paling baik
dari semua
solusi yang ada.
2.3.2
Macam-Macam Permasalahan Optimisasi
Persoalan
yang
berkaitan dengan
optimisasi sangat
kompleks
dalam
kehidupan
sehari-hari. Nilai optimal yang
didapat dalam optimisasi dapat berupa besaran panjang,
waktu,
jarak,
dan
lain-lain.
Berikut
ini
adalah
beberapa
persoalan yang
memerlukan
optimisasi:
a. Menentukan lintasan terpendek dari suatu tempat ke tempat yang lain.
b. Menentukan
jumlah pekerja seminimal
mungkin untuk
melakukan suatu proses
produksi
agar
pengeluaran biaya
pekerja dapat
diminimalkan dan
hasil
produksi
tetap maksimal.
c. Mengatur jalur kendaraan umum agar semua lokasi dapat dijangkau.
d. Mengatur
routing jaringan
kabel telepon
agar biaya pemasangan
kabel tidak
terlalu besar dan penggunaannya tidak boros.
|
|
21
Selain
beberapa
contoh
di
atas,
masih
banyak
persoalan lainnya
yang
terdapat
dalam kehidupan sehari-hari.
2.3.3
Penyelesaian Masalah Optimisasi
Secara umum, penyelesaian masalah pencarian jalur terpendek dapat dilakukan
dengan menggunakan dua metode, yaitu:
1. Metode Konvensional
2. Metode Heuristik
2.3.3.1 Metode Konvensional
Metode
konvensional
ialah
metode
yang
menggunakan perhitungan
matematis
biasa. Semua kemungkinan yang ada dicoba dengan mencatat nilai yang didapat, cara ini
kurang efektif karena optimasi akan berjalan secara lambat (polynomial time).
A.
Dynamic Programming
Dynamic Programming
(DP)
adalah
prosedur
matematika
yang didesain
utama
untuk
meningkatkan efisien
komputerisasi dalam
memilih
permasalahan-permasalahan
pemograman matematika dengan memecah permasalahan tersebut menjadi bagian-bagian
lebih kecil [Hamdy A. Taha, 1995, p.345]. Setiap bagian-bagian tersebut
menghasilkan
satu variabel optimasi. Hasil komputasi untuk bagian-bagian yang berbeda dihubungkan
dengan
recursive
computations yang
akan
menghasilkan solusi
optimal
yang
feasible
untuk semua permasalahan.
|
|
22
B.
Branch and Bound
Teknik
branch and bound (B&B)
terdiri
dari dua prosedur dasar.
Branching
adalah
proses
mempartisi masalah
yang
besar
menjadi
dua
atau
lebih
masalah
kecil.
Bounding adalah proses menghitung batas bawah pada solusi optimal dari
masalah kecil
tersebut.
Bounding
function
yang
digunakan yaitu
pemrosesan
hanya
dilakukan
pada
branch yang baik; yang buruk tidak akan diproses. Diharapkan bahwa branch yang baik
akan memberikan hasil yang optimal pada proses selanjutnya.
C.
Branch and Cut
Teknik branch and cut
merupakan teknik yang
menggunakan branch dan bound
dengan penambahan algoritma cutting pada solusi
yang didapatkan. Proses
yang
dilakukan
ialah
dengan
mengaplikasikan branch
and
bound
pada solusi
yang
nantinya
akan dipotong dengan algoritma tertentu untuk mendapatkan hasil yang lebih baik. Proses
tersebut akan diulang sampai tidak ada pemotongan lagi.
2.3.3.2 Metode Heuristik
Metode heuristik adalah subbidang dari kecerdasan buatan yang digunakan untuk
melakukan pencarian dan optimasi. Menurut Judea Peral (April, 1984),
metode heuristik
berkerja
berdasarkan
strategi
pencarian
pintar pada pemecahan
masalah
dengan
komputer,
dengan
menggunakan beberapa
pendekatan
Heuristic _algorithm].
Dua tujuan dasar dalam pemecahan
masalah optimisasi pada ilmu komputer
adalah mencari algoritma yang cepat menyelesaikan masalah dan memperoleh hasil yang
|
 23
optimal.
Metode
heuristik
ialah
metode
yang
menghilangkan salah
satu
atau
dua
dari
tujuan
tersebut.
Misalnya,
pada
pemecahan masalah
optimisasi, dihasilkan
solusi
yag
cukup optimal, tetapi secara manual, belum tentu solusi yang lebih optimal dapat
diperoleh
karena
kompleksnya
permasalahan yang
ada.
Atau,
solusi
yang
didapat
dihasilkan dengan waktu yang sangat cepat, namun secara manual masih dapat ditemukan
hasil yang lebih optimal.
Jadi,
hasil yang diperoleh belum tentu yang paling optimal.
Tetapi penggunaan
metode
heuristik
yang
umum
tetap
diterapan
di
dunia
nyata. Karena
terdapat
beberapa
masalah, di mana hanya metode heuristik yang memungkinkan untuk memperoleh solusi
yang optimal dalam waktu yang sangat singkat.
Sistem yang
menggunakan AI
MASALAH
SOLUSI
Basis
Pengetahuan
Inference
Engine
Gambar 2.13 Sistem yang menggunakan kecerdasan buatan
(Sumber: Sri Kusumadewi, 2005, p.1)
Pada
gambar
2.14
[Sri
Kusumadewi
dan
H.
Purnomo, 2005,
p.1],
input
yang
diberikan
pada
sistem
yang
menggunakan
kecerdasan
buatan
adalah
masalah.
Sistem
harus
dilengkapi
dengan
sekumpulan
pengetahuan yang
ada
pada
basis
pengetahuan.
Sistem harus memiliki inference engine agar mampu mengambil kesimpulan berdasarkan
fakta atau
pengetahuan. Output
yang diberikan berupa
hasil
masalah
sebagai hasil
dari
inferensi.
|
|
24
A.
Algoritma Generate and Test
Pada
prinsipnya
metode
ini
merupakan
penggabungan
antara
depth-first
search
dengan pelacakan mundur (backtracking), yaitu bergerak ke belakang menuju pada suatu
keadaaan awal. Nilai pengujian berupa jawaban ‘ya’ atau ‘tidak’.
Algoritmanya adalah
sebagai berikut.
1. Bangkitkan suatu kemungkinan
solusi (membangkitkan suatu titik atau lintasan
tertentu dari keadaan awal).
2. Uji
untuk
melihat
apakah node
tersebut
benar-benar
merupakan
solusi
dengan
cara
membandingkan verteks tersebut atau
verteks akhir dari suatu
lintasan yang
dipilih dengan kumpulan tujuan yang diharapkan.
3. Jika solusi ditemukan, keluar. Jika tidak, ulangi kembali langkah yang pertama.
B.
Simulated Annealing
Simulated
Annealing
(SA)
adalah
metode
pencarian
lokal
yang
acak,
di
mana
solusi sementara
dimodifikasi sehingga
mengarah pada
hasil
yang
lebih
baik,
dengan
beberapa kemungkinan. Mekanisme ini dapat mengantisipasi local optima yang buruk
Ide
dasar
SA
terbentuk dari
pemrosesan
logam.
Annealing
(memanaskan
kemudian
mendinginkan) dalam
pemrosesan
logam
ini
adalah
suatu proses
bagaimana
membuat bentuk cair berangsur-angsur menjadi bentuk
yang
lebih padat seiring dengan
penurunan temperature. SA
biasanya digunakan
untuk penyelesaian masalah yang
mana
perubahan keadaan dari suatu kondisi ke kondisi yang lainnya membutuhkan ruang yang
sangat luas.
|
|
25
Pada
SA,
ada
3
parameter
yang
sangat
menentukan adalah
tetangga,
gain,
dan
temperatur.
Tetangga
akan
sangat
berperan
dalam
bentuk
perubahan pada
solusi.
Pembangkitan bilangan random akan berimplikasi adanya probabilitas.
C.
Tabu Search
Tabu Search (TS) merupakan suatu
metode optimisasi yang
menggunakan short-
term
memori atau
memori
jangka
pendek
untuk
menjaga
agar
proses
pencarian tidak
terjebak pada
nilai
optimum
lokal. Metode
ini
menggunakan Tabu List
untuk
menyimpan sekumpulan solusi yang telah dievaluasi. Pada setiap iterasi, solusi yang akan
dievaluasi akan dicocokkan terlebih dahulu dengan tabu list untuk melihat apakah solusi
tersebut sudah ada pada tabu list. Apabila solusi tersebut sudah ada pada tabu list, maka
solusi tersebut tidak akan dievaluasi lagi pada iterasi berikutnya. Apabila sudah tidak ada
lagi
solusi
yang
tidak
menjadi
anggota tabu
list,
maka
nilai
terbaik
yang
baru
saja
diperoleh merupakan solusi yang sebenarnya.
D.
Algoritma Genetika
Genetic
Algorithm
(GA)
pertama
kali
dikembangkan oleh
John
Holland
dari
universitas Michigan
(1975).
GA
adalah
algoritma
heuristik
yang
didasarkan
atas
mekanisme
evolusi
biologis.
Keberagaman pada
evolusi
biologis
adalah
variasi
dari
kromosom antar individu organisme. Individu yang lebih kuat (fit) akan memiliki
tingkat
survival dan reproduksi yang lebih tinggi jika dibandingkan dengan individu yang kurang
fit. Pada dasarnya ada 4 kondisi yang sangat mempengaruhi proses evalusi adalah sebagai
berikut.
|
|
26
•
Kemampuan organisme untuk melakukan reproduksi
•
Keberadaan populasi organisme yang bisa melakukan reproduksi
•
Keberagaman organisme dalam suatu populasi
•
Perbedaan kemampuan untuk survive
Pada GA,
teknik pencarian dilakukan sekaligus atas sejumlah solusi
yang
mungkin dikenal
dengan
istilah
populasi. Individu
yang
terdapat
dalam
satu
populasi
disebut dengan
istilah kromosom.
Kromosom
ini merupakan suatu solusi
yang
masih
berbentuk
simbol.
Populasi
awal dibangun
secara
acak,
sedangkan populasi berikutnya
merupakan hasil evaluasi kromosom-kromosom
melalui iterasi yang disebut dengan
istilah
generasi.
Pada
setiap
generasi,
kromosom
akan
melalui
proses
evaluasi
dengan
menggunakan alat ukur yang disebut dengan fungsi fitness. Nilai fitness dalam kromosom
menunjukkan kualitas
kromosom dalam populasi tersebut.
Generasi
berikutnya
dikenal
dengan
istilah
anak
(off-spring)
terbentuk
dari
gabungan
2
kromosom yang bertindak
sebagai induk (parent) dengan operator penyilangan. Selain operator penyilangan, suatu
kromosom dapat dimodifikasi
dengan menggunakan operator mutasi.
E. Harmony Search
Harmony
search
(HS)
ialah
algoritma
metaheuristic
(algoritma
soft
computing
atau
algoritma
evolusioner)
meniru
proses
]. Setiap
musisi
memainkan
nada
untuk
mencari
harmoni
yang
terbaik
bersama-sama, sama
seperti
setiap
variabel
keputusan
dalam
proses
optimasi
memiliki
nilai
untuk
menemukan vektor
terbaik
serentak. HS
mencoba mencari vektor x yang meminimalkan beberapa pengeluaran fungsi.
|
|
27
F.
Particle Swarm Optimization
Particle
Swarm
Optimization (PSO)
merupakan
teknik
komputasi
heuristik
berbasis
populasi
parallel
yang
diajukan oleh
Kennedy dan
Eberhart (1995),
yang
dimotivasikan dari
perilaku
organisme
seperti
populasi
ikan
atau
populasi
burung.
Andaikan ada sejumlah burung
yang sedang mencari
makanan di sebuah daerah secara
Di
daerah tersebut hanya ada satu
potong makanan. Semua burung tidak mengetahui posisi makanan berada. Tetapi mereka
tahu seberapa
jauh
makanan tersebut dengan setiap
perulangan. Jadi strategi
yang baik
untuk menemukan makanan tersebut adalah mengikuti posisi burung yang terdekat
dengan makanan.
2.4
Travelling Salesman Problem
Traveling Salesman Problem (TSP) adalah permasalahan pada matematika diskrit
dan
optimalisasi
kombinatorial
l]. TSP
pertama kali dikemukakan pada
tahun 1800-an oleh seorang
matematikawan asal
Irlandia, sir William Howard Hamilton dan seorang matematikawan asal inggris, Thomas
Penyngton Kirkman.
Bentuk
umum
dari
TSP
pertama
dipelajari
oleh
para
matematikawan
mulai
tahun 1930.
Diawali oleh
Karl
Menger
di
Vienna dan Harvard,
permasalahan TSP dipublikasikan oleh Hassler Whitney dan Merrill Flood di Princeton.
TSP memerlukan keputusan dari siklus biaya atau panjang yang minimal, melalui
penerusuran setiap node pada graf yang relevan [Thammapimookkul dan Chamsethikul,
2001, p.5]. Jika biaya antar dua
lokasi tidak tergantung pada arah
lintasan,
maka TSP
|
 28
jenis ini bersifat simetris. Sedangkan TSP yang bersifat asimetris, yang disebut direcred
TSP.
TSP
sebagai
salah
dari
NP-complete problems
dapat
diselesaikan
dengan
Pendekatan heuristik yang terbagi dalam tiga kelas, sebagai beikut.
•
Tour
construction procedures,
menghasilkan perkiraan
perjalanan
optimal
dari
jarak
matriks.
Seperti
prosedur
Nearest
Neighbor, Clarke and
Wright
Saving,
prosedur Insertion, Minimal Spanning Tree, dan Christofides heuristic.
•
Tour improvement procedures, berusaha mencari perjalanan yang lebih baik dari
perjalanan awal. Seperti 2-opt dan 3-opt heuristik dan prosedur k-opt.
•
Tour composite procedures,
membuat perjalanan awal dari salah satu composite
procedures dan kemudian mencari perjalanan yang lebih baik menggunakan satu
atau lebih dengan tour improvement procedures.
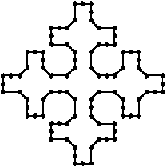
Gambar 2.14 Solusi TSP dengan 91 verteks
2.5
Multi Travelling Salesman Problem
Multi Travelling Salesman Problem (M-TSP) adalah generalisasi dari TSP, yang
merupakan
persoalan
yang
lebih
mendekati
permasalahan dalam
dunia
nyata.
Dalam
|
|
29
masalah ini diperlukan lebih dari satu kendaraan pengangkut untuk pendistribusian
barang. Pada M-TSP, keadaan pengangkut berjumlah m akan mengunjungi semua verteks
yang ada dengan total jarak yang minimum. M-TSP dapat selalu dikonversikan ke dalam
TSP
yang
sama
dengan
membuat
perbanyak
sebanyak
m
kali
dari
lokasi
yang
sama,
tetapi tidak
berhubungan satu
sama
lain.
Bebearapa
formula M-TSP
diturunkan secara
independent oleh Bellmore dan Hong (1974), Orloff (1974), Svetska dan Huckfeltz
(1973).
Pada
M-TSP
harus terdapat
m
=
2
salesman
yang
mengunjungi
n
kota
secara
bebas.
Tidak
ada
kota
yang
dikunjungi oleh
lebih
dari
satu
salesman
dan
setiap
m
salesman dapat memulai dari kota awal yang berbeda atau yang sama dan berakhir pada
kota yang sama dengan kota awal pada masing-masing salesman.
2.6 Vehicle Routing Problem
Vehicle Routing Problem (VRP) adalah salah satu problem atau permasalahan dari
combinatorial optimization di mana sebuah set rute akan dibentuk dari sejumlah kota atau
pelanggan didasarkan atas satu
atau
beberapa
depot. Setiap
kota atau
pelanggan
akan
dilayani oleh satu kendaraan dengan batasan-batasan tertentu; rute tersebut di awali dan
diakhiri di depot [http://neo.lcc.uma.es/radi-aeb/WebVRP].
Permasalahan
ini
pertama
kali
diformulasikan oleh
Dantzing dan
Ramser
pada
tahun 1959 sebagai pusat permasalahan utama dalam bidang transportasi, distribusi, dan
logistik. Dalam beberapa sektor pasar, transportasi memiliki nilai persentase yang tinggi
yang
dimasukkan
dalam
keuntungan.
Setelah
itu
dikembangkan metode komputerisasi
untuk transportasi yang menghasilkan penghematan total biaya yang signifikan.
|
 30
VRP adalah generalisasi dari TSP. Maka, TSP adalah sebuah VRP tanpa batasan
seperti depot, pelanggan dan permintaan. M-TSP adalah VRP dengan sebuah depot dan m
kendaraan pengangkut, termasuk bila tidak ada permintaan dari pelanggan. MTSP adalah
transformasi dari TSP dengan memperbanyak jumlah depot.
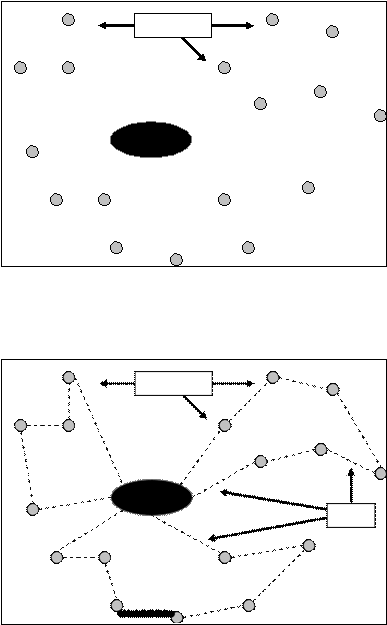
Pelanggan
Depot
Gambar 2.15 Contoh visualisasi input dari Vehicle Routing Problem
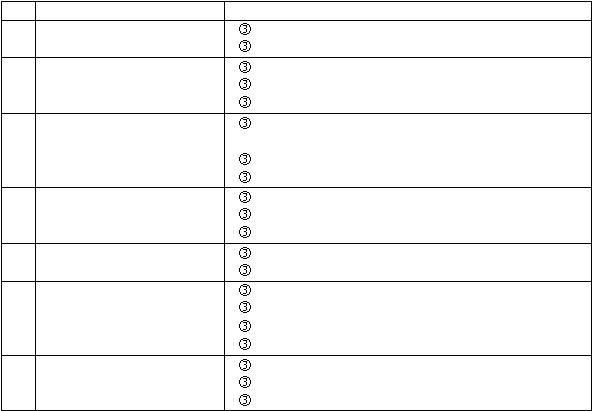
Pelanggan
Depot
Rute
Gambar 2.16 Salah satu output dari VRP dari input gambar 2.15
|
 31
Tujuan dari Vehicle Routing Problem
ialah untuk meminimalkan
jarak yang
dilalui oleh armada kendaraan yang melayani sekumpulan pelanggan seperti pada gambar
2.18 dan
menghasilkan salah
satu
rute
seperti
pada
gambar
2.19 dengan
banyaknya
kendaraan yang disediakan atau digunakan.
Pada
perkembangannya
[Titiporn Thammapimookkul,
2001, p.3],
VRP
memiliki
beberapa karateristik sehingga dapat dibagi-bagi dalam beberapa kategori masalah,
seperti
yang
dapat
ditunjukkan
dalam
tabel
2.2.
Kategori
ini
dibuat
oleh
Bodin
dan
Golden (1981), yang memaparkan berbagai karakteristik umum, yang membedakan VRP.
Keseluruhan tabel memberikan gambaran singkat tentang masalah routing.
Tabel 2.2 Kategori masalah dalam VRP
(Sumber: Titiporn Thammapimookkul, 2001, p.3)
No
Karateristik
Varian yang mungkin
1
Jumlah kendaraan
pengangkut
Satu kendaraan pengangkut
Multi kendaraan pengangkut
2
Tipe kendaraan
pengangkut
Homogen (satu tipe)
Heterogen (multi tipe)
Tipe khusus
3
Tipe permintaan
Permintaan deterministik (telah dikethui
sebelumnya)
Permintaan stokastik
Permintaan kepuasan sebagian
4
Lokasi permintaan
Simpul
Garis
campuran
5
Tenpat asal kendaraan
(pusat)
Satu pusat
Multi pusat
6
Jaringan yang mendasari
Tidak berarah
Berarah
Campuran
Euclid
7
Batasan kapasitas
kendaraan pengangkut
Semuanya sama
Jalur yang berbeda
Kapasitas tak terbatas
|
 32
8
Rute maksimum
Sama untuk semua rute
Berbeda untuk setiap rute
Tidak ditentukan
9
Sistem pengoperasian
Pengambilan saja
Pengiriman saja
Pengambilan dan pengantaran
10
Biaya
Variable atau biaya rute
Biaya tetap pengoperasian atau biaya tetap
kendaraan pengangkut
Biaya pengangkut umum
11
Tujuan
Meminimalkan biaya total rute
Meminimalkan jumlah kendaraan yang diperlukan
Meminimalkan fungsi kegunaan berdasarkan pada
pelayanan dan kenyamanan
Meminimalkan fungsi kegunaan berdasarkan pada
prioritas pelanggan
Jika VRP salah satu permasalahan kombinatorial direpresentasikan dalam sebuah
graf G
=
(V, E)
notasi
yang
digunakan
ialah sebagai berikut.
•
V
=
{v
0
,
v1, …, v
n
}
ialah set atau sekumpulan verteks yang menggambarkan depot,
pelanggan ataupun persimpangan jalan, di mana:
o
v
0
sebagai depot.
o
v1
,
…, v
n
sebagai pelanggan
o
Misalakan V` = V tanpa elemen {v
0
}
digunakan sebagai himpunan n kota
•
C
ialah matriks c
ij
sebagai biaya atau jarak antara pelanggan v
i
dan v
j
yang bernilai
non-negatif.
•
A
=
{(v
i
,
v
j
)
|
v
i
,
v
j
?
V; i ? j} adalah himpunan rusuk atau edge. Edge dapat yang
berarah (i, j) ? A dan tidak berarah e ? E
•
d ialah vektor dari permintaan / demand pelanggan.
•
R
i
ialah rute dari kendaraan ke-i.
|
|
33
•
k
ialah banyaknya kendaraan (semuanya identik) dengan kapasitas Q. Satu rute
untuk tiap kendaraan.
Dengan setiap verteks v
i
dalam V’ diasosiasikan dengan sejumlah barang q
i
,
yang
akan diantarkan oleh satu
kendaraan. VRP bertujuan untuk
menentukan sejumlah k rute
kendaraan dengan
total
biaya
yang
minimum,
bermula
dan
berakhir
di
sebuah
depot,
yang
setiap
verteks
dalam V’ dikunjungi
tepat
sekali oleh
satu kendaraan.
Akhirnya,
biaya dari solusi permasalahan ini S adalah:
k
F
VRP
(S ) =
?
C
(R
i
)
i
=1
2.7
Local Search
Local
search
(LS)
ialah
metaheuristik
untuk
menyelesaikan permasalahan
perhitungan optimisasi
yang
berat.
LS
dapat digunakan pada permasalahan yang
bertujuan
memaksimalkan solusi
yang
standar
di
antara
banyaknya
kandidat
Algoritma LS
berpindah dari
solusi ke solusi dalam kandidat solusi sampai dianggap solusi tersebut optimal. Algoritma
LS
dipergunakan secara
luas
untuk
permasalahan perhitungan
yang
berat,
meliputi
permasalahan computer science (artificial intelligence), matematika, operations research,
engineering, and bioinformatics.
Dalam
algoritma
LS
yang
paling
dasar,
dilakukan
penyelusuran dalam
neighborhood
terhadap
perjalanan
tertentu
untuk kemajuan perjalanan. Jika
perjalanan
tersebut ditemukan maka rute tersebut menggantikan yang lama dan proses tersebut akan
diteruskan
sampai
kemajuan
perjalanan
tidak
dapat
ditemukan lagi.
Hal
ini
disebut
iterative
improvement algorithm.
Algoritma
tersebut
dapat
diterapkan
dalam
hal-hal
sebagai berikut.
|
 34
A.
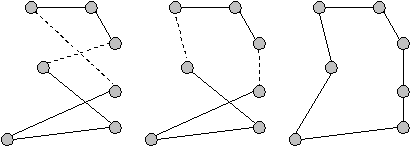
2-Opt
2-Opt ialah algoritma LS yang pertama kali diusulkan oleh Croes pada tahun 1958
untuk
menyeleseikan TSP. Ide
dasar
dibelakang algoritma tersebut
ialah
memindahkan
atau
menghapus
pasangan
rute
yang bersilangan dan
mengembalikan suatu
perjalanan
yang memungkinkan [http://en.wikipedia.org/wiki/2-opt].
Menghapus 2 edge
reconnect
(a)
(b)
Gambar 2.17 2-Opt move (a) dan 2-Opt optimal (b)
B.
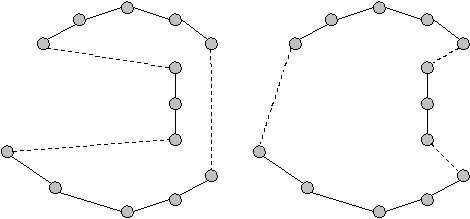
3-Opt
Analisis
3-Opt
meliputi
penghapusan tiga
edge
dalam
perjalanan,
kemudian
menghubungkan kembali
perjalanan tersebut ke
dalam
perjalanan
yang
memungkinkan
dan
kemudian
mengevaluasi tiap
metode
pengembalian
untuk
mencari
yang
paling
optimum. Proses
ini kemudian diulang untuk set tiga set koneksi yang berbeda [http://en.
wikipedia.org/wiki/3-opt].
|
 35
Menghapus 3 edge
reconnect
Gambar 2.18 3-Opt move
2.8
Algoritma Ant Colony Optimization
Algoritma
Ant
Colony
Optimization merupakan
teknik
probabilistik untuk
menjawab masalah komputasi
yang bisa dikurangi dengan
menemukan jalur
yang baik
dengan graf. ACO pertama kali dikembangkan oleh Marco Dorigo pada tahun 1991.
Sesuai
dengan
nama
algoritmanya,
ACO
di
inspirasi
oleh
koloni semut
karena
tingkah laku semut yang menarik ketika mencari makanan [Heitor S. Lopes et al., 2005,
p.2].
Semut-semut
menemukan jarak
terpendek
antara
sarang
semut
dan
sumber
makanannya. Ketika
berjalan
dari
sumber
makanan
menuju
sarang
mereka,
semut
memberikan
tanda
dengan
zat
feromon
sehingga akan
tercipta jalur
feromon.
Feromon
adalah zat kimia yang berasal dari kelenjar endokrin dan digunakan oleh makhluk hidup
untuk
mengenali sesama
jenis,
individu
lain,
kelompok,
dan
untuk
membantu
proses
reproduksi. Berbeda dengan
hormon,
feromon
menyebar ke
luar tubuh dan
hanya dapat
mempengaruhi dan dikenali oleh
individu lain
yang sejenis, proses peninggalan feromon
ini dikenal sebagai stigmergy. Semut dapat mencium feromon dan ketika mereka memilih
|
|
36
jalur
mereka,
mereka
cenderung memilih
jalur
yang
ditandai
oleh
feromon
dengan
konsentrasi
yang
tinggi.
Apabila
semut
telah
menemukan jalur
yang
terpendek
maka
semut-semut akan terus melalui jalur tersebut. Jalur lain yang ditandai oleh feromon lama
akan
memudar atau
menguap,
seiring berjalannya waktu.
Jalur-jalur yang pendek akan
mempunyai ketebalan feromon dengan probabilitik yang tinggi dan membuat jalur
tersebut akan dipilih dan
jalur
yang panjang akan ditinggalkan. Jalur feromon membuat
semut dapat menemukan jalan kembali ke sumber makanan atau sarang mereka.
Algoritma ACO
telah
banyak digunakan untuk
menghasilkan penyelesaian yang
mendekati optimal [Bernd Bullnheimer et al., 1997, p.1]. Aplikasi algoritma semut dalam
kehidupan sehari-hari mencakup beberapa persoalan sebagai berikut.
a. Traveling Salesman Problem (TSP), yaitu mencari jalur terpendek dalam sebuah
graf menggunakan jalur Hamilton.
b.
Quadratic
Assignment Problem
(QAP)
yang
berusaha
menempatkan sejumlah
sumber
n
ditempatkan
pada
sejumlah
m
lokasi
dengan
meminimalkan biaya
assignment.
c. Job-shop
Scheduling
Problem
(JSP),
juga
salah
satu contoh aplikasi
algoritma
semut untuk menjadwalkan sejumlah j pekerjaan menggunakan sejumlah m mesin
sehingga seluruh pekerjaan diselesaikan dalam waktu yang minimal.
d. Vehicle Routing Problem (VRP), pengaturan jalur kendaraan
e. Pewarnaan graf
Koloni semut yang nyata dan artificial terdapat banyak kemiripan [Marco Dorigo
et
al.,
2006, p.3]. Keduanya
terbentuk dari
sebuah
populasi
yang
terdiri
dari
individu-
individu
yang
berkerja
sama
untuk
mencapai
tujuan. Semut
artificial
hidup
di
dunia
|
|
37
virtual, karenanya
mereka
hanya
memodifikasi nilai
numerik (disebut analogi artificial
pheromones)
yang
berhubungan
dengan
keadaan-keadaan
permasalahan
yang
berbeda.
Sebuah
rangkaian
dari
nilai-nilai
feromon
yang
berhubungan dengan
keadaan
permasalahan disebut pheromone trail atau jejak feromon. Mekanisme untuk evaporation
atau penguapan feromon pada koloni semut
nyata
yang
membuat semut artificial dapat
melupakan sejarah (jalur-jalur yang pernah diambil) dan fokus pada arah pencarian baru
yang menjanjikan.
Seperti semut-semut nyata, semut-semut artificial membuat solusi secara berurut
dengan bergerak dari
satu
keadaan permasalahan ke
lainnya. Semut-semut nyata
hanya
berjalan, memilih arah berdasarkan konsentrasi feromon
lokal dan kebijakan keputusan
stokastik. Semut artificial membuat solusi sedikit demi sedikit, dan bergerak dari
keadaan
permasalahan
yang
tersedia
dan
membuat
keputusan
stokastik setiap
langkah.
Meskipun
begitu,
terdapat
perbedaan antara
yang
nyata
dan
semut
artificial
sebagai
berikut.
•
Semut artificial hidup di dunia dan pada waktu diskrit, mereka berpindah secara
sekuen melewati set batasan dari permasalahan.
•
Update feromon (penumpukan dan penguapan feromon) tidak dilakukan dengan
jalan
yang
sama
pada semut
yang
nyata
dan
semut
arficial. Update
feromon
dilakukan oleh beberapa dari semut artificial dan terkadang dilakukan saat solusi
telah dibangun.
•
Beberapa implementasi dari semut artificial menggunakan mekanisme tambahan
yang tidak ada pada semut-semut nyata, seperti local search, backtracking, dan
lain-lain.
|
 38
?
ij
ij
2.8.1
Algoritma Elitist Ant System
Ant System (AS) adalah bentuk awal dari algoritma ACO yang telah dimodifikasi
oleh para peneliti sampai saat ini [Ayan Acharya et al., 2008, p.1]. Algoritma Elitist Ant
System (EAS) adalah salah satu dari model yang dikembangkan
dari algoritma
AS.
Strategi
dari
EAS
mirip
dengan
AS
tetapi
berbeda
dalam
penerapan
memberikan jejak
feromon karena elite ant atau best ant disertakan sebagai feromon tambahan dalam meng-
update jejak semut. Aturan dasar meng-update jejak feromon dalam algoritma AS adalah
sebagai berikut.
m
t
new
=
(1
-
?
)
t
old
+
?
?
t
k
……………..……….….…… (1)
ij
ij
ij
k
=
1
Sedangkan aturan dalam meng-update feromon dengan algoritma elitist ant
system adalah sebagai berikut.
new
= (1
-
m
old
+
?
?
k
+ ?
bs
t
ij
? t
)
ij
k
=1
t
ij
e
t
ij
………..…………..…… (2)
dengan
k
adalah
perubahan
harga
intensitas
jejak
semut
antar
kota setiap
semut yang dihitung berdasarkan persamaan 3 sebagai berikut.
?t
k
=
?
1
L
k
ij
?
?
0
untuk (i,j) ?
kota asal dan tujuan dalam tabu
k,v
lainnya
e
adalah
parameter yang
mendefinisikan bobot
yang
diberikan pada
rute
yang
terbaik pada tabu
bs
dengan panjang L
bs
.
?
1
L
untuk (i,j) ?
kota asal dan tujuan dalam tabu
bs
?
t
bs
=
?
bs
?
0
lainnya
|
|
39
2.9
Capacitated Vehicle Routing Problem dengan Algoritma Elitist Ant System
Capacitated
Vehicle
Routing
Problem
(CVRP)
dapat
didefinisikan sebagai
pemberangkatan armada dari pusat depot, dengan sejumlah pelanggan yang
mesti
dilayani, dengan permintaan yang berbeda untuk produk sejenis [Heitor S. Lopes et al.,
2005, p.3]. Armada kendaraan terbatas dan mempunyai kapasitas
yang sama. Batasan-
batasan pada CVRP adalah sebagai berikut.
•
Setiap pelanggan hanya dilayani oleh satu pelanggan saja
•
Total permintaan
yang
dilayani
kendaraan
tidak
boleh
melebihi
kapasitas
kendaraan.
•
Masing-masing perjalanan kendaraan dimulai dan diakhiri di depot
•
Total panjang perjalanan tidak boleh melebihi batas otonomi kendaraan.
CVRP
ialah
permasalahan yang
lebih
rumit
dari
TSP,
karena
memerlukan
dua
tahap
penyelesaian. Pada tahap awal, setiap
semut menyusun beberapa perjalanan yang
independen, dan set-set perjalanan melayani semua pelanggan. Pada tahap kedua, setiap
perjalanan disampaikan pada sebuah
populasi
baru,
yang sistemnya sama
dalam
algoritma Ant
System
(AS)
untuk
TSP.
Pada
tahap
ini,
algoritma
berkerja
untuk
menetapkan
banyaknya
siklus,
yang
mengarah
pada
optimisasi
lokal
perjalanan.
Dua
tahap proses tersebut, diulang sampai kriteria pemberhentian dipenuhi. Dengan keadaan
total
permintaan semua pelanggan
yang
dilayani
tidak
melebihi
batas
kendaraan yang
digunakan pada rute R
i
,
Notasinya adalah sebagai berikut.
m
?
d
i
=
Q
i
=1
…………………..………….….…… (4)
|
 40
j
i
2
d
Dalam
algoritma
EAS
untuk
CVRP,
diperlukan
langkah-langkah
untuk
menentukan jalur terpendek sebagai berikut.
i.
Inisialisasi
Parameter-parameter yang di inisialisasi adalah:
Intensitas jejak semut antar antar kota dan perubahannya (t
ij
).
Banyak pelanggan (n) termasuk koordinat pelanggan (x, y).
Jarak antar pelanggan (d
ij
).
d
ij
=
(
x -
-
x
)
2
+
(
y
-
y
j
)
……………………………… (5)
Permintaan atau demand pelanggan (q
n
).
Banyak kendaraan (v) dengan kapasitas kendaraan (Q).
Banyak semut (k).
Tetapan pengendali intensitas jejak semut (a), nilai
a
=
0.
Tetapan pengendali visibilitas (ß), nilai
ß
=
0.
Tetapan penguapan jejak semut (?),
nilai harus 0
>
?
>
1
untuk mencegah
jejak feromon yang tak hingga.
Visibilitas antar kota (?
ij
).
?
=
1
………………………………………… (6)
ij
ij
Jumlah siklus maksimum (NC
max
).
|
 41
p
k
[t
ij
ij
[t
ij
=
0
ij
ii.
Proses iterasi sampai NC
max
a. Untuk setiap semut k = 1, …, n menbangun solusi yang baru.
Pengisian
depot dan kota pertama k semut ke dalam tabu list semut
kendaraan awal.
Tabu
list
semut ditulis
sebagai tabu
k,v
di
mana tabu
k,v
digunakan menyimpan rute semut k pada kendaraan v.
Penyusunan rute kunjungan semut ke setiap kota.
Perjalanan koloni semut berlangsung terus-menerus sampai semua
kota telah dikunjungi dan tidak melebihi batas kapasitas kendaraan yang
sesuai
dengan
rumus
4.
Untuk
menentukan kota
tujuan
digunakan
persamaan probabilitas kota untuk dikunjungi sebagai berikut.
]
a
[? ]
ß
p
ij
=
?
h?O
ij
]
a
[
?
]
ß
untuk v
j
?
?
……………….……… (7)
k
untuk lainnya ………………………………… (8)
Dengan ? = {v
j
?
V
:
v
j
yang boleh dikunjungi}
?
{v
0
}, kota v
j
dipilih
untuk dikunjungi setelah kota v
i
.
Bila kendaraan v pada semut k
telah melebihi batas dari kapasitas kendaraan Q maka semut k akan
menggunakan kendaraan selanjutnya.
b. Perbaiki semua rute kendaraan menggunakan 2-opt heuristik.
c. Perhitungan panjang rute kendaraan
untuk setiap semut.
Perhitungan panjang rute tertutup
(length closed
tour)
atau L
k
setiap
semut dilakukan setelah satu siklus diselesaikan oleh semua semut.
Perhitungan
ini
dilakukan
berdasarkan
tabu
k,v
masing-masing dengan
persamaan sebagai berikut.
|
 42
v
n
L
k
=
??
d
tabu
k
,i
(
j), d
tabu
k
,v
(
j
+
1)
……………….……… (9)
i
=0
j
=0
d. Pencarian rute terpendek.
Setelah L
k
setiap semut dihitung, akan didapat harga minimal panjang
rute tertutup
setiap
siklus
atau L
bs
dan
harga
minimal panjang rute tertutup
secara keseluruhan adalah L
min
.
e. Update jejak feromon.
Koloni semut
akan
meninggalkan jejak-jejak pada
lintasan
antar
kota
yang dilaluinya. Adanya penguapan dan perbedaan jumlah semut yang lewat,
menyebabkan kemungkinan terjadinya perubahan harga intensitas jejak semut
antar kota. Aturan dasar dalam
meng-update jejak feromon dengan algoritma
Elitist Ant System yaitu dengan persamaan 2 yang telah disebutkan terdahulu.
2.10 Flowcart
Salah
satu
bentuk
untuk
menyatakan
alur
pikiran
dalam
menyelesaikan suatu
pekerjaan adalah dalam bentuk gambar atau bagan yang disebut program flowchart atau
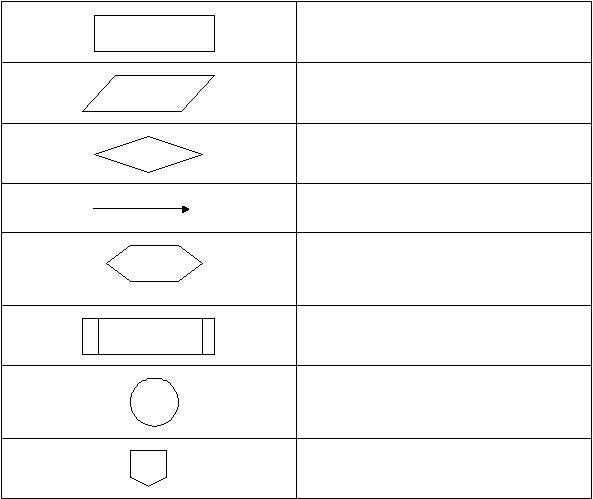
bagan alir suatu program [Moh. Sjukani, 2004, p.5]. Berikut adalah simbol-simbol yang
digunakan untuk menggambarkan diagram alur.
Tabel 2.3 Tabel simbol flowchart
(Sumber: Moh. Sjukani, 2004, p.9)
Notasi
Arti notasi
Terminal, untuk menyatakan mulai dan
selesei
sebagai
tanda,
tidak melakukan
suatu pekerjaan khusus.
|
 43
Process, untuk menyatakan assignment
statement
Input/Output operation, untuk menyatakan
proses baca dan proses tulis
Decision, untuk menyatakan pengambilan
keputusan sesuai dengan suatu kondisi
Garis, untuk menyatakan pelaksanaan, atau
alur proses
Preparation, pemberi nilai awal suatu
variabel
Call, memanggil suatu subprogram
Titik connector yang berada pada halaman
yang sama.
Titik connector yang berada pada halaman
yang lain.
2.11 State Transition Diagram
State
Transition
Diagram
(STD)
adalah
kumpulan
keadaan/atribut yang
menggambarkan seseorang atau suatu benda pada waktu tertentu, bentuk keberadaan atau
kondisi tertentu, seperti menunggu
instruksi
berikutnya, menunggu
pengisian password,
dan lain-lain.
STD merupakan modeling tools yang sangat kuat untuk mendekripsikan kelakuan
yang dibutuhkan pada sistem yang mempunyai sifat real-time, dan juga bagian interface
manusia pada berbagai sistem online
(Yourdan, 1989,
p.270).
Cara kerja sistem
ini ada
dua macam sebagai berkut.
|
 44
Passive
Sistem
ini
melakukan
kontrol
terhadap
lingkungan, tetapi
lebih bersifat
memberikan atau
menerima
data.
Kontrol
suatu
sistem
bertugas
mengumpulkan/menerima data melalui sinyal yang dikirim oleh satelit.
Active
Sistem ini melakukan kontrol terhadap lingkungan secara aktif dan dapat
menberikan respon terhadap lingkungan sesuai dengan program yang ditentukan.
Komponen-komponen utama STD sebagai berikut.
1. State, yang disimbolkan dengan
State adalah kumpulan atribut yang mencirikan seseorang atau suatu
benda pada waktu atau kondisi tertentu.
2. Transition State, yang disimbolkan dengan
Transition State yang diberi label dengan ekspresi atau arah, label tersebut
menunjukkan kejadian yang menyebabkan transisi terjadi.
3. Condition dan Action
Condition
adalah
suatu
peristiwa
pada
lingkungan eksternal
yang
dapat
dideteksi oleh sistem. Dan action adalah apa yang dilakukan oleh sistem apabila
terjadi
perubahan
state,
atau bisa
juga
dikatakan
sebagai reaksi
sistem
terhadap
suatu kondisi, aksi akan menghasilkan keluaran/tampilan.
Gambar 2.19 Contoh STD
(Sumber: Yourdan, 1989, p.265)
|