|
BAB II LANDASAN
TEORI
2.1
Definisi Aljabar Boolean
Aljabar
Boolean
merupakan
salah
satu
cabang
ilmu
matematika
yang
pertama
kali
dikemukanan
oleh
seorang
matematikawan
Inggris
yang
bernama
George
Boole
pada
tahun 1854.
Aljabar
Boolean dapat didefinisikan secara
abstrak
dalam beberapa
cara. Cara yang paling umum adalah dengan menspesifikasikan unsur–unsur
pembentuknya dan operasi–operasi yang menyertainya [Rinaldi Munir, 2005, p282].
Misalkan B adalah himpunan yang didefinisikan pada dua operator biner, + dan ., dan
sebuah operator uner,’. Misalkan 0 dan 1 adalah dua elemen yang berbeda dari B. Maka,
tupel
<B,
+,
.,
‘,
0,
1> disebut
aljabar
Boolean
jika
untuk
setiap a, b, c
0
B
berlaku
aksioma (sering dinamakan juga postulat Huntington) berikut :
1. Identitas
(i) a + 0 = a
(ii) a . 1 = a
2. Komutatif
(i) a + b = b + a
(ii) a . b = b . a
3. Distributif
(i) a . (b + c) = (a . b) + (a . c)
(ii) a + (b . c) = (a + b) . (a + c)
|
|
7
4. Komplemen
Untuk setiap a € B terdapat elemen unik a’ € B sehingga
(i) a + a’ = 1
(ii) a . a’ = 0
Elemen
0
dan 1
adalah
dua
elemen
unik
yang
berada
di
dalam
B.
0
disebut
elemen terkecil dan 1 disebut elemen terbesar. Kedua elemen unik dapat berbeda– beda
pada beberapa aljabar Boolean (misalnya 0 dan U pada himpunan, False dan True pada
proPosisi), namun secara umum tetap digunakan 0 dan 1 sebagai dua elemen unik yang
berbeda.
Elemen
0
disebut
elemen zero,
sedangkan
elemen
1
disebut
elemen
unit.
Operator + disebut operator penjumlahan, . disebut operator perkalian, dan ‘ disebut
operator komplemen.
Terdapat perbedaan antara aljabar Boolean dengan aljabar biasa untuk aritmetika
bilangan riil sebagai berikut.
1. Hukum distributif yang pertama, a . (b + c) = (a . b) + (a . c) sudah dikenal di
dalam aljabar biasa, tetapi hukum distributif yang kedua, a + (b . c) = (a + b) . (a
+ c), benar untuk aljabar Boolean, tetapi tidak benar untuk aljabar biasa.
2. Aljabar Boolean tidak memiliki kebalikan perkalian (multiplicative inverse) dan
kebalikan
penjumlahan; karena
itu, tidak ada operasi pembagian dan
pengurangan di dalam aljabar Boolean.
3. Aksioma
nomor 4 pada definisi aljabar Boolean yang
mendefinisikan operator
yang dinamakan komplemen yang tidak tersedia pada aljabar biasa.
4. Aljabar biasa memperlakukan himpunan bilangan riil dengan elemen yang tidak
berhingga banyaknya. Sedangkan aljabar Boolean memperlakukan himpunan
|
|
8
elemen B yang sampai sekarang belum didefinisikan, tetapi pada aljabar Boolean
dua-nilai, B didefinisikan sebagai himpunan dengan hanya dua nilai, 0 dan 1.
Hal lain yang penting adalah membedakan elemen himpunan dan peubah
(variable) pada
sistem aljabar. Sebagai contoh,
pada
aljabar
biasa,
elemen
himpunan
bilangan riil adalah angka, sedangkan peubahnya seperti a, b, c dan sebagainya. Dengan
cara
yang sama pada aljabar Boolean, orang mendefinisikan
elemen–elemen
himpunan
dan peubah seperti x, y, z sebagai simbol–simbol yang merepresentasikan elemen.
Berhubung
elemen–elemen B
tidak
didefinisikan
nilainya
(kita
bebas
menentukan anggota–anggota B), maka untuk mempunyai sebuah aljabar Boolean, harus
diperlihatkan:
1. elemen–elemen himpuan B,
2. kaidah/aturan operasi untuk dua operator biner dan operator uner,
3. himpunan
B, bersama–sama dengan dua operator tersebut,
memenuhi keempat
aksioma di atas.
Jika ketiga persyaratan di atas dipenuhi,
maka aljabar
yang didefinisikan dapat
dikatakan sebagai aljabar Boolean.
2.2
Aljabar Boolean Dua-Nilai
Aljabar
Boolean
yang
terkenal dan
memiliki
terapan
yang luas
adalah aljabar
Boolean
dua-nilai
(two-valued
Boolean
algebra).
Aljabar Boolean
dua-nilai
didefinisikan
pada
sebuah
himpunan B dengan dua buah elemen 0 dan 1 (sering
dinamakan bit – singkatan dari binary digit), yaitu B = {0, 1}, operator biner, + dan .
operator uner, ‘ [Rinaldi Munir, 2005, p285].
|
 9
Kaidah untuk operator biner dan operator uner ditunjukkan pada Tabel 2.1, 2.2,
dan 2.3 di bawah ini.
Tabel 2.1 Tabel kaidah operasi .
(Sumber: Rinaldi Munir, 2005, p285)
a
b
a . b
0
0
0
0
1
0
1
0
0
1
1
1
Tabel 2.2 Tabel kaidah operasi +
(Sumber: Rinaldi Munir, 2005, p285)
a
b
a + b
0
0
0
0
1
1
1
0
1
1
1
0
Tabel 2.3 Tabel kaidah operasi ‘
(Sumber: Rinaldi Munir, 2005, p285)
a
a’
0
1
1
0
Harus diperhatikan bahwa keempat aksioma di dalam definisi 2.1 terpenuhi pada
himpunan
B =
{0, 1} dengan dua operator biner dan satu operator
uner yang
didefinisikan di atas.
|
 10
1. Identitas: jelas berlaku karena dari tabel:
(i)
0 + 1 = 1 + 0 = 1
(ii)
1 . 0 = 0 . 1 = 0
yang memenuhi elemen identitas 0 dan 1 seperti yang didefinisikan pada
postulat Huntington.
2. Komutatif : jelas berlaku dengan melihat simetri tabel operator biner.
3. Distributif :
(i)
a
.
(b + c) = (a . b) + (a . c) dapat ditunjukkan benar dari tabel operator
biner di atas, dengan membentuk tabel kebenaran untuk semua nilai yang
mungkin dari a, b, dan c (Tabel 7.4). Oleh karena nilai–nilai pada kolom a
.
(b
+
c)
sama dengan
nilai –
nilai pada
kolom
(a
.
b)
+
(a
.
c),
maka
kesamaan a . (b + c) = (a . b) + (a . c) adalah benar.
(ii)
Hukum distributif a + (b . c) = (a + b) . (a + c) dapat ditunjukkan benar
dengan membuat tabel kebenaran dengan cara yang sama seperti (i).
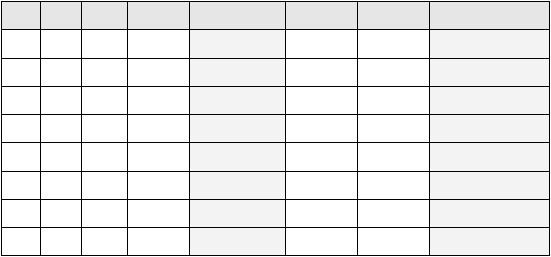
Tabel 2.4 Tabel kebenaran a . (b + c) = (a . b) + (a . c)
(Sumber: Rinaldi Munir, 2005, p286)
a
b
c
b + c
a . (b + c)
a . b
a . c
(a . b) + (a . c)
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
|
|
11
4. Komplemen : jelas berlaku karena Tabel 2.4 memperlihatkan bahwa :
(i)
a + a’ = 1, karena 0 + 0’ = 0 + 1 = 1 dan 1 + 1’ = 1 + 0 = 1
(ii)
a . a = 0, karena 0 . 0’ = 0 . 1 dan 1 . 1’ = 1 . 0 = 0
Karena keempat aksioma terpenuhi, maka terbukti bahwa B = {0 , 1} bersama–
sama dengan operator biner + dan ., operator komplemen ‘ merupakan aljabar Boolean.
Untuk selanjutnya, jika disebut aljabar Boolean, maka aljabar Boolean yang
dimaksudkan di sini adalah aljabar Boolean dua-nilai.
2.3
Ekspresi Boolean
Pada aljabar Boolean dua-nilai, B = {0, 1}. Kedua elemen B ini seringkali
disebut elemen biner atau bit (singkatan binary bit). Peubah (variable) x disebut peubah
Boolean atau peubah biner jika
nilainya
hanya dari B.
Ekspresi Boolean dibentuk dari
elemen–elemen B dan/atau peubah–peubah yang dapat dikombinasikan satu sama
lain
dengan operator +, ., dan ‘ [Rinaldi Munir, 2005, p286]. Secara formal, ekspresi Boolean
dapat didefinisikan secara rekursif sebagai berikut.
Misalkan (B, +, ., ‘, 0, 1) adalah sebuah aljabar Boolean. Suatu ekspresi Boolean
dalam (B, +, ., ‘) adalah:
(i)
Setiap elemen di dalam B,
(ii)
setiap peubah,
(iii) jika e1
dan e
2
adalah ekspresi Boolean, maka e
1
+
e
2
,
e1
.
e2, e1’ adalah ekspresi
Boolean.
|
|
12
Jadi menurut definisi di atas, setiap ekspresi di bawah ini,
0
1
a
b
c
a + b
a . b
a’ . (b + c)
a . b’ + a . b . c + b’, dan sebagainya
adalah
ekspresi Boolean.
Ekspresi
Boolean yang
mengandung n peubah
dinamakan ekspresi Boolean bagi n peubah [Rinaldi Munir, 2005, p287].
Dalam penulisan
ekspresi
Boolean selanjutnya,
digunakan
perjanjian
berikut:
tanda kurung ‘()’ mempunyai prioritas pengerjaan paling tinggi, kemudian diikuti
dengan operator ‘, + dan ·. Sebagai contoh, ekspresi a + b . c berarti a + (b . c), bukan (a
+ b) . c dan ekspresi a . b’ berarti a . (b’), bukan (a . b)’.
2.4
Prinsip Dualitas
Di dalam aljabar Boolean, banyak ditemukan kesamaan (identity) yang dapat
diperoleh
dari
kesamaan
lainnya,
misalnya pada
dua
aksioma
distributif yang sudah
disebutkan pada definisi aljabar Boolean sebelumnya:
(i)
a . (b + c) = (a . b) + (a . c)
(ii)
a + (b . c) = (a + b) . (a + c)
Aksioma
yang kedua diperoleh dari aksioma pertama dengan cara
mengganti ·
dengan + dan mengganti + dengan ·. Prinsip ini dikenal dengan prinsip dualitas, prinsip
|
 13
yang juga kita temukan di dalam teori himpunan maupun logika [Rinaldi Munir, 2005,
p289]. Definisi prinsip dualitas di dalam aljabar Boolean adalah sebagai berikut.
Misalkan
S adalah
kesamaan (identity) di dalam
aljabar Boolean yang
melibatkan operator +, ·, dan ‘,
maka
jika pernyataan S* diperoleh dari
S dengan cara
mengganti · dengan +, + dengan ·, 0 dengan 1, 1 dengan 0 dan membiarkan operator
komplemen tetap apa adanya,
maka kesamaan S* juga benar. S* disebut sebagai dual
dari S.
2.5
Hukum–Hukum Aljabar Boolean
Ada banyak hukum di dalam aljabar Boolean. Beberapa literatur bervariasi
dalam mengungkapkan jumlah hukum pada aljabar Boolean, tetapi hukum–hukum yang
paling penting ditampilkan pada tabel berikut.
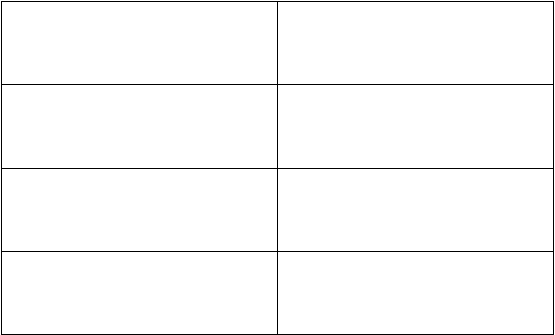
Tabel 2.5 Tabel hukum–hukum aljabar Boolean
(Sumber: Rinaldi Munir, 2005, p290)
1. Hukum identitas:
(i) a + 0 = a
(ii) a . 1 = a
2. Hukum idempoten:
(i) a + a = a
(ii) a . a = a
3. Hukum komplemen:
(i) a + a’ = 1
(ii) a . a’ = 0
4. Hukum dominansi:
(i) a . 0 = 0
(ii) a + 1 = 1
5. Hukum involusi:
(i)
(a’)’ = a
6. Hukum penyerapan:
(i) a + (a . b) = a
(ii) a . (a + b) = a
7. Hukum komulatif:
(i) a + b = b + a
(ii) a . b = b . a
8. Hukum asosiatif:
(i) a + (b + c) = (a + b) + c
(ii) a . (b . c) = (a . b) . c
|
 14
9. Hukum distributif:
(i) a + (b . c) = (a + b) . (a + c)
(ii) a . (b + c) = (a . b) + (a . c)
10. Hukum De Morgan :
(i) (a + b)’ = a’b’
(ii) (a . b)’ = a’ + b’
11. Hukum komplemen:
(i) 0’ = 1
(ii) 1’ = 0
Selanjutnya dapat memperoleh hukum–hukum aljabar Boolean dari hukum–
hukum aljabar dengan cara mempertukarkan
?
dengan +,
atau
0
dengan +
n
dengan ·,
atau
0
dengan ·
U dengan 1,
atau
T dengan 1
0
dengan 0,
atau
F dengan 0.
Perhatikanlah bahwa hukum yang ke-(ii) dari setiap hukum di atas merupakan
dual dari hukum yang ke-(i). Sebagai contoh,
Hukum komutatif:
a + b = b + a
dualnya:
a . b = b . a
Hukum asosiatif:
a + (b + c) = (a + b) + c
dualnya:
a . (b . c) = (a . b) . c
Hukum distributif:
a + (b . c) = (a + b) . (a + c)
dualnya:
a . (b + c) = (a . b) + (a . c)
|
|
15
2.6 Fungsi Boolean
Fungsi Boolean (disebut juga fungsi biner) adalah pemetaan dari B
n
ke B melalui
ekspresi Boolean, dapat dituliskan sebagai
f : B
n
B
yang dalam hal ini B
n
adalah himpunan yang beranggotakan pasangan terurut
ganda-n (ordered n-tuple) di dalam daerah asal B [Rinaldi Munir, 2005, p293].
Misalkan
ekspresi
Boolean
dengan
n
peubah
adalah
E(x1, x2
,
..., x
n
). Menurut
definisi di atas, setiap pemberian nilai–nilai kepada peubah x1
,
x2, ..., x
n
merupakan suatu
pasangan
terurut
ganda-n
di
dalam daerah
asal B
n
dan
nilai
ekspresi
tersebut
adalah
bayangannya di dalam daerah hasil
B. Dengan kata
lain, setiap ekspresi Boolean tidak
lain merupakan fungsi Boolean. Misalkan sebuah fungsi Boolean adalah f(x, y, z) = xyz
+
x’y
+
y’z.
Fungsi
f
memetakan nilai–nilai pasangan terurut ganda-3 (x,
y,
z) ke
himpunan {0, 1}. Contoh pasangan terurut ganda-3 misalnya (1, 0, 1) yang berarti x = 1,
y = 0, dan z = 1 sehingga f(1, 0, 1) = 1 . 0 . 1 + 1’ . 0 + 0’ . 1 = 0 + 0 + 1 = 1.
Selain secara aljabar, fungsi Boolean juga
dapat
dinyatakan
dengan
tabel
kebenaran dan dengan rangkaian logika. Tabel kebenaran berisi nilai–nilai fungsi untuk
semua
kombinasi
nilai–nilai
peubahnya.
Jika
fungsi Boolean
dinyatakan
dengan
tabel
kebenaran, maka untuk fungsi Boolean dengan n buah peubah, kombinasi dari nilai
peubah–peubahnya adalah sebanyak
2
n
.
Ini
berarti
terdapat
2
n
baris
yang berbeda di
dalam tabel kebenaran tersebut. Misalkan n = 3, maka akan terdapat 2
3
=
8
baris tabel.
Cara yang praktis membuat semua kombinasi tersebut adalah sebagai berikut.
1.
Untuk peubah pertama, isi 4 baris pertama pada kolom pertama dengan
sebuah 0 dan 4 baris selanjutnya dengan sebuah 1 berturut–turut.
|
 16
2.
Untuk peubah kedua, isi 2 baris pertama pada kolom kedua dengan 0 dan 2
baris berikutnya
dengan
1,
2
baris
berikutnya 0 lagi, dan 2 baris terakhir
dengan 1.
3.
Untuk peubah ketiga, isi kolom ketiga secara berselang–seling dengan 0 dan
1 mulai baris pertama sampai baris terakhir.
Fungsi
Boolean
tidak selalu
unik pada
representasi
ekspresinya.
Artinya,
dua
buah fungsi yang ekspresi Booleannya berbeda dapat menyatakan dua buah fungsi yang
sama. Misalkan
f dan g adalah ekspresi dari suatu fungsi Boolean. Fungsi
f dan g
dikatakan
merupakan fungsi
yang sama jika keduanya
memiliki
nilai
yang
sama pada
tabel kebenaran untuk setiap kombinasi peubah–peubahnya. Sebagai contoh, fungsi:
f(x, y, z) = x’y’z + x’yz + xy’ dan g(x, y, z) = x’z + xy’
adalah
dua
buah
fungsi
Boolean
yang
sama.
Kesamaan
ini
dapat
dilihat
pada
tabel berikut.
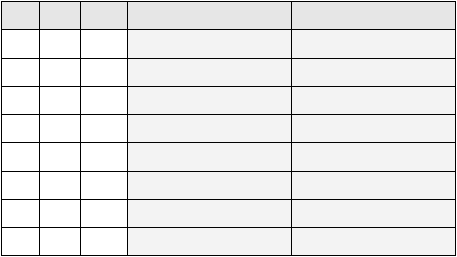
Tabel 2.6 Tabel kebenaran fungsi f dan g
(Sumber: Rinaldi Munir, 2005, p295)
x
y
z
f = x’y’z + x’yz + xy’
g = x’z + xy’
0
0
0
0
0
0
0
1
1
1
0
1
0
0
0
0
1
1
1
1
1
0
0
1
1
1
0
1
1
1
1
1
0
0
0
1
1
1
0
0
|
|
17
Jika
sebuah
fungsi
Boolean
tidak
unik
dalam
representasi
ekspresinya,
dapat
ditemukan ekspresi Boolean lainnya
yang menspesifikasikan
fungsi yang sama dengan
melakukan
manipulasi
aljabar terhadap
ekspresi
Boolean.
Yang
dimaksud
dengan
memanipulasi
atau
menyederhanakan
fungsi Boolean
adalah
menggunakan
hukum–
hukum aljabar Boolean untuk menghasilkan bentuk yang ekivalen. Sebagai contoh:
f(x, y, z) = x’y’z + x’yz + xy’
= x’z(y’ + y) + xy’
(Hukum distributif)
= x’z . 1 + xy’
(Hukum komplemen)
= x’z + xy’
(Hukum identitas)
Manipulasi aljabar pada ekspresi Boolean disebut juga dengan penyederhanaan
fungsi Boolean.
2.7 Komplemen Fungsi Boolean
Bila sebuah fungsi
Boolean dikomplemenkan, kita memperoleh fungsi
komplemen. Fungsi komplemen berguna pada saat kita melakukan penyederhanaan
fungsi Boolean [Rinaldi Munir, 2005, p296].
Fungsi komplemen dari suatu fungsi
f, yaitu
f
’
dapat dicari dengan dua cara
berikut.
1. Cara pertama: menggunakan hukum De Morgan
Hukum De Morgan untuk dua buah peubah, x1
dan x2 adalah
(i)
(x1
+ x
2
)’ = x
1
’x
2
’
(ii)
dan dualnya: (x1 . x2
)’ = x1
’
+ x2’
|
|
18
Hukum De Morgan untuk tiga buah peubah, x1
,
x2
dan x3 adalah
(i)
(x1
+ x
2
+ x
3
)’ = (x1 + y’) , yang dalam hal ini y = x2
+ x3
= x1’y’
= x1’(x2 + x3)’
= x1’x
2
’x3’
(ii)
dan dualnya : (x1
.
x2 . x3
)’ = x1
’
+ x2’ + x
3
’
Hukum De Morgan untuk n buah peubah, x1, x2, ... ,x
n
,
adalah
(iii)
(x1
+ x
2
+ ... + x
n
)’ = x
1
’
x2
’
... x
n
’
(iv)
dan dualnya : (x1
.
x2 . ... . x
n
)’ = x1’ + x
2
’
+ ... + x
n
’
2. Cara kedua: menggunakan prinsip dualitas.
Tentukan
dual
dari
ekspresi Boolean
yang
merepresentasikan
f,
lalu
komplemenkan setiap literal di dalam dual tersebut. Bentuk akhir yang diperoleh
menyatakan fungsi komplemen.
Misalkan f(x, y, z) = x(y’z’ + yz), maka dual dari ekspresi Boolean nya adalah
x + (y’ + z’) (y + z)
Komplemenkan tiap literal dari dual di atas menjadi
x’ + (y + z) (y’ + z’) = f ’
Jadi, f‘(x, y, z) = x’ + (y + z) (y’ + z’)
2.8
Bentuk Kanonik
Ekspresi Boolean yang menspesifikasikan suatu fungsi dapat disajikan dalam dua
bentuk. Pertama, sebagai penjumlahan dari hasil kali dan kedua sebagai perkalian dari
hasil jumlah.
Misalnya,
|
|
19
f(x, y, z) = x’y’z + xy’z’ + xyz
dan
g(x, y, z) = (x + y + z) (x + y’ + z) (x + y’ + z’) (x’ + y + z’) (x’ + y’ + z)
adalah
dua
buah
fungsi
yang
sama
(dapat ditunjukkan
dengan
tabel kebenarannya).
Fungsi yang pertama, f,
muncul dalam bentuk penjumlahan dari
hasil
kali, sedangkan
fungsi yang kedua, g, muncul dalam bentuk perkalian dari hasil jumlah [Rinaldi Munir,
2005, p298].
Perhatikan juga bahwa setiap suku (term) di dalam ekspresi mengandung literal
yang
lengkap
dalam
peubah
x,
y
dan
z,
baik
peubahnya
tanpa
komplemen
maupun
dengan komplemen. Ada dua macam bentuk term, yaitu minterm (hasil kali) dan
maxterm (hasil jumlah).
Ekspresi Boolean yang dinyatakan sebagai penjumlahan dari satu atau lebih
minterm atau perkalian dari satu atau lebih maxterm disebut dalam bentuk kanonik. Jadi,
ada dua macam bentuk kanonik:
1.
Penjumlahan dari hasil kali (Sum-of-Product atau SOP)
2.
Perkalian dari hasil jumlah (Product-of-Sum atau POS)
Fungsi f(x, y, z) = x’y’z + xy’z’ + xyz dikatakan dalam bentuk SOP dan
fungsi
g(x, y, z) = (x + y + z) (x + y’ + z) (x + y’ + z’) (x’ + y + z’) (x’ + y’ + z) dikatakan dalam
bentuk POS. Nama lain untuk SOP adalah bentuk normal disjungtif (disjunctive normal
form) dan nama lain POS adalah bentuk normal konjungtif (conjunctive normal form).
Minterm dilambangkan sebagai huruf m kecil berindeks. Indeks menyatakan nilai
desimal
dari
string biner yang
merepresentasikan
term.
Misalnya pada term
dengan
2
peubah x dan y, indeks 0 pada m
0
menyatakan nilai desimal dari 00 (x = 0 dan y = 0),
indeks 1 pada m1
menyatakan
nilai desimal dari 01 (x = 0 dan y = 1) dan seterusnya.
|
 20
Jadi, untuk minterm dari 3 peubah (x, y, dan z), jika ditulis m
6
maka ini berarti minterm
xyz’ karena 6 (desimal) = 110
(biner); di sini x = 1, y = 1 dan
z
= 0. Peubah x dan y
dinyatakan tanpa komplemen sedangkan peubah z dinyatakan dengan komplemen
karena bernilai 0, sehingga ditulis xyz’.
Maxterm
dilambangkan sebagai
huruf
M
besar berindeks.
Indeks
menyatakan
nilai desimal dari string biner yang merepresentasikan x + y. Misalnya pada term dengan
2
peubah x dan y, indeks 0 pada M
0
menyatakan nilai desimal dari 00 (x = 0 dan y = 0),
indeks 1 pada
M1 menyatakan
nilai desimal dari 01 (x = 0 dan y = 1) dan seterusnya.
Jadi, untuk maxterm dari 3 peubah (x, y, dan z), jika ditulis M
6
maka ini berarti maxterm
x’ + y’ + z karena 6 (desimal) = 110 (biner); di sini x = 1, y = 1 dan z = 0. Peubah x dan y
dinyatakan dengan komplemen sedangkan peubah z dinyatakan tanpa komplemen
karena bernilai 0, sehingga ditulis x’ + y’ + z.
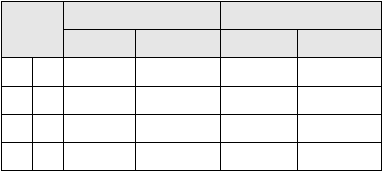
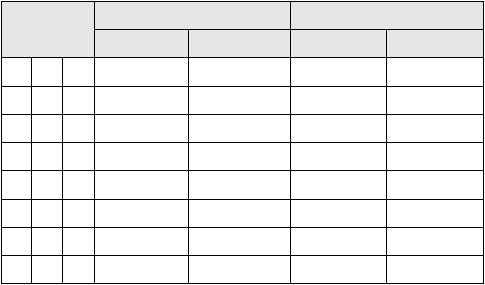
Tabel 2.7 Tabel minterm dan maxterm dengan 2 peubah
(Sumber: Rinaldi Munir, 2005, p299)
Minterm
Maxterm
x
y
Suku
Lambang
Suku
Lambang
0
0
x’y’
m
0
x + y
M
0
0
1
x’y
m1
x + y’
M1
1
0
xy’
m2
x’ + y
M2
1
1
xy
m3
x’ + y’
M3
|
 21
Tabel 2.8 Tabel minterm dan maxterm dengan 3 peubah
(Sumber: Rinaldi Munir, 2005, p300)
Minterm
Maxterm
x
y
y
Suku
Lambang
Suku
Lambang
0
0
0
x’y’z’
m
0
x + y + z
M
0
0
0
1
x’y’z
m1
x + y + z’
M1
0
1
0
x’yz’
m2
x + y’ + z
M2
0
1
1
x’yz
m3
x + y’ + z’
M3
1
0
0
xy’z’
m
4
x’ + y + z
M
4
1
0
1
xy’z
m
5
x’ + y + z’
M
5
1
1
0
xyz’
m
6
x’ + y’ + z
M
6
1
1
1
xyz
m
7
x’ + y’ + z’
M
7
Untuk membentuk fungsi dalam bentuk SOP, tinjau kombinasi nilai–nilai peubah
yang
memberikan
nilai
fungsi
sama
dengan 1. Misalkan
kombinasi
nilai–nilai peubah
yang
memberikan
nilai
fungsi sama dengan 1 adalah 001, 100, dan 111,
maka bentuk
SOP fungsi tersebut adalah:
f(x, y, z) = x’y’z + xy’z’ + xyz
atau (dengan menggunakan lambang minterm) dapat ditulis
f(x, y, z) = m1
+ m
4
+ m
7
= 3(1, 4, 7).
Untuk membentuk fungsi dalam bentuk POS, tinjau kombinasi nilai–nilai peubah
yang
memberikan
nilai
fungsi sama dengan 0. Misalkan kombinasi
nilai–
nilai peubah
yang memberikan nilai fungsi sama dengan 0 adalah 000, 010, 101, dan 110, maka
bentuk POS fungsi tersebut adalah
f(x, y, z) = (x + y + z) (x + y’ + z) (x’ + y + z’) (x’ + y’ + z)
atau (dengan menggunakan lambang maxterm) dapat ditulis
f(x, y, z) = M
0
+ M2 + M
5
+ M
6
= ?(0, 2, 5, 6).
|
|
22
Notasi 3
dan
?
berguna untuk
mempersingkat penulisan ekspresi dalam bentuk
SOP dan POS.
2.9
Konversi Antar Bentuk Kanonik
Fungsi Boolean dalam bentuk kanonik SOP dapat ditransformasi ke bentuk
kanonik POS, demikian pula sebaliknya [Rinaldi Munir 2005, p303]. Misalkan f adalah
fungsi Boolean dalam bentuk SOP dengan tiga peubah:
f(x, y, z) = ³(1, 4, 5, 6, 7)
dan f ’ adalah fungsi komplemen dari f,
f ‘(x, y, z) = 3(0, 2, 3) = m
0
+ m2 + m3
Dengan menggunakan hukum De Morgan, kita dapat memperoleh fungsi f dalam
bentuk POS:
f ‘(x, y, z) = (f ‘(x, y, z))‘ = (m
0
+
m2
+ m3)’
= m
0
’
. m2’ . m3
’
= (x’y’z’)’ . (x’yz’)’ . (x’yz)’
= (x + y + z) . (x + y’ + z) . (x + y’ + z’)
= M
0
M2 M3
= M
0
M2 M3
Jadi,
f
(x, y, z) = ?(0, 2, 3) = ³(1, 4, 5, 6, 7)
|
|
23
2.10
Bentuk Baku
Dua bentuk kanonik adalah bentuk dasar yang diperoleh dengan membaca fungsi
dari
tabel kebenaran.
Bentuk
ini
umumnya sangat
jarang
muncul, karena setiap
suku
(term) di dalam bentuk kanonik
harus mengandung literal
lengkap, baik dalam bentuk
normal (x) atau dalam bentuk komplemennya (x’) [Rinaldi Munir, 2005, p304].
Cara lain untuk mengekspresikan fungsi Boolean adalah bentuk baku (standard).
Pada bentuk ini, suku–suku yang membentuk fungsi dapat mengandung satu, dua, atau
sejumlah
literal. Dua tipe bentuk baku adalah bentuk baku SOP dan bentuk baku POS.
Contohnya,
f(x, y, z) = y’ + xy + x’yz
(bentuk baku SOP)
f(x, y, z) = x(y’ + z)(x’ + y + z’)
(bentuk baku POS)
Perbedaan antara bentuk kanonik dan bentuk baku adalah, pada bentuk kanonik,
setiap term harus mengandung literal lengkap, sedangkan pada bentuk baku setiap term
tidak mengandung literal lengkap.
2.11
Penyederhanaan Fungsi Boolean
Fungsi Boolean seringkali mengandung operasi–operasi yang tidak perlu, literal
atau suku–suku yang berlebihan. Oleh karena itu, fungsi Boolean dapat disederhanakan
lebih
lanjut. Menyederhanakan
fungsi
Boolean artinya
mencari bentuk fungsi
lain
yang
ekivalen tetapi dengan jumlah literal atau operasi yang lebih sedikit. Penyederhanaan
fungsi Boolean disebut juga minimisasi fungsi [Rinaldi Munir, 2005, p308].
Dipandang
dari
segi
aplikasi
aljabar Boolean,
fungsi
Boolean
yang
lebih
sederhana berarti rangkaian logikanya juga lebih sederhana (menggunakan jumlah
|
|
24
gerbang logika lebih sedikit). Ada tiga metode yang dapat digunakan untuk
menyederhanakan fungsi Boolean:
1.
Secara aljabar, menggunakan hukum–hukum aljabar Boolean.
2.
Metode Peta Karnaugh.
3.
Metode Quine-McCluskey (metode tabulasi).
2.11.1 Penyederhanaan Fungsi Boolean Secara Aljabar
Jumlah literal di dalam sebuah fungsi Boolean dapat diminimumkan dengan trik
manipulasi aljabar. Sayangnya, tidak ada aturan khusus yang harus diikuti yang akan
menjamin
menuju
ke
jawaban
akhir. Metode
yang
tersedia adalah prosedur
yang cut-
and-try yang memanfaatkan postulat, hukum–hukum dasar, dan metode manipulasi lain
yang sudah dikenal [Rinaldi Munir, 2005, p309]. Sebagai contoh :
f(x, y, z) = xz’ + y’z + xyz’
= xz’ . 1 + y’z + xyz’
(Hukum identitas)
= xz’ (1 + y) + y’z
(Hukum distributif)
= xz’ . 1 + y’z
(Hukum dominansi)
f(x, y, z) = xz’ + y’z
(Hukum identitas)
2.11.2 Metode Peta Karnaugh
Metode
Peta
Karnaugh
(atau K-map)
merupakan
metode
grafis
untuk
menyederhanakan
fungsi Boolean. Metode
ini ditemukan oleh Maurice Karnaugh pada
tahun 1953. Peta Karnaugh adalah sebuah diagram/peta yang terbentuk dari kotak–kotak
(berbentuk bujursangkar) yang bersisian. Tiap kotak merepresentasikan sebuah minterm.
|
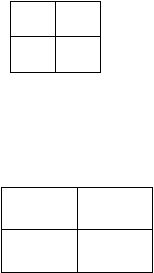 25
x’y’
x’y
xy’
xy
Tiap
kotak
dikatakan
bertetangga
jika minterm–minterm
yang
merepresentasikannya
berbeda hanya 1 buah literal [Kenneth H. Rosen, 2000, p612].
Peta Karnaugh dapat dibentuk dari fungsi Boolean yang dispesifikasikan dengan
ekspresi Boolean maupun fungsi yang direpresentasikan dengan tabel kebenaran.
a. Peta Karnaugh dengan Dua Peubah
Misalkan dua peubah di dalam
fungsi
Boolean adalah x dan y. Baris pada peta
Karnaugh untuk peubah x dan kolom untuk peubah y. Baris pertama diidentifikasi nilai
0
(menyatakan
x’),
sedangkan
baris
kedua dengan
1
(menyatakan x).
Kolom pertama
diidentifikasi nilai 0 (menyatakan y’), sedangkan kolom kedua dengan 1 (menyatakan y).
Setiap
kotak
merepresentasikan minterm dari
kombinasi
baris
dan
kolom
yang
bersesuaian.
Berikut terdapat tiga cara
yang lazim digunakan
sejumlah literatur dalam
menggambarkan peta Karnaugh untuk dua peubah.
m
0
m1
m2
m3
Gambar 2.1 Penyajian 1 - Peta Karnaugh dengan 2 peubah
(Sumber: Rinaldi Munir, 2005, p310)
y
0
1
x
0
1
Gambar 2.2 Penyajian 2 - Peta Karnaugh dengan 2 peubah
(Sumber: Rinaldi Munir, 2005, p310)
|
 26
x’y’
x’y
xy’
xy
x’y’z’
x’y’z
x’yz
x’yz’
xy’z’
xy’z
xyz
xyz’
y’
y
x’
x
Gambar 2.3 Penyajian 3 - Peta Karnaugh dengan 2 peubah
(Sumber: Rinaldi Munir, 2005, p285)
Perhatikan bahwa dua kotak yang bertetangga pada peta Karnaugh hanya
berbeda satu bit atau satu literal.
b.
Peta Karnaugh dengan Tiga Peubah
Untuk fungsi Boolean dengan tiga peubah (misalkan x, y dan z), jumlah kotak di
dalam
peta
Karnaugh
meningkat
menjadi
2³
=
8.
Baris
pada
peta
Karnaugh
untuk
peubah x dan kolom untuk peubah yz. Baris pertama diidentifikasi nilai 0 (menyatakan
x’), sedangkan baris kedua dengan 1 (menyatakan x). Kolom pertama diidentifikasi nilai
00
(menyatakan
x’y’),
kolom
kedua
diidentifikasi
nilai
01
(menyatakan
xy’),
kolom
ketiga diidentifikasi 11 (menyatakan xy). Perhatikanlah bahwa antara satu kolom dengan
kolom berikutnya hanya berbeda satu bit. Setiap kotak
merepresentasikan minterm dari
kombinasi baris dan kolom yang bersesuaian.
yz
00
01
11
10
x
0
1
Gambar 2.4 Peta Karnaugh dengan 3 peubah
(Sumber: Rinaldi Munir, 2005, p312)
|
 27
w’x’y’z’
w’x’y’z
w’x’yz
w’x’yz’
w’xy’z’
w’xy’z
w’xyz
w’xyz’
wxy’z’
wxy’z
wxyz
wxyz’
wx’y’z’
wx’y’z
wx’yz
wx’yz’
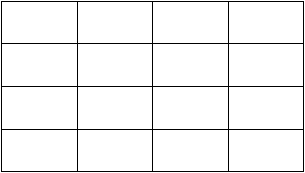
c.
Peta Karnaugh dengan Empat Peubah
Misalkan empat peubah di dalam
fungsi
Boolean adalah w, x, y dan z. Jumlah
kotak di dalam peta Karnaugh meningkat
menjadi 2
4
=
16. Baris pada peta Karnaugh
untuk
peubah
wx
dan
kolom untuk
peubah
yz.
Baris
pertama
diidentifikasi
nilai
00
(menyatakan w’x’),
baris kedua
dengan 01
(menyatakan w’x),
baris ketiga
dengan 11
(menyatakan
wx)
dan
baris
keempat
dengan
10
(menyatakan
wx’).
Kolom pertama
diidentifikasi nilai 00 (menyatakan y’z’), kolom kedua diidentifikasi nilai 01
(menyatakan yz’), kolom ketiga diidentifikasi nilai 11 (menyatakan yz), sedangkan
kolom keempat
diidentifikasi
dengan
nilai
00
(menyatakan yz’).
Setiap
kotak
merepresentasikan minterm dari kombinasi baris dan kolom yang bersesuaian.
yz
00
01
11
10
wx
00
01
11
10
Gambar 2.5 Peta Karnaugh dengan 4 peubah
(Sumber: Rinaldi Munir, 2005, p315)
2.11.3 Metode Quine-McCluskey
Metode peta Karnaugh hanya cocok digunakan jika fungsi Boolean mempunyai
jumlah peubah yang tidak banyak. Jika peubah yang terlibat pada suatu fungsi Boolean
dalam
jumlah
yang
besar
maka
penggunaan
peta
Karnaugh
menjadi
semakin
rumit,
sebab
ukuran
peta
bertambah
besar.
Selain
itu,
metode
peta Karnaugh
lebih sulit
diprogram
dengan komputer karena
diperlukan pengamatan
visual
untuk
|
|
28
mengidentifikasi minterm–minterm yang
akan
dikelompokkan.
Untuk
itu
diperlukan
metode
penyederhanaan
yang
lain
yang
dapat
diprogram dan
dapat
digunakan
untuk
fungsi Boolean
dengan
sembarang
jumlah
peubah.
Metode
alternatif tersebut
adalah
metode Quine-McCluskey [ Kenneth H. Rosen, 2000, p619].
Metode Quine-McCluskey adalah sebuah metode yang digunakan untuk
menyederhanakan
fungsi Boolean,
khususnya
fungsi Boolean
yang
memiliki
jumlah
peubah yang besar (di atas 6 buah). Metode Quine-McCluskey dikembangkan oleh W.V.
Quine dan E.J. McCluskey pada tahun 1950 [Rinaldi Munir, 2005, p334].
Metode
ini
mengubah sebuah
fungsi Boolean
menjadi sebuah
himpunan bentuk
prima, di mana sebanyak mungkin peubah dieliminasi (dihilangkan) secara maksimal,
hingga
didapat
fungsi Boolean
yang
paling
sederhana.
Ini
dapat
dilakukan
dengan
melakukan
perulangan
penggunaan
hukum komplemen,
a
+
a’ =
1.
Sebagai
contoh,
fungsi
Boolean
dengan empat
peubah dalam
bentuk
SOP:
f(a,
b,
c,
d)
=
3(3,
11)
=
3(0011, 1011) = a’b’cd + ab’cd dan f(a, b, c, d) = 3(7, 11) = 3(0111, 1011) = a’b’©d +
ab’cd.
a b c d
a b c d
-------
-------
3
0 0 1 1
7
0 1 1 1
11
1
0 1 1
11
1 0 1 1
-------
-------
BENTUK PRIMA -> (3,11)
-
0 1 1
?
Contoh (a)
Contoh (b)
Pada
contoh(a),
kedua minterm tersebut dapat
dikombinasikan
menjadi sebuah
bentuk
prima
yaitu
(3,11),
karena
memiliki
tepat
satu
perbedaan bit
pada
posisi
bit
nomor satu. Hasil kombinasi dalam bentuk prima (3,11) menyatakan bahwa peubah ‘a’
telah dieleminasi. Hal ini sesuai dengan hukum komplemen, a + a’ = 1.
|
|
29
Pada contoh(b), kedua minterm tersebut tidak dapat dikombinasikan menjadi
sebuah bentuk prima, karena memiliki dua perbedaan bit pada posisi bit nomor satu dan
dua. Setiap kombinasi dari minterm yang dapat
membentuk sebuah bentuk prima baru
harus memiliki tepat satu perbedaan bit pada posisi yang sama.
Secara
umum,
langkah–langkah
metode Quine-McCluskey untuk
menyederhanakan ekspresi Boolean dalam bentuk SOP adalah sebagai berikut.
1.
Nyatakan tiap minterm dalam n peubah menjadi string bit yang panjangnya n, yang
dalam hal
ini
peubah
komplemen
dinyatakan
dengan
‘0’,
peubah
yang
bukan
komplemen dengan ‘1’.
2.
Kelompokkan tiap minterm berdasarkan jumlah ‘1’ yang dimilikinya.
3.
Kombinasikan minterm dalam n peubah dengan kelompok
lain yang jumlah ‘1’-nya
berbeda satu, sehingga diperoleh bentuk prima (prime-implicant) yang terdiri dari n
-
1 peubah. Minterm yang dikombinasikan diberi tanda “v”.
4.
Kombinasikan minterm dalam n – 1 peubah dengan kelompok lain yang jumlah ‘1’-
nya berbeda satu, sehingga diperoleh bentuk prima yang terdiri dari n – 2 peubah.
5.
Teruskan langkah 4 sampai diperoleh bentuk prima yang sesederhanan mungkin.
6.
Ambil semua bentuk prima yang tidak bertanda “v”. Buatlah tabel baru yang
memperlihatkan minterm dari ekspresi
Boolean semula
yang dicakup oleh bentuk
prima tersebut (tandai dengan “×”). Setiap minterm harus dicakup oleh paling sedikit
satu buah bentuk prima.
7.
Pilih
bentuk
prima
yang
memiliki
jumlah
literal
paling
sedikit
namun
mencakup
sebanyak
mungkin minterm dari ekspresi
Boolean semula. Hal
ini dapat dilakukan
dengan cara berikut.
|
|
30
a.
Tandai kolom–kolom yang
mempunyai satu buah tanda
“
×
”
dengan tanda “*”,
lalu beri tanda “v” di sebelah kiri bentuk prima
yang berasosiasi dengan tanda
“*” tersebut. Bentuk prima ini telah dipilih untuk fungsi Boolean sederhana.
b.
Untuk setiap bentuk prima yang telah ditandai dengan
“v”, beri tanda minterm
yang
dicakup
oleh
bentuk
prima
tersebut
dengan
tanda
“v” (di baris bawah
setelah “*”).
c.
Periksa apakah masih ada minterm yang belum
dicakup oleh bentuk prima
terpilih. Jika ada, pilih dari bentuk prima yang tersisa yang mencakup sebanyak
mungkin minterm tersebut.
Beri tanda “v” bentuk prima
yang dipilih
itu serta
minterm yang dicakupnya.
d.
Ulangi
langkah c
sampai
seluruh
minterm
sudah dicakup
oleh
semua bentuk
prima.
Langkah–langkah
penyederhanaan
metode Quine-McCluskey di
atas
juga
berlaku
untuk
penyederhanaan
fungsi
Boolean dalam bentuk
POS.
Perhatikan
bahwa
bentuk fungsi output selalu sama dengan bentuk fungsi input, artinya input dalam bentuk
SOP
akan
menghasilkan output dalam bentuk
dalam SOP,
dan
demikian
pula
untuk
bentuk POS.
Agar lebih jelas, perhatikan contoh berikut. Bentuk input dalam bentuk SOP:
f(w, x, y, z)
= 3(1, 4, 6, 7, 8, 9, 10, 11, 15)
|
 31
Langkah–langkah minimisasi yang dilakukan adalah sebagai berikut.
(Langkah 1 dan langkah 2) Konversikan
nilai minterm ke bentuk biner dengan
panjang sebesar n peubah (4 bit) dan kelompokkan tiap minterm berdasarkan jumlah bit
‘1’ yang dimilikinya.
))))))))))))))))
term
w x y z
))))))))))))))))
1
0 0 0 1
(Jumlah bit '1 ' = 1 buah).
4
0 1 0 0
8
1 0 0 0
))))))))))))))))
6
0 1 1 0
(Jumlah bit '1' = 2 buah).
9
1 0 0 1
10
1 0 1 0
))))))))))))))))
7
0 1 1 1
(Jumlah bit '1 ' = 3 buah).
11
1 0 1 1
))))))))))))))))
15
1 1 1 1
(Jumlah bit '1' = 4 buah).
))))))))))))))))
(Langkah 3 sampai 5) Kombinasikan
term atau bentuk prima yang memiliki
perbedaan
tepat satu
bit pada
posisi
yang
sama.
Hasil
kombinasi
merupakan
bentuk
prima
baru.
Lakukan
hingga
didapat
bentuk
prima
sesederhana
mungkin.
Term
atau
bentuk prima yang dikombinasikan diberi tanda ‘v’.
))))))))))))))))
))))))))))))))))
)))))))))))))))))))
term
w x y z
term
w x y z
term
w x y z
))))))))))))))))
))))))))))))))))
)))))))))))))))))))
1
0 0 0 1
v
1,9
-
0 0 1
8,9,10,11
1 0 - -
v
4
0 1 0 0
v
4,6
0 1 – 0
8,10,9,11
1 0 - -
v
8
1 0 0 0
v
8,9
1 0 0 -
v
))))))))))))))))))))
))))))))))))))))
8,10
1 0 – 0
v
6
0 1 1 0
v
))))))))))))))))
9
1 0 0 1
v
6,7
0 1 1 -
10
1 0 1 0
v
9,11
1 0 – 1
v
))))))))))))))))
10,11
1 0 1 -
v
7
0 1 1 1
v
))))))))))))))))
11
1 0 1 1
v
7,15
-
1 1 1
))))))))))))))))
11,15
1 - 1 1
15
1 1 1 1
v
))))))))))))))))
|
 32
(Langkah 6) Ambil semua bentuk prima yang tidak bertanda “
v
”. Buatlah tabel
baru
yang
memperlihatkan
minterm
dari
ekspresi
Boolean
semula
yang
dicakup
oleh
bentuk prima
tersebut (tandai dengan
“×”). Setiap minterm harus dicakup oleh paling
sedikit satu buah bentuk prima.
(Langkah 7.a) Tandai kolom–kolom yang mempunyai satu buah tanda “×”
dengan
tanda
“*”,
lalu
beri
tanda
“v” di
sebelah
kiri
bentuk
prima
yang berasosiasi
dengan
tanda “*” tersebut. Bentuk prima
ini telah dipilih untuk fungsi Boolean
sederhana.
|
 33
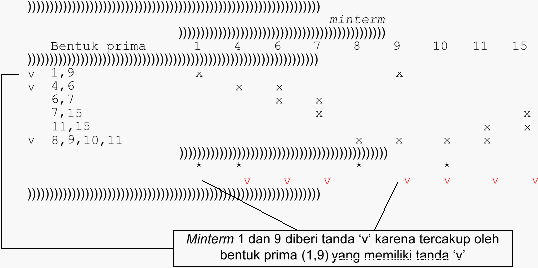
(Langkah 7.b) Untuk setiap bentuk prima yang telah ditandai dengan
“
v
”, beri
tanda minterm
yang dicakup
oleh
bentuk
prima tersebut
dengan
tanda
“v” (di baris
bawah setelah “*”).
(Langkah 7.c dan 7.d) Sampai tahap ini, masih ada minterm yang belum tercakup
dalam bentuk
prima
terpilih,
yaitu
7,
15.
Untuk
mencakup minterm tersebut,
dipilih
bentuk prima (7,15), karena mencakup minterm 7 dan 15 sekaligus.
))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))
minterm
)))))))))))))))))))))))))))))))))))))))))))))))
Bentuk prima
1
4
6
7
8
9
10
11
15
))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))
v
1,9
x
x
v
4,6
x
x
6,7
x
x
v
7,15
x
x
11,15
x
x
v
8,9,10,11
x
x
x
x
)))))))))))))))))))))))))))))))))))))))))))))))
*
*
*
*
v
v
v
v
v
v
v
v
v
))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))))
|
|
34
Sekarang, semua minterm sudah tercakup dalam bentuk prima terpilih. Bentuk prima
yang terpilih adalah sebagai berikut.
1,9
yang bersesuaian dengan term x' y' z
4,6
yang bersesuaian dengan term w' xz'
7,15
yang bersesuaian dengan term xyz
8,9,10,11
yang bersesuaian dengan term wx'
Dengan demikian, fungsi Boolean hasil penyederhanaan dengan metode Quine-
McCluskey adalah:
f(w, x, y, z) = x' y' z + w' xz' + xyz + wx'.
2.12. Teori Perancangan Program
Menurut Pressmann (2005, p.36), perangkat lunak didefinisikan sebagai berikut.
a.
Instruksi-instruksi
yang
jika dijalankan memberikan fungsi dan kerja yang
diinginkan.
b.
Struktur data yang membuat program mampu memanipulasi suatu informasi.
c.
Dokumen-dokumen yang menjelaskan operasi dan pemakaian suatu program.
Perangkat lunak dapat dibagi menjadi dua kategori besar, yaitu:
a.
Sistem operasi, yang mengontrol jalannya komputer.
b.
Aplikasi
yang
dapat
mengerjakan
berbagai
fungsi
atau
tugas
yang
diinginkan
manusia dalam menggunakan komputer.
Perangkat
lunak berbeda dengan
perangkat keras. Perangkat
lunak
merupakan
suatu elemen sistem yang bersifat logis, bukan fisik dan tidak berwujud nyata. Perangkat
lunak memiliki beberapa karakteristik sebagai berikut.
a.
Perangkat
lunak dikembangkan
dan
direkayasa.
Perangkat
lunak
tidak dirakit
seperti perangkat keras.
|
 35
b.
Perangkat
lunak tidak
dapat dirusak,
tetapi dapat
mengalami kegagalan
fungsi,
walaupun kegagalan ini dapat diperbaiki. Sedangkan perangkat keras dapat rusak
karena pengaruh lingkungan, sehingga harus diganti jika sudah tidak mungkin
diperbaiki. Pemeliharaan perangkat lunak lebih rumit daripada perangkat keras.
c.
Perangkat
lunak
dibuat
mulai
dari
komponen
terkecil
kemudian
digabungkan,
sehingga
dapat
membentuk
suatu
fungsi tertentu.
Sedangkan
perangkat
keras
dirakit dari berbagai komponen yang sudah ada.
Untuk membuat sebuah perangkat lunak, Pressmann (2005, p.79), mengusulkan
paradigma yang dapat dipakai sebagai pendekatan yang digunakan untuk perancangan
perangkat
lunak.
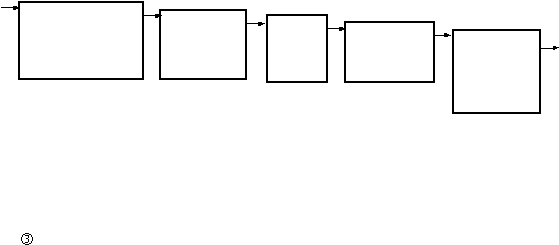
Model waterfall
merupakan pendekatan paradigma
paling
kuno
dan
paling banyak dipakai dalam pembuatan perangkat lunak yang sudah menjadi pola dasar
dalam paradigma-paradigma lainnya.
Communication
Planning
Modeling
Construction
project initiation
requirements
gathering
estimating
schedulin
g tracking
analysis
design
code
test
Deployment
delivery
support
feedback
Gambar 2.6 The Waterfall Model
(sumber: Roger S. Pressman, 2005, p.79)
Communication
Aktivitas dalam kerangka ini melibatkan komunikasi dan kolaborasi/kerja
sama dengan pelanggan. Meliputi pengumpulan persyaratan-persyaratan dan
aktivitas lain yang berhubungan.
|
|
36
Planning
Aktivitas
dalam kerangka
ini
adalah
menetapkan
satu
rencana
untuk
rekayasa perangkat lunak.
-
Menguraikan tugas-tugas teknis yang akan dilakukan
-
Memikirkan resiko yang mungkin terjadi
-
Mengumpulkan sumber daya yang diperlukan
-
Menentukan produk-produk yang ingin dihasilkan
-
Membuat satu rencana kerja
Modeling
Aktivitas dalam
kerangka ini meliputi analisa permasalahan yang
dihadapi, pembuatan model-model yang memudahkan pengembang dan
pelanggan untuk lebih memahami persyaratan-persyaratan perangkat lunak dan
juga menjelaskan bagaimana suatu sistem akan bekerja.
Construction
Aktivitas dalam kerangka ini adalah menerjemahkan spesifikasi desain ke
dalam bahasa komputer dan memeriksa apakah pemrograman telah menghasilkan
hasil yang diinginkan. Testing didesain untuk
mendeteksi
adanya error didalam
coding.
|
|
37
Deployment
Aktivitas dalam kerangka ini adalah sebagai berikut.
-
Mengirimkan perangkat lunak/sistem kepada para pelanggan
-
Mengevaluasi
kembali
perangkat
lunak
yang
dikirimkan
untuk
mengakomodasi perubahan dalam situasi bisnis
-
Menyediakan
umpan
balik
yang
didasarkan
pada
evaluasi
(menambah
fungsi atau feature baru ke dalam sistem).
2.13
Interaksi Manusia dan Komputer
Menurut Shneiderman (2005, p4), Interaksi manusia dan komputer merupakan
disiplin ilmu yang berhubungan dengan, perancangan, evaluasi, dan implementasi sistem
komputer interaktif untuk digunakan oleh manusia, serta studi fenomena-fenomena
besar yang berhubungan dengannya.
Pada interaksi manusia dan komputer ditekankan pada pembuatan antarmuka
pemakai (user interface), dimana user interface yang dibuat diusahakan sedemikian rupa
sehingga seorang user dapat dengan baik dan nyaman menggunakan aplikasi perangkat
lunak dibuat. Antar muka pemakai (user interface) adalah bagian sistem komputer
yang
memungkinkan
manusia
berinteraksi
dengan
komputer.
Tujuan antar
muka
pemakai adalah agar
sistem komputer
dapat digunakan
oleh pemakai (user interface),
istilah tersebut digunakan untuk menunjuk kepada kemampuan yang dimiliki oleh
piranti
lunak
atau
program aplikasi
yang
mudah
dioperasikan
dan
dapat
membantu
menyelesaikan
suatu
persoalan dengan
hasil
yang
sesuai
dengan
keinginan
pengguna
atau biasa disebut user friendly.
|
|
38
Pedoman
untuk
menghasilkan
suatu
rancangan
antar
muka
program yang
user
friendly adalah dengan menggunakan pedoman Eight Golden Rules. Eight Golden Rules
tersebut
menjelaskan
mengenai
beberapa aturan
yang
diperbolehkan
dan
tidaj
diperbolehkan sebagai pedoman untuk merancang antar muka program. Kedelapan
aturan tersebut, yaitu:
a. Strive for consistency, konsistensi dalam perancangan antar muka;
b. Enable frequent user to use shorcuts, memungkinkan pengguna
menggunakan shortcuts secara berkala;
c. Offer
informative
feed
back,
memberikan
umpan
balik
yang
informative;
d. Design
dialogs
to
yield
closure,
merancang
dialog
untuk
menghasilkan keadaan akhir;
e. Offer simple error handling, memberikan penanganan kesalahan yang
sederhana;
f.
Permit
easy
reversal
of actions, mengijinkan pembalikkan
aksi
dengan mudah;
g. Support
internal
locus
of
control,
mendukung
pengguna
menguasai
system yang dibuat;
h. Short-term
memory
load,
mengurangi
beban
jangka
pendek
kepada
pengguna.
|
|
39
2.14
UML (Unified Modelling Language)
UML
(Unified
Modeling
Language) adalah
sebuah
bahasa
yang
berdasarkan
grafik/gambar
untuk
memvisualisasi, menspesifikasikan,
membangun,
dan
pendokumentasian
dari
sebuah
sistem pengembangan
software
berbasis
OO(Object-
Oriented). UML
sendiri
juga
memberikan
standar penulisan
sebuah
sistem blue
print,
yang
meliputi konsep bisnis proses, penulisan kelas-kelas dalam bahasa program yang
spesifik,
skema
database,
dan
komponen-komponen
yang
diperlukan
dalam sistem
software [Joseph Schmuller 1999, p6].
UML sebagai sebuah bahasa yang memberikan vocabulary dan tatanan penulisan
kata-kata dalam ‘MS Word’ untuk kegunaan komunikasi. Sebuah bahasa model adalah
sebuah bahasa yang mempunyai vocabulary dan konsep tatanan / aturan penulisan serta
secara
fisik mempresentasikan dari sebuah sistem. Seperti
halnya UML adalah
sebuah
bahasa
standar
untuk
pengembangan
sebuah
software yang
dapat
menyampaikan
bagaimana membuat dan membentuk model-model, tetapi tidak menyampaikan apa dan
kapan model yang seharusnya dibuat yang merupakan salah satu proses implementasi
pengembangan software.
UML
tidak
hanya
merupakan
sebuah
bahasa
pemograman
visual
saja,
namun
juga dapat secara langsung dihubungkan ke berbagai bahasa pemograman, seperti JAVA,
C++, Visual Basic, atau bahkan dihubungkan secara langsung ke dalam sebuah object-
oriented database. Begitu juga mengenai pendokumentasian dapat dilakukan seperti;
requirements, arsitektur, design, source code, project plan, tests, dan prototypes. Untuk
dapat
memahami UML membutuhkan bentuk
konsep
dari
sebuah bahasa
model,
dan
mempelajari 3 (tiga) elemen utama dari UML seperti building block, aturan-aturan yang
|
|
40
menyatakan
bagaimana building
block diletakkan
secara bersamaan,
dan
beberapa
mekanisme umum (common).
Obyek
dalam ‘software
analysis
&
design’ adalah
sesuatu
berupa
konsep
(concept), benda (thing), dan sesuatu yang membedakannya dengan lingkungannya.
Secara sederhana obyek adalah mobil, manusia, alarm dan lainlainnya. Tapi obyek dapat
pula merupakan sesuatu yang abstrak yang hidup didalam sistem seperti tabel, database,
event, system messages.
Obyek dikenali dari keadaannya dan juga operasinya. Sebagai contoh sebuah
mobil dikenali dari warnanya, bentuknya, sedangkan manusia dari suaranya. Ciri-ciri
ini yang akan membedakan obyek tersebut dari obyek lainnya. Alasan mengapa saat ini
pendekatan
dalam pengembangan
software
dengan
object-oriented,
pertama
adalah
scalability dimana obyek lebih mudah dipakai untuk menggambarkan sistem yang besar
dan komplek. Kedua dynamic modeling, adalah dapat dipakai untuk permodelan sistem
dinamis dan real time.
2.13.1 Teknik Dasar OOA/D (Object-Oriented Analysis/Design)
Dalam dunia pemodelan, metodologi implementasi obyek walaupun terikat
kaidah-kaidah standar,
namun
teknik pemilihan obyek
tidak
terlepas pada subyektifitas
software analyst & designer. Beberapa obyek akan diabaikan dan beberapa obyek
menjadi perhatian untuk diimplementasikan di dalam sistem. Hal ini sah-sah saja karena
kenyataan bahwa suatu permasalahan sudah tentu memiliki lebih dari satu solusi. Ada 3
(tiga) teknik/konsep dasar dalam OOA/D,
yaitu pemodulan (encapsulation), penurunan
(inheritance) dan polymorphism.
|
|
41
a.
Pemodulan (Encapsulation)
Pada dunia nyata, seorang ibu rumah tangga menanak nasi dengan menggunakan
rice cooker, ibu tersebut menggunakannya hanya dengan menekan tombol. Tanpa harus
tahu bagaimana proses itu sebenarnya terjadi. Disini terdapat penyembunyian informasi
milik rice cooker, sehingga tidak perlu diketahui seorang ibu. Dengan demikian
menanak nasi oleh si
ibu menjadi sesuatu
yang menjadi dasar bagi konsep information
hiding.
b.
Penurunan (Inheritance)
Obyek-obyek memiliki banyak persamaan, namun ada sedikit perbedan. Contoh
dengan beberapa buah mobil yang mempunyai kegunaan yang berbeda-beda. Ada mobil
bak terbuka
seperti
truk, bak
tertutup seperti sedan
dan
minibus.Walaupun
demikian
obyek-obyek ini memiliki kesamaan yaitu teridentifikasi sebagai obyek mobil, obyek ini
dapat dikatakan sebagai
obyek
induk
(parent). Sedangkan
minibus
dikatakan
sebagai
obyek anak (child), hal ini juga berarti semua operasi yang berlaku pada mobil berlaku
juga pada minibus.
c.
Polymorphism
Pada
obyek
mobil, walaupun
minibus dan truk
merupakan jenis
obyek
mobil
yang sama, namun memiliki juga perbedaan. Misalnya suara truk lebih keras dari pada
minibus,
hal
ini juga
berlaku pada
obyek
anak (child)
melakukan
metoda
yang sama
dengan
algoritma berbeda dari obyek
induknya. Hal
ini
yang disebut
polymorphism,
teknik atau konsep dasar lainnya adalah ruang lingkup/pembatasan. Artinya setiap obyek
mempunyai ruang lingkup kelas, atribut, dan metoda yang dibatasi.
|
 42
2.13.2. Komponen UML
Pemodelan
dengan
UML
terdiri
dari
8
tipe
diagram yang
berbeda
untuk
memodelkan
sistem perangkat
lunak.
Masing-masing
diagram
UML
didesain
untuk
menunjukkan satu sisi dari bermacam-macamsudut pandang (perspektif) dan terdiri dari
tingkat abstraksi yang berbeda.
•
Use Case Diagram
Use case
merupakan
sebuah
deskripsi dari
sifat
suatu
sistem yang
bersal dari
pendirian seorang user. Use case diagram dibutuhkan untuk pengembangan sistem
karena merupakan alat yang dapat menunjukkan perilaku dan apa yang dikerjakan oleh
seorang user atau pengguna. Use-case diagram merupakan suatu bentuk diagram yang
menggambarkan
fungsi-fungsi
yang
diharapkan
dari
sebuah
sistem yang
dirancang.
Dalam Use-case
diagram
penekanannya
adalah
“apa”
yag
diperbuat
oleh sistem,
dan
bukan “bagaimana”. Sebuah use-case akan merepresentasikan sebuah interaksi antara
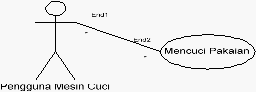
pelaku atau actor dengan sistem.
Use-case diagram yang digunakan dalam mercancang suatu sistem dapat sangat
membantu pada saat kita menyusun requirement sebuah sistem, mengomunikasikannya
dengan klien, dan merancang pengujian untuk semua fitur yang terdapat dalam sistem.
Dalam suatu sistem aplikasi database, use-case diagram sangat membantu requierement
apa saja yang diperlukan.
Contoh :
Gambar 2.7 Contoh Use Case Diagram
|
 43
•
Class Diagram
Sebuah
Class
Diagram menunjukkan
struktur
yang
statis
dari
beberapa
class
dalam suatu sistem. Class-class
merepresentasikan suatu keadaan (atribut/properti) dan
yang akan dikerjakan oleh sistem (metoda/fungsi).
Class memiliki tiga area pokok yaitu:
1. Nama (dan stereotype)
2. Atribut
3. Metoda
Atribut dan metoda dalam class diagram dapat memiliki salah satu sifat seperti berikut di
bawah ini:
•
Private, hanya dapat diakses oleh class itu sendiri.
•
Protected, hanya dapat diakses oleh class itu sendiri dan turunan dari class
tersebut.
•
Public, dapat diakses oleh class selain dari class yang bersangkutan.
Class
dapat
direpresentasikan
dalam sebuah
interface
atau
sebaliknya
merupakan
implementasi dari sebuah interface yang berupa class abstrak yang hanya tidak memiliki
attribute dan hanya memiliki metoda.
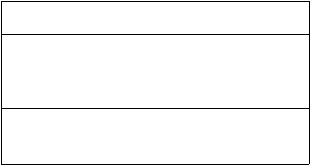
Contoh:
Mesin Cuci
Merk
Model
Nomor seri
Kapasitas
Add pakain()
Add deterjen()
Remove pakain()
Gambar 2.8 Contoh Class Diagram
|
 44
•
Object Diagram
Salah satu
alat
dalam
perancangan
sistem
yang
digunakan
untuk
menjelaskan
tentang nama obyek, atribut dan metode yang dipakai.
Contoh:
Kendaraan : Mobil dan motor
Gambar 2.9 Contoh Object Diagram
•
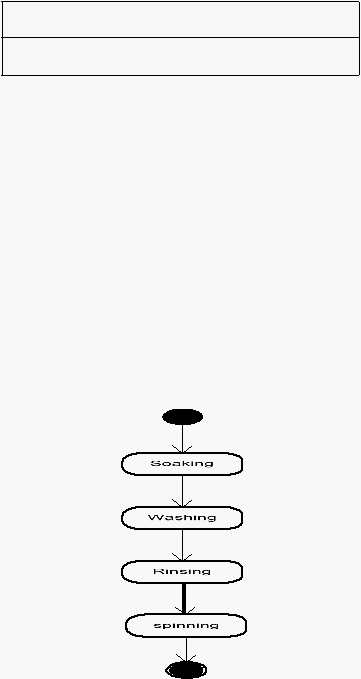
State Diagram
State Diagram
mengambarkan seluruh state yang memungkinkan yang mana
obyek-obyek dalam class dapat dimiliki dan kejadian-kejadian yang menyebabkan state
berubah.
Perubahan
dalam suatu
state
disebut
juga
transisi
(transition).
Suatu transisi
juga dapat
memiliki
sebuah aksi yang dihubungkan pada state, lebih spesifik apa yang
harus dilakukan dalam hubungannya dengan transisi state.
Contoh:
Gambar 2.10 contoh State Diagram
(Sumber: Joseph Schmuller, 1999, p11)
|
 45
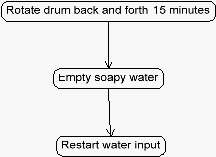
•
Activity Diagram
Sebuah Activity Diagram
menunjukkan suatu alur kegiatan secara berurutan.
Activity
Diagram
digunakan
untuk
mendiskripsikan
kegiatan-kegiatan
dalam sebuah
operasi
meskipun
juga
dapat
digunakan
untuk mendeskripsikan
alur
kegiatan
yang
lainnya seperti use case atau suatu interaksi.
Contoh:
Gambar 2.11 Contoh Activity Diagram
(Sumber: Joseph Schmuller, 1999, p13)
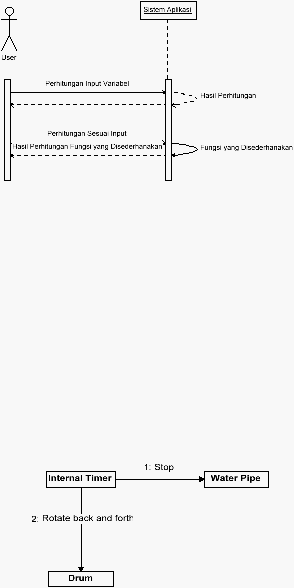
•
Sequence Diagram
Sequence
Diagram
merupakan
diagram yang
mengambarkan
kolaborasi
yang
dinamis antara obyek satu dengan yang lain. Kolaborasi ini ditunjukkan dengan adanya
interaksi antar obyek di dalam dan di sekitar sistem
yang berupa
instruksi atau pesan
yang berurutan.
Sequence diagram umumnya digunakan untuk menggambarkan suatu skenario
atau
urutan
langkah-langkah
yang
dilakukan
baik
oleh
actor
maupun
sistem
yang
merupakan respon dari sebuah kejadian untuk mendapatkan hasil atau output.
Contoh:
|
 46
Gambar 2.11 Contoh Sequence Diagram
•
Collaboration Diagram
Sebuah collaboration diagram menunjukkan kolaborasi yang dinamis yang mirip
dengan sequence diagram. Collaboration diagram digambarkan sebagai sebuah object
diagram dimana
sejumlah
obyek
ditunjukkan
disekitarnya
dengan
hubungan-
hubungannya.
Contoh:
Gambar 2.13 Contoh Collaboration Diagram
(Sumber: Joseph Schmuller, 1999, p13)
•
Component Diagram
Component Diagram menunjukkan struktur dan hubungan antar komponen
software termasuk ketergantungan (dependency) diantara komponen-komponen tersebut.
Contoh:
|
 47
Gambar 2.14 Contoh Component Diagram
•
Deployment Diagram
Deployment diagram menunjukkan arsitektur fisik pada hardware dan software
pada suatu sistem yang dirancang. Deployment diagram juga dapat
menunjukkan
perangkat-perangkat dan nodes diantara hubungan yang dimilikinya antar komponen.
Contoh:
Gambar 2.15 Gambar contoh Deployment Diagram
(Sumber: Joseph Schmuller, 1999, p14)
2.13.3 Flowchart
Flowchart
adalah penggambaran secara grafik dari langkah-langkah dan urut-
urutan prosedur dari suatu program. Flowchart menolong analis danprogrammer untuk
memecahkan
masalah kedalam segmen-segmen
yang
lebih
kecil
dan
menolong
dalam
menganalisis alternatif-alternatif lain dalam pengoperasian. Flowchart biasanya
mempermudah penyelesaian suatu masalah khususnya masalah yang perlu dipelajari dan
dievaluasi lebih lanjut.
|
|
48
Jenis-Jenis Flowchart
•
Flowchart Sistem (System Flowchart)
Flowchart sistem merupakan bagan yang menunjukkan alur kerja atau apa yang
sedang
dikerjakan
di
dalam sistem
secara
keseluruhan
dan
menjelaskan
urutan
dari
prosedur-prosedur yang ada di dalam sistem. Dengan kata lain, flowchart ini merupakan
deskripsi secara grafik dari urutan prosedur-prosedur yang terkombinasi yang
membentuk suatu sistem. Flowchart sistem terdiri dari data yang mengalir melalui
sistem dan proses
yang mentransformasikan data itu.
Data dan proses dalam flowchart
sistem dapat digambarkan secara online (dihubungkan langsung dengan komputer) atau
offline (tidak dihubungkan langsung dengan komputer, misalnya mesin tik, cash register
atau kalkulator).
•
Flowchart Paperwork / Flowchart Dokumen (Document Flowchart)
Flowchart paperwork menelusuri
alur
dari
data
yang
ditulis
melalui
sistem.
Flowchart paperwork
sering
disebut
juga
dengan
Flowchart
dokumen.
Kegunaan
utamanya
adalah
untuk
menelusuri alur
form dan
laporan
sistem dari
satu bagian ke
bagian lain baik bagaimana alur form dan laporan diproses, dicatat dan disimpan.
•
Flowchart Skematik
Flowchart skematik mirip dengan Flowchart Sistem yang menggambarkan suatu
sistem atau prosedur. Flowchart skematik ini bukan hanya menggunakan simbol-simbol
flowchart standar, tetapi juga menggunakan gambar-gambar komputer, peripheral, form-
form atau peralatan
lain
yang digunakan dalam sistem. Flowchart skematik digunakan
sebagai alat komunikasi antara analis sistem dengan seseorang yang tidak familiar
dengan simbol-simbol flowchart yang konvensional. Pemakaian gambar sebagai ganti
|
|
49
dari simbol-simbol flowchart
akan
menghemat
waktu
yang dibutuhkan oleh
seseorang
untuk
mempelajari simbol abstrak
sebelum
dapat
mengerti
flowchart.
Gambar-gambar
ini
mengurangi
kemungkinan salah pengertian tentang
sistem,
hal
ini disebabkan oleh
ketidak-mengertian tentang simbol-simbol yang digunakan. Gambar-gambar juga
memudahkan
pengamat
untuk
mengerti segala sesuatu
yang
dimaksudkan oleh
analis,
sehingga hasilnya lebih menyenangkan dan tanpa ada salah pengertian.
•
Flowchart Program
Flowchart
program dihasilkan
dari
flowchart
sistem.
Flowchart
program
merupakan keterangan yang lebih rinci tentang bagaimana setiap langkah program atau
prosedur
sesungguhnya
dilaksanakan. Flowchart
ini
menunjukkan
setiap
langkah
program atau
prosedur
dalam urutan
yang
tepat
saat
terjadi.
Programmer
menggunakan
flowchart
program untuk
menggambarkan
urutan
instruksi dari program komputer. Analis sistem
menggunakan
flowchart program untuk
menggambarkan
urutan
tugas-tugas
pekerjaan
dalam suatu prosedur atau operasi.
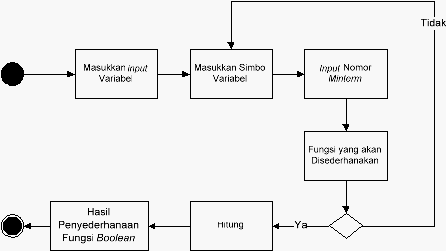
•
Flowchart Proses
Flowchart proses merupakan teknik penggambaran rekayasa industrial yang
memecah
dan
menganalisis
langkah-langkah
selanjutnya
dalam suatu
prosedur
atau
sistem.
Contoh Flowchart:
|
 50
Gambar 2.16 Contoh Flowchart
|