 BAB 2
TINJAUAN PUSTAKA
2.1. Saluran Terbuka
2.1.1. Aliran Pada Saluran Terbuka
Aliran air dalam suatu saluran dapat berupa aliran saluran terbuka
(open
channel
flow)
maupun
aliran-pipa
(pipe flow).
Kedua
jenis
aliran
tersebut
sama
dalam banyak
hal,
namun
berbeda
dalam satu
hal
yang
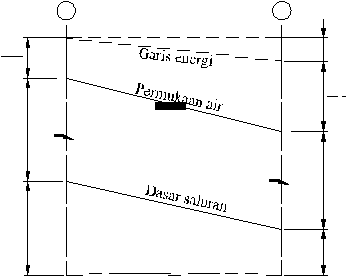
penting. Aliran saluran terbuka harus memiliki permukaan bebas (Gambar
2.1), sedangkan aliran pipa tidak demikian, karena air harus mengisi
seluruh saluran (Gambar 2.2).
1
2
V¹²
2g
y
1
V¹
h
f
V²²
2g
V2
y
2
z
1
z
2
G
aris persamaan
Gambar 2.1 Aliran Saluran Terbuka
6
|
 7
1
2
V1²
2g
y1
h
f
V2²
2g
V1
y
2
V2
z1
z
2
G aris persamaan
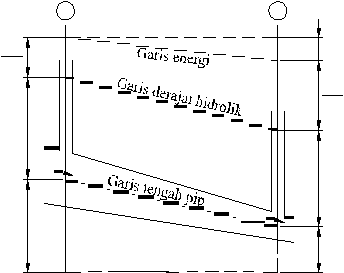
Gambar 2.2 Aliran Pipa
Pada gambar 2.2 aliran pipa, dua tabung pizometer dipasangkan ke
pipa pada penampang 1 dan 2. Permukaan air dalam tabung diatur dengan
tekanan
dalam pipa
pada
ketinggian
yang
disebut
garis
derajat
hidrolik.
Tekanan yang ditimbulkan oleh air pada setiap penampang pipa
ditunjukkan
dalam tabung
yang
bersesuaian
dengan
kolom
air
setinggi
y
diatas
garis
tengah
pipa.
Jumlah
energi
dalam aliran
di
penampang
berdasarkan
suatu
garis
persamaan
adalah
jumlah
tinggi
tempat
z
diukur
dari garis tengah pipa, tinggi tekan y dan tinggi kecepatan V²/2g, dengan V
adalah
kecepatan
rata-rata
aliran. Energi
ini
dinyatakan
dalam gambar
dengan
suatu
garis derajat energi atau disingkat garis energi.
Energi
yang
hilang ketika air mengalir dari penampang 1 ke penampang 2 dinyatakan
dengan hf. Bagan yang serupa untuk aliran saluran terbuka diperlihatkan
dalam gambar 2.1 aliran terbuka.
|
 8
V2
V2
Energi
yang
terdapat pada
aliran saluran
terbuka dan aliran
pipa
diatas dapat dinyatakan dalam persamaan yaitu :
z
1
+
y
1
+
1
2g
=
z
1
+
y
1
+
1
2g
+
h
f
pers (2.1)
Persamaan diatas dikenal juga sebagai persamaan energi (energi
equation) atau dapat disebut juga sebagai persamaan energi dari Bernoulli.
Aliran pada saluran terbuka dapat diklasifikasikan menjadi berbagai
tipe tergantung kriteria yang digunakan. Berdasarkan perubahan kedalaman
dan/atau
kecepatan
mengikuti
fungsi
waktu,
maka
aliran
dibedakan
menjadi
permanen
(steady)
dan tidak
permanen
(unsteady).
Sedangkan
berdasarkan fungsi, maka aliran dibedakan menjadi aliran seragam
(uniform)
dan tidak seragam/berubah
(nonuniform
or
varied).
Klasifikasi
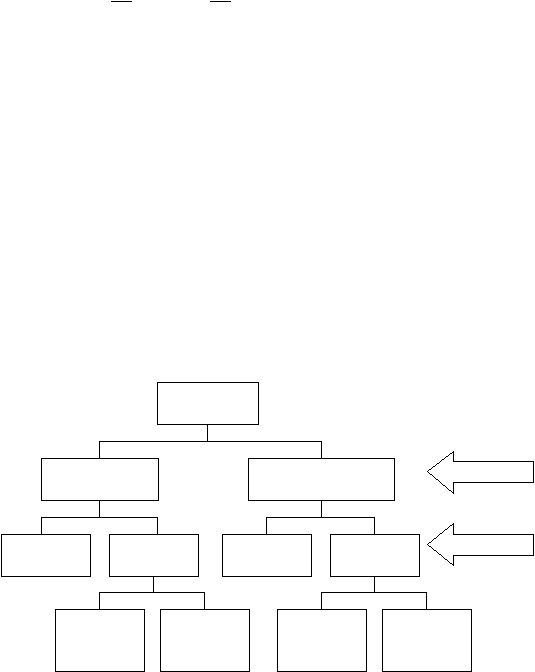
aliran pada saluran terbuka dapat dilihat pada gambar 2.3.
Aliran
(flow)
Aliran Permanen
(steady)
Aliran tak Permanen
(unsteady)
Fungsi Waktu
Seragam
(uniform)
Berubah
(varied)
Seragam
(uniform)
Berubah
(varied)
Fungsi Ruang
Berubah
Lambat Laun
(gradually)
Berubah
Tiba-Tiba
(rapidly)
Berubah
Lambat Laun
(gradually)
Berubah
Tiba-Tiba
(rapidly)
Gambar 2.3 Klasifikasi Aliran Pada Saluran Terbuka
|
|
9
a. Aliran Permanen dan Tidak Permanen
Jika kecepatan aliran
pada suatu titik
tidak
berubah terhadap
waktu, maka aliran disebut aliran permanen atau tunak (steady flow),
jika kecepatan pada suatu lokasi tertentu berubah terhadap waktu
maka alirannya disebut aliran tidak permanen atau tidak tunak
(unsteady flow).
b. Aliran Seragam dan Berubah
Jika kecepatan aliran pada suatu waktu tertentu tidak berubah
sepanjang saluran yang di tinjau, maka alirannya disebut aliran
seragam (uniform
flow).
Namun,
jika
kecepatan
aliran
pada
saat
tertentu berubah terhadap jarak, maka aliran disebut aliran tidak
seragam/berubah (nonuniform flow or varied flow).
Berdasarkan laju
perubahan
kecepatan
terhadap jarak,
maka
aliran dapat diklasifikasikan menjadi aliran berubah lambat laun
(gradually varied flow) atau aliran berubah tiba-tiba (rapidly varied
flow).
c. Aliran Laminer dan Turbulen
Jika partikel zat cair yang bergerak mengikuti alur tertentu dan
aliran tampak seperti gerakan serat-serat atau lapisan-lapisan tipis
yang paralel, maka alirannya disebut aliran laminer. Sebaliknya, jika
partikel zat cair bergerak mengikuti alur yang tidak beraturan, baik
ditinjau terhadap ruang maupun waktu, maka alirannya disebut aliran
turbulen.
|
|
10
Faktor yang
menentukan keadaan aliran adalah pengaruh
relatif antara
kekentalan
(viskositas)
dan
gaya
inersia.
Jika
gaya
viskositas yang dominan, maka alirannya laminer, sedangkan jika
gaya inersia yang dominan, maka aliran turbulen. Nisbah antara gaya
kekentalan dan inersia dinyatakan dalam bilangan Reynold (Rey),
yang didefinisikan seperti rumus berikut :
Rey =
V
×
L
v
pers (2.2)
dimana :
Rey
= bilangan Reynold
V
= kecepatan aliran (m/det),
L
=
panjang karakteristik (m) pada saluran
muka air
bebas, L = R,
R
= jari-jari hidrolik saluran (m),
v
= kekentalan kinematik (m²/det).
Batas peralihan antara aliran laminer dan turbulen pada aliran
bebas terjadi pada bilangan Reynold, Rey
±
600, yang dihitung
berdasarkan jari-jari hidrolik sebagai panjang karakteristik. Dalam
kehidupan sehari-hari, aliran laminer pada saluran terbuka sangat
jarang
ditemui.
Aliran
jenis
ini
mungkin
dapat
terjadi
pada
aliran
yang
kedalaman
sangat
tipis
diatas permukaan
gelas
sangat
halus
dengan kecepatan yang sangat kecil.
|
|
11
d. Aliran Subkritis, Kritis dan Superkritis
Aliran dikatakan kritis (Fr = 1) apabila kecepatan aliran sama
dengan kecepatan gelombang gravitasi dengan amplitudo kecil.
Gelombang gravitasi dapat dibangkitkan dengan merubah kedalaman.
Jika
kecepatan
aliran
lebih
kecil dari
pada
kecepatan
kritis,
maka
alirannya
disebut
subkritis
(Fr <
1),
sedangkan
jika
kecepatannya
alirannya lebih besar dari pada kecepatan kritis, maka alirannya
disebut superkritis (Fr > 1).
Parameter yang menentukan ketiga jenis aliran tersebut adalah
nisbah antara gaya gravitasi dan gaya inersia, yang dinyatakan dengan
bilangan Froude (Fr). Bilangan Froude untuk saluran berbentuk
persegi didefinisikan sebagai :
Fr
=
V
g
×
h
pers (2.3)
dimana :
Fr = bilangan Froude
V = kecepatan aliran (m/dt),
h
= kedalaman aliran (m),
g
= percepatan gravitasi (m²
/dt).
|
|
12
2.1.2. Aliran Permanen Seragam
a. Kualifikasi Aliran Seragam
Aliran
seragam (uniform
flow)
dianggap
memiliki
ciri-ciri
pokok yaitu :
1. Kedalaman, luas basah, kecepatan dan debit pada setiap
penampang pada bagian seluran yang lurus adalah konstan,
2. Garis energi,
muka air dan dasar saluran
saling sejajar, berarti
kemiringannya sama atau Sf = Sw = So = S.
Aliran
seragam
dianggap
sebagai suatu
aliran
permanen
(steady
flow).
Aliran
dalam saluran
terbuka
dikatakan
permanen
(steady)
bila
kedalaman
aliran tidak berubah
atau dianggap
konstan
selama suatu selang waktu tertentu.
Bila air
mengalir dalam saluran terbuka, air akan
mengalami
hambatan saat mengalir ke hilir. Hambatan ini biasanya dilawan oleh
komponen
gaya berat
yang
bekerja
dalam air
dalam arah
geraknya.
Aliran seragam akan terjadi bila hambatan ini seimbang dengan gaya
berat.
Besarnya tahanan bila
faktor-faktor
lain dari saluran dianggap
tidak
berubah, tergantung
pada
kecepatan aliran. Bila
air
memasuki
saluran secara
perlahan,
kecepatan
mengecil
dan
oleh
karenanya
hambatannya juga mengecil, dan hambatan lebih kecil dari gaya berat
sehingga terjadi aliran percepatan di bagian yang lurus disebelah
hulu.
|
|
13
Kecepatan
dan
hambatan
akan
meningkatkan lambat
laun
sampai terjadi keseimbangan antara hambatan dengan gaya-gaya
berat. Pada keadaan ini dan selanjutnya aliran menjadi seragam.
Bagian
lurus di
hulu
yang diperlukan
untuk
membentuk
aliran
seragam dikenal sebagai zona peralihan (transitory zone). Dalam zona
ini aliran dipercepat dan berubah. Bila saluran lebih pendek daripada
panjang peralihan yang diperlukan untuk kondisi yang ditetapkan,
maka tidak dapat terjadi aliran seragam. Pada bagian hilir saluran,
hambatan
mungkin akan
terjadi
lebih kecil dari gaya berat, sehingga
aliran menjadi tidak seragam lagi atau berubah.
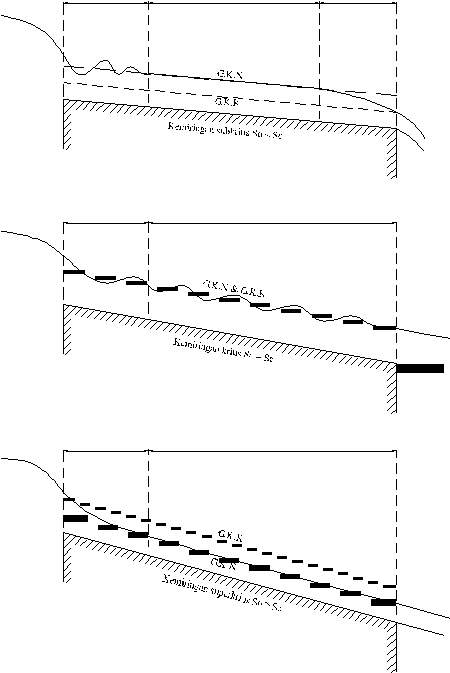
Untuk menjelaskan hal ini, diperlihatkan suatu saluran
panjang dengan tiga jenis kemiringan; subkritis, kritis dan superkritis
(Gambar 2.4). Pada kemiringan subkritis (Gambar 2.4.(a)) permukaan
air di zona peralihan tampak bergelombang.
Aliran dibagian
tengah
saluran
bersifat
seragam namum
kedua
ujungnya
bersifat
berubah.
Pada kemiringan kritis (Gambar 2.4.(b)) permukaan air dari aliran
kritis ini tidak stabil. Dibagian tengah dapat terjadi gelombang tetapi
kedalaman rata-ratanya konstan dan alirannya dapat dianggap
seragam. Pada kemiringan subkritis (Gambar 2.4.(c)) permukaan air
beralih dari keadaan subkritis menjadi superkritis setelah melalui
terjunan hidrolik lambat laun. Di hilir zona peralihan aliran mendekati
seragam.
Kedalaman
aliran
seragam disebut
kedalaman
normal
(normal
depth).
Pada
gambar
2.4
tersebut,
garis
panjang terputus-
putus menyatakan garis kedalaman normal, disingkat dengan G.K.N.,
|
 14
dan garis pendek terputus-putus atau garis titik-titik menyatakan garis
kedalaman kritis atau G.K.K.
Aliran Berubah
Zona Peralihan
Aliran Seragam
Aliran Berubah
Zona Peralihan
(a)
Aliran Berubah
Zona Peralihan
Dapat dianggap Aliran Seragam
(b)
Aliran Berubah
Zona Peralihan
Aliran Seragam
(c)
Gambar 2.4. Pembentukan Aliran Seragam Pada Saluran
|
|
15
b. Kecepatan Rata-Rata Aliran Seragam
Untuk perhitungan hidrolika, kecepatan rata-rata aliran
seragam dalam saluran terbuka biasanya dinyatakan dengan perkiraan
yang
dikenal dengan
rumus
aliran
seragam (uniform
flow
formula).
Sebagian besar rumus-rumus aliran seragam dapat dinyatakan dalam
bentuk umum sebagai berikut :
V = C R
x
S
y
pers (2.4)
dimana :
V = kecepatan rata-rata (m/det),
C
=
faktor tahanan aliran yang bervariasi menurut kekasaran
saluran, kekentalan dan berbagai faktor lainnya,
R
=
jari-jari hidrolik (m),
S
=
kemiringan energi/saluran,
x,y = eksponen.
Rumus aliran seragam yang baik untuk saluran aluvial dengan
pengangkutan
dan
aliran
turbulen harus
memperhitungkan
semua
besaran-besaran berikut ini :
•
Luas basah (A)
•
Kecepatan rata-rata (V)
•
Kecepatan permukaan yang maksimum (Vmaks)
•
Keliling basah (P)
•
Jari-jari hidrolis (R)
•
Kedalaman luas basah maksimum (y)
|
|
16
•
Kemiringan muka air (Sw)
•
Koefisien yang menyatakan kekasaran saluran (n)
•
Muatan sedimen yang melayang (Qs)
•
Muatan dasar (Qb)
Banyak sekali rumus-rumus praktis
mengenai
aliran seragam
yang telah dibuat dan dipublikasikan tetapi tidak satupun dari rumus-
rumus tersebut memenuhi persyaratan rumus yang baik. Rumus yang
paling terkenal dan banyak dipakai adalah rumus Manning.
c. Rumus Manning
Pada tahun 1889 seorang insinyur Irlandia,
Robert
Manning
mengemukakan
sebuah rumus yang akhirnya diperbaiki
menjadi
rumus yang sangat dikenal sebagai.
V
=
1
n R
2
1
3
S
2
pers (2.5)
dimana :
V = kecepatan rata-rata (m/dt),
R
= jari-jari hidrolik (m),
S
= kemiringan saluran,
n
= kekasaran dari Manning.
Rumus
ini
dikembangkan
dari tujuh rumus
yang berbeda,
berdasarkan data percobaan Bazin yang selanjutnya dicocokkan
dengan 170 percobaan. Akibat sederhananya rumus ini dan hasilnya
yang memuaskan dalam pemakaian praktis, rumus Manning
menjadi
sangat
banyak
dipakai
dibandingkan
dengan
rumus
aliran
seragam
|
|
17
lainnya
untuk
menghitung aliran
saluran
terbuka.
Nilai-nilai
n
dari
Manning dapat dilihat pada Lampiran A.
2.2. Irigasi
Irigasi adalah suatu usaha penyediaan dan pengaturan air untuk menunjang
pertanian, baik air permukaan (berasal dari saluran irigasi) maupun air tanah.
Irigasi bertujuan untuk membantu para petani dalam mengolah lahan pertaniannya,
terutama bagi para petani di pedesaan yang sering kekurangan air.
2.2.1. Saluran Irigasi
Saluran irigasi adalah saluran yang membawa atau mengalirkan air
ke daerah irigasi. Saluran irigasi utama terbagi atas 3 jenis yaitu :
a. Saluran primer
Saluran primer adalah saluran yang membawa air dari jaringan
utama ke saluran sekunder dan ke petak-petak tersier yang diairi. Petak
tersier
adalah
kumpulan
petak-petak
kuarter,
petak
kuarter
memiliki
luas kurang lebih 8-15 ha. Sedangkan petak tersier memiliki luas antara
50-150 ha.
b. Saluran sekunder
Saluran sekunder adalah saluran yang membawa air dari saluran
primer ke petak-petak tersier yang dilayani oleh saluran sekunder
tersebut.
|
|
18
c. Saluran tersier
Saluran tersier adalah saluran yang membawa air dari bangunan
sadap tersier dari jaringan utama ke dalam petak tersier saluran kuarter.
Saluran kuarter
membawa air dari boks bagi kuarter melalui bangunan
sadap tersier atau parit sawah ke sawah-sawah.
2.2.2. Kebutuhan Air Irigasi
Analisis kebutuhan
air
irigasi
merupakan salah satu tahap penting
yang
diperlukan
dalam
perencanaan
dan
pengelolaan
sistem irigasi.
Kebutuhan air tanaman didefinisikan sebagai jumlah air yang dibutuhkan
oleh tanaman pada suatu periode untuk dapat tumbuh dan produksi secara
normal. Kebutuhan air nyata untuk areal usaha pertanian meliputi
evapotranspirasi
(ET), sejumlah air
yang dibutuhkan untuk pengoperasian
secara khusus seperti penyiapan lahan dan penggantian air, serta kehilangan
selama pemakaian. Sehingga kebutuhan air dapat dirumuskan sebagai
berikut (Sudjarwadi 1990):
KAI
= ET + KA + KK
pers (2.6)
dimana :
KAI
= kebutuhan air irigasi
ET
= evapotranspirasi
KA
= kehilangan air
KK
= kebutuhan khusus
Untuk memenuhi kebutuhan air irigasi
terdapat dua sumber
utama.
yaitu
pemberian
air
irigasi
(PAI)
dan
hujan
efektif
(HE).
Disamping
itu
|
|
19
terdapat sumber lain yang dapat dimanfaatkan adalah kelengasan yang ada
di daerah perakaran serta kontribusi
air bawah permukaan. Pemberian Air
Irigasi dapat dipandang sebagai kebutuhan air dikurangi
hujan efektif dan
sumbangan air tanah.
PAI = KAI -HE – KAT
pers (2.7)
dimana :
PAI = pemberian air irigasi
KAI
= kebutuhan air
HE
= hujan efektif
KAT = kontribusi air tanah
2.2.3. Kebutuhan Air Sawah Untuk Padi
Kebutuhan air di sawah
untuk
padi
ditentukan
oleh
faktor-faktor
berikut :
1. Penyiapan lahan
2. Penggunaan konsumtif
3. Perkolasi dan rembesan
4. Pergantian lapisan air
5. Curah hujan efektif
Kebutuhan total air di sawah (GFR) mencakup faktor 1 sampai 4.
Kebutuhan bersih air di
sawah
(NFR) juga
memperhitungkan curah hujan
efektif.
Kebutuhan
air
di
sawah
dinyatakan
dalam mm/hari
atau
l/dt.ha.
Tidak disediakan kelonggaran untuk efisiensi irigasi di jaringan tersier dan
|
|
20
utama.
Efisiensi
juga
dicakup
dalam
memperhitungkan
kebutuhan
pengambilan irigasi (m³/dt).
1. Penyiapan Lahan Untuk Padi
Kebutuhan air untuk penyiapan lahan umumnya menentukan
kebutuhan maksimum air irigasi pada suatu proyek irigasi. Faktor-
faktor
penting
yang
menentukan besarnya
kebutuhan
air
untuk
penyiapan lahan adalah:
a. Lamanya
waktu
yang
dibutuhkan
untuk
menyelesaikan pekerjaan
penyiapan lahan.
Faktor-faktor penting yang menentukan lamanya jangka
waktu penyiapan lahan adalah:
-
Tersedianya tenaga kerja dan ternak penghela atau traktor
untuk menggarap tanah,
-
Perlu
memperpendek
jangka waktu tersebut agar tersedia
cukup
waktu
untuk
menanam padi
sawah
atau
padi
ladang
kedua.
Faktor-faktor tersebut saling berkaitan. Kondisi sosial
budaya yang ada di daerah penanaman padi akan mempengaruhi
lamanya waktu yang diperlukan untuk penyiapan lahan. Untuk
daerah-daerah proyek baru, jangka waktu penyiapan lahan akan
ditetapkan berdasarkan kebiasaan yang berlaku di daerah-daerah di
dekatnya. Sebagai pedoman diambil jangka waktu 1,5 bulan untuk
menyelesaikan penyiapan lahan di seluruh petak tersier.
|
|
21
Bilamana untuk penyiapan lahan diperkirakan akan dipakai
peralatan mesin secara luas, maka jangka waktu penyiapan lahan
akan
diambil
satu
bulan.
Perlu diingat
bahwa
transplantasi
(pemindahan
bibit
ke sawah)
mungkin
sudah
dimulai
setelah
3
sampai
4
minggu
di
beberapa
bagian petak tersier dimana
pengolahan lahan sudah selesai.
b. Jumlah air yang diperlukan untuk penyiapan lahan.
Pada umumnya jumlah air yang dibutuhkan untuk penyiapan
lahan dapat ditentukan berdasarkan kedalaman serta porositas tanah
di sawah. Rumus berikut dipakai untuk memperkirakan kebutuhan
air untuk penyiapan lahan:
(S - S
)
N
·
d
PWR
=
a
b
+
Pd
+
Fl
10
4
pers (2.8)
dimana :
PWR = kebutuhan air untuk penyiapan lahan (mm),
Sa
=
derajat
kejenuhan
tanah
setelah
penyiapan
lahan
dimulai (%),
Sb
=
derajat kejenuhan tanah sebelum penyiapan lahan
dimulai (%),
N
=
porositas tanah dalam
%
pada
harga rata-rata
untuk
kedalaman tanah
d
=
asumsi kedalaman tanah setelah pekerjaan penyiapan
lahan (mm),
|
|
22
Pd
=
kedalaman
genangan setelah pekerjaan penyiapan
lahan (mm),
Fl
=
kehilangan air di sawah selama 1 hari (mm).
Untuk tanah bertekstur berat tanpa retak-retak kebutuhan air
untuk penyiapan lahan diambil 200 mm ini termasuk air untuk
penjenuhan
dan
pengolahan
tanah.
Pada permulaan transplantasi
tidak akan ada lapisan air yang tersisa di sawah. Setelah
transplantasi selesai, lapisan air di sawah akan ditambah 50 mm.
secara
keseluruhan,
ini
berarti bahwa
lapisan
air
yang
diperlukan
akan menjadi 250 mm untuk penyiapan lahan dan untuk lapisan air
awal setelah transplantasi selesai.
Bila lahan telah dibiarkan bera selama
jangka waktu yang
lama (2,5 bulan atau lebih), maka lapisan air yang diperlukan untuk
penyiapan
lahan
diambil
300
mm,
termasuk
yang
50
mm untuk
penggenangan setelah transplantasi.
c. Kebutuhan air selama penyiapan lahan.
Untuk
perhitungan
kebutuhan
irigasi
selama
penyiapan
lahan, digunakan metode yang dikembangkan oleh van de Goor dan
Zijlstra (1968). Metode tersebut didasarkan pada laju air konstan
dalam 1/dt selama periode penyiapan lahan dan menghasilkan
rumus berikut:
IR =
M
e
k
pers (2.9)
(
e
k
-
1
)
|
|
23
dimana :
IR
=
kebutuhan air irigasi di tingkat persawahan (mm/hari),
M = kebutuhan
air
untuk
mengganti/mengkompensari
kehilangan air akibat evaporasi dan perkolasi di sawah
yang sudah dijenuhkan M = Eo + p (mm/hari),
Eo = evaporasi air terbuka yang diambil 1,1 ETo selama
penyiapan lahan (mm/hari),
p
=
perkolasi (mm/hari),
k
=
M
×
t
,
s
t
=
jangka waktu penyiapan lahan (hari),
s
=
kebutuhan air,
untuk penjenuhan ditambah dengan
lapisan air
50
mm,
mm yakni 200
+
50
=
250
mm
seperti yang sudah diterangkan di atas (mm),
e
=
bilangan eksponensial : 2,7182.
2. Penggunaan Konsumtif
Penggunaan air untuk kebutuhan tanaman dapat didekati dengan
menghitung evapotranspirasi tanaman, yang besarnya dipengaruhi oleh
jenis tanaman, umur tanaman dan faktor klimatologi. Nilai
evapotranspirasi
merupakan
jumlah dari evaporasi dan
transpirasi.
Yang dimaksud dengan evaporasi adalah proses perubahan molekul air
di permukaan menjadi molekul air di atmosfir. Sedangkan transpirasi
adalah proses fisiologis alamiah pada tanaman, dimana air yang dihisap
|
|
24
oleh akar diteruskan lewat
tubuh tanaman dan diuapkan kembali
melalui pucuk daun.
Nilai
evapotranspirasi
dapat diperoleh
dengan
pengukuran
di
lapangan atau dengan rumus-rumus empiris. Untuk keperluan
perhitungan kebutuhan air irigasi dibutuhkan
nilai
evapotranspirasi
potensial (ETo) yaitu evapotranspirasi yang terjadi apabila tersedia
cukup air. Kebutuhan air untuk tanaman adalah nilai ETo dikalikan
dengan suatu koefisien tanaman.
ETc
= c x ET
o
pers (2.10)
dimana :
ETc
= evapotranspirasi tanaman (mm/hari),
ETo = evapotranspirasi tanaman acuan (mm/hari),
c
= koefisien tanaman.
Kebutuhan air konsumtif ini dipengaruhi oleh jenis dan usia
tanaman (tingkat pertumbuhan tanaman). Pada saat tanaman mulai
tumbuh, nilai kebutuhan air konsumtif
meningkat
sesuai
pertumbuhannya dan mencapai maksimum pada saat pertumbuhan
vegetasi
maksimum.
Setelah
mencapai
maksimum dan
berlangsung
beberapa
saat
menurut
jenis
tanaman,
nilai
kebutuhan
air
konsumtif
akan
menurun
sejalan
dengan
pematangan
biji.
Pengaruh
watak
tanaman terhadap kebutuhan tersebut dengan faktor tanaman (c).
Nilai koefisien pertumbuhan tanaman ini tergantung jenis
tanaman yang ditanam. Untuk tanaman jenis yang sama juga berbeda
menurut varietasnya. Sebagai contoh padi dengan varietas unggul masa
|
 25
tumbuhnya
lebih
pendek
dari
padi
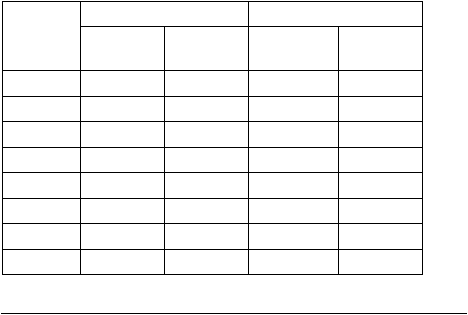
varietas biasa. Pada Tabel 2.1
disajikan
harga-harga
koefisien
tanaman padi dengan varietas unggul
dan varitas biasa menurut Nedeco/Prosida dan FAO.
Tabel 2.1 Harga-Harga Koefisien¹
)
Tanaman Padi
Bulan
Nedeco/Prosida
FAO
Varietas
2)
biasa
Varietas
3)
unggul
Varietas
biasa
Varietas
unggul
0,5
1,20
1,20
1,10
1,10
1
1,20
1,27
1,10
1,10
1,5
1,32
1,33
1,10
1,05
2
1,40
1,30
1,10
1,05
2,5
1,35
1,30
1,10
0,95
3
1,24
0
1,05
0
3,5
1,12
0,95
4
0
4)
0
Sumber: Dirjen Pengairan, Bina Program PSA 010, 1985
1) Harga-harga
koefisien
ini
akan dipakai
dengan
rumus
evapotranspirasi
Penman yang sudah dimodifikasi, dengan
menggunakan metode yang diperkenalkan oleh Nedeco/Prosida atau
FAO,
2)
Varietas padi biasa adalah varietas padi yang mana tumbuhnya
lama,
3)
Varietas unggul adalah varietas padi yang jangka waktu tumbuhnya
pendek,
4)
Selama
setengah
bulan terakhir
pemberian
air
irigasi
ke sawah
dihentikan; kemudian keofisien tanaman diambil “nol” dan padi
akan menjadi masak dengan air yang tersedia
|
|
26
Yang dimaksud ETo, adalah evapotranspirasi tetapan yaitu laju
evaportranspirasi dari suatu permukaan luas tanaman rumput hijau
setinggi 8 sampai 15 cm yang menutup tanah dengan ketinggian
seragam dan
seluruh
permukaan
teduh
tanpa
suatu
bagian
yang
menerima sinar secara langsung serta rumput masih tumbuh aktif tanpa
kekurangan
air.
Evapotranspirasi
tetapan disebut juga dengan
evapotranspirasi referensi/keluar. Terdapat beberapa cara untuk
menentukan
evapotranspirasi
tetapan, salah satunya seperti yang
diusulkan oleh Kriteria Perencanaan Irigasi 1986 sebagai berikut :
ET
o
= K
p
. E
pan
pers (2.11)
dimana :
ETo = Evaporasi tetapan/tanaman acuan (mm/hari),
Epan = Pembacaan panci Evaporasi,
Kp
= koefisien panci.
3. Perkolasi
Laju perkolasi sangat bergantung kepada
sifat-sifat tanah. Pada
tanah-tanah lempung berat dengan karakteristik pengolahan (puddling)
yang
baik,
laju
perkolasi
dapat
mencapai
1-3
mm/hari.
Pada
tanah-
tanah yang lebih ringan; laju perkolasi bisa lebih tinggi
Dari
hasil-hasil
penyelidikan tanah pertanian dan penyelidikan
kelulusan, besarnya
laju perkolasi serta tingkat kecocokan tanah untuk
pengelohanan tanah dapat diterapkan dan dianjurkan pemakaiannya.
Guna menentukan
laju perkolasi, tinggai muka air tanah juga harus di
|
|
27
perhitungkan. Perembesan terjadi akibat meresapnya air melalui
tanggul sawah.
4. Penggantian Lapisan Air
Setelah pemupukan, usahakan untuk
menjadwalkan dan
menganti lapisan air menurut kebutuhan. Jika tidak ada penjadwalan
semacam itu, lakukan penggantian
sebanyak 2 kali,
masing-masing 50
mm (3,3 mm/hari selama setengah bulan) selama sebulan dan 2 bulan
setelah transplantasi.
5. Curah Hujan Efektif
Untuk irigasi padi curah hujan efektif bulanan diambil 70% dari
curah hujan minimum tengah-bulanan dengan periode ulang 5 tahun.
Re = 0,7 ×
1
× R
15
(setengah bulan)
5
pers (2.12)
dimana :
Re
=
curah hujan efektif (mm/hari),
R(setengah bulan)
5
=
curah
hujan
minimum
tengah bulanan
dengan periode ulang 5 tahun/mm.
Di
daerah-daerah yang
besar
dimana
tersedia
data-data
curah
hujan
harian,
harus
dipertimbangkan untuk
diadakan
studi
simulasi
untuk menghasilkan criteria yang lebih terinci.
2.2.4. Kebutuhan Air Sawah Untuk Tanaman Selain Padi
Tanaman selain padi yang dibudidayakan oleh petani pada
umumnya berupa palawija. Yang dimaksudkan dengan palawija adalah
|
|
28
berbagai jenis tanaman yang dapat ditanam di sawah pada musim kemarau
ataupun pada
saat kekurangan
air. Lazimya
tanaman
palawija
ditanam di
lahan tegalan.
Dari jumlah air yang dibutuhkan, palawija dapat dibedakan menjadi
3 (tiga) jenis, yaitu.
a)
palawija yang butuh banyak air, seperti bawang, kacang tanah, ketela,
b) palawija yang butuh sedikit air, misalnya cabai, jagung, tembakau dan
kedelai,
c)
palawija yang membutuhkan sangat sedikit air, misalnya ketimun dan
lembayung.
Maksud analisis kebutuhan air untuk tanaman palawija terutama
untuk mengetahui luas lahan yang direncanakan untuk tanaman padi
maupun
palawija
berkaitan
dengan ketersedian
air
pada
bangunan
pengambilan sehingga kegagalan usaha pertanian dapat dihindari. Dengan
kata lain hitungan kebutuhan air untuk palawija digunakan sebagai dasar
untuk melakukan usaha pertanian sesuai dengan jumlah air yang tersedia.
Pemberian air untuk palawija akan ekonomis
jika sampai kapasitas
lapang,
lalu
berhenti
dan
diberikan
lagi
sampai
sebelum
mencapai
titik
layu. Analisis kebutuhan air untuk tanaman palawija dihitung seperti untuk
tanaman padi, namun ada dua hal yang membedakan, yaitu pada tanaman
palawija tidak memerlukan genangan serta koefisien tanaman yang
digunakan sesuai dengan jenis palawija yang ditanam.
|
|
29
a. Penyiapan Lahan
Masa prairigasi diperlukan guna menggarap lahan untuk
ditanami
dan untuk menciptakan kondisi kelembaban yang memadai
untuk persemaian tanaman. Jumlah air yang dibutuhkan tergantung
pada
kondisi
tanah
dan
pola
tanam yang
diterapkan.
Kriteria
Perencanaan Irigasi mengusulkan air untuk pengolahan lahan sejumlah
50 -120
mm
untuk tanaman
ladang dan 100 -120
mm untuk tanaman
tebu, kecuali jika terdapat kondisi-kondisi khusus misalnya ada
tanaman lain yang segera ditanam setelah tanaman padi
b.
Penggunaan Konsumtif
Untuk menentukan penggunaan konsumtif cara yang digunakan
seperti pada tanaman padi hanya koefisien tanaman yang berbeda. Nilai
koefisien beberapa jenis tanaman
yang direkomendasikan oleh Kriteria
Perencanaan
Irigasi
seperti
terlihat pada
Tabel
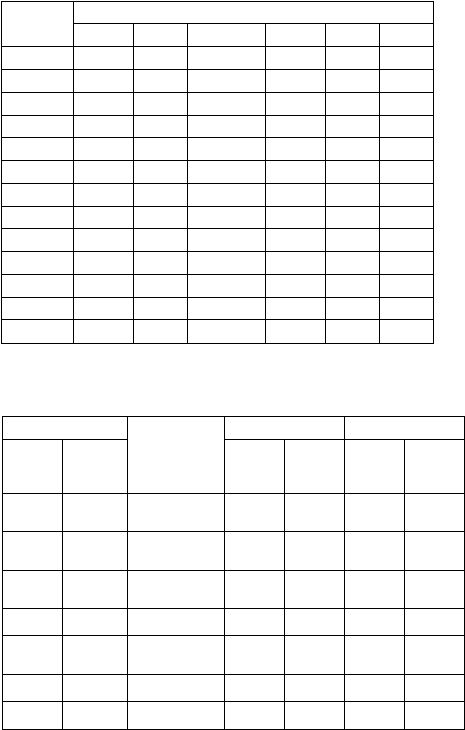
2.2.
Sedangkan
nilai
koefisien tanaman tebu diperlihatkan pada Tabel 2.3.
|
 30
Tabel 2.2 Harga-Harga Koefisien Tanaman Untuk Beberapa Palawija
Setengah
bulan ke
Koefisien Tanaman
Kedelai
Jagung
Kac.Tanah
Bawang
Buncis
Kapas
1
0,50
0,50
0,50
0,50
0,50
0,50
2
0,75
0,59
0,51
0,51
0,64
0,50
3
1,00
0,96
0,66
0,69
0,89
0,58
4
1,00
1,05
0,85
0,90
0,95
0,75
5
0,82
1,02
0,95
0,95
0,88
0,91
6
0,45
0,95
0,95
-
-
1,04
7
-
-
0,55
-
-
1,05
8
-
-
0,55
-
-
1,05
9
-
-
-
-
-
1,05
10
-
-
-
-
-
0,78
11
-
-
-
-
-
0,65
12
-
-
-
-
-
0,65
13
-
-
-
-
-
0,65
Sumber : Kriteria Perencanaan Irigasi, KP-01
Tabel 2.3 Harga-Harga Koefisien Tanaman Untuk Tebu
Umur Tanaman
Tahap
Pertumbuhan
RH < 70% min
RH < 20% Min
12
bulan
24 bulan
Angin
kecil s/d
sedang
Angin
kencang
Angin
kecil s/d
sedang
Angin
kencang
0 -1
0 -2,5
saat tanam sd
0,25 rimbun
0,55
0,6
0,4
0,45
1-2
2,5 -3,5
0,25 -0,5
rimbun
0,8
0,85
0,75
0,8
2 -2,5
3,5 -4,5
0,5 -0,75
rimbun
0,9
0,95
0,95
1,0
2,5 -4
4,5 -6
0,75 – rimbun
1,0
1,1
1,1
1,2
4 -10
6 -17
Penggunaan
air puncak
1,05
1,15
1,25
1,3
10 -11
17 -22
Awal berbunga
0,8
0,85
0,95
1,05
11 -12
22 -24
Menjadi masak
0,6
0,65
0,7
0,75
Sumber : Kriteria Perencanaan Irigasi, KP – 01
|
 31
2.2.5. Debit Rencana
Debit rencana adalah debit yang akan digunakan sebagai debit
saluran dalam perancangan saluran. Besaran debit rencana dipengaruhi oleh
kebutuhan bersih air sawah, luas area yang diairi dan efisiensi irigasi
saluran.
Debit rencana sebuah saluran dihitung dengan rumus
umum
sebagai berikut :
NFR A
Q
petak
rencana
=
E
pers (2.13)
Q
Q
petak
rencana
=
E
pers (2.14)
dimana :
Q
rencana
= debit rencana (l/dt),
Q
petak
= debit petak (l/dt),
NFR
= kebutuhan bersih (netto) air sawah (m.l/t.ha),
A
petak
= luas daerah yang diairi (ha),
E
= efisiensi saluran.
a. Kebutuhan air di sawah
Kebutuhan air di sawah ditentukan oleh faktor-faktor berikut:
•
Cara penyiapan lahan,
•
Kebutuhan air untuk tanam,
•
Perkolasi dan rembesan,
•
Pergantian lapisan air,
•
Curah hujan efektif.
|
|
32
Kebutuhan total air di sawah (GFR) mencakup faktor 1 sampai
4. Kebutuhan bersih (netto) air di sawah (NFR) juga memperhitungkan
curah
hujan
efektif. Besarnya
kebutuhan air di
sawah
bervariasi
menurut tahap dan pertumbuhan tanaman dan bergantung kepada cara
pengolahan lahan. Besarnya kebutuhan air di sawah dinyatakan dalam
mm/hari.
b.
Efisiensi
Untuk tujuan-tujuan perencanaan, dianggap bahwa seperempat
sampai sepertiga dari jumlah air
yang diambil akan
hilang sebelum air
itu sampai di sawah. Kehilangan air disebabkan oleh kegiatan
eksploitasi, evaporasi, dan perembesan.
Pada
umumnya kehilangan air di jaringan irigasi dapat dibagi-
bagi sebagai berikut :
•
15 - 22,5% dipetak tersier, antara bangunan sadap tersier dan
sawah,
•
7,5 – 12,5% di saluran sekunder,
•
7,5 – 12,5% di saluran primer.
2.3. Perancangan Saluran Untuk Aliran Seragam
2.3.1. Geometri Saluran
Penampang
saluran
terbagi
atas dua,
yang
pertama
adalah
penampang saluran alam dan kedua adalah saluran penampang buatan.
Penampang saluran
alam
umumnya
sangat
tidak
beraturan,
biasanya
|
 33
bervariasi dari bentuk seperti parabola
sampai
trapesium.
Sedangkan
penampang saluran buatan biasanya di rancang berdasarkan geometris yang
umum seperti
persegi
panjang,
trapesium,
segitiga,
lingkaran,
parabola,
persegi panjang sisi dibulatkan dan segitiga dasar dibulatkan.
Penampang
yang paling
umum digunakan adalah penampang
yang
berbentuk trapesium,
sebab penampang
ini
mempunyai
stabilitas
kemiringan
dinding
yang
dapat
disesuaikan
untuk
saluran
pasangan
ataupun saluran
tanpa
pasangan
(tanah).
Dibawah
ini
adalah
unsur-unsur
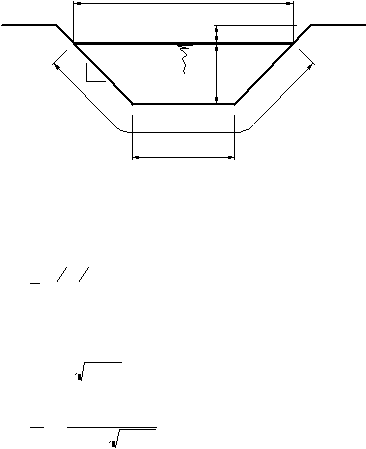
geometris untuk penampang saluran berbentuk trapesium.
T
w
1
y
z
P
b
Gambar 2.5 Unsur geometris penampang saluran berbentuk trapesium
Q =
V
×
A
pers (2.15)
Q =
1
R
2
3
S
1
2
A
n
pers (2.16)
A = ( b + zy ) y
pers (2.17)
P
= b + 2y
1
+
z
2
pers (2.18)
R
=
A
=
(b +
zy)y
pers (2.19)
P
b
+
2y
1
+
z
2
T
= b + 2zy
pers (2.20)
|
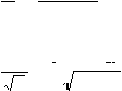 34
D =
A
=
T
A¹
,5
Z
=
(b + zy)y
b
+
2zy
[(b +
zy)y
]=
1
,5
=
pers (2.21)
pers (2.22)
T
b
+
2zy
dimana :
Q = debit saluran (m3
/det),
V = kecepatan rata-rata (m/det),
A = luas penampang melintang (m2
),
P
= keliling basah (m),
R = jari-jari hidrolik (m),
T
= lebar puncak (m),
D = kedalaman hidrolik (m),
Z
= faktor penampang,
b
= lebar dasar (m),
y
= tinggi air/tinggi saluran (m)
z
= kemiringan talut,
w = tinggi jagaan (m).
2.3.2. Saluran Tahan Erosi
Sebagian besar saluran yang diberi lapisan dan saluran yang bahan-
bahannya merupakan hasil rakitan pabrik dapat menahan erosi dengan baik,
sehingga dianggap tahan erosi (nonerodible). Saluran
tanpa lapisan
biasanya
peka
erosi,
kecuali
digali pada
dasar yang
keras
misalnya
dasar
yang terbuat dari batu. Dalam merancang saluran tahan erosi, faktor-faktor
|
 35
seperti kecepatan maksimum yang diizinkan dan gaya tarik yang diizinkan
tidak perlu dipertimbangkan. Perancang cukup menghitung ukuran-ukuran
saluran dengan rumus aliran seragam, kemudian memutuskan ukuran akhir
berdasarkan efisiensi
hidrolika, atau hukum pendekatan untuk penampang
terbaik, praktis dan ekonomis.
Faktor-faktor
yang
harus
dipertimbangkan
dalam perancangan
adalah jenis bahan yang membentuk tubuh saluran; yang menentukan
koefisien kekasaran; kecepatan
minimum yang diizinkan untuk
mencegah
pengendapan bila air
mengangkut
lanau (silt) atau serpihan kasar
lainnya;
kemiringan dasar saluran dan kemiringan dinding; jagaan (freeboard); dan
penampang yang paling efisien, ditentukan secara hidrolika maupun secara
pendekatan.
2.3.3. Kecepatan Maksimum yang Diizinkan
Kecepatan maksimum yand diizinkan adalah kecepatan aliran (rata-
rata)
maksimum yang
tidak
akan
menyebabkan
erosi/gerusan
terhadap
permukaan saluran. Kecepatan-kecepatan maksimum berikut ini dianjurkan
pemakaiannya dapat dilihat pada tabel 2.4 dibawah ini.
Tabel 2.4
Kecepatan Maksimum yang Diizinkan
Pasangan
Kecepatan Maksimum
(m/dt)
Pasangan batu
2
Pasangan beton
3
Pasangan Tanah
Dapat dilihat pada
Lampiran B
Sumber : Standar Perencanaan Irigasi : KP-03
|
|
36
2.3.4. Kecepatan Minimum yang Diizinkan
Kecepatan minimum
yang
diizinkan
atau
kecepatan
tanpa
pengendapan
merupakan
kecepatan
terendah yang
tidak
menimbulkan
sedimentasi dan mendorong pertumbuhan tanaman air dan ganggang.
Kecepatan ini sangat tidak menentu dan
nilainya
yang
tepat
tidak dapat
ditentukan dengan mudah. Bagi air yang tidak mengandung lanau, hal ini
tidak membawa pengaruh besar kecuali terhadap pertumbuhan tanaman.
Umumnya dapat dikatakan bahwa kecepatan rata-rata 0,5 m/dt sampai
1
m/dt dapat digunakan bila persentase lanau ditunjukkan dalam saluran kecil
dari 0,75 m/dt dapat mencegah pertumbuhan tanaman air yang dapat
mengurangi kapasitas saluran tersebut.
2.3.5. Kemiringan Saluran
Kemiringan memanjang dasar saluran biasanya diatur oleh
keadaaan topografi
dan
tinggi energi
yang
diperlukan
untuk
mengalirkan
air. Dalam berbagai hal, kemiringan
ini
dapat
pula
tergantung
pada
kegunaan saluran. Misalnya saluran yang digunakan sebagai distribusi air
seperti
yang
dipakai
dalam irigasi, persediaan
air
minum,
penambangan
hidrolika dan proyek pembangkit dengan tenaga air, memerlukan taraf yang
tinggi pada titik penghantar, sebab itu diusahakan kemiringan yang sekecil-
kecilnya untuk menjaga agar kehilangan tinggi tekan akan sekecil-kecilnya.
Kemiringan dinding saluran terutama tergantung pada jenis bahannya.
Tabel 2.5 memuat kemiringan yang dapat dipakai untuk berbagai jenis
bahan.
|
 37
Tabel 2.5
Kemiringan Dinding Saluran
Bahan
Kemiringan dinding
Batu
Hampir tegak lurus
Tanah gambut (peat), rawang (muck)
1 : ¼
Lempung teguh atau tanah berlapis beton
1 : ½ sampai 1 : 1
Tanah berlapis batu, atau tanah bagi saluran
yang lebar
1 : 1
Lempung kaku atau tanah bagi parit kecil
1 : 1½
Tanah berpasir lepas
1 : 2
Lempung berpasir atau lempung berpori
1 : 3
Sumber : Open-Channel Hydraulics(Chow, Ven Te)
2.3.6. Tinggi Jagaan
Tinggi
jagaan suatu saluran adalah
jarak
vertikal dari puncak
saluran
ke
permukaan
air
pada
kondisi rancang. Jarak ini harus cukup
mencegah gelombang atau kenaikan muka air yang melimpah ke tepi.
Tinggi jagaan minimum dapat dilihat pada tabel 2.6.
Tabel 2.6
Tinggi Jagaan
Debit
(m
3
/dt)
Tinggi Jagaan
(m)
< 0,5
0,40
0,5 – 1,5
0,50
1,5 – 5,0
0,60
5,0 – 10,0
0,75
10,0 – 15,0
0,85
> 15,0
1,00
Sumber : Standar Perencanaan Irigasi : KP-03
2.3.7. Penampang Hidrolik Terbaik
Telah diketahui bahwa hantaran suatu penampang saluran akan
meningkat
sesuai
dengan
peningkatan
jari-jari
hidrolik
atau
berkurangnya
keliling
basah.
Dari
segi
pandangan
hidrolika
maka
penampang
saluran
|
 38
yang
memiliki
basah
terkecil
akan
memiliki
hantaran
maksimum;
penampang seperti ini disebut penampang hidrolik terbaik.
Penampang hidrolik terbaik
juga dapat diartikan sebagai
penampang
saluran
yang
dapat
melewatkan
debit
maksimum untuk
luas
penampang basah, kekasaran dan kemiringan dasar tertentu. Berdasarkan
persamaan kontinuitas, tampak jelas bahwa untuk luas penampang
melintang tetap, debit maksimum dicapai jika kecepatan aliran maksimum.
Dari rumus Manning dapat dilihat bahwa untuk kemiringan saluran
dan kekasaran tetap, kecepatan maksimum dicapai jika jari-jari hidrolik (R)
maksimum.
Selanjutnya, untuk luas penampang tetap, jari-jari hidrolik
maksimum jika keliling basah (P) minimum.
Dari penjelasan rumus Manning diatas, persamaan dapat ditulis
A = min maka R = max
?
A
bilamana P
?
minimum
P
Dari
hal
tersebut dapat
ditunjukkan
bahwa
persoalannya
ekivalen
dengan melakukan minimizing untuk suatu harga A yang konstan.
A = ( b + zy ) y
pers (2.17)
= by + zy²
pers (2.23)
P
= b + 2y
1
+
z
2
pers (2.18)
b
= P - 2y
1
+
z
2
pers (2.24)
Nilai b pada pers (2.24) dapat disubtitusi ke nilai A pada pers
(2.23), menjadi :
A =
(
P
-
2y
1
+
z
2
)
y
+
zy
2
|
 39
(
2
P
=
A
+
2y
y
1
+
z
2
-
zy
pers (2.25)
P minimum bilamana
dP
=
0
dy
dP
=
-
A
+
(
2
1
+
z
2
)
-
z
=
0
dy
A
=
(
2
y
2
y
2
1
+
z
2
)
-
z
A =
(
2
1
+
z
2
)
y
2
-
zy
2
pers (2.26)
Nilai A pada pers (2.26)
merupakan disubtitusikan
nilai P ke pers
(2.25) akan menghasilkan persamaan sebagai berikut :
P
=
2 1 + z
)
y
2
-
zy
2
+
(
2y
1
+
z
2
)
-
zy
=
(
2
y
1
+
z
2
)
y
-
zy
+
(
2y
1
+
z
2
)
-
zy
=
2
(
2y
=
(
4y 1 +
1
+
z
2
)
-
2zy
z
2
)
-
2zy
pers (2.27)
Nilai
A
pada
pers
(2.26)
dan
nilai P
pada
pers
(2.27)
merupakan
luas penampang dan keliling basah untuk penampang hidrolik terbaik. Nilai
A dan P dapat disubtitusikan ke persamaan geometris lain untuk
mendapatkan unsur geometris penampang hidrolis terbaik pada penampang
berbentuk trapesium. Unsur-unsur geometris
penampang
hidrolis
terbaik
untuk penampang saluran berbentuk trapesium dapat dilihat pada tabel 2.7.
|
 40
Tabel 2.7
Unsur-unsur
Geometris Penampang Hidrolis
Terbaik
Untuk
Penampang Saluran Berbentuk Trapesium
Unsur
Geometris
Persamaan
Debit
saluran
(Q)
?
?
=1
?
?
(2
1
+
z
2
)y
2
-
zy
2
?
1
?
?
2
3
?
Q
=
?
?
??
(
)
?
(S)
2
?
×
{(2 1 +
z
2
)y
2
-
zy
2
}
?
?
n
?
?
?
4y 1
+
z
2
-
2zy
?
?
?
?
?
Kecepatan
rata-rata
(V)
?
(
)
?
2
3
?
1
?
2 1
+
z
2
y
2
-
zy
2
(
)
1
2
V
=
?
??
?
S 2
?
n
?
?
?
(
4y 1 +
z
2
)
-
2zy ?
?
Luas
penampang
(A)
A
=
(
2 1
+
z
2
)
y
2
-
zy
2
Keliling
basah
(P)
P
=
(
4y 1
+
z
2
)
-
2zy
Jari-jari
hidrolik
(R)
(2 1 +
z
2
)y
2
-
zy
2
R
=
(
2
4y 1 + z
)
-
2zy
Lebar
puncak
(T)
T
=
(
4y 1
+
z
2
)
-
(
2y 1
+
z
2
)
Kedalaman
hidrolik (D)
(
2 1
+
z
2
)
y
2
-
zy
2
D
=
(
2
2
4y 1 +
z
)
-
(
2y 1 + z
)
Faktor
penampang
(Z)
[
(
2 1
+
z
2
)
y
2
-
zy
2
]
1,5
Z
=
(
4y 1
+
z
2
)- (
2y 1
+
z
2
)
2.4. Metode Numerik
Metode numerik adalah teknik dimana masalah matematik diformulasikan
sedemikian rupa sehingga dapat diselesaikan oleh pengoperasian aritmatika.
Metode-metode
yang
dapat
sering
digunakan
dalam penyelesain
masalah
dalam
analisa numerik antara lain metode langsung, metode grafik, metode bagidua,
metode Newton-Raphson dan metode Secant. Dalam penelitian ini, digunakan
|
|
41
r
metode bagidua dalam penyelesain masalah matematik dalam perhitungan
penampang saluran ekonomis.
Metode Bagidua (biseksi) disebut juga pemotongan biner (binary
chopping), pembagian 2 (interval halving) atau
metode
Bolzano. Metode Bagidua
adalah
suatu
jenis pencarian
inkremental
dimana
interval
senantiasa
dibagi
separuhnya. Kalau suatu fungsi berubah tanda sepanjang interval, harga fungsi
ditengahnya di evaluasi. Letak akarnya kemudian ditentukan ada ditengah-tengah
subinterval dimana perubahan tanda terjadi. Proses ini diulang untuk memperoleh
taksiran yang diperhalus.
Langkah-langkah
penyelesain
masalah
matematik dalam metode
Bagidua
yaitu :
•
Langkah
1
:
Memilih
taksiran
terendah
(x
i
)
dan
tertinggi
(x
u
)
untuk
akar
fungsi
berubah
tanda
sepanjang
interval.
Ini
dapat
diperiksa dengan
:
f(x
i
)
f(x
u
)
< 0.
•
Langkah 2 : Taksiran pertama akar xr
ditentukan oleh :
x
=
x
i
+
x
u
2
•
Langkah
3
:
Buat
evaluasi
yang
berikut
untuk
menentukan
subinterval,
di
dalam mana akar terletak :
o
Jika f(x
i
) f(xr) < 0, akar terletak pada subinterval pertama, maka x
u
= xr,
dan lanjutkan ke step 2,
o
Jika f(x
i
)
f(xr) > 0, akar terletak pada subinterval kedua, maka
xi = xr,
dan lanjutkan ke step 2,
o
Jika f(xi) f(xr) = 0, akar = xr, komputasi selesai.
|