 BAB
2
LANDASAN TEORI
2.1 Teori-Teori Umum
2.1.1 Pengertian Suara
Suara
adalah
fenomena
fisik
yang
dihasilkan oleh
getaran
benda
atau
getaran suatu benda yang berupa sinyal analog dengan amplitudo yang berubah
secara
kontinyu
terhadap
waktu,
Suara
berhubungan erat
dengan
rasa
“mendengar”. Suara atau bunyi biasanya merambat melalui udara. Suara atau
bunyi tidak bias merambat melalui ruang hampa.
Benda
Bergetar
Perbedaan
Tekanan di Udara
Melewati
Udara(Gelombang)
Pendengar
Gambar 2.1 Proses Terjadinya Suara
Suara dihasilkan oleh getaran suatu benda. Selama bergetar, perbedaan tekanan
terjadi
di
udara
sekitarnya.
Pola
osilasi
yang
terjadi
dinamakan sebagai
“Gelombang”. Gelombang mempunyai pola sama yang berulang pada interval
tertentu,
yang
disebut sebagai
“Periode”. Contoh
suara
periodik
:
instrument
musik,
nyanyian
burung,
dll
dan
contoh
suara
nonperiodik
:
batuk, percikan
ombak, dll.
Suara berkaitan erat dengan :
1.
Frekuensi
-
Banyaknya getaran dalam 1 detik.
-
Satuan : Hertz (Hz) atau cycles per second (cps)
-
Panjang gelombang suara (wavelength) dirumuskan = c/f
Dimana c = kecepatan rambat bunyi
7
|
|
8
Dimana f = frekuensi
Panjang gelombang suara bias dihitung juga dengan rumus :
?= c/f.
Berdasarkan frekuensinya, suara dibagi menjadi 4, yaitu :
1.
Infrasound
=
0Hz – 20 Hz
2.
Pendengaran manusia = 20Hz – 20 KHz
3.
Ultrasound
=
20KHz – 1 GHz
4.
Hypersound
=
1GHz – 10 THz
Manusia membuat suara dengan frekuensi : 50Hz – 10KHz. Sinyal suara
musik
memiliki frekuensi
:
20Hz
–
20Khz.
Maka
Sistem multimedia
menggunakan
suara
yang
berada
dalam
range
pendengaran
manusia.
Suara
yang
berada
pada
range
pendengaran manusia
sebagai
“Audio”
dan
gelombangnya sebagai “Accoustic Sinyal”.
Suara diluar range pendengaran manusia dapat dikatakan sebagai “Noise”
(getaran yang tidak teratur dan tidak berurutan dalam berbagai frekuensi, tidak
dapat didengar manusia).
1. Amplitudo
-
Keras lemahnya bunyi atau tinggi rendahnya gelombang.
-
Satuan amplitudo adalah decibel (db)
-
Bunyi mulai dapat merusak telinga jika tingkat volumenya lebih
|
|
9
-
besar dari 85 dB dan pada ukuran 130 dB akan mampu membuat hancur
gendang telinga
2. Velocity
-
Kecepatan perambatan gelombang bunyi sampai ke telinga
pendengar.
-
Satuan yang digunakan : m/s
-
Pada udara kering dengan suhu 20 °C (68 °F)m kecepatan
rambat suara sekitar 343 m/s.
2.1.2 Representasi Suara
Gelombang
suara
analog
tidak
dapat
langsung
direpresentasikan pada
komputer. Komputer
mengukur
amplitudo pada
satuan
waktu
tertentu
untuk
menghasilkan sejumlah
angka.
Tiap
satuan
pengukuran
ini
dinamakan
“SAMPLE”.
untuk
itu
kita
harus
melakukan
conversion data
analog
untuk
dijadikan data digital.
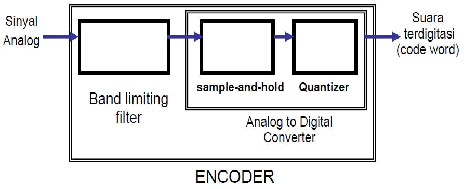
2.1.2.1 Analog to Digital Conversion (ADC)
Adalah
proses
mengubah
amplitudo
gelombang
bunyi
ke
dalam
waktu interval tertentu (disebut juga sampling), sehingga menghasilkan
representasi
digital
dari
suara.
Sampling
rate
:
beberapa
gelombang
yang
diambil
dalam satu
detik.
Contoh
:
jika
kualitas CD
Audio
dikatakan
memiliki frekuensi sebesar 44100
Hz, berarti jumlah sample
sebesar 44100 per detik.
|
 10
Gambar 2.2 Proses Sampling
1. Membuang frekuensi tinggi dari source sinyal
2. Mengambil sample pada interval waktu tertentu (sampling)
3. Menyimpan amplitudo sample dan mengubahnya ke dalam bentuk
diskrit (kuantisasi).
4. Merubah bentuk menjadi nilai biner.
2.1.2.2 Digital to Analog Converter (DAC)
Digital
to
Analog
Converter (DAC)
Adalah
proses
mengubah
digital
audio
menjadi
sinyal
analog.
DAC
biasanya hanya
menerima
sinyal digital Pulse Code Modulation (PCM). PCM adalah representasi
digital dari sinyal analog, dimana gelombang disample secara beraturan
berdasarkan interval
waktu
tertentu,
yang
kemudian
akan
diubah
ke
biner. Proses pengubahan ke biner disebut Quantisasi. PCM ditemukan
oleh
insinyur dari
Inggris,
bernama Alec
Revees
pada
tahun
1937.
Contoh DAC adalah: soundcard, CDPlayer, IPod, mp3player.
|
|
11
2.2 Teori - Teori Khusus
2.2.1 Analisis Fitur Pengekstrasi Sinyal digital.
Penelitian yang dapat memproses sinyal digital merupakan suatu metode
yang
khusus.
Sehingga sinyal
digital
diubah
menjadi
suatu
data
yang dapat
dihitung dan memiliki nilai ukur.Di antara metode- metode itu seperti :
1. Fast Fourier Transform (FFT)
2. Linear Predictive Coding (LPC)
3. Wavelet Transform (WT)
Dari
ketiga
metode
yang
ada,
akan
di
analisis
oleh
peneliti
sebagai
kajian
penelitian
ini
agar
dapat
memperbaiki penelitian
sebelumnya.
Dan
diharapkan ada pun cara yang terbaik dari ketiga metode.
2.2.1.1 Fast Fourier Transform (FFT)
FFT
merupakan sebuah kelas khusus
yang mengimplementasikan
algoritma
transform fourier
dengan
cukup
dalam
waktu
komputasi.
Dalam FFT biasanya
yang
lakukan setelah gelombang telah diperoleh
dan digital, FFT ditransformasikan ke frekuensi domain. Hasil FFT bisa
baik
nyata
dan
imajiner,
atau
magnitudo dan
fasa,
fungsi
frekuensi.
Pemilihan format output milik pengguna.
Karena
menghasilkan
FFT
spektrum
frekuensi
untuk
waktu
domain gelombang, beberapa aplikasi yang cukup sederhana, misalnya,
analisis
harmonik, distorsi
analisis,
analisis
getaran,
dan
modulasi
pengukuran, mungkin menyarankan diri segera.
Wilayah penting
lainnya
adalah
bahwa
dari
estimasi respons
frekuensi.
Sebuah
linier, sistem
invarian-waktu dapat
dirangsang
|
|
12
dengan
fungsi
impuls.,
kemudian dapat
diperoleh dan
cepat-Fourier-
ditransformasikan ke frekuensi
domain.
FFT dari respon
impuls,
yang
disebut
sebagai
fungsi respon frekuensi, sepenuhnya
menjadi ciri
sistem.
Sekali
sistem fungsi
respons
frekuensi
dikenal, orang
dapat
memprediksi bagaimana sistem itu akan bereaksi terhadap setiap bentuk
gelombang. Hal ini dilakukan dengan konvolusi. (Smith, 1997)
2.2.1.2 Linear Predictive Coding (LPC)
Linear
Predictive
Coding
(LPC)
adalah
suatu teknik
untuk
analisis
pidato
dan
merupakan metode
yang
paling
berguna
untuk
pengkodean dalam
pidato
pada
bit
rate
yang
rendah.
Memberikan
perkiraan yang sangat akurat pada parameter pidato, dan relatif efisien
untuk komputasi. Oleh karena itu prinsip kerja LPC menganalisis
ujaran dengan memperkirakan
forman, menghilangkan
efek mereka
dari
pidato
sinyal,
dan
memperkirakan intensitas
dan
frekuensi
buzz
yang
tersisa. Proses
mengeluarkan forman disebut invers
filtering, dan
sinyal sisanya disebut residu.
Angka-angka
yang
menjelaskan forman
dan residu dapat disimpan atau dikirimkan ke tempat lain. Sintesis LPC
tanda
ujaran
dengan
membalik
proses:
menggunakan sisa
untuk
menciptakan sumber sinyal, gunakan forman untuk membuat penyaring
(yang
mewakili tabung),
dan
menjalankan
source
melalui
filter,
sehingga dalam berbicara. Karena sinyal pidato bervariasi dengan
waktu, proses
ini dilakukan pada potongan pendek tanda ujaran, yang
|
|
13
disebut frame. Biasanya 30-50 frame per detik memberikan
pidato
dipahami dengan kompresi yang baik.
2.2.1.3 Alih Ragam Gelombang Singkat (ARGS)
ARGS
mulai
diperkenalkan pada tahun 1980-an oleh
Morlet dan
Grossman sebagai
fungsi matematis untuk
merepresentasikan data atau
fungsi
sebagai
alternatif
transformasi-transformasi matematika
yang
lahir
sebelumnya untuk
menangani
masalah
resolusi.
Sebuah
gelombang
singkat
merupakan gelombang yang
energinya
terkonsentrasi pada suatu selang waktu untuk
memberikan kemampuan
analisis
transien,
ketidakstasioneran,
atau
fenomena
berubah terhadap
waktu (time
varying). Karakteristik dari
gelombang
singkat antara
lain
adalah
berosilasi
singkat,
translasi
(pergeseran), dan
dilatasi
(skala).
Bentuk Gelombang Sinus dan gelombang singkat Skala (dilatasi) dalam
sebuah
gelombang singkat
berarti
pelebaran
atau
penyempitan
gelombang singkat.
Hubungan antara skala gelombang singkat dengan frekuensi yang
dihasilkan oleh
analisis
gelombang singkat
adalah
nilai
skala
kecil
(compressed
wavelet)
menyebabkan perubahan
koefisien
yang
menyatakan frekuensi
tinggi.
Nilai
skala
besar
(stretched
wavelet)
menyebabkan perubahan koefisien yang menyatakan
frekuensi rendah.
Tahap
pertama
analisis
gelombang
singkat
adalah
menentukan tipe
gelombang singkat atau mother
wavelet yang akan digunakan. Hal ini
perlu dilakukan
karena
fungsi gelombang
singkat
sangat
bervariasi.
|
|
14
Beberapa
contoh
mother
wavelet
adalah
Haar,
Daubechies. Setelah
pemilihan mother
gelombang singkat,
tahap
selanjutnya adalah
membentuk basis
gelombang
singkat
yang
akan
digunakan
untuk
mentransformasikan sinyal.
ARGS
memiliki
kemampuan
untuk
menganalisis suatu
data
dalam
domain
waktu
dan
domain
frekuensi
secara
simultan. Analisis data
pada
alih
ragam
gelombang
singkat
dilakukan
dengan
mendekomposisikan suatu
sinyal
ke
dalam
komponen
komponen
frekuensi
yang
berbeda-beda dan
selanjutnya
masing-masing komponen frekuensi
tersebut
dapat
dianalisis
sesuai
dengan
skala
resolusinya
atau
level
dekomposisinya. Hal
ini
seperti
proses filtering, dimana sinyal dalam domain waktu dilewatkan
ke
dalam High
Pass
Filter
dan
Low
Pass
Filter
untuk
memisahkan
komponen frekuensi tinggi dan frekuensi rendah.
ARGS
adalah
sebuah
alih
ragam
matematika yang
digunakan
untuk menganalisis sinyal bergerak. Sinyal bergerak ini dianalisis untuk
didapatkan informasi spectrum
frekuensi
dan
waktunya secara
bersamaan.
ARGS
menyediakan
penggambaran
frekuensi
waktu dari
sinyal.
Pada
awalnya,
alih
ragam
gelombang singkat
digunakan
untuk
menganalisis sinyal
bergerak (non-stationary sinyals). Sinyal bergerak
ini
dianalisis
dalam
alih
ragam
gelombang singkat
dengan
menggunakan teknik
multi-resolution analysis.
Secara
umum
teknik
multi-resolution analysis
adalah
teknik
yang
digunakan
untuk
menganalisis
frekuensi dengan cara
frekuensi
yang berbeda dianalisis
|
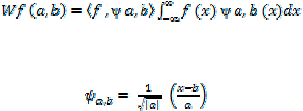 15
menggunakan resolusi berbeda. Resolusi dari sinyal merupakan ukutan
jumlah
informasi
di
dalam
sinyal
yang
dapat
berubah
melalui operasi
filterisasi.
ARGS
merupakan alat
yang
biasa
digunakan untuk
menyajikan
data atau fungsi atau operator ke dalam komponen-komponen frekuensi
yang berlainan, dan kemudian mengkaji setiap komponen dengan suatu
resolusi
yang sesuai dengan skalanya. ARGS
mempunyai kemampuan
membawa keluar ciri-ciri (features) khusus dari citra yang diteliti.
Secara umum
ARGS
kontinu
untuk
sinyal
f(x)
berdimensi 1-D,
didefinisikan pada persamaan (1).
Dengan
(1)
(2)
Fungsi ? disebut dengan induk gelombang singkat a, b ? R, a ? 0
(R
=
bilangan
nyata). Dalam
hal
ini,
a
adalah
parameter
lebar
dan
b
adalah parameter penggeseran posisi terhadap sumbu-x. Persamaan (1)
dapat dibentuk
ke
dalam bentuk diskret
dengan
memberikan
a
dan
b
nilai
diskret
(a=2n,
b
?
Z).
Pada
penelitian
ini
digunakan induk
gelombang singkat
Haar.
Pada
gelombang singkat
terdapat
istilah
dekomposisi. Secara
umum,
dekomposisi
gelombang
singkat
didapatkan melalui filterisasi subbidang dengan dua filter, yaitu grader
|
|
16
filter dan detail filter. Pengembangan untuk kasus sinyal berdimensi 2-
D
(sinyal citra 2-D) biasanya dilakukan dengan menerapkan bank filter
secara terpisah terhadap sinyal citra.
Biasanya digunakan sebuah pass
filter - down (H) dan pass filter - up (G). Konvolusi citra dengan pass
filter
-
down
menghasilkan sinyal
yang
biasa
disebut
dengan
citra
pendekatan
(approximation image)
dan
konvolusi dengan
pass
filter -
up pada arah spesifik menghasilkan citra detil (details images).
Setelah
berbagai
teori
yang
menjelaskan tentang pengekstrasian
data sinyal, kami memilih memakai metode gelombang singkat, hal ini
disebabkan
dari
perbandingan- perbandingan
yang
menyatakan
antara
metode
gelombang singkat
terhadap
metode
fast
fourier
Transform.
Diantara lain
menyebutkan bahwa pada
FFT
hanya
mempersentasikan
sinyal untuk jangkauan sinus, FFT hanya mengembangkan sinyal hanya
terjadi pada
frekuensi domain
tetapi
tidak
memberikan informasi pada
waktu domain. Sedangkan pada metode gelombang singkat, gelombang
singkat
bekerja
pada
waktu
yang
berbeda namun
juga
mempunyai
gelombang
yang
kecil.
Selain
itu
jika
pada
pengektrasian sinyal
tidak
berlanjut
pada
FFT
terdapat
kekurangan
dibandingkan dengan
gelombang
singkat
diantaranya pada
fungsi
kernel
yang
merupakan
window
dengan
panjang
yang
tak
terbatas
membuat syarat
stasioner
tidak terpenuhi dan
tidak dapat memberikan
informasi waktu
&frekuensi secara
bersamaan.
Selain
itu
dalam
mother
gelombang
singkatnya. Beberapa jenis alih
ragam gelombang singkat diantaranya
Alih Ragam Gelombang Singkat Diskrit (Discrete Wavelet Transform)
|
|
17
dan
Alih
Ragam
Gelombang
Singkat
Kontinyu (Continuous
Wavelet
Transform).
2.2.1.3.1 Alih Ragam Gelombang Singkat Kontinyu (ARGSK)
ARGSK
adalah
metoda
dekomposisi waktu-frekuensi
(time-frequency decomposition) yang
dikenal
juga
dengan
dekomposisi spectral
yang ditujukan
untuk mengkarakterisasi
respon
seismik pada frekuensi tertentu.
Dekomposisi spectral
adalah
penampang
seismik
konvensional yang
anda
amati
merupakan komposit
dari
rentang
frekuensi
gelombang
(umumnya 10
s/d 70 Hz, dengan
frekuensi dominant sekitar
30Hz).
Perbedaan penampang pada
frekuensi
yang
berbeda
akan
menampilkan fitur
geologi
yang
berbeda
pula,
karena
pada
hakikatnya sifat
geologi
seperti
ketebalan,
kandungan
fluida, dll.
hanya akan
lebih jelas dilihat pada level
frekuensi
yang
sesuai.
Metoda
dekomposisi
spectral
digunakan untuk
menampilkan
penampang
seismik
pada level frekuensi
tertentu, katakanlah pada frekuensi 10Hz, 20Hz, 30Hz, dll.
Ide dasar dari
metoda
ini
adalah dilakukannya FFT
(Fast
Fourier Transform) dari setiap window waktu secara menerus
(continuous) sehingga
diperoleh
gambaran
kisaran
frekuensi
pada
zona
target
(reservoar).
Gambar dibawah
ini
adalah
contoh
penerapan ARGSK
pada
salah
satu
trace
seismik
sintetik:
|
 18
Gambar 2.3 Trace Seismik Sintetik
Gambar
atas
sebelah kiri
adalah
trace
seismik
sintetik
sedangkan gambar sebelah kanan adalah hasil ARGSK dengan
menggunakan persamaan
Perhatikan
bahwa
ARGSK
ditampilkan dalam kawasan waktu terhadap
frekuensi. Waktu
tersebut adalah
waktu TWT
(Two
Way
Travel
Time)
dari
penampang seismik itu sendiri.
Lalu
dengan
menganalisis gambar
ARGSK,
katakanlah
target reservoar anda berapa pada kisaran 0.9 detik, maka anda
akan
mendapatkan
gambaran
frekuensi
dominan dari
target
|
|
19
anda, katakanlah 32Hz. Lalu dengan menggunakan persamaan
(2),
penampang ARGSK
diinversi
kembali
untuk
mendapatkan penampang seismik pada
frekuensi 32Hz,
yang
harapannya
dapat
meng-emphasize target
reservoar
anda.
Lihat
subjek
dekomposisi spectral
pada
blog
ini
yang
menujukkan hasil dari aplikasi metoda ARGSK terhadap data
real. (Polikar, Robi, 1999)
2.2.1.3.2 Alih Ragam Gelombang Singkat Diskrit (ARGSD)
Dasar dari ARGSD dimulai pada tahun 1976 dimana
teknik untuk mendekomposisi sinyal waktu diskrit ditemukan.
Di dalam ARGSK, sinyal dianalisis menggunakan seperangkat
fungsi dasar yang saling berhubungan dengan penskalaan dan
transisi sederhana. Sedangkan dalam ARGSD,
penggambaran
sebuah
skala
waktu
sinyal
digital
didapatkan dengan
menggunakan teknik
filterisasi
digital.
Secara
garis
besar
proses dalam teknik ini adalah dengan melewatkan sinyal
yang
akan
dianalisis pada
filter dengan
frekuensi dan
skala
yang berbeda.
Filterisasi sendiri merupakan sebuah funsi yang digunakan
dalam
pemprosesan sinyal.
Gelombang
singkat
dapat
direalisasikan
menggunakan
iterasi
filter
dengan penskalaan.
Resolusi
dari
sinyal,
yang
merupakan
rata-rata
dari
jumlah
detil
informasi dalam
sinyal,
ditemukan melalui
filterasi
ini
|
|
20
dan
skalanya
didapatkan
dengan
upsampling
dan
downsampling (subsampling). (Mallat, 1999)
Sebuah
sinyal
harus
dilewatkan dalam
dua
filterisasi
ARGSD yaitu highpass filter dan lowpass filter agar frekuensi
dari sinyal tersebut dapat dianalisis. Analisis sinyal dilakukan
terhadap
hasil
filterisasi
highpass
filter
dan
lowpass
filter
di
mana highpass
filter digunakan
untuk
menganalisis frekuensi
tinggi
dan
lowpass
filter
digunakan untuk
menganalisis
frekuensi rendah. Analisis terhadap frekuensi dilakukan
dengan
cara
menggunakan resolusi
yang
dihasilkan
setelah
sinyal
melewati filterisasi.
Analisis
frekuensi
yang
berbeda
dengan
menggunakan resolusi
yang
berbeda
inilah
yang
disebut
dengan
multi-resolution analysis,
seperti
yang
telah
disinggung pada bagian Transformasi Gelombang singkat.
sinyal
menjadi
frekuensi
tinggi dan
frekuensi
rendah
dalam proses
filterisasi
highpass
filter
dan
lowpass
filter
disebut
sebagai
dekomposisi. Proses
dekomposisi
dimulai
dengan melewatkan sinyal
asal
me
lewati highpass
filter dan
lowpass
filter.
Misalkan
sinyal
asal
ini
memiliki rentang
frekuensi dari
0
sampai
dengan
p
rad/s.
Dalam
melewati
highpass
filter
dan
lowpass
filter
ini,
rentang
frekuensi di-
subsample
menjadi dua,
sehingga rentang
frekuensi
tertinggi
pada
masing-masing subsample
menjadi
p/2
rad/s.
Setelah
filterisasi, setengah
dari sample atau salah satu subsample
|
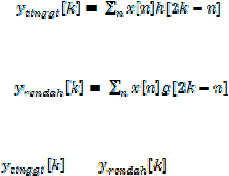 21
dapat dieliminasi berdasarkan aturan Nyquist. Sehingga sinyal
dapat
selalu di-subsample oleh 2 (?2 ) dengan cara
mengabaikan setiap sample yang kedua.
Proses dekomposisi
ini dapat
melalui satu atau
lebih
tingkatan.
Dekomposisi satu
tingkat
ditulis
dengan
ekspresi
matematika pada persamaan 3 dan 4.
(3)
(4)
dan
adalah hasil dari highpass filter
dan
lowpass
filter,
x[n]
merupakan sinyal
asal,
h[n]
adalah
highpass
filter,
dan
g[n]
adalah lowpass
filter.
Untuk
dekomposisi
lebih
dari
satu
tingkat,
prosedur
pada
rumus
3
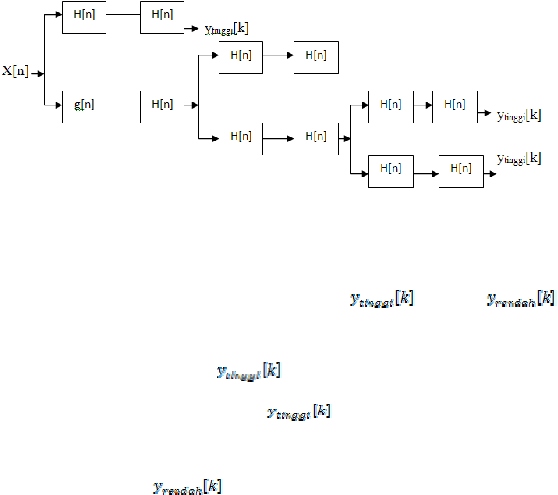
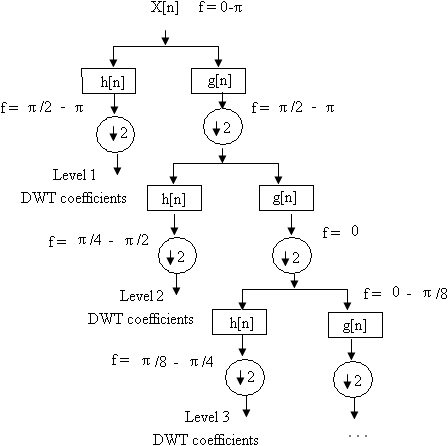
dan 4 dapat digunakan pada masing-masing tingkatan. Contoh
penggambaran dekomposisi
dipaparkan
pada
Gambar
2.1
dengan menggunakan dekomposisi tiga tingkat.
|
 22
Gambar 2.4 Dekomposisi Gelombang Singkat Tiga Tingkat
Pada
gambar
2.4,
dan
yang
merupakan hasil
dari
highpass
filter dan
lowpass
filter,
y
disebut
sebagai
koefisien
ARTGSD
.
merupakan
detil
dari
informasi
sinyal,
sedangkan
merupakan
t kisiran kasar dari fungsi
pensakalaan. Dengan
menggunakan koefisien
ARGSD ini
maka
dapat
dilakukan proses
Inverse
Discrete Wavelet
Transform (IDWT) untuk merekonstruksi menjadi sinyal asal.
ARGSD
menganalisis sinyal
pada
frekuensi
berbeda dengan
resolusi
yang
berbeda
melalui
dekomposisi sinyal
sehingga
menjadi
detil
informasi dan
taksiran kasar.
ARGSD bekerja
pada dua kumpulan fungsi yang disebut fungsi penskalaan dan
fungsi
gelombang
singkat
yang
masingmasing berhubungan
dengan lowpass filter
dan
highpass
filter.
Seperti
yang
telah
dijelaskan sebelumnya
dekomposisi
ini didasarkan pada
|
 23
aturan
Nyquist
yang
salah
satunya
mengatakan bahwa
frekuensi
komponen sample
harus
kurang
atau
sama dengan
setengah
dari
frekuensi sampling.
Jadi
diambil
frekuensi
sample p/2 dari
frekuensi sampling p dalam subsample oleh 2
pada
dekomposisi gelombang singkat. Sebagai penggambaran
dekomposisi gelombang singkat dengan
sinyal asal x[n]
yang
memilki frekuensi maksimum f = p dipaparkan pada Gambar
2.5.
Gambar 2.5 Dekomposisi Gelombang Singkat dengan Frekuensi Sinyal Asal f = 0
|
 24
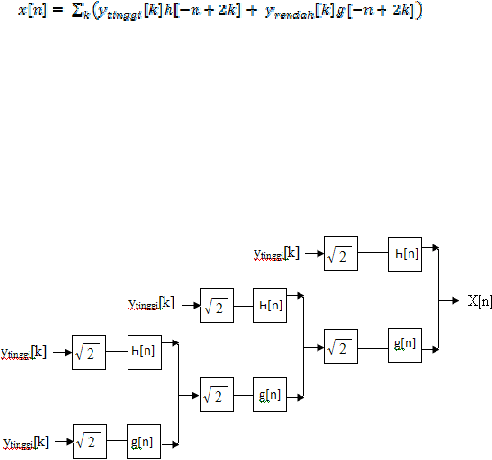
Proses
rekonstruksi diawali
dengan
menggabungkan
koefisien ARGSD
dari
yang
berada
pada
akhir
dekomposisi
dengan
sebelumnya meng-upsample
oleh
2
(?2)
melalui
highpass
filter
dan
lowpass
filter.
Proses
rekonstruksi ini
sepenuhnya merupakan
kebalikan
dar
i
proses
dekomposisi
sesuai
dengan
tingkatan
pada
proses
dekomposisi. Sehingga
persamaan
rekonstruksi pada
masing-masing tingkatan dapat
ditulis sbb :
Proses
rekonstruksi
gelombang
singkat
untuk
mendapatkan sinyal asal
dengan tiga tingkatan digambarkan
pada Gambar 2.6.
Gambar 2.6 Rekonstruksi Gelombang Singkat Tiga Tingkat
|
 25
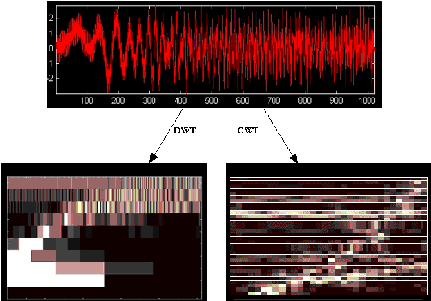
ARGSD mempunya kelebihan dalam hal ketelitian analisis
transformasi terhadap
isyarat
Transformasi.
Gambar
dibawah
ini merupakan perbandingan antara representation of a noisy
chrip sinyal dari ARGSD dan ARGSK.
Gambar 2.7 Representation of a Noisy Chrip Sinyal
Dari
gambar tersebut dapat terlihat ARGSD (DWT)
lebih
baik
dibandingkan dengan
ARGSK
(CWT)
dalam
proses
pengekstrasian sinyal
suara,
maka
kami
memakai
ARGSD
untuk mengekstrasi sinyal suara pada aplikasi yang kami buat.
Beberapa
jenis
ARGS
diantanya Haar
dan
Daubechies
dengan penjelasan di bawah ini.
|
|
26
2.2.1.3.3 Gelombang Singkat Haar
Gelombang
singkat
Haar
merupakan gelombang
singkat
yang
simple
dalam bentuk diskrit.
gelombang singkat
Haar
biasanya
berelasi
dengan
fungsi
matematika yang
disebut
dengan
alih
ragam
haar.
Aloh
ragam
haar berguna sebagai
prototype untuk semua alih ragam gelombang singkat
lainnya.
Seperti
contohnya pada
alih
ragam
gelombang
singkat, alih ragam haar
menguraikan sinyal diskrit
menjadi
dua
subsinyal dari
setengah
dari
panjang
record.
Salah satu
subsinyal berproses
pada
rata-rata
atau
trend
dan
sinyal
satunya lagi berproses pada perbedaan atau fluktuasi.
Alih
ragam
gelombang
singkat
Haar
memiliki
keuntungan
yaitu :
1. mempunyai konsep yang simple.
2. Prosesnya cepat
3. Memiliki memory yang efesien, dimulai dari perhitungan
langusng tanpa adanya array sementara.
4. Dapat
mengulang
kembali
proses
yang
dilakukan
tanpa
mempengaruhi efek terhadap problem lainnya.
Alih
ragam
Haar
mempunyai
keterbatasan yang
merupakan problem
bagi
beberapa
aplikasi.
Pada
umunya
setiap
rata-rata
untuk
tingkat
selanjutnya dan
setiap
set
koefisien, Tampilan haar transform merupakan sepasang nilai
dari rata-rata dan perbedaan. Kemudian pertukaran algoritma
|
|
27
melalui kedua
nilai dan perhitungan. Selain itu
rata-rata dan
perbedaan adanya
pada
sepasang
selanjutnya.Spectrum
koefisien
frekuensi
yang
tinggi
seharusnya dialihkan
ke
perubahan frekuensi yang tinggi. Layar Haar hanya memiliki
2
elemen
luas.
Jika
perubahan
yang
besar
menempati
dari
nilai genap ke nilai ganjil, perubahan tidak akan dialihkan ke
dalam
koefisien
frekuensi
tinggi.
Maka
gelombang singkat
haar
transform tidak
berguna
dalam
kompresi
dan
pengilangan noise pada proses sinyal suara.
2.2.1.3.4 Gelombang Singkat Daubechies
Daubechies gelombang
singkat
dinamakan
dari
Ingrid
Daubechies seorang profesor dari departemen matematika
dan
penggunaan matematika di
universitas Princeton.
dia
sangat ahli
dengan
pekerjaannya dengan
gelombang singkat
di dalam image compression.
daubechies adalah keluarga
dari
gelombang
singkat
orthogonal
didefinisikan dengan
discrete
gelombang singkat
transform
dan
dikarakteristikan
dengan
vanishing moment
jumlah
maksimal dari
beberapa
pemberi
dukungan. dengan
tiap
ripe
gelombang
singkat
di
setiap
class, ada sebuah
fungsi
scaling
(di
sebut
juga
father
gelombang
singkat)
yang
menghasilkan analisis
multiresolution orthogonal.
|
|
28
Alih
ragam
gelombang
singkat
Daubechies didefinisikan
hampir
sama
dengan
Alih
ragam
gelombang singkat
Haar
dengan
mengkomputasi rata-rata
yang
berjalan
dan
perbedaan
menggunakan scalar product
dengan
sinyal
scaling
dan
gelombang
singkat
satu-satunya perbedaan
diantara mereka terdiri dari bagaimana sinyal scaling ini dan
gelombang singkat didifinisikan.
Tipe
gelombang singkat ini memepunyai respon
frekuensi
yang
seimbang
tapi
fase
responnya
non-linear. daubecies
gelombang
singkat
digunakan
bertumpuk dengan
windows,
jadi
tingginya reflek
koifisien spectrum
semuanya
mempunyai perubahan
frekuensi
yang
tinggi.
Gelombang
singkat
daubechies
juga
berguna
untuk
mengkompresi dan
menghilangkan noise dalam proses sinyal audio.
Umumnya
daubechies gelombang
singkat
dipilih
karena
mempunyai
nilai
A
terttiggi
saat
menghilang, untuk
memberikan dukungan width N=2A, dan diantara 2
A-1
solusi
yang
mungkin salah
satunya
di
pilih
yang
filter
scalingnya
mempunyai
fase extremal.
Alih
ragam
gelombang
singkat
juga
sangat
mudah
di
tempatkan untuk
di
tranning
menggunakan alih
ragam
gelombang
singkat.
Gelombang
singkat
daubechies digunakan
secara
luas
dalam
memecahkan
berbagai
masalah, contohnya
fractal
problem
sinyal, sinyal diskontinuitas, dan lain-lain.
|
 29
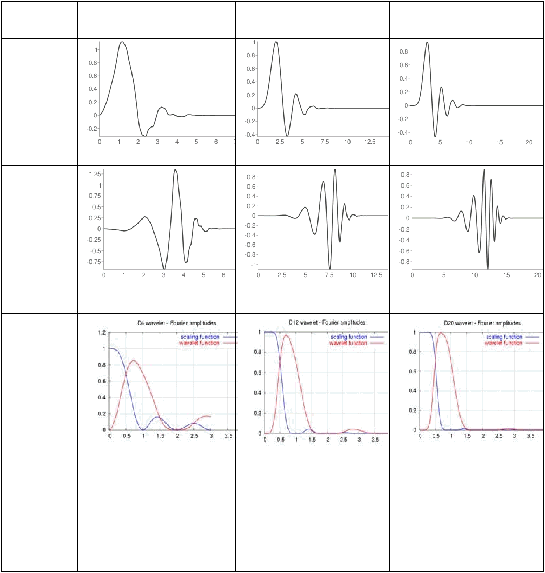
Db4
Db8
Db12
Scaling
functions
gelomba
ng
singkat
functios
amplitud
es of the
frequenc
y spectra
of the
above
functios
Gambar 2.8 Contoh Gelombang Singkat Daubechies
Gelombang sinyal tersebut tidak menunjukkan respon
frekuensi tinggi
dan
rendah
pass filter,
tapi
menuncukkan
|
|
30
amplitudo
dari Continuous
Forier
Transforms
dari scaling
(biru) dan fungsi gelombang singkat (merah).
Daubechies
orthogonal
gelombang
singkats D2-D20
paling banyak digunakan. nomer index mengacu pada nomer
koefesien
N. tiap gelombang
singkat
memiliki
number
of
zero
moments
atau
vanishing moments
sama
dari setengah
masa
maksilmal
kemampuan gelombang
singkat
untuk
mewakili sifat
polynomial atau
informasi dari sebuah sinyal.
untuk
contoh, D2,
dengan satu
momen,
dengan mudah
mengencode polynomials koefisien satu, atau constant sinyal
components. D4
mengencode polynomial
dengan
dua
koefisien,
seperti
konstan
dan
linear
komponen
sinyal;
dan
D6
mengencode
3-polynomial, seperti
konstan,
linier
dan
kuadrat
komponen
sinyal.
kemampuan untuk
mengencode
sinyal ini tidak memperhitungkan fenomena kebocoran sinyal
yang
terjadi
dan
kurangnya pergeseran-konstanan,
yang
timbul
dari
pergeseran diskrit
operasi
(di
bawah)
selama
transformasi aplikasi.
Sub-urutan yang
mewakili
linear,
kuadrat
(misalnya)
komponen
sinyal
diperlakukan berbeda
oleh alih ragam tergantung pada apakah poin sejajar dengan-
atau bahkan urutan lokasi yang
ganjil. Kekurangan dari sifat
penting
dari
pergeseran-konstanan, telah
menyebabkan
pembangunan beberapa
versi
berbeda
dari
sebuah
pergeseran-invarian (diskrit) alih ragam gelombang singkat.
|
 31
Tabel 2.1 Perbandingan Daubechies dan Haar
Gelombang singkat
Transform
No of bits
BER
Daubechies
16384
0%
Haar
16384
46%
Kami
memilih
daubechius gelombang
singkat
transform karena
pada
daubechius
gelombang
singkat
secara lengkap didukung
oleh
gelombang singkat dengan
fasa
ekstremal dan
memiliki
jumlah
vanishing moment
paling
tinggi
untuk
lebar
yang
ditentukan. Vanishing
moment menunjukan kemampuan gelombang singkat
dalam
merepresentasikan sifat polinomial. Filter
skala
yang dihubungkan adalah filter fasa minimum
Berdasarkan artikel Mohamed I. Mahmoud, Moawad I.
M. Dessouky, Salah Deyab, and Fatma H. Elfouly tentang
yang kami baca
tentang FPGA
technologi yang
meneliti
tentang ARGS
yang
paling
efektif
dalam
menganalisa
sinyal
dengan
berbagai
aplikasi
di
dapatkan
bahwa
nilai
Bit
Error
Ratio
(BER)
dari
daubechies
lebih
kecil
dari
Haar
gelombang singkat.
Sehingga
dapat
dilihat
bahwa
|
|
32
pemakayan daubechies lebih efektif daripada Haar dalam
menganalisa sinyal.
2.2.1.4 Metode Pencarian Linear
Metode
paling
sederhana
dalam
mengimplementasikan sebuah
direktori
adalah
dengan
menggunakan linear
list
dari
nama
berkas
dengan penunjuk ke blok
data.
Linear
list dari
direktori
memerlukan
pencarian
searah
untuk
mencari
suatu
direktori
didalamnya. Metode
sederhana
untuk
di
program tetapi
memakan
waktu
lama
ketika
dieksekusi.
Untuk
membuat berkas baru
kita
harus
mencari
di
dalam
direktori untuk meyakinkan
bahwa tidak ada berkas yang bernama
sama.
Lalu
kita
tambahkan sebuah berkas baru
pada
akhir
direktori.
Untuk
menghapus
sebuah
berkas, kita
mencari berkas
tersebut dalam
direktori,
lalu
melepaskan
tempat
yang
dialokasikan
untuknya.
Untuk
menggunakan kembali
suatu
berkas
dalam
direktori
kita
dapat
melakukan beberapa
hal. Kita dapat
menandai berkas tersebut sebagai
tidak
terpakai
(dengan
menamainya secara
khusus,
seperti
nama
yang
kosong,
atau
bit
terpakai
atau
tidak
yang
ditambahkan
pada
berkas),
atau kita dapat menambahkannya pada daftar direktori bebas. Alternatif
lainnya kita dapat menyalin ke tempat yang dikosongkan pada direktori.
Kita juga bisa menggunakan linked
list untuk
mengurangi waktu untuk
menghapus berkas. Kelemahan dari linear list ini adalah percarian
searah
untuk
mencari
sebuah
berkas.
Direktori yang berisi
informasi
sering digunakan, implementasi yang
lambat pada cara aksesnya akan
|
|
33
menjadi
perhatian
pengguna. Faktanya,
banyak
sistem
operasi
mengimplementasikan 'software
cache'
untuk
menyimpan
informasi
yang
paling
sering
digunakan.
Penggunaan 'cache'
menghindari
pembacaan
informasi
berulang-ulang pada
disk.
Daftar
yang
telah
diurutkan memperbolehkan pencarian biner dan mengurangi waktu
rata-rata
pencarian.
Bagaimana pun
juga penjagaan
agar daftar
tetap
terurut dapat
merumitkan operasi pembuatan dan penghapusan berkas,
karena
kita
perlu
memindahkan sejumlah
direktori
untuk
mengurutkannya. Tree
yang
lebih
lengkap
dapat
membantu seperti B-
tree.
Keuntungan
dari daftar
yang
terurut
adalah
kita
dapatkan
daftar
direktori yang terurut tanpa pengurutan yang terpisah.
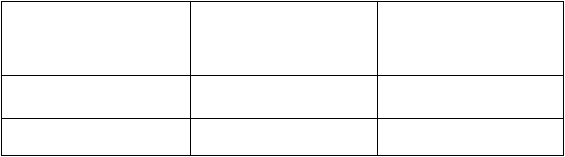
2.2.1.5 Euclidean Distance
Dalam matematika, jarak Euclidean atau Euclidean metrik adalah
jarak antara dua yang diukur dengan penggaris, dan diberikan oleh
rumus Pythagoras. Dengan menggunakan formula ini sebagai jarak,
ruang Euclides menjadi ruang metrik. Norma yang terkait disebut
norma Euklidean. Sastra lebih tua mengacu pada metrik sebagai metrik
Pythagoras.
Euclidean distance antara titik p dan q adalah panjang segmen
garis Dalam koordinat Cartesian, jika p = (p1, p2 ,..., pn) dan q = (Q1,
q2 ,..., qn) adalah dua titik dalam ruang-n Euclides, maka jarak dari p
untuk q adalah diberikan oleh :
|
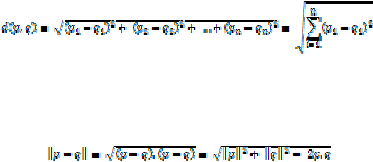 34
Aturan Euclidean Distance untuk mengukur jarak titik ke ruang Euclides
asal:
2.2.2 Analisis Fitur Vektor
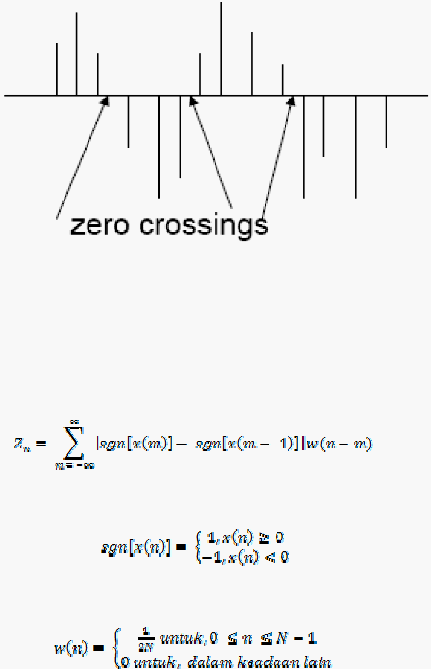
2.2.2.1 Zero Crossing Rate
Zero
-
crossing
rate adalah
parameter
penting
dalam klasifikasi
suara
pembicara dan
suara
yang
tidak
terucap. hal
ini
juga
sering
digunakan sebagain
front-end
processing
di
dalam
sistem
pengenalan
suara
otomatis. nilai
zero
-
crossing
adalah
indikator dari
frekuensi
dimana energi sinyal terkonsentrasi di dalam spektrum. suara
pembicara dihasilkan karena eksistasi dari vokal periodik yang terbawa
oleh udara di celah suara dan biasanya menunjukan nilai zero - crossing
yang
rendah.
sedangkan suara
yang
tak
terucap
dihasilkan karena
penyempitan saluran vokal
yang cukup
untuk
menyebabkan terjadinya
aliran
udara
turbulen yang
akhirnya menghasilkan
noise
dan
menunjukan nilai zero - crossing yang tinggi.
|
 35
Gambar 2.9 Definisi Zero - Crossing Rate
Definisi untuk zero – crossings rate adalah
Dimana
Dan
Model
untuk
produksi
suara
menyarankan bahwa
kisaran
energi
suara
harus
terkonsentrasi di
bawah
3kHz
karena
jatuhnya
spektrum
diperkenalkan oleh gelombang
glottal, sedangkan suara
yang
tak
terucap, sebagian besar energinya ditemukan pada frekuensi yang lebih
|
|
36
tinggi.
karena
frekuensi tinggi
maka
zero-crossing
rates
tinggi,
dan
frekuensi rendah
menyiratkan zero-crossing
rates
rendah,
ada
kolerasi
kuat
antara
zero-crossing
rate
dan
distribusi energi
dengan
frekuensi.
sebuah generalisasi yang masuk akal adalah jika tingkat zero-crossing
rate tinggi, sinyal suara adalah suara yang tidak diucapkan, sedangkan
jika zero-crossing rate rendah,
sinyal suara adalah
suara yang
diucapkan.
Zero
-
crossing
rate adalah
manipulasi
sederhana
dari besarnya
sinyaldapat
menyediakan sejumlah
properti
berguna.
beberapa
pengukuran ini secara tradisional termasuk energi, rata-rata ukurannya,
zero
crossings,
dan
fungsi
otokorelasi. Properti
ini
dapat
digunakan
untuk analisa
yang
lebih kompleks,
seperti
estimasi
lapangan.
Dalam
konteks
sinyal
diskrit,
zero
crossing
dikatakan terjadi
jika
sampel
mempunyai tanda aljabar yang berbeda. Ini berarti bahwa ada hubungan
antara zero - crossing dan konten frekuensi sinyal.
Koefisien gelombang singkat
sinyal audio dalam
setiap
subband
mengambil suatu
bentuk
osilasi
gelombang. Zero
crossing
di
dalam
tranformasi
domain
menggambarkan
seberapa
sering
frekuensi
sinyal
telah berubah dalam periode
waktu
tertentu di dalam sebuah
subband.
Normalisasi zero – crossing rate didefinisikan sebagai berikut :
|
 37
2.2.2.2 Mean
Karakteristik frekuensi
waktu
dari
audio
yang
sesuai
untuk
amplitudo dari koefisien
gelombang
singkat.
dua
notes
dari
frekuensi
dan besarnya suara yang sama dapat menghasilkan suara yang berbeda.
besarnya rata
-
rata
dari
suatu
urutan
dari koefisien adalah
semacam
ukuran sinyal.
fitur yang kami
gunakan ini adalah
nilai rata - rata dari
koefisien X(i), yang didefinisikan sebagai:
Dimana N adalah nilai dari koefisien di dalam sebuah subband.
2.2.2.3 Variances
Koefisien gelombang singkat audio dapat dilihat sebagai distribusi
dalam teori probabilitas. Kita tahu bahwa distribusi
probabilitas secara
unik
dicirikan oleh
momen.
Audio
adalah
sinyal
dengan
rata
-
rata
hampir
nol,
jadi
kami
memilih momen sentral kedua, seperti
varians
sebagai salah satu fitur kami. Jika kita mengasumsikan bahwa distribusi
gelombang
singkal
dimodelkan sebagai
fungsi
kepadatan
Laplace,
distribusinya juga
dapat
secara
langsung
terhubung
dengan
deviasi
standart.
Fitur yang kami gunakan adalah
|