|
6
BAB 2
LANDASAN
TEORI DAN
KERANGKA PEMIKIRAN
2.1 Landasan Teori
2.1.1 Analisis Rantai Markov
Analisis
Markov
merupakan
sebuah teknik
yang
berhubungan
dengan
probabilitas
akan
state
di
masa mendatang
dengan menganalisa probabilitas
saat
ini (Render
et
al,
2006, p652).
Teknik
ini
memiliki
beragam
aplikasi
dalam dunia
bisnis,
di
antaranya
analisis
pangsa
pasar,
prediksi
kerugian,
prediksi
penerimaan
mahasiswa
baru di universitas,
dan menentukan apakah sebuah mesin akan mengalami kerusakan di masa
mendatang.
Definisi
lain
menyatakan
bahwa
Analisa Markov
merupakan
sebuah
metode
dalam
menganalisa perilaku
saat
ini
dari
beberapa
variabel
dengan
tujuan
untuk memprediksi
perilaku dari variabel yang sama di masa mendatang (Levin et al., 1992, p802).
Analisa
Markov
hampir
sama
dengan
decision analysis,
bedanya adalah analisa
rantai Markov
tidak
memberikan
keputusan rekomendasi, melainkan
hanya
informasi
probabilitas
mengenai situasi
keputusan
yang
dapat
membantu
pengambil
keputusan.Dengan
demikian. Analisa
rantai
Markov bukanlah teknik optimisasi,
tetapi adalah
teknik deskriptif yang menghasilkan informasi probabilitas dimasa mendatang.
Menurut
Hamdy A.Taha :
“Sebuah
proses
markov adalah sebuah sistem stokhastik yang untuk
pemuculan
suatu
keadaan
di
masa
mendatang
bergantung
pada
keadaan
yang
segera
mendahuluinya
dan
hanya
bergantung pada itu
“(hlm.344).
(Taha,AHamdy. Riset
Operasi ,Jakarta
:
Binarupa
Aksara ,Th 1996 ).
Analisa
Markov
hampir
sama
dengan
decision
analysis,
bedanya
adalah
analisa
rantai Markov
tidak memberikan keputusan rekomendasi, melainkan hanya informasi
|
 7
probabilitas
mengenai situasi
keputusan
yang
dapat
membantu
pengambil
keputusan.Dengan
demikian. Analisa
rantai
Markov bukanlah teknik optimisasi,
tetapi adalah
teknik deskriptif yang menghasilkan informasi probabilitas dimasa mendatang.
2.1.2 Sejarah Markov
Andrey Andreyevich Markov
Markov
ditemukan oleh seorang
matematikawan terkenal
dari Rusia bernama
Andrey
Andreyevich
Markov
yang lahir
pada tanggal 14
Juni 1856
di
Ryazan, Russia
dan wafat pada
tanggal 20 Juli 1922 di Petrograd, Russia.
Pria
yang
bertempat
tinggal
dan
berkewarganegaraan
Rusia
ini
pernah
belajar
di
Universitas St. Petersburg pada tahun 1874 dibawah bimbingan Chebyshev yang juga
sebagai
pembimbing
doctoralnya.
Pada
tahun 1886,
Markov
menjadi
anggota St.Petersburg
Academy
Of Science.
Markov
terkenal
lewat
teori
yang
ditemukannya tentang
proses
stokastik, yang kemudian dikenal dengan nama Markov Chain.
|
|
8
2.1.3. State
State digunakan untuk mengidentifikasi
seluruh kondisi yang mungkin
dari suatu
proses
atau sistem
(Render
et
al,
2006,
p652). Misalnya saja, sebuah
mesin dapat
berada
dalam satu state
dari
dua state
yang ada
dalam satu waktu. Mesin tersebut
dapat
berfungsi
dengan baik atau dapat juga
berfungsi secara tidak baik (rusak). Kondisi dimana mesin dapat
berfungsi
disebut
dengan
state pertama.
Sedangkan
kondisi
dimana
mesin
tidak
dapat
berfungsi
disebut
dengan
state kedua.
Contoh
lainnya
adalah mahasiswa manajemen di
Universitas Bina Nusantara dapat memilih satu diantara peminatan yang ada
yaitu peminatan
E-Business, Marketing,
dan
Entrepreneurship.
Masing-masing
peminatan
ini
dapat
dianggap
sebagai sebuah state.
Menurut Render et al (2004, p652), dalam analisis Markov diasumsikan bahwa state
memiliki dua buah sifat yaitu:
•
Collectively
exhaustive
–
peneliti
dapat
membuat
daftar
seluruh
state
yang
mungkin
timbul atau
dimiliki oleh suatu sistem atau
proses
dimana
asumsinya
adalah terdapat jumlah state yang terbatas untuk sistem.
•
Mutually
exclusive
–
sebuah
sistem
hanya
dapat
berada
dalam
satu
state
dalam
satu waktu (sistem
tidak
dapat
berada
dalam
lebih
dari
satu state).
Misalnya,
mahasiswa
manajemen UBinus hanya
dapat
memilih
satu
peminatan
dari tiga peminatan yang ada.
2.1.4 Probabilitas State
Setelah
state
dari
sistem
atau
proses yang
akan
diteliti
telah
diidentifikasi,
langkah
selanjutnya adalah
menentukan
probabilitas
sistem
berada
dalam state tertentu dengan
menggunakan vektor probabilitas state.
|
|
9
p
(i) = vektor dari probabilitas state untuk periode i
= (p
1
,p2
,p3
,…,p
n
)
dimana
n
= jumlah state
p
1
,p2
,p
3
,…,p
n
=
probabilitas berada dalam state
ke-1, state ke-2, state ke-n
Untuk
beberapa
kasus
dimana
hanya
terdapat
satu
item
,
misalnya
sebuah
mesin.
Maka
dapat
ditentukan
dengan
pasti state
dari
item tersebut.
Misalnya
saja,
jika
penelitian
dilakukan
hanya
pada
satu
buah
mesin,
maka kita
dapat
mengetahui
dengan
pasti
bahwa
pada
saat
ini mesin
dapat
berfungsi
dengan
baik,
atau
tidak
berfungsi.
Maka vektor
untuk
mesin tersebut dapat diggambarkan sebagai berikut:
p(1) = (1,0)
dimana
p1
= 1 = probabilitas berada dalam state ke-1
p2
= 0 = probabilitas berada dalam state ke-2
Hal
ini
menunjukkan
bahwa
probabilitas
mesin berfungsi
dengan
baik, state
ke-1,
adalah
1
dan
probabilitas
mesin
tidak berfungsi, state
ke-2, adalah
0
untuk
periode
pertama.
Namun
dalam
beberapa
kasus,
penelitian
dilakukan
tidak
hanya
pada
satu
item saja
melainkan beberapa
item.
Contoh
lainnya
penelitian
dilakukan
di
suatu
kota
yang
memiliki
tiga
buah
toko
bahan
makanan
(Render et
al,
2006,
pp653-656).
Terdapat
total
100.000 orang
yang
berbelanja
di ketiga
toko bahan
makanan
tersebut
pada
bulan
tertentu.
Terdapat
40.000
orang
yang
berbelanja di
American
Food Store, dinamakan
dengan state 1. Terdapat
30.000
orang
yang
berbelanja
di
Food
Mart,
dinamakan
dengan
state
2.
Terdapat
30.000
orang
yang
berbelanja di
Atlas Foods,
dinamakan dengan state 3.
Probabilitas
dari satu orang
yang
berbelanja pasa satu diantara tiga
toko bahan makanan tersebut yaitu:
|
|
10
State 1 – American Food Store
40.000/100.000 = 0.40 = 40%
State 2 – Food Mart
30.000/100.000 = 0.30 = 30%
State 3 – Atlas Foods
30.000/100.000 = 0.30 = 30%
Jika
probabilitas
tersebut
diletakkan
dalam
vektor probabilitas
state
maka
akan
menjadi:
p
(1) = (0.4, 0.3, 0.3)
dimana
p
(1) = vektor probabilitas state ketiga
toko bahan
makanan untuk periode 1
p
1
=
0.4
=
probabilitas satu
orang
yang akan berbelanja di
American Food
Store,
state 1
p
2
= 0.3 = probabilitas satu orang yang akan berbelanja di Food Mart, state 2
p
3
= 0.3 = probabilitas satu orang yang akan berbelanja di Atlas Foods, state 3
Probabilitas
yang
ditunjukkan
oleh
vektor
di
atas
menggambarkan
pangsa
pasar
untuk
ketiga
toko
bahan makanan
untuk
periode pertama,
dimana
American
Food
Store
memiliki
pangsa
pasar sebesar
40%, Food
Mart
memiliki
pangsa
pasar
sebesar
30%,
Atlas
Food
memiliki
pangsa
pasar
sebesar 30%. Tentunya
pangsa
pasar ini memiliki
kondisi
yang
tidak
stabil dimana
tiap toko
dapat mengalami
perubahan
pangsa
pasar untuk
periode
berikutnya. Pihak manajemen tentunya
ingin mengetahui bagaimana pangsa pasar mereka
mengalami perubahan seiring
berjalannya
waktu.
Pelanggan
tidak selalu
tetap berbelanja
di
toko
tertentu,
tetapi
bisa
saja
berpindah
ke
toko
lain
untuk
melakukan
pembelian
selanjutnya.
Penelitian
untuk
ketiga
toko
bahan
makanan
menetapkan
bahwa
80%
pelanggan
American Food
Store pada
periode
pertama akan kembali
untuk berbelanja di
toko
itu
pada
periode
berikutnya.
10%
pelanggan
American
Food
Store
berpindah
ke
Food
Mart
dan
|
 11
sisanya sebesar
10%
berpindah
ke
Atlas
Food.
Untuk
pelanggan yang
berbelanja
di
Food
Mart,
70%
pelanggan akan
kembali,
10%
berpindah
ke
American
Food
Store,
dan
20%
berpindah
ke
Atlas
Food.
Untuk
pelanggan
yang berbelanja
di
Atlas
Food,
60%
pelanggan
akan
kembali,
20%
berpindah
ke
American
Food
Store, dan
20% berpindah
ke
Food
Mart.
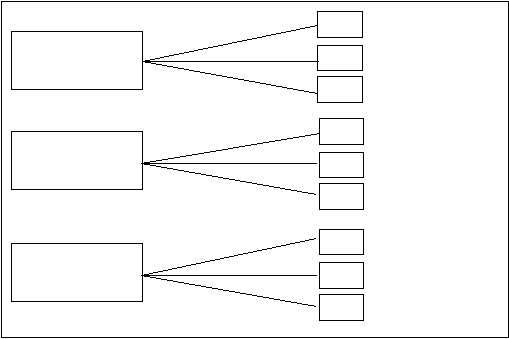
Gambar 2.1 memperlihatkan diagram pohon untuk menggambarkan situasi ini.
Perhatikan bahwa
dari 40%
pangsa pasar American Food Store untuk periode
pertama,
32% (0.4 x 0.8 =
0.32) akan
kembali,
4% akan
berpindah
ke Food
Mart,
dan 4%
akan
berpindah
ke
Atlas
Food. Untuk menghitung
pangsa
pasar American
Food
Store
pada
periode
berikutnya, tambahkan nilai 32%
yang
berasal
dari
pelanggan yang
kembali
dengan
nilai 3%
yang berasal
dari pelanggan Food Mart yang berpindah ke American Food Store dan
nilai
6%
yang
berasal
dari
pelanggan
Atlas
Food
yang
berpindah
ke
American
Food
Store.
Sehingga American Food Store akan memiliki 41% pangsa pasar pada periode berikutnya.
American Food
#1
0 4
Food Mart #2
0.3
Atlas Food #3
0.3
0.
#1
0.
#2
0.
#3
0.
#1
0.
#2
0.
#3
0.
#1
0.
#2
0.
#3
0.32 = 0.4
0.04 = 0.4
0.04 = 0.4
0.03
0.21
0.06
0.06
0.06
0.18
Gambar 2.1 Contoh Diagram Pohon
(Sumber: Render et al, 2006, p654)
|
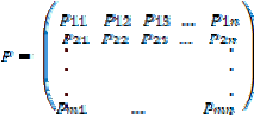 12
Dibandingkan dengan
menggunakan
diagram
pohon,
penggunaan matriks
probabilitas
state
lebih
memudahkan
dalam
melakukan
perhitungan.
Matriks
ini
digunakan
bersama dengan probabilitas state saat ini
untuk memprediksi kondisi di masa mendatang.
2.1.5
Matriks Transisi Probabilitas
Matriks Transisi
Probabilitas
memungkinkan
untuk
melakukan
perhitungan
probabilitas
state
di
masa
mendatang
berdasarkan pada
state
saat
ini.
Pij
=
probabilitas
kondisi
berada dalam
state j
di masa mendatang
berdasarkan pada state
i
saat ini. Misalkan
P
12
adalah
probabilitas
berada
pada state
2
di
masa mendatang
dimana sebelumnya
berada
pada state 1 ( Render et al. 2006, p655 ).
P
= matriks transisi probabilitas
Nilai
Pij
biasanya ditentukan secara empiris. Misalkan, penelitian
menunjukkan
bahwa 10% orang
yang saat
ini berbelanja pada
toko
ke-1
(state 1) pada
periode berikutnya
akan berbelanja di toko ke-2 (state 2),maka P
12
= 0.1 atau 10%( Render et al. 2006, p655 ).
Berdasarkan contoh soal sebelumnya mengenai
tiga toko bahan makanan
selanjutnya akan dbuat matriks transisi probabilitasnya untuk menentukan
berapa persentase
pelanggan akan berpindah tiap periodenya. Matriksnya adalah sebagai berikut :
|
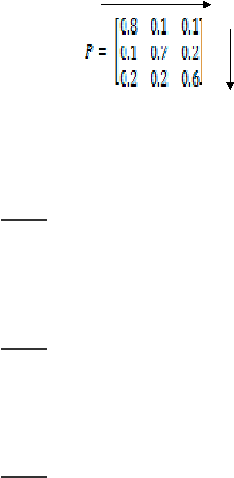 13
Mempertahankan
dan kehilangan
Mempertahankan dan
memperoleh
Toko American Food
mewakili state
1, Food Mart
state 2, dan
Atlas Food
state 3. Arti
dari probabilitas di atas dapat digambarkan seperti berikut :
Baris 1
0.8 = P
11
= probabilitas berada pada state 1 setelah sebelumnya berada pada state 1
0.1 = P
12
= probabilitas berada pada state 2 setelah sebelumnya berada pada state 1
0.1 = P
13
= probabilitas berada pada state 3 setelah sebelumnya berada pada state 1
Baris 2
0.1 = P
21
= probabilitas berada pada state 1 setelah sebelumnya berada pada state 2
0.7 = P
22
= probabilitas berada pada state 2 setelah sebelumnya berada pada state 2
0.2 = P
23
= probabilitas berada pada state 3 setelah sebelumnya berada pada state 2
Baris 3
0.2 = P
31
= probabilitas berada pada state 1 setelah sebelumnya berada pada state 3
0.2 = P
31
= probabilitas berada pada state 2 setelah sebelumnya berada pada state 3
0.6 = P
31
= probabilitas berada pada state 3 setelah sebelumnya berada pada state 3
2.1.6
Memprediksi Kondisi di Masa Mendatang
Menurut Render et
al ( 2006,
p656
)
Salah satu tujuan
analisis Markov adalah
untuk
memprediksi masa
depan.
Berdasarkan contoh
kasus
sebelumnya,
dimana
probabilitas
sama
dengan
pangsa
pasar,
maka
dimungkinkan untuk
menghitung
pangsa
pasar
di
masa
mendatang
untuk
American Food Store, Food Mart
,
dan
Atlas Food.
Jika
periode
saat
ini
adalah
0,
menghitung
probabilitas
state untuk
periode
berikutnya
(
periode
1
)
dapat
dilakukan sebagai berikut:
|
 14
p(1) = p(0)P
Jika penghitungan dilakukan pada periode n, maka probabilitas state untuk periode n
+ 1 adalah sebagai berikut:
p(n + 1) = p(n)P
Persamaan
di
atas
dapat
digunakan
untuk
menjawab
pertanyaan
atas pangsa
pasar
di
masa
mendatang untuk
ketiga
toko
bahan
makanan.
Perhitungannya
adalah
sebagai
berikut:
p(1)
= p(0)P
= (0.4, 0.3, 0.3)
= [(0.4)(0.8) + (0.3)(0.1)
+ (0.3)(0,2), (0.4)(0.1) (0.3)(0.7) + (0.3)(0.2),
(0.4)(0.1) + (0.3)(0.2)
+ (0.3)(0.6)]
= (0.41, 0.31, 0.28)
2.2
Kondisi Ekuilibrium
Pada masa-masa awal,
kehilangan
maupun memperoleh pelanggan merupakan hal
yang lazim
terjadi.
Namun
lama-kelamaan kehilangan
dan perolehan pelanggan akan
menjadi
semakin
kecil.
Merupakan
sebuah
kondisi yang
sangat
masuk
akal
jika
di
masa
mendatang
akan
tercapai suatu
kondisi
yang stabil
dimana
semua
state
yang
ada
tidak
mengalami
perubahan
lagi
atau disebut
juga
dengan
kondisi
ekuilibrium.
Kondisi
ini
akan
tercapai
hanya
jika
tidak
ada state
yang melakukan tindakan
yang dapat
mengubah
matriks
transisi
probabilitas.
Berdasarkan pada
kasus toko
bahan
makanan
yang
dibahas sebelumnya
maka
kita
dapat
mengetahui
pada saat
kondisi
pasar
stabil,
maka
berapakah
pangsa
pasar
dari masing-masing toko bahan makanan tersebut.
Ekuilibrium satu toko
Untuk
mengilustrasikan
ekuilibrium
ini,
diasumsikan
terdapat
sebuah
matriks
transisi
probabilitas yang baru
|
 15
Mempertahankan
Mempertahankan
dan kehilangan
A
B
C
A
B
C
Mempertahankan dan
memperoleh
Karena
C
tidak
pernah
kehilangan
pelanggannya dan
karena kedua
toko
kehilangan
pelanggannya beralih
ke
toko C
maka hanya tinggal menunggu waktu saja
hingga toko C
akan
meraih seluruh
pelanggan yang ada.
Kondisi yang
seperti ini
dikenal
dengan
istilah
sink
atau
basin
dari
suatu
state
yang
berarti
salah
satu
toko
yaitu
C
akhirnya
akan
meraih seluruh pelanggan. C juga disebut sebagai
absorbing
state.
Ekuilibrium dua toko
Ekuilibrium
jenis
kedua
diilustrasikan
melalui sebuah
matriks
transisi
probabilitas
yang
baru seperti berikut ini.
A
B
C
dan kehilangan
A
Mempertahankan dan
B
memperoleh
C
Dari
matriks di
atas
dapat
terlihat
bahwa
toko
B
dan
C
pada
akhirnya
akan
merebut
seluruh
pelanggan
toko A. Hal ini terjadi karena
A
kehilangan 0.05 pelanggannya beralih
ke
toko
B
dan
0.05
pelanggannya
beralih
ke
toko
C
dan
tidak
memperoleh
pelanggan
baru
baik
dari toko B maupun C. kondisi ekuilibrium pasar hanya dialami
oleh toko
B
dan
C. Kedua toko tersebut harus berbagi pelanggan yang ada di pasar.
|
 16
Ekuilibrium tiga toko
Ekuilibrium jenis ketiga yaitu
ketika
tidak
terjadi sink
atau basin. Berdasarkan contoh
kasus
toko
bahan
makanan
sebelumnya,
kita
akan
mencari
kondisi
ekuilibrium
pangsa
pasar ketiga toko bahan makanan tersebut.
Mempertahankan
dan kehilangan
A
B
C
A
B
C
Mempertahankan dan
memperoleh
Berdasarkan matriks
tersebut maka
dapat
dibentuk
sebuah persamaan
dimana
pangsa
pasar A merupakan jumlah
dari
pangsa pasar
A
+
pangsa
pasar A
yang
berasal
B +
pangsa
pasar A yang berasal C.
Hal
yang
sama juga dapat diterapkan
untuk pangsa
pasar B
dan
C
sehingga
jika
dituliskan
dalam
bentuk
persamaan
matematika
akan
menjadi
seperti
berikut :
A = 0.8A + 0.1B + 0.2C (1)
B = 0.1A + 0.7B + 0.2C (2)
C = 0.1A + 0.2B + 0.6C (3)
Karena
jumlah
probabilitas
pangsa
pasar
ketiga
toko
tersebut
sama
dengan
1
maka
dapat ditambahkan persamaan :
1 = A + B +C
Pada
persamaan
(1)
hingga
(3)
terdapat tanda
persamaan
yang
sama
sehingga
persamaan tersebut dapat diubah menjadi:
0 = –0.2A + 0.1B + 0.2C
(1)
0 = 0.1A – 0.3B + 0.2C
(2)
0 = 0.1A + 0.2B –
0.4C
(3)
|
 17
1 = A + B +C
Karena
terdapat
4
persamaan
dan
hanya
3
yang tidak
diketahui,
maka
kita
dapat
menghilangkan salah
satu dari tiga persamaan yang ada (
hilangkan persamaan
3
)
dan
memecahkan
tiga persamaan lainnya untuk mencari pangsa pasar ekuilibrium.
0 = -0.2A + 0.1B + 0.2C
x3
0 = -0.6A + 0.3B + 0.6C
(1)
0 =
0.1A -
0.3B + 0.2C
x1
0 = 0.1A -
0.3B + 0.2C
(2)
0 = -0.5A +0.8C
0.8C = 0.5A
C = 0.625A
0 = -0.2A + 0.1B + 0.2C
x1
0 = -0.2A + 0.1B + 0.2C
(1)
0 = 0.1A - 0.3B + 0.2C
x1
0 = 0.1A -
0.3B + 0.2C
(2)
0 = -0.3A + 0.4B
0.4B = 0.3A
B = 0.75A
Setelah
mendapatkan
nilai
B
dan
C,
maka
kita
dapat
mencari
nilai
A
dengan
memasukkannya ke dalam
persamaan:
1 = A + B + C
1 = A + 0.75A + 0.625A
1 = 2.375A
A = 0.421052631 ˜ 0.421
Langkah terakhir adalah mencari nilai dari B dan C yaitu:
B = 0.75A
= 0.75(0.421)
= 0.31575
˜
0.316
C = 0.625A
= 0.625(0.421)
= 0.263125 ˜ 0.263
Maka
pada
kondisi ekuilibrium,
pangsa
pasar
untuk
toko A
=
0.421 (42.1%),
B
=
0.75
(75%), C = 0.263 (26.3%).
|
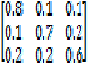 18
Untuk
membuktikan kondisi
ekuilibrium ini, maka kita dapat
melakukan
perhitungan nilai
pangsa pasar ekuilibrium dengan matriks transisi probabilitas.
= (0.421, 0.75, 0.263)
= (0.421, 0.75, 0.263)
2.3
Pengantar QM For
Windows
QM
for
Windows
merupakan
sebuah
paket
software untuk
teknik
kuantitatif
yang
dikembangkan
oleh
Professor
Howard
Weiss.
Software ini
berbasiskan
menu
dan
sangat
mudah
digunakan
bahkan oleh
pengguna
yang
tidak
memiliki
pengalaman
komputer.
Fitur
yang
disediakan
QM
for
Windows
memberikan
kemudahan
bagi
penggunanya (Render
et al,
2006, p712), antara lain:
•
Pengguna
yang
telah
mengenal
program
kertas kerja
(spreadsheet) atau
pengolah
kata
(word
processing)
di
Windows
dapat dengan
mudah
menggunakan
QM
for Windows.
Semua modul yang ada dapat diakses kapan pun.
•
Walaupun
QM
for
Windows
memiliki
19
modul
dan
40
submodul,
tampilan
untuk
tiap
modul sangat konsisten, sehingga
jika pengguna telah terbiasa menggunakan satu
modul maka untuk modul berikutnya akan menjadi lebih mudah.
•
Editor
dengan jenis
kertas
kerja memungkinkan
untuk
melakukan
proses editing
dengan
layar penuh.
•
File
dibuka
dan
disimpan
sama
seperti pada
Windows dimana
file dinamai
sesuai
modul
yang
digunakan
sehingga memudahkan
jika
ingin mencari
file
yang
disimpan
sebelumnya.
•
Mudah
untuk
melakukan
perubahan
dari
satu
metode
solusi
ke
metode
lainnya
untuk
melakukan perbandingan metode dan jawaban yang dihasilkan.
Gambar grafik dapat dengan mudah dihasilkan dan dicetak.
|
 19
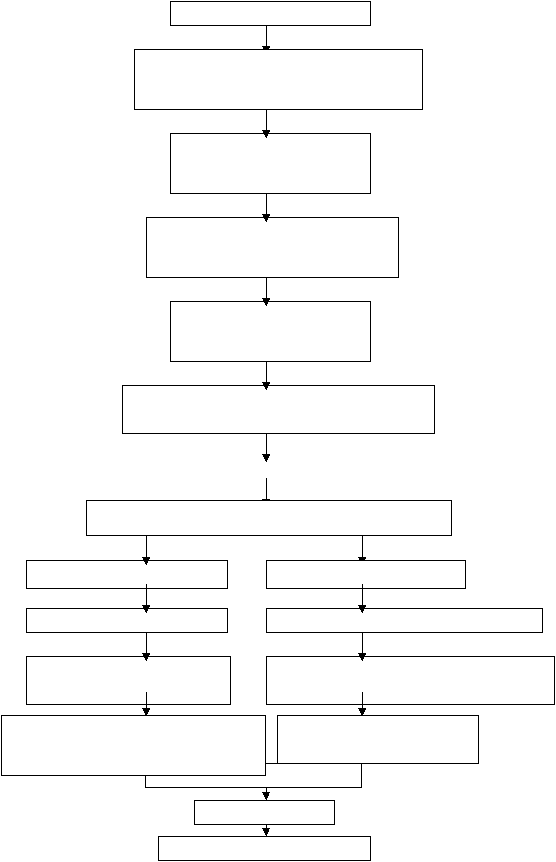
2.4
Kerangka Pemikiran
STUDI PENDAHULUAN
IDENTIFIKASI MASALAH
1. Latar Belakang Masalah
2.
Perumusan Masalah
TUJUAN PENELITIAN
Menjawab ke-empat rumusan
permasalahan diatas
LANDASAN TEORI
1. Analisis Markov
2.
QM for Windows
PENGUMPULAN DATA
Wawancara Kuisioner
DATA PEMILIHAN UNIVERSITAS OLEH
SISWA SMA DI BOGOR
Latar Belakang Menggunakan Pendekatan Rantai Markov
PENGOLAHAN DATA
Analisis Rantai Markov
Statistik Deskriptif
Penentuan
State
Analisis Menggunakan Program SPSS
Pembuatan Matriks
Probabilitas Transisi
Analisis Sumber Referensi Pelajar
dalam PemilihanUniversitas
Melakukan Analisis Pendugaan
Peminatan Periode Berikutnya dan
Titik Ekuilibrium
Analisis Penilaian Pelajar
pada Kelima Universitas
OUTPUT
KESIMPULAN DAN SARAN
|