2010100394MNBab2

BAB 2

LANDASAN TEORI dan

KERANGKA

PEMIKIRAN

2.1 Riset Operasi (Operating Research)

2.1.1 Pengertian Riset Operasi

Menurut Pendapat Mulyono

(2004, p2), secara harfiah

kata operations

dapat

didefinisikan sebagai

tindakan-tindakan yang

diterapkan

pada

beberapa masalah

atau

hipotesa.

Sementara kata

research

adalah

suatu

proses

yang

terorganisasi

dalam mencari kebenaran akan masalah atau

hipotesa

tadi. Kenyataannya,

sangat

sulit

untuk

mendefinisikan

Operating Research,

terutama

karena

batas-

batasnya tidak

jelas.

Operating

Research

memiliki

bermacam-macam

penjelasan,

namun hanya beberapa yang biasa digunakan dan diterima secara umum.

Definisi 1

Riset

operasi adalah

penerapan

motode-metode

ilmiah

terhadap masalah-

masalah

rumit

yang

muncul

dalam pengarahan

dan

pengelolahan

dari

suatu

sistem

besar manusia, mesin,

bahan

dan uang

dalam

industri, bisnis, pemerintah

dan pertahanan. Pendekatan khusus ini bertujuan membentuk suatu model

ilmiah dari sistem, menggabungkan ukuran-ukuran faktor-faktor seperti

kesempatan dan

risiko,

untuk

meramalkan

dan

membandingkan hasil-hasil

dan

beberapa keputusan, strategi

atau

pengawasan. Tujuannya adalah

membantu

pengambil keputusan menentukan kebijaksanaan dan tindakannya secara ilmiah

(

Operational

Research

Society Of Great Britain).

Definisi 2

Riset operasi berkaitan dengan

menentukan

pilihan secara ilmiah

bagaimana

merancang dan menjalankan sistem manusia

dan mesin secara terbaik, biasanya

membutuhkan

alokasi

sumber

daya

yang

langka.

(

Operations

Research Society

Of America).

Definisi 3

Operating Research,

adalah seni memberikan jawaban buruk terhadap

masalah-masalah yang jika

tidak, memiliki jawaban yang lebih buruk (T.L. Saaty)

Definisi 4

Operating

Research

adalah pendekatan

dalam

pengambilan

keputusan

yang

ditandai dengan penggunaan pengetahuan ilmiah melalui usaha kelompok antara

disiplin yang bertujuan menentukan penggunaan terbaik sumber daya terbatas.

Definisi 5

Operating Research dalam arti luas,

dapat

diartikan sebagai penerapan

metode-metode,

teknik-teknik,

dan

alat-alat

terhadap masalah-masalah

yang

menyangkut

operasi-operasi

dari

sistem-sistem, sedemikian

rupa

sehingga

memberikan penyelesaian optimal.

Menurut

Modul

Lab MKB, Analisis

Kuantitatif merupakan suatu

pendekatan

ilmiah

terhadap

pengambilan

keputusan

managerial.

Pendekatan

tersebut

dimulai dengan data yang kemudian diolah atau

diproses menjadi informasi yang

berguna bagi

decision maker.

2.1.2

Model dalam Riset Operasi

Model

adalah

abstraksi

atau

penyederhanaan

realitas

sistem

yang

kompleks

mana

hanya

komponen-komponen

yang relevan

atau

faktor-faktor

yang

dominan dari masalah

yang dianalisis diikutsertakan. Ia menunjukkan

hubungan-

hubungan (langsung dan tidak langsung) dari aksi dan reaksi dalam pengertian

sebab dan akibat. Karena sebuah model adalah suatu

abstraksi realitas,

ia akan

tampak kurang

kompleks

dibandingkan

realitas

itu

sendiri.

Model

itu,

agar

menjadi lengkap, perlu mencerminkan semua realitas yang sedang diteliti.

Model

dapat

diklasifikasikan dalam banyak cara, misalnya menurut

jenisnya,

dimensi,

fungsinya,

tujuannya, subyeknya,

atau

derajat abstraksinya.

Kriteria

yang paling biasa adalah jenis model. Jenis dasar itu meliputi:

Iconic (

Physical)

model

Model

Iconic adalah

suatu

penyajian

fisik

yang

tampak

seperti

aslinya

dari

suatu

sistem nyata

dengan

skala

yang

berbeda.

Contoh

model

ini

adalah

mainan

anak-anak,

potret,

histogram, market

dan lain-lain.

Model

iconic

dikatakan

diperkecil (scale down)

atau

diperbesar

(

scale up

)

sesuai

dengan

ukuran model apakah lebih kecil atau besar dibanding sistem nyata.

Model iconic

mudah

diamati,

dibentuk

dan

dijelaskan,

tetapi sulit

untuk

memanipulasi dan

tak

berguna

untuk

tujuan

peramalan.

Biasanya

model

ini

menunjukkan peristiwa statistik.

b. Analogue Model

Model Analogue

lebih abstrak

dibanding model iconic,

karena

tak kelihatan

sama

antara

model

dengan

sistem

nyata.

Contohnya

jaringan

pipa

tempat

air

mengalir

dapat

digunakan

dengan

pengertian

yang

sama

sebagai

distribusi aliran

listrik. Peta

dengan

bermacam-macam

warna merupakan

model

analog

dimana

perbedaan warna

menunjukkan

pegunungan,

hijau

sebagai

dataran

rendah dan

lain-lain.

Kurva

permintaan,

kurva

frekuensi

dalam statistika adalah contoh lain model analog dari tingkah laku peristiwa-

peristiwa. Model

analog lebih

mudah

untuk memanipulasi

dan

dapat

menunjukkan situasi

dinamis. Model

ini umumnya

lebih

berguna

daripada

model

iconic karena

kapasitasnya

yang

besar

untuk

menunjukkan

ciri-ciri

sistem nyata

yang dipelajari.

Mathematic (Simbolic

)

Model

Diantara

jenis

model

yang

lain,

model

matematik sifatnya

paling

abstrak.

Model

ini menggunakan seperangkat simbol

matematik

untuk menunjukkan

komponen-komponen (dan hubungan antara mereka) dari sistem nyata.

Namun, sistem nyata tidak selalu dapat diekspresikan dalam rumusan

matematik. Model

ini dapat

dibedakan

menjadi dua

kelompok,

yaitu

deterministik dan

probabilistik.

Model deterministik dibentuk

dalam

situasi

kepastian

(

certainty). Model

ini

memerlukan

penyederhanaan-

penyerdehanaan

dari realitas

karena kepastian

jarang

terjadi.

Namun,

keuntungan

model

ini

adalah

bahwa

ia dapat

dimanipulasi

dan

diselesaikan

lebih mudah. Jadi, sistem

yang rumit dapat

dimodel

dan

dianalisa jika

dapat

diasumsikan bahwa

semua

komponen sistem

itu dapat

diketahui

dengan

pasti.

Ada beberapa cara

untuk membuat model menjadi

lebih sederhana,

misalnya:

1. Melinierkan hubungan yang tidak linier

2. Mengurangi banyaknya variabel atau kendala

3. Mengubah sifat variabel, misalnya dari diskrit menjadi kontinyu

4. Mengganti tujuan ganda menjadi tujuan tunggal

5. Mengeluarkan unsur dinamik (membuat model menjadi statistik)

6. Mengasumsikan

variabel

random

menjadi

suatu

nilai

tunggal

(deterministik)

Pembentukan

model

adalah

esensi

dari

pendekatan

Operation Research

karena

solusi

dari

pendekatan ini

tergantung

pada ketepatan model

yang

dibuat. Philips, Ravindran,

dan

Solberg (1976) mengingatkan sepuluh prinsip

dalam pembentukan model yaitu:

1. Jangan membuat model yang rumit jika yang sederhana akan cukup

2. Hati-hati

dalam

merumuskan

masalah,

agar

disesuaikan

dengan

teknik

penyelesaian

3. Hati-hati

dalam

memecahkan

model,

jangan

membuat

kesalahan

matematik

4. Pastikan kecocokan model sebelum diputuskan untuk diterapkan

5. Model jangan sampai keliru dengan sistem nyata

6. Jangan membuat model yang tidak diharapkan

7. Hati-hati dengan model yang terlalu banyak

8. Pembentukan

model

itu

sendiri

hendaknya

memberikan

beberapa

keuntungan

9. Sampah masuk, sampah keluar artinya

nilai

suatu model

tidak

lebih baik

dari pada datanya

10. Model tidak dapat menggantikan pengambil keputusan

2.1.3

Tahap-tahap dalam Riset Operasi

Pembentukan model

yang

cocok

hanyalah

salah satu

tahap

dari

aplikasi

Operating Research. Pola

dasar

penerapan

Operating Research

terhadap

suatu

masalah dapat dipisahkan menjadi beberapa tahap.

a. Merumuskan masalah

Dalam

perumusan

masalah

diakibatkan karena

pertanyaan

penting

yang

harus dijawab :

•

Variabel

keputusan

yaitu

unsur-unsur

dalam

persoalan

yang

dapat

dikendalikan

oleh

pengambil

keputusan. Sering

juga disebut sebagai

instrumen.

•

Tujuan

(objective

Penerapan

tujuan

membantu

pengambil

keputusan memusatkan

perhatian

pada

persoalan dan

pengaruhnya

terhadap organisasi. Tujuan ini

diekspresikan dalam variabel

keputusan

•

Kendala

(

constraints)

adalah pembatas-pembatas terhadap alternatif

tindakan yang tersedia

b. Pembentukan

model

Model

merupakan ekspresi

kuantitatif dari

tujuan

dan

kendala-kendala

persoalan

dalam

variabel

keputusan.

Jika

model

yang

dihasilkan cocok

dengan mudah diperoleh dengan program linier.

Jika hubungan

matematik

model

begitu

rumit

untuk

penerapan

solusi

nalaitik, maka

suatu model

probabilita mungkin lebih cocok.

Mencari penyelesaian masalah

Pada

tahap

ini bermacam-macam

teknik

dan

metode solusi

kuantitatif

yang merupakan

bagian

utama

dari

Operating Research memasuki

proses.

Penyelesaian

masalah

sesungguhnya

merupakan

aplikasi satu

atau lebih teknik-teknik ini terhadap model. Seringkali, solusi terhadap

model

berarti nilai-nilai

variabel

keputusan yang

mengoptimumkan salah

satu fungsi tujuan dengan nilai fungsi tujuan lain dengan dapat diterima.

d. Validasi model

Asumsi-asumsi

yang

dapat

digunakan

dalam

pembentukan

model harus

absah. Dengan kata lain, model harus diperiksa apakah ia mencerminkan

berjalannya sistem

yang diwakili. Suatu

model

yang biasa

digunakan

untuk

menguji

validitas

model

adalah

membandingkan performancenya

dengan data masa

lalu

yang

tersedia. Model

dikatakan

valid jika

dengan

kondisi

input

yang

serupa, ia dapat

menghasilkan

kembali

performance

seperti

masa lampau.

Masalahnya adalah bahwa

tak ada

yang

menjamin

performance masa depan akan berlanjut meniru cerita lama.

e. Penerapan hasil akhir

Tahap

akhir adalah

menerapkan

hasil model

yang telah

diuji.

Hal

ini

membutuhkan

suatu

penjelasan

yang hati-hati tentang solusi yang

digunakan

dan

hubungannya

dengan realitas.

Suatu

tahap

kritis

pada

tahap

ini

adalah

mempertemukan

ahli

Operating Research (pembentuk

model) dengan mereka yang bertanggung jawab terhadap pelaksanaan

sistem.

2.1.4 Metode-Metode

Umum Mencari Solusi

Pada

umunya

terdapat tiga

metode

untuk

mencari

solusi

terhadap

model

Operating

Research

yaitu metode analitis

yang

bersifat deduktif, metode numerik

yang bersifat indukatif dan metode monte carlo

a. Pendekatan

Analitik

(metode

analitik)

memerlukan

perwujudan

model

dengan solusi grafik dengan perhitungan matematik. Jenis matematik yang

digunakan tergantung pada sifat-sifat model.

b. Pendekatan Numerik (model numerik) berhubungan dengan perulangan atau

coba-coba

dari

prosedur-prosedur kesalahan,

melalui

penggunaan

perhitungan

numerik

pada

setiap

tahap.

Metode numerik

digunakan

jika

beberapa

metode analitik gagal

untuk mencari solusi.

Urutannya

dimulai

dengan

solusi

awal

(

initial

solution

)

dan

diteruskan

dengan

seperangkat

aturan-aturan untuk

perbaikan

menuju

optimum. Solusi awal kemudian

diganti

dengan

sokusi

yang

diperbaiki

dan

proses

itu

diulang

sampai

tidak

mungkin

adanya

perbaikan

lagi

atau biaya

perhitungan

lebih

lanjut

dapat

diterima.

Model Monte Carlo

Model

ini

memerlukan

penggunaan

konsep

probabilitas

dan

sampling.

Beberapa langkah pendekatan ini :

Untuk model yang cocok terhadap suatu sistem, pengamatan sampel

dilakukan dan kemudian distribusi probabilitas variabel yang

bersangkutan ditentukan

ii.

Ubah distribusi probabilitas itu menjadi distribusi kumulatif

iii.

Pilih urutan bilangan random dengan bantuan tabel random

iv.

Tentukan

urutan

nilai

variabel

yang

bersangkutan

dengan

urutan

bilangan random yang didapat dari langkah c.

Cocokkan

suatu

fungsi

matematik

standar

dengan

nilai-nilai

pada

tahap d.

Metode

Monte Carlo pada

dasarnya

adalah

suatu

teknik

simulasi

dimana

fungsi distribusi statistik dibuat melalui seperangkat

bilangan random.

2.1.5 Sifat-Sifat Riset Operasi

Teknik-teknik Operating Resear©h

Saat

ini

Operating Research telah

berkembang

begitu

luas,

sehingga

dirasa

tak

perlu

untuk

menyebutkan

satu

demi

satu

teknik

Operating Research yang

ada.

Namun, beberapa masalah

Operating

Research

yang

didefinisikan dengan

baik dan

diterima umum dapat digolongkan sebagai berikut :

1. Masalah alokasi

2. Masalah pertarungan

3. Masalah antri

4. Masalah jaringan

5. Masalah persediaan

Ciri-ciri

Operating Research

Ada beberapa

ciri-ciri Operating

Research

yang menonjol, antara lain :

1. Operating Resear©h merupakan pendekatan kelompok antar

disiplin untuk

mencari hasil

optimum

Operating

Research

menggunakan

teknik

penelitian ilmiah untuk

mendapatkan

solusi optimum

3. Operating ®esearch hanya memberikan jawaban yang jelek

terhadap

persoalan jika tersedia jawaban yang lebih jelek. Ia

tidak memberikan jawaban

sempurna

terhadap

masalah

itu,

sehingga

Operating Research

hanya

memperbaiki kualitas solusi.

2.1.6 Keterbatasan Riset Operasi

Operating Research berbeda

dengan

optimasi

klasik,

karena

dalam

metode

optimasi

nonklasik

(

Operating Research)

dapat

menangani

kendala

pertidaksamaan

maupun persamaan.

Dengan

kendala

yang

lebih

bebas

ini,

metode optimasi

nonklasik

menjadi

lebih menarik dan

lebih

realistis.

Tetapi, ini

membutuhkan metode solusi yang baru, karena

kendala pertidaksamaan tak

dapat ditangani dengan teknik kalkulus klasik.

2.1.7 Penerapan dan Peranan Riset Operasi dalam Membuat Keputusan

Riset

operasi

adalah suatu

metode

pengambilan

keputusan

yang

dikembangkan

dari studi

operasional

militer selama

Perang

Dunia

II.

Keberhasilan-keberhasilan penelitian

dari

kelompok-kelompok

studi

militer

ini

telah

menarik

kalangan

industriawan untuk

membantu

memberikan

berbagai

solusi terhadap masalah-masalah

manajerial yang rumit. Dewasa ini riset operasi

telah mendapat pengakuan sebagai mata ajaran yang penting di tingkat

perguruan

tinggi, sesuai

perkembangan kurikulum

pendidikan tinggi

maka

teknik-teknik

pendekatan dalam mengidentifikasi masalah

dan

mengambil

keputusan

menjadi

suatu kebutuhan penting

bagi

peserta

didik.

Selain

itu

kalangan

professional, manajer, akademisi dapat

memanfaatkan

metode-metode

riset

operasi

yang

disajikan

dalam

buku

ini.

Materi

riset

operasi

yang

disampaikan mencakup berbagai bidang

pengetahuan

seperti ekonomi,

manajemen produksi,

manejemen operasi,

transportasi, teknik industri dan

lain-

lain.

Riset

operasi

adalah penerapan

metode-metode

ilmiah

terhadap

masalah

rumit

yang

muncul

dalam pengarahan dan

pengelolaan

dari suatu

sistem

besar

manusia, mesin, bahan dan uang dalam industri, bisnis, pemerintahan, dan

pertahanan.

Pendekatan

khusus

ini

bertujuan

membentuk

suatu

model

ilmiah

dari

sistem, menggabungkan

ukuran-ukuran,

faktor-faktor

seperti

kesempatan

dan

resiko,

untuk

meramalkan

dan membandingkan

hasil-hasil

dari

beberapa

keputusan, strategi

atau

pengawasan.

Tujuannya

adalah

membantu

pengambilan keputusan menentukan kebijakan

dan

tindakannya

secara

ilmiah

(

Operational

Research

Society of Grreat Britain).

2.2 Program Linear (

Linear Programming)

2.2.1

Sejarah Program

Linear

George

Dantzig diakui

umum

sebagai

pioner Linear Programming

karena

jasanya

dalam

menemukan

metode dalam

mencari

solusi

masalah

Linear

Programming

dengan

banyak

variabel

keputusan.

Dantzig

bekerja

pada

penelitian

teknik

matematik

untuk

memecahkan

masalah

logistik

militer

ketika

dia

dipekerjakan

oleh

angkatan

udara

Amerika Serikat

selama Perang

Dunia

II.

Penelitiannya

didukung

oleh ahli-ahli lainnya.

Nama asli teknik

ini adalah

program saling

ketergantungan

kegiatan-kegiatan

dalam

suatu struktur linear

yang kemudian dipendekkan menjadi

Linear Programming.

Linear

Programming lahir tahun

40-an

Departemen Pertahanan

Inggris

dan

Amerika

menjawab

masalah

optimisasi perencanaan

operasi

perang

melawan

Jerman dalam Perang Dunia ke-II dan dikembangkan

oleh Dantzig (1947) dan

para pakar lainnya.

Wujud

permasalahan

yaitu

mengoptimumkan

suatu

fungsi

linear

yang

terbatas oleh

kendala-kendala berupa persamaan dan

pertidaksamaan linear.

2.2.2

Pengertian Program Linear

Mulyono

(2004,

p13)

menyatakan

bahwa Program

linear

(

Linear

Programming yang

disingkat

LP)

merupakan

salah

satu

teknik

Operating

Research

yang digunakan paling luas dan

diketahui dengan

baik. Program

Linear

merupakan metode

matematik

dalam mengalokasikan sumber daya

yang langka

untuk mencapai tujuan.

Program

Linear

(

Linear Programming

)

merupakan

sebuah

teknik

matematik

yang

didesain untuk membantu

para manajer

operasi dalam

merencanakan

dan

membuat

keputusan

yang

diperlukan

untuk

mengalokasikan sumber

daya

berdasarkan pendapat Heizer dan Render (2006, p588).

“Linear

Programming

(LP)

adalah suatu

cara

untuk

menyelesaikan

persoalan

pengalokasian

sumber

yang

terbatas

diantara

beberapa aktivitas yang

bersaing,

dengan

cara terbaik

yang mungkin

dilakukan. Persoalan

pengalokasian

itu akan

muncul

manakala seseorang harus

memilih

tingkat aktivitas

tertentu

yang

bersaing

dalam

hal

penggunaan sumber

daya

langka

yang

dibutuhkan

untuk

melaksanakan

aktivitas

tersebut.”

(sumber:

Bahtiar

Saleh

Abbas,

Robert Tang

Herman; Shinta,

Jurnal Piranti Warta ; 2008)

“Linear programming

menggunakan

model

matematis

untuk

menjelaskan

persoalan

yang

dihadapinya.

Sifat

linier disini memberi

arti bahwa

seluruh fungsi

matematis

dalam

model

ini

merupakan

fungsi yang

linier

sedangkan

kata

“

program” merupakan

sinonim

untuk

perencanaan.

Dengan

demikian,

program

linier

adalah perencanaan aktivitas

untuk memperoleh suatu

hasil yang optimum,

yaitu

suatu

hasil

yang

mencapai

tujuan terbaik

diantara

seluruh

alternatif

yang

fisibel.”. (sumber: Merlyana, Bahtiar Saleh Abbas,

Jurnal Piranti Warta; 2008).

Program

Linear

menyatakan

penggunaan

teknik matematik tertentu

untuk

mendapatkan kemungkinan

terbaik

atas

persoalan

yang melibatkan sumber yang

serba

terbatas.

Program

Linear

adalah

suatu

cara

untuk

menyelesaikan

persoalan

pengalokasian

sumber-sumber

yang terbatas

antara aktivitas

yang

bersaing dengan cara terbaik yang mungkin dilakukan.

Linear progamming

merupakan

suatu

teknik

yang

membantu

pengambilan

keputusan dalam mengalokasikan sumber daya (mesin tenaga kerja, uang,

waktu,

kapasitas

gudang,

dan

bahan

baku).

Linear programming merupakan

penggunaan

secara

luas

dari

teknik model

matematika

yang

dirancang

untuk

membantu manajer dalam

merencanakan

dan

mengambil

keputusan dalam

mengalokasikan sumber daya.

2.2.3

Tujuan dari Program Linear

•

Mempelajari

program

linear

sebagai

penunjang

pengambilan

keputusan.

•

Memahami syarat-syarat pemecahan program linear

dan

pemecahannya.

•

Memperkenalkan

metode

grafik

untuk

pemecahan

maksimisasi

dan

minimisasi persoalan program linear.

•

Mempelajari

masalah

teknik

dalam

program

linear

seperti

titik

ekstrim

dan

alternatif

pemecahan optimum

dan

memperlihatkannya

dengan

metode grafik.

2.2.4 Syarat pembentukan Model Program Linear

Sebelum melihat

pemecahan program linear,

kita harus

mempelajari

syarat-syarat utama

persoalan

program

linear

dalam

perusahaan

tertentu.

Berikut adalah syarat pembentukan model program linear:

Variabel

keputusan

merupakan

unsur-unsur

dalam

persoalan

yang

dapat

dikendalikan oleh pengambil keputusan.

Persoalan

Linear

Programming bertujuan

untuk

memaksimalkan atau

meminimalkan

kuantitas (pada

umumnya

berupa

laba

atau

biaya).

Sifat

umum

ini

disebut

sebagai

fungsi

tujuan

(obje©tive function) dari

suatu

persoalan Linear Prog®amming. Tujuan utama suatu perusahaan pada

umumnya

untuk memaksimalkan

keuntungan

pada jangka

panjang.

Dalam

kasus

sistem distribusi

suatu

perusahaan

angkutan

atau

penerbangan,

tujuan pada

umumnya berupa meminimalkan biaya.

Adanya

batasan

(

constraints

)

atau

kendala,

yang membatasi

tingkat

sampai di mana sasaran

dapat dicapai. Sebagai contoh, keputusan untuk

memproduksi berapa

banyak

unit

dari tiap produk

dalam

suatu lini

produk

perusahaan,

dibatasi

oleh tenaga

kerja

dan

mesin

yang

tersedia.

Oleh

karena itu, untuk memaksimalkan atau meminimalkan suatu kuantitas

(fungsi

tujuan)

bergantung

kepada

sumber

daya

yang jumlahnya

terbatas

(batasan).

Harus ada

beberapa alternatif tindakan yang dapat

diambil. Sebagai

contoh,

jika

suatu

perusahaan

menghasilkan

tiga

produk berbeda,

manajemen

dapat

menggunakan

Linear Programming

untuk

memutuskan

bagaimana

cara

mengalokasikan

sumber

dayanya yang

terbatas

(tenaga

kerja,

permesinan,

dan

seterusnya).

Jika

tidak

ada

alternatif

yang

dapat

diambil, maka Linear

Programming tidak diperlukan.

Kita

harus

dapat

menyatakan

tujuan

perusahaan

dan

segenap

keterbatasannya

sebagai kesamaan

atau

ketidaksamaan

matematik,

dan

harus

ada

kesamaan

dan ketidaksamaan

linear

Tujuan

perusahaan

yakni

keuntungan.

“Model

Pemrograman

Linear

(MPL)

memiliki

sebuah

fungsi

objektif

dan

satu atau

lebih kendala.

Pada fungsi objektif terdapat

parameter yang

disebut

koefisien fungsi objektif (objective function coefficients). Koefisien fungsi

objektif

menggambarkan kontribusi satu

satuan

variabel

keputusan

terhadap

nilai

fungsi

objektif.

Koefisien

fungsi objektif

yang

selama

ini

dikenal

dalam

pembahasan

MPL

bersifat

tegas,

demikian

pula

dengan

kendala”.

(sumber:

Sani

Susanto,

Dedy

Suryadi,

Hari

Adianto,

YMK

Aritonang Jurnal

Teknik

Industri, Vol 8, No 1 (2006))

Fungsi Tujuan

merupakan suatu pernyataan

matematik

dalam

pemrograman

linear

yang

memaksimalkan

atau

meminimalkan

kuantitas

(sering

berupa

laba

atau

biaya,

tetapi

setiap tujuan

dapat

digunakan).

Sedangkan batasan merupakan pembatas yang membatasi tingkat sampai

dimana seorang manajer dapai mencapai suatu tujuan.

Uji

linearitas

dipergunakan

untuk

melihat apakah model

yang dibangun

mempunyai hubungan linear atau tidak. Uji ini jarang digunakan pada

berbagai

penelitian,

karena

biasanya

model

dibentuk

berdasarkan

telah teoritis

bahwa

hubungan antara variabel bebas dengan variabel terikatnya adalah linear.

Hubungan

antar

variabel

yang

secara

teori

bukan

merupakan

hubungan

linear sebenarnya

sudah

tidak dapat

dianalisis

dengan

regresi linear, misalnya

masalah elastisitas.

Asumsi

linearlitas adalah asumsi

yang

menetapkan

atau

memastikan

apakah data yang kita miliki sesuai dengan garis linear atau tidak.

2.2.5 Kesamaan dan Ketidaksamaan Matematik dalam Program Linear

Meskipun

kesamaan

lebih

populer

dibandingkan dengan

ketidaksamaan

namun

ketidaksamaan

merupakan suatu

hubungan

yang

penting

dalam

program

linear.

Apakah

perbedaannya?

Kesamaan

digambarkan

oleh

tanda

”=” dan merupakan pernyataan khusus dalam matematik.

Namun

banyak

persoalan

perusahaan

yang

tidak

dapat

dinyatakan

dalam

bentuk

kesamaan yang jelas dan rapi. Hitungan

yang dicari

tidak selalu satuan

bulat

tetapi

bisa

juga

berupa

angka

kira-kira.

Untuk

itu

dibutuhkan

ketidaksamaan yakni hubungan lain yang dinyatakan dalam bentuk matematik.

Sebagian besar

batasan

dalam

persoalan

program

linear

dinyatakan sebagai

ketidaksamaan.

Seperti akan

terlihat

nanti,

kebanyakan

di atas atau di bawah

batas

dan tidak

dinyatakan

pada

tingkat

yang

pasti,

sehingga

membuka

banyak kemungkinan.

2.2.6 Metode Grafik untuk Pemecahan Program Linear

Ada

kemungkinan

untuk memecahkan masalah program linear secara

grafik

sepanjang jumlah

variabel

(produk, misalnya)

tidak

lebih

dari 2. Metode

grafik

merupakan cara

yang

baik

untuk

mulai

mengembangkan suatu

pengertian

teknik kuantitatif.

Berikut

adalah

tahap-tahap

dalam

menyelesaikan program

linear

dengan

metode grafik :

Menentukan

variabel

keputusan

atau

barang

apa

saja

yang

akan

produksi

oleh

suatu

perusahaan atau

pabrik

dengan

memberikan

pemisalan pada variabel keputusan.

Menentukan

fungsi

tujuan

yaitu

memaksimalkan

profit

atau

meminumkan biaya.

Menentukan

fungsi

kendala

yang

ada

(batasan

yang

berkaitan

dengan

kasus).

Menyelesaikan

permasalahannya atau

persamaan fungsi

yang

ada

dengan persamaan atau petidaksamaan matematika.

Menentukan

titik-titik

yang

memenuhi

daerah

yang

memenuhi syarat.

Daerah

bagian

atas

yang

dibatasi

titik-titik

merupakan

daerah

minimum dan

daerah

bawah

yang dibatasi titik-titik

merupakan daerah

maksimum.

2.2.7

Penerapan dari Program Linear

Semua

organisasi

harus membuat

keputusan

bagaimana

mengalokasikan

sumber-sumbernya,

dan

tiada

organisasi yang

beroperasi

secara

permanent

dengan

sumber yang

tidak

terbatas,

akibatnya manajemen harus secara

terus-

menerus

mengalokasikan

sumber

yang

langka

untuk

mencapai

tujuan

organisasi,

bagaimanapun caranya.

Dan

organisasi bisa

mencapai banyak

tujuan ini.

Beberapa contoh dari penerapan program linear:

Sebuah

bank

hendak

mengalokasikan

dananya

untuk

mencapai

kemungkinan hasil

tertinggi.

Ia harus beroperasi

dalam

peraturan

likuiditas

yang

dibuat pemerintah, dan

harus

mampu

menjaga

fleksibilitas

yang

memadai untuk memenuhi permintaan pinjaman daripada nasabahnya.

Agen

periklanan juga

harus mencapai kemungkinan

terbaik bagi

nasabah

produknya

dengan

biaya

advertising terendah.

Ada

berlusinan

kemungkinan

yang

dapat

jadikan tempat,

masing-masing

dengan

tarif

dan pembaca yang berbeda.

Perusahaan

mebel

juga

harus

memaksimumkan

labanya.

Kedua

departemennya

menghadapi

batas waktu produksi yang

tidak

bisa ditawar

untuk memenuhi permintaan para pelanggannya.

Membuat

suatu

jadwal

produksi

yang

akan

mencukupi permintaan di

masa

mendatang akan suatu produk perusahaan dan

pada saat yang

bersamaan

meminimalkan biaya persediaan dan biaya produksi total.

Memilih

bauran

produk pada

suatu pabrik untuk

memanfaatkan

penggunaan mesin

dan

jam

kerja

yang

tersedia sebaik

mungkin

selagi

memaksimalkan laba perusahaan.

Mengalokasikan ruangan untuk para penyewa yang bercampur dalam

pusat

pembelanjaan

baru untuk

memaksimalkan

pendapatan

perusahaan

penyewaan.

Tiap

organisasi mencoba untuk mencapai tujuan

tertentu

(tingkat hasil atau

pendapatan maximum dengan biaya

minimum) sesuai

dengan

batasan sumber

(tabungan, anggaran advertensi nasabah, tersedianya bahan-bahan).

2.3 Metode Simpleks (

Simplex Method)

2.3.1 Sejarah Metode Simpleks

Metode

ini

kembangkan

oleh

George

Dantzig

pada

tahun

1946

dan

sepertinya cocok untuk komputerisasi

masa kini.

Pada tahun 1946,

Narendra

Karmarkar

dari Bell Laboratories

menemukan

suatu cara

untuk

memecahkan masalah-masalah program

linear yang lebih

besar,

sehingga

memperbaiki

dan

meningkatkan

hasil

dari metode simpleks. Metode ini

menyelesaikan

masalah program

linear

melalui perhitungan

berulang-ulang

(iteration)

dimana

langkah-langkah

perhitungan

yang

sama

diulang

berkali-kali

sebelum solusi optimum dicapai.

2.3.2 Pengertian Metode Simpleks

Metode simpleks

merupakan

prosedur

algoritma yang

digunakan

untuk

menghitung

dan

menyimpan

banyak angka

pada iterasi-iterasi yang

sekarang

dan

untuk pengambilan keputusan pada iterasi berikutnya.

Metode Simpleks

merupakan

suatu

metode

untuk

menyelesaikan masalah-masalah

program linear yang meliputi banyak pertidaksamaan dan banyak variabel.

Dalam

menggunakan

metode simpleks

untuk menyelesaikan masalah-

masalah program linear, model program linear harus diubah ke dalam suatu

bentuk umum yang dinamakan

”bentuk baku”. Ciri-ciri dari bentuk baku model

program

linear

adalah

semua

kendala berupa

persamaan

dengan

sisi

kanan non

negatif, fungsi tujuan dapat memaksimumkan atau meminimumkan.

Salah

satu

teknik

penentuan

solusi

optimal

yang

digunakan

dalam

pemrograman

linier

adalah

metode

simpleks.

Penentuan solusi optimal

menggunakan

metode

simpleks

didasarkan pada

teknik

eleminasi

Gauss

Jordan.

Penentuan

solusi

optimal

dilakukan

dengan memeriksa

titik

ekstrim

satu

per

satu

dengan

cara

perhitungan

iteratif. Sehingga

penentuan

solusi

optimal dengan

simpleks

dilakukan

tahap

demi

tahap

yang

disebut

dengan

iterasi.

Iterasi

ke-i

hanya tergantung dari iterasi sebelumnya.

2.3.3 Bentuk Baku dan

Bentuk Tabel Metode Simpleks

Sebelum

melakukan perhitungan

iteratif

untuk

menentukan solusi

optimal,

pertama

sekali

bentuk

umum

pemrograman

linier

diubah

dalam

bentuk

baku

terlebih dahulu. Bentuk baku dalam metode simpleks tidak hanya mengubah

persamaan

kendala

dalam

bentuk

sama

dengan,

tetapi

setiap

fungsi

kendala

harus

diwakili

oleh

satu

variabel

basis

awal.

Variabel

basis

awal

menunjukkan

status

sumber

daya

pada

kondisi

sebelum

ada

aktivitas

yang

dilakukan.

Dengan

kata

lain,

variabel

keputusan semuanya

masih bernilai

nol.

Dengan

demikian,

meskipun

fungsi

kendala

pada

bentuk

umum

pemrograman linier sudah

dalam

bentuk persamaan, fungsi kendala tersebut masih harus tetap berubah.

Ada

beberapa

hal

yang

harus

diperhatikan

dalam

membuat

bentuk

baku,

yaitu:

1. Fungsi

kendala

dengan

pertidaksamaan

dalam

bentuk

umum,

diubah

menjadi

persamaan

(=)

dengan

menambahkan satu

variabel

slack.

2. Fungsi

kendala

dengan

pertidaksamaan

dalam

bentuk

umum,

diubah menjadi persamaan (=) dengan mengurangkan satu variabel

surplus.

3. Fungsi

kendala dengan persamaan dalam

bentuk

umum,

ditambahkan

satu artificial variabel (variabel buatan).

Dalam

perhitungan

iterative, kita akan

bekerja

menggunakan

tabel.

Bentuk

baku yang sudah diperoleh, harus dibuat ke dalam bentuk tabel.

Semua

variabel

yang

bukan

variabel

basis

mempunyai

solusi

(nilai

kanan)

sama

dengan

nol

dan

koefisien

variabel

basis

pada

baris

tujuan

harus

sama

dengan 0. Oleh karena itu kita harus membedakan pembentukan tabel awal

berdasarkan

variabel basis awal.

Berikut adalah contoh kasus:

600,

Bentuk

ini

merupakan

bentuk

umum.

Perubahan

dalam

bentuk

baku hanya

membutuhkan

variabel

slack,

karena

semua

fungsi

kendala

menggunakan

bentuk

pertidaksamaan =

dalam

bentuk

umumnya.

Maka

bentuk

bakunya adalah sebagai berikut : 10 x1

+ 5 x2

+ s1

= 600

2.3.4 Tahap-Tahap Metode Simpleks

Berikut

adalah

tahap-tahap

dalam

menyelesaikan

program

linear

dengan

metode simpleks:

Periksa apakah tabel layak atau tidak.

Kelayakan tabel simpleks dilihat dari solusi

(nilai

kanan).

Jika

solusi ada

yang bernilai negatif, maka

tabel tidak

layak. Tabel

yang tidak layak tidak dapat diteruskan untuk dioptimalkan.

2. Tentukan kolom pivot. Penentuan kolom pivot dilihat dari koefisien fungsi

tujuan

(nilai

sebelah

kanan

baris

dan

tergantung

dari bentuk

tujuan. Jika tujuan

maksimisasi,

maka

kolom

pivot

adalah

kolom

dengan

koefisien

paling

negatif.

Jika tujuan minimisasi, maka kolom pivot adalah kolom dengan koefisien positif

terbesar.

Jika

kolom

pivot

ditandai dan

ditarik

atas,

maka

kita

akan

mendapatkan variabel keluar.

Jika nilai

paling negatif (untuk tujuan maksimisasi)

atau

positif

terbesar

(untuk

tujuan

minimisasi)

lebih

dari

satu,

pilih

salah

satu

secara sembarang.

3. Tentukan baris

pivot.

Baris

pivot ditentukan

setelah

membagi

nilai solusi dengan

nilai

kolom pivot

yang

bersesuaian

(nilai yang

terletak

dalam satu baris).

Dalam

hal

ini,

nilai

negatif dan 0 pada

kolom

pivot

tidak

diperhatikan, artinya

tidak

ikut

menjadi

pembagi.

Baris pivot adalah

baris

dengan rasio

pembagian

terkecil.

Jika

baris

pivot

ditandai

dan

ditarik

kiri,

maka

kita

akan

mendapatkan

variabel

keluar.

Jika

rasio

pembagian

terkecil lebih

dari

satu,

pilih

salah

sau secara

sembarang.

Tentukan

elemen

pivot. Elemen

pivot merupakan nilai

yang

terletak

pada

perpotongan kolom dan baris pivot.

Bentuk tabel simpleks baru. Tabel simpleks baru

dibentuk dengan pertama sekali

menghitung nilai

baris pivot

baru.

Baris

pivot

baru adalah baris

pivot lama dibagi

dengan elemen pivot. Baris baru lainnya merupakan pengurangan nilai kolom

pivot

baris

yang

bersangkutan dikali

baris

pivot baru dalam satu kolom

terhadap

baris lamanya yang terletak pada kolom tersebut.

6. Periksa

apakah

tabel

sudah

optimal.

Keoptimalan

tabel

dilihat

dari

koefisien

fungsi

tujuan

(nilai

pada

baris

dan

tergantung

dari

bentuk

tujuan.

Untuk

tujuan

maksimisasi,

tabel

sudah

optimal

jika

semua

nilai

pada

baris

sudah

positif atau

0. Pada

tujuan minimisasi,

tabel sudah optimal jika semua

nilai pada

baris

z sudah negatif

atau 0.

Jika

belum,

kembali ke

langkah no.

jika sudah

optimal baca solusi optimalnya.

2.3.5 Metode Revised Simplex

(Metode Simpleks yang diperbaiki)

Metode

ini

didesain

untuk mencapai

hal

yang

tepat

seperti

pada

metode

simpleks

yang

asli. Metode

ini

menghitung

dan

menyimpan

hanya

informasi yang

diperlukan

sekarang

dan

data

yang

penting

disimpan

dalam

bentuk

lebih

padat.

Metode

revised

simplex

secara eksplisit memakai manipulasi

matriks

maka masalah

harus dinyatakan dalam notasi matriks.

2.3.6 Istilah-Istilah dalam Metode Simpleks

Ada

beberapa

istilah

yang sangat

sering

digunakan dalam metode

simpleks,

diantaranya :

•

Iterasi adalah

tahapan

perhitungan

dimana

nilai

dalam perhitungan

itu

tergantung dari nilai tabel sebelumnya.

•

Variabel

non

basis

adalah

variabel

yang

nilainya

diatur

menjadi

nol

pada sembarang iterasi. Dalam terminologi umum, jumlah variabel non

basis selalu sama dengan derajat bebas

dalam sistem persamaan.

•

Variabel

basis

merupakan

variabel

yang

nilainya

bukan nol

pada

sembarang

iterasi.

Pada

solusi awal,

variabel

basis merupakan variabel

slack

(jika

fungsi

kendala merupakan

pertidaksamaan =

)

atau

variabel

buatan

(jika

fungsi

kendala

menggunakan

pertidaksamaan

atau

=).

Secara

umum, jumlah

variabel basis selalu sama

dengan

jumlah fungsi

pembatas (tanpa fungsi non negatif).

•

Solusi

atau

nilai

kanan

merupakan

nilai

sumber

daya

pembatas yang

masih

tersedia.

Pada

solusi

awal,

nilai

kanan

atau solusi

sama

dengan

jumlah

sumber

daya

pembatas

awal

yang

ada,

karena

aktivitas

belum

dilaksanakan.

•

Variabel

slack

adalah

variabel yang ditambahkan

model

matematik

kendala

untuk mengkonversikan

pertidaksamaan

menjadi

persamaan

(=).

Penambahan

variabel ini

terjadi pada

tahap

inisialisasi.

Pada solusi

awal, variabel slack akan berfungsi sebagai variabel basis.

•

Variabel

surplus

adalah

variabel

yang

dikurangkan dari

model

matematik

kendala

untuk

mengkonversikan

pertidaksamaan

menjadi

persamaan

(=).

Penambahan

ini

terjadi

pada

tahap

inisialisasi.

Pada

solusi awal, variabel surplus tidak dapat berfungsi sebagai variabel basis.

•

Variabel

buatan

adalah

variabel

yang ditambahkan ke model

matematik

kendala

dengan

bentuk =

atau

untuk

difungsikan

sebagai

variabel basis awal. Penambahan variabel ini

terjadi pada tahap

inisialisasi.

Variabel

ini

harus

bernilai 0

pada

solusi

optimal,

karena

kenyataannya variabel ini tidak ada. Variabel hanya ada di atas kertas.

•

Kolom

pivot

(kolom

kerja)

adalah

kolom yang memuat

variabel

masuk.

Koefisien

pada

kolom

ini

akan

menjadi

pembagi

nilai

kanan

untuk menentukan baris pivot (baris kerja).

•

Baris

pivot

(baris

kerja)

adalah salah

satu

baris dari

antara

variabel

basis yang memuat variabel keluar.

•

Elemen

pivot

(elemen

kerja)

adalah elemen yang terletak pada

perpotongan kolom

dan

baris

pivot. Elemen

pivot

akan

menjadi dasar

perhitungan untuk tabel simpleks berikutnya.

•

Variabel

masuk

adalah

variabel

yang

terpilih

untuk

menjadi

variabel

basis

pada

iterasi

berikutnya.

Variabel masuk

dipilih

satu

dari antara

variabel non basis pada

setiap

iterasi. Variabel ini pada

iterasi

berikutnya

akan bernilai positif.

•

Variabel

keluar

adalah

variabel

yang

keluar

dari

variabel

basis

pada

iterasi

berikutnya

dan

digantikan

oleh variabel

masuk.

Variabel

keluar

dipilih

satu

dari

antara

variabel

basis

pada

setiap

iterasi.

Variabel

ini

pada iterasi berikutnya akan bernilai nol.

2.4 Produksi (

Production)

2.4.1 Pengertian Produksi

Dalam

kehidupan

sehari-hari,

apabila

kita

mendengar

kata

produksi,

maka

yang

terbayang

pikiran kita adalah suatu

kegiatan

besar

yang

memerlukan

peralatan

yang

serba

canggih,

serta menggunakan

ribuan

tenaga

kerja

untuk

mengerjakannya. Sebenarnya dugaan tersebut tidak benar.

Produksi artinya, kegiatan

menambah

nilai

guna

suatu

barang atau jasa untuk

keperluan

orang

banyak.

Dari

pengertian

diatas

dapat

ditarik suatu

kesimpulan

bahwa,

tidak semua

kegiatan

yang

menambah

nilai

guna

suatu

barang

dapat

dikatakan proses produksi.

Produksi

adalah suatu kegiatan

yang menghasilkan

output dalam

bentuk

barang

maupun

jasa.

Contoh:

pabrik

baterai

yang

memproduksi batu

baterai,

tukang

mie ayam

yang membuat

mie

yamin,

tukang

pijet

yang

memberikan

pelayanan jasa pijat dan urut kepada para pelanggannya, dan lain sebagainya.

2.4.2 Kegunaan Produksi

Salah satu

yang

dilakukan

dalam proses

produksi ialah menambah

nilai guna

suatu barang atau jasa.

Dalam

kegiatan menambah nilai

guna

barang atau

jasa

ini, dikenal lima jenis kegunaan, yaitu :

1. Guna bentuk

Yang

dimaksud dengan guna

bentuk yaitu, didalam melakukan

proses

produksi,

kegiatannya ialah

merubah

bentuk

suatu

barang sehingga

barang

tersebut

mempunyai nilai ekonomis. Contohnya: keramik.

2. Guna jasa

Guna jasa ialah kegiatan produksi yang memberikan pelayanan jasa. Contohnya:

tukang becak, buruh, dll.

3. Guna tempat

Guna

tempat adalah kegiata

produksi yang

memanfaatkan tempat-

tempat

dimana suatu

barang

memiliki nilai ekonomis.

Contoh:

pengangkutan

pasir dari

tempat

yang pasirnya

melimpah

ketempat

dimana

orang

membutuhkan

pasir

tersebut.

4. Guna waktu

Guna

waktu

ialah

kegiatan

produksi yag

memanfaatkan

waktu-

tertentu.

Misalnya: pembelian

beras

yang

dilakukan

oleh

Bulog

pada saat

musim

panen,

dan dijual kembali pada saat masyarakat membutuhkan.

5. Guna milik

Guna

milik

ialah,

kegiatan

produksi

yang

memanfaatkan

modal

yang

dimiliki

untuk dikelola orang lain dan dari hasil tersebut ia mendapatkan keuntungan.

2.5 Biji Plastik

2.5.1 Pengertian Biji Plastik

Plastik

merupakan

bahan baru

yang semakin

berkembang.

Dewasa ini,

plastik banyak

digunakan untuk berbagai macam bahan

dasar.

Penggunaan

plastik

dapat

dipakai

sebagai

bahan pengemas,

konstruksi,

elektroteknik,

automotif, mebel, pertanian, peralatan rumah tangga, bahan

pesawat, kapal

mainan

dan

lain sebagainya.

Penggunaan

plastik di

berbagai

bidang seperti

atas

dasarkan

pada

alasan

bahwa

bahan

plastik

mempunyai

keunggulan dibandingkan

dengan

bahan

lain

antara

lain, seperti tidak

mudah

berkarat,

kuat,

tidak

mudah

pecah,

ringan,

dan

elastis.

Ada

beberapa

proses

yang

terjadi

pada

industri

plastik,

yaitu

bahan

dasar

biji

plastik mengalami pemanasan,

kemudian

dikirim

tempat

pembentukan.

Pembentukan

bisa

dilakukan

dengan

berbagai

cara

antara

lain:

pencetakan,

pengepresan,

dan pembentukan

dengan

pemanasan

atau

dengan

vakum.

Setelah mengalami

pembentukan,

selanjutnya

dilakukan

proses

pendinginan.

Proses

ini

bertujuan

agar

plastik yang

sudah terbentuk

tidak mengalami perubahan bentuk lagi.

2.5.2 Jenis-Jenis Biji Plastik

Secara umum plastik dikategorikan menjadi dua kelompok yaitu :

1. Thermo Halus

Thermo

halus

adalah

plastik

yang

mempunyai

sifat

apabila

dipanaskan

akan menjadi halus. Jenis plastik ini sering kita

gunakan

karena sifat plastik

ini mudah dibentuk sesuai keinginan kita.

2. Thermo Kasar

Thermo

kasar

adalah

plastik

yang

mempunyai

sifat apabila

dipanaskan

akan

menjadi keras

dan

tidak

akan

menjadi

lunak. Jenis

plastik

ini

sering

digunakan

pada

industri-industri

besar dan

juga

digunakan

pada

pesawat

ruang angkasa.

Selain pengelompokan plastik seperti di atas, plastik secara komersial dikenal

dengan

berbagai

macam nama.

Penamaan

ini

dibuat

berdasarkan

bahan

penyusunnya.

Jenis-jenis plastik tersebut adalah :

a. Polyetheen (PE).

b. Poly Vinyl Chlorida (PVC).

c. Poly Propylen

(PP)

d. Poly Methil Meth Acrylaat (PMMA)

e. Acrylonitrit butadieen Styreen (ABS).

f. Poly Amide (PA).

g. Polyester (Cairan pengeras dan perapat).

h. Poly Ethen Three (PET).

Masing-masing jenis plastik di atas mempunyai karakteristik yang berbeda.

Berikut ini beberapa karakteristik jenis-jenis plastik.

1. Polyetheen lunak,

Bersifat mengambang di air, mudah dibentuk, kalau dibakar terjadi

tetesan

api, asap warna hitam dan

bau seperti lilin.

Poly Methil Meth Acrylaat (PMMA),

Bersifat tenggelam di air, mudah terbakar, kalau dibakar terjadi percikan api,

bau sedikit manis, dan nyala api kuning kebiru-biruan.

3. Polystreen

(PS),

Bersifat tenggelam di air, mudah terbakar, asap tebal, dan nyala api oranye

kekuningan.

Poly Vynil Chlorida (PVC) lunak,

Bersifat tenggelam di air, relatif sulit dibakar, bau menyengat dan menusuk

(keasam-asaman),

dan mudah dibentuk.

Poly Vynil Chlorida (PVC) keras,

Bersifat tenggelam di air, relatif sulit dibakar, bau menyengat dan menusuk

(keasam-asaman), dan susah dibentuk.

Yang digunakan untuk injection gesper plastik adalah Poly Propylen (PP)

karena bahan dibentuk sesuai dengan cetakan dan bisa mengeras setelah

diinject.

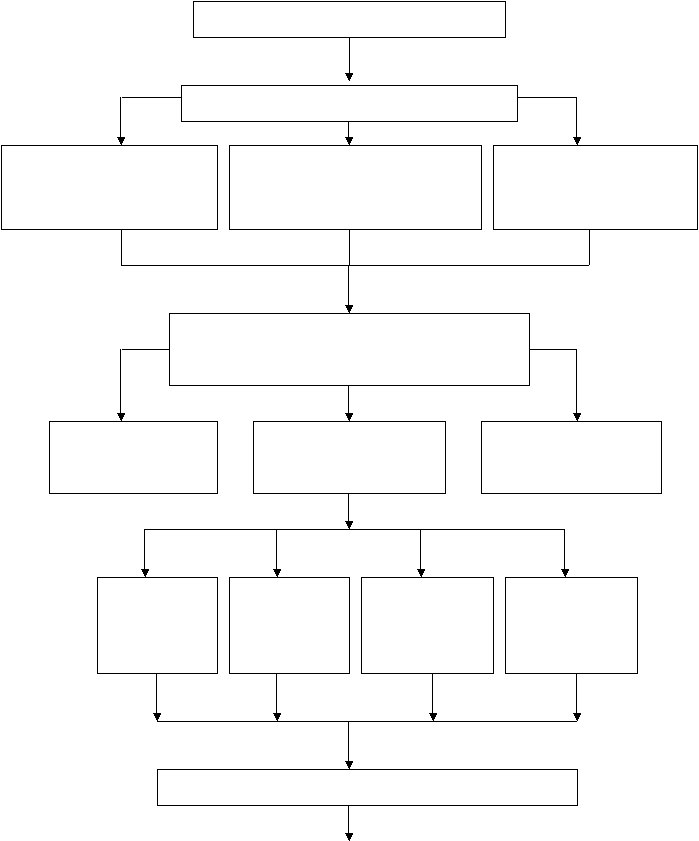
2.6 Kerangka Pemikiran

Input

Identifikasi Permasalahan

kendala-kendala yang ada

dalam memproduksi variasi

gesper plastik agar

memperoleh laba maksimal

jumlah produksi yang optimal

untuk variasi gesper plastik agar

sesuai dengan kapasitas produksi

yang dimiliki oleh perusahaan

hasil produksi variasi

gesper plastik dan laba

maksimal yang dapat

dicapai

Menganalisis dan memformulasikan masalah

dalam Program Linear (Linear Programming)

Menetapkan Variabel

Keputusan

Menetapkan Fungsi

Kendala

Menetapkan Fungsi

Tujuan

Jumlah

Bahan

Baku

Jumlah

jam

kerja mesin

Jumlah

jam

kerja tenaga

kerja

Permintaan

masing-masing

Produk

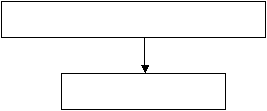
Membuat Perhitungan dengan Metode Simpleks

Solusi Optimal

Output

Sumber : Kerangka Pemikiran Penulisan Skripsi