|
BAB 2
LANDASAN TEORI
Teorema
Shannon-Nyquist
menyatakan agar
tidak
ada
informasi
yang
hilang
ketika
pencuplikan
sinyal,
maka
kecepatan
pencuplikan
harus
minimal
dua
kali
dari
lebar pita sinyal tersebut. Pada kebanyakan aplikasi, termasuk kamera digital video dan
citra,
nilai Nyquist-rate sangat tinggi sehingga
menghasilkan jumlah data yang banyak
sehingga pemampatan sangat diperlukan sebelum data
disimpan atau
dikirimkan. Pada
aplikasi-aplikasi lain
seperti
pencitraan
medis
dan
high-speed
ADC
meningkatkan
kecepatan pencuplikan memerlukan biaya yang sangat mahal.
2.1
Representasi dan Aproksimasi
Representasi adalah
bagaimana
menyatakan suatu
sinyal
dalam
basis
pembentuknya. Representasi sinyal satu dimensi adalah menyatakan suatu sinyal
satu dimensi dalam basis pembentuknya. Representasi tidak
mengubah banyak
data sinyal asli. Representasi dilakukan dengan harapan suatu sinyal dinyatakan
dalam
basis
pembentuk
yang
tepat
sehingga
menghasilkan pemampatan
atau
sparsity. Dengan sparsity maka
hanya sebagian nilai koefisien yang besar
yang
memuat sebagian besar informasi dari sinyal. Sedangkan sebagian besar lainnya
memiliki nilai
koefisien
yang
kecil
yang
tidak
memuat
informasi
dari
sinyal
sehingga dapat dihilangkan.
7
|
|
8
N
?
N
?
Rumus representasi adalah sebagai berikut:
f
=
?
a ?
i
i
i?I
………(1)
Dimana :
f
:
suatu sinyal
a
i
:
koefisien
?
i
:
basis
Basis
dalam suatu
transformasi berguna
untuk
merepresentasikan sebuah
sinyal
dan
nilai.
Misalkan
pada
fourier
transform
yang
memiliki
basis
sinus
maka dapat dikatakan bahwa
sinyal
yang dihasilkan
akan berbentuk sinus dan
memiliki nilai-nilai tertentu. Basis sinus digunakan juga pada teorema sampling
yang
dapat
merepresentasikan setiap
fungsi
yang
dibatasi (finite
function)
dan
prosesnya
dapat
diselesaikan dengan
sampel-sampel. Selain
itu
basis
juga
berpengaruh dalam
aproksimasi. Basis
yang
berbeda
dapat
memberikan
nilai
aproksimasi yang berbeda pula.
Aproksimasi
merupakan pendekatan dalam
mengambil suatu
data.
Data
yang
diambil
hanya
sebagian
sedangkan sisa
datanya
dijadikan
nol.
Ketika
melakukan aproksimasi maka
akan terdapat selisih antara data asli dengan data
yang diaproksimasi. Selisih ini yang dikenal dengan sebutan norm error. Berikut
adalah bentuk persamaannya
[7]
:
f
(t)
-
f
ˆ
(t )
2
?
8
=
?
?
?
-8
f
(t)
-
f
ˆ
(t ) 2
?
dt
?
?
1 2
/ 2
………(2)
|
|
9
Aproksimasi dapat dibedakan menjadi dua jenis yaitu:
•
Aproksimasi linier
Pada aproksimasi linier sebagian data
yang diambil adalah data
yang
terletak
di
bagian
depan
sedangkan
sisanya
dijadikan
nol.
Banyak
data
yang diambil
tergantung
dari
persentase
data
yang diinginkan.
Contohnya dapat dilihat di bawah ini:
Misalkan terdapat data sinyal input: - 0,03 - 0,01
-
0,07 - 0,02
0,12 0,01 0,08 - 0,43 - 0,27 0,09
Bila
persentase
data
yang diinginkan
adalah
20
%
maka data
yang
diambil adalah sebanyak 2 data. Hal ini didapat dari 20 % dikalikan
dengan
banyaknya jumlah
data
sinyal
input.
Dari
contoh
di
atas
jumlah
data
sinyal
input
adalah
sebanyak 10
data.
Jadi
data
yang
diambil = 20 % x 10 = 2 data.
Sehingga data sinyal input akan menjadi: - 0,03 - 0,01 0 0 0 0 0 0
0 0
•
Aproksimasi nonlinier
Pada
aproksimasi
nonlinier
sebagian data
yang
diambil
adalah
data
yang paling besar setelah data-data
tersebut diabsolutkan. Data-data
yang
tidak
diambil
dijadikan
nol.
Sama
seperti
aproksimasi linier
banyak data yang diambil pada aproksimasi nonlinier tergantung dari
|
|
10
persentase
data
yang
diinginkan.
Contohnya
dapat
dilihat
di
bawah
ini:
Misalkan terdapat data sinyal input: - 0,03 - 0,01
-
0,07 - 0,02
0,12 0,01 0,08 - 0,43 - 0,27 0,09
Berikut adalah data sinyal input di atas yang telah diabsolutkan:
0,03 0,01 0,07 0,02 0,12 0,01 0,08 0,43 0,27 0,09
Bila
persentase
data
yang diinginkan
adalah
40
%
maka data
yang
diambil adalah sebanyak 4 data. Hal ini didapat dari 40 % dikalikan
dengan
banyaknya jumlah
data
sinyal
input.
Dari
contoh
di
atas
jumlah
data
sinyal
input
adalah
sebanyak 10
data.
Jadi
data
yang
diambil = 40 % x 10 = 4 data.
Sehingga data sinyal input akan menjadi: 0 0 0 0 0,12 0 0 - 0,43
-
0,27 0,09
2.2
Sparsity
Kebanyakan sinyal
alami
memiliki
representasi
yang
padat
ketika
dinyatakan ke dalam basis yang tepat. Sebagai contoh, pada Gambar 2.1 (a) dan
transformasi wavelet-nya pada Gambar 2.1 (b). Walaupun hampir seluruh
piksel citra
memiliki
nilai
tidak
nol,
namun kebanyakan koefisien wavelet-nya
bernilai
kecil dan
hanya
sedikit
koefisien
yang bernilai
besar
dimana
memuat
sebagian besar informasi dari citra.
|
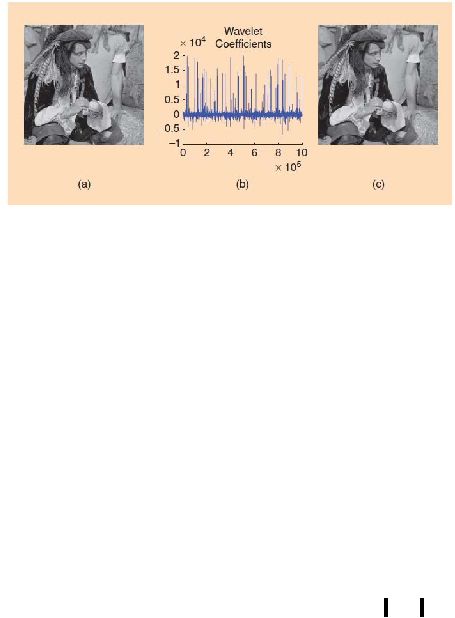 11
Gambar 2.1
(a) Citra asli berukuran 1 Megapiksel.
(b) Koefisien-koefisien wavelet.
(c) Rekontruksi citra yang didapatkan dengan hanya menggunakan 25.000
koefisien wavelet terbesar.
Secara
matematik,
jika
suatu
vektor
x
?
R
n
yang
direpresentasikan
menggunakan basis orthonormal (misalnya basis wavelet)
?
=
[? ?
1
2
...
?
N
]
seperti persamaan berikut:
N
x
=
?
s
i
?
i
(t
)
i
=1
………(3)
Dimana s
i
adalah koefisien dari x didapatkan dari,
s
i
=
x,
?
i
,
biasanya
(3) dituliskan dalam bentuk matriks
x
=
?
s
(dimana
?
adalah matriks
N
×
N
sedangkan x dan s berupa vektor kolom
N
×
1
). Sinyal x dikatakan K-sparse jika
hanya K dari koefisien-koefisien s bernilai tidak nol sedangkan sejumlah (N-K)
koefisien bernilai nol. Jika
K
<<
N
,
maka sinyal x dikatakan compressible
[8]
.
Dengan
hanya
mengambil koefisien-koefisien bernilai besar dan mengabaikan
sisanya menjadi prinsip dasar pemampatan data seperti JPEG-2000 dan standar
|
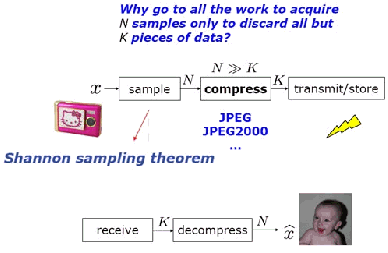 12
pemampatan data
lainnya
[9]
.
Teknik
pemampatan data
seperti
di
atas
disebut
dengan
transform-coding,
walaupun
memberikan
pemampatan
data
yang
baik
dan
digunakan
pada
banyak
standar
pemampatan saat
ini,
namun
memiliki
ketidakefisien-an yaitu
pertama
jumlah
data
semula
N
mungkin
sangat
besar
walaupun jumlah K kecil, ke-dua seluruh N koefisien transformasi harus dihitung
walaupun nantinya hanya sejumlah K koefisien terbesar yang diambil sedangkan
sisanya dibuang, ke-tiga lokasi dari K koefisien terbesar tersebut harus disimpan,
Gambar 2.2 memperlihatkan ketidakefisien-an tersebut
[10]
.
Gambar 2.2 Blok diagram standar transform-coding yang saat ini digunakan.
2.3
Fourier Transform (Transformasi Fourier)
Diperkenalkan pertama kali oleh Jean Baptiste Joseph Fourier pada tahun
1807.
Dia
menyatakan bahwa
semua
sinyal
periodik
yang
kontinu
dapat
dinyatakan
sebagai
jumlah
dari
sinyal-sinyal sinusoidal
dengan
frekuensi,
amplitudo, dan fasa yang tertentu
[11][12]
.
Dengan fourier transform, suatu sinyal
|
|
13
dalam domain waktu dapat direpresentasikan ke dalam domain frekuensi. Nilai-
nilai
frekuensi
dari sinyal
tersebut
dapat
diketahui setelah direpresentasikan ke
dalam domain frekuensi.
Namun
dalam
domain
frekuensi tidak
terdapat
informasi waktu
kapan
frekuensi-frekuensi tersebut
muncul.
Karena
hal
inilah
maka fourier transform
hanya cocok
untuk sinyal stasioner dan
tidak cocok
untuk sinyal
non-stasioner.
Hal
ini
disebabkan fourier
transform
menganalisa sinyal
dalam
keseluruhan
waktu
(dari
awal
sampling
hingga
akhir
sampling) sehingga muncul
asumsi
bahwa
informasi
frekuensi
sinyal
tersebut
terjadi
dalam
setiap
waktu.
Padahal
belum tentu
frekuensi-frekuensi tersebut terjadi dalam setiap waktu pada sinyal
tersebut.
Inilah
yang
menjadi
kekurangan dari
fourier
transform
dalam
menganalisa suatu sinyal.
2.4
Discrete Cosine Tansform (DCT)
Discrete Cosine Transform (DCT) merupakan suatu teknik yang digunakan
untuk melakukan konversi
sinyal ke
dalam komponen
frekuensi pembentuknya
dengan
cara
memperhitungkan
nilai
riil
dari
hasil
transformasinya.
Dari
namanya dapat
diketahui bahwa DCT
hanya
menggunakan
gelombang cosinus
(cosine waves). DCT merupakan transformasi yang berhubungan dengan fourier
transform, namun DCT hanya menggunakan bilangan-bilangan riilnya
[13]
.
DCT
dapat dikelompokkan menjadi dua yaitu DCT maju dan DCT balik.
|
 14
N
N
2.4.1
Discrete Cosine Transform Maju (Forward DCT)
Persamaan forward DCT yang digunakan yaitu:
y(k ) =
w(k )
?
x(n)
cos
p
(2n - 1)(k - 1)
,
k
=
1,..., N
……….(4)
n
=1
2N
Dimana
?
?
w(k )
=
?
1
,
k
=
1
N
………(5)
?
2
, 2
?
?
N
=
k
=
N
N
adalah panjang dari x(n), x(n) adalah
nilai sinyal asli, y(k) adalah nilai dari
forward DCT, x(n) dan y(k) mempunyai ukuran yang sama.
2.4.2
Discrete Cosine Transform Balik (Inverse DCT)
Pada inverse DCT dilakukan proses rekonstruksi yaitu mengembalikan
komponen frekuensi menjadi komponen sinyal semula. Persamaan yang
digunakan yaitu:
x(n)
=
?
w(k ) y(k )
cos
p
(2n
-
1)(k
-
1)
,
n
=
1,..., N
………(6)
k
=1
2N
Dimana
?
?
w(k )
=
?
1
,
k
=
1
N
?
2
, 2
?
?
N
=
k
=
N
|
|
15
N
adalah panjang dari y(k), y(k) adalah nilai dari forward DCT, x(n) adalah nilai
dari inverse DCT, x(n) dan y(k) mempunyai ukuran yang sama.
2.5
Wavelet Transform (Transformasi Wavelet)
Dengan berkembangnya teknik-teknik analisa sinyal maka muncullah suatu
konsep baru yang dapat mengatasi kekurangan dari fourier transform dan teknik
analisa sinyal tersebut dinamakan dengan Wavelet Transform. Wavelet transform
mulai diperkenalkan pada tahun 1980-an oleh Morlet
dan Grossman sebagai
fungsi matematis untuk merepresentasikan data atau fungsi sebagai alternatif
transformasi-transformasi matematika yang lahir sebelumnya untuk menangani
masalah
resolusi.
Sebuah wavelet merupakan
gelombang
singkat (small
wave)
yang
energinya
terkonsentrasi
pada suatu selang waktu untuk memberikan
kemampuan
analisis
transien, ketidakstasioneran, atau fenomena
berubah
terhadap
waktu
(time
varying).
Karakteristik
dari
wavelet
antara
lain adalah
berosilasi singkat, translasi (pergeseran), dan dilatasi (skala).
Wavelet transform
memiliki
kemampuan
untuk
menganalisa
suatu data
dalam domain waktu dan domain frekuensi secara bersamaan. Analisa data pada
wavelet transform dilakukan dengan
mendekomposisikan suatu sinyal ke dalam
komponen-komponen frekuensi yang berbeda-beda dan selanjutnya masing-
masing komponen frekuensi tersebut dapat dianalisa sesuai dengan skala
resolusinya
atau
level
dekomposisinya.
Hal
ini
seperti
proses filtering,
dimana
sinyal dalam domain waktu dilewatkan ke dalam low-pass filter (LPF) dan high-
|
|
16
pass filter (HPF) untuk memisahkan komponen frekuensi tinggi dan frekuensi
rendah
[14]
. Tahap pertama analisis wavelet adalah menentukan tipe wavelet atau
mother wavelet yang akan digunakan. Hal ini perlu dilakukan karena fungsi
wavelet
sangat
bervariasi.
Beberapa
contoh mother
wavelet
adalah
Haar,
Daubechies, Biortoghonal, Coiflets, Symlets, Morlet, Mexican
Hat, dan Meyer.
Setelah pemilihan mother
wavelet,
tahap selanjutnya adalah
membentuk
basis
wavelet yang akan digunakan untuk mentransformasikan sinyal.
Berdasarkan jenis sinyal yang diprosesnya, wavelet transform dapat dibagi
menjadi
dua
bagian
besar,
yaitu Continuous Wavelet Transform (CWT)
dan
Discrete Wavelet Transform (DWT).
2.5.1
Discrete Wavelet Transform (Transformasi Wavelet Diskrit)
Discrete wavelet transform (DWT) secara
umum
merupakan dekomposisi
sinyal
pada
frekuensi subband
sinyal
tersebut.
Komponen
subband
wavelet
transform dihasilkan dengan
cara penurunan level
dekomposisi.
Implementasi
DWT dapat dilakukan dengan cara
melewatkan
sinyal
melalui sebuah LPF dan
HPF serta melakukan downsampling pada keluaran masing-masing filter seperti
yang ditunjukkan pada Gambar 2.3
[15]
.
|
 17
Gambar 2.3 Proses DWT.
Dimana :
x[n]
: Sinyal asli
g[n]
: Low-Pass Filter (LPF)
h[n]
: High-Pass Filter (HPF)
Keluaran dari
LPF
merupakan
koefisien
aproksimasi
dari
DWT
dan
keluaran dari HPF merupakan koefisien detail dari DWT. DWT yang digunakan
dalam penelitian ini adalah Lifting Wavelet Transform (LWT).
2.5.2
Lifting Wavelet Transform (Transformasi Wavelet Lifting)
Lifting wavelet transform (LWT) adalah salah satu bagian dari
DWT
yang
dikenalkan
oleh
Wim Sweldens.
LWT
ini
kemudian
disebut
sebagai
generasi
kedua
DWT.
Pada
DWT dilakukan proses beberapa filter secara terpisah,
sedangkan dengan LWT operasi proses dibagi dan diproses secara bersamaan
[16]
.
Proses pada LWT dinamakan dengan Predict (P) dan Update (U).
|
 18
Gambar 2.4 Proses LWT.
Dapat dilihat pada Gambar
2.4
bahwa pada proses LWT, proses Predict
(P) dan Update (U) dibagi menjadi dua bagian dan diproses
secara bersamaan.
Cara kerja LWT seperti inilah yang membuat teknik ini lebih efisien
dibandingkan
dengan
DWT.
Dalam
penelitian
ini,
tipe wavelet
atau
mother
wavelet yang akan digunakan adalah jenis Biortoghonal 4.4.
2.5.2.1 Lifting Wavelet Transform Maju (Forward LWT)
Gambar 2.5 Skema Lifting Wavelet Transform Maju.
Proses forward LWT adalah dengan membagi (split) sinyal Sj yang masuk
ke dalam 2 tahap
yaitu untuk
ganjil (even
j+1
)
dan genap (odd
j+1
). Dimana pada
|
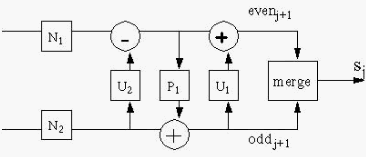 19
tahap ganjil (even
j+1
)
diambil nilai sinyal dari S
0
sampai (S/2)-1, sedangkan pada
tahap genap (odd
j+1
) diambil
nilai sinyal dari (S/2)-1 sampai Sj-1. Tahap
ganjil
dilakukan dengan koefisien Predict (P) sedangkan tahap genap dilakukan dengan
koefisien Update (U).
2.5.2.2 Lifting Wavelet Transform Balik (Inverse LWT)
Gambar 2.6 Skema Lifting Wavelet Transform Balik.
Inverse LWT adalah proses rekonstruksi yaitu mengembalikan komponen
frekuensi menjadi komponen sinyal semula.
2.6
Mean Square Error (MSE)
Mean
Square
Error (MSE)
merupakan
ukuran kontrol kualitas yang
digunakan untuk mengetahui kualitas
dari
suatu proses. MSE menghitung
seberapa besar pergeseran data antara sinyal sumber dan sinyal hasil keluaran,
dimana
sinyal
sumber
dan
sinyal
hasil
keluaran
memiliki
ukuran
yang
sama.
Nilai MSE yang baik adalah mendekati nol (MSE ˜ 0).
|
|
20
n
2
Rumus dari perhitungan MSE adalah
[17]
:
1
n
MSE =
?
(S -
S
e
)
………(7)
i
=
1
Dimana :
MSE
: Mean Square Error
S
: Sinyal sumber
S
e
: Sinyal Hasil Keluaran
n
: Panjang sinyal
2.7
Peak Signal to Noise Ratio (PSNR)
Peak
Signal
to
Noise
Ratio (PSNR)
adalah
perbandingan
antara
nilai
maksimum sinyal sumber dengan nilai rata-rata kuadrat error (MSE). Nilai
PSNR
yang baik
adalah tak hingga (PSNR ˜
8). PSNR dihitung dalam satuan
desibel (dB). Desibel adalah satuan yang seringkali digunakan dalam
menyatakan
perbedaan
relatif
kekuatan
sinyal. Desibel dinyatakan
sebagai
logaritmik basis 10 yang merupakan rasio dari dua sinyal.
|
|
21
Rumus dari perhitungan PSNR adalah
[18]
:
PSNR(dB) = 10 x log
10
Max sinyal²
MSE
………(8)
Dimana :
PSNR(dB)
: Peak Signal to Noise Ratio dalam desibel
Max Sinyal
: Nilai maksimum sinyal sumber
MSE
: Mean Square Error
|