|
BAB II
TINJAUAN PUSTAKA
2.1
Infiltrasi
Infiltrasi adalah proses masuknya air dari atas ( Surface ) kedalam tanah.
Didalam tanah air mengalir dalam arah lateral, sebagai aliran antara ( interflow ) menuju
mata
air
danau
dan
sungai;
atau
secara
vertikal, yang
dikenal
dengan
perkolasi
(percolation) menuju
air
tanah.
Gerak
air
di
dalam
tanah
melalui
pori
–
pori
tanah
dipengaruhi
oleh
gaya
gravitasi
dan
gaya
kapiler.
Gaya
gravitasi
menyebabkan
aliran
selalu
menuju ke
tempat
yang
lebih rendah,
sementara
gaya
kapiler
menyebabkan air
bergerak
ke
segala
arah. Air
kapiler selalu
bergerak
dari
daerah
basah
menuju
daerah
yang
lebih
kering.
Tanah
kering
mempunyai gaya
kapiler
lebih besar daripada
tanah
basah.
Gaya
tersebut
berkurang
dengan
bertambahnya
kelembaban
tanah.
Selain
itu,
gaya kapiler bekerja lebih kuat pada tanah butiran halus seperti lempung daripada tanah
butiran
kasar
seperti
pasir.
Apabila
tanah
kering,
air
terinfiltrasi
melalui
permukaan
tanah karena pengaruh gaya gravitasi dan gaya kapiler pada seluruh permukaan. Setelah
tanah menjadi basah, gerak kapiler berkurang karena berkurangnya gaya kapiler. Hal ini
menyebabkan penurunan laju infiltrasi. Sementara aliran kapiler pada lapisan permukaan
berkurang, aliran karena pengaruh gravitasi berlanjut mengisi pori – pori tanah. Dengan
terisinya
pori
–
pori
tanah,
laju
infiltrasi berkurang
secara
berangsur
–
angsur
sampai
dicapai kondisi konstan; di mana laju infiltrasi sama dengan laju perkolasi melalui tanah.
|
 Dalam infiltrasi dikenal
dua
istilah
yaitu kapasitas infiltrasi
dan
laju
infiltrasi,
yang
dinyatakan dalam
mm/jam.
Kapasitas infiltrasi
adalah
laju
infiltrasi
maksimum
untuk suatu jenis tanah tertentu; sedangkan laju infiltrasi ( f
t
)
adalah kecepatan infiltrasi
yang
nilainya
tergantung pada
kondisi
tanah
dan
intensitas
hujan.
Gambar
2.1.
menunjukkan
kurva
kapasitas
infiltrasi
(f
p
),
yang
merupakan
fungsi
waktu.
Apabila
tanah
dalam
kondisi
kering
ketika
infiltrasi
terjadi,
kapasitas
infiltrasi
tinggi
karena
kedua
gaya
kapiler
dan
gaya
gravitasi
bekerja
bersama
–
sama
menarik
air
kedalam
tanah.
Ketika
tanah
menjadi
basah,
gaya
kapiler
berkurang
yang
menyebabkan laju
infiltrasi
menurun.
Akhirnya kapasitas infiltrasi
mencapai
suatu
nilai
konstan,
yang
dipengaruhi terutama oleh gravitasi dan laju perkolasi.
Gambar 2.1. Kurva Kapasitas infiltrasi ( f
p
)
(
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2008 )
2.1.1
Faktor – Faktor Yang Mempengaruhi Infiltrasi
Laju
infiltrasi dipengaruhi oleh beberapa
faktor,
yaitu kedalaman
genangan dan
tebal
lapisan
jenuh,
kelembaban tanah,
pemadatan oleh
hujan,
tanaman
penutup,
intensitas hujan dan sifat – sifat fisik tanah.
|
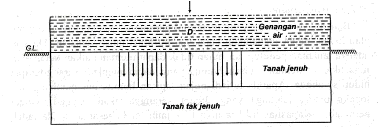 2.1.2
Kedalaman Genangan Dan Tebal Lapisan Jenuh
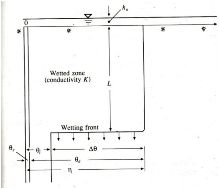
Seperti
ditunjukan
dalam
gambar
2.2.,
air
yang
tergenang
di
atas
permukaan
tanah terinfiltrasi ke dalam tanah, yang menyebabkan suatu lapisan dibawah permukaan
tanah
menjadi jenuh air. Apabila tebal dari
lapisan jenuh air adalah L, dapat dianggap
bahwa
air
mengalir kebawah melalui
sejumlah tabung
kecil.
Aliran
melalui
lapisan
tersebut
serupa
dengan
aliran
melalui
pipa.
Kedalaman
genangan
di
atas
permukaan
tanah (D)
memberikan tinggi tekanan pada
ujung atas tabung, sehingga tinggi tekanan
total
yang
menyebabkan aliran
adalah
D+L.
Tahanan terhadap
aliran
yang
diberikan
tanah adalah sebanding dengan tebal lapis jenuh air L. Pada awal hujan, dimana L adalah
kecil
dibanding D,
tinggi
tekanan
adalah
besar
dibanding tahanan
terhadap
aliran,
sehingga air
masuk ke dalam
tanah dengan cepat. Sejalan dengan waktu, L bertambah
panjang
sampai
melebihi D,
sehingga tahanan
terhadap
aliran
semakin
besar.
Pada
kondisi tersebut kecepatan infiltrasi berkurang. Apabila L sangat lebih besar daripada D,
perubahan L
mempunyai
pengaruh
yang
hampir
sama
dengan
gaya
tekanan
dan
hambatan, sehingga laju infiltrasi hampir konstan.
Gambar 2.2. Genangan Pada Permukaan Tanah
(
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2008 )
2.1.3
Kelembaban Tanah
Jumlah kadar air
tanah
mempengaruhi kapasitas
infiltrasi. Ketika air jatuh pada
tanah
kering,
permukaan
atas dari tanah
tersebut
menjadi
basah,
sedangkan
bagian
|
|
bawahnya
relatif
masih
kering.
Dengan
demikian terdapat perbedaan
yang besar
dari
gaya
kapiler
antara
permukaan
atas
tanah
dan
yang
ada
dibawahnya. Karena
adanya
perbedaan tersebut, maka terjadi gaya kapiler yang bekerja bersama – sama dengan gaya
berat,
sehingga
air bergerak ke bawah
(infiltrasi) dengan cepat. Dengan bertambahnya
waktu,
permukaan bawah
tanah
menjadi
basah,
sehingga
perbedaan
gaya
kapiler
berkurang, sehingga infiltrasi berkurang. Selain
itu, ketika
tanah
menjadi basah koloid
yang terdapat dalam tanah akan mengembang dan menutupi pori – pori tanah, sehingga
mengurangi kapasitas infiltrasi pada periode awal hujan.
2.1.4 Pemampatan Oleh Hujan
Ketika hujan jatuh di atas tanah, butir tanah
mengalami pemadatan oleh butiran
air hujan. Pemadatan tersebut mengurangi pori – pori tanah yang berbutir halus (seperti
lempung),
sehingga dapat
mengurangi kapasitas
infiltrasi. Untuk
tanah pasir, pengaruh
tersebut sangat kecil.
2.1.5 Penyumbatan Oleh Butir Halus
Ketika tanah sangat kering, permukaannya sering terdapat butiran halus. Ketika
hujan turun dan infiltrasi terjadi, butiran
halus tersebut terbawa
masuk ke dalam tanah,
dan mengisi pori – pori tanah, sehingga mengurangi kapasitas infiltrasi.
2.1.6 Tanaman Penutup
Banyaknya tanaman yang menutupi permukaan tanah, seperti rumput atau hutan,
dapat menaikan kapasitas infiltrasi tanah tersebut. Dengan adanya tanaman penutup, air
hujan tidak dapat
memampatkan tanah, dan
juga
akan terbentuk
lapisan humus
yang
|
|
dapat menjadi tempat hidup serangga. Apabila terjadi hujan lapisan humus mengembang
dan
lubang –
lubang
(
sarang
)
yang
dibuat serangga akan
menjadi sangat
permeabel.
Kapasitas infiltrasinya bisa jauh menjadi lebih besar dari pada tanah yang tanpa penutup
tanaman.
2.1.7 Topografi
Kondisi
topografi juga
mempengaruhi infiltrasi. Pada
lahan
dengan kemiringan
besar,
aliran permukaan
mempunyai kecepatan
besar
sehingga air
kekurangan
waktu
untuk
infiltrasi.
Akibatnya sebagian
besar
air
hujan
menjadi
aliran
permukaan.
Sebaliknya, pada lahan yang datar
air
menggenang sehingga
mempunyai
waktu cukup
banyak untuk infiltrasi.
2.1.8 Intensitas Hujan
Intensitas
hujan
juga
berpengaruh terhadap
kapasitas
infiltrasi,
jika
intensitas
curah hujan I
lebih kecil dari kapasitas infiltrasi, maka laju infiltrasi aktual adalah sama
dengan
intensitas hujan.
Apabila
intensitas hujan
lebih besar dari
kapasitas infiltrasi,
maka laju infiltrasi aktual sama dengan kapasitas infiltrasi.
2.1.9 Pengukuran Infiltrasi
Metode
yang
biasa
digunakan
untuk
menentukan kapasitas
infiltrasi
adalah
pengukuran dengan infiltrometer dan analisis hidrograf. Infiltrometer dibedakan menjadi
infiltrometer genangan dan simulator hujan ( rainfall simulators ).
|
|
2.1.10 Infiltrometer Genangan
Infiltrometer genangan yang banyak digunakan adalah dua silinder kosentris atau
tabung yang dimasukkan kedalam tanah. Untuk tipe pertama, dua silinder kosentris yang
terbuat
dari
logam
dengan
diameter antara
22,5
dan
90
cm
ditempatkan dengan
sisi
bawahnya berada beberapa sentimeter di bawah tanah seperti terlihat dalam gambar 2.3.
Ke dalam kedua ruangan diisikan air yang selalu dijaga pada elevasi sama. Fungsi dari
silinder
luar adalah
untuk
mencegah air di dalam ruang sebelah dalam menyebar pada
daerah yang
lebih
besar
setelah
merembes di
bawah dasar
silinder.
Kapasitas
infiltrasi
dan perubahannya dapat ditentukan dari kecepatan penambahan air pada silinder dalam
yang diperlukan untuk mempertahankan elevasi konstan.
Infiltrometer tipe kedua terdiri dari tabung dengan diameter sekitar 22,5 cm dan
panjang 45 sampai 60 cm yang dimasukkan kedalam tanah sampai kedalaman minimum
sama dengan kedalaman dimana air
meresap selama percobaan ( sekitar 37,5
sampai
52,5 cm ),
sehingga tidak terjadi penyebaran. Laju air
yang
harus ditambahkan untuk
menjaga kedalaman yang konstan di dalam tabung dicatat.
Infiltrometer
genangan
ini
tidak
memberikan kondisi
infiltrasi
yang sebenarnya
terjadi
di
lapangan,
karena
pengaruh
pukulan butir
–
butir
hujan
tidak diperhitungkan
dan
struktur
tanah
di
sekeliling dinding
silinder
telah
terganggu
pada
waktu
pemasukannya kedalam tanah.
Tetapi
meskipun mempunyai kelemahan, alat
ini
mudah
dipindah
dan
dapat
digunakan
untuk
mengetahui kapasitas
infiltrasi
di
titik
yang
dikehendaki sesuai dengan tata guna lahan, jenis tanaman dan sebagainya.
|
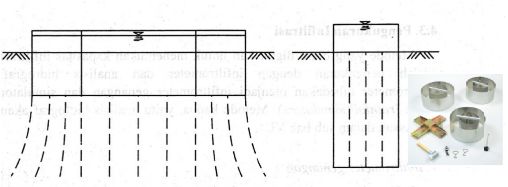 Gambar 2.3. Infiltrometer Genangan
( Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2008 )
2.1.11
Simulator Hujan
Untuk
mengurangi kelemahan dari penggunaan alat diatas, dibuat hujan tiruan
dengan
intensitas
merata yang lebih
tinggi dari kapasitas
infiltrasi. Luas bidang yang
disiram antara 0,1 sampai 40
m².
Besar
infiltrasi dihitung dengan
mencatat
besarnya
hujan dan limpasan.
Gambar 2.4. adalah sket simulator hujan. Hujan tiruan dengan intensitas hujan I
jatuh pada bidang yang akan dicari kapasitas infiltrasinya. Intensitas hujan lebih besar
dari kapasitas infiltrasi f sehingga terjadi genangan diatas permukaan tanah. Pada suatu
saat genangan air
akan meluap dan luapan air ditampung dalam ember.
Dengan
mengetahui
intensitas hujan I,
volume tampungan dalam ember dan tinggi
genangan,
maka akan dapat dihitung kapasitas infiltrasi f.
|
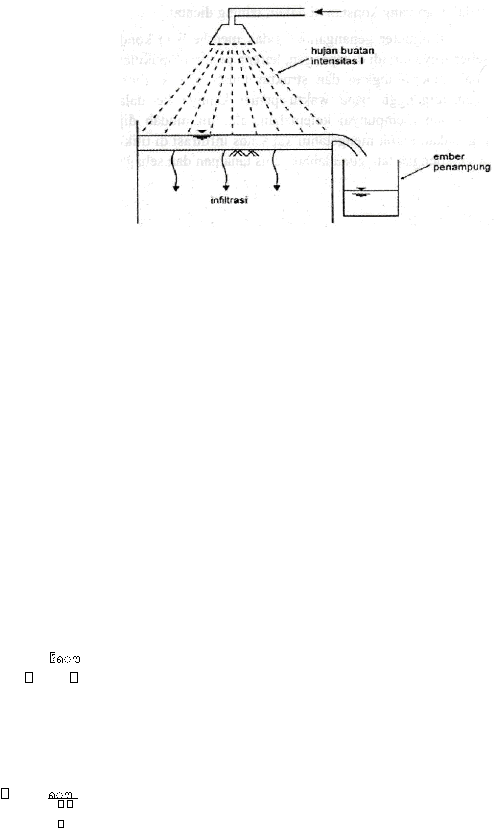 Gambar 2.4. Simulator hujan
(
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2008 )
2.1.12 Kapasitas Infiltrasi
Laju
infiltrasi
f,
dinyatakan
dalam
in/jam
atau
cm/jam,
adalah
kecepatan
air
masuk
kedalam
tanah
dari
permukaan
tanah.
Jika
air
menggenang
pada
permukaan
tanah, maka kapasitas infiltrasi telah mencapai batas kemampuan. Jika laju distribusi air
pada permukaan, sebagai contoh hujan, lebih kecil dari pada kemampuan
laju
infiltrasi
maka laju infiltrasi sebenarnya akan juga lebih kecil dari pada laju potensial. kumulatif
infiltrasi
F
adalah
akumulasi dari
kedalaman
air
yang
masuk
kedalam
tanah
selama
jangka waktu
tertentu
dan
itu
sama
dengan
integral
dari
laju
infiltrasi pada periode
tersebut :
????
?
???
?
?
( 2.1 )
Dimana
t
adalah
variabel buatan dari
fungsi
waktu
dalam
integral.
Sebaliknya,
laju
infiltrasi adalah turunan terhadap waktu dari infiltrasi kumulatif :
???
?
??
?
( 2.2 )
Metode perhitungan kapasitas infiltrasi dapat dilakukan dengan metode Horton, metode
Philip, dan Metode Green – Ampt.
|
 2.1.13 Metode Horton
Salah
satu
persamaan
infiltrasi
paling
awal
yang
dikembangkan oleh
Horton
(1933, 1939
),
yang
mengamati bahwa
infiltrasi
berawal dari
suatu
nilai
baku
f
o
dan
secara eksponen menurun sampai pada kondisi konstan fc
:
f(t) = fc
+
(f
o
–
fc)e
-kt
( 2.3 )
dimana
k
adalah
pengurangan konstan
terhadap
dimensi
[T
-1
].
f
o
adalah
kapasitas
infiltrasi awal sedangkan fc
adalah kapasitas infiltrasi konstan yang tergantung pada tipe
tanah.
Parameter
f
o
dan
fc
adalah
didapat
dari
pengukuran dilapangan
dengan
menggunakan
alat
double ring
infiltrometer.
Parameter
f
o
dan
f
c
nilainya dipengaruhi
oleh
fungsi jenis
tanah dan
tutupan.
Untuk
tanah berpasir atau berkerikil nilai
tersebut
tinggi, sedang tanah
berlempung
yang
gundul
nilainya kecil, dan
apabila
permukaan
tanah
ada
rumput
nilainya
bertambah. Untuk
menghitung laju
infiltrasi
dengan
menggunakan metode horton maka perlu diketahui nilai k. Karena nilai k tidak diketahui
maka persamaan tersebut kemudian ditrasnposisikan sebagai berikut :
f(t) - f
c
=
(f
o
–
f
c
)e
-kt
setelah ditrasnposisikan maka persamaan tersebut di log kan menjadi :
log (f(t) - fc ) =log (f
o
–
f
c
)
–
kt log e ( 2.4 )
atau
?
?
?
??
?
?
?
?
???
?
?
?
??
?
?
?
?
?
–
?
( 2.5 )
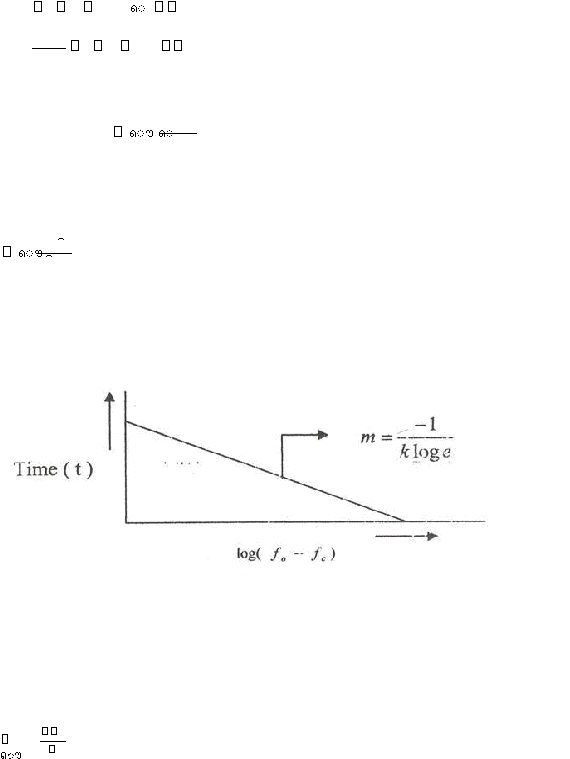
Persamaan diatas sama dengan persamaan garis lurus dengan kemiringan m berikut ini
y
=
mx + c
( 2.6 )
dengan :
m
=
?
?
??? ?
|
 y = t
x =
?
?
?
?
?
?
c =
?
?
??
?
?
?
?
?
–
?
Dengan demikian persamaan ini dapat diwakilkan dalam sebuah garis lurus yang
mempunyai nilai
?
?
??? ?
.
Bentuk dari garis lurus persamaan tersebut di perlihatkan
dalam
gambar
2.5 di bawah
ini dengan
m merupakan
garis miring
maka
m dapat
dihitung dengan persamaan berikut ini.
?
?
?
?
?
?
?
?
( 2.7 )
Dengan y2 dan
y1 nilai dari
log ( f
o
–
fc )
dari
fungsi
waktu x2 dan
x1
.
Dari
nilai
m
kemudian dihitung nilai k maka dapat diketahui laju infiltrasi menurut Horton.
Gambar 2.5. Grafik Hubungan t terhadap log (f
o
–
fc)
(
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2008 )
Jumlah total air yang terinfiltrasi pada
suatu periode tergantung
pada laju
infiltrasi dan
fungsi waktu. Apabila laju infiltrasi pada suatu saat adalah f
(t)
,
maka laju infiltrasi kumulatif atau
jumlah air yang terinfiltrasi adalah F
(t)
.
laju infiltrasi dan jumlah air yang terinfiltrasi adalah :
?
?
?
???
( 2.8 )
?
dan
|
 ?
?
???
?
?
?
?
?
?
?
?
???
( 2.9)
Persamaan 2.9 menunjukan bahwa jumlah air yang terinfiltarasi F
(t)
merupakan integral dari laju
infiltrasi maka persamaan 2.9 menjadi :
?
?
?
?
??
?
?
?
?
?
?
?
?
?
?
?1
??
?
?
( 2.10 )
?
2.1.14 Metode Philip
Philip
(1957,
1969)
memberikan solusi
pada
persamaan
Richard
pada
kondisi
yang
bersifat
membatasi
dengan
mengasumsikan
tersebut
K
dan
D
dapat
diketahui
dengan
kadar
kelembaban
?.
Philip menggunakan Boltzmann
transformasi B(? ) =
zt
-1/2
untuk konversi
(2.3) ke
dalam
satu persamaan
diferensial
biasa
di
B, dan
penyelesaian
persamaan
ini untuk
menghasilkan satu
rangkaian
tanpa
batas
untuk
kumulatif
infiltrasi
F(t),
dengan
pendekatan
sebagai berikut :
F(t) = St1
/2
+Kt
( 2.11 )
Dimana S
adalah parameter yang disebut sorptivity, merupakan fungsi dari kemampuan resapan
tanah, dan K adalah konduksi daya hidrolik.
Dengan turunan
f(t)=
?
St
—1/2
+
K
( 2.12 )
?
sebagai t Æ8, f(t)
sama dengan
K. Dua kondisi
pada persamaan Philip
mewakili
akibat
dari
gaya
kapiler
tanah
dan gaya
gravitasi, berturut –
turut. Untuk arah mendatar tanah, gaya
kapiler tanah
hanya
gaya
yang
membawa
air
kedalam
lubang
–
lubang
kecil,
dan
persamaan
Philip
mengurangi sampai pada F(t) = St1
/2
.
|
 2.1.15 Metode Green – AMPT
Dalam sub bab sebelumnya, persamaan infiltrasi yang dikembangkan dari solusi
pendekatan persamaan Richard.
Pendekatan alternatif
untuk
lebih
mengembangkan
pendekatan teori
fisika
itu
hanya
solusi
analisa
exact.
Green
dan
Ampt
bertujuan
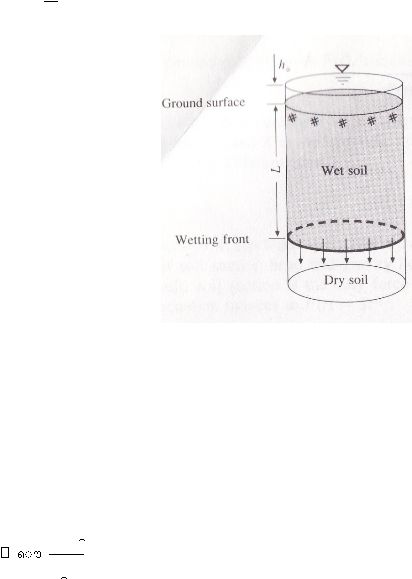
mempermudah gambar
infiltrasi
yang
ditunjukan
pada
gambar 2.6.
permukaan
basah
adalah batas
yang
memisahkan tanah dari kadar kelembaban ?
i
bawah dari tanah
jenuh
dengan
kadar
kelembaban ?
diatas.
Permukaan
yang
basah
mendesak
masuk
ke
kekedalaman L dalam waktu t sejak
infiltrasi berawal. Genangan air dengan kedalaman
kecil h
o
diatas permukaan tanah.
Gambar 2.6. Variable Dari Model Infiltrasi Green-Ampt
(
Sumber : Hidrologi, BR Sri Harto, 2000 )
Memodelkan lubang tanah arah vertikal dari unit horizontal yang bersinggungan dengan
area bersekat ( gambar 2.7 ) dan biarkan satu volume kedali jadi terdefinisi sekitar tanah
basah di antara permukaan dan kedalaman L. Jika tanah memiliki kadar kelembaban ?
i
sepanjang
masuk
kedalaman
tanah,
kadar
kelembaban akan
meningkat dari
?
i
ke
?
(porositas)
dengan
melewati
permukaan
basah. Kadar
kelembaban ?
adalah
rasio
dari
volume
air
sampai
volume
total
dengan
pengendali
permukaan, karena
itu
kenaikan
dalam simpanan air dengan pengendali isi sebagai hasil dari infiltrasi adalah L(? - ?
i
).
|
 Definisi quantitas ini sama dengan F, kedalaman kumulatif dari air yang teresap
kedalam tanah. Hence
F(t) = L(? - ?
i
)
( 2.13 )
=
L??
Dimana ?? = (? - ?
i
)
Hukum Darcy menunjukkan
q = -K
??
??
( 2.14 )
Gambar 2.7. Infiltrasi Dalam Kolom Tanah Dari Unit Area Trasnsisi Dari Model Green-
Ampt
(
Sumber : Hidrologi, BR Sri Harto, 2000 )
dalam kasus
ini aliran Darcy q adalah tetap sepanjang kedalaman dan persamaan dari f,
karena q adalah positif meningkat sedangkan f adalah positif menurun. Jika nilai 1 dan 2
berada berturut – turut di permukaan tanah dan hanya pada sisi kering dari permukaan
basah, dapat melalui pendekatan berikut
? ?
?
?
?
?
?
(
2.15 )
?
?
?
?
|
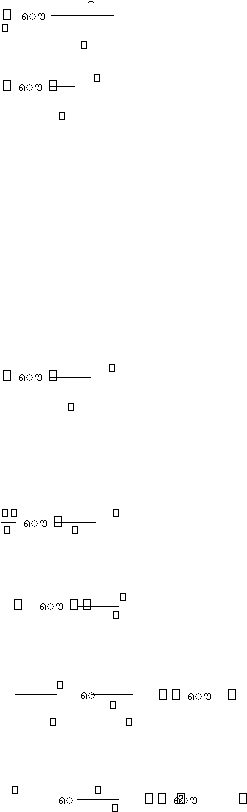 h1 pada
permukaan
sama
dengan
dalam
genangan
h
o
. Nilai
h
2
dalam
tanah
kering
dibawah permukaan basah sama dengan –? – L. Hukum Darcy pada sistem ini dituliskan
sebagai berikut
?
?
?
?
?–? –
?
?
?
?
–
?
(
2.16 )
Jika dalam genangan h
o
, adalah sama dengan perbandingan ? dan L. Asumsi ini
biasanya
mendekati
masalah
hidrologi
air
permukaan karena
itu
asumsi
genangan
menjadi
limpasan
permukaan.
Setelah
itu,
akan
ditunjukkan
bagaimana
menghitug
h
o
jika tidak disamakan.
Dari
persamaan
2.13. permukaan
basah
memiliki
kedalaman
L = F/??, dan
asumsi h
o
=
0, disubtitusikan kedalam persamaan 2.16 menjadi
?
??? –
?
(
2.17 )
dari f = dF/dt, persamaan 2.17 dapat dinyatakan dalam persamaan diferensial dengan F
tidak diketahui
?
??? –
?
?
Untuk memberikan solusi F,digunakan pembagian jamak untuk memperoleh
?
?
?
?
??? –
Kemudian dibagi menjadi 2 bagian
??
??? –
?
?
??
?
?
??? –
??? –
Dan diintegral
???
?
?1
?
??
?
?
?
?
??? –
?
|
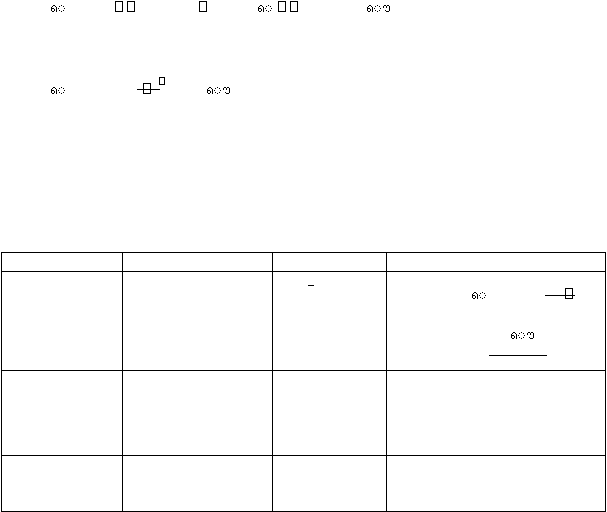 untuk memperoleh
?
?
?
?
???
?
?
?
?
?
?
???
?
?
???
??
??
atau
????
??? ln ?1
?
?
?
?
??
( 2.18 )
?
??
Dari tabel 4.1. dibawah ini dapat dilihat perbandingan parameter yang digunakan
pada masing – masing metode dalam menghitung laju infiltrasi pada tanah.
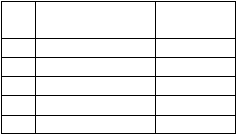
Tabel 2.1. Perbandingan Persamaan Laju Infiltrasi Dari Ketiga Metode
Keterangan
Horton
Philip
Green - Ampt
Laju Infiltrasi
f(t) = fc
+
(f
o
–
fc
)e
-kt
f(t)=
?
St
—1/2
+
K
?
?
?
?
?
?
?
?
?
??? ln ?1
?
???
??
??? – ?
Kekurangan
Tidak cukup akurat
Laju
infiltrasi
yang
didapat
tidak
sesuai
dengan
kondisi
dilapangan
Membutuhkan banyak
uji
lab
untuk
mendapatkan setiap
parameternya.
Keunggulan
Parameter
yang
diperoleh dari
lokasi
penelitian
Mudah
dalam
penerapannya
Hasil yang didapat akurat
Dari
tabel
tersebut
diketahui parameter dari
setiap
persamaan
ketiga
metode
tersebut.
Beberapa parameter tersebut diperoleh dari hasil pengamatan pada daerah penelitian dan
di
laboratorium. Persamaan
laju
infiltrasi pada
metode Green –
Ampt
memiliki
parameter terbanyak
yang didapat
dari
hasil
pengamatan
di
laboratorium
tanah.
Sama
dengan
metode
Green
–
Ampt
pada
metode
Philip
kedua
parameter
yaitu
S
dan
K
didapat
dari
hasil
pengamatan
laboratorium juga.
Kedua
persamaan
tersebut
banyak
menggunakan parameter yang diperoleh dari hasil laboratorium karena itu kedua metode
tersebut, yaitu Green – Ampt dan Philip tidak sesuai dengan kebutuhan penelitian ini,
|
 yang
banyak
menggunakan
data
dari pengamatan
daerah
penelitian,
selain
itu
pengaplikasian persamaan pada kedua metode tersebut tergolong cukup rumit.
2.1.16 Hubungan Laju Infiltrasi dengan Permeabilitas Tanah
Permeabilitas tanah
merupakan
sifat
bahan
berpori
yang
memungkinkan aliran
rembesan
yang
berupa
air
mengalir
melewati
rongga
pori
yang
menyebabkan tanah
bersifat
permeable.
Koefisien
permeabilitas (
k
)
memiliki
satuan
sama
dengan
laju
infiltrasi
tanah
(
cm/jam
).
Koefisien
permeabilitas
tanah
tergantung
pada
beberapa
faktor yaitu : kekentalan cairan, distribusi ukuran pori, distribusi ukuran butiran, angka
pori,
kekerasan
permukaan butiran
tanah,
dan
derajat
kejenuhan
tanah.
Karena
nilai
koefisien permeabilitas tanah sama dengan laju infiltrasi tanah maka semakin permeabel
sifat
tanah
maka
akan
semakin besar
laju
infiltrasi
pada
tanah.
Berikut
ini
adalah
koefisien permeabilitas pada umumnya.
Tabel 2.2. Harga Koefisien Resapan Pada Umumnya
No
Jenis Tanah
k
( cm/s )
1
Kerikil bersih
1 – 10²
2
Pasir kasar
10
-2
–
1
3
Lanau
10
-3
–
10
-2
4
Lanau Lempung
10
-3
–
10
-5
5
Lempung
<
10
-6
Sumber : Prinsip – Prinsip Rekayasa Geoteknis, Braja. M. Das, 1998
Nilai
dari
koefisien
dari
permeabilitas
sangat
berpengaruh
pada
penelitian
ini
karena
nilai tersebut dijadikan pembanding dengan laju
infiltrasi yang dihitung dengan metode
Horton,
jika
nilai
koefisien
permeabilitas tersebut
mendekati
laju
infiltrasi
dengan
menggunakan
metode
Horton
maka
penggunaan
metode
Horton pada
penelitian
ini
dapat digunakan.
|
|
2.2
Proses Limpasan ( run off )
Daya infiltrasi menentukan besarnya air hujan yang dapat diserap kedalam tanah.
Sekali air hujan tersebut masuk kedalam tanah maka tidak dapat diuapkan kembali dan
tetap
akan
berada
dibawah
permukaan
tanah
yang
akan
mengalir
sebagai
air
tanah.
Aliran
air
tanah
sangat
lambat,
makin
besar
daya
infiltasi
mengakibatkan limpasan
permukaan makin kecil sehingga debit puncaknya akan lebih kecil (Soemarto, 1995).
Faktor – faktor yang mempengaruhi limpasan secara umum dapat dikelompokan
menjadi 2 kelompok, yaitu faktor meteorologi dan karakteristik daerah tangkapan
saluran
atau
daerah aliran
sungai
(DAS).
Faktor
meteorologi yang berpengaruh pada
limpasan
terutama
adalah
karakteristik hujan,
yang
meliputi
intensitas
hujan,
durasi
hujan, dan distribusi curah hujan. Sedangkan karakteristik DAS yang berpengaruh besar
pada aliran permukaan meliputi luas dan bentuk DAS, topografi, dan tata guna lahan.
Pemakaian
metode rasional
untuk
menghitung debit
puncak
yang ditimbulkan
paling
sering
digunakan
dalam
perencanaan drainasi
perkotaan.
Beberapa
parameter
hidrologi
yang
diperhitungkan
adalah
intensitas
hujan,
durasi
hujan,
frekuensi
hujan,
luas
DAS,
kehilangan air
dan
kosentrasi
aliran.
Metode
rasional
didasarkan pada
persamaan berikut :
Q = 0,278 CIA
( 2.19 )
dengan :
Q
:
debit puncak
I
:
intensitas hujan
A
:
luas daerah tangkapan
C
:
koefisien
aliran
yang
tergantung pada jenis
permukaan
lahan, yang
nilainya
diberikan dalam tabel 2.1 koefisien aliran
|
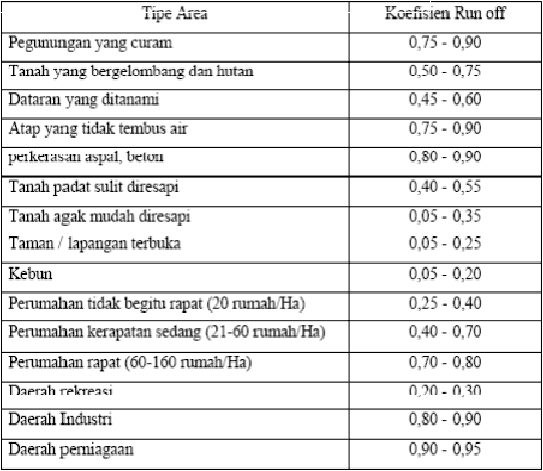 Tabel 2.3. Koefisien Run Off
Sumber : Hidrologi, BR Sri Harto, 2000
2.3
Penentuan Hujan Kawasan
Stasiun
penakar
hujan
hanya
memberikan kedalaman
hujan
di
titik
di
mana
stasiun tersebut berada; sehingga
hujan pada
suatu
luasan
harus
diperkirakan dari
titik
pengukuran tersebut.
Apabila
pada
suatu
daerah
terdapat
lebih
dari
satu
stasiun
pengukuran yang ditempatkan secara terpencar, hujan
yang tercatat dimasing –
masing
stasiun dapat tidak sama. Dalam analisis hidrologi sering diperlukan untuk menentukan
hujan
rerata
pada
daerah
tersebut,
yang
dapat
dilakukan
dengan
tiga
metode
berikut
yaitu metode rerata aritmatik, metode poligon Thissen, dan metode Isohiet.
|
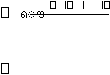 2.3.1
Metode Rerata Arimatik ( Aljabar )
Metode
ini adalah
yang
paling
sederhana
untuk
menghitung
hujan
rerata
pada
suatu
daerah.
Pengukuran yang
dilakukan
di
beberapa
stasiun
dalam
waktu
yang
bersamaan
dijumlahkan kemudian
dibagi
dengan jumlah
stasiun.
Stasiun
hujan
yang
digunakan
dalam
hitungan
biasanya
yang
berada
didalam
DAS;
tetapi stasiun
di
luar
DAS yang masih berdekatan juga bisa diperhitungkan.
Metode rerata aljabar memberikan hasil yang baik apabila :
a.
Stasiun hujan tersebar merata di DAS
b. Distribusi hujan relatif merata pada seluruh DAS
Hujan rerata pada seluruh DAS diberikan dalam bentuk berikut :
?
?
?
……
?
?
( 2.20 )
Dengan :
?
=
hujan rerata kawasan
P1, P2
,…P
n
=
hujan distasiun 1,2,…..,n
n
=
jumlah stasiun
2.3.2
Metode Thiessen
Metode ini memperhitungkan bobot dari masing – masing stasiun yang mewakili
luasan
di
sekitarnya.
Pada
suatu
luasan
di
dalam DAS
dianggap
bahwa
hujan
adalah
sama dengan yang terjadi pada stasiun terdekat, sehingga hujan yang tercatat pada suatu
stasiun
mewakili
luasan
tersebut.
Metode
ini digunakan
apabila
penyebaran
stasiun
hujan di daerah yang ditinjau tidak merata. Hitung curah hujan rerata dilakukan dengan
memperhitungkan daerah pengaruh dari setiap stasiun.
Pembentukan poligon Thiessen adalah sebagai berikut ini.
|
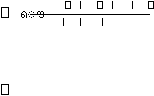 a.
Stasiun pencatat hujan digambarkan pada peta DAS yang ditinjau termasuk stasiun
hujan di luar DAS yang berdekatan, seperti ditunjukan dalam gambar 2.8.
b.
Stasiun – stasiun tersebut dihubungkan dengan garis lurus ( garis terputus ) sehingga
membentuk
segitiga
–
segitiga,
yang
sebaiknya
mempunyai
sisi
dengan
panjang
yang kira – kira sama.
c.
Dibuat
garis
berat
pada
sisi
–
sisi
segitiga
seperti
yang
ditunjukan
dengan
garis
penuh pada gambar 2.8.
d.
Garis – garis berat tersebut membentuk poligon yang mengelilingi tiap stasiun. Tiap
stasiun mewakili luasan
yang dibentuk oleh poligon. Untuk stasiun yang berada di
dekat batas DAS, garis batas DAS membentuk batas tertutup dari poligon.
e.
Luas tiap poligon diukur dan kemudian dikalikan dengan kedalaman hujan di
stasiun yang berada di dalam poligon.
f.
Jumlah dari
hitungan pada butir e untuk semua stasiun dibagi dengan luas daerah
yang ditinjau menghasilkan hujan rerata daerah tersebut, yang dalam bentuk
matematik mempunyai bentuk berikut ini
?
?
?
?
?
?
?
……
?
?
?
?
?
?
?
……
?
?
( 2.21 )
Dengan :
?
=
hujan rerata kawasan
P1, P2
,…P
n
=
hujan distasiun 1,2,…..,n
A1, A2
,…A
n
=
luas daerah yang mewakili stasiun 1,2,…..,n
|
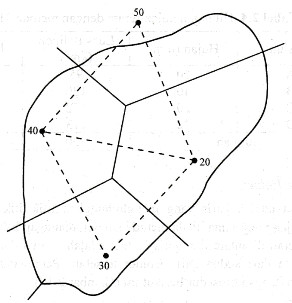 Gambar 2.8. Poligon Thiessen
(
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2008 )
2.3.3
Metode Isohiet
Isohiet adalah
garis
yang
menghubungkan titik – titik dengan
kedalaman
hujan
yang sama. Pada metode isohiet, dianggap bahwa hujan pada suatu daerah di antara dua
garis isohiet adalah merata dan sama dengan nilai rerata dari kedua garis isohiet tersebut.
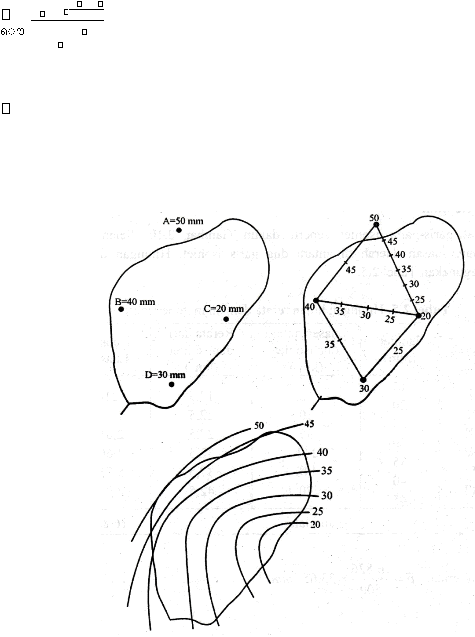
Pembuatan garis isohiet dilakukan dengan prosedur berikut ini ( gambar 2.9 ).
a. Lokasi stasiun hujan dan kedalaman hujan digambarkan pada peta daerah yang ditinjau. b.
Dari
nilai
kedalaman
hujan
di
stasiun
yang
berdampingan
dibuat
interpolasi
dengan
pertambahan nilai yang ditetapkan.
c. Dibuat kurva
yang menghubungkan titik – titik
interpolasi
yang
mempunyai
kedalam
hujan yang sama. Ketelitian tergantung pada pembuatan garis isohiet dan intervalnya.
d. Diukur
luas daerah antara dua
isohiet
yang berurutan dan kemudian dikalikan dengan
nilai rerata dari nilai kedua garis isohiet.
|
 ?
?
e. Jumlah dari hitungan pada butir d untuk seluruh garis isohiet dibagi dengan luas daerah
yang
ditinjau
menghasilkan kedalam hujan
rerata
daerah
tersebut.
Secara
matematis
hujan rerata tersebut dapat ditulis :
?
?
??
?
?
?
?
?
?? ?
?
( 2.22 )
??
Dengan :
?
=
hujan rerata kawasan
I
n
=
garis isohiet ke n, n+1
A
n
=
luas daerah yang dibatasi oleh gari isohiet ke n dan n+1
Gambar 2.9. Metode Isohiet
(
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2008 )
|
|
2.4
Analisis Frekuensi Curah Hujan
Sistem
hidrologi kadang – kadang di pengaruhi oleh peristiwa – peristiwa yang
luar
biasa,
seperti
hujan
lebat,
banjir
dan
kekeringan. Besaran
peristiwa
ekstrim
berbanding terbalik
dengan
frekuensi
kejadiannya,
peristiwa
yang
luar
biasa
ekstrim
kejadiannya sangat langka.
Tujuan analisis
frekuensi adalah berkaitan dengan besaran peristiwa – peristiwa
ekstrim
yang
berkaitan
dengan
frekuensi
kejadiannya melalui
penerapan
distribusi
kemungkinan. Frekuensi
hujan
adalah jumlah
kemungkinan
suatu besaran
hujan
disampai
atau
dilampaui.
Sebaliknya
kala
ulang adalah
waktu
hipotetik
dimana
hujan
dengan suatu besaran tertentu akan disampai atau dilampaui.
Analisis
frekuensi
memerlukan seri data
hujan
yang diperoleh dari pos penakar
hujan, baik yang manual maupun yang otomatis. Analisis frekuensi ini di dasarkan pada
sifat statistik data kejadian yang telah lalu untuk memperoleh probabilitas besaran hujan
dimasa
yang akan datang.
Dengan anggapan sifat
statistik
kejadian
hujan
yang
akan
datang masih sama dengan sifat statistik kejadian hujan masa lalu.
Dalam
ilmu
statistik
dikenal
beberapa
macam
distribusi
frekuensi
dan
empat
jenis distribusi yang banyak digunakan dalam bidang hidrologi adalah :
a.
Distribusi Normal
b.
Distribusi Log Normal
c.
Distribusi Log Pearson Type III
d.
Distribusi Gumbel
Dalam statistik dikenal beberapa parameter
yang berkaitan dengan analisis data
yang
meliputi
rata
–
rata,
simpangan baku,
koefisien variasi dan
koefisien skewness
(kecondongan atau kemencengan).
|
|
Dalam analisa data hidrologi diperlukan ukuran –
ukuran numerik yang menjadi
ciri
data
tersebut. Sembarang
nilai
yang
menjelaskan ciri susunan
data
disebut
parameter.
Parameter
yang
digunakan dalam
analisis susunan data
dari
suatu
variabel
disebut
dengan
parameter statistik,
seperti
nilai
rerata,
deviasi,
dsb.
Pengukuran
parameter yang
sering
digunakan dalam
analisis
data
hidrologi
meliputi
pengukuran
tendensi sentral dan dispersi.
2.4.1
Tendensi Sentral
Nilai
rerata
merupakan
nilai
yang
cukup reprensentatif
dalam
suatu
distribusi.
Nilai rerata dapat digunkan untuk pengukuran suatu distribusi; dan mempunyai bentuk
berikut ini.
?
?
?
?
?
?
( 2.23 )
?
?
?
?
dengan :
?
?
:
rerata
x : variabel random
n : jumlah data
2.4.2
Dispersi
Tidak
semua
variat
dari
variabel
hidrologi
sama
dengan
nilai reratanya,
tetapi
ada yang
lebih besar
atau lebih kecil. Besarnya derajad sebaran
variant disekitar nilai
reratanya
disebut
varian
atau dispersi
(
penyebaran ) penyebaran dapat
diukur
dengan
deviasi standar dan varian.
|
 ?
Varian dapat dihitung dengan menggunkan persamaan berikut dimana s²
adalah varian.
Akar dari varian, s, adalah deviasi standar :
?
?
?
??
?
?
?
??
?
?
?
?
?
( 2.24 )
Koefisien varian ( C
v
) adalah nilai perbandingan antara deviasi standar dan nilai rerata
?
?
( 2.25 )
?
?
Deviasi
standar
dan
koefisien
varian
dapat
digunakan untuk
mengetahui
variabilitas daari distribusi. Semakin besar deviasi standar dan koefisien varian, semakin
besar penyebaran dari distribusi.
Kemencengan C
s
dapat digunakan untuk
mengetahui derajat ketidak simetrisan
dari suatu bentuk distribusi. Kemencengan diberikan oleh bentuk berikut :
?
?
?
?
?
?
??
?
??
??
?
?
?
?
??
?
?
?
?
( 2.26 )
Koefisien kurtosis C
k
diberikan oleh persamaan berikut :
?
?
?
?
?
?
??
??
?
?
??
??
?
?
?
?
??
?
?
?
?
( 2.27 )
2.4.3
Distribusi Normal
Distribusi normal adalah simetris terhadap sumbu vertikal dan berbentuk lonceng
yang
juga
disebut distribusi Gauss. Distribusi nomal
punya
2
parameter
yaitu
rerata
µ
dan deviasi standar s dari populasi. Dalam praktek, nilai rerata ?
?
dan standar deviasi
s diturunkan
dari
data
sampel
untuk
menggantikan
µ
dan
s.
Fungsi
distribusi
normal mempunyai bentuk :
?
?
?
?
?
??
?
/???
?
?
( 2.28 )
?v??
|
 ?
? /?
/?
dengan X adalah variable random dan p(X) adalah fungsi probabilitas kontinyu. Apabila
variable X ditulis dalam bentuk berikut
?
?
?
( 2.29 )
Maka persamaan ( 2.28 ) menjadi :
????
?
?
?
/
?
( 2.30 )
?
v
??
Dengan z adalah satuan standar, yang terdistribusi normal dengan rerata nol dan deviasi
standar satu. Persamaan ( 2.29 ) dapat ditulis dalam bentuk :
X
=
µ + z s
Dimana z adalah faktor frekuensi dari distribusi normal. Pada umumnya faktor frekuensi
dari distribusi statistik diberi notasi K.
Fungsi densitas kumulatif (CDF) dapat diturunkan dengan integrasi dari
fungsi
densitas probabilitas ( persamaan 2.30), yang menghasilkan:
????
?
?
?
v
??
?
( 2.31 )
dengan
F(z)
adalah
probabilitas kumulatif.
Distribusi normal
adalah
simetris
terhadap
sumbu
vertikal.
Dalam pemakaian praktis,
biasanya
hitungan dilakukan dengan
tidak
menggunakan persamaan – persamaan tersebut, tetapi telah dibuat tabel seperti diberikan
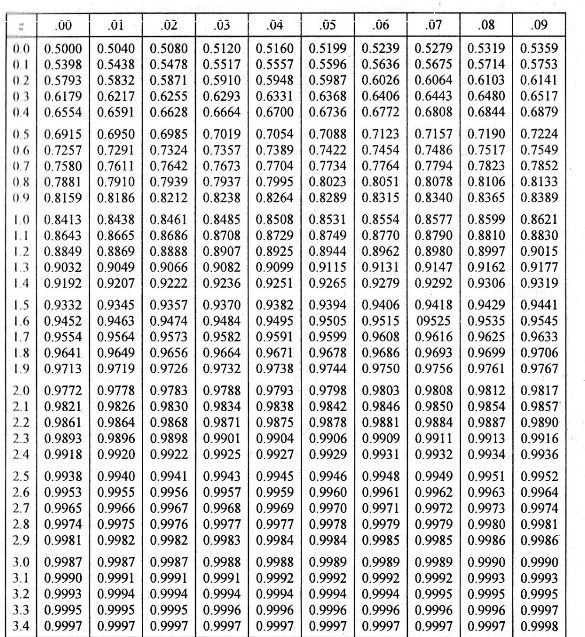
dalam tabel 2.2 tabel distribusi normal.
Sri Harto ( 1993 ) memberikan sifat – sifat distribusi normal, yaitu nilai koefisien
kemencengan sama dengan nol ( C
s
˜
0
)
dan nilai koefisien kurtosis C
k
˜
3. Selain
itu
terdapat sifat – sifat distribusi frekuensi kumulatif berikut ini.
P ( ?
?
-
s ) =
15,87% P ( ?
?
) =
50%
|
|
P ( ?
?
+
s ) =
84,14%
|
 Kemungkinan variat berada pada daerah ( ?
?
-
s ) dan ( ?
?
+
s ) adalah 68,27% dan yang
berada antara ( ?
?
-
2s ) dan ( ?
?
+
2s ) adalah 95,44%.
Tabel 2.4. Probabilitas Kumulatif Distribusi Normal Standar
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2000
2.4.4
Distribusi Log Normal
distribusi log normal digunakan apabila nilai – nilai dari variable random tidak
mengikuti distribusi normal, tetapi nilai logaritmanya memenuhi distribusi normal.
|
 ?
?
?
?
/?
??
?
v
v
Dalam hal ini fungsi densitas probabilitas ( PDF ) diperoleh dengan melakukan
trasnformasi, yang dalam hal ini digunakan persamaan trasnformasi berikut :
y
=
ln x
atau
y = log x
parameter dari distribusi log normal adalah rerata dan standar deviasi dari y yaitu µ
y
dan
s
y
.
Dengan menggunakan transformasi tersebut maka
?
?
?
?
?
?
?
?
/???
?
?
?
?
?
v
??
fungsi densitas kumulatif ( CDF ) dapat diturunkan dengan integrasi dari fungsi densitas
probabilitas, yang menghasilkan :
?
?
?
?
?
???
?
?
?
?
?
?
( 2.32 )
dengan F(z) adalah probabilitas kumulatif.
Hitungan distribusi log normal dilakukan dengan menggunakan tabel yang sama
dengan distribusi normal yaitu tabel 2.2. tabel distribusi normal.
Sri Harto ( 1993 ) memberikan sifat – sifat distribusi log normal, berikut :
Nilai kemencengan : C
s
=
Cv³ + 3C
v
Nilai Kortosis : C
k
=
C
8
+
6C
6
+
15C
4
+
16C ²
+
3
2.4.5
Distribusi Gumbel
Distribusi
Gumbel banyak
digunakan
untuk
analisis
data maksimum,
seperti
untuk analisis frekuensi banjir. Fungsi densitas kumulatif mempunyai bentuk :
?
?
?
?
?
??
( 2.33 )
dimana :
|
 ?
??
?
?
v
?
?
?
( 2.34 )
( 2.35 )
u = ?
?
-
0,5772a
( 2.36 )
dengan :
y
:
faktor reduksi Gumbel
u : modulus dari distribusi ( titik dari densitas probabilitas maksimum )
s : Deviasi Standar
distribusi Gumbel mempunyai sifat bahwa koefisien skewness C
v
=
1,1396 dan koefisien
kurtosis C
k
=
5,4002.
Penyelesaian dari persamaan 2.36. menghasilkan :
?
?
?
?
??
( 2.37 )
???
Dari persamaan 2.24
?
??
?
?
( 2.38 )
Subtitusi persamaan 2.38 kedalam persamaan 2.37 menghasilkan :
?
?
?
??
( 2.39 )
?
Dari persamaan 2.21 diperoleh :
x
T
=
u + ay
T
( 2.40 )
analisis
frekuensi dengan
menggunakan metode Gumbel
juga
sering dilakukan dengan
persamaan berikut ini.
x = ?
?
+
Ks
(
2.41 )
dengan K adalah frekuensi faktor yang bisa dihitung dengan persamaan berikut :
y
=
y
n
+Ks
n
( 2.42 )
|
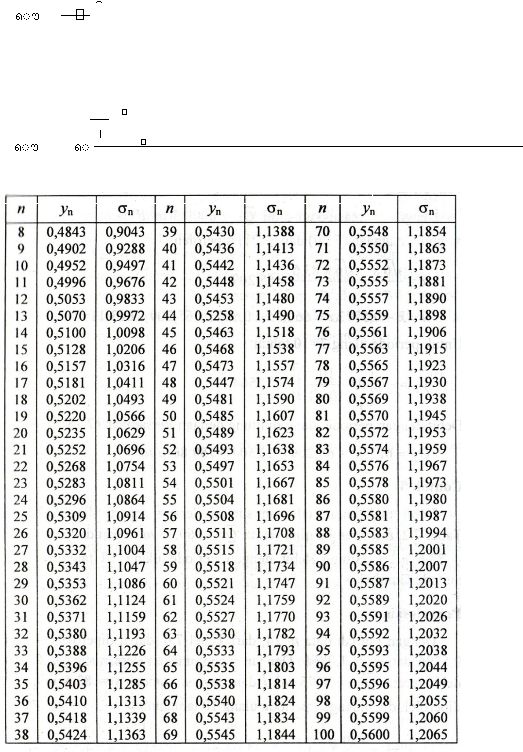 dengan y adalah faktor reduksi Gumbel seperti diberikan oleh persamaan 2.31, y
n
dan s
n
adalah nilai rerata dan deviasi standar dari variant gumbel, yang nilainya tergantung dari
jumlah data seperti diberikan pada tabel 2.3. nilai y
n
dan s
n
fungsi jumlah data.
dari persamaan 2.41 dan 2.42 diperoleh :
?
?
?
??
?
?
(
2.43 )
?
?
dan dengan persamaan 2.36 diperoleh :
??????
??
?
?
?
?
?
??
?
( 2.44
)
?
?
Table 2.5. Nilai y
n
Dan s
n
Fungsi Jumlah Data
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2000
|
 ?
2.4.6
Distribusi Log Pearson III
Pearson Telah banyak mengembangkan model matematika fungsi distribusi
untuk membuat persamaan empiris dari suatu distribusi. Ada 12 tipe distribusi pearson,
namun hanya distribusi log Pearson III yang banyak digunakan dalam hidrologi,
terutama dalam analisis data
maksimum. Bentuk distribusi
log Pearson III
merupakan
hasil transformasi dari distribusi Pearson III mempunyai bentuk berikut :
?
?
?
?
?
??
?
?
( 2.45 )
?
??
?
?
dengan ß dan ? adalah parameter.
Rerata dari distribusi
gamma adalah ß?,
varians adalah ß²?, dan kemencengan
adalah 2/(?)
1/2
.
Persamaan CDF mempunyai bentuk :
G???
?
x
??
e
?
dx
( 2.46 ) Bentuk kumulatif dari distribusi log Pearson III dengan
nilai
variant
X
apabila digambarkan pada kertas probabilitas logaritmik akan membentuk
persamaan garis
lurus. Persamaan tersebut mempunyai bentuk berikut :
y
T
=
??+K
j
s
y
( 2.47 )
dengan :
y
T
:
nilai logaritmik dari x dengan priode ulang T
??
:
nilai rerata dari y
t
s
y
:
deviasi standar dari y
t
K
j
:
faktor frekuensi, yang merupakan fungsi dari probabilitas ( atau priode ulang ) dan
koefisien
kemencengan C
sy
,
yang
diberikan
dalam
tabel
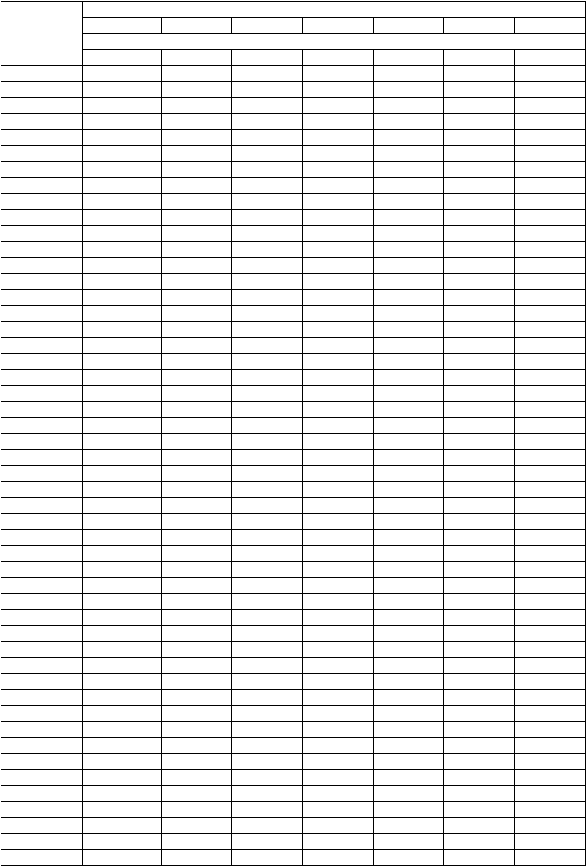
2.4.
Nilai
KT
untuk
distribusi Pearson
|
 Skew
coefficient
C
s
or C
w
Return Period in Years
2
5
10
25
50
100
200
Exceedence Probability
0.50
0.20
0.10
0.04
0.02
0.01
0.005
3.0
-0.396
0.420
1.180
2.278
3.152
4.051
4.970
2.9
-0.390
0.440
1.195
2.277
3.134
4.013
4.909
2.8
-0.384
0.460
1.210
2.275
3.114
3.973
4.847
2.7
-0.376
0.479
1.224
2.272
3.093
3.932
4.783
2.6
-0.368
0.499
1.238
2.267
3.071
3.889
4.718
2.5
-0.360
0.518
1.250
2.262
3.048
3.845
4.652
2.4
-0.351
0.537
1.262
2.256
3.023
3.800
4.584
2.3
-0.341
0.555
1.274
2.248
2.997
3.753
4.515
2.2
-0.330
0.574
1.284
2.240
2.970
3.705
4.444
2.1
-0.319
0.592
1.294
2.230
2.942
3.656
4.372
2.0
-0.307
0.609
1.302
2.219
2.912
3.605
4.298
1.9
-0.294
0.627
1.310
2.207
2.881
3.553
4.223
1.8
-0.282
0.643
1.318
2.193
2.848
3.499
4.147
1.7
-0.268
0.660
1.324
2.179
2.815
3.444
4.069
1.6
-0.254
0.675
1.329
2.163
2.780
3.338
3.990
1.5
-0.240
0.690
1.333
2.146
2.743
3.330
3.910
1.4
-0.225
0.705
1.337
2.128
2.706
3.271
3.828
1.3
-0.210
0.719
1.339
2.108
2.666
3.211
3.745
1.2
-0.195
0.732
1.340
2.087
2.626
3.149
3.661
1.1
-0.180
0.745
1.341
2.066
2.585
3.087
3.575
1.0
-0.164
0.758
1.340
2.043
2.542
3.022
3.489
0.9
-0.148
0.769
1.339
2.018
2.498
2.957
3.401
0.8
-0.132
0.780
1.336
1.993
2.453
2.891
3.312
0.7
-0.116
0.790
1.333
1.967
2.407
2.824
3.223
0.6
-0.099
0.800
1.328
1.939
2.359
2.755
3.132
0.5
-0.083
0.808
1.323
1.910
2.311
2.686
3.041
0.4
-0.066
0.816
1.317
1.880
2.261
2.615
2.949
0.3
-0.050
0.824
1.309
1.849
2.211
2.544
2.856
0.2
-0.033
0.836
1.301
1.818
2.159
2.472
2.763
0.1
-0.017
0.836
1.292
1.751
2.054
2.326
2.576
0
0
0.842
1.282
1.751
2.054
2.326
2.576
-0.1
0.017
0.846
1.270
0.716
2.000
2.252
2.482
-0.2
0.033
0.850
1.258
1.680
1.945
2.178
2.388
-0.3
0.050
0.853
1.245
1.643
1.890
2.104
2.294
-0.4
0.066
0.855
1.231
1.606
1.834
2.029
2.201
-0.5
0.083
0.856
1.216
1.567
1.777
1.955
2.108
-0.6
0.099
0.857
1.200
1.528
1.720
1.880
2.016
-0.7
0.116
0.857
1.183
1.488
1.663
1.806
1.926
-0.8
0.132
0.856
1.166
1,448
1.606
1.733
1.837
-0.9
0.148
0.854
1.147
1.407
1.549
1.660
1.749
-1.0
0.164
0.852
1.128
1.366
1.492
1.588
1.664
-1.1
0.180
0.848
1.107
1.324
1.435
1.518
1.581
-1.2
0.195
0.844
1.086
1.282
1.379
1.449
1.501
-1.3
0.210
0.838
1.064
1.240
1.324
1.383
1.424
-1.4
0.225
0.832
1.041
1.198
1.270
1.318
1.351
-1.5
0.240
0.825
1.018
1.157
1.217
1.256
1.282
-1.6
0.254
0.817
0.994
1.116
1.166
1.197
1.216
-1.7
0.268
0.808
0.970
1.075
1.116
1.140
1.155
-1.8
0.282
0.799
0.945
1.035
1.069
1.087
1.097
-1.9
0.294
0.788
0.920
0.996
1.023
1.037
1.044
Tabel 2.6. Nilai KT Untuk Distribusi Pearson III
|
 Skew
coefficient
C
s
or C
w
Return Period in Years
2
5
10
25
50
100
200
Exceedence Probability
0.50
0.20
0.10
0.04
0.02
0.01
0.005
-2.1
0.319
0.765
0.869
0.923
0.939
0.946
0.949
-2.2
0.330
0.752
0.844
0.888
0.900
0.905
0.907
-2.3
0.341
0.739
0.819
0.855
0.864
0.867
0.869
-2.4
0.351
0.725
0.795
0.823
0.830
0.832
0.833
-2.5
0.360
0.711
0.771
0.793
0.798
0.799
0.800
-2.6
0.368
0.696
0.747
0.764
0.768
0.769
0.769
-2.7
0.376
0.681
0.724
0.738
0.740
0.740
0.741
-2.8
0.384
0.666
0.702
0.712
0.714
0.714
0.714
-2.9
0.390
0.651
0.681
0.683
0.689
0.690
0.690
-3.0
0.396
0.636
0.666
0.666
0.666
0.667
0.667
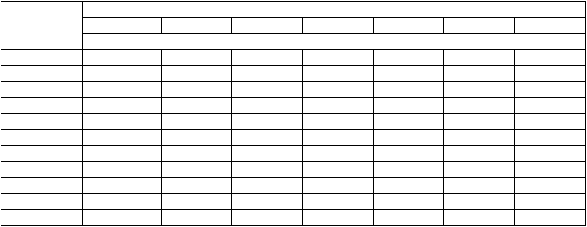
Tabel 2.6. Nilai KT Untuk Distribusi Pearson III ( Lanjutan )
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2000
Distribusi log
Pearson
III
digunakan
apabila
parameter statistik
C
s
dan
C
k
mempunyai nilai selain dari parameter statistik untuk distribusi yang lain (
normal, log
normal, Gumbel ). Penggunaan metode log Pearson III dilakukan dengan menggunakan
langkah – langkah berikut ini.
a.
Data maksimum tahunan disusun dalam tabel
b.
Hitung nilai logaritma dari data tersebut dengan transformasi
y
i
=
ln x
i
atau
y
i
=
log x
i
c.
Hitung nilai rerata ?
?
,
deviasi standar s
y
, koefisien kemencengan C
sy
dari nilai logaritma y
i
.
d.
Dihitung
nilai y
j
untuk
berbagai
priode
ulang yang dikehendaki
dengan
menggunakan
persamaan 2.47
e.
Hitung x
T
untuk setiap periode ulang dengan menghitung nilai anti-lognya :
x
T
=arc ln y atau
x
T
=arc ln y
Pada setiap perhitungan distribusi diatas memiliki persyaratan – persyaratan yang
harus di penuhi sebagai dasar dalam pemilihan penggunan
metode distribusi.
Persyaratan tersebut dapat dilihat pada tabel 2.5. berikut ini.
Tabel 2.7. Persyaratan Masing – Masing Distribusi
|
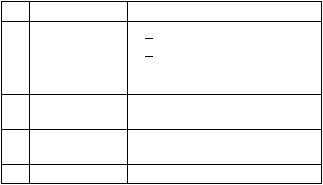 no
Distribusi
Persyaratan
1
Normal
(x+s) = 68,27
(x+2s) = 95,44
Cs ˜ 0
Ck ˜ 3
2
Log Normal
Cs = Cv³+3Cv
Ck = Cv
8
+6Cv
6
+15Cv
4
+16Cv²
+3
3
Gumbel
Cs = 1,14
Ck = 5,4
4
Log Pearson III
Selain Dari nilai Diatas
Sumber : Hidrologi Terapan, Bambang Triatmodjo, 2000
2.4.7
Analisa Intensitas Curah Hujan
Intensitas hujan adalah tinggi atau kedalaman air hujan per satuan waktu. Dengan kata
lain bahwa intensitas curah hujan menyatakan besarnya curah hujan dalam jangka pendek yang
memberikan gambaran derasnya hujan perjam.
Untuk mengelola data curah hujan menjadi intensitas hujan di gunakan cara
statistik dari data pengamatan curah hujan yang terjadi. Dan bila tidak dijumpai data
untuk setiap durasi hujan, maka diperlukan pendekatan secara empiris dengan pedoman
kepada durasi 60 menit ( 1 jam ) dan pada curah hujan harian maksimum yang terjadi
setiap tahun. Cara lain yang lazim digunakan adalah dengan mengambil pola intensitas
hujan untuk kota lain yang mempunyai kondisi yang hampir sama. Untuk mengubah
curah hujan menjadi intensitas hujan dapat digunakan berbagai metode diantaranya:
a.
Metoda Van Breen
b. Metoda Hasper Der Weduwen
2.4.8
Metode Van Breen
|
 ?
Penurunan rumus yang dilakukan Van Breen didasarkan atas anggapan bahwa lamanya
durasi hujan yang ada dipulau jawa terkonsentrasi selama 4 jam dengan hujan efektif sebesar
90% hujan total selama 24 jam. Persamaan tersebut adalah:
?
??
%
?
( 2.48 )
Dengan,
I
:
intensitas hujan (mm/jam)
R²
4
:
curah hujan harian maksimum (mm/24jam)
Dengan persamaan diatas dapat dibuat suatu kurva intensitas durasi hujan dimana
Van Breen
mengambil
kota
Jakarta
sebagai kurva
basis bentuk
kurva
IDF. Kurva
ini
dapat memberikan kecenderungan bentuk kurva untuk daerah – daerah lain di Indonesia
pada umumnya. Berdasarkan pada kurva pola Van Breen kota Jakarta, besarnya
intensitas hujan dapat didekati dengan persamaan:
?
??
?,???
?
?
?,??
( 2.49 )
?
Dengan,
I
T
:
Intensitas hujan (mm/jam) pada PUH T pada waktu konsentrasi tc
Tc
:
waktu konsentrasi (menit)
R
T
:
curah hujan harian maksimum PUH T,(mm/24jam)
2.4.9
Metode Hasper Der Weduwen
Metode
ini
merupakan
hasil
penyelidikan di
Indonesia
yang
dilakukan
olen
Hasper dan Der Weduwen. Penurunan
rumus diperoleh
berdasarkan
kecenderungan
curah
hujan
harian yang dikelompokan atas dasar
anggapan bahwa
hujan
mempunyai
|
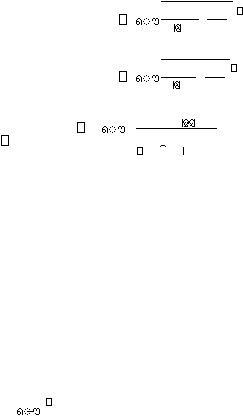 distribusi yang simetris dengan durasi hujan (t) lebih kecil dari 1 jam dan durasi hujan
dari 1 jam sampai 24 jam. Persamaan yang digunakan adalah:
2< t = 24
,maka
?
??????
?
?
?
( 2.50 )
?
,??
???
0 < t = 2
,maka
?
?????
?
?
?
( 2.51 )
?
,?
?
???
Dan
?
?
?
?
?
?
?
?
( 2.52 )
?
?
??
?
?????
Dengan,
t
:
durasi hujan ( menit)
R, R
t
: curah hujan menurut Hasper - Der Weduwen
X
t
:
curah hujan harian maksimumyang terpilih, (mm/ 24jam)
Untuk
menentukan
intensitas hujan
menurut Hasper
Der
Weduwen digunakan rumus
sebagai berikut:
?
?
( 2.53 )
Dengan,
I
:
intensitas hujan ( mm/jam)
R
:
curah hujan
Setelah
kedua
metode
tersebut
dilakukan
maka
selanjutnya dilakukan
perhitungan
penentuan/pendekatan intensitas
hujan.
Cara
ini
di
maksudkan
untuk
menentukan persamaan intensitas
yang
paling
mendekati
untuk
daerah
perencanaan.
Metoda
yang
di
gunakan
adalah
metode
perhitungan dengan
cara
kuadrat
terkecil.
Adapun caranya sebagai berikut :
a. Rumus Talbot (1881)
|
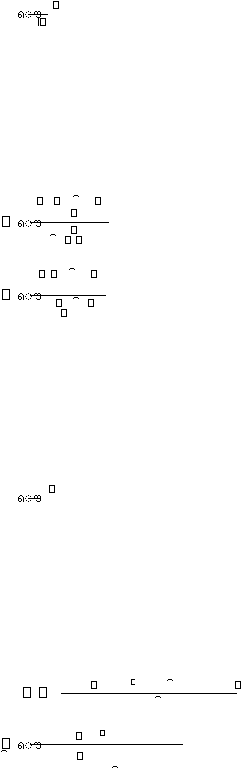 ??
Rumus ini banyak digunakan karena mudah diterapkan dan tetapan – tetapan a
dan b ditentukan dengan harga – harga yang terukur.
?
?
( 2.54 )
Dengan,
I
:
intensitas hujan ( mm/jam )
t
:
lamanya hujan ( jam )
a
dan b konstanta yang tergantung pada lamanya hujan yang terjadi di DAS
: konstanta yang tergantung pada lamanya hujan yang terjadi di DAS
?
?
?
?
??
?
?
?
?
?
?
?
?
?
.
?
( 2.55 )
?
.
????
?
????
?
?
?
?
?
.
?
( 2.56 )
b. Rumus Ishiguro (1905 )
Rumus ini mungkin cocok untuk jangka waktu curah hujan yang lamanya lebih
dari 2 jam.
?
?
?
( 2.57 )
Dengan,
I
:
intensitas hujan ( mm/jam )
t
:
lamanya hujan ( jam )
n
:
konstanta
????
?????? ??
????? ?.???
????? ??
?
?
?
??
?
??
?
?
?
??
?
???
??
?
??
( 2.58 )
????
?????? ??
?????? ?.???
?
?
?
?
??
?
??
?
?
?
??
?
???
??
?
??
( 2.59 )
c. Rumus Sherman (1953 )
|
 ?
v
?
( 2.60 )
Dengan,
I
:
intensitas hujan ( mm/jam )
t
:
lamanya hujan ( jam )
a
dan b konstanta
: konstanta
??
?
??
v???
?
v???
?
?
?
?
?
?
.
?
( 2.61 )
??
??
v????
?
v??
?
?
?
?
?
.
?
( 2.62 )
Dengan,
[ ]
:
jumlah angka- angka dalam tiap suku
n
:
banyaknya data.
Kemudian
dilakukan
penggambaran kurva
IDF
yang
dimaksudkan
untuk
menggambarkan persamaan persamaan intensitas hujan wilayah perencanaan yang dapat
di
gunakan untuk
perhitungan
limpasan (run
off)
dengan
rumus
rasional dan besarnya
kemungkinan terjadinya
intensitas
hujan
yang
berlaku
untuk
lamanya
curah
hujan
sembarang.
2.5
Biopori
Lubang
resapan biopori
adalah
lubang
silindris
yang
dibuat
secara
vertikal
kedalam
tanah
dengan
diameter
10
cm
dan
kedalam
sekitar
80
–
100
cm,
atau
dalam
kasus
tanah
dengan permukaan air tanah dangkal, tidak sampai melebihi kedalaman muka air tanah.
Lubang diisi dengan sampah organik untuk memicu terbentuknya biopori. Biopori adalah pori –
pori berbentuk lubang yang dibuat oleh aktivitas fauna tanah atau akar tanaman.
|
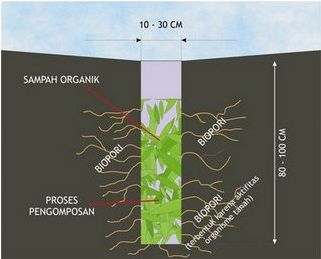 Gambar 2.10. Biopori
2.5.1
Keunggulan dan manfaat
Lubang resapan biopori adalah teknologi tepat guna dan ramah lingkungan untuk
mengatasi banjir dengan cara:
a.
meningkatkan kapasitas infiltrasi
b. mengubah sampah organik menjadi kompos dan
mengurangi emisi
gas rumah kaca
(CO2 dan Metan)
c.
memanfaatkan peran aktivitas fauna tanah dan akar tanaman, dan mengatasi masalah
yang ditimbulkan oleh genangan air seperti penyakit deman berdarah dan malaria.
2.5.2
Meningkatkan kapasitas Infiltrasi
Kehadiran lubang resapan biopori secara langsung akan menambah bidang resapan air,
setidaknya sebesar
luas
kolom/
dinding
lubang.
Sebagai
contoh
bila
lubang
dibuat
dengan
diameter 10cm dan dalam 100
cm maka luas bidang resapan bertambah sebanyak 7850 cm2
dengan kata lain suatu permukaan tanah berbentuk lingkaran dengan
diameter 10
cm,
yang
|
|
semula mempunyai bidang
resapan
78,5
cm2
setelah
dibuat lubang
resapan biopori dengan
kedalaman 100 cm, luas bidang resapan menjadi 7850 cm2.
Dengan
adanya aktivitas fauna
tanah pada
lubang resapan
maka
biopori
akan
terbentuk dan
senantiasa terpelihara keberadaannya. Oleh karena itu
bidang resapan ini akan
selalu terjaga kemampuannya dalam meresapkan air.
Dengan demikian kombinasi antara
luas
bidang
resapan
dengan
kehadiran biopori
secara
bersama
–
sama
akan
meningkatkan
kemampuan dalam meresapkan air.
2.5.3
Mengubah Sampah Organik Menjadi Kompos
Lubang
resapan
biopori
“ diaktifkan
“ dengan
memberikan
sampah
organik
kedalamnya. Sampah
ini
akan
dijadikan
sebagai
sumber energi
bagi
organisme
tanah
untuk
melakukan kegiatan melalui proses dekomposisi. Sampah yang telah didekomposisi ini
dikenal
sebagai kompos. Dengan melalui proses seperti itu maka lubang resapan biopori selain
berfungsi sebagai
bidang
peresapan air
juga
sekaligus
berfungsi sebagai
“pabrik”
pembuat
kompos. Kompos dapat dipanen pada setiap periode tertentu dan dapat dimanfaatkan sebagai
pupuk organik pada berbagai jenis tanaman.
2.5.4
Memanfaatkan Fauna Tanah Dan Atau Akar Tanaman
Seperti disebutkan diatas lubang resapan biopori diaktifkan oleh organisme
tanah,
khususnya
fauna
tanah
dan
perakaran
tanaman.
Aktivitas
merekalah yang
selanjutnya akan
menciptakan
rongga
–rongga
atau
liang –
liang
didalam
tanah
yang
akan dijadikan “saluran“ air untuk meresap kedalam tubuh tanah. Dengan memanfaatkan
aktivitas
mereka
maka
rongga –
rongga
atau
liang
–
liang
tersebut
akan
senantiasa
|
|
terpeliharadan terjaga
keberadaannya
sehingga
kemampuan
peresapannya
akan
tetap
terjaga
tanpa
campur
tangan
langsung
dari
manusia
untuk
pemeliharaannya. Hal
ini
tentunya akan sangat menghemat tenaga dan biaya. Kewajiban factor manusia dalam hal
ini
adalah
memberikan pakan
kepada
mereka
berupa
sampah
organik
pada
periode
tertentu. Sampah organik
yang
dimasukkan
kedalam
lubang akan
menjadi
humus
dan
tubuh biota dalam tanah, tidak cepat di emisikan ke
atmosfir sebagai gas
rumah kaca;
berarti mengurangi pemanasan global dan memelihara biodiversitas dalam tanah.
2.5.5 Jumlah Lubang Resapan Biopori
Jumlah lubang yang perlu dibuat dapat dihitung dengan menggunakan persamaan:
Jumlah LRB = Q
limpasan
/F(t)
(
2.63 )
Bila
lubang
yang
dibuat
berdiameter
10cm
dengan
kedalaman
100cm
maka
setiap
lubang
mampu
menampung
7,8 liter
sampah
organik, ini berarti
bahwa
setiap lubang
dapat
diisi
dengan sampah organik selama 2 – 3 hari.
2.6 Pengambilan Sampel
Sampel
adalah
sebagian
dari
populasi. Artinya
tidak
akan
ada
sampel
jika
tidak
ada
populasi. Populasi adalah keseluruhan elemen atau unsur yang akan kita teliti. Penelitian yang
dilakukan atas
seluruh elemen dinamakan sensus. Idealnya, agar hasil penelitiannya lebih
bisa
dipercaya, seorang
peneliti
harus
melakukan sensus.
Namun
karena sesuatu hal
peneliti
bisa
tidak meneliti keseluruhan elemen tadi, maka yang bisa dilakukannya adalah meneliti sebagian
dari keseluruhan elemen atau unsur tadi.
|
|
Berbagai alasan yang masuk akal mengapa peneliti tidak melakukan sensus antara lain
adalah:
a.
populasi
demikian
banyaknya sehingga
dalam
prakteknya
tidak
mungkin
seluruh
elemen
diteliti
b. keterbatasan waktu penelitian, biaya, dan sumber daya manusia.
c. Penelitian yang
dilakukan
terhadap
sampel
bisa
lebih reliabel daripada
terhadap
populasi,
karena elemen sedemikian banyaknya maka akan memunculkan kelelahan fisik dan mental
para pencacahnya sehingga banyak terjadi kekeliruan. (Uma Sekaran, 1992)
d. Jika elemen populasi homogen, penelitian terhadap seluruh elemen dalam populasi menjadi
tidak masuk akal, misalnya untuk meneliti kualitas jeruk dari satu pohon jeruk.
Agar hasil penelitian yang dilakukan terhadap sampel masih tetap bisa dipercaya dalam
artian
masih
bisa
mewakili
karakteristik populasi,
maka
cara
penarikan
sampelnya
harus
dilakukan secara seksama. Cara pemilihan sampel dikenal
dengan
nama teknik
sampling
atau
teknik pengambilan sampel.
2.6.1
Syarat Sampel Yang Baik
Secara umum, sampel yang baik adalah yang dapat mewakili sebanyak mungkin
karakteristik populasi. Dalam bahasa pengukuran, artinya sampel harus valid, yaitu bisa
mengukur sesuatu yang seharusnya diukur. Kalau
yang ingin diukur adalah masyarakat
Sunda sedangkan yang dijadikan sampel adalah hanya orang Banten saja, maka sampel
tersebut
tidak
valid,
karena
tidak
mengukur
sesuatu
yang
seharusnya diukur
(orang
Sunda). Sampel yang
valid ditentukan oleh dua pertimbangan yaitu akurasi atau
ketepatan dan presisi.
|
|
2.6.2 Akurasi atau Ketepatan
Akurasi atau
ketepatan,
yaitu tingkat
ketidakadaan “bias”
(kekeliruan) dalam
sample.
Dengan kata lain makin sedikit tingkat kekeliruan yang ada dalam sampel, makin akurat sampel
tersebut. Tolok ukur adanya “bias” atau kekeliruan
adalah populasi.
Cooper dan Emory (1995) menyebutkan bahwa “there is no systematic variance” yang
maksudnya
adalah tidak
ada
keragaman
pengukuran yang disebabkan karena pengaruh yang
diketahui
atau
tidak
diketahui,
yang menyebabkan
skor
cenderung
mengarah
pada
satu
titik
tertentu.
Sebagai
contoh,
jika
ingin
mengetahui
rata-rata
luas
tanah
suatu
perumahan,
lalu
yang dijadikan sampel
adalah rumah
yang terletak di setiap sudut jalan, maka hasil atau skor
yang diperoleh akan bias. Kekeliruan semacam ini bisa terjadi pada sampel yang diambil secara
sistematis
2.6.3 Presisi
Kriteria
kedua
sampel
yang
baik
adalah
memiliki
tingkat
presisi
estimasi. Presisi
mengacu pada persoalan sedekat mana estimasi kita
dengan karakteristik populasi. Makin kecil
tingkat
perbedaan di
antara
rata-rata
populasi
dengan
rata-rata
sampel,
maka
makin
tinggi
tingkat presisi sampel tersebut.
Belum pernah
ada sampel yang bisa mewakili karakteristik populasi
sepenuhnya.
Oleh karena itu dalam setiap penarikan sampel senantiasa melekat kesalahan – kesalahan, yang
dikenal
dengan
nama
“sampling
error” Presisi
diukur
oleh
simpangan
baku
(standard
error).
Makin
kecil
perbedaan di
antara
simpangan baku
yang
diperoleh
dari
sampel
(S)
dengan
simpangan baku dari populasi (
s)
,
makin tinggi pula tingkat presisinya. Walau tidak selamanya,
|
|
tingkat presisi
mungkin bisa
meningkat
dengan
cara
menambahkan jumlah sampel, karena
kesalahan mungkin bisa berkurang kalau jumlah sampelnya ditambah ( Kerlinger, 1973 ).
2.6.4 Ukuran Sampel
Ukuran sampel atau jumlah sampel yang diambil menjadi persoalan yang penting
manakala jenis
penelitian
yang
akan
dilakukan
adalah
penelitian
yang
menggunakan
analisis kuantitatif. Pada penelitian yang menggunakan analisis kualitatif, ukuran sampel
bukan
menjadi
nomor
satu,
karena
yang
dipentingkan alah
kekayaan
informasi. Walau
jumlahnya sedikit tetapi jika kaya akan informasi, maka sampelnya lebih bermanfaat.
Dikaitkan dengan besarnya sampel,
selain
tingkat kesalahan, ada lagi beberapa faktor
lain yang perlu memperoleh pertimbangan yaitu:
a. derajat keseragaman
b. rencana analisis
c. biaya, waktu, dan tenaga yang tersedia (Singarimbun dan Effendy, 1989).
Makin tidak seragam sifat atau karakter setiap
elemen populasi,
makin banyak
sampel
yang
harus
diambil.
Jika
rencana
analisisnya mendetail atau
rinci
maka
jumlah
sampelnya pun harus banyak.
2.6.5 Teknik-Teknik Pengambilan Sampel
Secara umum, ada dua jenis teknik pengambilan sampel yaitu, sampel acak atau
random sampling /
probability sampling, dan
sampel tidak
acak atau nonrandom
|
|
samping/nonprobability sampling.
Yang
dimaksud
dengan
random
sampling
adalah
cara
pengambilan
sampel
yang
memberikan kesempatan yang
sama
untuk
diambil
kepada
setiap
elemen
populasi.
Artinya
jika
elemen
populasinya ada
100
dan
yang
akan
dijadikan
sampel
adalah
25,
maka
setiap
elemen
tersebut mempunyai kemungkinan
25/100
untuk
bisa
dipilih
menjadi
sampel. Sedangkan yang
dimaksud
dengan
nonrandom sampling atau nonprobability
sampling,
setiap
elemen populasi
tidak mempunyai kemungkinan yang
sama
untuk
dijadikan
sampel. Lima
elemen
populasi dipilih
sebagai
sampel
karena
letaknya dekat
dengan
rumah
peneliti, sedangkan yang lainnya, karena jauh, tidak dipilih, artinya kemungkinannya 0 (nol).
Dua jenis
teknik
pengambilan sampel di
atas
mempunyai tujuan
yang berbeda. Jika
peneliti
ingin
hasil penelitiannya bisa
dijadikan
ukuran
untuk
mengestimasikan populasi,
atau
istilahnya
adalah
melakukan
generalisasi
maka
seharusnya
sampel
representatif
dan
diambil
secara
acak.
Namun
jika
peneliti
tidak
mempunyai kemauan
melakukan
generalisasi hasil
penelitian maka sampel bisa diambil secara tidak acak. Sampel tidak acak biasanya juga diambil
jika peneliti tidak mempunyai data pasti tentang ukuran populasi dan informasi lengkap
tentang setiap elemen populasi.
Di setiap jenis teknik pemilihan tersebut, terdapat beberapa teknik yang lebih spesifik
lagi.
Pada
sampel
acak
(random sampling) dikenal
dengan
istilah
simple
random
sampling,
stratified random
sampling, cluster
sampling, systematic sampling,
dan area
sampling. Pada
nonprobability sampling
dikenal
beberapa
teknik,
antara
lain
adalah
convenience
sampling,
purposive sampling, quota sampling, snowball sampling. Namun dalam penelitian ini digunakan
tehnik Area Sampling.
2.6.6 Area Sampling atau Sampel Wilayah
|
 Teknik
ini
dipakai
ketika
peneliti
dihadapkan pada
situasi
bahwa
populasi
penelitiannya tersebar di berbagai wilayah. Misalnya, seorang marketing manajer sebuah
stasiun
TV
ingin
mengetahui
tingkat
penerimaan
masyarakat
Jawa
Barat
atas
sebuah
mata
tayangan,
teknik
pengambilan sampel
dengan
area
sampling
sangat
tepat.
Prosedurnya :
a.
Susun sampling frame yang menggambarkan peta wilayah (Jawa Barat) – Kabupaten,
Kotamadya, Kecamatan, Desa.
b. Tentukan wilayah yang akan dijadikan sampel ( Kabupaten, Kotamadya, Kecamatan,
Desa )
c.
Tentukan berapa wilayah yang akan dijadikan sampel penelitiannya.
d. Pilih beberapa wilayah untuk dijadikan sampel dengan cara acak atau random.
e.
Kalau ternyata masih terlampau banyak responden yang harus diambil datanya, bagi
lagi wilayah yang terpilih ke dalam sub wilayah.
Untuk
menghitung jumlah sampel
wilayah
yang dapat
mewakili
suatu
luasan
wilayah maka dibutuhkan persamaan probabilitas sebagai berikut :
?
?
???
?????
?
??
?????
?
100
( 2.64 )
dimana I : intensitas nilai jelajah nominal
kemudian hitung luasan area sampel dan jumlah titik sampel dengan persamaan berikut
ini :
Luas area contoh = luas area total x I
( 2.65 )
??
?
?
?
?
??
?
?????
( 2.66 )
Setelah
diketahui
jumlah
titik
contoh
hitung
luas
area
yang
diwakili
oleh
satu
titik
contoh dengan persamaan sebagai berikut
|
 ?
??
?
?
?
?
??
?
?
?
???
?????
( 2.67 )
Karena metode perhitungan ini menggunakan garis sistematik yang memanfaatkan
tehnik perputaran seperti gambar 2.11 dibawah
ini maka cari jarak antara titik contoh
dan garis titik contoh dengan persamaan dibawah ini.
?
?
?
?
?
????
???
?
?
?
?
?
?
?
???
?
?
??
?
?
( 2.68 )
( 2.69 )
Gambar 2.11. Diagram Rencana Garis Sistematik Yang Memanfaatkan Tehnik
Perputaran
|