 BAB 2
LANDASAN TEORI
2.1
Sinyal Analog dan Sinyal Digital
Suatu
sinyal
didefinisikan
sebagai
besaran fisis
yang
berubah-ubah
menurut
waktu, ruang, atau variabel lainnya. Secara matematik, kita mendefinisikan sinyal
sebagai fungsi dari dua atau lebih variabel bebas. Ada sinyal yang termasuk kelas sinyal
yang secara presisi didefinisikan dengan menetapkan ketergantungan fungsional pada
variabel bebas. Namun, terdapat kasus yaitu hubungan fungsional seperti itu
tidak
diketahui atau terlalu rumit untuk setiap penggunaan praktis.
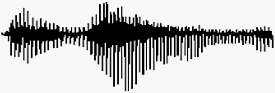
Sebagai contoh, suatu sinyal suara tidak dapat didiskripsikan secara fungsional.
Umumnya, suatu segmen suara dapat dinyatakan dengan derajat ketelitian yang tinggi
sebagai jumlah dari beberapa sinusoida dengan amplitudo dan
frekuensi yang berbeda,
yakni seperti
N
?
i
=
1
A
i
(
t
)
sin
[²
p
F
i
(
t
)
t
+
?
i
( )
t )
]
dengan
{A
i
(t)},
{F
i
(t)},
dan
{
?
i
(t)} secara berturut-turut
adalah
himpunan
amplitudo,
frekuensi, dan fase sinusoida yang bervariasi
menurut waktu. Faktanya, salah satu cara
untuk
menginterpretasikan
isi
informasi
atau pesan
yang
disampaikan
dalam setiap
segmen waktu yang pendek dari sinyal suara adalah dengan mengukur amplitudo,
frekuensi, dan fase yang terdapat dalam segmen waktu sinyal yang pendek.
Gambar 2.1 Contoh Sinyal Suara
|
|
6
6
2.1.1
Sinyal Analog
Sebuah sinyal
analog
atau sinyal
waktu kontinu
adalah
sinyal dengan variabel
apapun
yang
merupakan sinyal
kontinu dalam hal
waktu,
sehingga
untuk
setiap
nilai
waktu dapat diambil nilai-nilai dalam selang kontinu (a,b), dengan a dapat menjadi - 8
dan b dapat menjadi 8 . Perbedaannya dengan sinyal digital adalah pada sinyal analog,
pergerakan
naik turun
dari
sinyal
–
walaupun kecil –
sangatlah
berarti.
Sinyal
analog
menggunakan beberapa sifat dari perantara untuk menyampaikan informasi sinyal.
Kerugian dari
penggunaan
sinyal
analog adalah
di
setiap
sistem terdapat
gangguan
(noise), sebagai
contoh
adalah variasi
acak.
Ketika
sinyal
ditransmisikan
dengan jarak jauh, noise akan menjadi dominan. Efek dari noise akan membuat sinyal
menghilang dan menyimpang, dan untuk mengembalikannya sangat susah, karena ketika
sinyal dikuatkan untuk mengembalikan bagian sinyal yang lemah, maka noise juga akan
dikuatkan.
2.1.2
Sinyal Digital
Sinyal digital adalah suatu sinyal waktu-diskrit yang mempunyai himpunan nilai-
nilai diskrit. Biasanya, nilai-nilai sinyal dari suatu himpunan tebatas ini seimbang dan
karena itu dapat dinyatakan sebagai suatu kelipatan integer dari jarak antara dua nilai
berurutan.
2.1.3
Keuntungan Pemrosesan Sinyal Digital Dibandingkan Sinyal Analog
Suatu
sistem digital
yang
dapat
diprogram
memiliki
keluwesan
untuk
mengkonfigurasi ulang operasi-operasi sinyal digital secara sederhana dengan mengubah
program. Sedangkan konfigurasi ulang suatu sistem analog biasanya menuntut
mendesain ulang perangkat keras yang diikuti dengan pengkajian dan pembuktian untuk
melhat apakah sistem itu beroperasi dengan baik.
Pertimbangan
keakuratan
juga
memainkan
peranan
penting
dalam penentuan
bentuk prosesor
sinyal.
Toleransi pada komponen rangkaian analog membuat hal itu
sangat sulit bagi pendesain sistem untuk mengontrol ketepatan suatu sistem pemrosesan
sinyal analog. Dengan kata lain, suatu sistem digital menyediakan kontrol
yang
lebih
baik untuk syarat keakuratan.
|
 7
7
Sinyal digital mudah disimpan pada media magnetik tanpa mengalami penurunan
atau kehilangan keaslian sinyalnya. Sehingga sinyal-sinyal itu menjadi mudah dipindah-
pindah dan dapat diproses secara tidak terhubung (offline).
2.1.4
Elemen Dasar Sistem Pemrosesan Sinyal Digital
Sebagian besar sinyal-sinyal yang ditemukan dalam sains dan
teknologi adalah
analog. Yaitu, sinyal-sinyal yang merupakan fungsi dari suatu variabel kontinu, seperti
waktu atau ruang, dan yang biasanya mengambil nilai-nilai dalam interval yang kontinu.
Sinyal-sinyal seperti itu dapat diproses secara langsung dengan sistem analog yang tepat
atau pengganda frekuensi yang bermaksud mengubah karakteristiknya atau mengambil
beberapa informasi yang diinginkan. Itu artinya sinyal telah diproses secara langsung
dalam
bentuk
analognya,
dengan
sinyal
masukan
maupun
keluarannya
adalah
sinyal
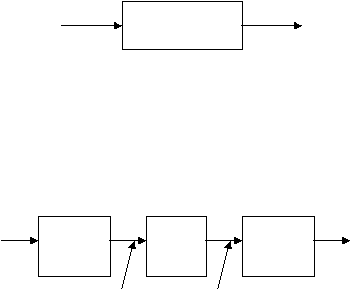
analog. Proses ini diilustrasikan pada gambar berikut :
Sinyal Masukan
Analog
Prosesor Sinyal
Analog
Sinyal Keluaran
Analog
Gambar 2.2 Sistem Proses Sinyal Analog
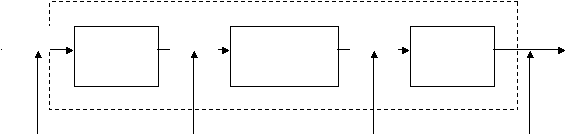
Pemrosesan
sinyal
digital
menyediakan
suatu
metode
alternatif
untuk
pemrosesan sinyal analog, seperti yang diilustrasikan pada gambar berikut :
Sinyal
Masukan
Analog
Konverter
Analog
Digital
Proses
Sinyal
Digital
Konverter
Digital
Analog
Sinyal
Keluaran
Analog
Sinyal
Masukan
Digital
Sinyal
Keluaran
Digital
Gambar 2.3 Sistem Proses Sinyal Digital
|
|
8
8
Untuk
melakukan
pemrosesan
sinyal
digital,
diperlukan
suatu interface
yang
dinamakan
pengkonversi
sinyal
analog
menjadi
sinyal
digital (A/D).
Keluaran
pengkonversi A/D adalah sinyal digital yang cocok dengan masukan terhadap prosesor
digital.
Untuk pemakaian dengan keluaran digital dari prosesor sinyal digital akan
disampaikan
kepada
pemakai
dalam bentuk
analog.
Untuk
itu,
diperlukan
sebuah
interface lain untuk mengubah sinyal digital menjadi sinyal analog, yang dinamakan
dengan pengkonversi sinyal digital menjadi sinyal analog (D/A). Namun pada beberapa
aplikasi,
pengkonversi
D/A
tidak
diperlukan, dikarenakan
aplikasi
tersebut
hanya
melakukan analisis sinyal dengan informasi yang ingin disampaikan dalam bentuk
digital. Program aplikasi yang diteliti oleh penulis merupakan salah satu aplikasinya.
2.1.5
Konversi Sinyal Analog Menjadi Sinyal Digital
Sebagian besar sinyal-sinyal, seperti sinyal biologis, sinyal seismik, sinyal radar,
dan khususnya adalah suara adalah sinyal analog. Untuk memproses sinyal analog
dengan alat digital tidak dapat langsung diproses begitu saja. Tentunya, pertama kali
adalah
harus dikonversi dulu
menjadi sinyal digital, yaitu
mengkonversi
menjadi suatu
deret angka
yang mempunyai presisi terbatas. Prosedur
ini dinamakan konversi analog
ke digital (A/D) dengan alat yang dinamakan pengkonversi A/D.
Secara
konsepsi,
kita
memandang
konversi
A/D
sebagai
proses
tiga
langkah,
yaitu :
1. Pencuplikan (Sampling)
Ini adalah konversi suatu sinyal waktu-kontinu menjadi suatu sinyal waktu
diskrit yang diperoleh dengan
mengambil
cuplikan
(sample)
sinyal
waktu
kontinu pada saat waktu diskrit. Diketahui hubungan :
x(n) = x
a
(nT),
-
8
< n < 8
dengan
x(n) adalah
sinyal
waktu diskrit
yang
diperoleh dengan
mengambil
cuplikan-cuplikan sinyal analog x
a
(t)
setiap T detik. Selang waktu T antara
cuplikan
yang berurutan dinamakan
periode pencuplikan
dan
kebalikannya
1/T = F
s
dinamakan laju pencuplikan.
|
 9
9
2. Kuantisasi
Ini adalah konversi sinyal yang bernilai kontinu waktu diskrit menjadi sinyal
bernilai diskrit, waktu diskrit (digital). Nilai setiap cuplikan sinyal
digambarkan dengan suatu nilai terpilih dari himpunan berhingga nilai-nilai
yang
mungkin.
Selisih
antara
cuplikan
x(n) yang
tidak
terkuantisasi
dan
keluaran x
q
(n) yang terkuantisasi dinamakan
Galat Kuantisasi (Quantization
Error).
3. Pengkodean
Dalam proses pengkodean, setiap nilai diskrit x
q
(n) digambarkan dengan
suatu barisan biner-b.
Pengkonversi A/D
x
a
(t)
x(n)
x
q
(n)
Pencuplikan
Pengkuantisasi
Pengkodean
01
01
1...
Sinyal
Analog
Sinyal Waktu
Diskrit
Sinyal
Terkuantisasi
Sinyal
Digital
Gambar 2.4 Bagian Dasar Konversi Analog ke Digital
2.2
File Audio Wave
File Wave adalah format sebuah file untuk menyimpan audio digital yang dibuat
oleh Microsoft dan menjadi standar dari format file audio komputer untuk segala sesuatu
mulai dari
suara sistem dan permainan,
hingga
format
file
untuk CD audio. File Wave
dapat diidentifikasi dengan nama file berekstension WAV (.wav). File Wave merupakan
format umum yang paling sederhana untuk menyimpan data sinyal audio.
|
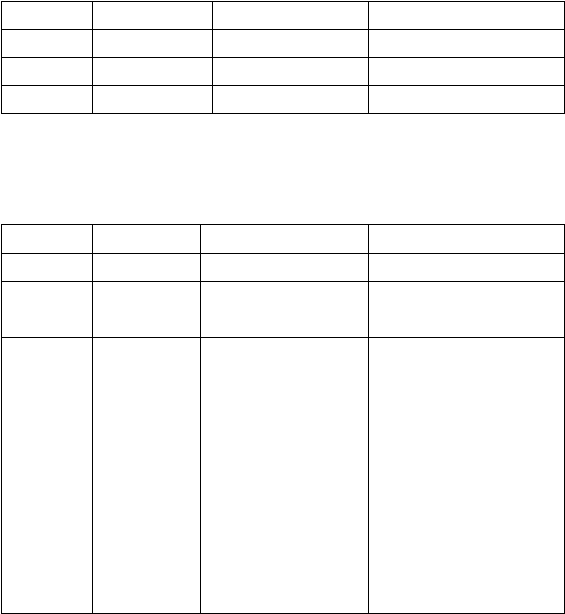 10
10
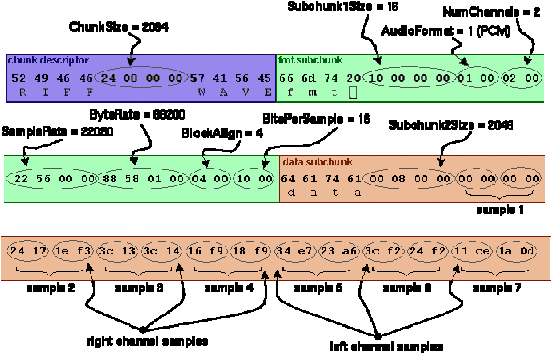
File Wave terdiri dari 3 chunk (potongan) informasi yaitu :
1. RIFF chunk yang mengidentifikasikan bahwa file tersebut adalah file Wave.
2. Format chunk yang berisi format dari informasi file suara seperti jumlah channel,
sample rate, resolusi..
3. Data chunk yang menunjukkan ukuran dari informasi file suara dan di dalamnya
terdapat kumpulan data.
Setiap chunk mengandung informasi-informasi sebagai berikut :
1. RIFF chunk
Tabel 2.1 Informasi pada RIFF Chunk
Offset File
Ukuran (byte)
Deskripsi
Nilai
0x00
4
ID Chunk
”RIFF” (0x52494646)
0x04
4
Ukuran Chunk
(ukuran file) – 8
0x08
4
Tipe
”WAVE” (0x57415645)
2. Format chunk
Tabel 2.2 Informasi pada Format Chunk
Offset File
Ukuran (byte)
Deskripsi
Nilai
0x00
4
ID Chunk
”fmt” (0x666D7420)
0x04
4
Ukuran Chunk
16
+
jumlah
byte
untuk
format extra
0x08
2
Kode Kompresi
0 = PCM tidak terkompresi
1
= Microsoft ADPCM
6 = ITU G.711 a-law
7 = ITU G.711 µ-law
17 = IMA ADPCM
20 = ITU G.273 ADPCM
(Yamaha)
49 = GSM 6.10
64 = ITU G.721 ADPCM
80 = MPEG
|
 11
11
0x0a
2
Channel
number
(banyak saluran suara)
1 = mono
2 = stereo
0x0c
4
Sample
rate
(banyak
cuplikan per detik)
1 – 0xFFFFFFFF
Contoh : 44100 Hz
0x10
4
Rata-rata
byte
yang
dimainkan per detik
= Sample rate * Channel
number * Bits per Sample
0x14
2
Block
align
(jumlah
byte satu sample
untuk
semua channel)
= Channel number * Bits
per Sample / 8
0x16
2
Bits
per
Sample
(banyak
bit
untuk
1
cuplikan)
1 – 65535
Contoh : 8 = 8 bit (1 byte)
16 = 16 biy (2 byte)
0x18
2
Tempat untuk
parameter lainnya
(tidak terdapat pada
format PCM)
0 – 65535
3. Data chunk
Tabel 2.3 Informasi pada Data Chunk
File Offset
Ukuran (byte)
Deskripsi
Nilai
0x00
4
ID Chunk
”data” (0x64617461)
0x04
4
Ukuran Chunk
Tergantung
banyaknya
cuplikan
0x08
Data Sample
|
 12
12
Gambar 2.5 Contoh Format File .WAV
2.3
Transformasi Diskrit Fourier
Transformasi
Fourier,
yang
ditemukan oleh Joseph Fourier, sering digunakan
untuk mentransformasikan sebuah sinyal domain waktu yang bersifat kontinu menjadi
sinyal domain frekuensi. Transformasi Fourier merupakan sebuah transformasi integral
yang menyatakan ulang sebuah fungsi ke dalam bentuk fungsi berbasis sinus, yaitu
sebagai sebuah penjumlahan ataupun integral dari fungsi sinus yang dikalikan dengan
suatu koefisien
Ada empat
macam jenis dari
transformasi Fourier,
yaitu
transformasi
kontinu
Fourier, transformasi diskrit Fourier, transformasi diskrit Fourier berbasis waktu, dan
deret Fourier. Keempat macam jenis
transformasi Fourier itu dapat dibedakan
menurut
sifat waktu dan frekuensinya yang dapat dilihat pada tabel 2.4 di bawah ini.
|
 13
13
Tabel 2.4 Perbedaan Empat Macam Jenis Transformasi Fourier
Transformasi
Waktu
Frekuensi
Transformasi kontinu Fourier
Kontinu, Aperiodik
Kontinu, Aperiodik
Deret Fourier
Kontinu, Periodik
Diskrit, Aperiodik
Transformasi diskrit Fourier
berbasis waktu
Diskrit, Aperiodik
Kontinu, Periodik
Transformasi diskrit Fourier
Diskrit, Periodik
Diskrit, Periodik
Transformasi kontinu Fourier menggambarkan spektrum dari sebuah sinyal
waktu
non-periodik
yang
bersifat
kontinu.
Transformasi
kontinu
Fourier
X
(
f
)
dari
sebuah fungsi waktu bersifat kontinu x(t )
dapat ditulis sebagai berikut :
X
(
f
)
=
8
?
x
(
t
)
e
-
j 2
p
f
t
dt
-
8
(Pers 2-1)
Transformasi kontinu Fourier merupakan sebuah metode yang sangat berguna
untuk menentukan komponen frekuensi dari sebuah sinyal waktu, menentukan distribusi
momentum dari
partikel,
dan
untuk
berbagai
aplikasi
lainnya.
Transformasi
kontinu
Fourier sebetulnya merupakan dekomposisi dari sebuah fungsi menjadi bentuk fungsi
berbasis sinus, yang biasanya diekspresikan sebagai eksponensial yang rumit.
Oleh karena untuk mengerjakan transformasi kontinu Fourier diperlukan
kalkulus
untuk
menghitung
integral
yang
ada, di
mana
komputer
dapat
menampilkan
transformasi Fourier berupa fungsi-fungsi yang diskrit, membuat Joseph Fourier
menciptakan
transformasi
diskrit
Fourier
dengan mengganti fungsi integral menjadi
fungsi penjumlahan yang terbatas.
Transformasi diskrit Fourier (DFT) atau yang sering disebut sebagai transformasi
Fourier terbatas, adalah sebuah transformasi Fourier yang seringkali digunakan dalam
pemrosesan sinyal dan bidang-bidang yang berkaitan dengan analisis frekuensi yang
terkandung di dalam sebuah sinyal, untuk menyelesaikan persamaan diferensial parsial,
dan untuk operasi seperti konvolusi.
|
|
14
14
DFT diperkenalkan sebagai aproksimasi metode numerik untuk mengerjakan
fungsi
transformasi
Fourier. DFT
dapat ditulis sebagai berikut :
X
(m)
dari sebuah sinyal
waktu
yang diskrit
x(n)
N
-1
X
(
m
)
=
?
n
=
0
x
(
n
)e
-
j
2
pnm / N
(Pers 2-2)
Dari persamaan 2-2, komponen dari bilangan natural dipisahkan menjadi bagian
riil dan imajinernya menggunakan persamaan Euler, yaitu :
e
-
j?
=
cos(? )+
j
sin(? )
(Pers 2-3)
Dengan
menggabungkan persamaan 2-2 dan 2-3 maka didapat persamaan DFT
yang baru yaitu :
N
-1
X
(m)
=
?
x(n)[cos(2
p
nm / N )
-
j
sin(2
p
nm / N )]
n=0
(Pers 2-4)
Seperti yang terlihat pada persamaan 2-2 dan 2-4, kalkulus tidak lagi dibutuhkan
untuk menghitung DFT. Dengan fungsi penjumlahan yang terbatas, tidak dijumpai
kesulitan dengan
fungsi
yang tak terbatas bersifat kontinu. Dalam bidang proses sinyal
digital, sinyal dan spektra diproses hanya dalam bentuk sampel, sehingga DFT adalah
sesuatu yang benar-benar dipakai untuk memrosesnya.
Implementasi dari
DFT dapat
menggunakan transformasi Fourier cepat atau fast Fourier transform.
DFT merupakan metode yang lebih relevan untuk komputasional serta lebih
sederhana secara matematika dibandingkan dengan transformasi Fourier.
2.4 Fast Fourier Transform
Walaupun DFT adalah prosedur matematika yang paling tepat untuk menentukan
isi
frekuensi
dari berbasis-waktu,
namun penggunaannya tidak efisien. Ketika jumlah
cuplikan
dalam DFT
bertambah,
maka
perhitungannya
akan
bertambah
jauh
lebih
banyak.
Pada
tahun 1965,
ilmuwan
Cooley
dan
Tukey
menciptakan
suatu
algoritma
yang
sangat
efisien
dalam
mengimplementasikan
DFT.
Algoritma
itu dikenal
dengan
|
 15
15
N
W
W
nama
fast
Fourier
transform
(FFT).
Dalam perkembangannya,
ada
berbagai
macam
algoritma
yang dikembangkan untuk FFT
ini, namun
yang akan dipakai adalah
algoritma FFT radix-2.
Algoritma FFT radix-2 sangat efisien ketika menghitung DFT dengan batasan
adalah
ukuran dari DFT
haruslah dalam bentuk perpangkatan dari 2 (N = 2
k
). Jumlah
dari perhitungan yang dibutuhkan untuk memproses FFT sejumlah N-titik adalah
N
log
2
N .
2
Dari persamaan pada N-titik pada DFT, yaitu
N -1
X
(m) =
?
x(n)e
-
j
2
pnm
/
N
n
=
0
(Pers 2-5)
FFT memisahkan input data
x(n)
menjadi dua bagian, yaitu elemen ganjil dan elemen
genap, sehingga persamaan 2-5 berubah menjadi
X
(m) =
(
N
/
2)-1
?
n=0
x(2n)e
-
j
2p
(2n)m/ N
+
(
N
/
2)-1
?
x(2n +1)e
-
j
2p (2n+1)m/ N
n=0
(Pers 2-6)
Dengan mengeluarkan fase sudut yang konstan dari penjumlahan tersebut
X
(m) =
(
N 2)-1
/ 2)-1
?
n=0
x(2n)e
-
j
2p (2n)m/ N
+
e
-
j
2pm/ N
(
N
/
2)-1
?
x(2n +1)e
-
j
2p (2n)m/ N
n=0
(Pers 2-7)
-
j2
p N
/ N
Persamaan berikut disederhanakan dengan menetapkan notasi baku, yaitu
W
N
=
e
sehingga persamaan 2-7 berubah menjadi
X
(
m
)
=
(
N
/
2 -1
) -1
?
n
=
0
x 2 n )W 2
( 2 n )W 2
nm
+
W
m
(
N
/
2
)
-1
?
x
(
2
n
+
1)W 2
nm
n
=
0
(Pers 2-8)
Karena
2
=
e
-
j
2p 2 /( N )
=
e
-
j
2p
/( N / 2 )
,
kita
bisa
menggantikan
2
dengan
W
N
/
2
,
sehingga persamaan 2-8 berubah menjadi
|
|
16
16
nm
/
2
X
(m) =
(
N
/
2)-1
?
x(2n)W
/
2
+W
(
N
/
2)-1
m
?
x(2n +1)W
nm
n=0
N
N
n=0
N
(Pers 2-9)
Sekarang kita
mempunyai 2 buah penjumlahan
N / 2
yang akan
menghasilkan N-titik
DFT. Dengan menggantikan nilai
m
pada persamaan 2-9 dengan
didapat
m
+
N / 2 , maka
(
N
/
2)-1
+ N / 2)
=
?
n(m+N / 2)
+
(m+N / 2)
(
N
/
2)-1
?
+1
n(m+N / 2)
X
(m
n=0
x(2n)W
N
/
2
W
N
n=0
x(2n
)W
N
/
2
(Pers 2-10)
Melihat hubungan
n m + N / 2 )
( m + N / 2 )
nm
nN / 2
nm
(e
-
j
2
pn 2 N / 2 N
)
W
N
/
2
=
W
N
/
2
W
N
/
2
=
W
N
/
2
nm
nm
=
W
N
/
2
(1) = W
N
/
2
(Pers 2-11)
untuk semua n bilangan bulat, maka faktor yang disebut dengan twiddle factor di depan
penjumlahan dapat disederhanakan menjadi
(m+N / 2)
m
N
/
2
m
- 2pN / 2N
j 2pN / 2N
m
m
W
N
=W
N
W
N
=W
N
(e
)
=W
N
(-1) = -W
N
(Pers 2-12)
Dengan
menggunakan persamaan 2-11 dan
2-12, maka
nilai
persamaan 2-10 berubah menjadi
X
(m + N / 2)
pada
X
(m + N / 2) =
(
N
/
2)-1
?
x(2n)W
N
/
2
-W
N
(
N
/
2)-1
?
x(2n +1)W
N
/
2
nm
m
nm
n=0
Sehingga didapat 2 buah persamaan baru yaitu
n=0
(Pers 2-13)
X
(m) =
(
N
/
2)-1
?
x(2n)W
N
/
2
+W
N
(
N
/
2)-1
?
x(2n +1)W
/
2
dan
n=0
nm
m
n=0
nm
N
(Pers 2-14)
|
 17
17
n
N
/
2
X
(m + N / 2) =
(
N
/
2)-1
?
x(2n)W
/
2
-W
(
N
/
2)-1
m
?
x(2n +1)W
nm
n=0
N
N
n=0
N
(Pers 2-14’)
Dengan hanya merubah tanda pada twiddle factor maka kita mendapatkan 2 buah
persamaan,
yaitu
X
(m)
dan
X
(m + N / 2) . Sehingga kita hanya
membutuhkan m
sebanyak
N / 2
mulai
dari
0
hingga
(
N / 2) - 1
untuk
mendapatkan semua
nilai
outputnya.
Dengan
mengambil
contoh
kasus
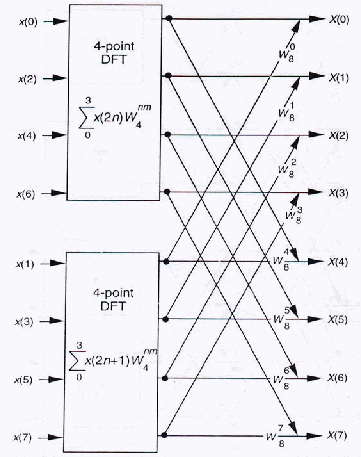
N=8,
persamaan
2-14
dan
2-14’
dapat
diimplementasikan pada gambar 2.6
Gambar 2.6
Implementasi FFT dari 8-titik DFT menggunakan dua buah 4-titik DFT
Jika kita menyederhanakan persamaan 2-14 dan 2-14’ menjadi
X
(m) = A(m) + W
m
B(m)
(Pers 2-15)
dan
|
|
18
18
N
N
/
2
N
/
2
1)W
p
+
/
/
4
X
(m + N / 2) = A(m) - W
m
B(m)
(Pers 2-15’)
kita
dapat
memecah
dua
buah
4-titik
DFT
menjadi
empat
buah
2-titik
DFT,
yaitu
dengan cara seperti sebelumnya, memecahnya menjadi bagian ganjil dan bagian genap.
atau
A(m)
(
N
/
2)-1
=
?
n=0
x(2n)W
nm
(
N
/
4)-1
=
?
2n=0
x(4n)W
4
nm
+
(
N
/
4)-1
?
x(4n
2
n=0
(
4
n+1)
m
N
/
2
A(m) =
(
N
/
4)-1
?
x(4n)W
2
nm
+
W
m
(
N
/
4)-1
?
x(4n + 1)W
2
nm
2
n
=0
N 4
/ 4
N
/
2
2
n
=0
N 4
/ 4
(Pers 2-16)
Dengan
mengganti
nilai 2n
menjadi
menjadi
p
,
maka persamaan
2-16 dapat
disederhanakan
A(m) =
(
N
/
4)-1
?
x(2 p)W
/
4
+
W
(
N
/
4)-1
m
?
x(2 p + 1)W
pm
p
=0
N
N
N
p
=0
(Pers 2-17)
Ada kemiripan bentuk antara persamaan 2-14 dengan 2-17. Dengan
ini, FFT
memiliki
kemampuan
untuk
mengurangi jumlah perhitungan pada DFT. Dengan
langkah
sama,
maka nilai
B(m)
pada persamaan 2-14’ dapat diubah menjadi
B(m) =
(
N
/
4)-1
?
x(2 p)W
/
4
-W
N
/
2
(
N
/
4)-1
?
x(2 p +1)W
N
/
4
p=0
pm
m
N
p=0
pm
(Pers 2-18)
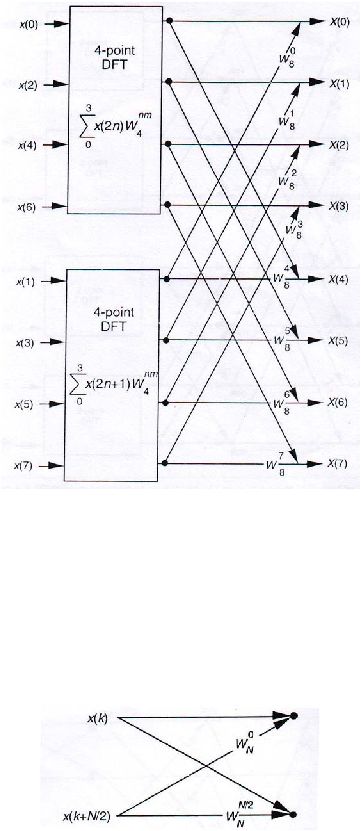
Untuk contoh kasus N=8, persamaan 2-17 dan 2-18 dapat diimplementasikan pada
gambar 2.7
|
 19
19
N
N
Gambar 2.7 Implementasi FFT dari 8-titik DFT menggunakan
dua buah 4-titik DFT dan empat buah 2-titik DFT
Bentuk pola yang tertera pada gambar 2.6 disebut dengan butterfly pattern. Pada
gambar, telah
terdapat empat buah 2-titik DFT yang
tidak dapat dibagi
lagi, sehingga
proses pembagian N-titik telah selesai.
Dari definisi
W
N
,
maka W
0
=
e
-
j
2p
0 N
/ N
=
1
dan
W
N
/
2
=
e
-
j
2p
N
/
2
N
=
e
-
jp
=
-1 , sehingga bagian 2-titik DFT ditunjukkan oleh gambar 2.8
Gambar 2.8 Sebuah 2-titik DFT butterfly
|
 20
20
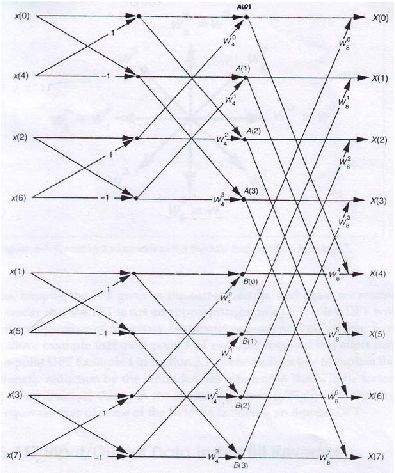
Susunan lengkap dari contoh kasus 8-titik DFT terlihat pada gambar 2.9
Gambar 2.9 Implementasi lengkap FFT dari 8-titik DFT
Untuk penentuan komponen ganjil dan genap, dilakukan suatu proses pemecahan
yang
disebut
dengan
bit reversal.
Proses
ini
melakukan
penukaran
bit-bit biner dari
angka desimal. Misalkan ada sejumlah n bit. Cara kerja dari bit reversal adalah dengan
menukar bit ke-0 dengan bit ke n-0, bit ke-1 dengan bit ke n-1, dan seterusnya. Untuk
lebih jelasnya, dapat dilihat di tabel 2.5.
|
 21
21
Tabel 2.5 Input Index Bit Reversal untuk 8-titik DFT
Normal order of
index n
Binary bits of
index n
Reversed bits of
index n
Bit-reversed
order of index n
0
1
2
3
4
5
6
7
000
001
010
011
100
101
110
111
000
100
010
110
001
101
011
111
0
4
2
6
1
5
3
7
2.5
Algoritma Divide And Conquer
Algoritma
Divide and Conquer
merupakan algoritma yang
sangat
popular
di
dunia Ilmu
Komputer. Divide and Conquer
merupakan algoritma yang berprinsip
memecah-mecah
permasalahan
yang terlalu
besar
menjadi
beberapa bagian
kecil
sehingga lebih mudah untuk diselesaikan. Langkah-langkah umum algoritma Divide and
Conquer :
Divide
: Membagi masalah menjadi beberapa submasalah yang memiliki kemiripan
dengan masalah semula namun berukuran lebih kecil (idealnya berukuran
hampir sama).
Conquer
: Memecahkan masing-masing submasalah secara rekursif.
Combine
: Menggabungkan solusi masing-masing submasalah sehingga membentuk
solusi masalah semula.
Objek
masalah
yang
dibagi
adalah
masukan
(input)
atau
instances
yang
berukuran n: tabel
(larik),
matriks, dan sebagainya, bergantung pada masalahnya. Tiap-
tiap
sub-masalah
mempunyai
karakteristik
yang
sama
(the
same
type) dengan
karakteristik
masalah
asal,
sehingga
metode Divide and Conquer lebih natural
diungkapkan
dalam skema
rekursif.
Sesuai
dengan
karakteristik
pembagian
dan
pemecahan
masalah
tersebut,
maka
algoritma
ini
dapat
berjalan
baik
pada
persoalan
yang bertipe
rekursif (perulangan
dengan
memanggil
dirinya
sendiri ).
Dengan
|
 22
22
demikian, algoritma ini dapat diimplementasikan dengan cara iteratif (perulangan biasa),
karena
pada
prinsipnya iteratif
hampir
sama
dengan rekursif. Salah
satu
penggunaan
algoritma ini yang paling populer adalah dalam hal pengolahan data yang bertipe array
(elemen larik). Mengapa?
Karena
1
pengolahan array
pada
umumnya
selalu
menggunakan
prinsip
rekursif
atau iteratif.
Penggunaan
secara
spesifik
adalah
untuk
mencari nilai minimal dan maksimal serta untuk mengurutkan elemen array. Dalam hal
pengurutan
ini
ada empat
macam algoritma pengurutan
yang
berdasar
pada
algoritma
Divide and Conquer, yaitu merge sort, insert sort, quick sort, dan selection sort. Merge
sort dan Quick sort mempunyai kompleksitas algoritma O(n ²log
n). Hal ini
lebih baik
jika dibandingkan dengan pengurutan biasa dengan menggunakan algoritma brute force.
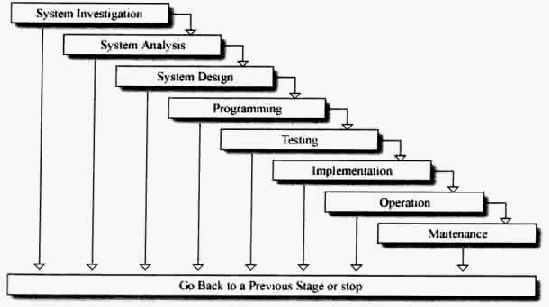
2.6 Software Development Life Cycle
Menurut
Turban,
et. al.,
Software
Development Life
Cycle
(SDLC)
adalah
kerangka terstruktur
yang terdiri dari
beberapa proses
yang berurutan vang diperlukan
untuk
membangun
suatu sistem
informasi.
Pendekatan
waterfall
digunakan
untuk
menggambarkan
SDLC. SDLC
dirancang
dengan
tujuan
untuk
membangun
alur
pemrograman yang
terstruktur
dan
untuk
membantu
manajemen
proyek
dalam
perhitungan estimasi waktu dan sumber yang dibutuhkan suatu proyek.
Gambar 2.10 Eight Stage SDLC
|
|
23
23
Tahap-tahap SDLC adalah sebagai berikut
:
1.
System Investigation.
System Investigation adalah
tahap
yang
mengutamakan
pembelajaran
terhadap
segala kemungkinan yang dapat terjadi. Dengan pembelajaran maka suatu sistem
dapat terhindar dari kesalahan yang dapat
mengakibatkan peningkatan usaha,
waktu dan jumlah pengeluaran.
2. System Analysis.
System Analysis adalah tahap yang menganalisis masalah yang perlu diselesaikan.
Tahap ini
mendefinisikan permasalahan, mengidentifikasikan penyebab,
menspesifikasikan solusi, serta mengidentifikasikan informasi-informasi yang
diperlukan.
3. System Design
System Design
adalah
tahap
yang
menjelaskan
bagaimana
suatu
sistem
akan
bekerja. Hasil dari tahap ini adalah output, input dan user interface dari sistem
serta hardware, software, database dan prosedur.
4. Programming
Programming adalah
tahap
yang
menerjemahkan
spesifikasi
desain
sistem
menjadi bahasa pemrograman yang dapat dimengerti oleh komputer.
5. Testing
Testing adalah
tahap
yang
digunakan
untuk
memeriksa apakah
pemrograman
telah
menghasilkan
hasil yang diinginkan dan diharapkan atas situasi
tertentu.
Testing dirancang untuk mendeteksi adanya kesalahan coding.
6. Implementation
Implementation adalah proses perubahan dari penggunaan sistem lama menjadi
sistem yang baru.
7. Operation and Maintenance
8. Operation and Maintenance adalah tahap untuk
memelihara
sistern baru yang
akan dioperasikan dalam suatu periode waktu.
|
|
24
24
2.7
Bentuk Program
Arsitektur aplikasi program dirancang dengan dua tipe konsep yaitu :
•
Object Oriented Programming.
•
Procedural Programming.
Object
Oriented Programming
(OOP) adalah
sebuah
paradigma
pemrograman
yang
menggunakan
class
dan object dan interaksinya
untuk mendesain
aplikasi dan
program komputer Deitel. Keunggulan yang membuat OOP sering digunakan adalah
karena
sifatnya
yang
reusable, di
mana
programmer
tidak
perlu
berulang-ulang
membuat
program untuk
modul-modul
yang mempunyai
kegiatan
fungsional
yang
mirip, sehingga penerapan OOP sangat cocok untuk membuat aplikasi atau program
yang rumit. OOP terdiri dari tiga bagian konsep, antara lain adalah :
•
Encapsulation.
•
Inheritance.
•
Polymorphism.
Encapsulation adalah konsep untuk membungkus atribut-atribut dan method-
method
yang ada pada
suatu
bagian
menjadi
sebuah class. Tujuan
dari
encapsulation
adalah untuk memudahkan konsep pemrograman,
menyembunyikan informasi yang
rahasia, dan untuk
memungkinkan pembuatan objek-objek yang mempunyai sifat yang
sama.
Inheritance
adalah
konsep
penurunan
sifat yang terdapat pada OOP,
yang
bertujuan
untuk
memudahkan
pemrograman dari
yang
sederhana
menjadi yang rumit
sehingga tidak akan membuat konsep pemrograman menjadi rumit. Tujuan dari
inheritance selain
untuk
memudahkan
pemrograman
adalah
untuk
menjaga
hubungan
antar class. Sehingga balik programmer maupun user dapat dengan mudah memengerti
aliran program apabila program telah berkembang menjadi rumit.
Polymorphism adalah konsep OOP di mana sebuah objek dapat berubah bentuk
sifatnya
ditengah
jalannya
program.
Dasar
dari
konsep polymorphism
adalah
konsep
inheritance. Pada dasarnya polymorphism adalah sebuah abstract class yang mempunyai
virtual
method
yang
diturunkan
menjadi
beberapa class yang
harus
mengimplementasikan virtual method tersebut. Tujuan dari polymorphism adalah untuk
|
 25
25
memantapkan
arsitektur
pemrograman,
karena
dengan
adanya
polymorphism arah
hubungan antar class akan menjadi jelas dan method-method dari class tersebut juga akan
menjadi jelas.
Dengan adanya tiga konsep OOP tersebut, OOP menjadi konsep pemrograman yang
handal dan dapat diimplementasikan dalam segala situasi.
Procedural programming adalah pemrograman dengan pemanggilan function atau
procedure,
disebut
juga
dengan
istilah
umum
routines. Biasa
dikenal
juga
sebagai
imperative programming. Setiap
dari procedure harus
mengandung sederetan
langkah-
langkah algoritma. Sejumlah Procedure
tersebut
dapat dipanggil
dari program
setiap
saat. Procedural Programming adalah konsep pemrograman sederhana dengan
menerapkan urutan-urutan langkah.
2.8 State Transition Diagram
STD merupakan suatu modeling tool yang menggambarkan sifat ketergantungan
sistem.
Pada
mulanya
hanya digunakan untuk menggambarkan suatu
sistem yang
memiliki sifat real time seperti proses control, telephone switching system, dan control
system.
State adalah kumpulan keadaan dan atribut yang mencirikan objek pada waktu
atau kondisi tertentu. Disimbolkan dengan segi empat.
Gambar 2.11 Notasi State
Transition adalah simbol perpindahan keaktifan dari sebuah objek menjadi
objek lain. Transition disimbolkan dengan anak panah.
Gambar 2.12 Notasi Transition
|
|
26
26
Condition adalah suatu keadaan pada lingkungan eksternal yang dapat dideteksi
oleh
sistem.
Condition menggambarkan
syarat
yang
biasanya
digunakan
dalam
hubungan seleksi.
Action
adalah
yang
dilakukan sistem
bila
terjadi perubahan
state
atau merupakan reaksi terhadap kondisi. Aksi akan menghasilkan keluaran atau output.
Display adalah hasil yang merupakan STD.
2.9
User Interface Design
User Interface (UI) Design adalah perancangan tampilan antarmuka yang bersifat
visual dari suatu aplikasi agar aplikasi tersebut dapat berinteraksi dengan baik dengan
user dan dapat digunakan dengan maksimal.
Proses perancangan UI
harus mengandung arti dari unsur-unsur visual yang
seimbang, yang dapat memodelkan inti dari operasi aplikasi yang akan dijalankan.
Selain itu perancangan UI yang baik juga harus dapat membuat aplikasi hingga mudah
digunakan dan dapat disesuaikan dengan kebutuhan masing-masing user.
Dalam perancangan UI, terdapat delapan aturan emas
yang mendukung sebuah
perancangan UI yang baik. Delapan aturan emas tersebut antara lain:
1. Usaha untuk konsistensi dalam tampilan.
2. Memungkinkan user yang rutin untuk menggunakan shortcut.
3. Memberikan umpan balik yang informatif.
4. Memunculkan dialog box pada penutupan.
5. Mempunyai error-handling sederhana.
6. Memungkinkan user untuk membatalkan tindakan.
7. Mendukung komponen dan control.
8. Mengurangi penggunaan memori jangka pendek.
|