|
BAB 2
LANDASAN TEORI
2.1 Ruang Sampel dan Kejadian
Di
dalam
suatu
kegiatan,
seringkali dilakukan berbagai
percobaan atau
eksperimen. Hasil eksperimen akan memberikan informasi tentang masalah yang sedang
dihadapi
dalam
kegiatan
tersebut.
Eksperimeneksperimen tersebut
memiliki
karakteristik:
“Hasil eksperimen tak dapat diduga sebelumnya dengan tingkat keyakinan yang
pasti.
Semua
hasil yang mungkin dapat diberikan.Eksperimen dapat dilakukan
berulang-ulang dalam kondisi yang sama.”
(Djauhari, 1990: 3)
Definisi 1
“Eksperimen-eksperimen yang
memiliki
karakteristik
tersebut,
selanjutnya
disebut
eksperimen
acak.
Kemudian,
himpunan
semua
hasil
yang
mungkin dari
suatu
eksperimen acak disebut ruang sampel (sample space) dan diberi lambang S.”
(Djauhari, 1990: 3)
Contoh 1:
Misalkan
kita
melakukan
eksperimen,
melantunkan
sebuah
mata
uang,
dan
setelah
jatuh
ke tanah,
kita
amati
bagian
atasnya.
Hasilnya
yang
mungkin
dari eksperimen ini bisa M (bagian muka), bisa pula B (bagian belakang). Jika
dianggap bahwa eksperimen tersebut dapat dilakukan berulang-ulang pada
|
 8
kondisi yang sama, maka eksperimen
tersebut merupakan
eksperimen
acak.
Ruang sampelnya S = {M,B}.
Definisi 2
“Kejadian adalah himpunan bagian dari ruang sampel.”
(Walpole, 1986 : 4)
Contoh 2:
Misalkan
?
?
?
|
0
? ? 5
?
himpunan
bagian
ruang
sampel
?
?
|
?
0
?
,t
menyatakan umur (dalam tahun) suatu komponen mesin tertentu dan A
menyatakan kejadian bahwa komponen akan rusak
sebelum akhir tahun ke
lima.
Definisi 3
“Koleksi himpunan ?
? yang tertutup terhadap komplemen dan irisan hingga
disebut lapangan.”
(Djauhari, 1990: 16)
Definisi 4
“Koleksi
himpunan
?
?
yang tertutup terhadap komplemen dan
irisan
terbilang disebut lapangan sigma.”
(Djauhari, 1990: 16)
Definisi 5
Misalkan S
ruang sampel
dari
suatu
eksperimen
acak
dan
A
suatu
lapangan
sigma yang terdiri atas himpunan bagian dari S. Peluang adalah fungsi P dari A pada [0,
1] yang bersifat:
|
 9
•
?
?
?
0 untuk setiap A di A
•
?
?
1
?
?
•
?
?
?
?
?
?
?
?
?
??
?
?, untuk setiap A1, A2, A3, … di A
dimana ?
?
?
?
?
? bila
(Djauhari, 1990: 17)
Teorema 1
Bila suatu percobaan dapat menghasilkan N macam hasil yang berkemungkinan
sama, dan bila tepat sebanyak n dari hasil berkaitan dengan kejadian A, maka peluang
kejadian A adalah :
?
?
?
??
??
(Walpole, 1986: 17)
Definisi 6
Diketahui S adalah ruang sampel. Fungsi X dari S ke  dinamakan peubah acak.
Jelajah (range) dari X yakni Ax = {x|x = X(c), c di S}dinamakan ruang peubah acak X
atau ruang dari X.
(Djauhari, 1990: 28)
F.k.p. (Fungsi Kepekatan Peluang) dari Peubah Acak Diskrit
Definisi 7
Misalkan A ruang dari peubah acak diskrit X. Jadi A terbilang. Fungsi f dari A
ke dalam ?
yang bersifat:
•
???
0, untuk setiap x di A
•
?
?
?
?
?
1
|
 10
dinamakan fungsi kepadatan peluang (f. k.p.) dari peubah acak diskrit X. Jika peubah
acak X diskrit dengan f.k.p f(x), maka peluang suatu A diberikan oleh:
•
?
?
?
?
?
?
(Djauhari, 1990: 41)
Definisi 8
Distribusi kumulatif F(x) suatu variabel random X dengan distribusi peluang f(x)
dinyatakan oleh
?
?
?
?
?
?
?
???
???
(Walpole, 1986: 38)
F.k.p. dari Peubah Acak Kontinu
Definisi 9
Misalkan A ruang peubah
acak
kontinu X. Fungsi
f
dari
A
ke
dalam ?
yang
memenuhi:
•
???
0, untuk setiap ? ? ?
•
?
???
?
1
?
dinamakan
f.k.p.
dari peubah acak kontinu X.
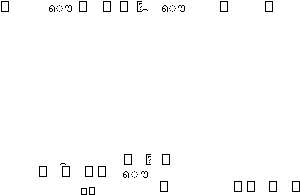
Jika peubah acak kontinu X
memiliki
f.k.p. f(x) maka peluang suatu peristiwa A diberikan oleh :
?
?
?
?
??
?
?
?
?
(Djauhari, 1990: 42)
|
 11
?
?
????
?
?
? ?
?
?
?
Definisi 10
Distribusi kumulatif F(x) suatu variabel random kontinu X dengan fungsi padat
f(x) diberikan oleh :
???
?
??
?
???
?
?
(Walpole, 1986: 44)
Definisi 11
Misalkan u(x) suatu fungsi dari X. Besaran :
?
?
? ?
?
?;
?
?
?
?
?
?
??
?
?
?
?
?
?
?
;
?
?
?
?
, dinamakan ekspektasi matematik atau nilai harapan dari u(x).
(Djauhari, 1990: 66)
Bila dalam pendekatan klasik estimator yang diperoleh hanya berdasarkan pada
informasi
sampel,
dalam pendekatan
Bayes
di
samping
informasi
sampel
juga
diperlukan informasi tentang parameter.
Definisi 12
“Suatu
informasi
pada
ruang parameter disebut
informasi
prior.
Informasi
ini
dipandang
sebagai
distribusi
peluang
pada ruang parameter
yang disebut distribusi
prior.”
(Soejoeti, 1988: 1.29)
Definisi 13
“Distribusi bersyarat ?
jika diberikan observasi sampel X disebut distribusi
posterior ?
dari X dan dinyatakan dengan ???|??.”
(Soejoeti, 1988)
Dalam menentukan distribusi posterior, khususnya untuk kasus kontinu kadang
diperlukan perhitungan integral yang tidak mudah, yaitu apabila fungsi matematikanya
|
|
12
tidak
sederhana,
salah satu cara
mengatasi kesulitan
ini
adalah dengan
menggunakan
distribusi prior sekawan.
Definisi 14
Misalkan F adalah
klas dari distribusi
peluang
dengan
fkp
f(x;
q). Klas P dari
distribusi prior
disebut
distribusi keluarga
sekawan
untuk
F
jika
distribusi posterior
berada dalam P
untuk semua
?
?, semua prior dalam P dan semua ?
?
.
Tiga sifat
yang merupakan sifat yang disenangi bagi keluarga prior sekawan adalah :
“Secara
matematik dapat
ditelusuri,
yaitu
cukup
mudah
untuk
menentukan
distribusi
posterior
dari
distribusi prior
dan
fungsi
likelihood
yang
dipunyai,
menghasilkan distribusi
posterior
yang
juga
anggota
sekawan
yang
sama,
sehingga
tidak
sulit
menggunakan teorema
Bayes
berturut-turut,
serta
mudah
dihitung
nilai
harapannya.
Keluasannya, yaitu
keluarga
distribusi
sekawan
meliputi distribusi dengan parameter-parameter yang berbeda, sehingga
mewakili
berbagai
macam
informasi
prior
yang
berbeda. Mudah
diinterpretasikan, yaitu
keluarga
distribusi
sekawan
dapat
dengan
mudah
diinterpretasikan oleh orang yang mempunyai informasi prior tersebut.”
(Soejoeti, 1988: 4.7)
Definisi 15
Misalkan
X1,
X2,
X3,…,Xn
sampel
random
dari
fungsi
probabilitas f(x;q).
Statistik W=h(X1,X2,X3,…,Xn) dikatakan cukup (sufien) untuk ?
apabila untuk semua
?
dan semua hasil yang mungkin, fungsi probabilitas X1, X2, X3,…,Xn jika diketahui w
tidak tergantung pada ? , baik dalam fungsi itu sendiri atau dalam wilayah fungsi itu.
|
 13
Untuk menentukan
statistik cukup biasanya
tidak menggunakan
definisi 15,
tetapi lebih mudah mengerjakannya dengan kriteria Fisher-Neyman.
(Soejoeti, 1990)
Teorema 2 (Kriteria Fisher-Neyman)
Misalkan
X1,
X2,
X3,…,Xn
sampel
random
dari
fungsi
probabilitas
f(x; ?
).
statistik
W=h(X1,X2,X3,…,Xn)
dikatakan
cukup
untuk ?
jika
dan
hanya
jika fungsi
probabilitas bersama X1, X2, X3,…,Xn terurai menjadi hasil kali fungsi probabilitas W
dan suatu fungsi lain yang hanya tergantung pada ?. Yakni W cukup jika dan hanya jika
f(x1,x2,x3,…,xn) =g(w; ?)h(x1,x2,x3,…,xn).
(Soejoeti, 1990)
Teorema 3
Jika T adalah statistik cukup untuk q dengan
fungsi kepadatan peluang g(t; ?)
maka
???|??
???|??
??.???;??
,
???
?
dengan ?
(?)distribusi prior untuk ? dan m(t) fungsi probabilitas marginal untuk t.
(Berger, 1980: 93)
Bukti
•
???|??
????.???;??
?
????.???;??
?
?
?
?
?
.?
?
?
?
.???;
??
?
????.????.???;??
?
?
?
?
?
.???;??
???|??
????
Definisi 16
Resiko Bayes dari ?
(terhadap prior ?) ditulis r(?; ?)didefinisikan sebagai
?
?
?; ?
?
?
?
?
??|??
?
.
(Berger, 1980: 125)
|
 14
Definisi 17
Dalam
klas
semua
estimator
bila
?
?
?;
?
?
berhingga,
estimator
d
dikatakan estimator Bayes jika ?
?
?;
?
?
?
?
?;
?
?
?
untuk setiap estimator ?
?
yang
lain.
(Berger, 1980: 126)
Fungsi-fungsi
pada
distribusi
waktu
hidup
merupakan suatu
fungsi
yangmenggunakan
variabel
random.
Waktu
hidup
adalah
interval
waktu
yang
diamati
dari suatu
individu saat
pertama kali
masuk ke
dalam
pengamatan
hingga
keluar dari
pengamatan. Misalnya
interval waktu sampai rusaknya suatu barang produksi,
matinya
suatu
makhluk
hidup,
kambuhnya
suatu
penyakit
atau
sampai
terjangkitnya suatu
penyakit. Variabel random non negatif waktu hidup biasanya dinotasikan dengan huruf
“T”, dan akan membentuk suatu distribusi.
Distribusi dari waktu hidup dapat disajikan oleh tiga fungsi berikut.
•
Fungsi Densitas Peluang/f.d.p. f(t)
Fungsi densitas
peluang
adalah
probabilitas
kegagalan
suatu
individu
pada
suatu
interval
yang
kecil
(t, t + ?t) persatuan
waktu.
Fungsi densitas
peluang (f.d.p) dinyatakan dengan f(t).
???
??
?
??
?
?
?
lim
????
?
?
......(2.1)
??
Sebagai ilustrasi, dalam sebuah penelitian mengenai lama hidup suatu individu.
Kejadian yang diamati adalah waktu kematian individu tersebut. Dalam kasus ini
?
?
?
??
?
??
?
,
?
????
???
lim
????
?
?
?
?
|
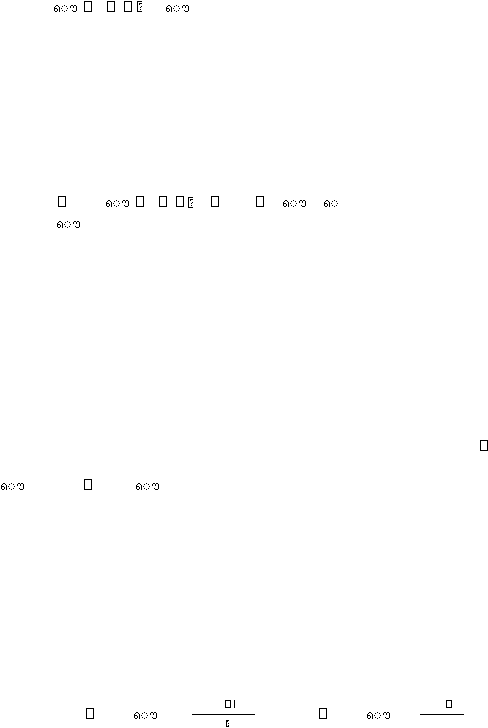 15
?
Fungsi distribusi kumulatif pada waktu t untuk suatu individu adalah probabilitas
bahwa suatu individu mengalami kegagalan sebelum waktu t atau pada interval
waktu [0,8].
????
?
??
?
f?x?dx
?
......(2.2)
•
Fungsi Survivor S(t)
Fungsi survivor adalah peluang suatu individu bertahan hidup lebih dari
waktu t dengan t > 0. Fungsi survivor dinyatakan dengan S(t).
???
?
??
?
?
?
?
?
?
1
????
......(2.3)
Mengacu pada ilustrasi di depan:
S(t) = P[individu hidup lebih lama dari waktu t]
Dalam
beberapa
hal,
khususnya
yang
mencakup tahan
hidup dari komponen-
komponen
industri,
S(t)
ditentukan sebagai
fungsi
reliabilitas. S(t)
merupakan
fungsi
kontinu menurun secara kontinu dengan S(0) = 1, artinya peluang suatu
individu bertahan hidup lebih lama dari waktu nol adalah 1
dan
?
8
?
lim
?
?
?
0, artinya peluang suatu
individu
bertahan
hidup pada
waktu yang tak terhingga adalah 0.
•
Fungsi Hazard h(t)
Fungsi
hazard adalah suatu fungsi yang
menunjukkan tingkat kegagalan
atau resiko dalam interval (t, t + ?t) dan diketahui bahwa individu tersebut telah
bertahan hidup selama waktu t. Fungsi hazard dinyatakan dengan:
P?
???
???
P?
?
???
?
?
?
lim
????
?
?
atau
?
?
?
lim
????
?
??
?
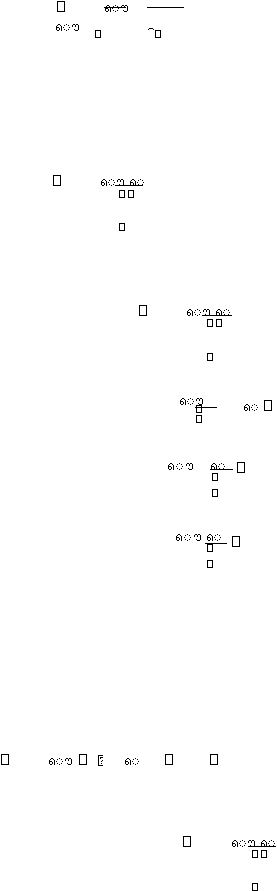
fungsi hazard dapat pula dinyatakan oleh dua buah fungsi yaitu fungsi survivor
dan fungsi densitas peluang.
|
 16
?
?
?
????
??
?
?
......(2.4)
???
?
???
Teorema 4
Jika T
variabel random
yang
menyatakan waktu
hidup dimana T ³ 0, dan
f(t)
merupakan f.d.p serta S(t) merupakan fungsi survivor, maka :
?
?
?
?
??
??
?
Bukti :
Dari (2.2) dan (2.3) maka
?
?
?
?
??
??
?
??
?
?1
???
?
0
?
?
?
???
?
?
?
???
Teorema 5
Jika T
variabel random
yang
menyatakan waktu
hidup dimana T = 0 dan S(t)
merupakan fungsi survivor
dan h(r) menyatakan fungsi hazard maka
???
?? ?
?
???
??
?
Bukti.
Berdasarkan teorema 4 diketahui bahwa
?
?
?
?
??
??
?
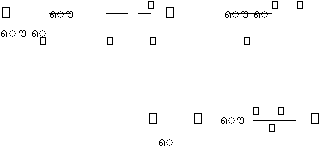
dan persamaan (2.4) adalah
|
 17
???
?
?
?
?
?
?
????
??
???
???
???
?
?
Dengann menggunakan salah satu sifat S(t) bahwa S(0) = 1, maka
?
?
??
?
?
?
?
?
???
?
?
?
?
?
?
?
|
 18
?
?
ln
?
?
??
?
ln
?
?
?
ln
?0?
ln
?
?
?
Sehingga
???
exp ?
?
?
???
??
Akibat Teorema 5
Berdasarkan teorema 4 dan teorema 5, f(t) dapat dinyatakan dalam h(t)
sebagai
???
???. exp ?
?
?
???
??
Bukti:
?
?
?
???
?
??
?
maka
?
?
?
?
?
?
.
??? sehingga terbukti bahwa
???
???. exp ?
?
???
??
?
Dari
teorema 4
dan
teorema 5
serta akibat dari teorema 5 di atas, dapat dilihat
bahwa
ketiga
fungsi
pada
distribusi waktu
hidup
yaitu
f(t),
S(t),
dan
h(t)
saling
berhubungan satu dengan yang lainnya.
Dalam
uji
sampel
lengkap,
eksperimen
akan
dihentikan
jika
semua
komponen
yang
diuji
telah
mati
atau
gagal.
Cara
seperti
ini
mempunyai keuntungan
yaitu dapat
dihasilkan observasi terurut dari semua komponen yang diuji.
(Lawless, 1982: 231)
Definisi 18
F.k.p
untuk
waktu
kegagalan
T
berdistribusi Weibull
dengan
parameter
q
dinyatakan sebagai :
|
|
19
?
?|?; ?
?
?
?
?? ?
?
?
?
,?
0,? ? 0,? ?
0
?
?
|
|
20
(Sinha, 1979: 136)
Penerapan distribusi Weibull pada analisis uji hidup antara lain dilakukan oleh
Kao
(1959)
dengan
menerapkan distribusi Weibull dalam
uji
hidup
tabung
elektron,
kemudian Leiblain dan Zeln (1956) melakukan penelitian penerapan distribusi ini dalam
bidang
rekayasa
(Zanzawi,
1996:7).
Selanjutnya banyak
peneliti
yang
mengembangkannya antara
lain Thomas dan Wilson (1972),(Lawless, 1982:145),
Pandey dan Malik (1989).
Menurut William
W.
Hines
dan Douglas C. Montgomery (1990: 268), sebuah
metode
yang
paling
baik
untuk
memperoleh sebuah
estimator
yang
tunggal
adalah
metode
maksimum likelihood.
Karena
secara
konsep
prosedur
metode
maksimum
likelihood sangat sederhana dan metode ini lebih umum
digunakan untuk mengestimasi parameter-parameter distribusi waktu hidup.
Definisi 19
Misalkan
x
variabel random
dengan
p.d.f
f(x;q),
dimana
parameter
q
tidak diketahui.
Misalkan X1, X2, …, Xn menjadi nilai yang diobservasi di dalam suatu sampel random
yang besarnya n. Maka fungsi likelihood sampel tersebut adalah :
L(?)
=
f(x1; ?).
f(x2; ?). …. f(xn;
?)
(Hines, 1990: 268)
?ˆ
merupakan
nilai
maksimum
likelihood
estimator
atau
dengan
kata
lain
maksimum
likelihood adalah
nilai ?
yang
memaksimumkan
fungsi
likelihood.
Fungsi
likelihood
lebih cocok apabila dikerjakan dengan menggunakan natural logaritma dan dinotasikan
dengan ln L(?).
|
|
21
2.2 Java dengan builder NetBeans dan database MySQL.
Java
adalah
sebuah
bahasa
pemrograman dengan
basik
Object
Oriented
Programing (OOP)
yang
sangat
efisien
dan
mempunyai sifat
“global”.
Hal
ini
dikarenakan aplikasi desktop ataupun aplikasi web dapat berjalan sepenuhnya di
semua
“Operating System”
yang
sudah
terinstal
Java
Enviroment. Penulis
menggunakan
dukungan bahasa Java
dan
NetBeans
ini
seutuhnya
legal
dan
tidak
memerlukan ijin
apapun juga. Karena Java dan Netbeans ini bersifat “freeware”. Ini juga menjadi
salah
satu alasan kenapa penulis memilih menggunakan bahasa pemrograman Java.
Dalam
distribusinya
Java
dibagi
kebanyak
jenis
dan
bagian.
Tiga
kelompok
besar Java adalah :
•
Java Standart Edition yang di gunakan untuk mendukung aplikasi dengan basic
Java di PC
•
Java Enterprise Edition yang lebih fokus pada aplikasi – aplikasi yang digunakan
server besar
•
Java Micro
Edition
yang
fokusnya kedalam pembuatan program program
berukuran micro yang biasa di gunakan di ponsel – ponsel.
Program Java bisa langsung diunduh secara gratis di http://java.sun.com. Di situ
bisa didapatkan
versi
dari
java yang
terbaru. Penulis
menggunakan Java Development
Kit versi 6 update ke 21. Lalu di dukung dengan NetBeans versi 6.9.1.
NetBeans
adalah
sebuah
developer kit
untuk
membuat
program berbasi
Java.
NetBeans
mempunyai tampilan
yang
cukup
rumit
untuk
sebuah
developer
kit.
Tapi
|
 22
tentunya hal tersebut tidak akan dirasakan lagi apabila pengguna mulai tebiasa dengan
tampilan tersebut.
Penulis
akan
memulai
pembuatan program simulasi
dimulai
dari
user
interfacenya. Setelah user
interfacenya tersusun makan penulis akan mulai memasukan
kode-kode
dan
event-event
yang
dibutuhkan.
Tahap
pengembangan aplikasi
yang
demikian dinamakan “Bottom Up”.
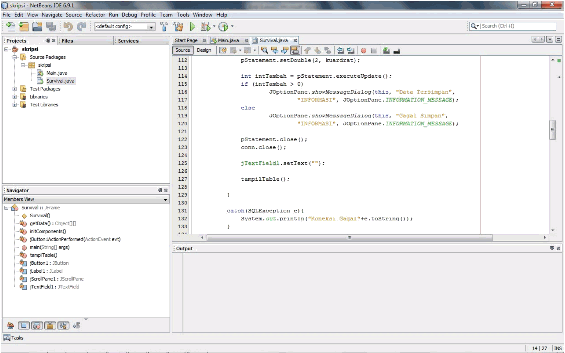
Berikut
adalah
tampilan dari NetBeans 6.9.1 padasaat
penulisan
source
code
Java.
Gambar (2.1)
|
 23
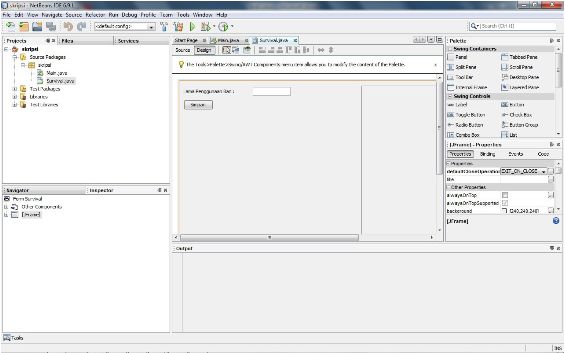
Berikut adalah tampilan NetBeans saat pembuatan User Interface.
Gambar (2.2)
Dikedua gambar di
atas dapat kita
lihat tab
project
yang berisikan data dan kumpulan
file dari project yang sedang dikerjakan. Di bawahnya terdapat navigator dan inspector
untuk
memudahkan kita
melihat smua element element
yang ada saat
membuka suatu
form
atau
class
java.
Pada
saat
penulisan source
code,
tampilan
NetBeans cukup
sederhana, di bagian kanan hanya terdiri dari tempat penulisan source code dan dibawah
nya
terdapat
kolom
output
yang
memberikan kita
laporan
setiap kali kita
men-debug
program yang sedang dibuat. Pada
saat pembuatan User Interface, kolom output
tetap
ada,
tetapi
di
atasnya
terdapat
tempat
design
User
Interface, Palette
control
dan
Properties.
Pada
tempat
mendisign
kita bisa
mengatur posisi
dan
letak
tombol
sesuai
dengan yang kita inginkan. Sedangkan semua tampilan grafis yang kita butuhkan seperti
|
|
24
tombol, text box, panel scroll dan lain – lainnya dapat kita dapatkan dari colom Palette.
Di
situ
terdapat banyak
sekali
jenis
yang
tentunya
tidak
perlu
dibahas
penulis
disini.
Pada properties, kita bisa mengatur semua tentang object grafis yang kita masukan, dari
nama akses,
ukuran, jenis huruf, tampilan, dan sebagainya. Di propeties, kita juga bisa
melihat binding dari object tersebut, event yang ada padaobject tersebut, ataupun bentuk
dari code yang digunakan.
MySQL
adalah
sistem
penyimpanan database
yang
pengoperasiannya
menggunakan perintah SQL. MySQL adalah database dasar yang
menggunakan bahasa
Java
dalam
pembuatannya. Untuk
mengakses
database
bisa
menggunakan banyak
program
tambahan
yang
mendukung
untuk
mempermudah
pengoperasian dan
akses
database tanpa perlu melalui perintah di “command promt”. Untuk penulisan skripsi ini,
penulis
menggunakan program
tambahan
phpMyAdmin.
Sehingga
database
MySQL
dioperasikan dan
dapat
diatur
dengan
mudah
melalui
tampilan
web
yang
cukup
sederhana.
|
 25
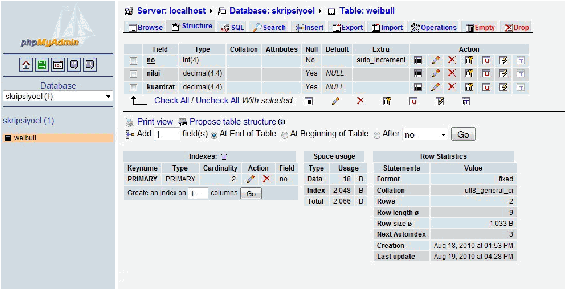
Berikut adalah contoh tampilan dari phpMyAdmin.
Gambar (2.3)
Dari
gambar di
atas
dapat
kita
lihat,
tampilan dari
phpMyAdmin
cukup
sederhana.
Tombol kecil yang ada di sisi kiri urut dari kiri ke kanan adalah :
•
Home untuk kembali ke halaman muka.
•
Log Out untuk keluar dari phpMyAdmin
•
SQL query window untuk membuka jendela query SQL
•
phpMyAdmin documentation untuk membuka dokumentasi – dokumentasi yang
ada tentang phpMyAdmin
•
SQL documentation untuk membuka dokumentasi tentang database SQL
Di
sisi kiri
terdapat tab
untuk
memilih database
yang ada.
Disusul
di
sisi
bawahnya
terdapat keterangan database yang sedang dibuka dan isi dari tabel yang ada. Di sebelah
kanannya terdapat keterangan posisi window saat ini. Gambar di atas menyatakan posisi
|
|
26
pada saat membuka tabel weibull. Di bawahnya terdapat banyak tab, dari kiri ke kanan
adalah :
•
Browse untuk membuka dan membaca isi dari tabel yang dipilih
•
Structure untuk melihat struktur dari tabel yang dipilih
•
SQL untuk membuka window tempat mengimput query – query SQL
•
Search untuk masuk ke mode pencarian
•
Insert untuk membuka halaman input data
•
Export untuk mengekspor data
•
Import untuk mengimpor data database atau file lain
•
Operation
untuk
membuka halaman
pengaturan bagaimana
cara kerja
sebuah
tabel tersebut
•
Empty untuk mengosongkan tabel yang dipilih
•
Drop untuk menghapus tabel yang dipilih
Walaupun memiliki tampilan yang cukup sederhana tetapi bisa dikatakan bahwa
MySQL dengan phpMyAdmin memiliki kemampuan yang cukup rumit untuk
menangani server server besar. Dan satu yang tidak boleh kita lupakan bahwa MySQL
dan
phpMyAdmin
adalah
jenis
program
berdistribusi freeware,
sama
seperti
Java dan
NetBeans,
sehingga
tidak
membutuhkan
lisensi
ataupun
ijin
khusus untuk
menggunakannya.
|