|
18
BAB 2
LANDASAN TEORI
2.1
Preventive Maintenance
2.1.1
Pengertian Perawatan (Maintenance)
Menurut
Assauri
(1999,
p59)
perawatan
merupakan kegiatan
untuk
memelihara atau
menjaga
fasilitas
dan
peralatan pabrik,
dan
mengadakan
perbaikan, penyesuaian atau penggantian yang diperlukan untuk mendapatkan
suatu
kondisi
operasi
produksi
yang
memuaskan, sesuai
dengan
yang
direncakan. Dengan
adanya perawatan diharapkan semua
fasilitas dan
mesin
yang dimiliki oleh perusahaan dapat dioperasikan sesuai dengan jadwal yang
telah ditentukan.
Perawatan
mempunyai peranan
yang
sangat
menentukan
dalam
kegiatan produksi dari suatu perusahaan
yang
menyangkut kelancaran atau
kemacetan produksi,
kelambatan
dan
volume
produksi.
Dengan
demikian
perawatan memiliki
fungsi
yang sama
pentingnya dengan
fungsi-fungsi
lain
dari suatu perusahaan.
Karena pentingnya aktivitas perawatan
maka diperlukan perencanaan
yang
matang
untuk
menjalankannya, sehingga
terhentinya
proses
produksi
akibat mesin rusak dapat dikurangi seminimum mungkin. Aktivitas perawatan
yang benar-benar baik dapat mengurangi biaya untuk merawat mesin.
|
|
19
Menurut
sumber
yang
didapat
dari
jurnal
ilmiah
internasional,
=68814&RQT=309&VName=PQD, manajemen pabrik-pabrik terutama
yang
berhubungan dengan
bagian
perawatan
atau
maintenance
biasanya
dihadapkan pada pertimbangan-pertimbangan
yang saling berbenturan.
Sebagai
contoh,
jika
peralatan
mengalami
perawatan
yang
berlebih,
maka
biaya
untuk
perawatan akan
semakin
tinggi,
namun
apabila
perawatannya
kurang,
maka
akan berakibat
pada
meningkatnya kerusakan-kerusakan
pada
peralatan tersebut. Pada situasi seperti ini, dimana keperluan untuk perawatan
bergantung pada macam-macam kondisi, akan sangat sulit
untuk menentukan
strategi perawatan dan pemeliharaan yang optimal yang akan memaksimalkan
keuntungan
yang
diperoleh
dari
peralatan-peralatan tersebut
dengan
berdasarkan kepada berbagai kriteria.
Pengertian
lain
mengenai pemeliharaan
menurut
Heizer
adalah
suatu
aktivitas
yang berkaitan dengan
usaha mempertahankan peralatan/sistem
dalam kondisi layak bekerja.
2.1.2
Tujuan Maintenance
Adapun tujuan utama dari fungsi maintenance, menurut Assauri (1999,
p95) adalah:
|
|
20
1. Kemampuan
berproduksi dapat
memenuhi kebutuhan sesuai
dengan
rencana produksi.
2.
Menjaga
kualitas
pada
tingkat
yang
tepat
untuk
memenuhi apa
yang
dibutuhkan oleh
produk
itu
sesuai
dan
kegiatan
produksi
yang
tidak
terganggu.
3. Untuk
membantu
mengurangi pemakaian dan penyimpangan
yang diluar
batas
dan
menjaga
modal
yang
diivestasikan dalam
perusahaan
selama
waktu
yang
ditentukan sesuai dengan kebijaksanaan perusahan
mengenai
investasi tersebut.
4.
Untuk
mencapai
tingkat
biaya
maintenance
serendah
mungkin
dengan
melaksanakan kegiatan maintenance secara efektif dan efisien.
5. Menghindari
kegiatan
meintenance
yang
dapat
membahayakan
keselamatan para pekerja.
6. Mengadakan suatu kerjasama yang erat dengan
fungsi-fungsi utama
lainnya
dari
suatu
perusahaan,dalam ranka
mencapai
tujuan
utama
perusahaan yaitu tingkat keuntungan atau return of investment yang sebaik
mungkin dan total biaya yang terendah.
|
|
21
2.1.3
Jenis-Jenis Perawatan
Aktivitas perawatan (maintenance)
dapat dibedakan dalam
lima
jenis
yaitu preventive maintenance, corrective maintenance, reactive maintenance,
proactive maintenance dan predictive maintenance.
2.1.3.1 Pengertian Preventive Maintenance
Preventive
maintenance
adalah
kegiatan
perawatan yang
dilakukan
untuk
mencegah
timbulnya
kerusakan
dan
menemukan kondisi
yang
dapat
menyebabkan fasilitas atau mesin produksi
mengalami kerusakan pada waktu
melakukan kegiatan produksi.
Dengan demikian semua
fasilitas atau
mesin
yang
mendapat tindakan
preventive
akan
terjamin
kelancaran kerjanya
dan
selalu
dalam
keadaan
optimal untuk melakukan kegiatan proses produksi.
Dalam pelaksanaannya preventive maintenance dapat dibedakan atas
routine maintenance dan periodic maintenance.
Routine maintenance adalah kegiatan perawatan yang dilakukan secara
rutin. Contohnya pelumasan, pengecekan isi bahan bakar.
Periodic maintenance
adalah kegiatan perawatan yang dilakukan
secara periodik atau dalam jangka waktu tertentu (Assauri, p90).
|
|
22
2.1.3.2 Corrective Maintenance
Corrective
maintenance
merupakan kegiatan
perawatan
yang
dilakukan
setelah
mesin
atau
fasilitas
mengalami
kerusakan
atau
gangguan.
Dalam
hal
ini
kegiatan
corrective
maintenance
bersifat
perbaikan yaitu
menunggu sampai kerusakan terjadi terlebih dahulu, kemudian baru diperbaiki
agar dapat beroperasi kembali.
Tindakan corrective
ini
dapat
memakan biaya
perawatan
yang
lebih
murah
daripada tindakan preventive.
Hal
tersebut
dapat
terjadi
apabila
kerusakan terjadi disaat mesin atau fasilitas tidak melakukan proses produksi.
Namun saat kerusakan terjadi selama proses produksi berlangsung maka biaya
perawatan akan mengalami peningkatan akibat terhentinya proses produksi.
Dengan
demikian
dapat
disimpulkan bahwa
tindakan
corrective
memusatkan
permasalah
setelah
permasalahan tersebut
terjadi,
bukan
menganalisa masalah untuk mencegahnya agar tidak terjadi.
2.1.3.3 Reactive Maintenance
Reactive
maintenance
adalah
kegiatan pemeliharaan yang
dilakukan
sebagai
respon
terhadap
breakdown unit
yang
tidak
terencana,
umumnya
sebagai hasil dari kegagalan baik yang bersifat internal ataupun yang bersifat
eksternal.
Yang
termasuk
kedalam reactive
maintenance
adalah
corrective
maintenance.
|
|
23
2.1.3.4 Proactive Maintenance
Proactive
maintenance
adalah
pemeliharaan yang
dilakukan
secara
teratur dan terencana tanpa
menunggu
mesin rusak terlebih dahulu, sehingga
dapat
meminimasi kemungkinan terjadinya breakdown akibat kerusakan
mesin.
Yang
termasuk
dalam proactive
maintenance
adalah
preventive
maintenance dan predictive maintenance.
2.1.3.5 Predictive Maintenance
Predictive
maintenance
adalah
pemeliharaan
yang
dilakukan
melalui
analisa
secara
fisik
terhadap
peralatan
atau
komponen dengan
bantuan
pengukuran instrumen
tertentu
seperti
alat
pengukur
getaran,
temperatur,
pengukur suara dan lain-lain untuk mendeteksi kerusakan sedini mungkin.
2.1.4
Langkah-Langkah Pengambilan Tindakan Maintenance
Dalam
menentukan tindakan
Maintenance
yang diambil
ada
4
tahap
yang harus dilewati terlebih dahulu yaitu:
1. What
Menentukan
jenis
komponen yang perlu diberlakukannya pemeliharaan
rutin. Tipe komponen digolongkan dalam jenis:
•
Komponen Kritis
Komponen yang frekuensi kerusakannya sangat sering.
|
|
24
•
Komponen Mayor
Komponen yang frekuensi kerusakannya cukup tinggi.
•
Komponen Minor
Komponen yang frekuensi kerusakannya jarang.
2. How
Berarti bagaimana cara atau tindakan pemeliharaan yang diambil
•
Inspeksi Rutin
•
Preventive Maintenance
•
Corrective Maintenance
3. Who
Siapa yang akan bertanggung jawab atas kerusakan dan yang bertanggung
jawab untuk mereparasikan.
4. Where
Menunjukan tempat yang akan digunakan untuk mereparasinya.
2.1.5
Konsep-Konsep Pemeliharaan
2.1.5.1 Konsep Reliability (Keandalan)
Menurut
Ebeling
reliability
adalah
probabilitas suatu
komponen atau
sistem yang akan berjalan sesuai dengan fungsi
yang ditetapkan dalam jangka
waktu
tertentu
saat
komponen tersebut
beroperasi. Reliability
adalah
probabilitas mesin tidak rusak walaupun telah beroperasi overtime, sedangkan
|
|
25
menurut Heizer & Render, Reliability adalah peluang suatu mesin dapat
berfungsi secara benar pada waktu tertentu dibawah kondisi tertentu pula.
2.1.5.2 Konsep Keterawatan
Adalah
suatu
probabilitas suatu
komponen
atau
sistem
yang
menunjukan kemampuan yang
diharapkan
pada
suatu
waktu
tertentu
saat
perawatan dilakukan sesuai
dengan prosedur
yang
diharuskan.
Keterawatan
suatu
komponen
juga
dapat
dikatakan sebagai
probabilitas
suatu komponen
dapat diperbaiki sesuai dengan waktu yang diberikan.
2.1.5.3 Konsep Avaibility (Ketersediaan)
Adalah
probabilitas suatu
komponen
atau
sistem
yang
menujukan
kemampuan
yang diharapkan
pada
suatu
waktu
tertentu
ketika
dioperasikan
dalam kondisi operasional tertentu. Ketersediaan juga dapat dikatakan sebagai
presentase waktu
operasional
sebuah komponen
atau
sistem
selama
interval
waktu tertentu.
Yang
membedakan avaibility
dan
reliability
adalah
probabilitas
saat
komponen dalam keadaan tidak rusak walaupun pada masa lampau telah rusak
tetapi
telah
diperbaiki kekondisi semulanya. Makanya
nilai
Avaibility
tidak
akan pernah rendah dari nilai Reliability.
|
|
26
2.1.6
Konsep Preventive Maintenance
Konsep preventive maintenance pertama
kali diterapkan
di Jepang
pada tahun 1971. Konsep ini
mencakup semua hal
yang berhubungan dengan
maintenance dengan
segala
implementasinya
di lapangan.
Konsep ini
mengikut sertakan
pekerja
dari
bagian
produksi
untuk
ambil
bagian
dalam
kegiataan
maintenance
tersebut.
Dengan
demikian
maka
diharapkan terjadi
kerjasama yang baik antara bagian maintenance dan bagian produksi.
Inti dasar dari preventive maintenance adalah
inspeksi dan reparasi
bila
terjadi
kerusakan pada
fasilitas.
Inspeksi
dilakukan untuk
mencegah
kerusakan yang akan mengganggu proses produksi.
Ada tiga hal utama dalam maintenance adalah:
•
Membersihkan ( Cleaning )
Pekerjaan ini adalah tugas yang harus dilakukan setiap mesin atau fasilitas
lainnya
setelah
digunakan.
Pembersihan dapat
dilakukan
dengan
pembersihan
dari
debu-debu
sisa
produksi
dan
juga
mencuci
peralatan
yang telah dipakai.
•
Memeriksa ( Inspection )
Pekerjaan
kedua adalah memeriksa bagin-bagian
dari mesin yang
dianggap
perlu. Pemeriksaan rutin
perlu
dilakukan
sesuai
dengan
waktu
yang telah ditentukan.
|
|
27
•
Memperbaiki ( Repair )
Pekerjaan
selanjutnya adalah
memperbaiki bila
terdapat
kerusakan-
kerusakan sehingga dapat digunakan kembali seperti kondisi normal.
2.1.7
Distribusi Kerusakan
Distribusi kerusakan adalah informasi dasar mengenai umur pakai
suatu peralatan dalam suatu populasi. Distribusi yang umum digunakan adalah
distribusi eksponensial, lognormal, normal dan Weibull. Distribusi kerusakan
ini dapat memenuhi berbagai
fase kerusakan. Jika sampelnya
tergolong kecil
maka
penaksiran parameter
distribusi
dilakukan
dengan
metode
kuadrat
terkecil (least squares curve fitting). Distribusi exponensial biasanya
digunakan
jika
laju
kerusakannya konstan
terhadap
waktu.
Distribusi
lognormal
memiliki kemiripan dengan distribusi Weibull sehingga jika
pada
suatu kasus memiliki distribusi Weibull maka distribusi Lognormal, juga
cocok untuk digunakan. Distribusi normal biasanya digunakan pada fenomena
terjadinya
wear
out
region.
Distribusi
Weibull
dapat
digunakan pada
model
yang mengalami laju kerusakan menaik maupun menurun.
Dalam perhitungan nilai
fungsi distribusi kumulatif
(F(ti)) digunakan
metode pendekatan median
rank
karena
metode
ini
memberikan
hasil
yang
lebih
baik
untuk
distribusi
kerusakan
yang
mempunyai
penyimpangan
|
 28
distribusi (skewed distribution).
Adapun
nilai F(ti) tersebut didekati dengan
persamaan :
F ti) =
(ti) =
i
-
0.3
n
+
0.4
2.1.7.1 Distribusi Eksponensial
Distribusi ini
memiliki laju kerusakan yang tidak berubah dan kostan
terhadap
waktu
(Constant Failure Rate Model). Penaksiran
parameter
distribusi Eksponensial
dilakukan dengan
metode
kuadrat
terkecil
(least
squares method) yaitu :
•
xi = ti
•
yi = ln [1/(1-F ( ti ))]
•
F(ti) = ( i-0.3 ) / ( n+ 0.4)
•
Parameter :
n
?
x
i
y
i
?
=
b
=
i
=1
?
x
i
2
i 1
=1
Dimana :
ti
=
data kerusakan ke i
i
=
1,2,3,…..,n
n = jumlah data kerusakan
F(ti) dihitung dengan menggunakan pendekatan median rank
|
|
29
Fungsi kerusakan distribusi Eksponensial adalah
•
Fungsi Kepadatan Probabilitas
f
(t )
=
?
e
-
?t
•
Fungsi Distribusi Kumulatif
f
(t )
=
1
-
e
-
?t
•
Fungsi Keandalan
R(t ) = 1
-
e
-
?t
•
Fungsi Laju Kerusakan
?
(t)
=
f
(t )
=
?
R(t )
•
Nilai Rata-Rata Distribusi Eksponensial
MTTF
=
1
?
2.1.7.2 Distribusi Lognormal
Distribusi
lognormal
memiliki
dua
parameter
yaitu parameter
bentuk
(s) dan parameter lokasi (t
med
). Seperti distribusi Weibull, distribusi
Lognormal
memiliki
bentuk
yang
bervariasi.
Yang
sering
terjadi,
biasanya
data yang dapat didekati dengan distribusi Weibull
juga bisa didekati dengan
distribusi lognormal.
Distribusi lognormal
dilakukan
dengan
menggunakan
metode kuardrat terkecil (least square method) yaitu:
•
xi = ln ti
|
 30
?
?
•
yi = zi = F
-1
[F (ti)]
•
F(ti) = ( i- 0.3 ) / ( n + 0.4)
n
?
n
?
n
?
x
i
y
i
-
?
?
y
i
?
•
b
=
i 1
=1
n
?
i
=1
?
n
2
2
n
?
x
i
i 1
=1
-
?
?
x
i
?
?
i
=1
?
n
n
?
y
i
?
x
i
•
a
=
1
i 1
=1
-
b
i 1
=1
n
n
•
Parameter
s
=
1
b
dan t
med
=
e
-
(
as
)
Dimana :
ti = data kerusakan ke i
i = 1,2,3,…..,n
n = jumlah data kerusakan
zi = nilai dari tabel distribusi normal
F(ti) dihitung dengan menggunakan pendekatan median rank
Fungsi kerusakan distribusi lognormal adalah
•
Fungsi Kepadatan Probabilitas
f
(t ) =
1
e
st 2p
2
1
?
t
?
2
2
ln
?
?
s
?
t
med
?
|
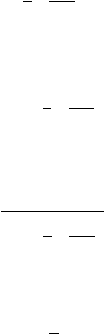 31
?
?
?
?
•
Fungsi Distribusi Kumulatif
f
(t ) = F
?
1
ln
t
?
?
s
t
med
?
•
Fungsi Keandalan
R(t ) = 1 - F
?
1
ln
t
?
?
s
t
med
?
•
Fungsi Laju Kerusakan
?
(t) =
f
(t
)
?
1
t
?
1
-
F
?
?
s
ln
?
t
med
?
•
Nilai Rata- Rata Distribusi lognormal
s
2
MTTF
=
t
med
e
2
2.1.7.3 Distribusi Normal
Bentuk distribusi normal memyerupai lonceng sehingga memilki nilai
simetris
terhadap
nilai
rataan
dengan
dua
parameter
bentuk
yaitu
µ
(nilai
tengah) dan
s
(standart deviasi). Parameter µ (nilai tengah)
memiliki
sembarang
nilai,
positif
maupun negatif.
Sedangkan parameter
s
(standart
deviasi) selalu memiliki nilai positif.
Distribusi normal dilakukan dengan menggunakan metode kuadrat
terkecil (least square method) yaitu:
•
xi = ti
|
 32
2
?
?
?
•
yi = zi = F
-1
[F (ti)]
•
F(ti) = ( i- 0.3 ) / ( n + 0.4)
n
?
n
?
n
?
x
i
y
i
-
?
?
y
i
?
•
b
=
i
=1
n
?
i
=1
?
n
2
2
n
?
x
i
i
=1
-
?
?
x
i
?
?
i
=1
?
n
n
?
y
i
?
x
i
•
a
=
i
=1
-
b
i
=1
n
n
•
Parameter
µ
=
-
a
b
dan
s
=
1
b
Dimana :
ti = data kerusakan ke i
i = 1,2,3,…..,n
n = jumlah data kerusakan
zi = nilai dari tabel distribusi Normal
F(ti) dihitung dengan menggunakan pendekatan median rank
Fungsi kerusakan distribusi Normal adalah:
•
Fungsi Kepadatan Probabilitas
?
=
(t - µ )
?
?
f
(t ) =
1
e
?
st 2
p
?
2s ²
?
|
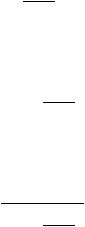 33
•
Fungsi Distribusi Kumulatif
?
t -
µ
?
f
(t ) = F
?
?
?
s
?
•
Fungsi Keandalan
?
t -
µ
?
R(t ) = 1
-
F
?
?
?
s
?
•
Fungsi Laju Kerusakan
?
(t) =
f
(t
)
?
t
-
µ
?
1
-
F
?
?
?
s
?
•
Nilai Rata- Rata Distribusi Lognormal
MTTF = µ
2.1.7.4 Distribusi Weibull
Distribusi Weibull
sering
dipakai
sebagai
pendekatan untuk
mengetahui
karakteristik fungsi
kerusakan
karena
perubahan
nilai
akan
mengakibatkan distribusi Weibull mempunyai sifat tertentu ataupun ekuivalen
dengan distribusi tertentu. Distribusi Weibull dilakukan dengan menggunakan
metode kuadrat terkecil (least square method) yaitu:
•
xi = ti
•
yi = ln[ln(1/(1-F(ti)))]
•
F(ti) = ( i- 0.3 ) / ( n + 0.4)
|
 34
?
?
ß
n
?
n
?
n
?
x
i
y
i
-
?
?
y
i
?
•
b
=
i 1
=1
n
?
i
=1
?
n
2
2
n
?
x
i
i 1
=1
-
?
?
x
i
?
?
i
=
1
?
n
n
?
y
i
?
x
i
•
a
=
1
i 1
=1
-
b
i 1
=1
n
n
•
Parameter
?
a
?
-? ?
?
=
e
?
ß
?
Dimana :
ti
=
data kerusakan ke i
i
=
1,2,3,…..,n
n = jumlah data kerusakan
F(ti) dihitung dengan menggunakan pendekatan median rank
Fungsi kerusakan distribusi Weibull adalah:
•
Fungsi Kepadatan Probabilitas
-1
?
t
?
ß
?
?
-
? ?
?
ß
f
(t)
=
t
?
?
?
?
?
?
e
?
?
?
•
Fungsi Distribusi Kumulatif
?
t
?
ß
-
? ?
?
f
(t )
=
1
-
e
?
?
?
|
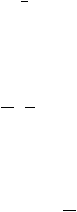 35
•
Fungsi Keandalan
?
t
?
ß
-
?
?
R(t ) = e
?
a
?
•
Fungsi Laju Kerusakan
ß
?
t
?
ß
-1
?
(t) =
?
?
?
?
?
?
•
Nilai Rata- Rata Distribusi lognormal
?
1
?
MTTF
=
?G?
1
+
?
ß
?
?
G
(
x)
=
(
x
-
1).
G
(
x
-
1)
Dimana
G
(
x)
adalah fungsi gamma
2.1.8
Identifikasi Distribusi
Identifikasi distribusi dilakukan
melalui
2
tahap
yaitu
Least
Square
Curve dan Goodness of Fit Test
2.1.8.1 Least Square Curve Fitting
Metode
ini
digunakan
utnuk
menghitung nilai
index
of
fit (r).
Distribusi dengan
nilai
r
yang
terbesar
akan
dipilih
untuk
diuji
dengan
menggunakan Goodness of Fit Test
|
 36
2
2
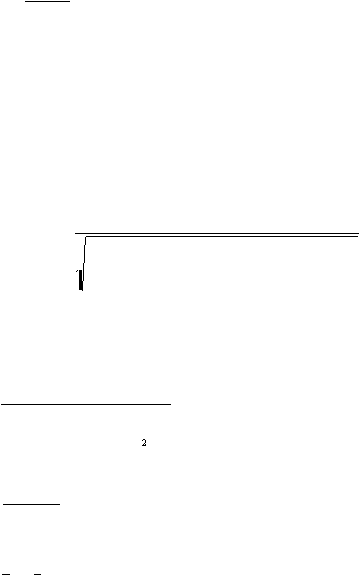
Rumus umum yang terdapat dalam metode Least Square Curve Fitting
adalah:
F t
(t
i
)
=
i
-
0.3
n
+
0.4
Dimana :
i
=
data waktu ke-t
n = Jumlah data kerusakan
n
?
n
??
n
?
n
?
X Y
i
i
-
?
?
Xi
??
?
Yi
?
index of
fit r
=
?
n
i
=1
?
n
?
i
=1
?
?
?
??
i
=1
?
n
?
n
?
?
?
n
?
Xi
2
-
?
?
Xi
?
?
?
n
?
Yi
2
-
?
?
Yi
?
?
?
?
i
=1
?
i
=1
?
?
? ?
?
i
=1
?
i
=1
?
?
?
n
?
n
??
n
?
n
?
XiYi - ?
?
Xi ??
?
Yi ?
b
=
i 1
=1
?
n
?
i
=1
?
n
?? i
=
1
?
?
?
untuk Weibull, Normal, Lognormal
?n
?
Xi
2
-
?
?
Xi
?
?
?
?
i
=1
?
i
=1
?
?
?
n
?
XiYi
b
=
i
=1
untuk Eksponensial
?
n
?
?
?
Xi
2
?
?
i
=1
?
a
=
y
-
b
x
Rumus yang dimiliki masing-masing distribusi adalah :
•
Distribusi Weibull
Xi
=
ln ti dimana ti adalah data waktu ke i
|
 37
-1
-1
?
?
1
?
?
yi
=
ln
?
ln
?
?
?
?
?
1
-
F
(ti)
?
?
?
a
?
-
?
?
Parameter : ß = b dan ? = e
?
b
?
•
Distribusi Eksponensial
x
i
=
t
i
dimana t
i
adalah data waktu ke-i
ln
?
1
?
y
i
=
?
?
1
-
F
(t
)
?
i
?
Parameter : ? = b
•
Distribusi Normal
x
i
=
t
i
dimana t
i
adalah data waktu ke-i
y
i
=
z
i
=
f
[F t
(t
i
)]
?
a
?
Parameter : s =
1
dan µ = -
?
?
b
?
b
?
•
Distribusi Lognormal
Xi =
ln ti dimana ti adalah data waktu ke i
y
i
=
z
i
=
f
[F t
(t
i
)]
Parameter : s =
1
dan t
b
med
=
e
-
sa
|
 38
2
2.1.8.2 Goodness of Fit Test
Setelah
perhitungan index
of
fit
dilakukan
maka
tahap
selanjutnya
dilakukan pengujian Goodness of Fit untuk nilai
index of fit terbesar. Uji ini
dilakukan dengan membandingkan antara hipotesa nol (H
0
)
yang menyatakan
bahwa data kerusakan mengikuti distribusi pilihan dan hipotesis alternatif (H1)
yang menyatakan bahwa data kerusakan tidak mengikuti distribusi pilihan.
Pengujian yang dilakukan dalam Goodness of Fit Test ada tiga macam
yaitu
Mann’s
Test
untuk distribusi Weibull,
Bartlett’s Test
untuk
distribusi
Eksponensial
dan
Kolmogorov-Smirnov untuk
distribusi
Normal
dan
Lognormal
2.1.8.2.1
Mann’s Test
Menurut Ebeling, (1997, p400) hipotesa untuk melakukan uji ini
adalah :
H
o
:
Data kerusakan berdistribusi Weibull
H1
:
Data kerusakan tidak berdistribusi Weibull
Uji statistiknya adalah :
r
-1
?
ln t
-
ln t
?
k k1
?
?
i
+1
i
?
M
=
i k1
- k1
+1
?
k1
?
ln t
M
i
?
-
ln t
?
k
?
?
i
+1
i
?
i
=1
?
Mi
?
|
 39
Dimana :
k
=
r
k
=
r
-
1
1
2
2
2
M
i
=
Z
i
+1
-
Z
i
?
?
i
-
0.5
?
?
Z
i
=
ln
?
-
ln
?
1
-
n
_
0.25
?
?
?
?
?
?
Jika
nilai M < M
crit
maka Ho diterima. Nilai M
crit
diperoleh dari tabel
distribusi F dengan v
1
=
2k
1
dan v2
=
2k2
2.1.8.2.2
Bartlett’s Test
Menurut Ebeling, (1997, p399) hipotesa untuk melakukan uji ini
adalah :
H
o
:
Data kerusakan berdistribusi Eksponential
H1
:
Data kerusakan tidak berdistribusi Eksponential
Uji statistiknya adalah :
?
?
r
?
r
?
2r
?
ln
?
(1/ r
)
?
t
i
?
-
(1 r
/ r
)
?
ln t
i
?
B
=
?
?
i 1
=1
1
+
?
(
r
+
1
)
6r
i
=1
?
dimana :
t
i
=
data waktu kerusakan ke-i
r = jumlah kerusakan
B
=
nilai uji statistic untuk uji Bartlett’s Test
|
 40
s
n
i
H
0
diterima jika :
2
2
X
(1-a / 2,r -1)
<
B
< X
(a / 2,r -1)
2.1.8.2.3
Kolmogorov-Smirnov Test
Menurut Ebeling, (1997, p402) hipotesa untuk melakukan uji ini
adalah :
H
o
:
Data kerusakan berdistribusi Normal atau Lognormal
H1
:
Data kerusakan tidak berdistribusi Normal atau Lognormal
Uji statistiknya adalah :
D
n
=
max
(D
1
,
D
2
)
D =
max
?
?
?
t
i
-
t
?
i
-
1?
?
?
1
?
f
?
1<i <n
?
?
?
?
?
-
?
?
?
?
D
=
max
?
?
-
f
?
i
?
?
?
i
?
t s
1
?
?
-
t
?
?
?
1<i < n
?
?
n
n
t
?
?
?
?
n
(t
-
t
)
2
t
=
?
i
s
2
=
?
i
i
=1
n
i
=1
n
-
1
Untuk Lognormal
:
n
t
=
?
ln t
i
n
s
2
=
?
(
ln t
-
t
)
2
i
=1
n
i
=1
n
-
1
ti = data waktu kerusakan ke-i
s = standar deviasi
|
 41
Jika Dn < Dcrit maka terima H0. Nilai Dcrit diperoleh dari tabel
critical value for Kolmogorov-Smirnov Test for normality.
2.1.9
Mean Time To Failure
Mean
Time
To
Failure
merupakan
rata-rata
selang
waktu
kerusakan
dari suatu distribusi kerusakan. Perhitungan nilai MTTF untuk masing-masing
distribusi adalah:
•
Distribusi Weibull
?
1
?
MTTF =
f
.G?1 +
?
ß
?
?
•
Distribusi Eksponensial
MTTF
=
1
?
•
Distribusi Normal
MTTF =
a
•
Distribusi Lognormal
MTTF = t
med
e
s
2
/
2
2.1.10 Mean Time To Repair
Untuk dapat menghitung
rata-rata perbaikan,
distribusi data untuk
waktu perbaikan perlu diketahui terlebih dahulu. Pengujian untuk menentukan
|
 42
distribusi data
dilakukan dengan cara
seperti
yang telah
dijelaskan.
Rumus
yang digunakan untuk masing-masing distribusi adalah:
•
Distribusi Weibull
?
1
?
MTTR
=
f
.
G?
1
+
?
ß
?
?
•
Distribusi Eksponensial
MTTR
=
1
?
•
Distribusi Normal dan Lognormal
MTTR
=
t
med
e
s
2
/
2
2.1.11 Interval Waktu Penggantian Pencegahan Kerusakan untuk Minimasi
Total Downtime
Penggantian pencegahan
dilakukan
untuk
menghindari terhentinya
mesin akibat kerusakan komponen. Untuk melakukan tindakan perawatan ini,
maka
harus
diketahui
interval
waktu antara
tindakan penggantian
(tp)
yang
optimal
dari
suatu
komponen
sehingga
dicapai
minimasi
downtime yang
maksimal.
•
Block Replacement
Jika pada selang waktu tertentu tidak terdapat kerusakan, maka
tindakan penggantian dilakukan pada suatu
interval
yang tetap.
Jika sistem rusak
sebelum tercapainya
tp,
maka dilakukan
|
|
43
penggantian
kerusakan dan penggantian
selanjutnya
akan
tetap
dilakukan pada
saat
tp
dengan
mengabaikan
pergantian
perbaikan sebelumnya.
•
Age Replacement
Dalam metode ini tindakan penggantian
dilakukan
pada saat
pengoperasiannya sudah
mencapai
waktu
yang ditetapkan
yaitu
tp. Jika pada
selang
waktu
tp terdapat
kerusakan,
maka
dilakukan
penggantian sebagai
tindakan
korektif.
Perhitungan
umur
tindakan
penggantian tp
dimulai
dari
awal
lagi
dengan
mengambil acuan dari saat sistem mulai bekerja kembali setelah
dilakukan tindakan perawatan korektif tersebut.
Rumus yang digunakan dalam metode ini adalah :
D
(tp
)
=
(total ekspektasi downtime per siklus)
(ekspektasi panjang waktu siklus
)
Rumus dari total ekspektasi downtime per siklus adalah :
Total
Ekspektasi
Downtime per siklus
=
Tp
.
R(tp) +Tf .
(1-
R(Tp))
Tp
=
Interval waktu tindakan penggantian pencegahan
R(tp)
=
Probabilitas suatu siklus tindakan pencegahan Tf
=
Interval waktu tindakan perbaikan kerusakan Reliability
waktu
silus pencegahan
sama dengan probabilitas dari kerusakan
yang terjadi setela waktu tp yaitu :
|
 44
?
8
R
(
tp
)
=
?
(
t dt
)
tp
Jadi probability dari suatu siklus rusak yaitu : 1 – R(ti)
Ekspektasi
panjang
waktu
siklus
=
(tp
+
Tp)
.
R(tp) +
(ekspektasi panjang siklus kegagalan) . (1 – R(tp))
Dimana :
R(tp) = Probabilitas suatu siklus tindakan pencegahan
(1-R(tp)) = Probabilitas suatu siklus tindakan kegagalan
Untuk
menentukan ekspektasi
panjang
siklus
kegagalan.
Perlu
diperhatikan waktu rata-rata kegagalan / MTTF (Mean Time To
Failure), dimana untuk preventve maintenance diperoleh :
MTTF
=
?
t. f (t)dt
Nilai tengah distribusi kerusakan yaitu :
t. f
(t dt
)dt
M
(tp
)
=
1
-
R
(
tp
)
Ekspektasi panjang siklus kegagalan =
?
t. f
(t dt
)dt
1
-
R
(tp
)
+
Tf
Jadi ekspektasi panjang waktu siklus yaitu :
?
?
t. f
(
t dt
)
?
?
.
?
?
?
?
?
.
=
(tp + Tp
)
R
(tp
)
+
+
Tf
(1 - R(tp
))
?
?
1
-
R
(tp)
?
?
?
?
?
?
=
(tp
+
Tp .R(tp)
).R(tp)
+
?
t. f t dt
(t dt
)dt
+
Tf
.
(1
-
R
(tp )
))
|
 45
Dan total downtime per siklus yaitu :
D
(tp
)
=
Tp
×
R
(
tp
)
+
Tf
(
1
-
R
(
tp
))
(
tp + Tp
)
×
R
(
tp
)
+
(
M
(
tp
)
+
Tf
)
×
(
1
-
R
(
tp
))
2.1.12 Interval Waktu Pemeriksaan
Selain penggantian pencegahan maka pemeriksaan (inspeksi) juga
diperlukan
dalam Preventive
Maintenance untuk
meningkatkan availability.
Tujuan dari
inspeksi adalah
untuk
mencega
kegagalan
yang
tidak terdeteksi
terutama pada saat
mesin
tidak beroperasi yang disebabkan oleh korosi atau
kerusakan mekanik. Yang harus diingat adalah bahwa inspeksi dapat
meningkatkan availability tetapi tidak dapat meningkatkan reliabilitas.
Menurut Jardine, (1993, p108) tindak pemeriksaan juga bertujuan untuk
meminimasi downtime
mesin akibat kerusakan
yang terjadi secara
tiba-tiba.
Konstruksi model interval waktu pemeriksaan optimal tersebut adalah :
•
1
=
waktu rata - rata perbaikan
µ
•
1
=
waktu rata -
rata pemeriksaan
i
Menurut Jardine, (1993, p109) total downtime per unit waktu
merupakan fungsi dari frekuensi pemeriksaan (n) dan dinotasikan dengan
D(n) yaitu sebagai berikut:
|
 46
D(n)
=
downtime untuk
perbaikan
kerusakan
dan
downtime
untuk
pemeriksaan.
D
(
n
)
=
?
(
n
)
+
n
µ
i
Keterangan :
?(n)
= laju kerusakan yang terjadi
n
= jumlah pemeriksaan per satuan waktu
µ
= berbanding terbalik dengan 1/µ
i
= berbanding terbalik dengan 1/i
Diasumsikan bahwa
laju kerusakan berbanding terbalik dengan jumlah
pemeriksaan :
?
(n)
=
k
n
Dan karena
:
D
(
n
)
=
?
(n)
+
n
µ
i
Dimana
: k = nilai konstan dari banyaknya kerusakan tiap
satuan waktu, maka diperoleh : n =
ki
µ
2.1.13 Kehandalan (Reliabity) Dengan dan Tanpa Preventive Maintenance
Peningkatan kehandalan dapat ditempuh melalui perawatan
pencegahan. Perawatan pencegahan dapat mengurangi pengaruh wear out dan
menunjukkan hasil yang signifikan terhadap umur sistem.
|
|
47
Menurut Ebeling (1997, p204),
model kehandalan berikut ini
mengasumkan
sistem kembali
ke
kondisi baru
setelah
menjalani preventive
maintenance.
Kehandalan pada saat t dinyatakan sebagai berikut :
R
m
(t)=R(t)
untuk 0 = t = T
R
m
(t)=R(t) . R(t-T)
untuk T = t =2T
Keterangan :
T
= interval waktu penggantian pencegahan kerusakan.
Rm(t)
=
kehandalan
(reliability)
system
dengan
perawatan
pencegahan.
R(t)
= Kehandalan (reliability) system tanpa perawatan pencegahan.
R(T)
= peluang kehandalan hingga perawatan pencegahan pertama.
R(t-T)
= peluang
kehandalan
antara
waktu
t-T
setelah
system
dikembalikan pada kondisi awal (T)
Ini adalah bukti yang merefleksikan
bahwa
distribusi
eksponensial,
yang memiliki laju kerusakan konstan, bila dilakukan preventive maintenance
tidak akan menghasilkan dampak apapun. Dengan demikian, tidak ada
peningkatan reliability seperti yang diharapkan.
|
 48
2
i
i
2.2
Koefisien Korelasi
Secara aritmetika nilai koefisien korelasi bias didapatkan berdasarkan
hasil analisis regresi sederhana, akan tetapi
nilai
ini
tidak akan memiliki arti.
Dalam model
hipotetik
untuk
persamaan
regresi,
tidak
dikenal
keberadaan
parameter korelasi ( yang dilambangkan dengan ? atau rho) karena X
dianggap peubah
tetap. Dalam
hal
ini koefisien korelasi
tersebut
tidak
berperan sebagai penduga parameter atau statistic tetapi melulu sebagai angka.
Koefisien ini dapat dihitung dengan rumus:
n
?
n
??
n
?
n
?
x
i
y
i
-
?
?
x
i
??
?
y
i
?
r
=
i
=1
?
n
?
n
?
i
=1
?
?
?
?? i =1
?
n
?
n
?
?
?
n
?
x
²
-
?
?
x
?
?
?
n
?
y
²
-
?
?
y
?
?
?
?
i 1
=1
?
i
=1
?
?
? ?
?
i
=1
?
i
=1
?
?
?
2.3
Langkah-langkah Minitab 14
2.3.1
Diagram Pareto
Menurut Meyer dan Krueger (A Minitab Guide to Statistcs, p59), “A
pareto chart that ordersthe bars from largest to smallest along with a line that
shows the cummultive percentageand count of the bars. This chart often used
with analyzing defect in a manufacturing process to help determine the types
of defects which are most prevalent in a process.”
Langkah-langkah
menggunakan software
Minitab 14 untuk
membuat
diagram Pareto adalah:
|
|
49
•
Pilih menu Stat > Quality Tools > Pareto Chart
•
Klik opsi Chart defects table > Isikan dengan data yang sesuai
•
Masukan angka 99 dalam Combine defects after the first
•
Tambahkan judul diagram > lalu klik OK
2.3.2
Goodness of Fit Test
Goodness of fit
test dilakukan
untuk
menguji
apakah nilai r terbesar
dari perhitungan
index of fit merupakan
distribusi
yang sesuai dengan data
kerusakakan
yang
ada.
Dalam
menggunakan
software
Minitab 14,
uji
goodness of fit dilakukan dengan
metode Anderson-Darling. Distribusi yang
memiliki nilai koefisien Anderson-Darling terkecil, beararti distribusi tersebut
semakin cocok dengan data yang diujikan.
Berikut
ini
merupakan
langkah-langkah dalam melakukan
uji
goodness of fit dengan menggunakan software Minitab 14:
•
Pilih menu Stat > Quality Tools > Individual Distribution Identification
•
Masukkan data pada Single column
•
Pilih semua distribusi yang ingin diujikan pada opsi Specify
•
Klik OK
|
|
50
2.3.3
Korelasi
Menurut Nur Iriawan dan Septin Puji Astuti (Mengolah Data Statistik
dengan Mudah menggunakan Minitab 14, p173), “Koefisien korelasi Pearson
berguna untuk mengukur tingkat keeratan hubungan linear antara 2 variable.
Nilai korelasi berkisar antara -1 sampa +1. Nilai korelasi negatif berarti
hubungan antara 2 variabel negative. Sebaliknya nilai korelasi positif berarti
hubungan antara 2 variabel adalah positif. Suatu hubungan antara 2 variabel
dikatakan berkorelasi kuat apabila makin mendekat 1 atau
-
1
.
Sebaliknya,
suatu hubungan antara 2 variabel dikatakan lemah apabila semakin
mendekati 0.”
Berikut merupakan
langkah-langkah uji korelasi dua
variable dengan
menggunakan Minitab 14:
•
Pilih menu Basic Statistics > Correlation.
•
Masukkan data yang akan diolah ke dalam kolom Variables.
•
Jika
ingin menampilkan p-value, pilih Display p-values > kemudian klik
OK
|