|
BAB 2
LANDASAN TEORI
2.1
Simulasi
2.1.1
Defenisi Simulasi
Menurut Kakiay (2003, p1), mengemukakan defenisi simulasi
sebagai suatu sistem yang digunakan
untuk memecahkan atau
menguraikan
persoalan-persoalan
dalam kehidupan
nyata
yang
penuh
dengan
ketidakpastian dengan tidak atau menggunakan model tertentu dan lebih
ditekankan pada pemakaian komputer untuk mendapatkan solusinya.
Menurut Harrel et al. (2000, p5), mengemukakan bahwa simulasi
adalah imitasi dari sistem dinamis
dengan
menggunakan
model
komputer
untuk mengevaluasi dan meningkatkan performansi sistem.
Menurut Schriber (1987), simulasi adalah model dari suatu proses
atau sistem dimana dengan cara tertentu
model
tersebut
melakukan
respon
yang
sama dengan sistem
yang sebenarnya terhadap suatu kejadian dengan
waktu yang tidak dibatasi.
Menurut Emshoff dan Simon (1970), simulasi didefinisikan sebagai
suatu
model
sistem dimana
komponennya
direpresentasikan
oleh
proses-
proses aritmatika dan logika yang dijalankan komputer untuk
memperkirakan sifat-sifat dinamis sistem tersebut.
|
|
27
Menurut Shannon (1975), simulasi merupakan proses perancangan
model
dari
sistem nyata
yang
dilanjutkan
dengan
pelaksanaan
eksperimen
terhadap model untuk mempelajari perilaku sistem atau evaluasi strategi.
Menurut Banks dan Carson (1984), simulasi adalah tiruan dari
sistem nyata
yang dikerjakan secara manual atau komputer, yang kemudian
diobservasi dan disimpulkan untuk mempelajari karakterisasi sistem.
Menurut Hoover dan Perry (1990), simulasi merupakan proses
perancangan
model
matematis
atau
logis
dari
sistem nyata,
melakukan
eksperimen terhadap model dengan menggunakan komputer untuk
menggambarkan, menjelaskan dan memprediksi perilaku sistem.
Menurut Law dan Kelton (1991), simulasi didefinisikan sebagai
sekumpulan metode dan aplikasi untuk menirukan atau merepresentasikan
perilaku
dari
suatu
sistem nyata,
yang
biasanya
dilakukan
pada
komputer
dengan menggunakan perangkat lunak tertentu.
Menrut Khosnevis (1994), simulasi merupakan proses aplikasi
membangun
model
dari
sistem nyata
atau
usulan
sistem,
melakukan
eksperimen
dengan
model
tersebut untuk
menjelaskan
perilaku
sistem,
mempelajari kinerja sistem atau untuk membangun sistem baru sesuai
dengan kinerja yang diinginkan.
|
|
28
2.1.2
Keuntungan dan Kekurangan Model Simulasi
Menurut
Suryani
(2006,
p5),
simulasi
mempunyai
kelebihan
dan
kekurangan. Kelebihan tersebut antara lain:
•
Tidak
semua
sistem
dapat
direpresentasikan
dalam
model
matematis,
simulasi merupakan alternatif yang tepat.
•
Dapat
bereksperimen
tanpa
adanya
resiko pada
sistem
nyata.
Dengan
simulasi
memungkinkan
untuk
melakukan
percobaan
terhadap
sistem
tanpa harus menanggung resiko terhadap sistem yang berjalan.
•
Simulasi
dapat
mengestimasi
kinerja
sistem pada
kondisi
tertentu dan
memberikan alternatif desain terbaik sesuai dengan spesifikasi yang
diinginkan.
•
Simulasi
memungkinkan untuk
melakukan studi
jangka panjang dalam
waktu relatif singkat.
•
Dapat menggunakan input data bervariasi.
Menurut Suryani (2006, p5), simulasi
mempunyai kekurangan,
antara lain:
•
Kualitas dan analisis model tergantung pada si pembuat model.
•
Hanya mengestimasi karakteristik sistem berdasarkan masukan tertentu.
Menurut
Render
et
al. (2003,
p603),
menyatakan bahwa simulasi
merupakan suatu alat yang semakin banyak digunakan karena beberapa
alasan, yaitu:
|
|
29
•
Simulasi relatif mudah dan fleksibel.
•
Perkembangan akhir dalam dunia software memungkinkan beberapa
model simulasi sangat mudah untuk dikembangkan.
•
Simulasi dapat digunakan untuk
menganalisa situasi dunia nyata
yang
kompleks
dan
luas
yang
tidak
dapat
diselesaikan
oleh
model
analisis
kuantitatif konvensional.
•
Simulasi memungkinkan analisa what-if. Dengan bantuan komputer,
manager
mampu
mencoba
beberapa
kebijakan
keputusan
dalam
hitungan menit.
•
Simulasi tidak mempengaruhi sistem dunia nyata.
•
Simulasi memungkinkan peneliti untuk mempelajari efek interaktif dari
komponen individu ataupun variabel untuk menentukan yang mana
yang penting.
•
Simulasi memungkinkan time compression.
•
Simulasi memungkinkan terlibatnya beberapa komplikasi yang terjadi di
dunia nyata,
yang
mana
tidak dimungkinkan
oleh
model
analisis
kuantitatif pada umumnya.
Menurut
Render
et
al.
(2003,
p604), kekurangan
utama
simulasi
adalah:
|
|
30
•
Model simulasi yang baik untuk situasi kompleks pada umumnya sangat
mahal.
Proses
pembuatannya
memakan
waktu
yang
lama dan
merupakan proses yang kompleks pula.
•
Simulasi
tidak
menghasilkan
solusi
yang
optimal
untuk
suatu
permasalahan seperti teknis analisis kuantitatif lainnya. Simulasi
merupakan
pendekatan trial
and
error,
yang
memberikan solusi
yang
berbeda setiap pengulangannya.
•
Manager harus membangkitkan kondisi dan batasan dengan solusi yang
hendak dicapai.
•
Masing-masing model simulasi bersifat unik. Solusi dan keputusan
simulasi tidak selalu dapat diaplikasikan untuk permasalahan lain.
Kakiay (2003,p3-5), menyebutkan terdapat berbagai keuntungan
lain yang bisa diperoleh dengan memanfaatkan simulasi dan simulasi
komputer, yaitu sebagai berikut:
1.
Menghemat Waktu (Compress Time)
Kemampuan didalam menghemat waktu ini dapat dilihat dari pekerjaan
yang bila dikerjakan akan memakan waktu tahunan tetapi kemudian
dapat
disimulasikan
hanya
dalam beberapa
menit,
bahkan
dalam
beberapa
kasus
hanya
dalam hitungan
detik.
Kemampuan
ini
dapat
dipakai oleh para peneliti untuk melakukan berbagai pekerjaan desain
operasional
yang
mana juga
memperhatikan bagian terkecil dari
waktu
|
|
31
untuk
kemudian
dibandingkan
dengan
yang
terdapat pada sistem
yang
nyata berlaku.
2.
Dapat Melebar-luaskan Waktu (Expand Time)
Hal ini terlihat terutama dalam dunia statistik dimana hasilnya
diinginkan dapat tersaji dengan cepat. Simulasi dapat digunakan untuk
menunjukkan perubahan struktur dari suatu sistem nyata yang
sebenarnya tidak dapat diteliti pada waktu yang seharusnya. Dengan
demikian
simulasi
dapat
membantu
mengubah
sistem nyata
hanya
dengan memasuki sedikit data.
3.
Dapat Mengawasi Sumber-sumber yang Bervariasi (Control Sources of
Variation)
Kemampuan
pengendalian
dalam simulasi
ini
tampak
apabila
statistik
digunakan untuk meninjau hubungan
antara variabel bebas
(independent) dengan variabel terkait (dependent)
yang
merupakan
faktor-faktor yang akan dibentuk dalam percobaan. Di dalam simulasi
pengambilan data dan pengolahannya
pada komputer, ada beberapa
sumber yang dapat dihilangkan atau sengaja ditiadakan. Untuk
memanfaatkan kemampuan ini, peneliti harus mengetahui dan mampu
menguraikan sejumlah input dari sumber-sumber yang bervariasi yang
dibutuhkan oleh simulasi tersebut.
|
|
32
4.
Mengoreksi
Kesalahan-kesalahn
Perhitungan
(Error
in
Meansurement
Correction)
Dalam prakteknya
pada
suatu
kegiatan
ataupun
percobaan
dapat
saja
muncul
kesalahan
dalam
mencatat hasil-hasilnya. Sebaliknya, dalam
simulasi komputer jarang ditemukan kesalahan perhitungan terutama
bila
angka-angka
diambil dari
komputer
secara teratur dan bebas.
Komputer mempunyai kemampuan untuk melakukan perhitungan
dengan akurat.
5.
Dapat
Dihentikan
dan
Dijalankan
Kembali
(Stop
Simulation
and
Restart)
Simulasi komputer dapat dihentikan untuk kepentingan peninjauan
ataupun pencatatan semua keadaan yang relevan tanpa berakibat buruk
terhadap program simulasi tersebut. Dalam dunia nyata, percobaan tidak
dapat dihentikan begitu saja. Dalam simulasi komputer, setelah
dilakukan penghentian maka
kemudian dapat dengan cepat dijalankan
kembali (restart).
6.
Mudah Diperbanyak (Easy to Replicate)
Dengan simulasi
komputer percobaan dapat
dilakukan
setiap
saat
dan
dapat diulang-ulang. Pengulangan dilakukan terutama untuk mengubah
berbagai
komponen
dan
variabelnya, seperti
dengan
perubahan
pada
parameternya, perubahan pada kondisi operasinya, ataupun dengan
memperbanyak output
|
|
33
2.2
Kriteria Waktu yang Tepat dalam Penggunaan Simulasi
Menurut Harrel et al. (2000, p12), simulasi sendiri memiliki batasan
yang
harus
diperhatikan
sebelum memutuskan
penggunaannya
terhadap
sebuah situasi. Beberapa petunjuk umum tentang kriteria yang cocok dalam
penggunaan simulasi:
•
Keputusan operasional (logis maupun kuantitatif) dibutuhkan.
•
Proses yang akan dianalisa terdefinisi dengan baik dan berulang-ulang.
•
Aktivitas
dan
kejadian
menunjukkan
sifat
ketergantungan
dan
keanekaragaman.
•
Biaya akibat penerapan keputusan
lebih besar dibandingkan biaya
pembuatan simulasi.
•
Biaya
eksperimen
pada
sistem
aktual
lebih besar dibandingkan
biaya
pembuatan simulasi.
2.3
Klasifikasi Simulasi
Menurut Suryani (2006, p6), simulasi dapat diklasifikasikan sebagai berikut:
1.
Menurut waktu:
a.
Simulasi statis. Pada simulasi ini output model tidak dipengaruhi
waktu.
b.
Simulasi
dinamis.
Pada
simulasi
ini
output
model
dipengaruhi
waktu. Waktu yang bertindak sebagai variabel bebas.
|
|
34
Contoh: model populasi yang berkembang sepanjang waktu, laju
penjualan, tingkat penjualan.
2.
Menurut perubahan status variabel:
a.
Simulasi kontinu, merupakan model simulasi yang status
variabel berubah secara kontinyu.
Contoh: model-model level cairan yang rate-nya (lajunya)
berubah setiap saat.
b.
Simulasi diskrit model yang status variabel berubah pada saat-
saat tertentu.
Contoh: model-model inventory yang materialnya datang dan
diambil pada waktu tertentu
3.
Menurut derajat ketidakpastiannya:
a.
Simulasi
deterministik,
merupakan
model
yang
outputnya
bisa
ditentukan secara pasti.
Contoh: model-model
matematis,
model
Economic
Order
Quantity.
b.
Simulasi stokastik, yaitu model yang model tidak bisa ditentukan
secara pasti (mengandung ketidakpastian).
Contoh: diagram pohon keputusan.
|
|
35
2.4
Jenis- jenis Simulasi
Terdapat
beberapa
jenis simulasi
yang biasa digunakan
(menurut
Kakiay, Pengantar Sistem Simulasi 2004). Yaitu:
•
Simulasi Identitas (Identity Simulation)
Simulasi
identitas
ini digunakan secara langsung dan cukup sederhana
dalam penggunaannya. Dengan banyak meniadakan berbagai macam hal
yang
mendasar
dari
aturan
permodelan. Kekurangan dari simulasi ini
adalah cukup mahal dan tidak begitu layak, hanya sedikit memberikan
kontrol atau mungkin tidak memberikan jawaban yang efektif.
•
Simulasi Identitas Semu (Ouasi Indentity Simulation)
Simulasi
ini memodelkan berbagai aspek yang terkait dari
sistem yang
sebenarnya sehingga dapat mengeluarkan unsur-unsur yang dapat
membuat setiap simulasi identitas tidak berfungsi dengan baik. Simulasi
ini setingkat lebih maju dibandingkan dengan simulasi identitas.
•
Simulasi Laboratorium (Laboratory Simulation)
Simulasi laboratorium biasanya memerlukan berbagai komponen seperti
operator, perangkat lunak dan keras, prosedur operational, fungsi-fungsi
matematis, distribusi probabilitas, dan lain sebagainya. Keuntungan dari
simulasi ini adalah simulasi ini
lebih murah dan lebih layak untuk
memberikan jawaban yang dapat dipertanggungjawabkan dibandingkan
|
|
36
dengan dua
simulasi diatas. Terdapat dua jenis simulasi laboratorium,
yaitu:
-
Operating Planning.
Disini komputer berperan sangat penting sebagai pengumpul
data dan sebagai pengolahan informasi.
-
Man Machine Simulation.
Didalam simulasi
ini,
aturan-aturan
dari
simulasi
tidak
terlalu
diperhatikan dan komputer hanya digunakan untuk mengolah
dan menganalisis data.
•
Simulasi Komputer (Computer Simulational)
Untuk simulasi jenis ini, digunakan komputer untuk menyelesaikan
masalah sesuai dengan kebutuhan yang kemudian komputer tersebut
diprogram sehingga nanti dapat digunakan
untuk
memecahkan
masalah
yang sama lagi. Untuk saat sekarang ini, lebih condong untuk dilakukan
simulasi komputer. Selain penggunaannya yang mudah juga karena hasil
yang diperoleh untuk pemecahan masalah lebih cepat dan akurat.
2.5
Pengertian Random Number dan Generator Random Number
Menurut Kakiay (2004, p21), Random Number Generator adalah
suatu algoritma yang digunakan untuk menghasilkan
urutan-urutan
atau
sequence dari angka-angka sebagai hasil dari perhitungan dengan komputer
|
|
37
yang diketahui distribusinya
sehingga angka-angka tersebut
muncul secara
random dan digunakan terus-menerus.
Menurut
Suryani
(2006,
p23),
bilangan
random
merupakan
bilangan yang berdistribusi uniform antara 0 dan 1.
Menurut Kakiay (2004, p22), dalam penentuan random number
pada umumnya terdapat beberapa sumber yang dipergunakan, antara lain:
•
Tabel Random Number
Tabel Random ini sudah banyak ditemukan mulai dari enam digit
sampai dengan dua belas digit.
•
Electronic Random Number
Electronic Random Number ini juga banyak digunakan dalam percobaan
penelitian.
•
Congruential Pseudo Random Number Generator
Random Number Generator ini terdiri dari tiga bagian:
-
Additve (Arithmatic) Random Number Generator.
-
Multiplicative Random Number Generator.
-
Mixed Congruential Random Number Generator.
|
|
38
2.6
Tipe Simulasi
2.6.1
Static versus Dynamic Simulation
Simulasi statis merupakan simulasi yang tidak berdasarkan
atau
dipengaruhi oleh waktu. Simulasi statis pada umumnya mencakup proses
pembuatan
sampel
random
untuk
menggeneralisasikan hasil statistik, yang
pada umunya dinamakan simulasi Monte Carlo.
Simulasi
dinamis,
merupakan
kebalikan dari simulasi statis yang
mencakup perubahan waktu. Simulasi dinamis mencakup perubahan status
yang terjadi sepanjang waktu. Simulasi dinamis sangat cocok digunakan
untuk
menganalisa
sistem
manufaktur dan jasa karena sangat dipengaruhi
waktu.
2.6.2
Stochastic versus Deterministic Simulation
Simulasi dimana satu atau lebih variabel masukan bersifat
inventory,
secara
natural
dikategorikan
sebagai
simulasi
stokastik atau
simulasi
probabilistik.
Simulasi
stokastik
menghasilkan
output yang
merupakan inventory sehingga hanya memberikan suatu pandangan data
bagaimana sistem mungkin beroperasi.
Simulasi yang mana komponen masukannya tidak besifat inventory
disebut dengan simulasi deterministik. Simulasi deterministik memiliki input
yang konstan dan output yang konstan pula.
|
|
39
2.6.3
Discrete-Event versus Continious Simulation
Discrete–event simulation
merupakan simulasi dimana perubahan
pada titik waktu yang diskrit yang dipicu oleh kejadian. Simulasi seperti ini
mungkin mencakup:
•
Kedatangan entitas pada suatu workstation.
•
Kegagalan/kerusakan dari sumber daya.
•
Penyeesaian dari suatu aktivitas.
•
Berhentinya shift.
Sedangkan pada
continious simulation, status variabel berubah
secara terus menerus sepanjang waktu.
2.7
Simulasi Monte Carlo
Menurut Kakiay (2004, p113), simulasi Monte Carlo dikenal juga
dengan
istilah Sampling Simulation atau Monte Carlo Sampling Technique.
Sampling simulasi ini menggambarkan kemungkinan penggunaan data
sampel
dalam
metode
Monte
Carlo
dan juga sudah dapat diketahui atau
diperkirakan distribusinya. Simulasi ini
menggunakan data
yang sudah ada
(historical data) yang sebenarnya dipakai pada simulasi untuk tujuan lain.
Dengan kata lain apabila
menghendaki model simulasi yang
mengikutsertakan inventory atau sampling dengan distribusi probabilitas
|
|
40
yang dapat diketahui dan ditentukan, maka secara simulasi Monte Carlo ini
dapat digunakan.
Metode
simulasi
Monte
Carlo
ini cukup sederhana didalam
menguraikan ataupun menyelesaikan persoalan, termasuk dalam penggunaan
program-programnya didalam komputer.
Menurut Render et al. (2003, p604), ketika sebuah sistem memiliki
elemen-elemen yang menunjukkan adanya suatu peluang dalam sifat
variabelnya, metode dari simulasi Monte Carlo ini dapat diaplikasikan.
Ide dasar dari simulasi Monte Carlo ini adalah menggenerate atau
menghasilkan
suatu
nilai
untuk
membentuk
suatu
model
dari
variabelnya
dan dipelajari. Ada banyak sekali variabel-variabel didalam sistem nyata ini
yang
merupakan
probabilitas
secara alami
dan
yang
mungkin
ingin
kita
simulasikan.
Berikut adalah beberapa contoh dari variabel-variabel berikut:
1.
Persediaan permintaan harian atau mingguan.
2.
Waktu menunggu untuk pemesanan persediaan sampai tiba ke kita.
3.
Waktu diantara breakdown mesin.
4.
Waktu antar kedatangan di fasilitas pelayanan.
5.
Waktu pelayanan.
6.
Waktu untuk menyelesaikan suatu proyek.
7.
Jumlah karyawan yang tidak hadir setiap harinya.
|
|
41
Dasar
dari
simulasi
Monte
Carlo
adalah
percobaan
dari
peluang
(probabilitas) elemen melalui penarikan contoh acak (inventory sampling).
Berikut ini lima langkah-langkah untuk melakukan simulasi Monte Carlo:
1.
Membuat suatu distribusi probabilitas dari variabel pentingnya.
2.
Kemudian menyusun distribusi probabilitas kumulatifnya dari setiap
variabel yang berasal dari langkah 1.
3.
Membuat suatu interval angka acak dari setiap variabelnya.
4.
Menggenerate angka acak.
5.
Dan terakhir lakukan simulasi secara berkala untuk percobaan-
percobaannya.
2.8
Metodologi Simulasi
Tahapan dalam metodologi simulasi adalah sebagai berikut :
1.
Mendefinisikan masalah.
Proses
mendefinisikan
masalah
yang
dilakukan
untuk
menentukan
tujuan dari simulasi sedikit berbeda dari proses mendefinisikan masalah
dalam teknik
analisis
lainnya.
Pada
intinya,
proses
mendefinisikan
masalah
dalam simulasi
mencakup
spesifikasi
tujuan
dan
indentifikasi
variabel
sistem yang
dapat
dikendalikan
dan
yang
tidak
dapat
dikendalikan untuk diteliti.
|
|
42
2.
Membangun model simulasi.
Perbedaan antara simulasi dengan teknik analisis lainnya seperti linear
programming ataupun teori antrian adalah bahwa dalam simulasi, model
harus dibangun secara khusus untuk suatu kondisi dimana terjadi
masalah.
Spesifikasi variabel dan parameter
Langkah awal dalam pembangunan
model simulasi adalah menentukan
karakteristik
dari
sistem
yang
harus diperbaiki, yang disebut dengan
parameter, dan karakteristik mana yang diizinkan untuk mengalami
perubahan-perubahan selama
simulasi, yang dinamakan dengan
variabel.
Spesifikasi aturan pengambilan keputusan
Aturan pengambilan keputusan merupakan kumpulan kondisi-kondisi
yang
merupakan sifat dari model simulasi yang dikembangkan. Pada
umumnya, aturan pengambilan keputusan adalah aturan prioritas dalam
suatu model simulasi.
Spesifikasi distribusi probabilitas
Dua kategori dari distribusi
yang dapat digunakan dalam siulasi adalah
distribusi
frekuensi
empiris dan juga distribusi
matematik
standar.
Distribusi empiris diperoleh dari observasi
terhadap frekuensi relatif
terjadinya suatu kejadian seperti kedatangan dalam suatu antrian. Denga
kata lain, distribusi empiris merupakan suatu distribusi yang khusus
|
|
43
dibangun dan
hanya
sesuai
untuk kondisi
tertentu.
Namun demikian,
distribusi
data
sering
kali diasumsikan
mengikuti
suatu
distribusi
matematik standar seperti distribusi normal atau distribusi poisson.
Spesifikasi time-incrementing procedure
Dalam suatu
model simulasi,
waktu dapat dimajukan dengan dua
metode, yaitu: (1) peningkatan waktu tetap (fixed-time increments) atau
(2) peningkatan waktu variabel (variabel-time
increments).
Kedua
metode
tersebut
membutuhkan
konsep
waktu
dalam simulasi.
Dalam
peningkatan waktu tetap, waktu (seperti: menit, jam ataupun hari) dalam
simulasi meningkat dengan interval yang tetap dari suatu periode waktu
ke
periode
lainnya.
Sedangkan
dalam peningkatan
waktu
variabel,
peningkatan waktu terjadi dengan suatu
variabel
yang
memerintahkan
suatu kejadian pindah ke kejadian lainnya.
3.
Membuat spesifikasi nilai dari variabel dan parameter.
Menentukan kondisi awal
Suatu variabel selama proses simulasi akan mengalami perubahan nilai,
namun
demikian
suatu
variabel
harus
memiliki
nilai
awal. Nilai
dari
parameter akan bersifat tetap, namun demikian, parameter dapat berubah
bila alternatif yang berbeda dipelajari dalam simulasi.
|
|
44
Menentukan lamanya program dijalankan
Lamanya suatu program simulasi dijalankan tergantung pada tujuan dari
simulasi.
Dengan
kata
lain,
suatu
program akan
dijalankan
hingga
mencapai equilibrium.
4.
Mengevaluasi hasil.
Hasil yang diperoleh dari suatu simulasi tergantung pada bagaimana
suatu
model
simulasi
dikembangkan
mendekati
sistem nyata.
Namun
demikian,
hasil
yang
diperoleh
juga tergantung pada perancangan
simulasi dalam suatu
area
statistik.
Pada
kondisi
tertentu,
model
simulasi
dikembangkan
dalam bentuk
percobaan
hipotesa,
sehingga
simulasi
dijalankan
dalam suatu
kumpulan
sampel
data
yang
menggambarkan analisis formal dalam statistik inferensia.
5.
Melakukan validasi.
Proses
validasi
dapat
digambarkan
sebagai
suatu
proses testing
pada
program komputer
untuk
meyakinkan
bahwa
program simulasi
yang
dikembangkan tepat dan benar. Untuk melakukan validasi, sistem analis
memiliki
tiga
alternatif yaitu
(1)
membandingkan
hasil
kalkulasi
dari
program
simulasi
dengan
hasil
kalkulasi
pada
program
yang
terpisah,
(2) melakukan
simulasi terhadap kondisi simulasi dan membandingkan
hasilnya dengan sistem yang sekarang, (3) memilih beberapa poin dalam
simulasi
yang
dijalankan
dan
membandingkannya
dengan
hasil
yang
|
|
45
diperoleh dengan model matematis yang sesuai untuk kondisi yang sama
pula.
6.
Membuat proposal penelitian baru.
Bedasarkan pada hasil simulasi, suatu proposal terhadap penelitian baru
dapat dibuat. Proposal penelitian baru yang diusulkan ini berkaitan
dengan
perubahan pada
parameter, variabel,
aturan
keputusan, kondisi
awal dan lamanya suatu simulasi dijalankan.
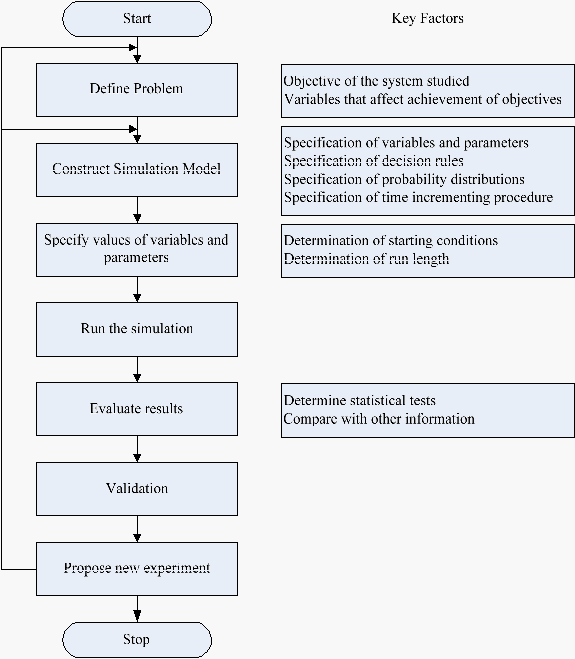
Diagram
berikut
ini
merupakan
diagram
alir
yang
menggambarkan
langkah-langkah penting dalam simulasi. (Chase et al, 2006, p693)
|
 46
Diagram 2.1 Diagram Langkah-langkah Penting dalam Simulasi
|
|
47
2.9
Identifikasi Distribusi
2.9.1
Uji Kebaikan Suia (Goodness of Fit)
Menurut Walpole (1995, p325), uji kebaikan suai (Goodness of Fit)
digunakan
untuk
menentukan apakah suatu populasi memiliki sebaran
teoritik tertentu
yang didasarkan
pada
seberapa
baik kesesuaian antara
frekuensi
yang teramati dalam data contoh
dengan
frekuensi
harapan
yang
didasarkan pada sebaran yang dihipotesiskan.
2.9.1.1 Kolmogorov-Smirnov Test
Uji Kolmogorov-Smirnov
merupakan salah satu uji kebaikan suai
yang digunakan untuk membandingkan tingkat kesesuaian sampel
dengan
suatu distribusi
tertentu seperti normal, uniform, poisson dan eksponensial.
Uji
ini didasarkan pada perbandingan frekuensi kumulatif dari data dengan
frekuensi kumulatif dari distribusi teoritis. Berikut adalah langkah pengujian
kolmogoro-smirnov:
1.
Tentukan frekuensi kumulatif data hasil observasi (F
0
).
2.
Tentukan frekuensi kumulatif distribusi data teoritis (F
e
).
3.
Tentukan nilai D
n
dengan menghitung absolute dari selisih F
e
–
F
0
.
4.
Tentukan D
n
Maksimal dari langkah nomor 3.
a
5.
Tentukan nilai kritis tabel D
n
Tabel =
n
n
dari tabel nilai kritis D untuk
uji kolmogorov-smirnov.
|
|
48
6.
Jika D
n
Max Hitung < D
n
Tabel maka terima hipotesis yang mengatakan
bahwa data mengikuti pola distribusi yang dihipotesiskan.
Menurut White (1975,
p338), mengemukakan bahwa sebaiknya
menggunakan kolmogorov-smirnov test dalam uji kebaikan suai dikarenakan
secara statistikal akan lebih baik dibandingkan dengan chi-square test.
2.9.2
Uji Hipotesis
Menurut Walpole (1995, p288), uji hipotesis adalah suatu
uji
yang
dilakukan dengan menggunakan pernyataan atau dugaan mengenai satu atau
lebih populasi. Dalam hal ini digunakan dua macam hipotesis yaitu hipotesis
nol yaitu hipotesis yang dirumuskan dengan harapan akan diterima (H
0
) dan
hipotesis alternatif
yaitu suatu hipotesis yang diharapkan untuk diterima
apabila hipotesis awal ditolak (H1). Suatu hipotesis awal akan ditolak apabila
nilai dari x hitung jatuh diwilayah kritis. Dan hipotesis awal akan diterima
apabila nilai dari x hitung jatuh di wilayah penerimaan.
2.10
Pola Distribusi Data
2.10.1
Frequency Distribution
Menurut Harrel (2000, p120-121), frequency distribution
merupakan
distribusi kelompok data
dalam
interval
atau kelas berdasarkan
frekuensi dari kejadian. Distribusi frekuensi dapat dibagi dua, yaitu:
|
|
49
1.
Discrete Frequency Distribution
Merupakan distribusi yang terbatas
pada nilai tertentu dan hanya
sekumpulan frekuensi yang terbatas saja yang ditampilkan. Sebagai
contoh dari discrete distribution adalah jumlah orang yang datang ke
suatu sistem pada interval waktu tertentu.
2.
Continuous Frequency Distribution
Merupakan
rentang
nilai
antara
sampel
dari
suatu
nilai
berada. Suatu
data dapat dikatakan memiliki continuous frequency distribution apabila
data tersebut dapat mewakili interval nilai yang sudah ditentukan.
2.10.2
Theoretical Distribution
Merupakan suatu distribusi yang
dapat dibedakan berdasarkan
parameter
yang
ditentukan
dari dispersion
(penyebaran)
dan
density
(kerapatan). Menurut Banks dan Gibsons (1997), berikut adalah statistikal
distribusi teoritis yang ada:
1.
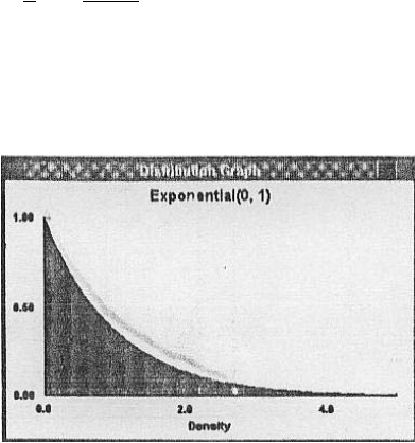
Exponential Distribution
Distribusi eksponensial adalah distribusi kontinu
dimana
dibatasi oleh
batas bawah. Bentuk dari distribusi ini akan selalu sama dimana dimulai
dari
nilai
minimum yang
terbatas
dan
terus
menurun
sampai
nilai
x
terbesar. Biasanya distribusi eksponensial mencerminkan waktu antar
kedatangan.
|
 50
1
?
[
x
-
min
]?
f (x) =
exp
?
-
?
ß
?
ß
?
dimana:
min = minimum x value
ß
= scale parameter
Grafik 2.1 Grafik Distribusi Eksponensial
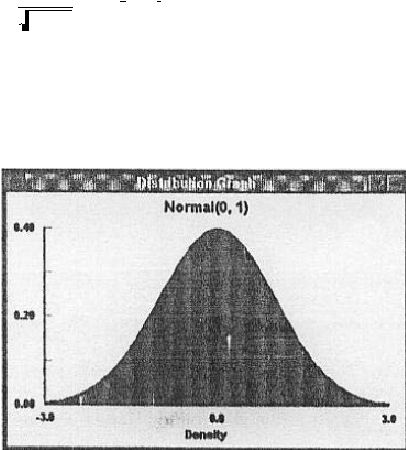
2.
Normal Distribution
Distribusi
normal
merupakan
distribusi kontinu yang tidak terbatas.
Biasanya kurva normal membentuk lonceng dengan nilai rata-ratanya
berada pada titik tengah kurva yang berarti jumlahnya paling banyak.
Berikut adalah rumusnya:
|
 51
?
1
?
[
x
-
µ
]
?
f (x) =
2
µ
s
2
?
exp
?
-
?
2
?
2
s
2
?
,
dimana:
µ
= shift parameter / mean
s
= scale parameter / standard deviation
Grafik 2.2 Grafik Distribusi Normal
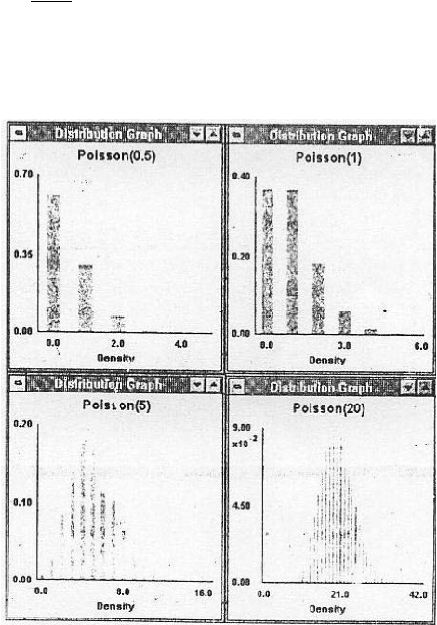
3.
Poisson Distribution
Distribusi poisson merupakan distribusi diskrit yang memiliki batas dari
0 pada batas bawah dan tidak terbatas pada batas atas. Biasanya
distribusi poisson berhubungan dengan tingkat kedatangan untuk suatu
sistem dan berkaitan erat dengan distribusi eksponensial. Berikut adalah
rumusnya:
|
 52
p(x) =
e
-
?
?
x
,
x!
dimana:
?
= rate of occurrence / mean
Grafik 2.3 Grafik Distribusi Poisson
|
 53
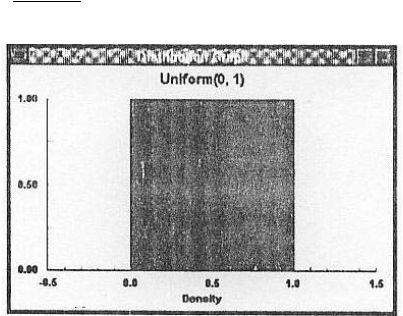
4.
Uniform Distribution
Distribusi
uniform
merupakan distribusi kontinu dimana dibatasi pada
kedua sisinya. Biasanya data berdistribusi uniform apabila nilai max dan
min tidak berbeda jauh. Berikut adalah rumusnya:
f (x) =
1
max - min
Grafik 2.4 Grafik Distribusi Uniform
2.11
Pareto Diagram
Diagram Pareto
adalah
grafik batang
yang
menunjukkan
masalah
berdasarkan urutan banyaknya kejadian. Masalah yang paling banyak terjadi
ditunjukan oleh grafik batang pertama
tertinggi serta ditempatkan pada sisi
paling kiri dan seterusnya sampai
masalah
yang paling sedikit terjadi
|
|
54
ditunjukkan oleh grafik batang terakhir yang terendah serta ditempatkan
pada sisi paling kanan.
Pada dasarnya diagram Pareto dapat digunakan sebagai alat
interprestasi untuk:
•
Menentukan
frekuensi
relatif
dan
urutan
pentingnya
masalah-masalah
atau penyebab-penyebab dari masalah yang ada.
•
Memfokuskan
perhatian
pada
isu-isu
kritis
daan
penting
melalui
pembuatan ranking terhadap masalah-masalah atau penyebab-penyebab
dari masalah itu dalam bentuk signifikan.
Menurut Mitra (1993) dan
Besterfield (1998), proses penyusunan diagram
Pareto meliputi enam langkah, yaitu:
1.
Menentukan atau arti pengklasifikasian data, misalnya berdasarkan
masalah, penyebab, jenis ketidaksesuaian dan sebagainya.
2.
Menentukan satuan yang digunakan untuk membuat urutan
karakteristik-karakteristik
tersebut, misalnya rupiah,
frekuensi,
unit dan
sebagainya.
3.
Mengumpulkan data
sesuai dengan
interval
waktu
yang telah
ditentukan.
4.
Merangkum data dan membuat ranking kategori data tersebut dari
yang
terbesar hingga yang terkecil.
|
|
55
5.
Menghitung frekuensi kumulatif atau persentase kumulatif yang
digunakan.
6.
Menggambar
diagram
batang,
menunjukkan
tingkat
kepentingan relatif
masing-masing
masalah.
Mengidentifikasi beberapa hal yang penting
untuk mendapatkan perhatian.
2.11.1
Memahami Hukum Pareto Diagram
Dinamakan
diagram pareto
sesuai
dengan
penemunya
seorang
bangsa
Italia
bernama
Wilfredo
Pareto
pada
tahun
1897.
Dalam diagram
pareto dikenal istilah “Vital Few – Trivial Many”, yang artinya sedikit tapi
vital atau sangat penting, banyak tetapi kurang vital atau kurang penting
(sedikit). Hal ini sesuai dengan kejadian sehari-hari yang menunjukkan
bahwa dalam banyak hal, permasalahan atau kerugian yang besar biasanya
disebabkan oleh hal-hal atau sebab-sebab yang jumlahnya
sedikit.
Dengan
demikian, timbul pemahaman lebih baik mengerjakan yang sedikit tetapi
bermanfaat
besar
daripada
mengerjakan banyak
hal
tapi
hasilnya
sedikit.
Konsep pareto mengajarkan agar kita pandai menerapkan prinsip skala
prioritas atau mendahulukan mana yang penting.
Sesuai dengan konsep pareto (pembagian 80 : 20), berlaku hal-hal
sebagai berikut:
•
80% dari sales dihasilkan oleh 20% jumlah salesman.
|
|
56
• 80% income RI dihasilkan oleh 20% dari jumlah jenis mata pencaharian
penduduk.
•
80% dari kesalahan yang terjadi diperusahaan dilakukan oleh 20% dari
seluruh karyawan.
• dsb.
Dalam kehidupan sehari-hari, analisa dan diagram pareto atau yang
biasa
disebut
dengan
diagram prioritas,
digunakan
dalam rangka
memilih
prioritas masalah yang dampaknya paling besar, yaitu kurang lebih 80%
disebabkan oleh kurang lebih 20% faktor penyebab,
sesuai
dengan
hukum
pareto.
2.11.2
Tipe-Tipe Diagram Pareto
Diagram pareto yang menunjukkan akibat suatu masalah:
-
Kualitas: jumlah kerusakan, cacat, kesalahan, keluhan, produk yang
dikembangkan, perbaikan.
-
Biaya:
jumlah
kerugian, pemborosan
biaya,
biaya
stock
(dead stock),
biaya bunga (piutang macet)
-
Pengiriman: keterlambatan pengiriman.
-
Metode kerja: jumlah kecelakaan kekeliruan kerja.
|
 57
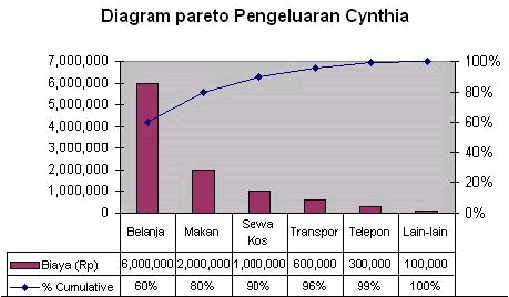
Diagram pareto yang menunjukkan penyebab-penyebab suatu masalah:
-
Operator:
giliran kerja,
kelompok
kerja,
umur
karyawan, pengalaman,
keterampilan.
-
Mesin: perlengkapan, peralatan, mesin-mesin, organisasi, instrumen.
-
Bahan baku: jenis bahan baku, produsen.
-
Metode kerja: kondisi kerja, order kerja.
Diagram 2.2 Contoh Diagram Pareto
2.12
Analisa Sensitivitas
Menurut
Pujawan
(2004,
p146),
analisa sensitivitas cocok
diaplikasikan pada permasalahan yang mengandung satu atau lebih faktor
ketidakpastian. Pertanyaan utama yang akan dijawab pada analisa
sensitivitas
adalah (1) bagaimana pengaruh yang
timbul pada
ukuran
hasil
|
|
58
(misalnya nilai NPW) bila suatu faktor individual berubah pada selang
(X%), dan (2) berapakah besarnya perubahan nilai suatu faktor sehingga
mengakibatkan keputusan pemilihan suatu alternatif bisa berubah.
Karena
nilai-nilai
parameter
dalam studi ekonomi
teknik biasanya
diestimasikan
besarnya
maka
jelas
nilai-nilai tersebut
tidak akan bisa
dilepaskan dari faktor kesalahan. Artinya,
nilai-nilai
parameter
tersebut
mungkin lebih besar atau lebih kecil dari hasil estimasi yang diperoleh, atau
perubah pada saat-saat tertentu. Perubahan-perubahan yang terjadi pada
nilai-nilai parameter tentunya akan mengakibatkan perubahan-perubahan
pula pada
tingkat output
atau
hasil
yang
ditunjukkan
oleh
suatu alternatif
investasi. Perubahan-perubahan
tingkat output atau
hasil
ini
memungkinkan
keputusan akan berubah dari satu alternatif ke alternatif
lainnya. Apabila
berubahnya faktor-faktor atau parameter-parameter tadi akan mengakibatkan
berubahnya
suatu
keputusan
maka
keputusan tersebut
dikatakan
sensitif
terhadap perubahan nilai parameter-parameter atau faktor-faktor tersebut.
Untuk mengetahui seberapa sensitif suatu keputuan terhadap
perubahan faktor-faktor atau parameter-parameter yang mempengaruhinya
maka setiap pengambilan keputusan pada ekonomi teknik hendaknya disertai
dengan analisa sensitivitas. Analisa ini akan memberikan gambaran sejauh
mana suatu keputusan akan cukup kuat berhadapan dengan perubahan
faktor-faktor atau parameter-parameter yang mempengaruhi.
|
|
59
Analisa sensitivitas dilakukan dengan mengubah nilai dari suatu
parameter pada suatu saat untuk selanjutnya dilihat bagaimana pengaruhnya
terhadap
akseptabilitas suatu
alternatif
investasi.
Parameter-parameter
yang
biasanya berubah dan perubahannya
bisa mempengaruhi keputusan-
keputusan
dalam
studi ekonomi
teknik adalah
ongkos
investasi, aliran kas,
nilai sisa, tingkat bunga, tingkat pajak, dan sebagainya.
|