|
5
BAB 2
LANDASAN TEORI
Struktur Aljabar
Struktur aljabar adalah ilmu yang mempelajari suatu sistem aljabar
dengan satu atau
lebih operasi biner yang diberlakukan pada sistem aljabar
tersebut. Struktur aljabar merupakan salah satu cabang matematika abstrak, yang
umumnya akan lebih rumit dibandingkan dengan cabang lain yang lebih konkret.
Secara
khusus,
struktur
aljabar
adalah
himpunan
tertutup
yang
terdiri
dari satu
atau lebih operasi matematika.
Operasi Biner (Tertutup)
Operasi
biner
adalah
operasi
dua elemen
dari
sebuah
himpunan,
yang
menghasilkan elemen yang masih merupakan anggota himpunan tersebut
(tertutup).
Contoh:
Himpunan A = { bilangan asli }, dengan operasi biner +
A tertutup terhadap operasi ”+”, bila untuk setiap a,b
?
A,
maka ( a + b )
?
A.
Dengan kata lain, hasil penjumlahan dua buah elemen
sembarang
dari
himpunan
A
yang berisi bilangan asli, akan
menghasilkan suatu bilangan asli yang juga merupakan suatu elemen
tunggal dari himpunan A.
|
|
6
Operasi Asosiatif
Operasi asosiatif adalah operasi biner “*” di mana untuk setiap a,b,c
?
A
maka :
( a * b ) * c = a * ( b * c )
Unsur Kesatuan (Identitas)
Unsur kesatuan atau identitas adalah suatu elemen yang jika dioperasikan
terhadap suatu elemen tunggal dari sebuah himpunan akan menghasilkan elemen
tunggal itu sendiri.
Ada 2 jenis identitas yaitu:
•
Identitas terhadap penjumlahan
Identitas
terhadap penjumlahan adalah suatu elemen yang
jika dilakukan operasi penjumlahan terhadap suatu elemen
tunggal dari sebuah himpunan akan menghasilkan elemen tunggal
itu sendiri.
Untuk setiap a
?
A, jika memenuhi :
a + e = e + a = a
maka, e merupakan identitas terhadap penjumlahan (unsur
kesatuan aditif).
•
Identitas terhadap perkalian
Identitas terhadap perkalian adalah suatu elemen yang jika
dilakukan operasi perkalian terhadap suatu elemen
tunggal dari
sebuah himpunan akan menghasilkan elemen tunggal itu sendiri.
|
|
7
Untuk setiap a
?
A, jika memenuhi :
a * e = e * a = a
maka, e merupakan identitas terhadap perkalian (unsur
kesatuan multiplikatif).
Invers
Invers adalah suatu elemen yang jika dioperasikan terhadap suatu elemen
tunggal dari sebuah himpunan akan menghasilkan suatu elemen yang merupakan
identitas.
Untuk
setiap
a,
a’
?
A
dan e
adalah
identitas
untuk
operasi biner “*”
memenuhi :
a * a’ = a’ * a = e
maka a’ adalah invers dari a untuk operasi biner “*”.
Operasi Komutatif
Operasi komutatif adalah operasi biner ”*” di mana untuk setiap a,b ?
A
berlaku :
a * b = b * a
|
|
8
Operasi Distributif
Operasi
biner # dikatakan distributif terhadap operasi biner * jika
memenuhi :
•
Distributif Kiri
Untuk setiap a,b,c ? A memenuhi :
a # ( b * c ) = ( a # b ) * ( a # c )
•
Distributif Kanan
Untuk setiap a,b,c ? A memenuhi :
( a* b ) # c = ( a # c ) * ( b # c )
Himpunan Bagian
Suatu himpunan B dikatakan merupakan himpunan bagian dari himpunan
A,
jika
semua
elemen
dari
himpunan
B
merupakan
elemen
dari
himpunan
A,
yang dilambangkan dengan B ? A.
Ring
Ring adalah suatu struktur aljabar yang terdiri dari dua operasi biner yaitu
penjumlahan
dan
perkalian,
di
mana
terhadap penjumlahan struktur tersebut
merupakan grup abelian, terhadap perkalian struktur tersebut merupakan
semigrup dan operasi perkalian bersifat distributif terhadap operasi penjumlahan.
Suatu ring (R,+,×) adalah suatu himpunan tak kosong R dengan operasi
biner penjumlahan (+) dan perkalian (×) pada R yang memenuhi aksioma-
aksioma berikut :
|
|
9
1.
Terhadap penjumlahan (+)
Tertutup : Untuk setiap a,b ? R, maka a + b ? R.
Asosiatif : Untuk setiap a,b,c ? R, maka (a + b) + c = a + (b + c).
Mempunyai unsur kesatuan : Adanya elemen identitas 0 sedemikian
hingga a + 0 = 0 + a = a.
Mempunyai invers : Untuk setiap a ?
R terdapat b sedemikian
hingga a + b = b + a = 0.
Komutatif : Untuk setiap a,b ? R, maka a + b = b + a.
2.
Terhadap perkalian (×)
Tertutup : Untuk setiap a,b ? R, maka a × b ? R.
Asosiatif : Untuk setiap a,b,c ? R, maka (a × b) × c = a × (b × c).
Mempunyai unsur kesatuan : Adanya elemen identitas 1 sedemikian
hingga a × 1 = 1 × a = a.
3.
Distributif perkalian (×) terhadap penjumlahan (+)
Untuk setiap a,b,c ? R, jika memenuhi :
•
Distributif Kiri
Untuk setiap a,b,c ?
R
memenuhi :
a × ( b + c ) = ( a × b ) + ( a × c )
•
Distributif Kanan
Untuk setiap a,b,c ?
R
memenuhi :
( a + b ) × c = ( a × c ) + ( b × c )
maka R bersifat distributif perkalian terhadap penjumlahan.
|
|
10
Ring Komutatif
Ring
komutatif
atau
gelanggang
komutatif
adalah
suatu ring, di mana
terhadap
penjumlahan
struktur
tersebut merupakan grup abelian, terhadap
perkalian struktur tersebut merupakan monoid komutatif dan operasi perkalian
bersifat distributif terhadap operasi penjumlahan.
Suatu ring komutatif (R,+,×) adalah suatu himpunan tak kosong R dengan
operasi biner penjumlahan (+) dan perkalian (×) pada R yang memenuhi aksioma-
aksioma berikut :
1.
Terhadap penjumlahan (+)
Tertutup : Untuk setiap a,b ? R, maka a + b ? R.
Asosiatif : Untuk setiap a,b,c ? R, maka (a + b) + c = a + (b + c).
Mempunyai unsur kesatuan : Adanya elemen identitas 0 sedemikian
hingga a + 0 = 0 + a = a.
Mempunyai invers : Untuk setiap a ?
R terdapat b sedemikian
hingga a + b = b + a = 0.
Komutatif : Untuk setiap a,b ? R, maka a + b = b + a.
2.
Terhadap perkalian (×)
Tertutup : Untuk setiap a,b ? R, maka a × b ? R.
Asosiatif : Untuk setiap a,b,c ? R, maka (a × b) × c = a × (b × c).
Mempunyai unsur kesatuan : Adanya elemen identitas 1 sedemikian
hingga a × 1 = 1 × a = a.
Komutatif : Untuk setiap a,b ? R, maka a × b = b × a.
|
|
11
3.
Distributif perkalian (×) terhadap penjumlahan (+)
Untuk setiap a,b,c ? R, jika memenuhi :
•
Distributif Kiri
Untuk setiap a,b,c
?
R
memenuhi :
a × ( b + c ) = ( a × b ) + ( a × c )
•
Distributif Kanan
Untuk setiap a,b,c
?
R
memenuhi :
( a + b ) × c = ( a × c ) + ( b × c )
maka R bersifat distributif perkalian terhadap penjumlahan.
Field
Field
adalah
suatu
struktur
aljabar
yang
terdiri
dari
dua operasi
biner
yaitu
penjumlahan dan perkalian, di mana
terhadap penjumlahan dan perkalian,
struktur tersebut merupakan grup abelian dan operasi perkalian bersifat distributif
terhadap operasi penjumlahan.
Suatu field (R,+,×) adalah suatu
himpunan tak kosong R dengan operasi
biner penjumlahan (+) dan perkalian (×) pada R yang memenuhi aksioma-
aksioma berikut :
1.
Terhadap penjumlahan (+)
Tertutup : Untuk setiap a,b ? R, maka a + b ? R.
Asosiatif : Untuk setiap a,b,c ? R, maka (a + b) + c = a + (b + c).
Mempunyai unsur kesatuan : Adanya elemen identitas 0 sedemikian
hingga a + 0 = 0 + a = a.
|
|
12
Mempunyai invers : Untuk setiap a ?
R terdapat b sedemikian
hingga a + b = b + a = 0.
Komutatif : Untuk setiap a,b ? R, maka a + b = b + a.
2.
Terhadap perkalian (×)
Tertutup : Untuk setiap a,b ? R, maka a × b ? R.
Asosiatif : Untuk setiap a,b,c ? R, maka (a × b) × c = a × (b × c).
Mempunyai unsur kesatuan : Adanya elemen identitas 1 sedemikian
hingga a × 1 = 1 × a = a.
Mempunyai invers : Untuk setiap a ?
R terdapat b sedemikian
hingga a × b = b × a = 0.
Komutatif : Untuk setiap a,b ? R, maka a × b = b × a.
3.
Distributif perkalian (×) terhadap penjumlahan (+)
Untuk setiap a,b,c ? R, jika memenuhi :
•
Distributif Kiri
Untuk setiap a,b,c
?
R
memenuhi :
a × ( b + c ) = ( a × b ) + ( a × c )
•
Distributif Kanan
Untuk setiap a,b,c
?
R
memenuhi :
( a + b ) × c = ( a × c ) + ( b × c )
maka R bersifat distributif perkalian terhadap penjumlahan.
|
|
13
Sub Ring
Misalkan (R,+,×) adalah suatu Ring, S adalah merupakan himpunan tidak
kosong
yang
merupakan bagian dari
R
(S ? R).
Bila
dilakukan
operasi
yang
sama dengan
(R,+,×),
yaitu (S,+,×)
membentuk
suatu
ring
maka
himpunan
S
disebut sub ring dari himpunan R.
Jadi (S,+,×) adalah subring dari (R,+,×) jika S memenuhi aksioma-
aksioma berikut :
1.
S adalah himpunan tak kosong
2.
Untuk setiap a,b ? S, maka a – b ? S.
3.
Untuk setiap a,b
?
S, maka a × b
?
S.
4.
Untuk setiap
a,b ? R dan b adalah
invers a
terhadap penjumlahan,
maka b harus di dalam S.
5.
Adanya elemen identitas perkalian 1 di dalam S.
Ideal
Ideal adalah sub ring khusus
yang memiliki sifat
istimewa yaitu
tertutup
terhadap perkalian unsur di
luar sub ring. Suatu sub ring disebut
ideal
jika sub
ring tersebut
merupakan ideal kiri dan
ideal kanan. Ideal kiri
yaitu bila tertutup
terhadap perkalian unsur di sebelah kiri. Ideal kanan
yaitu bila tertutup terhadap
perkalian unsur di sebelah kanan. Secara struktur aljabar, suatu subring disebut
ideal jika memenuhi aksioma-aksioma berikut:
|
 14
1. Ideal kiri
(S,+,×) adalah subring dari (R,+,×)
Untuk setiap a ? S dan r ? R, maka r × a ? S.
2. Ideal kanan
(S,+,×) adalah subring dari (R,+,×)
Untuk setiap a
?
S dan r
?
R, maka a × r
?
S.
Tabel Cayley
Tabel
Cayley adalah
daftar
yang
dibuat
untuk
memperlihatkan
operasi
antar dua elemen pada himpunan terbatas. Contoh Tabel Cayley:
Tabel 2.1 Tabel Cayley Penjumlahan Modulo 6
+
6
0
1
2
3
4
5
0
0
1
2
3
4
5
1
1
2
3
4
5
0
2
2
3
4
5
0
1
3
3
4
5
0
1
2
4
4
5
0
1
2
3
5
5
0
1
2
3
4
Interaksi Manusia dan Komputer
Interaksi Manusia dan Komputer adalah disiplin ilmu yang
mempelajari
hubungan antara manusia dan komputer yang meliputi perancangan, evaluasi, dan
implementasi antarmuka
pengguna komputer agar mudah digunakan oleh
|
|
15
manusia. Sedangkan interaksi manusia dan komputer sendiri adalah serangkaian
proses, dialog dan kegiatan yang dilakukan oleh manusia untuk berinteraksi
dengan komputer yang keduanya saling memberikan masukan dan umpan balik
melalui sebuah antarmuka untuk memperoleh hasil akhir yang diharapkan.
Beberapa aspek utama dalam perancangan sebuah antarmuka adalah :
1. Metodologi dan proses perancangan antarmuka.
2. Metode implementasi antarmuka.
3. Metode evaluasi dan perbandingan antarmuka.
4. Pengembangan antarmuka baru.
5. Mengembangkan sebuah deskripsi dan prediksi atau teori dari sebuah
antarmuka baru.
Menurut Shneiderman, seorang profesor dalam bidang Interaksi Manusia
dan
Komputer,
terdapat
8
aturan
emas
dalam
perancangan
desain
antarmuka,
yaitu:
1. Konsistensi.
Konsistensi dilakukan pada urutan tindakan, perintah, dan istilah yang
digunakan pada prompt, menu, serta layar bantuan.
2. Memungkinkan pengguna untuk menggunakan shortcut.
Ada kebutuhan dari pengguna yang sudah ahli untuk meningkatkan
kecepatan interaksi, sehingga diperlukan singkatan, tombol fungsi,
perintah tersembunyi, dan fasilitas makro.
3. Memberikan umpan balik yang informatif.
Untuk setiap tindakan operator, sebaiknya disertakan suatu sistem
umpan balik. Untuk tindakan yang sering dilakukan dan tidak terlalu
|
|
16
penting, dapat diberikan umpan balik yang sederhana. Tetapi ketika
tindakan merupakan hal yang penting, maka umpan balik sebaiknya
lebih substansial. Misalnya muncul suatu suara ketika salah menekan
tombol pada waktu input data atau muncul pesan kesalahannya.
4. Merancang dialog untuk menghasilkan suatu penutupan.
Urutan
tindakan sebaiknya diorganisir dalam suatu kelompok dengan
bagian awal, tengah, dan akhir. Umpan balik yang informatif akan
meberikan indikasi bahwa cara yang dilakukan sudah benar dan dapat
mempersiapkan kelompok tindakan berikutnya.
5. Memberikan penanganan kesalahan yang sederhana.
Sedapat
mungkin
sistem dirancang
sehingga
pengguna
tidak
dapat
melakukan kesalahan fatal. Jika kesalahan terjadi, sistem dapat
mendeteksi kesalahan dengan cepat dan memberikan mekanisme yang
sedehana dan mudah dipahami untuk penanganan kesalahan.
6. Mudah kembali ke tindakan sebelumnya.
Hal ini dapat mengurangi kekuatiran pengguna karena pengguna
mengetahui kesalahan yang dilakukan dapat dibatalkan; sehingga
pengguna
tidak
takut
untuk
mengekplorasi pilihan-pilihan lain yang
belum biasa digunakan.
7. Mendukung tempat pengendali internal (internal locus of control).
Pengguna ingin menjadi pengontrol sistem dan sistem akan merespon
tindakan yang dilakukan pengguna daripada pengguna merasa bahwa
sistem mengontrol pengguna. Sebaiknya sistem dirancang sedemikan
rupa sehingga pengguna menjadi inisiator daripada responden.
|
 17
8. Mengurangi beban ingatan jangka pendek.
Keterbatasan ingatan manusia membutuhkan tampilan yang sederhana
atau banyak tampilan halaman yang sebaiknya disatukan, serta
diberikan cukup waktu pelatihan untuk kode, mnemonic, dan urutan
tindakan.
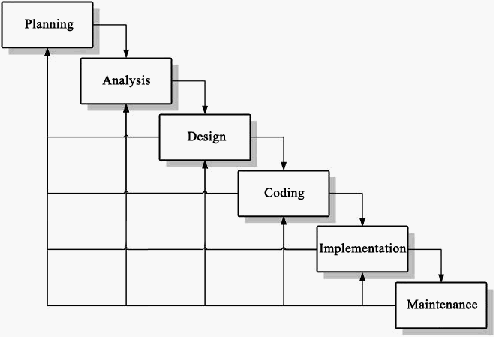
Waterfall Model
Waterfall Model adalah
sebuah
metode
pengembangan software yang
bersifat sekuensial dan terdiri dari 6 tahap yang saling terkait dan mempengaruhi
seperti terlihat pada gambar berikut.
Gambar 2.1 Metode Waterfall
|
|
18
Tahapan dalam Waterfall Model adalah sebagai berikut :
1.
Planning
Tahap perencanaan merupakan tahap awal dimana semua yang akan
dibuat
direncanakan
di
dalam tahap
ini,
termasuk
mengenai kebutuhan
tenaga kerja, biaya, dsb.
2. Analysis
Tahap
analisis
bertujuan
untuk mencari kebutuhan pengguna dan
organisasi
serta
menganalisa
kondisi
yang
ada,
sebelum diterapkan
sistem informasi yang baru.
3.
Design
Tahap desain bertujuan menentukan spesifikasi detil dari komponen-
komponen
sistem informasi
(manusia,
hardware,
software,
network
dan
data)
dan
produk-produk
informasi yang
sesuai
dengan
hasil
tahap
analisis.
4.
Coding
Pada
tahap
ini
dilakukan
pengaplikasian
dari
desain
ke
dalam
bentuk
kode program.
5.
Implementation
Tahap
implementasi
bertujuan untuk
mengimplementasikan
hasil
program
sekaligus menguji apakah program
sesuai dengan kebutuhan
dan desain yang telah dilaksanakan.
|
 19
6.
Maintenance
Tahapan
perawatan
(maintenance)
dilakukan
ketika
sistem informasi
sudah dioperasikan. Pada tahapan ini dilakukan monitoring proses,
evaluasi dan perubahan (perbaikan) bila diperlukan.
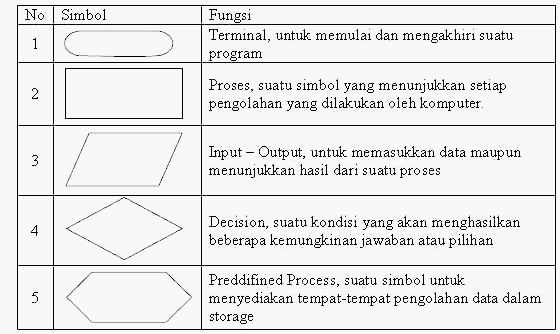
Flowchart
Flowchart
merupakan
sebuah
diagram dengan
symbol
symbol
symbol
grafis
yang
menyatakan tipe operasi program yang berbeda.Sebagai representasi
dari sebuah program, flowchart maupun algoritma dapat menjadi alat bantu untuk
memudahkan
perancangan
alur
urutan logika
suatu
program,
memudahkan
pelacakkan sumber kesalahan program, dan alat untuk menerangkan logika
program.
Tabel 2.2 Tabel Simbol Flowchart
|