 BAB 2
LANDASAN TEORI
2.1
TEORI
GRAF
2.1.1
Definisi
Definisi 2.1
(Munir, 2009,
p356)
Secara matematis, graf
G
didefinisikan sebagai pasangan
himpunan
(V,E),
ditulis
dengan
notasi
G
=
(V,E),
yang dalam hal
ini
V
adalah
himpunan
tidak
kosong
dari
simpul-sumpul
(vertices
atau node) dan E
adalah
himpunan sisi
(edges
atau
arcs) yang
menghubungkan
simpul.
Secara
geometri graf
digambarkan
sebagai sekumpulan
noktah
(simpul) di
dalam
bidang kartesius
yang dihubungkan
dengan sekumpulan
garis (sisi).
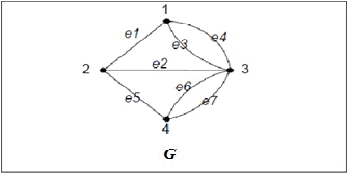
Gambar 2.1 Graf
(Munir, 2009, p356)
|
 8
Gambar
di halaman
sebelumnya
menunjukkan
sebuah graf G dengan:
• V = {1,2,3,4}
• E = {(1,2)
,
(2,3)
,
(1,3)
,
(1,3)
,
(2,4)
,
(3,4)
,
(3,4)}
=
{
e1
,
e
2
,
e
3
,
e
4
,
e
5
,
e
6
,
e
7
}
2.1.2
Jenis-jenis
Graf
Berdasarkan arah
dan
bobotnya,
graf
dibagi
menjadi
empat
bagian
sebagai
berikut.
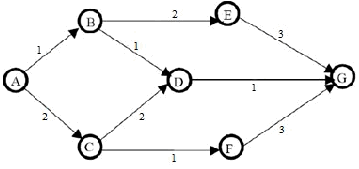
1. Graf berarah
dan berbobot: tiap edges mempunyai arah dan bobot
Gambar 2.2 Graf berarah
dan berbobot
Gambar 2.2 menunjukkan
graf berarah dan berbobot
yang terdiri dari
tujuh
simpul
(vertices),
yaitu
A,B,C,D,E,F,G.
Verteks
A
mempunyai
arah
ke
verteks B
dan
verteks
C,
verteks
B
mempunyai
arah
ke
verteks
D
dan
verteks E, dan seterusnya. Bobot antara satu verteks dengan
verteks lain
juga
diketahui.
|
 9
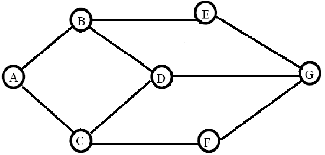
2. Graf
tidak
berarah
dan
berbobot:
tiap
edges
tidak
mempunyai
arah
tetapi
mempunyai
bobot
(nilai).
Gambar
2.3 Graf tidak
berarah
dan berbobot
Gambar 2.3
menunjukkan
graf
tidak
berarah
dan
berbobot
yang
terdiri
dari
tujuh
titik
(vertices), yaitu
A,B,C,D,E,F,G.
Verteks
A
tidak
mempunyai arah ke verteks B maupun
ke verteks C,
tetapi
memiliki
bobot
pada edgenya,
begitu
juga yang terjadi
dengan
verteks-
verteks
lainnnya.
3. Graf
berarah
dan
tidak
berbobot:
tiap
edges
mempunyai
arah
tetapi
tidak
mempunyai
bobot
(nilai).
Gambar
2.4 Graf berarah dan tidak
berbobot
|
 10
Gambar 2.4
menunjukkan
graf
berarah dan
tidak
berbobot yang
terdiri
dari
tujuh titik
(vertices),
yaitu
A,B,C,D,E,F,G.
Verteks
A
mempunyai
arah
ke
verteks
B dan
verteks
C,
tetapi
tidak
memiliki
bobot
untuk
setiap
edgenya.
4. Graf
tidak berarah dan
tidak
berbobot
:
Gambar
2.5 Graf tidak
berarah
dan tidak
berbobot
Gambar
2.5
menunjukkan graf tidak berarah
dan
tidak
berbobot yang
terdiri
dari
tujuh
titik
(vertices),
yaitu
A,B,C,D,E,F,G.
Verteks
A tidak
mempunyai
arah ke
verteks B dan verteks C,
verteks
C
juga
tidak
memiliki
arah
dengan
verteks
D
dan
verteks
B,
begitu
juga
yang
terjadi
dengan
verteks-verteks
lainnya. Setiap
edge
tidak memiliki
nilai.
2.1.2
Representasi
Graf
Suatu
graf
dapat direpresentasikan
ke beberapa
bentuk. Representasi
graf
dapat
digunakan
untuk
mengimplementasikan
graf
tersebut
ke
dalam
bentuk
tertentu,
sehingga
dapat digunakan
pada berbagai
kasus yang
berbeda.
|
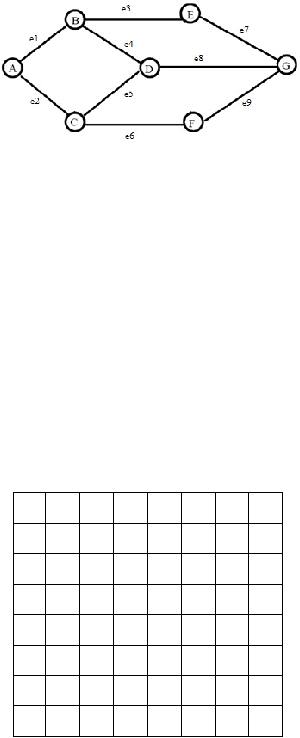 11
Gambar
2.6 Contoh Graf ABCDEFG
Representasi
graf yang
sering digunakan adalah sebagai berikut.
a.
Matriks
Kedekatan
(Adjacency Matrix)
Untuk
suatu
graf
dengan
jumlah
simpul
sebanyak
n, maka
matriks
kedekatan
mempunyai
ukuran
n
x n (n
baris
dan
n kolom).
Matriks
kedekatan untuk contoh
graf
ABCDEFG
dapat
dilihat
pada Tabel
2.1.
Tabel
2.1 Matriks kedekatan
graf
ABCDEFG
A
B
C
D
E
F
G
A
0
1
1
0
0
0
0
B
1
0
0
1
1
0
0
C
1
0
0
1
0
1
0
D
0
1
1
0
0
0
1
E
0
1
0
0
0
0
1
F
0
0
1
0
0
0
1
G
0
0
0
0
1
1
0
|
 12
b.
Matriks
Bersisian
(Incidency Matrix)
Untuk
suatu
graf
dengan
jumlah
simpul
sebanyak
n dan
jumlah
sisi
sebanyak
m,
maka
matriks
kedekatan
mempunyai
ukuran
n
x
m
(n
baris
dan m
kolom). Matriks
bersisian
untuk graf ABCDEFG dapat dilihat
pada tabel 2.2.
Tabel 2.2
Matriks
bersisian graf ABCDEFG
e1
e2
e
3
e
4
e
5
e
6
e
7
e
8
e
9
A
1
1
0
0
0
0
0
0
0
B
1
0
1
1
0
0
0
0
0
C
0
1
0
0
1
1
0
0
0
D
0
0
0
1
1
0
0
1
0
E
0
0
1
0
0
0
1
0
0
F
0
0
0
0
0
1
0
0
1
G
0
0
0
0
0
0
1
0
1
c.
List
Kedekatan (Adjacency
List)
Simpul
x
dapat
dianggap
sebagai
suatu
list
yang
terdiri
dari
simpul
pada
graf
yang
berdekatan
dengan x.
Adjacency list
untuk
graf
ABCDEFG
dapat
dilihat
pada gambar
di bawah
ini.
Tabel 2.3 Adjacency List
graf ABCDEFG
A
B,C
B
A,D,E
|
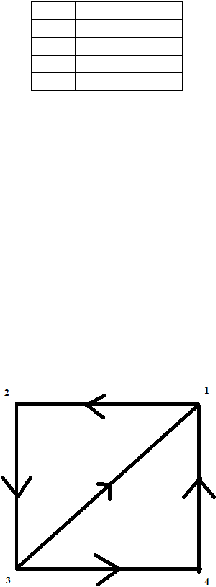 13
C
A,D,F
D
B,C,E,F,G
E
B,G
F
C,G
G
D,E,F
2.1.3
Graf Euler dan Graf
Hamilton
Definisi 2.2
(
Munir , 2009 , p404
)
Lintasan
Euler
ialah
lintasan
yang
melalui
masing-masing
sisi
di
dalam
graf
tepat
satu
kali.
Bila
lintasan
tersebut
kembali
ke simpul
asal,
membentuk
lintasan
tertutup (sirkuit), maka lintasan tertutup itu
dinamakan
sirkuit
Euler. Jadi,
sirkuit
Euler ialah
sirkuit
melewati
masing-masing
sisi
tepat satu
kali.
Gambar 2.7 Lintasan Euler
(Munir, 2009, p404)
Lintasan Euler pada Gambar 2.7: 3, 1, 2, 3, 4, 1.
|
 14
Gambar
2.8 Sirkuit
Euler (Munir,
2009,
p405)
Sirkuit Euler
pada Gambar 2.8: 1, 2,
3,
4, 7,
3, 5,
7, 6,
5, 2, 6, 1.
Definisi 2.3
(
Munir , 2009 , p408
)
Lintasan
Hamilton
ialah
lintasan
yang melalui
tiap
simpul
di dalam
graf
tepat
satu kali.
Bila
lintasan itu
kembali
ke
simpul
asal membentuk
lintasan
tertutup
(sirkuit),
maka
lintasan
tertutup
itu dinamakan
sirkuit
Hamilton.
Dengan
kata lain,
sirkuit
Hamilton
ialah
sirkuit
yang
melalui
tiap
simpul
di
dalam
graf
tepat
satu
kali,
kecuali simpul
asal
(sekaligus simpul
akhir)
yang
dilalui dua
kali.
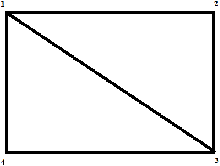
Gambar 2.9 Lintasan Hamilton (Munir,
2009, p409)
|
 15
Gambar 2.10 Sirkuit
Hamilton
(Munir, 2009, p409)
2.2
OPTIMASI
2.2.1
Definisi Masalah
Optimasi
Optimasi
ialah
suatu
proses
untuk mencapai
hasil
yang
ideal
atau
optimal
(nilai
efektif
yang
dapat
dicapai).
Dalam
disiplin
matematika
optimasi
merujuk
pada
studi
permasalahan
yang
mencoba
untuk
mencari
nilai
minimal
atau
maksimal
dari
suatu
fungsi
riil. Untuk
dapat
mencapai
nilai
minimal
atau
maksimal
tersebut,
secara
sistimatis
dilakukan
pemilihan
nilai
variabel
bilangan
bulat
atau
riil yang
akan
memberikan
solusi
optimal.
2.2.2
Macam-macam
Permasalahan
Optimasi
Permasalahan
optimasi
mempunyai
hubungan
yang
erat dalam
kehidupan
sehari-hari.
Nilai
optimal
yang
dapat
dioptimasi
dapat
berupa
besaran
waktu,
panjang,
jarak,
dan
jadwal.
Berikut
ini adalah
beberapa
contoh
dari
permasalahan
optimasi.
|
|
16
1. Travelling Salesman Problem
Sebuah
permasalahan
dalam menentukan
lintasan terpendek
dari suatu
kota
menuju seluruh kota lainnya dan kembali
ke kota
semula.
2. Quadratic Assignment Problem (QAP)
Sebuah
permasalahan
untuk
mengalokasikan
sejumlah
n
resources
untuk
ditempatkan pada
sejumlah
M
lokasi
dengan
meminimumkan
biaya
alokasi.
3. Job Scheduling Problem
(JSP)
Sebuah
permasalahan
untuk
menjadwalkan
sejumlah
j pekerjaan
menggunakan
sejumlah
m
mesin,
sehingga
seluruh
pekerjaan
diselesaikan
dengan waktu yang
minimal.
4. Pewarnaan
graf.
2.2.3
Permasalahan
Rute Terpendek
Masalah
rute terpendek
merupakan
masalah
yang
berkaitan
dengan
penentuan
edge-edge
dalam sebuah graf yang membentuk rute
terdekat antara
sumber
dan
tujuan.
Tujuan
dari
permasalahan
rute
terpendek
adalah
mencari
rute
yang
memiliki
jarak terdekat antara
titik asal dan titik tujuan.
|
 17
Gambar 2.11
Graph
ABCDEFG
Pada
gambar
2.11
dimisalkan
kota
A
merupakan
kota awal
dan kota
G adalah
kota
tujuan.
Dari
kota awal
sampai
dengan
kota
tujuan,
dapat
dipilih
beberapa
rute
sebagai
berikut.
•
A?
B
?C
?
D
?
E
?G
•
A?
B
?C
?
D
?
F
?G
•
A?
B
?C
?
D
?G
•
A?
B
?C
?
F
?G
•
A?
B
?
D
?
E
?G
•
A?
B
?
D
?
F
?G
•
A?
B
?
D
?G
•
A?
B
?
E
?G
•
A?C
?
D
?
E
?G
•
A?C
?
D
?
F
?G
•
A?C
?
D
?G
•
A?C
?
F
?G
|
|
18
Berdasarkan
data di halaman
sebelumnya,
dapat
dihitung
rute terpendek
dengan
mencari
jarak
antar
rute
tersebut.
Apabila
jarak
antar
rute
belum
diketahui,
jarak
dapat
dihitung
berdasarkan
koordinat dari
kota-kota tersebut,
kemudian
dihitung
jarak
yang
paling
pendek
yang dapat
dilalui.
2.2.4
Penyelesaian
Masalah
Optimasi
Secara
umum,
penyelesaian
masalah
pencarian
rute terpendek
dapat
dilakukan
dengan
menggunakan
dua
metode,
yaitu
metode
konvensional
dan
metode
heuristik.
1.
Metode Konvensional
adalah
metode
yang
menggunakan
matematika
biasa.
Contoh:
algoritma
Djikstra,
algoritma
Floyd-Warshall,
algoritma
Bellman-Ford.
2. Metode
heuristik adalah
suatu
metode
yang
merujuk pada
metode
komputasi
yang
mengoptimasi
sebuah
permasalahan
dengan
mencoba
secara
iteratif
mencari
kandidat
solusi
sehingga
mendapatkan
yang
paling
optimal.
Contoh: algoritma genetika
dan algoritma Ant Colony
Optimization.
(I’ing Mutakhiroh,
Indrato, Taufiq
Hidayat,
2007)
|
 19
2.3
Travelling Salesman
Problem
Sebuah
permasalahan
dalam
menentukan
lintasan
terpendek
dari suatu
kota
menuju
seluruh
n
kota
lainnya
dan
kembali
ke
kota
semula
dengan
sekali
kunjung
untuk
tiap kota.
Permasalahan
TSP
ini
dapat
dimisalkan
menjadi
persoalan
pada
graph,
yaitu
bagaimana
menentukan
sirkuit
hamilton
yang
memiliki
bobot
paling
minimum
pada
graph
tersebut.
Misalkan
terdapat n buah titik dalam sebuah
graph
lengkap
dengan n verteks , maka
jumlah sirkuit
hamiltonnya
adalah
(
n
-
1
)
!
/
2
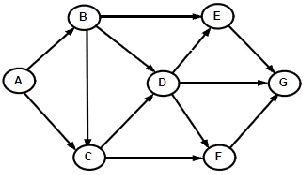
Contoh
:
Gambar 2.8 Graf
lengkap
(Munir
,
2009 , p423)
Graph di atas
memiliki ( 4 – 1 ) ! / 2 = 3 sirkuit
hamilton
I1 = (a, b, c, d, a) atau (a, d, c, b, a) ==> panjang
=
10 + 12 + 8 + 15 = 45
|
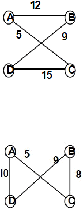 20
I2 = (a, c, d, b, a) atau (a, b, d, c, a) ==> panjang
=
12 + 5
+
9
+
15 = 41
I3 = (a, c, b, d, a) atau (a, d, b, c, a) ==> panjang
=
10 + 5 + 9 + 8 = 32
Jadi
dari
3
sirkuit
hamilton
yang
telah
didapat,
sirkuit
hamilton
yang
paling
pendek
adalah I3 = (a,
c, b,
d, a) atau
(a,
d,
b, c, a) dengan
panjang
sirkuit
=
10 + 5 +
9
+
8
=
32.
2.4
ALGORITMA
ANT
COLONY
Algoritma Semut
(Ant
Colony
Algorithm)
merupakan algoritma
yang
terinspirasi
dari
pengamatan
terhadap
suatu
koloni
semut.
Semut
merupakan
hewan
yang
hidup
sebagai
suatu
kesatuan
dalam koloninya.
Suatu
perilaku
penting
dan
menarik
untuk
ditinjau
dari suatu
koloni
semut
adalah
perilaku
mereka
pada saat
mencari
makan,
terutama
bagaimana
mereka
mampu
menemukan
rute yang
menghubungkan
antara sumber
makanan
dengan sarang
mereka. Ketika berjalan
menuju
sumber
makanan
dan
sebaliknya,
semut
meninggalkan
jejak
berupa
suatu
zat
yang
disebut
pheromone.
Semut-semut
dapat
mencium
pheromone,
dan
ketika
memilih
rute
yang
akan
dilalui,
semut
akan
memiliki
kecenderungan
untuk
memilih
rute
yang
memiliki
tingkat konsentrasi pheromone
yang
tinggi.
|
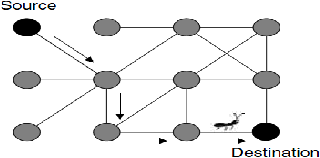 21
Gambar 2.12
Semut
menciptakan
solusi,
dari
sumber menuju tujuan (Dorigo,p10)
Proses
peninggalan
pheromone
ini merupakan
salah
satu
contoh
dari
proses
stigmergy,
yaitu
sebuah
proses
yang
meninggalkan
jejak
pada
lingkungan
oleh
suatu
aksi dan merangsang
perkembangan
pada
aksi berikutnya.
Proses
peninggalan
pheromone
ini sangat
berguna
bagi
semut
yang
memungkinkan
para
semut
untuk
mengingat
jalan
pulang
ke sarang
dan
juga
memungkinkan
para
semut
berkomunikasi
dengan
koloninya.
Seiring
waktu,
bagaimanapun
juga
jejak
dari pheromone
akan
menguap
dan
akan mengurangi kekuatan daya tariknya. Lebih cepat setiap semut pulang
pergi
melalui
rute tersebut,
maka
pheromone
yang menguap
lebih
sedikit.
Begitu
pula yang
terjadi
dengan
hal
sebaliknya
jika
semut
lebih
lama
pulang
pergi
melalui
rute,
maka
pheromone yang menguap akan lebih
banyak.
2.4.1
Cara
Kerja Algoritma Semut
Semut
secara
alamiah
dapat
mencari
jalan
terpendek
yang menghubungkan
antara
sumber
makanan
dengan
sarangnya.
Untuk
lebih jelasnya
diberikan
contoh
seperti di halaman berikut.
|
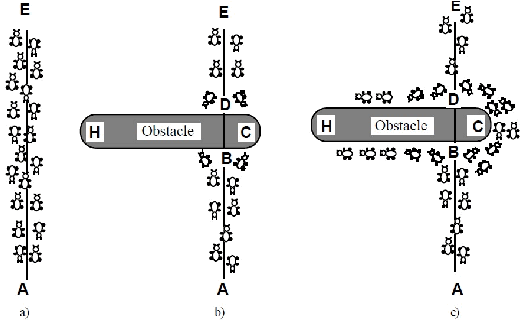 22
Gambar 2.13
Perjalanan semut dari sarang(A)
menuju sumber makanan(E)
Gambar
2.9.a
di atas
menunjukkan
ada
dua
kelompok
semut
yang
sedang
melakukan
perjalanan.
Kelompok
yang
berangkat
dari
bawah
yang
merupakan
sarang
semut
dan kelompok
lain
yang
berangkat
dari
atas yang
merupakan
sumber
makanan.
Pada
gambar
2.9.b
ada
sebuah
penghalang (obstacle)
yang
menghalangi
jalur
semut
dan
membagi
jalur
semut
menjadi
2,
yaitu
jalur
kiri
dan
jalur
kanan.
Semut
dengan
kecepatan
yang
sama
berjalan
sembari
meninggalkan
jejak
pheromone
di jalan
yang telah dilewatinya. Gambar 2.9.c
terlihat
jumlah
semut yang lebih
banyak
melewati
jalur
yang
kanan,
sehingga
lebih
banyak
jejak pheromone
yang
tertinggal.
Untuk
lebih
mudah
membayangkan
sistem
koloni
semut,
lihatlah
pemodelan
dari
sistem
koloni
semut
seperti gambar yang ada di bawah
ini.
|
 23
Gambar
2.14 Permodelan
Sistem
Koloni Semut
Misalkan
jarak
antara
D dan H,
antara B dan H,
dan antara
B dan D
(melalui
C)
adalah
sama
besar
yaitu
1.
Misalkan
C
berada
dalam
pertengahan
jalan
antara
D
dan
B
(Gambar
2.10a).
Misalkan
juga
ada
30 semut yang
datang
menuju
B
dari
A,
dan
30
semut
menuju
D
dari
E pada
suatu
waktu
yang
bergerak
dengan
kecepatan sama, dan setiap
langkah
semut
akan
meninggalkan
jejak pheromone.
Pada
gambar
2.10.b
menunjukkan
waktu
pada
saat
t=0.
Dalam
keadaan
ini
tidak ada
jejak feromon
sama sekali
pada
seluruh
edge, oleh
karena
itu kemungkinan
untuk
memilih
jalur kanan dan
kiri adalah sama besar.
Pada
gambar
2.10.c
menunjukkan
waktu
pada
saat
t=1.
Dalam
keadaan
ini
jejak
pheromone
pada
jalur
yang
lebih
pendek
akan
lebih
kuat,
oleh
karena
itu
lebih
banyak
semut
memilih
jalur
kanan, yang
merupakan
jalur
terpendek.
|
|
24
Semakin
sedikit
semut
yang melalui
suatu
jalur,
maka semakin
sedikit
pula
pheromone
yang
ditinggalkan,
dan pada akhirnya
jejak
pheromon
akan
benar-benar
hilang
ketika tidak ada semut
lagi yang
memilih
jalur tersebut.
2.5
Algoritma Elitist Ant System
Algoritma
Elitist
Ant System
merupakan
pengembangan
dari
algoritma
Ant
System.
Pada
dasarnya
algoritma
Elitist
Ant
System
memiliki
similiaritas
atau
kesamaan
dengan algoritma Ant
System dalam
menyelesaikan permasalahan TSP.
Yang
membedakan
antara
keduanya
adalah
pada saat
perhitungan
perubahan
nilai
intensitas
jejak
pheromone
antar kota. Pada algoritma Elitist
Ant System
terjadi
penambahan
sebesar
e
/
L
bs
pada
edge-edge
yang
merupakan
rute
terbaik,
dimana
e
adalah parameter
yang
menunjukkan
adanya rute terbaik
dan L
bs
adalah
panjang
rute
terbaik.
Dalam
algoritma Elitist
Ant
System, diperlukan beberapa variabel dan
langkah-langkah
untuk
menentukan
jalur
terpendek sebagai berikut.
Langkah 1 : Penetapan parameter
dan nilai pheromone
awal
a.
Inisialisasi
harga parameter-parameter
algoritma.
Parameter-parameter
yang diinisilisasikan
adalah:
1.
Intensitas
jejak
semut
antar kota dan
perubahannya
(t
ij
)
2.
Banyak kota (n) termasuk x dan y (koordinat)
atau d
ij
(jarak
antar
kota)
|
|
25
3.
Penentuan kota berangkat dan kota
tujuan
4.
Tetapan
siklus-semut
(Q)
5.
Tetapan
pengendali
intensitas
jejak
semut
(a)
6.
Tetapan
pengendali
visibilitas
(ß)
7.
Visibilitas antar
kota
=
1/d
ij
(?
ij
)
8.
Jumlah semut (m)
9.
Tetapan
penguapan
jejak
semut
(?)
10. Jumlah
siklus
maksimum
(NCmax)
bersifat
tetap
selama algoritma
dijalankan.
sedangkan
t
ij
akan selalu
diperbaharui
harganya
pada
setiap
siklus
algoritma
mulai
dari
siklus
pertama
(NC=1)
sampai
tercapai
jumlah
siklus
maksimum
(NC=NCmax)
atau
sampai
terjadi
konvergensi.
b.
Inisialisasi
titik
pertama
setiap
semut
Pengisian
kota pertama
ke dalam
tabu
list.
Hasil
inisialisasi
kota pertama
semut
pada
langkah
1
harus
diisikan
sebagai
elemen
pertama
tabu
list.
Hasil
dari
langkah
ini
adalah
terisinya
elemen
pertama tabu
list
setiap
semut
dengan
indeks
kota
pertama.
Langkah 2 : Penyusunan kunjungan
Penyusunan
jalur
kunjungan
setiap
semut
ke
setiap
kota.
Koloni
semut
yang
sudah
terdistribusi
ke
kota
tujuan.
Kemudian
dari
kota
kedua,
masing-masing
koloni
semut
akan
melanjutkan
perjalanan
dengan
memilih
salah
satu
dari
kota-kota
yang
tidak terdapat
pada
tabu k sebagai
kota
tujuan selanjutnya.
Perjalanan
pertama
semut
|
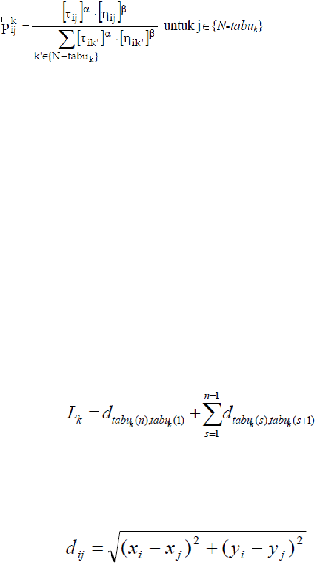 26
akan
mulai
melakukan
perjalanan
dari
kota
pertama
sebagai
kota
asal
dan
salah
satu
kota
lainnya
sebagai
kota
koloni
semut
berlangsung
terus-menerus
hingga
mencapai
kota
yang
telah
ditentukan.
Jika
s menyatakan
indeks
urutan
kunjungan,
kota
asal
dinyatakan sebagai
tabuk(s) dan
kota-kota
lainnya
dinyatakan sebagai
{N-tabuk},
maka
untuk
menentukan
kota tujuan
digunakan
persamaan
probabilitas
kota untuk
dikunjungi
sebagai
berikut.
=
0,
untuk
lainnya
dengan i sebagai
indeks
kota
asal dan j sebagai
indeks kota tujuan.
Langkah 3 : Mencari
rute
terbaik
a.
Perhitungan
panjang
jalur
setiap
semut.
Perhitungan panjang
jalur
tertutup
(length closed
tour)
atau
L
k
setiap
semut
dilakukan
setelah
satu siklus
diselesaikan
oleh semua
semut.
Perhitungan
dilakukan berdasarkan
tabu
k
masing-masing
dengan
persamaan
berikut:
dengan
d
ij
adalah
jarak
antara
kota
i
ke
kota
j
yang
dihitung
berdasarkan
persamaan
:
|
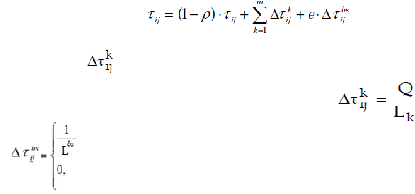 27
b.
Perhitungan
rute terpendek
Setelah
L
k
setiap semut
dihitung,
akan
diperoleh
harga minimal
panjang
jalur
tertutup
setiap
siklus
atau
LminNC
dan harga
minimal
panjang jalur tertutup secara
keseluruhan
adalah atau Lmin.
Langkah 4 : Perubahan
Intensitas Pheromone
Perhitungan
harga
intensitas
jejak
kaki semut
antar
kota untuk
siklus
selanjutnya.
Harga
intensitas
jejak
kaki
semut
antar
kota
pada
semua
lintasan
antar
kota
ada
kemungkinan
berubah,
karena
adanya
penguapan
dan
perbedaan
jumlah
semut
yang melewati.
Untuk
siklus
selanjutnya,
semut
yang akan
melewati
lintasan
tersebut
harga
intensitasnya
telah
berubah.
Harga
intensitas
jejak
kaki
semut
antar
kota
untuk
siklus selanjutnya
dihitung
dengan
persamaan:
dengan
adalah perubahan harga
intensitas
jejak pheromone antar
kota
setiap semut
dan
yang
dihitung berdasarkan
persamaan
dan
untuk edge
yang memiliki
tur terbaik
lainnya
Langkah 5 : Penyelesaian
Tabu list dikosongkan kembali untuk diisi
dengan urutan titik
baru pada
iterasi
selanjutnya,
jika
NCmax
belum
tercapai
atau
belum
terjadi
konvergensi
(semua
semut
hanya
menemukan
satu
tour
yang
sama
dengan jarak
yang
sama
pula).
Algoritma
diulang
lagi dari
langkah
2
dengan
harga
parameter
intensitas
pheromone
|
|
28
antar
titik
yang
sudah
diperbaharui.
Perhitungan
akan
dilanjutkan
hingga
semut
telah
menyelesaikan
perjalanannya
mengunjungi
tiap-tiap
titik. Hal
ini akan
berulang
hingga
sesuai
dengan
NCmax
yang
telah
ditentukan
atau telah
mencapai
konvergensi.
Kemudian
akan
ditentukan
jarak
terpendek
dari
masing-masing
iterasi.
Jarak
terpendek
inilah
yang
merupakan
solusi
terbaik
dari
algoritma
Elitist Ant
System.
2.6 Software Engineering
(Rekayasa
Piranti Lunak)
Menurut
Fritz
Bauer
(Pressman,
2001,
p19), rekayasa
piranti
lunak
adalah
penetapan
dan
pemakaian
prinsip-prinsip
rekayasa
dengan
tujuan
mendapatkan
piranti
lunak
yang
ekonomis,
terpercaya,
dan bekerja
efisien
pada
mesin
yang
sebenarnya (komputer).
Rekayasa
piranti
lunak
terbagi
menjadi
3 lapisan
yang
mampu
mengontrol
kualitas
dari
piranti
lunak
(Pressman, 2001,
p19),
yaitu:
a. Proses
(Process)
Proses
merupakan
lapisan
paling
dasar
dalam
rekayasa
piranti
lunak.
Proses
dari rekayasa
piranti
lunak
adalah
perekat
yang
menyatukan
lapisan-lapisan
teknologi
dan
memungkinkan
pengembangan
yang
rasional
dan
periodik
dari
pirantik lunak komputer.
b. Metode (Methods)
Metode
dari rekayasa
piranti
lunak
menyediakan
secara
teknis
bagaimana
membangun sebuah
piranti
lunak.
Metode
meliputi
sekumpulan tugas
yang
|
|
29
luas,
termasuk
di dalamnya
analisis
kebutuhan,
perancangan,
konstruksi
program,
pengujian,
dan pemeliharaan.
Metode
dari rekayasa
piranti
lunak
bergantung
pada
sekumpulan
prinsip
dasar
masing-masing
area
teknologi
dan
memasukkan
pemodelan aktivitas, serta
teknik
deskriptif
lainnya.
c. Alat Bantu (Tools)
Alat
bantu
dari rekayasa
piranti
lunak
menyediakan
dukungan
otomatis
atau
semi
otomatis
untuk
proses
dan
metode.
Ketika
alat
bantu
diintegrasi,
informasi
akan
diciptakan
oleh
sebuah
alat
bantu
yang
dapat
digunakan
oleh
lainnnya,
sebuah
sistem
untuk
mendukung
pengembangan
piranti
lunak,
yang
juga disebut
computer-aided
software
engingeering(CASE).
CASE
menggabungkan
piranti
lunak, perangkat keras, dan
database piranti
lunak
untuk
menciptakan
lingkungan
rekayasa
piranti
lunak
yang
sejalan dengan
CAD
/
CAE
(computer-aided design/engineering)
untuk perangkat
keras.
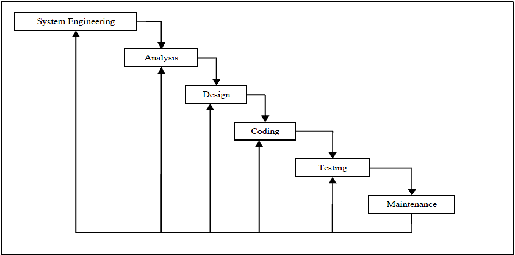
Dalam
perancangan
piranti
lunak,
dikenal
linear
sequential
model
atau yang
lebih
dikenal
dengan
sebutan
classic
life cycle
atau waterfall
model.
Model
ini
menyarankan pendekatan yang
sistematik
dan
berurutan
dalam
pengembangan
piranti
lunak yang
melalui
analisis,
desain,
pengkodean,
pengujian,
dan
pemeliharaan.
Model
ini
meliputi serangkaian
aktivitas,
yaitu:
a. Rekayasa
dan pemodelan
sistem
Karena
piranti
lunak
merupakan
sebuah
bagian
dari
sistem
yang
besar,
maka
yang
perlu
dilakukan
pertama
kali
adalah
menetapkan
kebutuhan
untuk
seluruh
elemen
sistem
dan
mengalokasikan
sebagian
dari
kebutuhan
tersebut
ke piranti
lunak.
|
 30
b. Analisis
kebutuhan piranti
lunak
Untuk dapat
mengerti
inti dari program
yang dibangun,
diperlukan
pengertian
akan
informasi
yang
diperlukan
oleh
piranti lunak.
c. Perancangan
Perancangan
piranti
lunak
sebenarnya
merupakan
sebuah
proses
yang
terdiri
dari
banyak
kegiatan,
yang
menitikberatkan
pada 4 atribut dari
program,
yaitu:
struktur
data,
arsitektur
piranti
lunak,
representasi
tampilan,
dan detil
prosedur.
d. Pengkodean
Dalam
pengkodean,
perancangan
yang
telah
dilakukan
diterjemahkan
ke
bentuk
yang dimengerti
komputer.
e. Pemeliharaan
Pemeliharaan
dilakukan
untuk mengantisipasi
terjadinya
kesalahan,
karena
perubahan
sistem atau peningkatan
kebutuhan pengguna
akan
fungsi baru.
Gambar
2.15
Waterfall Model (Pressman, 2002, p29)
|
 31
2.7
Flowchart
Salah
satu
bentuk
untuk
menyatakan
alur
pikiran
dalam
menyelesaikan
suatu
pekerjaan
adalah
dalam
bentuk
gambar
atau
bagan
yang
disebut
program
flowchart
atau
bagan
alir
program
(Moh.
Sjukani,
2004,
p5).
Berikut
adalah
simbol-simbol
yang digunakan
untuk menggambarkan
diagram alir.
Tabel
2.4 Tabel
simbol flowchart
(Sumber: Moh. Sjukani, 2004,p9)
Notasi
Arti Notasi
Terminal,
untuk
menyatakan
mulai dan
selesai sebagai
tanda, tidak
melakukan
suatu
pekerjaan khusus.
Process,
untuk
menyatakan
assignment
statement.
Input/Output
operation,
untuk
menyatakan
proses baca da proses tulis.
Decision,
untuk menyatakan
pengambilan
keputusan
sesuai dengan
suatu
kondisi
Garis,
untuk
menyatakan pelaksanaan,
atau alur
proses
Preparation,
pemberi
nilai
awal
suatu
variabel
Call,
memanggil
suatu subprogram
Titik
connector
yang
berada
pada
halaman
yang
sama.
Titik
connector
yang
berada
pada
halaman
yang
lain.
2.8
State
Transition
Diagram
State
Transition
Diagram
(STD)
adalah
kumpulan
keadaan/atribut yang
menggambarkan
seseorang
atau
suatu benda pada
waktu
tertentu,
bentuk
keberadaan
|
|
32
atau
kondisi
tertentu, seperti menunggu instruksi berikutnya,
menunggu pengisian
password, dan lain-lain.
STD
merupakan
modelling
tools yang
sangat
kuat untuk
mendeskripsikan
kelakukan
yang
dibutuhkan
pada
sistem
yang
mempunyai
sifat real-time
dan juga
bagian
interface
manusia
pada
berbagai
sistem
online.
Cara
kerja
sistem
ini
ada
dua
macam
sebagai berikut.
•
Passive
Sistem
ini
melakukan
kontrol terhadap lingkungan,
tetapi lebih
bersifat memberikan atau menerima data. Kontrol suatu sistem
bertugas
mengumpulkan/menerima
data
melalui
sinyal
yang
dikirim
oleh
satelit.
•
Active
Sistem
ini
melakukan
kontrol
terhadap
lingkungan
secara
aktif
dan
dapat
memberikan
respon
terhadap
lingkungan
sesuai dengan
program
yang ditentukan.
Komponen-komponen
utama STD sebagai berikut.
1. State
State adalah
kumpulan
atribut
yang
mencirikan
seseorang
atau suatu
benda
pada waktu atau kondisi
tertentu.
2. Transition State
Transition
State yang
diberi
label
dengan
ekspresi
atau
arah,
label
tersebut menunjukkan
kejadian yang menyebabkan
transisi
terjadi.
|
|
33
3. Condition
dan Action
Condition
adalah
suatu
peristiwa
pada
lingkungan
eksternal
yang
dapat
dideteksi
oleh
sistem. Dan
action adalah
apa
yang
dilakukan
oleh sistem
apabila
terjadi
perubahan
state,
atau
bisa
juga dikatakan
sebagai
reaksi
sistem
terhadap
suatu
kondisi,
aksi
akan
menghasilkan
keluaran/tampilan.
|