|
BAB 2
LANDASAN TEORI
2.1 Dasar Teori Antrian
Menurut Taha
(2002,
p72), dalam hampir setiap
organisasi
selalu
ada
contoh
proses
yang
menimbulkan deretan
tunggu
disebut antrian. Deretan bagian, mesin atau
unit harus menunggu untuk memperoleh pelayanan karena fasilitas pelayanan terbatas
dan tidak dapat memenuhinya secara bersamaan.
Bila berpergian dengan pesawat maka akan dihadapkan berbagai deretan antrian.
Untuk membeli karcis, orang harus berdiri dalam deretan menuju loker agen perjalanan.
Begitu tiba di lapangan udara, orang harus berdiri pada deretan pemeriksaan bagasi dan
pemeriksaan
parpor. Di
dalam pesawat,
penumpang
harus berdiri
lagi
dalam deretan
untuk mendapatkan tempat duduk. Ini adalah contoh dalam kehidupan sehari-hari
tentang antrian.
2.1.1 Pengertian Teori Antrian
Menurut
Taha
(2002,
p91),
Banyak
model
yang berbeda
tentang
sistem aliran
barang mencakup faktor-faktor yang ditandai dengan suatu sebaran peubah acak.
Yang
paling umum digunakan adalah pendekatan analitis pada sistem aliran acak seperti pada
analisis antrian atau teori antrian. Teori antrian mengacu kepada pengamatan matematis
dan fisik dari suatu kelompok masalah yang ditandai dengan ciri-ciri :
1. Ada masukan dari satuan yang memasuki sistem.
2. Satuan yang bergerak melewati sistem adalah diskrit.
|
|
9
3.
Satuan
yang
mulai
membutuhkan pelayanan
disusun
dengan
satu
cara
dan
menerima pelayanan menurut susunan tadi.
4. Mekanisme
yang
ada
yakni
yang
mengatur kapan
satu satuan
yang
melayani
selesai dilayani.
5. Paling
tidak
satu
dari dua
mekanisme, kedatangan atau
pelayanan,
tidak
ditentukan
seluruhnya
tetapi
dapat
diperhitungkan pada
satu
jenis
sistem
probabilistic (berpeluang).
Menurut
Taha
(2002,
p135),
teori
antrian
adalah
teori
yang
menyangkut
studi
matematis
dari
antrian-antrian atau
baris-baris
penungguan.
Formasi
baris-baris
penungguan merupakan
sesuatu
yang
biasa
terjadi
apabila
kebutuhan
akan
suatu
pelayanan melebihi kapasitas yang tersedia untuk menyelenggarakan pelayanan tersebut.
Apabila
pelayanan
terlalu
banyak
maka akan
memerlukan
ongkos
yang
besar,
sebaliknya
jika
kapasitas pelayanan kurang maka akan
terjadi baris penungguan dalam
waktu yang cukup lama yang juga akan menimbulkan ongkos baik berupa ongkos social,
kehilangan
langganan ataupun
pengangguran kerja.
Yang
menjadi
tujuan
utama
teori
antrian
ialah
mencapai
keseimbangan antara
ongkos
pelayanan
dengan
ongkos
yang
disebabkan oleh adanya waktu menunggu tersebut.
Ada dua kondisi yang dijumpai dalam sistem manusia-mesin :
•
Siklus
waktu
kegiatan permesinan
(machine cycle
time)
dan
kegiatan
pelayanan (operator
cycle
time)
berlangsung secara
konstan
dan
dapat
diprediksikan.
•
Kedua siklus kegiatan baik permesinan maupun pelayanan berlangsung
secara random atau acak.
Proses yang terjadi pada model antrian dapat digambarkan seperti berikut :
|
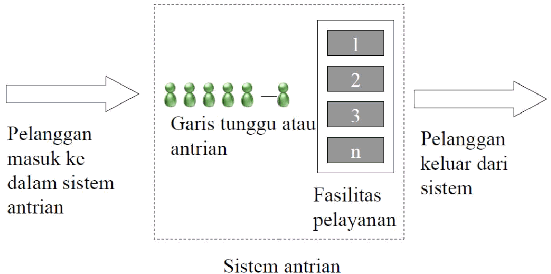 10
Sumber gambar : Taha, Hamdy A (2002) Riset Operasi. Jilid 3. Binarupa Aksara
Jakarta.
Gambar 2.1 Model Antrian
Unit-unit
langganan
yang
memerlukan pelayanan
yang
diturunkan
dari
suatu
sumber
input
memasuki
sistem
antrian
dan
ikut
dalam
antrian.
Dalam
waktu
tertentu,
anggota antrian
ini dipilih untuk dilayani. Pemilihan ini didasarkan pada
suatu antrian
tertentu
yang
disebut
“disiplin
pelayanan” atau
service
discipline.
Pelayanan
yang
diperlukan
dilaksanakan dengan
suatu
“mekanisme
pelayanan”
tertentu
(service
mechanism). Setelah itu, unit-unit langganan meninggalkan sistem antrian.
|
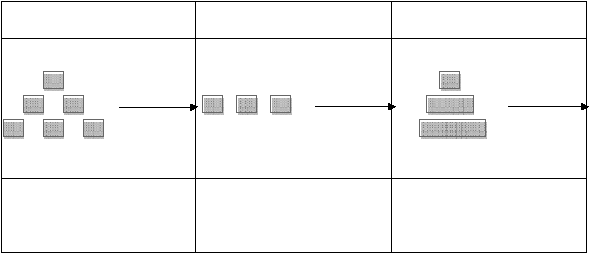 11
2.1.2 Teori Antrian Dengan Gabungan Kedatangan dan Kepergian
Menurut Taha
(2002,
p185),
notasi
yang
sesuai
dengan
untuk
meringkaskan
karakteristik dari antrian parallel telah secara
universal dibakukan dalam format berikut
ini :
(a/b/c) : (d/e/f)
Dengan pendekatan sistem, suatu antrian dapat dilihat pada gambar sebagai berikut :
INPUT
PROSES
OUTPUT
Masuk ke dalam sistem
Antrian
&
fasilitas
pelayanan
Keluar dari sistem
Sumber : Modul PSK&E Lab Teknik Industri
Gambar 2.2 Sistem Antrian
Dimana
simbol
a,
b,
c, d, e,
dan
f
adalah
unsure-unsur
dasar
dari
model
ini
sebagai berikut :
a
=
Distribusi kedatangan
b =
Distribusi waktu pelayanan (atau keberangkatan)
c
=
Jumlah pelayanan pararel (c = 1, 2, …8)
d = Peraturan pelayanan (FCFS)
e
=
Jumlah maksimum yang diijinkan dalam sistem
|
|
12
f = Ukuran sumber pemanggilan
Notasi
baku
tersebut
menggantikan simbol
a
dan
b
untuk
kedatangan
dan
keberangkatan dengan kode berikut ini,
M =
Distribusi kedatangan atau
keberangkatan
dalam poisson
(atau
Markov,
atau
distribusi antar-kedatangan atau pelayanan eksponensial yang setara)
D =
Waktu
antar
kedatangan
atau
waktu
pelayanan
yang
konstan
ataupun
deterministic
GI =
Distribusi independen umum dari kedatangan (atau waktu antar-kedatangan)
EK =
Distribusi
erlangian
atau
gamma
dari
distribusi
antar
kedatangan
atau
waktu
pelayanan dengan parameter k
G =
Distribusi umum dari keberangkatn (atau waktu pelayanan)
Teori antrian berhubungan dengan analisis suatu antrian dan perilakunya. Secara
umum dapat dikatakan bahwa suatu antrian terjadi bila tingkat jumlah orang atau sesuatu
yang
harus
dilayani
lebih
besar
daripada
tingkat
jumlah
pelayanannya. Jika
jumlah
orang/barang yang dating/harus dilayani
lebih kecil daripada
kecepatan
pelayanannya,
maka antrian akan berkurang atau mungkin tidak ada antrian lagi.
Pekerjaan
atau
orang
yang
dating
ke
sistem
dapat
berasal
dari
suatu
populasi
yang finite atau infinite. Bila jumlah pekerjaan atau orang/barang tidak mempunyai limit
yang
diperbolehkan
menunggu
dalam
suatu antrian,
maka
antrian
ini
disebut
infinite.
Sebaliknya, bila antrian mempunyai limit disebut antrian finite.
Karakteristik lain
yang
diperlukan
untuk
menjelaskan
situasi
antrian
adalah
disiplin
antrian.
Istilah
disiplin
antrian
menyatakan metode
suatu
set
aturan
yang
digunakan
untuk
menentukan
urutan pekerjaan atau
orang/barang
yang
akan dilayani.
Dalam teori antrian diasumsikan bahwa pekerjaan atau orang/barang yang akan dilayani
|
|
13
menurut “First Come, First Served Base”, yaitu menurut urutan yang sama sebagaimana
mereka datang dalam antrian.
Dalam
praktek,
beberapa
fasilitas pelayanan seperti
Kantor
Pos,
Supermarket,
Bank jika sistem antrian
yang dimiliki
mempunyai beberapa
fasilitas
pelayanan
yang
menganggur
ada
biayanya, demikian
pula
bagi
orang
yang
menunggu
fasilitas
pelayanan,
maka
dalam
kenyataannya kita
temui ketidak-seimbangan
antara
input
dan
proses
output-nya.
Karenanya
tujuan
daripada
teori
antrian
ini
adalah
meminimalkan
total biaya yang timbul dari fasilitas pelayanan yang menganggur dan waktu yang hilang
bagi orang/barang
karena menunggu pelayanan.
2.1.3 Situasi Antrian
Menurut Taha (2002, p190), situasi antrian yang terdapat di perusahaan industry,
antrian langganan di Supermarket ataupun di
Bank mempunyai kesamaan. Situasi yang
sama tersebut adalah nasabah membutuhkan perhatian atau layanan. Sebagai contoh dari
nasabah perusahaan industry adalah pembuatan mesin-mesin yang harus diuji coba oleh
operator mesin. Disini operator mesin bertindak sebagai pemberi jasa pelayanan.
Dari berbagai masalah penerapan teori antrian, perlu untuk dibuat beberapa dasar
asumsi tentang aspek-aspek dari sistem antrian. Dalam model dasar teori antrian,
asumsi-asumsi yang dibuat adalah :
1. Proses atau pola kedatangan
2. Proses pelayanan
3. Ukuran antrian
4. Disiplin Antrian
5. Jumlah fasilitas pelayanan
|
|
14
Nasabah dapat
datang
di
suatu
antrian
menurut berbagai
cara
yang
berbeda.
Mereka dapat datang dalam kelompok kecil atau besar, secara teratur atau tidak teratur
waktunya.
Dengan demikian
proses
atau pola
kedatangan dari
suatu
antrian
mungkin
sangat besar variabilitasnya.
Karena
waktu
kedatangan tidak
dapat
diketahui
dengan
pasti,
kita
harus
menentukan model distribusi probabilitas atas kedatangan tersebut. Dalam
model dasar
antrian, distribusi ini disebut “ exponential distribution”. Dari teori statistic kita ketahui
bahwa
pola
kedatangan adalah secara
random,
maka
interval
atau
jarak antara
kedatangan akan
mengikuti distribusi eksponensial ini. Bila
pola
kedatangan
ini
betul-
betul secara random,
maka dengan mengelompokkan data kedatangan ke dalam interval
waktu
yang
sama
akan
kita
peroleh
distribusi
Poisson.
Jadi
distribusi Poisson
juga
digunakan untuk menjelaskan proses kedatangan bila waktu diantara interval
mempunyai distribusi exponential.
2.1.4 Unsur-Unsur Dasar dari Model Antrian
Menurut Taha
(2002,
p190),
Dari
sudut pandang
model
antrian,
situasi antrian
disiptakan dengan
cara
berikut
ini.
Sementara
para
pelanggan tiba
di
satu
sarana
pelayanan,
mereka bergabung
dalam sebuah antrian. Pelayan memilih seorang
pelanggan dari
antrian
untuk
memulai
pelayanan. Setelah
selesai
pelayanan, proses
memilih
pelanggan
baru (yang
sedang
menunggu) diulangi.
Diasumsikan
tidak ada
waktu
yang
terhilang
antara
penyelesaian pelayanan
dengan
diterimanya
seorang
pelanggan baru di sarana pelayanan tersebut.
Pelaku-pelaku utama dala sebuah situasi antrian adalah pelanggan (customer)
dan
pelayan (server).
Dalam
model antrian,
interaksi
antara
pelanggan
dan
pelayan
|
|
15
adalah
menarik
hanya
dalam
hal
kaitannya dengan
periode
waktu
yang
diperoleh
pelanggan untuk
menyelesaikan sebuat pelayanan. Jadi, dari sudut pandang kedatangan
pelanggan, kita tertarik pada interval waktu yang memisahkan kedatangan yang berturu-
turut. Juga, dalam
kasus pelayanan,
yang
diperhitungkan adalah
waktu
pelayanan
per
pelanggan.
Dalam
model-model antrian,
kedatangan
pelanggan
dan
waktu
pelayanan
diringkas dalam bentuk distribusi yang umumnya disebut sebagai
distribusi
kedatangan
(arrival
distribution) dan
distribusi
waktu
pelayanan
(service
time
distribution). Kedua distribusi ini
mewakili situasi di
mana pelanggan tiba dan dilayani
secara
indivisual (misalnya, Bank atau Supermarket). Dalam situasi
lainnya, pelanggan
dapat
tiba
dan/atau
dilayani
dalam
kelompok
(misalnya
restoran). Kasus
terakhir
ini
umumnya disebut antrian kelompok (bulk queue).
Walaupun
pola
kedatangan
dan
kepergian
adalah
faktor-faktor yang
penting
dalam
analisis
antrian,
faktor-faktor
lain
juga
penting
dalam
pengembangan model-
model antrian. Faktor pertama adalah cara memilih pelanggan dari antrian untuk
memulai
pelayanan. Ini
disebut
sebagai
peraturan
pelayanan
(service
discipline).
Peraturan
yang
paling
umum
adalah FCFS
(First
Come
First
Served/datang pertama
dilayani
pertama),
LCFS
(Last
Come
First
Served/datang terakhir
dilayani
pertama),
SIRO (Service In Random Order/pelayanan dalam urutan acak) juga dapat timbul dalam
situasi
praktis.
Kita
juga
harus
menambahkan bahwa
sementar
peraturan
pelayanan
menentukan
pemilihan
pelanggan
dari satu
jalur antrian,
para pelanggan
yang
tiba
di
sebuah
sarana
pelayanan
dapat
juga
ditempatkan dalam
antrian
prioritas
(priority
queue) sedemikian rupa sehingga prioritas yang lebih tinggi akan menerima preferensi
|
|
16
untuk mulai dilayani lebih dahulu. Pemilihan pelanggan yang spesifik dari setiap antrian
prioritas dapat mengikuti peraturan pelayanan tertentu.
Faktor
kedua
berkaitan
dengan
rancangan sarana
tersebut
dan
pelaksanaan
pelayanan. Sarana
tersebut
dapat
mencakup
lebih
dari
satu
pelayan,
sehingga
memungkinkan
beberapa pelanggan
sebanyak
jumlah
pelayan
tersebut
untuk
dilayani
secara berbarengan (misalnya kasir Bank). Dalam kasus ini, semua pelayan menawarkan
pelayanan yang
sama
dan
sarana
pelayanan
tersebut
dikatakan
memiliki
pelayanan
sejajar
(pararel
servers).
Sebaliknya, sarana
pelayanan
dapat
pula
terdiri
dari
serangkaian stasiun
yang
dapat
dilalui
pelanggan
sebelum
pelayanan
diselesaikan
(misalnya
pengolahan sebuah
produk
di
serangkain mesin).
Situasi
yang
dihasilkan
umumnya
dikenal
sebagai antrian
serial
atau
antrian
tandem
(tandem
queue).
Rancangan yang
paling
umum
dari
sebuah
sarana
pelayanan
mencakup
baik
stasiun
pengolahan serial atau pararel. Ini
menghasilkan yang disebut antrian jaringan
(network queue).
Faktor ketiga
berkaitan
dengan
ukuran
antrian yang
diijinkan.
Dalam
beberapa
situasi
tertentu,
hanya
sejumlah
pelanggan
tertentu yang
diijinkan,
kemungkinan
karena
batasan
ruang (misalnya
ruang
untuk
mobil
di
tempat
pengisian
bahan bakar). Setelah antrian memenuhi kapasitas, pelanggan yang baru tiba tidak dapat
masuk dalam antrian.
Faktor
keempat
berkaitan dengan
sifat
sumber
yang
meminta pelayanan
(kedatangan
pelanggan).
Sumber
pemanggilan (calling
source)
dapat
menghasilkan
sejumlah
terbatas
pelanggan
atau
(secara
teoritis)
sejumlah tak
terbatas
pelanggan.
Sumber
terbatas
terjadi
ketika
kedatangan
mempengaruhi laju
kedatangan
pelanggan
baru.
Di
sebuah
bengkel dengan
M
mesin,
sumber pemanggilan sebelum ada
mesin
|
|
17
rusak
terdiri
dari
M
calon
pelanggan. Setelah
satu
mesin
rusak,
mesin
itu
menjadi
pelanggan dan karena itu tidak dapat menghasilkan pemanggilan baru sampai diperbaiki.
Perbedaan
yang ditarik
antara
situasi bengkel dengan
situasi
lain di
mana “penyebab”
dari pemanggilan terbatas, tetapi mampu menghasilkan kedatangan yang tidak terhingga.
Misalnya, dalam
sebuah
tempat pelayanan
jasa
pengetikan, jumlah
pengetik
terbatas,
tetapi setiap pengetik dapat
menhasilkan kedatangan sebanyak apapun, karena
ia
biasanya
tidal
perlu
menunggu
penyelesaian bahan
yang
diserahkan,
sebelum
menghasilkan pesanan-pesanan baru.
Model-model antrian
yang
mewakili situasi
di
mana
manusia
mengambil peran
sebagai pelanggan dan/atau pelayan harus dirancang
untuk
memperhitungkan pengaruh
perilaku
manusia
(human
behavior).
Pelayan
“manusia”
dapat
mempercepat laju
pelayanan ketika jalur
antrian
memanjang. Pelanggan
“manusia”
dapat berpindah dari
satu jalur
ke jalur
antrian
lainnya dengan
harapan dapat
mengurangi
waktu menunggu
(di saat berikutnya anda berada di Bank atau Supermarket. anda dapat
membuat waktu
menunggu
anda
menjadi
tidak
membosankan
dengan
memperhatikan fenomena
perpindahan ini). Beberapa pelanggan “manusia” juga menolak untuk bergabung dalam
satu
jalur
antrian
karena
mereka
memperhatikan waktu
menunggu
yang
lama,
atau
mereka dapat membatalkan setelah berada dalam antrian karena waktu menunggu
mereka
sudah
terlalu
panjang. (Catat
bahwa
dalam
hal
perilaku
manusia, waktu
menunggu yang panjang bagi satu orang tidak sama panjangnya bagi orang lainnya).
Tidak
diragukan lagi, terdapat
cirri-ciri
perilaku
manusia
yang
lainnya
dalam
situasi antrian sehari-hari. Tetapi, dari
sudut pandang model antrian, cirri-ciri ini hanya
dapat
diperhitungkan jika
perilaku
itu
dapat
dikuantifikasi dengan
cara
tertentu
yang
memungkinkannya untuk dimasukkan
dalam
model
yang
bersangkutan. Juga,
model-
|
|
18
model antrian tidak dapat
memperhitungkan sebuah perilaku
individual dari pelanggan
dalam
arti
bahwa
semua
pelanggan
dalam
antrian
diperkirakan
untuk
“berperilaku”
secara
setara,
sementara
mereka
berada
di
sarana pelayanan
yang
bersangkutan. Jadi
pelanggan yang
sika
mengobrol (dengan
pelayan
selama
dilayani)
dipertimbangkan
sebagai
kasus
yang
jarang
dan
perilakunya
itu
diabaikan
dalam perancangan sistem.
Sebaliknya, jika sebagian besar pelanggan
ternyata suka
mengobrol, sebuah rancangan
realistik dari sarana pelayanan tersebut
harus didasari oleh fakta bahwa kebiasaan ini,
walaupun
membuang-buang
waktu,
merupakan
bagian
integral
dari
operasinya.
Satu
cara yang logis untuk memasukkan pengaruh kebiasaan ini adalah dengan meningkatkan
waktu pelayanan per pelanggan.
Jadi,
dapat
kita
lihat
bahwa
unsur-unsur
dasar
dari
model
antrian
bergantung
pada faktor-faktor berikut ini :
1. Distribusi kedatangan (kedatangan tunggal atau kelompok)
2. Distribusi waktu pelayanan (pelayanan tunggal atau kelompok)
3. Rancangan saran pelayanan (statsiun serial, pararel, atau jaringan)
4. Peraturan pelayanan (FCFS, LCFS, SIRO) dan prioritas pelayanan
5. Ukuran antrian (terhingga atau tidak terhingga)
6. Sumber pemanggilan (terhingga atau tidak terhingga)
7. Perilaku manusia (perpindahan, penolakan, atau pembatalan)
Tujuan kita dalam
mempelajari
pengoperasian
sebuah
sarana
pelayanan
dalam
kondisi acak adalah
umtuk
memperoleh beberapa karakteristik yang mengukur
kinerja
sistem
yang
sedang
dipelajari
tersebut.
Misalnya,
satu
ukuran
yang
logis dari kinerja
adalah
seberapa
lama
seorang
pelanggan
diperkirakan
harus
menunggu
sebelum
dilayani. Satu
ukuran lainnya adalah persentase waktu sarana pelayanan tersebut tidak
|
|
19
dipergunakan. Ukuran
pertama
memandang sistem
dari
sudut
pandang
pelanggan,
sementar
ukuran kedua mengevaluasi derajat pemanfaatan sarana tersebut. Kita
secara
intuitif
melihat
bahwa
semakin
lama
seorang
pelanggan menunggu,
semakin
kecil
persentase waktu sarana tersebut tidak dipergunakan, dan sebaliknya. Keduanya ukuran
kinerja
ini
karena
itu dipergunakan
untuk
memilih
tingkat pelayanan (atau
laju
pelayanan) yang akan menghasilkan keseimbangan yang wajar antara kedua situasi yang
bertentangan ini.
2.1.5 Analisa Antrian dalam Sistem Manusia-Mesin
Dua kondisi/siklus yang biasa dijumpai dalam sistem manusia-mesin :
•
Siklus waktu kegiatan persiapan (machine cycle time) dan kegiatan pelayanan
(operator cycle time) yang berlangsung secara konstan dan dapat diprediksikan.
Artinya
:
Bilamana
kondisi
yang berlangsung
atau terjadi
adalah
bila
sistem
bekerja
sesuai
dengan
asumsi
awal
dari
operator
dan
operator
dapat
mengendalikan
sepenuhnya kinerja dari mesin yang bersangkutan sehingga
kegiatan produksi
dapat
berjalan sesuai dengan keinginan dari
operator
yang
bersangkutan.
•
Kedua
siklus
kegiatan, baik
siklus persiapan
maupun
pelayanan berlangsung
secara random/acak.
Artinya : Kondisi dimana baik waktu yang dihabiskan untuk
melakukan setup
dari
mesin
maupun
waktu
yang
diperlukan dalam
melakukan
pelayanan
tidak
dapat
diprediksikan sebelumnya,
sehingga
hal
itu
akan
berimbas
pada
tidak
menentunya waktu yang dihabiskan dalam suatu pelayanan.
Pemikiran Analitis dan Sintesa (Analitical thinking and Sintetical thinking) :
|
|
20
•
Pemikiran analitis
Merupakan suatu
proses
yang
berguna
untuk
melakukan
suatu
pengamatan
terhadap
bagian-bagian dari
suatu
sistem
kerja
yang
dianalisa
sebagai
suatu
bagian integral yang terdiri sendiri (sistem individual).
•
Pemikiran sintesa
Merupakan suatu proses untuk
melakukan analisa terhadap perilaku dari suatu
sistem sebagai
suatu
kesatuan yang
integral
dan
memperhitungkan bagaimana
suatu sub-sistem dapat saling mempengaruhi satu sama lain.
Agar suatu sistem kerja dapat berjalan dengan baik, kombinasi dari kedua proses
tersebut
mutlak
diperlukan,
terutama
dalam
menghadapi suatu
malfungsi
dari
suatu
sistem
kerja.
Dimana
dalam
hal
ini
pendiagnosisan
sistem
dilakukan melalui
proses
analitis, sedangkan pemecahan dan
integrasi sistem agar dapat berjalan normal kembali
merupakan proses sintesa.
2.1.6 Notasi Parameter dan Rumus-Rumus
Menurut White (2000,
p92),
parameter
model antrian ditentukan dengan
notasi
sebagai berikut :
?
=
rata-rata kecepatan kedatangan (jumlah kedatangan persatuan waktu).
1
?
=
rata-rata waktu antar kedatangan.
µ
=
rata-rata kecepatan pelayanan (jumlah
satuan
yang dilayani persatuan
waktu
bila pelayan sibuk).
P
=
faktor penggunaan pelayan (proporsi waktu pelayan ketika sedang (sibuk)).
Pn
=
probabilita bahwa n satuan (kedatangan) dalam sistem.
|
 21
Lq
=
rata-rata jumlah satuan dalam antrian (rata-rata panjang antrian).
Ls
=
rata-rata jumlah satuan dalam sistem.
Wq
=
rata-rata waktu tunggu dalam antrian.
Ws
=
rata-rata waktu tunggu dalam sistem.
Dalam skripsi ini permasalahan antrian didasarkan pada asumsi berikut :
a. Jumlah kedatangan per unit waktu digambarkan dengan distribusi Poisson dengan ?
=
rata-rata kecepatan kedatangan
b. Waktu pelayanan eksponensial dengan µ = rata-rata kecepatan pelayanan.
c. Disiplin antrian adalah First Come First Served (FCFS) seluruh kedatangan dalam
barisan hingga dilayani.
d. Dimungkinkan panjang barisan yang tak terhingga.
e. Populasi yang dilayani tidak terbatas.
f.
Rata-rata kedatangan lebih kecil dari rata-rata waktu pelayanan.
g. Rata-rata tingkat kedatangan lebih kecil
dari tingkat pelayanan semua channel (=
jumlah channel dikalikan rata-rata tingkat pelayanan per channel).
Dari asumsi tersebut dapat diperoleh hasil secara statistik sebagai berikut :
Po = probabilitas semua saluran (pemberi layanan) mengganggur
Po =
?
?µ
Dimana :
k = jumlah saluran
Pw = probabilitas semua saluran secara simultan (utilization factor)
Pw =
?
?
?
?
?µ
Po
?! µ
?µ ?
Ls = jumlah rata-rata dalam sistem.
|
 22
Ls =
?µ?
?
µ
?
Po +
?
?
??
?
!??µ ??
?
µ
Lq = jumlah rata-rata dalam antrian.
Lq = Ls -
?
µ
Ws = rata-rata waktu dalam sistem.
Ws =
?
?
Wq = rata-rata waktu dalam antrian.
Wq =
?
2.1.7 Empat Model Struktur Antrian Secara Umum
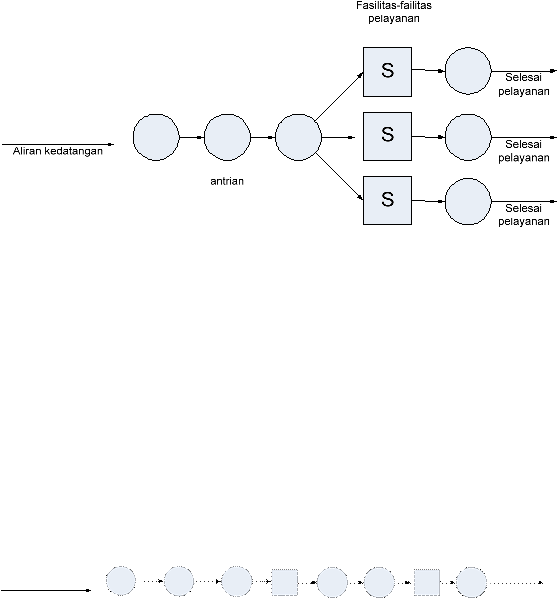
Menurut White (2000, p121), model struktur antrian adalah :
•
Antrian Single Channel, Single Phase System
Disini fasilitas yang dilayani akan datang, masuk dan
membentuk antrian pada
satu baris/aliran pelayanan dan selanjutnya akan berhadpan dengan satu fasilitas
operasi pelayanan. Seperti yang ditunjukkan pada gambar berikut :
Sumber : Modul PSK&E Lab Teknik Industri
Gambar 2.3 Antrian Single Channel, Single Phase System
|
 23
•
Antrian Multi Channel, Single Phase System
Disini fasilitas yang dilayani akan datang, masuk dan
membentuk antrian pada
satu
baris/aliran
pelayanan
dan
selanjutnya
akan
berhadapan dengan
beberapa
fasilitas operasi pelayanan. Seperti yang ditunjuk pada gambar berikut :
Sumber : Modul PSK&E Lab Teknik Industri
Gambar 2.4 Antrian Multi Channel, Single Phase System
•
Antrian Single Channel, Multi Phase System
Disini fasilitas yang dilayani akan datang, masuk dan
membentuk antrian pada
beberapa
baris/aliran
pelayanan dan selanjutnya akan
berhadapan
dengan satu
fasilitas operasi pelayan. Seperti yang ditunjukkan pada gambar berikut :
Fasilitas-failitas
pelayanan
Fasilitas-failitas
pelayanan
Aliran kedatangan
antrian
S
S
Selesai
pelayanan
Sumber : Modul PSK&E Lab Teknik Industri
Gambar 2.5 Antrian Single Channel, Multi Phase System
|
 24
•
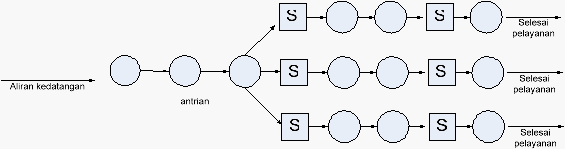
Antrian Multi Channel, Multi Phase System
Dimana disini kedatangan fasilitas yang akan dilayani akan masuk dalam sistem
pelayanan
yang
dioperasikan dari
satu
fasilitas
terus
menuju
ke
fasilitas
pelayanan yang lainnya. Seperti yang ditunjukkan pada gambar berikut :
Sumber : Modul PSK&E Lab Teknik Industri
Gambar 2.6 Antrian Multi Channel, Multi Phase System
Tingkat
kedatangan (?)
merupakan frekuensi
atau
rata-rata
waktu
datangnya
pekerjaan
dalam
satuan
waktu.
Dan
secara
umum
pola
kedatangannya berdistribusi
Poisson. Sedangkan tingkat pelayanan (µ)
merupakan rata-rata waktu pelayanan dalam
ukuran
pekerjaan per
satuan
waktu.
Dan
secara
umum
pola
pelayan
berdistribusi
Exponential.
2.1.8 Rumus-Rumus antrian Single Channel, Single Phase System
Menurut White (2000, p101) kuantitas nilai dari ?
merupakan nulai dari traffic intensity
terhadap suatu sistem, dalam beberapa
terminologi antrian,
simbol
ini
termasuk dalam
analisis beban yang berlebihan, beban angkat, dan utilitas dari server itu sendiri, dimana
:
|
 25
?
=
?
µ
Untuk perhitungan single server dan beberapa pendekatan model antrian lainnya.
Bilamana :
?
1,
maka
aliran
akan
bergerak
lancer
walaupun
dengan
antrian
didalamnya. ? > 1,
maka antrian akan terjadi dan sulit untuk
memperhitungkan rumus
dalam model antrian (M/M/1) : (GD/8/8).
Menurut White (2000, p104) dan Taha (2002. p192), jumlah kedatangan
orang/barang yang membentuk barisan :
Lq =
?
????
Waktu menunggu rata-rata dalam antrian :
Wq =
?
µ
??
?
?
Suatu model antrian sederhana mempunyai karakteristik sebagai berikut :
1. Waktu datangnya pekerjaan dapat dinyatakan polanya sebagai distribusi Poisson.
2. Waktu pelayanan dapat dinyatakan polanya sebagai distribusi exponential.
3. Single fasilitas pelayan.
4. Disiplin antrian adalah First Come, Fisrt Served Based atau General discipline.
5. Dalam infinite calling population.
2.1.9 Rumus-Rumus antrian Multi Channel, Single Phase System
?
=
?
µ
Menurut White (2000, p103), rumus untuk model antrian (M/M/c) : (GD/8/8).
Bilamana : ?
1, maka aliran akan bergerak lancer. ? > 1, maka antrian akan
terjadi. Dimana : S = Jumlah fasilitas pelayanan (server) yang tersedia.
|
 26
Probabilitas Sistem Antrian Kosong
Po = ?
??
?
?
?
?
?
?
?
!????
?
?
?!
Dimana :
Po
=
probabilitas sistem
antrian kosong
(tidak ada
fasilitas
yang harus dilayani/yang
masuk dalam sistem pelayanan/antrian).
Jumlah kedatangan orang/barang yang membentuk antrian :
Lq =
.
??
?
!.????
?
Waktu menunggu rata-rata dalam antrian :
Wq =
??
µ????
?
Ws = Wq +
?
?
2.1.10 Model serial K stasiun dengan kapasitas antrian tak terhingga (8)
Menurut Taha
(2002,p216),
suatu
sajian
teorema
tanpa
bukti
yang
dapat
diterapkan
dalam
serial
k
stasiun
mempertimbangkan
sistem
dengan
k
stasiun
dalam
serial, seperti diperlihatkan pada gambar berikut.
Sumber : Taha, Hamdy A. (2002). Riset Operasi. Jilid 3. Binarupa Aksara, Jakarta.
Gambar 2.7 Model Antrian Serial-k
|
|
27
Asumsikan
bahwa
kedatangan
di stasiun
1 dihasilkan
oleh
satu
populasi
taj
hingga sesuai
dengan distribusi
Poisson
dengan
laju
kedatangan
rata-rata ?.
Unit-unit
yang
dilayani
akan
bergerak
berurutan
dari
satu
stasiun ke
stasiun
berikutnya sampai
dikeluarkan di stasiun k
Pni = (1-?i)?
??
Dimana :
Ni = 0, 1, 2, …
i
=
1, 2, …, k
Dalam kondisi ini dapat dibuktikan bahwa untuk semua I, keluaran dari stasiun I
bersifat Poisson dengan nilai mean ? dan bahwa setiap stasiun dapat diperlakukan secara
independen sebagai
(M/M/c)
:
(GD/8/8).
Tetapi
haruslah
diingat
bahwa
hasil
steady
state dari stasiun tersebut akan berlaku jika ? < Ciµi, untuk I = 1, 2, .., k.
2.2 Peta Kerja
Menurut Sritomo (2000,p123), definisi peta kerja adalah suatu peta ataupun alat
yang menggambarkan kegiatan kerja secara sistematis dan jelas.
2.2.1 Jenis-jenis Peta Kerja
Menurut Sritomo
(2000,p124),
definisi
pemetaan pada peta
kerja
dpaat
dibagi
menjadi dua jenis, yaitu :
a. Peta Kerja Keseluruhan
Peta kerja keseluruhan merupakan peta kerja yang digunakan untuk menganalisa
kerja keseluruhan. Peta kerja keseluruhan yang umum dipakai adalah :
o
Peta Aliran Proses (Flow Process Chart)
|
|
28
Merupakan peta kerja
yang
menggambarkan semua aktivitas baik
yang
produktif
maupun
tidak
produktif yang
terlibat
dalam
proses
pelaksanaan kerja.
o
Peta Proses Operasi (Operation Process Chart)
Merupakan
peta
kerja
yang
mencoba
menggambarkan urutan
kerja
dengan
membagi
pekerjaan
tersebut
menjadi
elemen-elemen operasi
secara detail.
o
Diagram Aliran (Flow Chart)
Merupakan peta kerja yang serupa dengan peta aliran proses
hanya saja
penggambarannya dilakukan diatas layout kerja yang ada.
o
Peta Proses Produk Banyak (Multi Product Process Chart)
Merupakan
peta
kerja
yang
dibuat
unutk
memberikan gambaran
pekerjaan dari banyak produk secara mendetail untuk setiap produknya.
b. Peta Kerja Setempat
Peta
kerja setempat
merupakan peta
kerja
yang digunakan
untuk
menganalisa
kerja setempat. Peta kerja setempat yang umum dipakai adalah :
o
Peta Tangan Kiri dan Kanan (Left dan Right Hand Chart)
Merupakan peta kerja
yang digunakan
untuk
menganalisa
gerakan
tangan
kiri
atau
kanan
dari
pekerja
secara
mendetail dengan
menggunakan gerakan dasar therblig.
o
Peta Pekerja dan Mesin (Man and Machine Process Chart)
Merupakan peta
kerja
yang
memberikan
informasi
tentang
hubungan
waktu siklus pekerja dan waktu operasi mesin yang ditangani.
|
|
29
2.3 Pola Distribusi Data
Menurut
Harrel
(2000,
p118),
pola
distribusi data
dibagi
menjadi dua,
yaitu
frequency distribution dan theoretical distribution.
2.3.1 Frequency Distribution
Menurut
Harrel
(2000,
p120-121),
frequency
distribution
merupakan
distribusi
kelompok data dalam interval atau kelas berdasarkan frekuensi dari kejadian. Distribusi
frekuensi dibagi menjadi dua, yaitu :
a. Discrete Frequency Distribution
Merupakan distribusi
yang
terbatas pada
nilai
tertentu dan
hanya
sekumpulan
frekuensi
yang
terbatas
saja
yang
ditampilkan. Sebagai
contoh
dari
discrete
frequency
distribution adalah
jumlah orang
yang
datang
ke
suatu
sistem
pada
interval waktu tertentu.
b. Continuous Frequency Distribution
Merupakan rentang nilai antara sample dari suatu nilai berada. Suatu data dapat
dikatakan memiliki continuous frequency distribution apabila data tersebut dapat
mewakili interval nilai yang sudah ditentukan.
2.3.2 Theoretical Distribution
Menurut
Banks
dan
Gibsons
(2001,p203-207),
suatu
distribusi yang
dapat
dibedakan
berdasarkan parameter
yang
ditentukan
dari
dispersion
(penyebaran) dan
density (kerapatan). Berikut beberapa statistikal distribusi teoritis yang ada.
a. Normal Distribution
|
 30
Distribusi
normal
merupakan distribusi
kontinu
yang
tidak
terbatas.
Biasanya
kurva
normal
membentuk
lonceng
dengan
nilai
rata-ratanya
berada
pada titik tengah kurva yang
berarti
jumlahnya paling banyak. Berikut adalah
rumusnya :
f(x) =
?
v
???
?
exp
????
?
?
??
?
Dimana :
µ = shift parameter/mean
= scale parameter/standart deviation
Sumber : Plot Software Mat-Lab
Gambar 2.8 Distribusi Normal
|
 31
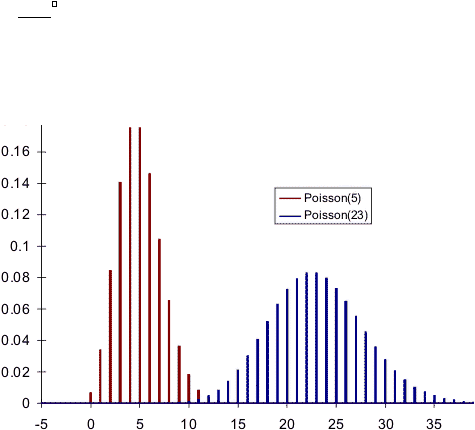
b. Poisson Distribution
Distribusi poisson merupakan distribusi diskrit yang memiliki batas dari 0
pada batas bawah dan tidak terbatas pada batas atas. Biasanya distribusi poisson
berhubungan
dengan
tingkat
kedatangan
untuk
suatu
sistem
dan
berkaitan
erat
dengan distribusi eksponensial. Berikut adalah rumusnya :
p(x) =
?
??
?
?!
Dimana :
?
=
rate of occurrence/mean
Sumber : VOSE Software
Gambar 2.9 Distribusi Poisson
|
 32
c. Uniform Distribution
Distribusi
uniform
merupakan distribusi
kontinu
dimana
dibatasi
pada
kedua
sisinya.
Biasanya
data
berdistribusi
uniform
apabila
nilai
max
dan
min
tidak berbeda jauh. Berikut adalah rumusnya :
f(x) =
?
??? ???
Dimana :
max = nilai maksimal
min = nilai minimal
Sumber : Crystal Ball software
Gambar 2.10 Distribusi Uniform
d. Exponential Distribution
Distribusi
eksponensial adalah
distribusi
kontinu
dimana
dibatasi
oleh
batas
bawah.
Bentuk
dari
distribusi
ini
akan
selalu
sama dimana
dimulai dari
nilai minimum yang terbatas dan terus menurun sampai nilai x terbesar. Biasanya
|
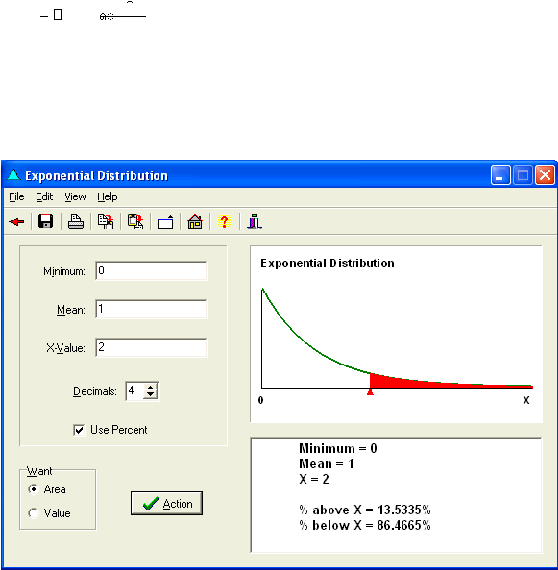 33
distribusi
eksponensial
mencerminkan
waktu
antar kedatangan. Rumusnya
adalah sebagai berikut :
f(x) =
?
?? ?
?
????
?
?
?
?
Dimana :
min = minimum x value
ß
=
scale parameter
Sumber : MVPStats Software
Gambar 2.11 Distribusi Eksponensial
2.4 Pengukuran Kerja
Menurut Sritomo (2000, p169-170), pengurukuran kerja merupakan bagian dari
penelitian cara kerja. Pengukuran kerja adalah pengukuran kerja dilihat dari waktu kerja
|
|
34
pada
saat operator
melakukan kerja.
Pengukuran
kerja
merupakan metode penetapan
keseimbangan antara kegiatan dengan manusia yang dikontribusikan dengan output yang
akan dihasilkan. Pengukuran kerja dibagi menjadi dua, yaitu :
a. Pengukuran kerja langsung
Pengukuran kerja langsung adalah pengukuran waktu kerja yang dilakukan
secara
langsung
di
tempat
dimana
pekerjaan
diukur
dan
dijalankan. Cara
pengukurannya
dilakukan
dengan
menggunakan
alat
bantuan
seperti
jam
henti
(stopwatch) dan sampling kerja.
b. Pengukuran kerja tidak langsung
Pengukuran tidak langsung adalah pengukuran kerja dengan cara dihitung
dengan
metode
stadar
data/formula, pengukuran kerja
dengan
analisa
regresi,
penetapan waktu baku dengan data gerakan. Atau dengan kata lain si pengamat
tidak harus berada di
tempat pengukuran kerja. Biasanya dilakukan dengan WF
(Work Factor) dan MTM (Methods Time Measurement).
2.5 Model Perancangan Program
Menurut
Shneiderman (2005,
p47),
model
RAD
(Rapid
Application
Development) adalah sebuah model pembangunan perangkat lunak sekuensial liner yang
menekankan
suatu
siklus
perkembangan yang
sangat
pendek
atau
singkat.
Dalam
perkembangannya
yang cepat
ini
dicapai dengan
menggunakan pendekatan konstruksi
berbasis komponen.
Kelemahan dalam model ini adalah :
a. Tidak cocok untuk proyek skala besar.
b. Proyek dapat gagal karena waktu yang disepakati tidak dipenuhi.
|
|
35
c. Sistem yang tidak dapat dimodularisasi tidak cocok untuk model ini.
d. Resiko teknis yang tinggi juga kurang cocok untuk model ini.
Model RAD ini merupakan suatu model yang mengadopsi dari M odel Waterfall
hanya saja
letak perbedaannya
pada
masalah waktu tadi. Pendekatan-pendekatan RAD
yang merupakan konstruksi berbasis komponen meliputi beberapa fase :
1. Business Modeling
Dimana
aliran
informasi di
antara
beberapa
fungsi
bisnis
dimodelkan
dengan cara menjawab pertanyaan mengenai apa, bagaimana dan ke mana aliran
informasi tersebut.
2. Data Modeling
Aliran informasi tadi disaring ke dalam serangkaian objek data kemudian
diidentifikasi dan hubungan dari objek itu didefinisikan.
3. Process Modeling
Dari
fase
data
aliran
informasi
didefinisikan dalam
modeling
fase
ditransformasikan untuk
mencapai
aliran
informasi
yang
perlu
bagi
sebuah
implementasi bisnis.
4. Application Generation
Dalam
menggunakan bahasa pemrograman,
RAD
banyak
menggunakan
komponen-komponen yang ada atau
menciptakan komponen yang dapat dipakai
lagi.
5. Testing and Turnover
Dalam
RAD
menekankan suatu
pemakaian
kembali
pada
komponen-
komponen,
hal
ini
mengurangi waktu pengujian karena komponen
yang
akan
dipakai telah teruji dahulu.
|
|
36
2.6 Interaksi Manusa dan Komputer
Menurut Shneiderman (2005, p15), suatu program yang interaktif dan baik harus
bersifat user friendly dengan lima kriteria sebagai berikut :
1. Waktu belajar yang tidak lama.
2. Kecepatan penyajian informasi yang tepat.
3. Tingkat kesalahan pemakaian rendah.
4. Penghafalan sesudah melampaui jangka waktu.
5. Kepuasan pribadi.
Menurut Shneiderman (2005,
p74),
dalam
rancangan sistem
interaksi
manusia
dan
computer
yang
baik
juga harus memperhatikan delapan
aturan emas (eight
golden
rules), yaitu :
1. Strive for consistency (berusaha untuk konsisten).
2. Enable frequent
user to use shortcuts
(memungkinkan
pengguna
untuk
menggunakan jalan pintas).
3. Offer informative feedback (memberikan umpan balik yang informative).
4. Design dialogs to yield closure (pengorganisasian yang baik sehingga pengguna
mengetahui kapan awal dan akhir dari suatu aksi).
5. Offer simple error handling (memberikan pencegahan kesalahan dan penanganan
kesalahan yang sederhana).
6. Permit easy
reversal
of
actions
(memungkinkan kembali
ke
aksi
sebelumnya
dengan mudah).
7. Support internal
locus
of
control
(memungkinkan pengguna
untuk
menguasai
dan mengontrol sistem).
|
|
37
8. Reduce
short term memory load
(mengurangi
beban
ingatan
jangka
pendek,
sehingga pengguna tidak perlu banyak menghafal).
|