 5
BAB 2
TINJAUAN KEPUSTAKAAN
2.1
Jembatan
Pengertian jembatan secara umum adalah suatu konstruksi yang berfungsi untuk
menghubungkan dua bagian jalan yang terputus oleh adanya rintangan-rintangan seperti
danau, lembah, jurang, saluran irigasi, jalan kereta api dan semacamnya. Jenis jembatan
berdasarkan fungsi, lokasi, bahan konstruksi dan tipe struktur sekarang ini telah
mengalami perkembangan yang pesat sejalan dengan kemajuan ilmu pengetahuan dan
teknologi, mulai dari yang sederhana sampai pada konstruksi yang kompleks.
Jenis jembatan sendiri dapat dibedakan berdasarkan fungsi, lokasi, dan bahan
konstruksinya. Berdasarkan fungsinya, jembatan dapat dibedakan sebagai berikut :
a.
Jembatan jalan raya (highway bridge)
Gambar 2.1 Jembatan Jalan Raya (Sumber : news.rutgers.edu
)
|
 6
b.
Jembatan jalan kereta api (railway bridge)
Gambar 2.2 Jembatan Jalan Kereta Api (Sumber : .theodora.com)
c.
Jembatan pejalan kaki atau penyeberangan (pedestrian bridge)
Gambar 2.3 Jembatan Pejalan Kaki (Sumber : galinsky.com)
Kalau berdasarkan lokasinya, jenis jembatan dapat dibedakan sebagai berikut :
a.
Jembatan di atas sungai atau danau
b.
Jembatan di atas lembah
|
|
7
c.
Jembatan di atas saluran irigasi/drainase (culvert)
d.
Jembatan di atas jalan yang sudah ada (fly over)
e.
Jembatan di dermaga (jetty)
Sedangkan berdasarkan bahan konstruksinya,jembatan dapat dibedakan sebagai berikut :
a.
Jembatan kayu (log bridge)
b.
Jembatan beton (concrete bridge)
c.
Jembatan beton prategang (prestressed concrete bridge)
d.
Jembatan baja (steel bridge)
e.
Jembatan komposit (composite bridge)
Jembatan memiliki beberapa bagian antara lain :
a.
Struktur atas (super structure), yaitu semua bagian jembatan atas tumpuan yang
terdiri dari tumpuannya sendiri, balok utama longitudinal atau stringer/girder,
sistem lantai dan pengaku (bracing/stiffener). Bagian-bagian sekunder lain
adalah parapet, dinding railing, anti kembang-susu, alat sambung dek dan
sebagainya.
b.
Struktur bawah (sub structure), dibagi menjadi 2 bagian yaitu kepala jembatan
(abutments) atau pilar (pier) dan pondasi untuk kepala jembatan atau pilar.
Struktur bangunan bawah perlu didesain khusus sesuai dengan jenis kekuatan
tanah dasar dan elevasi jembatan.
|
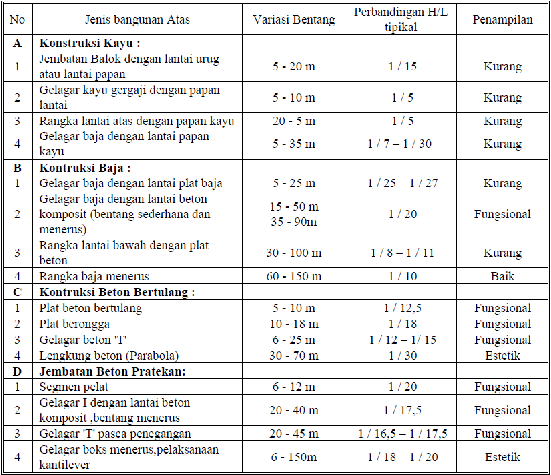 8
Tabel 2.1 Jenis Jembatan berdasarkan Bentang
Sumber : Bridge Management System 1992
2.2
Evaluasi Kekuatan Jembatan
Tata
cara evaluasi kelayakan jembatan berdasarkan kemampuan jembatan
menahan beban yang dimunculkan dalam bentuk faktor ketahanan (resistance factor)
dibahas dalam tulisan di bawah ini. Faktor ketahanan dibagi dalam dua jenis :
a.
Faktor ketahanan yang mendasarkan pada beban tertinggi (operating rating)
b.
Faktor ketahanan yang mendasarkan pada pada beban lebih rendah (inventory
rating, inv). Beban tertinggi (operating rating) bersifat sementara, tidak terlalu sering
dilakukan dan mendasarkan pada tegangan 75% tegangan lelehnya, sedang beban lebih
|
|
9
rendah (inventory rating) mendasarkan pada 55% tegangan lelehnya, sering dilakukan
dan berjangka panjang
2.3
Jembatan Beton Prategang
2.3.1
Pengertian Beton Prategang
Beton merupakan material yang lemah menahan gaya tarik tetapi kuat menahan
gaya tekan. Kuat tarik beton bervariasi mulai dari 8 sampai 14 persen dari kuat
tekannya. Rendahnya kapasitas tarik beton menimbulkan tejadinya retak lentur pada
taraf pembebanan yang masih rendah. Untuk mengurangi atau mencegah
berkembangnya retak tersebut, gaya konsentris atau eksentris diberikan dalam arah
longitudinal elemen struktural.
Gaya longitudinal tersebut disebut gaya prategang, yaitu gaya tekan yang
memberian prategang pada penampang di sepanjang bentang suatu elemen struktural
sebelum bekerjanya beban mati dan beban hidup transversal aau beban hidup horizontal
transien. Gaya prategang ini berupa tendon yang diberikan tegangan awal sebelum
memikul beban kerjanya yang berfungsi mengurangi atau menghilangkan tegangan tarik
pada saat beton mengalami beban kerja, menggantikan tulangan tarik pada struktur
beton bertulang biasa.
Beton prategang adalah material yang sangat banyak digunakan dalam
konstruksi. Beton prategang pada dasarnya adalah beton di mana tegangan-tegangan
internal dengan besar serta distribusi yang sesuai diberikan sedemikian rupa sehingga
tegangan-tegangan yang diakibatkan oleh beban-beban luar dilawan sampai suatu
tingkat yang diinginkan.
Beton yang digunakan dalam beton prategang adalah beton
yang mempunyai kuat tekan yang cukup tinggi dengan nilai f’c
min K-300, modulus
|
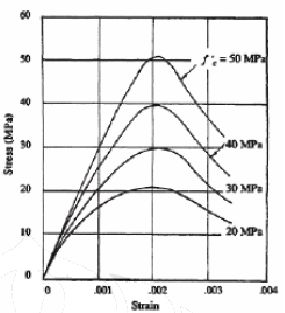 10
elastis yang tinggi dan mengalami rangkak ultimate yang lebih kecil yang menghasilkan
kehilangan prategangan yang lebih kecil pada baja.
Kuat tekan yang tinggi ini diperlukan untuk menahan tegangan tekan pada serat
tertekan, pengangkuran tendon, mencegah terjadinya keretakan.
Tipikal diagram
tegangan-regangan beton dapat dilihat pada gambar 2.4
Gambar 2.4 Diagram Tegangan-Regangan pada Beton
2.3.2
Pemakaian Baja Prategang
Baja (tendon) yang dipakai untuk beton prategang dalam prakteknya ada
tiga macam, yaitu :
a.
Kawat tunggal (wires), biasanya digunakan untuk baja prategang pada beton
prategang dengan sistem pratarik (pre-tension)
b.
Kawat untaian (strand), biasanya digunakan untuk baja prategang pada beton
prategang dengan sistem pasca tarik (post-tension)
|
 11
c.
Kawat batangan (bar), biasanya digunakan untuk baja prategang pada beton
prategang dengan sistem pratarik (pre-tension)
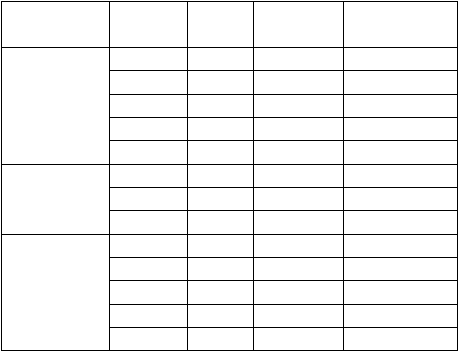
Pada tabel 2.2 di bawah akan ditunjukkan tipikal baja yang biasa digunakan
Tabel 2.2 Tipikal Baja Prategang
Jenis Material
Diameter
(mm)
Luas
(mm²)
Beban
Putus (kN)
Tegangan
Tarik (Mpa)
Kawat
Tunggal
(Wire)
3
7,1
13,5
1900
4
12,6
22,1
1750
5
19,6
31,4
1600
7
38,5
57,8
1500
8
50,3
70,4
1400
Untaian
Kawat
(Strand)
9,3
54,7
102
1860
12,7
100
184
1840
15,2
143
250
1750
Kawat
Batangan
(Bar)
23
415
450
1080
26
530
570
1080
29
660
710
1080
32
804
870
1080
38
1140
1230
1080
2.3.3
Prinsip Dasar Prategang
Pemberian gaya prategang ditentukan berdasarkan jenis sistem yang
dilaksanakan dan panjang bentang serta kelangsingan yang dikehendaki. Gaya
prategang yang diberikan secara longitudinal di sepanjang atau sejajar dengan
sumbu komponen struktur, maka prinsip-prinsip prategang dikenal sebagai
pemberian prategang linier.
Pemberian gaya prategang dapat dilakukan sebelum atau sesudah beton
dicor. Pemberian prategang yang dilakukan sebelum pengecoran disebut sistem
pratarik (pre-tensioned), sedangkan pemberian prategang setelah dilakukan
|
|
12
pengecoran disebut sistem pascatarik (post-tensioned). Pemberian gaya
prategang pada beton akan memberikan tegangan tekan pada penampang.
Tegangan ini akan menahan beban luar yang bekerja pada penampang.
Beton prategang sendiri dapat mengalami gaya prategang penuh (fully
stressed) atau gaya prategang sebagian (partial stressed). Prategang penuh
adalah struktur tidak diizinkan ada tegangan tarik pada penampang baik pada
tahap transfer sampai dengan masa layan dan tegangan pada serat bawah
dianggap tidak ada. Sedangkan prategang sebagian adalah penampang struktur
direncanakan untuk dapat menerima tegangan tarik pada lokasi penampang
selama masa transfer sampai
masa layan dan tegangan serat bawah tidak sama
dengan nol.
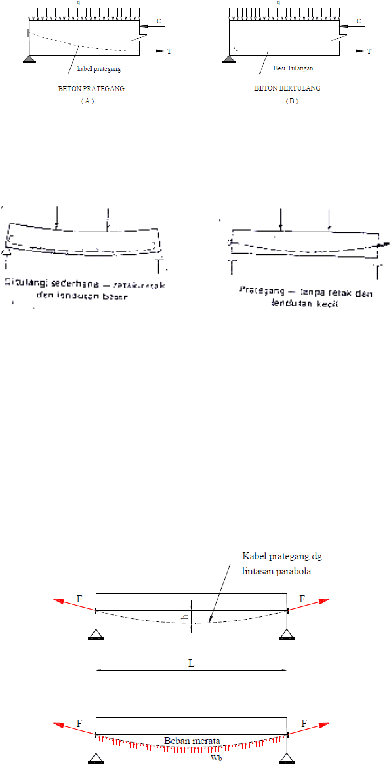
Ada tiga konsep berbeda yang dipakai untuk menjelaskan dan menganalisis sifat-
sifat dasar dari beton prategang :
a.
Konsep pertama, sistem prategang untuk mengubah beton menjadi bahan yang
elastis. Ini merupakan buah pemikiran Eugene Freyssinet yang
memvisualisasikan beton prategang pada dasarnya adalah beton yang
ditransformasikan dari bahan yang getas menjadi bahan elastis dengan
memberikan tekanan (desakan) terlebih dahulu (pratekan) pada bahan tersebut.
Dari konsep ini lahirlah kriteria “tidak ada tegangan tarik” pada beton. Pada
umumnya telah diketahui bahwa jika tidak ada tegangan tarik pada beton. berarti
tidak akan terjadi retak, dan beton tidak merupakan bahan yang getas lagi
melainkan berubah menjadi bahan yang elastis.
|
 13
Gambar 2.5 Distribusi Tegangan Beton Prategang
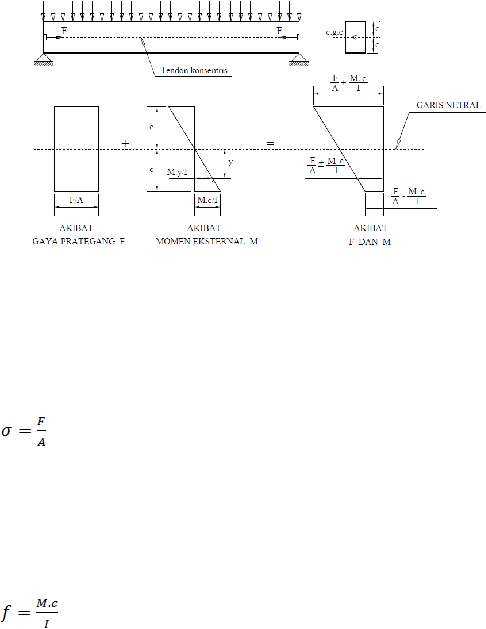
Dalam bentuk yang paling sederhana, ambillah balok persegi panjang yang diberi
gaya prategang oleh sebuah tendon sentris. Akibat gaya prategang F, akan timbul
tegangan tekan merata seperti pada gambar 2.6.
............................................................................................................. (2.1)
Akibat beban merata (termasuk berat sendiri beton) akan memberikan tegangan
tarik di bawah garis netral dan tegangan tekan di atas garis netral yang besarnya
pada serat terluar penampang adalah :
......................................................................................
(2.2)
Dimana
M
=
Momen lentur pada penampang yang ditinjau
c
= Jarak garis netral ke serat terluar penampang
I
= Momen Inersia Penampang
|
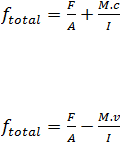 14
Kalau kedua tegangan akibat gaya prategang dan tegangan akibat momen lentur
ini dijumlahkan, maka tegangan maksimum pada serat terluar penampang
adalah:
?
Di atas garis netral:
(
tidak boleh melampaui tegangan hancur beton) .........(2.3)
?
Di bawah garis netral:
(tidak boleh < 0) ...........................................................(2.4)
Jadi dengan adanya gaya internal tekan ini, maka beton akan dapat memikul
beban tarik.
b.
Konsep kedua, sistem prategang untuk kombinasi baja mutu tinggi dengan beton.
Konsep ini mempertimbangkan beton prategang sebagai kombinasi (gabungan)
dari baja dan beton, seperti pada beton bertulang, dimana baja menahan tarikan
dan beton menahan tekanan, dengan demikian kedua bahan membentuk kopel
penahan untuk melawan momen eksternal (gambar 2.7). Pada beton prategang,
baja mutu tinggi ditanam pada beton, seperti pada beton bertulang biasa, beton di
sekitarnya akan menjadi retak berat sebelum seluruh kekuatan baja
digunakan
(gambar 2.8). Oleh karena itu, baja perlu ditarik sebelumnya (pratarik) terhadap
beton. Dengan menarik dan menjangkarkan ke beton dihasilkan tegangan dan
regangan pada baja. Kombinasi ini memungkinkan pemakaian yang aman dan
ekonomis dari kedua bahan dimana hal ini tidak dapat dicapai jika baja hanya
ditanamkan dalam bentuk seperti pada beton bertulang biasa.
|
 15
Gambar 2.6 Momen Penahan Internal pada Balok Beton Prategang dan Beton
Bertulang
Gambar 2.7 Balok Beton menggunakan Baja Mutu Tinggi
c.
Konsep ketiga, sistem prategang untuk mencapai keseiimbangan beban.
Konsep ini terutama menggunakan prategang sebagai suatu usaha untuk
membuat keseimbangan gaya-gaya pada sebuah balok. Penerapan dari konsep ini
menganggap beton diambil sebagai benda bebas dan menggantikan tendon
dengan gaya-gaya yang bekerja pada sepanjang beton.
Gambar 2.8 Balok Prategang dengan Tendon Parabola
|
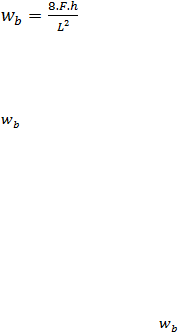 16
Suatu balok beton di atas dua perletakan (simple beam) yang diberi gaya
prategang F melalui suatu kabel prategang dengan lintasan parabola. Beban
akibat gaya prategang yang terdistribusi secara merata ke arah atas dinyatakan ;
......................................................................................................(2.5)
Dimana:
= Beban merata kearah atas, akibat gaya prategang F
h
= Tinggi parabola lintasan kabel prategang
L
= Bentangan Balok
F
= Gaya prategang
Jadi beban merata akibat beban (mengarah ke bawah) diimbangi oleh gaya
merata akibat prategang
yang mengarah ke atas.
2.4
Metode Prategangan
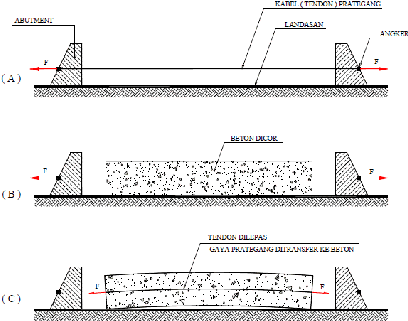
Ada dua jenis metode pemberian gaya prategang pada beton, yaitu :
a.
Metode Pratarik (Pre-Tension Method)
Metode ini yaitu baja prategang diberi gaya prategang dulu sebelum
beton dicor, oleh karena itu disebut metode pratarik. Adapun prinsip
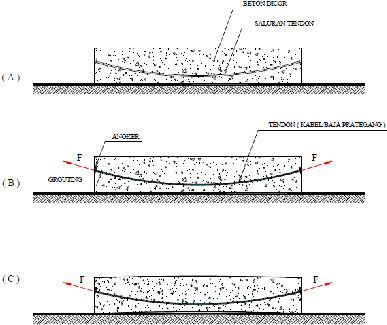
pratarik secara singkat dijelaskan seperti pada gambar 2.10
|
 17
Gambar 2.9 Prinsip Metode Pratarik
Tahap (A) : Kabel (tendon) prategang ditarik atau diberi gaya prategang
kemudian diangker pada suatu abutment tetap.
Tahap (B) : Beton dicor pada cetakan (formwork) dan landasan yang sudah
disediakan sedemikian sehingga melingkupi tendon yang sudah diberi gaya
prategang dan dibiarkan mengering.
Tahap (C) : Setelah beton mongering dan cukup umur dan kuat untuk menerima
gaya prategang, tendon dipotong dan dilepas, sehingga gaya prategang ditransfer
ke beton.
Setelah gaya prategang ditransfer ke beton, balok beton tersebut akan
melengkung ke atas sebelum menerima beban kerja. Setelah beban kerja bekerja,
maka balok beton tersebut akan rata.
|
 18
b.
Metode Pascatarik (Post-Tension Method)
Pada metode pascatarik, beton dicor terlebih dahulu, dimana sebelumnya
telah disiapkan saluran kabel atau tendon yang disebut duct. Metode
pascatarik dapat dijelaskan secara singkat seperti pada gambar 2.11.
Gambar 2.10 Prinsip Metode Pascatarik
Tahap (A) :
Dengan cetakan (formwork) yang telah disediakan lengkap
dengan saluran/selongsong kabel prategang (tendon duct) yang dipasang
melengkung sesuai bisang momen balok, beton dicor.
Tahap (B) : Setelah beton cukup umur dan kuat memikul gaya prategang,
tendon atau kabel prategang dimasukkan dalam selongsong (tendon duct),
kemudian ditarik untuk mendapat gaya prategang. Metode pemberian
gaya prategang ini, salah satu ujung kabel diangker, kemudian ujung
lainnya ditarik (ditarik dari satu sisi). Ada pula yang ditarik di kedua
|
|
19
sisinya dan diangker secara bersamaan. Setelah diangkur, kemudian saluran di
grouting melalui lubang yang telah disediakan.
Tahap (C) : Setelah diangkur, balok beton menjadi tertekan, jadi gaya prategang
telah ditransfer ke beton. Karena tendon dipasang melengkung, maka akibat gaya
prategang tendon memberikan beban merata ke balok yang arahnya ke atas,
akibatnya balok melengkung ke atas.
Karena alasan transportasi dari pabrik beton ke lokasi proyek, maka biasanya
beton prategang dengan sistem post-tension ini dilaksanakan secara segmental
(balok dibagi-bagi, misalnya dengan panjang 1-1,5 m), kemudian pemberian
gaya prategang dilaksanakan di lokasi proyek, setelah balok segmental tersebut
dirangkai.
2.5
Tahap Pembebanan
Tidak seperti pada perencanaan beton bertulang biasa, pada perencanaan beton
prategang ada dua tahap pembebanan yang harus dianalisa. Pada setiap tahap
pembebanan harus selalu diadakan pengecekan atas kondisi pada bagian yang tertekan
maupun bagian yang tertarik untuk setiap penampang. Dua tahap pembebanan pada
beton prategang yaitu tahap transfer dan tahap layan (service).
a.
Tahap transfer
Untuk metode pratarik, tahap transfer ini terjadi pada saat angker dilepas dan
gaya prategang ditransfer ke beton. Untuk metode pascatarik, tahap transfer ini
terjadi
pada saat beton sudah cukup umur dan dilakukan penarikan kabel
prategang. Pada saat ini beban yang bekerja hanya berat sendiri struktur, beban
pekerja dan peralatan, sedangkan beban hidup belum bekerja sepenuhnya, jadi
|
|
20
beban yang bekerja sangat minimum. Sementara gaya prategang yang bekerja
adalah maksimum karena belum ada kehilangan gaya prategang.
b.
Tahap layan
Setelah beton prategang digunakan atau difungsikan sebagai komponen struktur,
maka mulailah masuk ke tahap service atau tahap layan dari beton prategang
tersebut. Pada tahap ini beban luar seperti live load, angin, gempa, dan lain-lain
mulai harus bekerja, sedangkan pada tahap ini semua kehilangan gaya prategang
sudah harus dipertimbangkan di dalam analisa strukturnya.
2.6
Kehilangan Prategang
Gaya prategang pada beton mengalami proses reduksi yang progresif
(pengurangan secara perlahan) sejak gaya prategang awal diberikan. Pada dasarnya nilai
masing-masing kehilangan gaya prategang adalah kecil, tetapi apabila dijumlahkan
dapat menyebabkan penurunan gaya yang cukup signifikan yaitu ± 15% - 20%, sehingga
kehilangan gaya prategang harus dipertimbangkan.
Beberapa hal yang harus diperhatikan untuk meminimalkan kehilangan gaya prategang
adalah :
a.
Mutu beton yang digunakan minimal 40 MPa untuk memperkecil rangkak.
b.
Tendon yang digunakan adalah mutu tinggi yang memiliki relaksasi rendah.
Secara umum, reduksi gaya prategang dapat dikelompokkan menjadi dua kategori, yaitu:
a.
Kehilangan elastis segera yang terjadi pada saat proses fabrikasi atau konstruksi,
termasuk perpendekan (deformasi) beton secara elastis, kehilangan karena pengangkuran
dan kehilangan karena gesekan.
|
|
21
b.
Kehilangan yang bergantung pada waktu, seperti rangkak, susut dan kehilangan
akibat efek temperatur dan relaksasi baja, yang semuanya dapat ditentukan pada
kondisi limit tegangan akibat beban kerja di dalam beton prategang.
2.6.1
Kehilangan Akibat Gesekan
Kehilangan gaya prategang akibat gesekan antara tendon dan saluran
beton sekitarnya dan juga sistem pengangkuran yang digunakan. Gesekan dalam
saluran tendon disebabkan oleh :
a.
Gesekan fisis yang normal terjadi antara dua benda yang bergeser satu
terhadap lainnya, dalam hal ini tendon yang bergerak terhadap dinding
saluran yang diam, terutama pada tracee tendon berbentuk lengkung.
b.
Melendut-lendutnya letak saluran tendon disebut biasanya dengan efek
goyangan (Wobble effect)
c.
Karatan-karatan yang terdapat pada tendons dan dinding saluran tendons
yang terbuat dari baja.
d.
Kemungkinan adanya beton yang masuk (bocor) dalam saluran tendon.
e.
Kebersihan saluran.
Perhitungan berkurangnya prategangan sampai sekarang merupakan cara
pendekatan. Dalam garis besarnya hanya menghitung 2 (dua) macam gesekan
yaitu : gesekan pada tendons (
) yang melengkung dan wobble effect ( k1
).
|
 22
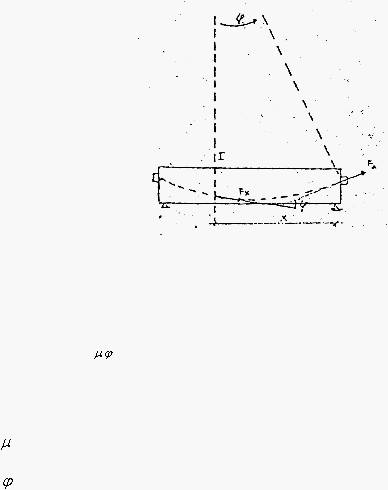
Gambar 2.11 Penampang beton
Prategangan
dalam penampang sejauh x
dari jack dihitung dengan rumus
EULER – COOLEY – MONTAGNON :
P
x
= P
o
. e
–
(
+ kx)
....................................................................................................................
(2.6)
dimana
:
= Koefisien gesekan tendon terhadap salurannya.
= Perubahan sudut lengkungan (radial)
k1
= Koefisien Wobble – Effect
x
= Panjang tendon dari tempat Jack
Rumus ini bisa mendekati keadaan sebenarnya bila dibarengi ketelitian
pelaksanaan sedemikian sehingga sebab-sebab yang membesarkan gesekan
diatas diperkecil, misalnya Wobble – effect, karatan, kebersihan dalam saluran.
Koefisien gesekan dan Wobble – effect ini memiliki nilai seperti tabel di bawah
sebagai berikut :
|
 23
Tabel 2.3 Koefisien gesekan dan Wobble – effect
Tipe tendon
Koefisien Wobble,
k1
tiap meter
Koefisien
Kelengkungan,
Tendon pada selubung logam fleksibel
Tendon kawat
0,0033 – 0,0049
0,15 – 0,25
Strand (7 kawat)
0,0016 – 0,0066
0,15 – 0,25
Batang baja mutu tinggi
0,0003 – 0,0020
0,08 – 0,30
Tendon pada selubung logam kaku
Strand (7 kawat)
0,0007
0,15 – 0,25
Tendon yang diminyaki terlebih dahulu
Tendon kawat dan strand (7 kawat)
0,0010 – 0,0066
0,03 – 0,15
Tendon yang diberi lapisan mastik
Tendon kawat dan strand (7 kawat)
0,0033 – 0,0066
0,05 – 0,15
2.6.2
Kehilangan Akibat Perpendekan Elastis Beton
Kehilangan gaya prategang akibat perpendekan elastis beton, harus
memperhitungkan secara cermat nilai modulus elastisitas beton pada saat transfer
tegangan, modulus elastisitas baja prategang, dan tegangan beton pada titik berat
baja prategang yang diakibatkan oleh gaya prategang dan beban mati segera
setelah transfer.
Jika tidak ada perhitungan yang lebih teliti, maka kehilangan tegangan
dalam tendon
akibat perpendekan elastis beton dapat dihitung sebagai
berikut:
Untuk komponen pratarik
..............................................................................
(2.7)
Untuk komponen pasca tarik
|
 24
................................................................................................(2.8)
2.6.3
Kehilangan Prategang Akibat Slip Pengangkuran
Pada komponen pasca tarik, kehilangan prategang saat transfer gaya
prategang dari alat penegang ke angkur harus diperhitungkan, berdasarkan
panjang pengaruh tendon yang diperkirakan mengalami pengaruh perubahan
tegangan akibat slip pengangkuran. Besar kehilangan dari hasil perhitungan
harus diperiksa di lapangan pada saat pra-penegangan, dan harus dilakukan
penyesuaian di mana perlu.
2.6.4
Kehilangan Akibat Susut pada Beton
Pada strktur beton prategang, susut beton harus diperhitungkan sebagai
faktor yang mempengaruhi kehilangan gaya prategang, yang besarnya tergantung
pada waktu. Jika tidak ada perhitungan yang lebih teliti, maka kehilangan
tegangan dalam tendon
akibat susut pada beton harus diambil sebesar :
...................................................................................................(2.9)
Dimana
menyatakan besarnya deformasi susut beton yang dihitung sesuai
ketentuan yang ada.
Bila tulangan baja non-prategang digunakan dan disebar ke seluruh
penampang komponen struktur prategang, maka pengaruhnya terhadap susut
perlu dipertimbangkan terutama dalam arah aksial, sehingga jika tidak ada
perhitungan yang lebih teliti, kehilangan gaya prategang dalam tendon
dapat
diambil sebesar :
|
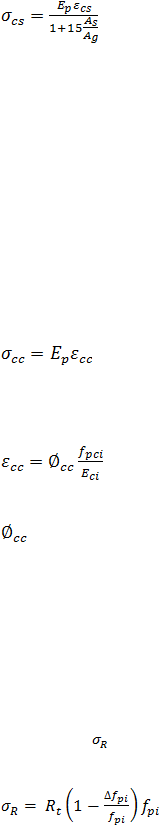 25
...............................................................................................(2.10)
2.6.5
Kehilangan Akibat Rangkak pada Beton
Kehilangan gaya prategang akibat rangkak pada beton harus
diperhitungkan dari analisis regangan rangkak yang tergantung pada waktu.
Kecuali jika ada perhitungan yang lebih rinci dan bila tegangan tekan (akibat
prategang) dalam beton pada posisi tendon tidak melebihi 0,5f’c
,
kehilangan
akibat rangkak tersebut dapat dihitung sebesar :
.................................................................................................(2.11)
Dimana :
...............................................................................................(2.12)
= Faktor rangkak rencana
2.6.6
Kehilangan Akibat Relaksasi Baja Prategang
Relaksasi baja prategang harus diperhitungkan sebagai faktor yang
mempengaruhi kehilangan gaya prategang, yang besarnya tergantung pada
waktu. Jika tidak ada perhitungan yang lebih teliti, maka kehilangan tegangan
dalam tendon
akibat relaksasi baja prategang harus diambil sebesar :
................................................................................(2.13)
|
|
26
Dimana
menyatakan faktor relaksasi rencana tendon, yang dipengaruhi oleh
jenis tendon.
2.6.7
Kehilangan Akibat Pengaruh Lain
Bilamana
dianggap perlu, dalam perencanaan harus diperhitungkan
kehilangan tegangan akibat pengaruh lain yang belum disebutka di atas,
tergantung dari jenis dan kepentingan struktur beton prategang, antara lain untuk
faktor kehilangan seketika :
a.
Perubahan suhu antara saat penegangan tendon dan saat pengecoran beton
b.
Deformasi pada sambungan struktur pracetak
c.
Relaksasi tendon sebelum transfer
d.
Deformasi acuan pada komponen pracetak
e.
Perbedaan suhu antara tendon yang ditegangkan dan struktur
yang di
prategang selama perawatan pemanasan beton.
Demikian juga bila dianggap perlu, diperhitungkan kehilangan yang tergantung
waktu, yang disebabkan oleh beberapa hal, antara lain :
a.
Deformasi pada sambungan struktur pracetak yang dipasang pada
penampang
b.
Pengaruh penambahan rangkak yang disebabkan oleh beban berulang yang
sering terjadi.
2.7
Perencanaan Beton Prategang
Ada dua metode perencanaan beton prategang, yaitu :
a.
Metode Beban Kerja (Working Stress Method)
|
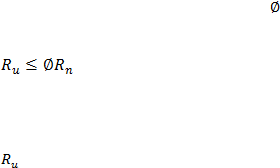 27
Prinsip perencanaan ini adalah menghitung tegangan yang terjadi akibat
pembebanan (tanpa dikalikan dengan faktor beban) dan membandingkan
dengan tegangan yang diijinkan. Tegangan yang diijinkan dikalikan dengan suat
faktor kelebihan tegangan (overstress factor) dan jika tegangan yang terjadi lebih
kecil dari tegangan yang diijinkan tersebut, maka struktur dinyatakan aman.
b.
Metode Beban Batas (Limit State Method)
Prinsip perencanaan ini didasarkan pada batas-batas tertentu yang dapat
dilampaui oleh suatu sistem struktur. Batas-batas ini ditetapkan terutama
terhadap kekuatan, kemampuan layan, keawetan, ketahanan terhadap beban, api,
kelelahan dan persyaratan-persyaratan khusus yang berhubungan dengan
penggunaan struktur tersebut. Dalam menghitung beban rencana maka beban
harus dikalikan dengan suatu faktor beban (load factor), sedangkan kapasitas
bahan dikalikan dengan suatu faktor reduksi kekuatan (reduction factor).
Tahap batas (limit state) adalah suatu batas tidak diinginkan yang berhubungan
dengan kemungkinan kegagalan struktur
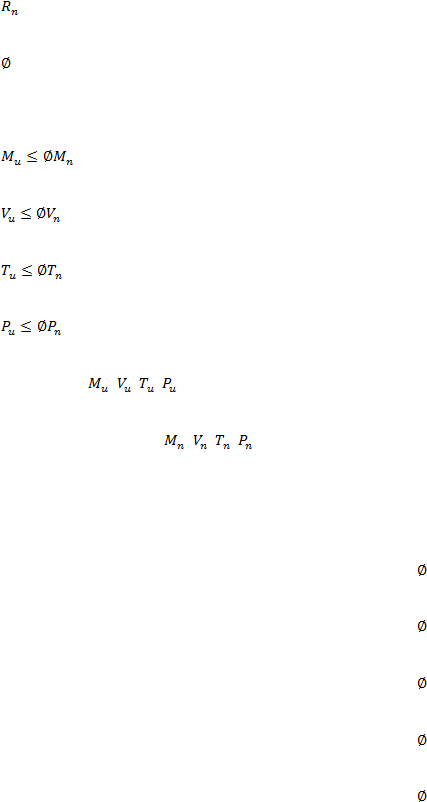
Perencanaan struktur untuk tahap batas kekuatan (strength limit state),
menetapkan bahwa aksi design (R
u
) harus lebih kecil dari kapasitas bahan
dikalikan dengan faktor reduksi kekuatan
.
......................................................................................................(2.14)
Dimana:
= Aksi desain
|
 28
= Kapasitas bahan
= Faktor reduksi
Sehingga untuk aksi desain momen, geser, puntir, dan gaya aksial berlaku:
.....................................................................................................(2.15)
.........................................................................................................(2.16)
........................................................................................................(2.17)
........................................................................................................(2.18)
Harga-harga
,
,
,
diperoleh dari kombinasi pembebanan yang paling
maksimum, sedangkan
,
,
,
adalah kapasitas penampang terhadap
momen.geser,puntir, dan gaya aksial.
Faktor reduksi kekuatan menurut SNI Beton 03-2847-2002
Lentur tanpa gaya aksial
:
= 0,80
Aksial tarik dan aksial tarik dengan lentur
:
= 0,80
Aksial tekan dan aksial tekan dengan lentur tulangan spiral
:
= 0,70
Aksial tekan dan aksial tekan dengan lentur tulangan sengkang :
= 0,65
Gaya geser dan Puntir
:
= 0,75
|
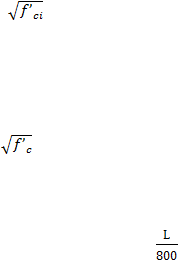 29
Sedangkan batas ijin tegangan untuk masa peralihan dan masa layan sesuai
dengan RSNI 2005 tentang pembebanan pada jembatan.
-
Masa peralihan
Serat Tertekan
= 0,6 f’
ci
....................................................................... (2.19)
Serat Tertarik
= 0,25
................................................................. (2.20)
-
Masa Layan
Serat Tertekan
= 0,45 f’c
..................................................................... (2.21)
Serat Tertarik
= 0,5
................................................................... (2.22)
Dengan f’
ci
= 0,8 f’c ...................................................................... (2.23)
Dan batas lendutan yang digunakan adalah sebesar
............................... (2.24)
2.8
Analisa Dinamik
Pada ilmu statika keseimbangan gaya-gaya didasarkan atas kondisi statik, artinya
gaya-gaya tersebut tetap intensitasnya, tetap tempatnya dan tetap arah/garis kerjanya.
Gaya-gaya tersebut dikategorikan sebagai beban statik. Kondisi seperti ini akan berbeda
dengan beban dinamik dengan pokok-pokok perbedaan sebagai berikut ini:
a.
Beban dinamik adalah beban yang berubah-ubah menurut waktu (time varying)
sehingga beban dinamik merupakan fungsi dari waktu.
b.
Beban dinamik umumnya hanya bekerja pada rentang waktu tertentu. Untuk
beban gempa bumi maka rentang waktu tersebut kadang-kadang hanya beberapa
detik saja. Walaupun hanya beberapa detik saja namun beban angin dan beban
gempa misalnya dapat merusak struktur dengan kerugian yang sangat besar.
|
|
30
c.
Beban dinamik dapat menyebabkan timbulnya gaya inersia pada pusat massa
yang arahnya berlawanan dengan arah gerakan.
d.
Beban dinamik lebih kompleks dibanding dengan beban statik, baik dari bentuk
fungsi bebannya maupun akibat yang ditimbulkan.
e.
Karena beban dinamik berubah-ubah intensitasnya menurut waktu, maka
pengaruhnya terhadap struktur juga berubah-ubah menurut waktu. Oleh karena
itu penyelesaian problem
dinamik harus dilakukan seara berulang-ulang
menyertai sejarah pembebanan yang ada. Kalau penyelesaian problem
statik
bersifat penyelesaian tunggal (single solution), maka penyelesaian problem
dinamik bersifat penyelesaian berulang-ulang (multiple solutions).
f.
Karena beban dinamik menimbulkan respon yang berubah-ubah menurut waktu,
maka struktur yang bersangkutan akan ikut bergetar/ada gerakan. Dalam hal ini
bahan akan melakukan resistensi terhadap gerakan dan umumnya dikatakan
bahan yang bersangkutan mempunyai kemampuan untuk meredam getaran. Dengan
demikian pada pembebanan dinamik, akan terdapat peristiwa redaman yang hal ini tidak
ada pada pembebanan statik.
Pada problem dinamik, setiap titik atau massa umumnya hanya diperhitungkan
berpindah tempat dalam satu arah saja yaitu arah horisontal. Karena simpangan yang
terjadi hanya terjadi dalam satu bidang (2-dimensi) maka simpangan suatu massa pada
setiap saat hanya mempunyai posisi/ordinat tertentu baik bertanda positif maupun
negatif. Pada kondisi 2-D tersebut simpangan suatu massa pada saat t dapat dinyatakan
dalam koordinat tunggal yaitu y(t). Struktur seperti itu dinamakan struktur dengan
derajat kebebasan tunggal. Secara umum bangunan 1-tingkat dianngap hanya
mempunyai derajat kebebasan tunggal (single degree of freedom, SDOF) dan struktur
|
|
31
yang mempunyai n-tingkat akan mempunyai n-derajat kebebasan atau struktur dengan
derajat kebebasan banyak (multi degree of freedom, MDOF). Banyaknya derajat
kebebasan menyatakan banyaknya perpindahan yang independent yang diperlukan untuk
mendefinisikan perpindahan posisi dari massa terhadap posisi awal.
Respon struktur akan bergantung pada properti dinamik struktur (kekakuan,
massa dan redaman) dan juga akan bergantung dari beban dinamik serta
macam/jenis/asumsi getaran yang dipakai. Secara umum struktur bangunan gedung
tidaklah selalu dapat dinyatakan di dalam suatu sistem yang mempunyai derajat
kebebasan tunggal (SDOF). Struktur bangunan gedung justru banyak yang mempunyai
derajat kebebasan banyak (MDOF). Pada struktur bangunan gedung bertingkat banyak
umumnya massa struktur dapat digumpalkan pada tempat-tempat tertentu (lumped mass)
yang umumnya pada tiap-tiap lantai-tingkat, maka struktur yang tadinya mempunyai
derajat kebebasan tak terhingga akan menjadi struktur dengan derajat kebebasan
terbatas.
2.8.1
Tipe Getaran
Secara umum gerakan massa suatu struktur dapat disebabkan baik oleh
adanya gangguan luar maupun adanya suatu nilai awal (initial conditions).
Peristiwa dengan gerakan massa akibat adanya nilai awal, misalnya simpangan
awal atau kecepatan awal, biasa disebut dengan getaran bebas (free vibration
systems). Sedangkan apabila goyangan suatu struktur yang diakibatkan oleh
adanya gaya luar ataupun adanya getaran tanah akibat gempa, biasa disebut
dengan getaran dipaksa (forced vibration systems). Namun gerakan suatu massa
|
|
32
umumnya akan dihambat/diredam baik karena gesekan dengan benda-benda
sekelilingnya maupun oleh peristiwa intern yang ada pada benda yang
bersangkutan, sehingga gerakan massa tersebut lambat laun akan melemah.
Gerakan massa struktur yang memperhitungkan adanya gaya redam disebut
damped systems atau sistem gerakan yang diredam. Walaupun demikian, suatu
struktur kadang-kadang dianggap tidak mempunyai redaman atau undamped
systems.
Tipe gerakan pada struktur dapat dirangkum menjadi:
a.
Getaran bebas tanpa redaman (Undamped Free Vibration Systems)
b.
Getaran bebas yang diredam (Damped free Vibration)
c.
Getaran dipaksa yang tidak diredam (Undamped Forced Vibration
Systems)
d.
Getaran dipaksa yang diredam (Damped Forced Vibration Systems)
2.8.2
Persamaan Differensial Struktur SDOF
Persamaan keseimbangan dinamik dapat diturunkan dari model
matematik dari struktur SDOF seperti yang ditunjukkan pada Gambar 2.13. Pada
Gambar 2.12, P(t)
merupakan beban dinamik yang intensitasnya merupakan
fungsi dari waktu. Akibat beban dinamik, struktur akan bergoyang berganti-ganti
ke kanan maupun ke kiri. Terdapat beberapa parameter penting yang
mempengaruhi besar kecilnya goyangan yaitu massa (m), kekakuan kolom (k)
dan koefisien redaman (c). Struktur tersebut kemudian digambar secara ideal
seperti pada Gambar 2.13
dimana pada gambar ini telah memperhatikan
parameter-parameter yang berpengaruh. Pada Gambar 2.15 ditampilkan model
matematik untuk struktur SDOF yang mempunyai redaman. Apabila beban
|
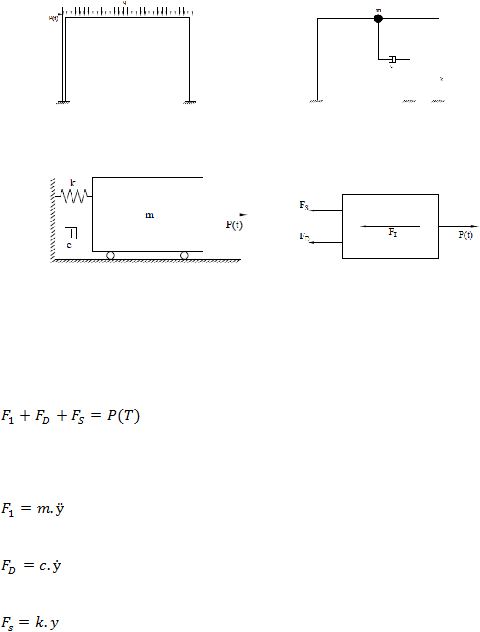 33
dinamik
P(t) seperti pada Gambar 2.14
bekerja ke arah kanan, maka akan
terdapat perlawanan pegas, damper dan gaya inersia. Gambar 2.15
adalah
gambar keseimbangandinamik yang bekerja pada massa (m), gambar ini
umumnya disebut free body diagram.
Gambar 2.12 Struktur SDOF Gambar 2.13 Model Fisik Struktur SDOF
Gambar 2.14 Model Matematik
Gambar 2.15 Free Body Diagram
Berdasarkan prinsip keseimbangan dinamik pada free body diagram tersebut,
maka dapat diperoleh hubungan:
.....................................................................................(2.25)
dimana:
........................................................................................................(2.26)
.........................................................................................................(2.27)
.........................................................................................................(2.28)
|
 34
dimana FI, FD, FS
berturut-turut adalah gaya inersia, gaya redaman dan gaya
pegas,
sedangkan ?, ? dan y
berturut-turut adalah percepatan, kecepatan dan
simpangan.
Apabila persamaan (2.26), (2.27), (2.28) disubstitusikan pada persamaan
(2.25) maka akan diperoleh persamaan kesimbangan dinamik sebagai berikut:
m
?
c
?
k
y
P(t) ............................................................................ (2.29)
Struktur/sistem seperti balok kantilever atau balok diatas 2 tumpuan sebenarnya
mempunyai infinite DOF (derajat kebebasan tak hingga) tetapi tidak dapat
disederhanakan menjadi suatu sistem SDOF dengan menggunakan shape
function = fungsi bentuk = ? (x).
Fungsi
bentuk ?
(x) menyatakan bentuk deformasi dari struktur yang
bergetar, sehingga jika nilai suatu deformasi di suatu lokasi tertentu diketahui,
maka dengan menggunakan fungsi bentuk tersebut dapat dicari nilai deformasi di
tiap lokasi pada struktur.
Dengan kata lain cukup 1 nilai deformasi yang harus dicari. Penyerdehanaan
seperti ini disebut generalized SDOF
MDOF
SDOF
Nilai massa m, kekakuan k, redaman c
dan gaya luar p
yang didapat dengan
memasukkan fungsi bentuk disebut:
-
Generalized massa
m*
-
Generalized spring constant
k*
-
Generalized damping coeffisient
c*
-
Generalized force
p*
|
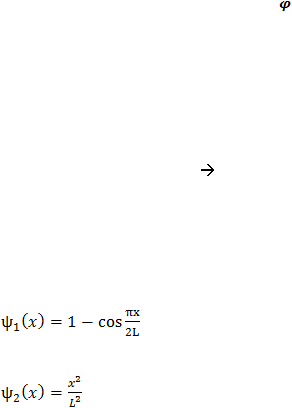 35
Ada 2 cara untuk memodelkan struktur MDOF menjadi SDOF dengan GSDOF :
-
Model kontinyu/distributed
-
Model tergumpal/diskrit
2.8.2.1 Fungsi bentuk / Shape Function /
(x)
Fungsi bentuk / shape function yang dipilih harus memenuhi syarat batas
untuk kasus struktur kantilever, ada banyak sekali kemungkinan bentuk
deformasi akibat gaya dinamik dan sebagainya. Sehingga dapat ditentukan syarat
batasnya. Misalnya pada x = 0
? (x = 0) = 0
Berdasarkan syarat batas tersebut, masih banyak kemungkinan persamaan
yang bisa memenuhi untuk digunakan sebagai fungsi bentuk / shape factor
diantaranya
......................................................................................(2.30)
...................................................................................................(2.31)
Dan sebagainya
Pada analisis GSDOF, diasumsikan bahwa struktur berdeformasi dalam 1 bentuk
tertentu atau mengikuti suatu shape function
tertentu. Shape function
sendiri
ditentukan sebagai suatu pendekatan sehingga hasil analisa juga merupakan
susatu hasil pendekatan. Setelah shape function ditentukan, langkah berikutnya
adalah menghitung:
-
Generalized m
= m*
-
Generalized k
= k*
|
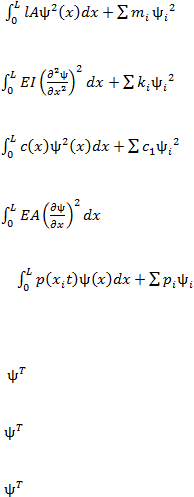 36
-
Generalized c
= c*
-
Generalized p(t)
= p(t)*
a.
Model kontinyu/distributed
m* =
....................................................................(2.32)
k* =
dalam arah lentur........................................(2.33)
c* =
...................................................................(2.34)
k* =
dalam arah aksial ..........................................................(2.35)
p(t)* =
................................................................(2.36)
b.
Model Tergumpal
M* =
M
?
..................................................................................................(2.37)
K* =
K
?
....................................................................................................(2.38)
P* =
F(t).....................................................................................................(2.39)
Dimana
M
: matriks massa
K
: matriks kekakuan
F
: matriks gaya luar dinamik
? : fungsi bentuk diskrit (berupa angka-angka/bukan persamaan)
|
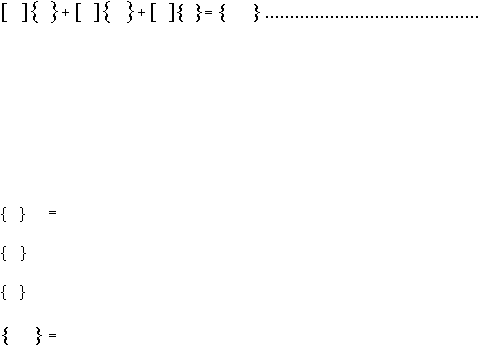 37
2.8.3
Persamaan Diferensial Struktur MDOF
Untuk menyatakan persamaan diferensial gerakan pada struktur dengan
derajat kebebasan banyak maka dipakai anggapan dan pendekatan seperti pada
struktur dengan
derajat kebebasan tunggal (SDOF). Untuk memeperoleh
persamaan diferensial tersebut maka tetap dipakai prinsip keseimbangan
dinamik (dynamic equation equilibrium) pada suatu massa yang ditinjau. Namun
pada struktur dengan derajat kebebasan banyak,
persamaan diferensial
gerakannya merupakan persamaan yang dependent atau coupled
karena
kesimbangan dinamik suatu massa yang ditinjau dipengaruhi oleh kekakuan,
redaman dan simpangan massa sebelum dan sesudahnya. Penyelesaian
persamaan coupled harus dilakukan secara simultan artinya dengan melibatkan
semua persamaan yang ada. Sehingga persamaan keseimbangan dinamik untuk
derajat kebebasan banyak dapat ditulis dalam matriks:
M
Ÿ
C
?
K
Y
F(t)
(2.40)
dimana:
[M]
= Matriks massa
[C]
= Matriks redaman
[K] = Matriks kekakuan
Ÿ
Vektor percepatan
?
= Vektor kecepatan
Y
= Vektor simpangan
F(t)
Vektor beban
|
|
38
2.8.4
Parameter Dinamis
Penilaian kondisi bangunan atas jembatan dengan menggunakan
frekuensi alami aktual dimaksudkan untuk penyerdehanaan analisis. Analisis
yang dimaksud berupa perhitungan ulang dari frekuensi alami (f
teoritis
)
berdasarkan dimensi dari balok/gelagar jembatan.
Parameter penilaian dinamis
adalah sebagai berikut :
a.
Frekuensi alami pertama atau fundamental terukur (f
aktual
)
yang berasal
dari rekaman getaran bebas.
b.
Kekakuan lentur (EI
aktual
)
c.
Redaman kritis (h
aktual
)
Penurunan frekuensi alami aktual (f
aktual
)
terhadap nilai frekuensi alami teoritis
(f
teoritis
) menunjukkan penurunan dari keutuhan struktural.
Parameter kekakuan lentur (EI) langsung terkait dengan frekuensi alami
aktual. Penurunan kekakuan lentur aktual (EI
aktual
) terhadap kekakuan lentur
teoritis (EI
teoritis
) menunjukkan penurunan kapasitas daya pikul. Peningkatan
redaman kritis aktual (h
aktual
) terhadap redaman kritis teoritis (h
teoritis
) dari beton
utuh menunjukkan tingkat kerusakan retakan.
2.8.5
Frekuensi Alami
Frekuensi alami merupakan jumlah perulangan gerakan dalam satu detik
pada getaran bebas (cps atau hertz). Model bentuk getaran dari sebuah struktur
adalah bentuk lendutan struktur pada frekuensi yang spesifik. Nilai frekuensi
alami dapat digunakan sebagai pedoman apakah suatu struktur akan mengalami
resonansi atau tidak. Suatu struktur akan mengalami resonansi apabila nilai
|
|
39
frekuensi beban yang diterima struktur mendekati atau sama dengan frekuensi
alaminya.
Frekuensi alami struktur dipengaruhi oleh properti internal struktur, yaitu
kekakuan dan massa struktur. Pada umumnya untuk jembatan yang relatif baru,
frekuensinya berkisar antara 3-5 Hz. Nilainya akan tetap kecuali apabila struktur
tersebut mengalami perubahan pada kekakuan dan massa strukturnya. Kerusakan
yang terjadi pada struktur akan menyebabkan degradasi pada kekakuannya. Hal
ini akan mempengaruhi secara langsung pada nilai frekuensi alaminya. Dengan
demikian frekuensi alami merupakan indikator yang baik terhadap kerusakan
yang dialami oleh suatu sistem struktur.
2.8.6
Analisa Penurunan Struktur
Getaran bebas adalah ketika tidak ada getaran eksternal yang
diaplikasikan dan redaman struktur diabaikan. Respon jembatan berkaitan erat
dengan kondisi kerusakan struktural. Nilai kerusakan struktural relatif
adalah
sebagai berikut :
.............................................................................(2.41)
Dimana:
D
relatif
= Nilai kerusakan struktural relatif
F
0
= Frekuensi alami awal
F
i
= Frekuensi alami ke-i
Pada analisis noda lebih tinggi akan terlihat perbedaan perubahan bentuk untuk
jembatan lurus dan jembatan miring (skew) seperti pada gambar 2.16. Jembatan
|
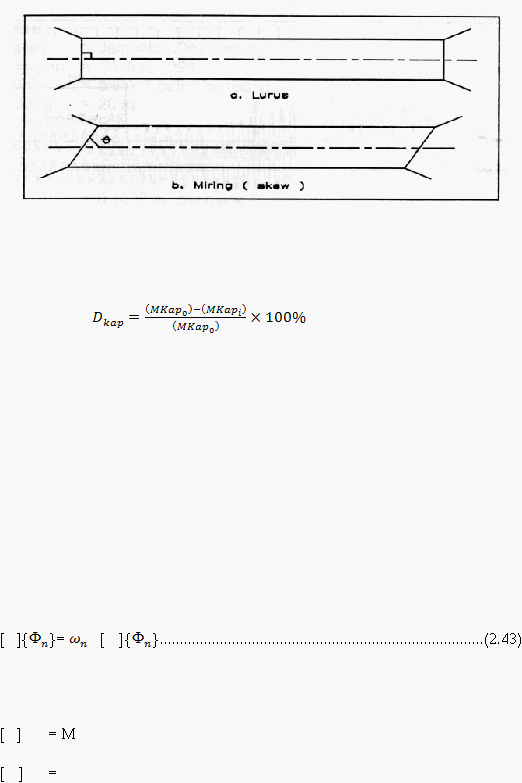 40
lurus mempunyai perubahan bentuk lentur yang terpisah dari punter sedangkan
jembatan miring (skew) mempunyai kombinasi antara lentur dan puntir.
Gambar 2.16 Jembatan (a) lurus, Jembatan (b) miring (skew)
Nilai penurunan kapasitas (D
kap
) dari bangunan atas adalah sebagai berikut :
.....................(2.42)
Dimana :
D
kap
= Nilai penurunan kapasitas
Mkap
0
= Momen kapasitas awal
Mkap
i
= Momen kapasitas ke-i
2.8.7
Analisis Eigenvalue
Mode bentuk dan periode alami dari getaran bebas tanpa redaman
diperoleh dari persamaan karakteristik di bawah :
K
²
M
Dimana :
K
atriks kekakuan
M
Matriks massa
|
|
41
²
= Mode ke-n eigenvalue
= Mode ke-n eigenvalue (mode bentuk)
Analisis eigenvalue
menyediakan properti dinamis dari struktur dengan
memecahkan karakteristik persamaan yang tersusun atas matriks massa dan
matriks kekakuan. Properti dianmis meliputi mode natural (mode bentuk),
periode alami (frekuensi) dan faktor partisipasi modal.
a.
Mode natural : Mode natural berkaitan dengan getaran bebas tanpa
redaman (undamped free vibration system). Mode pertama, mode kedua
dan mode ke-n mewakili urutan dimana energi yang paling sedikit
dibutuhkan untuk merusak struktur.
b.
Periode alami : Periode alami adalah waktu yang dibutuhkan untuk
menggetarkan struktur secara bebas ke dalam mode satu lingkaran penuh
koresponding alami.
c.
Faktor partisipasi modal : merupakan rasio dari pengaruh mode spesifik
ke mode total.
2.8.7.1 Tipe analisis
Eigen Vectors
-
Subspace Iteration
Kalkulasi matriks kecepatan iterasi digunakan untuk menjalankan
analisis eigenvalue. Metode ini secara efektif digunakan ketika
menjalankan analisis eigenvalue
untuk sistem finite
elemen dalam
|
|
42
skala besar (sistem matriks besar) dan umumnya digunakan di
kalangan engineer.
-
Lanczos
Matriks tridiagonal digunakan untuk menjalankan analisis eigenvalue.
Metode ini secara efektif digunakan ketika sedang menjalankan analisis
eigenvalue untuk mode lebih rendah.
Ritz Vectors
Tidak seperti mode alami eigenvalue, beban tergantung ritz vectors
menghasilkan hasil yang lebih bisa diandalkan dalam analisis dinamis dengan mode
yang lebih sedikit. Ritz vectors dihasilkan mencerminkan distribusi spasial atau
karakteristik dari pembebanan dinamis.
2.8.8
Evaluasi Hasil Analisis
Penilaian kondisi bangunan atas jembatan berdasarkan criteria yang diturunkan
dari hasil penelitian seperti terlihat pada tabel 2.3. Hasil pengamatan visual juga harus
diperhitungkan dalam penilaian kondisi bangunan atas jembatan.
Luas retakan dari pengamatan visual merupakan keterangan objektif dalam evaluasi
rasio redaman. Kondisi retakan dapat diklasifikasi sebagai kondisi baik, cukup, buruk
sesuai dengan pengamatan retak rambut, retak setempat, retak menyeluruh.
|
 43
Tabel 2.4 Penilaian Kondisi Bangunan Atas Jembatan
Nilai
Kondisi
Jenis Kerusakan
Nilai Kerusakan
Relatif
D
rel
Nilai Penurunan
Kapasitas
D
cap
baik
utuh
0% - 5%
0% -10%
cukup
rusak ringan (non struktural)
6% - 10%
11% - 20%
sedang
rusak ringan (struktural)
11% - 17%
21% - 34%
buruk
rusak berat (struktural)
18% - 20%
35% - 40%
Catatan :
-Nilai dalam tabel 2.3 berlaku untuk bahan bangunan atas yang sejenis, untuk penilaian bangunan atas komposit
perlu diperhitungkan penampang sisa.
-Penilaian objektif dibantu oleh pemeriksaan visual
2.9
MIDAS CIVIL
MIDAS CIVIL merupakan software yang berfungsi untuk pemodelan struktur
dan menganalisa struktur itu sendiri. Program MIDAS dapat menganalisa tahapan
metode pelaksanaan sekaligus dalam satu eksekusi program, dimana hasil analisa pada
saat analisa statis dibandingkan dengan hasil analisa pada saat pelaksanaan konstruksi.
MIDAS CIVIL dipilih karena mempunyai berbagai fitur untuk analisis yang bisa
menjawab kerumitan analisis struktur dengan proses input yang relatif mudah. Untuk
jembatan berbentang panjang seperti jembatan cable stayed dan jembatan gantung,
Midas Civil mempunyai pula wizard yang cukup canggih dalam membantu proses
analisis dan perencanaan yang rumit dengan derajat ketidak-tentuan statik yang
sangat tinggi.
|