 BAB 2
LANDASAN TEORI
2.1 Struktur Aljabar
2.1.1
Definisi Struktur Aljabar
Menurut Dr. Kusno Kromodihardjo (1988), yang dimaksud dengan suatu
struktur
aljabar
yaitu
suatu
himpunan tak
hampa
yang
dilengkapi
dengan
suatu
komposisi
biner
atau
lebih.
Misalkan
S adalah
suatu
himpunan
yang
dilengkapi
dengan dua komposisi biner + dan *, maka S menjadi satu struktur aljabar dan diberi
notasi (S, +, *).
2.1.2
Tabel Cayley
Dibutuhkan
suatu
alat
yang konkret untuk
mendefinisikan komposisi
biner
dalam suatu himpunan khususnya
himpunan terhingga yaitu Tabel Cayley. Dengan
tabel Cayley,
komposisi biner dapat
didefinisikan
secara analitik (deskriptif) atau
secara
geometrik.
Tabel Cayley
adalah
daftar
yang
dirancang
oleh Arthur Cayley
pada abad ke-19.
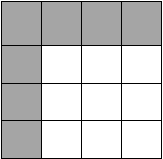
Tabel 2.1 Tabel Cayley untuk Operasi Penjumlahan Modulo 4
+
4
0
1
2
0
0
1
2
1
1
2
0
2
2
0
1
|
|
8
Dari tabel Cayley di atas, elemen yang dioperasikan adalah elemen di kolom
abu-abu kiri 0 1 2 dengan operasi
+
4
elemen di baris abu-abu atas 0 1 2. Kolom
putih
dan
baris
putih
merupakan
hasil
biner
antara masing-masing elemen
pada
himpunan.
Terlihat bahwa 0 +
4
0
=
0, 0 +
4
1
=
1, 0 +
4
2
=
2, 1 +
4
0
=
1, 1 +
4
1
=
2,
1
+
4
2
=
0
dan seterusnya.
Dalam sistem aljabar
perlu
diperhatikan
bahwa
operasi
+
4
di
atas
belum
tentu
berarti operasi
penjumlahan
yang
lazim
digunakan dalam aritmatika,
namun
dapat berarti pengurangan,
perkalian,
atau
lainnya
sesuai
dengan
definisi yang
diberikan pengguna.
Tabel Cayley banyak digunakan dalam sistem aljabar karena penyusunannya
dapat menggambarkan sifat-sifat grup. Sebagai contoh, operasi penjumlahan modulo
4
dari himpunan A
=
{0,1,2}
merupakan
grup abelian
(komutatif)
dengan
melihat
hasil bahwa hasil produk operasi pada
Tabel
2.1 saling simetris terhadap sumbu
diagonal utama tabel.
2.1.3 Sifat-Sifat Operasi Aljabar
Menurut
Connell
(2004),
operasi
biner
pada
sistem
aljabar
memiliki
sifat-
sifat yang digunakan untuk mengklasifikasikan sistem tersebut.
A. Operasi Biner (tertutup)
Misalkan
A
=
{2,4,6,8,..} yaitu bilangan asli genap dan dipandang operasi
+,
yaitu operasi penjumlahan,
maka
operasi
+
merupakan
operasi
biner
pada
A
karena jumlah dua bilangan
asli genap selalu merupakan
bilangan asli genap
dalam A.
|
|
9
(
?
a, b
?
A) a+b
?
A
Ö + tertutup
B. Operasi Asosiatif
Operasi
biner
*
pada
suatu
himpunan A
bersifat asosiatif jika
dan
hanya
jika
untuk setiap
a, b, c ? A
berlaku (a*b)*c = a*(b*c).
(?a, b, c ? A)
(a*b)*c = a*(b*c) Ö * asosiatif
C. Komutatif
Operasi biner * pada suatu
himpunan A bersifat komutatif
jika dan
hanya
jika
untuk setiap a,b
?
A berlaku sifat a*b = b*a.
(?a, b ? A)
a*b = b*a Ö
* komutatif
D. Memiliki Elemen Identitas (Unsur Kesatuan)
Unsur kesatuan atau elemen identitas adalah suatu elemen yang jika
dioperasikan
terhadap
sembarang elemen tunggal
dari sebuah
himpunan
akan
menghasilkan elemen itu sendiri.
Pada operasi
biner
*, suatu
elemen
e1
?
A
disebut
identitas
(unkes)
kiri
jika
untuk semua elemen a
?
A
berlaku e1
*a = a. Sedangkan suatu elemen
e2
?
A
disebut identitas (unkes) kanan jika untuk semua elemen a
?
A
berlaku a*e2
=
a.
Jika suatu elemen e
?
A
merupakan identitas kiri dan sekaligus identitas kanan,
maka e disebut elemen identitas. Dalam simbol matematika:
e1
?
A adalah identitas kiri
Ù
(?a ? A)
e2
?
A adalah identitas kanan
Ù
(
?
a
?
A)
e1*a = a
a*e2
= a
(?a ? A)
e*a = a*e = a Ö
*
memiliki elemen identitas
|
|
10
E. Memiliki Invers
Invers suatu elemen adalah elemen yang jika dioperasikan terhadap elemen
pertama akan menghasilkan elemen identitas.
Pada operasi biner *, suatu elemen e1
?
A
disebut invers kiri a jika untuk semua
elemen a
?
A
berlaku e1
*a = e. Sedangkan suatu elemen e
2
?
A
disebut
invers
kanan a jika untuk semua elemen a
?
A berlaku a* e
2
= e
Jika ada suatu anggota himpunan A yang merupakan invers kiri sekaligus invers
kanan
elemen
a,
maka anggota
tersebut
disebut
invers
a
(simbol
a
-1
). Dalam
simbol matematika:
a
-1
?
A adalah invers kiri
Ù
(?a ? A)
a
-1
?
A adalah invers kanan
Ù
(?a ? A)
a
-1
*a = e
a*a
-1
= e
(
?
a
?
A) a
-1
*a = a* a
-1
= e Ö
* memiliki invers dari a
2.1.4
Klasifikasi Struktur Aljabar Umum
Struktur
suatu
sistem aljabar dapat diklasifikasikan ke dalam beberapa
kategori berdasarkan sifat-sifat pada setiap operasi sebagai berikut.
A. Grupoid
Misalkan (A,*) adalah suatu struktur aljabar dan akan disebut grupoid jika
operasi * merupakan operasi biner (tertutup).
B. Semigrup
Misalkan (A,*) adalah
suatu
struktur aljabar.
(A,*) disebut semigrup jika
memenuhi kondisi-kondisi:
|
|
11
1. (A,*) merupakan operasi biner (tertutup)
2. (A,*) merupakan operasi asosiatif
C. Monoid
Misalkan
(A,*)
adalah
suatu
struktur
aljabar.
(A,*) disebut
monoid
jika
memenuhi kondisi-kondisi:
1. (A,*) merupakan semigrup
2. (A,*) memiliki elemen identitas
D. Grup
Misal
(A,*)
adalah
suatu
struktur
aljabar.
(A,*)
disebut
grup
bila
memenuhi
kondisi-kondisi:
1. (A,*) merupakan monoid
2. Setiap elemen dalam A memiliki invers
2.1.5
Bentuk-Bentuk Grup Khusus
Kategori-kategori seperti yang telah dijelaskan sebelumnya
merupakan
klasifikasi struktur aljabar secara umum. Kategori-kategori ini dapat dikelompokkan
lagi ke dalam kategori-kategori khusus berdasarkan sifat yang lebih spesifik.
Untuk
grup
sendiri
terdapat beberapa jenis grup khusus yang dapat dilihat
dengan
menganalisis
sifat-sifat
tambahan
pada
sistem aljabarnya.
Bentuk-bentuk
khusus ini adalah sebagai berikut.
|
 12
A. Grup Komutatif (Abelian)
Misalkan (A,*) adalah suatu grup G, maka G disebut grup komutatif atau
Abelian, jika
?a, b ? G berlaku ab = ba atau dapat dikatakan memenuhi kondisi-
kondisi:
1. (A,*) merupakan grup
2. (A,*) bersifat komutatif
Contoh:
Himpunan A = {0, 1, 2,3} dengan operasi penjumlahan modulo 4.
Tabel 2.2 Operasi Penjumlahan Modulo 4
+
4
0
1
2
3
0
0
1
2
3
1
1
2
3
0
2
2
3
0
1
3
3
0
1
2
Dengan
pembuktian
sifat akan
didapatkan
bahwa
(A, +
4
)
memenuhi sifat-sifat
grup abelian karena
matriks pada tabel Cayley merupakan
matrik yang simetris
terhadap diagonal utama.
B. Grup Siklik
Suatu grup G disebut siklik jika untuk sejumlah a
?
G
sedemikian hingga setiap
elemen x
?
G
dapat dinyatakan sebagai hasil operasi a
dengan dirinya sendiri
sebanyak n kali (n berhingga). Elemen a yang bersifat seperti itu disebut sebagai
|
 13
generator.
Jika
G
grup
siklik
dibangun
oleh a, maka
ditulis
G=(a),
elemen-
elemen tersebut dapat ditulis sebagai a
-²
,
a
-¹
,
a
0
=
e,
a
1
,
a
2
,...
Contoh:
Himpunan A = {0, 1, 2} dengan operasi penjumlahan modulo 3.
Tabel 2.3 Operasi Penjumlahan Modulo 3
+
3
0
1
2
0
0
1
2
1
1
2
0
2
2
0
1
Dengan pembuktian sifat akan didapatkan bahwa (A, +
3
)
memenuhi sifat-sifat
grup siklik, yakni:
1. (A, +
3
) bersifat biner (tertutup)
2. (A, +
3
) bersifat asosiatif
3. (A, +
3
) memiliki elemen identitas e = 0
4. Setiap elemen dalam A memiliki invers (0
-1
= 0, 1
-1
= 2, 2
-1
= 1)
Elemen 1 dan 2 pada himpunan A adalah generator untuk grup siklik.
0 = 1 +
3
1
+
3
1
n = 3
0 = 2 +
3
2
+
3
2
n = 3
1 = 1 +
3
1
+
3
1
+
3
1
n = 4
1 = 2 +
3
2
n = 2
2
= 1
+
3
1
n = 2
2 = 2
+
3
2
+
3
2
+
3
2
n = 4
|
|
14
C. Grup Periodik dan Aperiodik
Definisi C.1
(i)
Tingkat a = minimum
{a | a ? N a
, a
x
=
e}
jika himpunan
?
0
(ii)
Tingkat
a
=
0
(tak hingga) jika himpunan = 0
Tingkat suatu unsur dari suatu grup adalah
bilangan asli terkecil yang bila
dipangkatkan kepada unsur tersebut menghasilkan unsur kesatuan bila bilangan
itu ada seperti
dijelaskan pada pterhinggernyataan (i). Pernyataan (ii)
menunjukkan bila tidak ada satu bilangan asli pun yang dipangkatkan pada suatu
unsur a menghasilkan unsur kesatuan maka dikatakan tingkat a tak hingga.
Tingkat (atau ordo) dari a diberi notasi
t a).
(a).
Bila ada suatu bilangan asli
n
?
a
n
=
e,
dapat
dikatakan
tingkat
dari a
atau
tingkat a
terhingga.
Bila tidak
demikian maka dikatakan tingkat a tak hingga. (Kusno, 1988)
Definisi C.2 (Aperiodik, Periodik, Campuran)
Suatu grup G dinamakan periodik atau berkala jika tingkat setiap unsurnya
terhingga
dan
dinamakan aperiodik jika setiap
unsurnya selain
unsur
kesatuan
mempunyai tingkat tak
hingga. Akan dinamakan campuran jika sedikitnya
mempunyai satu
unsur
dengan
tingkat
tak
hingga dan satu
unsur
?
e
dengan
tingkat terhingga.
Akibat definisi di atas, terbentuk 2 pernyataan
(i)
Setiap grup terhingga adalah periodik
(ii)
Jika suatu grup aperiodik atau campuran maka grup tersebut tak hingga
Berhadapan dengan itu,
grup
tak
hingga tidak
mesti aperiodik. Bisa saja
aperiodik, bisa campuran,
dan bisa pula periodik. Jadi tak hingga
hanya
|
|
15
merupakan syarat perlu
agar
suatu grup aperiodik
atau
campuran. Istilah
aperiodik
tidak
berarti tidak
periodik,
bukan
ingkaran
dari
periodik.
Tidak
periodik
berarti bisa aperiodik
tetapi
bisa pula
campuran.
Sebaliknya,
tidak
aperiodik
tidak
mesti
periodik,
bisa
periodik
dan
bisa
pula campuran.
Oleh
karenanya istilah aperiodik tidak dapat diganti dengan tak berkala. (Kusno, 1988)
Contoh:
Pandangan grup
(R,+
S
)
yaitu grup dari semua bilangan nyata terhadap
penambahan sehari-hari. Unsur kesatuannya 0 dan notasi operasinya +.
Disini
notasi
a
n
artinya:
a
+
a
+
a.... + a
sebanyak
n-suku.
Jelas
bahwa
?x ? R dengan
X
?
0, t ( x) = 0, sedangkan
t
(0)
=
1
karena 0 unsur kesatuannya.
D. Subgrup Normal
Definisi D.1 (Koset)
Di dalam suatu
grup G
terdapat subgrup H
untuk a, b ? G , dikatakan bahwa a
kongruen
dengan
b
modulo
H
dan
ditulis
a
=
b
mod
H,
bila
dan
hanya
bila
ab
-¹
?
H. Relasi
a
=
b
mod H adalah suatu relasi ekuivalen pada G. Kelas
ekuivalen yang
memuat a dapat ditulis sebagai bentuk
Ha = {ah, h ? H} disebut
koset kanan terhadap subgrup H. Sedangkan
Ha = {ah, h ? H} disebut koset kiri
terhadap subgrup H. Unsur a disebut generator dari koset tersebut. Dengan
demikian, di dalam
grup
G
untuk setiap subgrup H dari G terdapat
himpunan
koset kanan
K
=
{Ha | a ? G} dan himpunan koset kiri
L
=
{aH | a ? G}.
Catatan
:
(i)
Banyak koset
kanan dan koset kiri di
grup G terhadap
suatu
subgrup H selalu
sama dinamakan indeks subgrup H di G yang
dinotasikan dengan [G:H]
|
|
16
(ii) Himpunan koset kanan (kiri) membentuk partisi di G, yaitu
untuk
setiap
a, b ? G berlaku Ha = Hb atau
Ha n Hb = Ø untuk
U
Ha = G.
a?G
Definisi D.2 (Subgrup)
Himpunan bagian dari suatu grup yang
merupakan grup terhadap operasi yang
sama, yaitu operasi yang ada dalam grup tersebut dinamakan subgrup. Berikut
adalah beberapa teorema mengenai subgrup.
Teorema D.1
:
Misalkan G adalah sebuah
grup dan S suatu
himpunan bagian
dari
G. S
dinamakan
suatu
subgrup
dari
G
jika S
merupakan
suatu grup terhadap operasi yang ada dalam G.
Teorema D.2
:
G
sebuah
grup dan S suatu
himpunan bagian dari
G
yang tak
kosong,
maka
S
merupakan
suatu
grup dari
G
jika dan
hanya
jika (i)
x
dan
y
?
S
(ii)
x
?
S
?
x ¹
-¹
?
S
Teorema D.3
:
G
suatu
grup dan
S
?
G
dengan
S
?
0. S suatu subgrup dari G
jika dan hanya jika ?x, y ? S berlaku xy
-1
?
S.
Dari ketiga teorema di atas, jika S adalah subgrup dari G maka dapat dinotasikan
H
=
G. Jika
H
adalah
proper
subgrup
dari
G,
yaitu
H
?
G,
maka
dituliskan
H
<
G.
Definisi D.3 (Subgrup Normal)
Misalkan
H
adalah suatu
subgrup
dari
grup
G,
subgrup
H
dikatakan subgrup
normal dari G bila
gH
=
Hg untuk
semua g ? G
maka dapat dibuktikan bahwa
|
 17
setiap koset
kiri
dari
H
dalam G
sama
dengan
koset
kanan
dari H dalam
G.
Berikut adalah teorema yang berlaku pada subgrup normal.
(i)
Subgrup H adalah normal di grup G
(ii)
Untuk semua
g
?
G, g 1
-1
Hg ? H
(iii) Untuk semua
g
?
G, g ¹
-¹
Hg = H
Contoh:
Misalkan
G
=
{1
,2,3,4,5,6
}
adalah suatu grup dan
H
=
{1
,6
}
adalah merupakan
subgrup dari G dengan operasi ×
7
.
Berikut tabel Cayley dari kedua himpunan.
Tabel 2.4 Operasi Perkalian Modulo 7
×
7
1
2
3
4
5
6
1
1
2
3
4
5
6
2
2
4
6
1
3
5
3
3
6
2
5
1
4
4
4
1
5
2
6
3
5
5
3
1
6
4
2
6
6
5
4
3
2
1
Tabel 2.5 Operasi Penjumlahan Modulo 7
×
7
1
2
1
1
2
2
2
1
|
|
18
7
7
7
7
7
7
7
7
7
Invers dari G
1
-1
=
1
2
-¹
=
4
3
-¹
= 5
4
-¹
=
2
5
-¹
= ³
6
-¹
=
6
Terbukti bahwa H subgrup dari
G atau dapat dinotasikan dengan
H
<
G.
Pembuktian selanjutnya:
1
×
7
H
×
7
1
-1
=
1
×
-¹
1
×
7
H
=
H
2
×
7
H
×
7
2
3
×
H
× ³
-¹
4
×
H
× 4
-1
5
×
H
×
5 ¹
-¹
6
×
H
× 6
-1
=
2
×
7
4
×
7
H
=
H
=
3
×
7
5
×
7
H
=
H
=
4
×
7
2
×
7
H
=
H
=
5
×
7
3
×
7
H
=
H
=
6
×
7
6
×
7
H
=
H
Terbukti bahwa H subgrup normal dari G sesuai dengan teorema di atas.
Dinotasikan dengan H < G.
E.
Grup Faktor (Grup Kuosien)
Definisi E.1 (Lagrange)
Bila G adalah suatu grup terhingga dan H subgrup dari G, maka
G
/
H
=
[
G
:
H
]
yaitu order dari subgrup H membagi order dari G.
Bukti:
Misalkan
n
adalah
order
dari G
dan k
adalah order dari
H. Maka setiap
koset
kanan dari H dalam G mempunyai order sebanyak k juga. Misal r adalah banyak
koset
kanan
yang
berlainan
dari
H
dalam
G.
Koset
kanan
dari
H
dalam G
membentuk partisi dari G, sehingga G dapat ditulis sebagai gabungan dari koset-
koset yang lepas (disjoint) yaitu
G
=
a
1
H
?
a
2
H
?
a
3
H
?
...
?
a
r
H
.
|
|
19
Oleh
karena
koset
kanan
merupakan
partisi
dari
G
maka
G
=| a
1
H
|
+
|
a
2
H
|
+...+ a
| a
r
H
|
=
H
+
H
+
... +
H
=
k
+
k
+
... + k
=
kr
Diperoleh n = kr sehingga k membagi n.
Definisi E.2 (Grup Faktor)
Misalkan N adalah subgrup
normal dari
grup
G, maka himpunan semua koset
kanan
dari
N
dalam
G (dinotasikan
dengan G / N ) terhadap
operasi
perkalian
himpunan
merupakan
suatu
grup
dan
G
/
N
disebut
grup
faktor.
G N = {aN | a ? G},
/ N = {aN | a ? G},
didefinisikan operasi pada
G N
/ N
,
aN.bN = ab
dengan
unsur aN disebut koset-koset dari N. (Fraleigh, 1997)
Teorema :
Himpunan
G
/
N
adalah
grup
dan
disebut
grup
faktor di bawah
operasi perkalian.
Operasi perkaliannya didefinisikan a.bN = ab.N
Bukti :
-
Menurut definisi operasi, pada
G
/
N
tertutup di bawah operasi perkalian
asosiatif (aN.bN ).cN = (ab)N.cN
=
((ab)c)N
=
aN ((bc)N ) = aN (bN.cN ).
-
Unsur
identitas
adalah
koset
N
sebab
aN.N
=
aNeN = (ae) N = aN
dan
N
=
aN = eN.N
=
(ea)N
=
aN.
-
Invers dari aN adalah
a ¹
-¹
N
sebab aN a 1
.a 1
-1
N
=
(aa
-1
)
N
=
eN = N
Terbukti bahwa G / N adalah grup.
|
 20
7
Contoh:
Misalkan
G
=
{1,2,3,4,5,6}
adalah suatu grup dan
H
= 1,6
{1,6
}
adalah merupakan
subgrup dari
G, dengan operasi
×
7
.
(Contoh soal
ini sama
seperti
contoh
soal
pada subgrup normal. Digunakan tabel Cayley yang sama)
Koset kiri = koset kanan
1×
7
H
×
7
=
1×
7
{1,6} = {1,6}
2
×
7
H
×
7
=
2
×
7
{1,6} = {2,5}
3
×
7
H
×
7
=
3
×
7
{1,6} = {3,4}
G
=
(1×
7
H
)
?
(2 ×
7
H
)
?
(3×
7
H
)
Sehingga tampak seperti tabel berikut.
Tabel 2.6 Operasi Perkalian
*
1
×
7
H
2
×
7
H
3
×
7
H
1
×
7
H
1
×
7
H
2
×
7
H
3
×
7
H
2
×
7
H
2
×
7
H
3
×
7
H
1
×
7
H
3
×
7
H
3
×
7
H
1
×
7
H
2
×
7
H
(2 ×
7
H
)
*
(2 ×
7
H
)
=
4
×
7
H
×
7
H
=
4
×
7
{1,6}×
7
{1,6}
=
4
×
7
{1, 6 , 6 ,1}
=
4
×
7
{1, 6}
=
{
4
,3}
=
3
×
7
{1, 6}
=
3
×
7
H
(
2
×
7
H ) * (3
×
7
H )
=
6
×
7
H
×
7
H
(3
×
7
H
)
*
(3
×
7
H
)
=
2
×
7
H
×
7
H
=
6
×
7
{1,6}
=
{6,1}
=
H
=
2
×
7
{1,6}
=
2
×
7
H
Maka
terbentuk
grup
factor atau kuosien dengan yang bersifat tertutup, asosiatif, memiliki unkes
1
×
7
H, dan memiliki invers
(1×
7
H
) ¹
-¹
-1
=
1×
7
H
(2 ×
7
H
)
(3
×
H
) ¹
-¹
=
³
×
7
H
=
²
×
7
H
|
|
21
+
+
F.
Homomorfisma Grup
Homomorfisma
grup
merupakan
suatu
pemetaan
pada
grup
yang
memenuhi
sifat-sifat tertentu. Berikut akan dibahas homomorfisma
grup beserta sifat-
sifatnya.
Definisi F.1 (Homomorfisma)
Diketahui
(G,*)
dan
(G',
•
)
merupakan
grup. Pemetaan
?
:
G
?
G'
disebut
homomorfisma
jika
dan
hanya
jika
untuk
setiap
a, b
?
G
berlaku
?
(a * b)
=
?
(a)
•
?
(b).
Definisi F.2
-
Suatu homomorfisma yang injektif disebut monomorfisma
-
Suatu homomorfisma yang surjektif disebut epimorfisma
-
Suatu homomorfisma yang bijektif disebut isomorfisma
Definisi F.3
Suatu
homorfisma
dari
suatu
grup
ke
dalam dirinya
sendiri
dinamakan
suatu
endomorfisma dan suatu endomorfisma yang dibjektif dinamakan automorfisma.
Contoh:
Ambil grup
G
1
=
(
R
,
x
s
)
yaitu grup multiplikatif dari himpunan semua bilangan
nyata positif dan grup
G
2
=
(
R
,
x
s
)
yaitu grup aditif dari himpunan semua
bilangan nyata.
Bangun
pemetaan
?
:
G
1
?
G
2
sebagai
berikut:
?
(
x)
=
log x
maka
?x, y ? G
1
=
®
+
akan
berlaku
?
(
xy)
=
log( xy)
=
log x
+
log y
=
?
(
x)
+
?
(
y).
Ini
berarti
bahwa
?
suatu
homomorfisma;
selanjutnya
?
injektif
dan
surjektif,
|
|
22
sebab
? x)
( x)
=
? y)
( y)
?
log x
=
log y
?
x
=
y;
selain
itu
?
x'
?
G
2
?
x
?
G
1
sedemikian
hingga
? x)
( x)
=
x'
yaitu bila diambil
x
=
10
x
.
Jadi
?
suatu isomorfisma.
Lemma F.1
Diketahui G, G’ grup dan
?
:
G
?
G'
merupakan homomorfisma grup, maka
keempat sifat berikut berlaku:
(i)
Jika
e merupakan
elemen
identitas
di
G,
maka ? e)
(e)
merupkan
elemen
identitas e' di G’.
(ii)
Jika a ? G maka ?(a
-¹
)
=
?(a) ¹
-¹
(iii)
Jika H merupakan subgrup pada G, maka
?
(
H
)
merupakan subgrup pada
G’.
(iv)
Jika K’ merupakan subgrup pada G’,
maka ?
-¹
(K ' ) merupakan subgrup
pada G.
Definisi F.4 (Kernel)
Diketahui
G,
G’
grup
dan
?
:
G
?
G'
homomorfisma
grup.
Himpunan
{a
?
G
|
?
(a)
=
e'}
dinamakan kernel
?
dari dan dinotasikan ker
(?
).
Lemma F.2
Diketahui G, G’ grup dan
?
:
G
?
G'
merupakan homomorfisma grup. Pemetaan
?
merupakan pemetaan injektif jika dan hanya jika ker ? =
(
) =
{e}.
Bukti ( ? )
Menurut
Lemma
G.1
(i)
berakitab
?
(e)
=
e'
dan
karena
?
merupakan pemetaan
injektif
maka
hanya elemen e di G yang
dipetakan ke elemen e’ di G’. Jadi ker
(?
)
=
{e}.
|
|
23
(
?
)
Diandaikan
pemetaan
?
bukan
pemetaan
injektif,
yaitu terdapat
a, b
?
G
dengan
a
?
b
dan
?
(a)
=
?
(b).
Karena
?
(a)
=
?
(b)
maka
?(a)?(b) 1
-1
=
e
-¹
.
Menurut
Lemma
G.1
(ii)
diperoleh
?(a)?(b) 1
-1
=
?(a)?(b
-¹
)
=
?(ab
-1
)
= e'.
Karena
diketahui
ker
(
?
)
=
{e}
akibatnya
ab
-¹
=
e
dan
dengan kata
lain
a = b.
Muncul kontradiksi dengan pengandaian bahwa
a ? b.
Jadi,
pengandaian diingkar dan terbukti
?
merupakan pemetaan injektif.
Definisi F.5 (Monomorfisma)
Diketahui G, G’ grup dan ?
:
G
?
G
'
merupakan homomorfisma grup. Pemetaan
?
disebut monomorfisma
grup jika dan hanya jika
?
suatu pemetaan
satu-satu
dari G ke G’. Dengan kata lain, jika
? x)
( x)
=
?
(y)
maka
x
=
y
untuk
x, y
?
G.
Definisi F.6 (Epimorfisma)
Diketahui G, G’ grup dan ?
:
G
?
G'
merupakan homomorfisma grup. Pemetaan
?
disebut epimorfisma grup apabila setiap
g
?
G'
ada
g
?
G
sehingga ?
(
g
)
=
g
'.
Dengan kata lain, setiap elemen G’
mempunyai
kawan
elemen G.
Dapat pula
dikatakan bahwa homomorfisma ? dari G onto G atau disingkat homomorfisma
?
onto.
Definisi F.7 (Isomorfisma)
Diketahui G, G’ grup dan
?
:
G
?
G'
merupakan homomorfisma grup. Pemetaan
?
disebut isomorfisma g®up jika dan hanya jika ?
merupakan pemetaan injektif
(satu-satu). Grup G dan G’ dikatakan isomorphic jika ada isomorfisma ? dari G
|
|
24
ke G’ dan dinotasikan dengan
G
?
G'.
Langkah-langkah untuk menunjukkan
grup G dan G’ isomorphic adalah:
1. Definisikan fungsi ? dari G ke G’.
2. Tunjukkan bahwa ? fungsi satu-satu dan pada.
3. Tunjukkan bahwa ? homomorfisma.
Sedangkan untuk
menunjukkan dua grup G dan G’ tidak isomorphic, pada
prinsipnya adalah
menunjukkan bahwa tidak ada homomorfisma
yang bersifat
satu-satu
dan
pada
dari G
ke
G’.
Namun
tidak
mungkin
dicoba
setiap
kemungkinan yang ada,
kecuali
jika
pemetaan
satu-satu
memang
tidak
dapat
dibuat. Cara praktis untuk
menunjukkan dua grup G dan G’ tidak isomorphic
adalah dengan mendapatkan sifat aljabar yang tidak dipenuhi kedua grup.
2.2 Interaksi Manusia dan Komputer
Definisi
dari
interaksi manusia
dan
komputer
adalah disiplin ilmu yang
menekankan
pada
aspek
desain,
evaluasi,
dan
implementasi
dari
sistem komputer
interaktif
untuk
kegunaan
manusia dengan
mempertimbangkan
fenomena-fenomena
disekitar manusia itu sendiri. Dalam interaksi manusia dan komputer itu sendiri interface
berperan penting sebagai penghubung antara kedua sistem. Oleh karena
itu dibutuhkan
user
interface
untuk
memudahkan
pengguna
mengetahui apa yang terjadi pada sistem
yang digunakannya.
Beberapa aspek utama dalam perancangan sebuah interface adalah :
1. Metodologi dan proses perancangan interface
2. Metode implementasi interface
|
|
25
3. Metode evaluasi dan perbandingan interface.
4. Pengembangan new interface.
5.
Mengembangkan
sebuah
deskripsi
dan
prediksi
atau
teori
dari sebuah
new
interface.
Berikut adalah 8 aturan emas dalam merancang desain interface yang dikemukakan oleh
Shneiderman, seorang profesor dalam bidang Interaksi Manusia dan Komputer:
1. Konsistensi
2. Memungkinkan pengguna (yang sudah ahli) untuk menggunakan shortcut.
3. Memberikan
umpan balik
yang
informatif.
Misalnya
muncul
suatu notification
ketika terjadi kesalahan saat melakukan masukan.
4. Merancang dialog untuk menghasilkan suatu penutupan yaitu berupa umpan
balik yang informatif akan meberikan indikasi bahwa cara yang dilakukan sudah
benar dan dapat mempersiapkan kelompok tindakan berikutnya.
5. Memberikan penanganan kesalahan yang sederhana jika terjadi kesalahan, sistem
dapat
mendeteksi
kesalahan
dengan
cepat
dan
memberikan
mekanisme yang
sedehana dan mudah dipahami untuk penanganan kesalahan.
6. Mudah kembali ke tindakan sebelumnya.
7.
Mendukung tempat pengendali internal (internal
locus
of
control) sehingga
pengguna menjadi inisiator daripada responden.
8. Mengurangi beban ingatan jangka pendek.
2.3 Bahasa Pemrograman Java
2.3.1
Latar Belakang Java
Java adalah
sebuah teknologi
yang
diperkenalkan
oleh Sun
Microsystems
pada pertengahan
tahun 1990an.
Awalnya
Java diciptakan
pada
tahun
1995
oleh
|
|
26
Patrick Naughton, Mike Sheridan, James Gosling, dan Bill Joy beserta programmer
dari
Sun
Microsystems.
Nama
Java terinspirasi ketika
mereka
sedang
menikmati
secangkir
kopi
tubruk
yang
berasal
dari Pulau
Jawa.
Akhirnya disepakati
untuk
memberikan nama bahasa pemrograman tersebut dengan nama Java. Menurut
definisi dari Sun Microsystems, Java adalah nama untuk sekumpulan teknologi
untuk
membuat dan
menjalankan
perangkat
lunak
pada
komputer standalone atau
pun pada lingkungan jaringan.
2.3.2 Teknologi Java
Kebanyakan orang
menyebut Java sebagai
sebuah teknologi dibandingkan
bahasa
pemrograman
karena Java
lebih
lengkap
dibandingkan
sebuah
bahasa
pemrograman konvensional. Berikut ulasan lengkap mengenai teknologi Java.
•
Sebuah Bahasa Pemrograman
Sebagai
sebuah
bahasa
pemrograman, Java
dapat
membuat
seluruh
bentuk
aplikasi, desktop, website, dan lainnya sebagaimana dibuat dengan menggunakan
bahasa pemrograman konvensional lain.
Java
adalah
bahasa pemrograman
yang
berorientasi
objek
(OOP)
dan
dapat
dijalankan
pada
berbagai
platform
sistem operasi.
Perkembangan
Java
tidak
hanya
terfokus
pada
satu
sistem operasi, tetapi
dikembangkan
untuk berbagai
sistem operasi dan bersifat open source.
•
Sebuah Development Environment
Sebagai sebuah
peralatan
pembangunan,
teknologi Java
menyediakan
banyak
tools
seperti
compiler,
interpreter,
penyusun dokumentasi,
paket
kelas,
dan
sebagainya.
|
|
27
•
Sebuah Aplikasi
Aplikasi dengan teknologi Java secara umum adalah aplikasi serba
guna yang
dapat dijalankan pada seluruh mesin
yang memiliki Java Runtime Environment
(JRE)
•
Sebuah Deployment Environment
Terdapat
dua
komponen
utama
dari Deployment
Environment.
Yang
pertama
adalah JRE, yang terdapat pada paket Java Development Kit (JDK), mengandung
kelas-kelas
untuk semua
paket
teknologi Java
yang
meliputi
kelas dasar dari
Java,
komponen
GUI,
dan
sebagainya. Komponen yang lain terdapat pada
Website
Browser.
Hampir
seluruh Website
Browser
komersial
menyediakan
interpreter dan runtime environment dari teknologi Java.
2.3.3
Karakteristik Java
Berdasarkan white paper resmi dari Sun Microsystems, Java
memiliki
karakteristik sebagai berikut.
1. Sederhana karena menggunakan sintaks mirip C++
2. Berorientasi objek yang membuat program
dapat dibuat secara modular dan
dapat dipergunakan kembali.
3. Java dibuat sehingga aplikasi terdistribusi secara mudah dengan adanya libraries
networking yang terintegrasi.
4.
Java
dijalankan
menggunakan
interpreter yaitu
Java
Virtual
Machine
(JVM)
sehingga source code Java yang telah dikompilasi menjadi Java bytecodes yang
dapat dijalankan pada platform yang berbeda-beda.
|
|
28
5. Compiler Java mempunyai kemampuan mendeteksi error secara lebih teliti
dibandingkan pemrograman lain. Selain itu, Java mempunyai Runtime Exception
Handling untuk membantu mengatasi error pada pemrograman.
6.
Java
memiliki
beberapa
mekanisme
keamanan
untuk
menjaga
aplikasi tidak
digunakan untuk merusak sistem komputer yang menjalankan aplikasi tersebut.
7. Program Java merupakan platform independent. Program cukup mempunyai satu
buah
versi
yang
dapat
dijalankan pada platform berbeda
dengan
Java Virtual
Machine (JVM).
8. Source code
maupun
program
Java
dapat
dengan
mudah dibawa
ke
platform
yang berbeda-beda tanpa harus dikompilasi ulang.
9. Performance
Java
meskipun
kurang
tinggi
namun
dapat
ditingkatkan
menggunakan kompilasi Java lain
seperti buatan Inprise, Microsoft, atau
Symantec yang menggunakan Just In Time Compilers (JIT).
10. Java
mempunyai
kemampuan
untuk
membuat suatu
program
yang
dapat
melakukan beberapa pekerjaan secara sekaligus dan simultan.
11. Java
didesain
sehingga
dapat
dijalankan
pada
lingkungan
yang
dinamis.
Perubahan pada suatu kelas dengan menambahkan properties ataupun metode dapat
dilakukan tanpa menganggu program yang menggunakan kelas tersebut.
|
 29
2.3.4
Fase Pemrograman Java
Gambar 2.1 Aliran Proses Kompilasi dan Eksekusi
Langkah pertama dalam pembuatan sebuah program berbasis Java adalah
menuliskan kode program pada text editor. Contoh text editor yang dapat digunakan
antara
lain:
notepad,
vi,
emacs
dan
lain sebagainya.
Kode
program yang
dibuat
kemudian tersimpan dalam sebuah berkas berekstensi .java.
Setelah
membuat
dan
menyimpan
kode
program,
kompilasi
file yang
berisi
kode
program tersebut
dengan
menggunakan
Java
Compiler.
Hasilnya
adalah
berupa
berkas bytecode dengan ekstensi
.class.
Berkas yang mengandung bytecode tersebut kemudian akan dikonversikan oleh Java
Interpreter menjadi bahasa mesin sesuai dengan jenis dan platform yang digunakan.
Table 2.7 Fase Pemrograman Java
Proses
Tool
Hasil
Menulis
kode
program
Text Editor
Berkas
berekstensi .Java
Kompilasi Program
Java compiler
Berkas
berekstensi
.class
(Java bytecodes)
Menjalankan
program
Java Interpreter
Program output
|
 30
2.4 Rekayasa Piranti Lunak
Rekayasa Piranti Lunak (RPL) adalah suatu disiplin ilmu yang membahas semua
aspek
produksi
perangkat
lunak,
mulai dari
tahap awal
yaitu
analisa
kebutuhan
pengguna, menentukan spesifikasi dari kebutuhan pengguna, disain, pengkodean,
pengujian sampai pemeliharaan sistem setelah digunakan. RPL tidak hanya berhubungan
dengan
cara
pembuatan
program komputer.
Pernyataan
”semua aspek
produksi”
pada
pengertian di atas, mempunyai arti semua hal yang berhubungan dengan proses produksi
seperti manajemen proyek, penentuan personil, anggaran biaya, metode, jadwal, kualitas
sampai dengan pelatihan pengguna merupakan bagian dari RPL.
2.4.1
Ruang Lingkup
Sesuai dengan definisi yang telah disampaikan sebelumnya, maka ruang
lingkup RPL dapat digambarkan sebagai berikut.
Gambar 2.2 Ruang Lingkup RPL (Abran et.al., 2004)
-
Software
Requirements
berhubungan
dengan
spesifikasi
kebutuhan
dan
persyaratan perangkat lunak
-
Software Design mencakup proses penampilan arsitektur, komponen, antar muka,
dan karakteristik lain dari perangkat lunak
|
|
31
-
Software Construction berhubungan dengan detil pengembangan perangkat lunak,
termasuk algoritma, pengkodean, pengujian dan pencarian kesalahan
-
Software Testing meliputi pengujian pada keseluruhan perilaku perangkat lunak
-
Software Maintenance mencakup upaya-upaya perawatan ketika perangkat lunak
telah dioperasikan
-
Software Configuration Management berhubungan dengan
usaha perubahan
konfigurasi perangkat lunak untuk memenuhi kebutuhan tertentu
-
Software
Engineering
Management
berkaitan
dengan
pengelolaan
dan
pengukuran RPL, termasuk perencanaan proyek perangkat lunak
-
Software Engineering Tools and Methods mencakup kajian
teoritis tentang alat
bantu dan metode RPL
-
Software
Engineering
Process
berhubungan
dengan definisi,
implementasi
pengukuran, pengelolaan, perubahan dan perbaikan proses RPL
-
Software Quality menitik beratkan pada kualitas dan daur hidup perangkat lunak
2.4.2
Metode Rekayasa Perangkat Lunak
Pada rekayasa perangkat lunak, banyak model yang telah dikembangkan
untuk
membantu proses pengembangan perangkat
lunak.
Model-model ini pada
umumnya
mengacu pada
model proses pengembangan
sistem
yang disebut System
Development Life Cycle (SDLC) seperti terlihat pada gambar berikut ini.
|
 32
Gambar 2.3 System Development Life Cycle (SDLC)
SDLC merupakan serangkaian kegiatan yang dilakukan selama masa pengembangan
software.
Pemakaian
metode SDLC
yang
cocok
ditentukan
oleh
beberapa
aspek
seperti jenis bahasa pemrograman yang digunakan atau kompleksitas aplikasi.
Berikut adalah beberapa hal
yang perlu diperhatikan selama proses pengembangan
sistem.
•
Kebutuhan terhadap definisi
masalah yang
jelas.
Input
utama dari setiap
model
pengembangan
perangkat
lunak
adalah
pendefinisian
masalah
yang
jelas.
Semakin jelas akan semakin baik karena akan memudahkan dalam penyelesaian
masalah.
•
Tahapan-tahapan pengembangan
yang teratur. Meskipun
model-model
pengembangan
perangkat
lunak
memiliki
pola yang
berbeda-beda, biasanya
model-model
tersebut
mengikuti
pola
umum
analysist
–
design
–
coding
–
testing - maintenance
•
Stakeholder berperan sangat penting dalam keseluruhan tahapan pengembangan.
Stakeholder
dalam
rekayasa perangkat
lunak
dapat
berupa
pengguna, pemilik,
|
|
33
pengembang, pemrogram dan orang-orang yang terlibat dalam rekayasa
perangkat lunak tersebut.
•
Dokumentasi
merupakan
bagian
penting
dari
pengembangan perangkat
lunak.
Masing-masing
tahapan dalam
model
biasanya menghasilkan
sejumlah tulisan,
diagram,
gambar atau bentuk-bentuk lain yang harus didokumentasi dan
merupakan bagian tak terpisahkan dari perangkat lunak yang dihasilkan.
2.4.3
Tahapan Rekayasa Perangkat Lunak
Meskipun dalam pendekatan berbeda-beda, namun
model-model pendekatan
memiliki
kesamaan,
yaitu
menggunakan
pola tahapan
analysist
–
design
–
coding(construction) – testing – maintenance.
1.
Analisis
sistem adalah
sebuah
teknik
pemecahan
masalah
yang
menguraikan
sebuah sistem menjadi komponen-komponennya dengan tujuan
mempelajari
seberapa bagus dan baik komponen-komponen tersebut bekerja dan berinteraksi
untuk meraih tujuan.
Analisis mungkin adalah bagian terpenting dari proses rekayasa perangkat lunak
karena semua proses lanjutan akan sangat bergantung pada baik atat
tidaknya
hasil analisis.
2. Disain
perangkat
lunak adalah tugas,
tahapan atau
aktivitas
yang
difokuskan
pada spesifikasi detil dari solusi berbasis komputer.
Disain perangkat lunak sering juga disebut sebagai physical design. Jika tahapan
analisis sistem menekankan pada masalah bisnis (business rule), maka
sebaliknya disain perangkat lunak fokus pada sisi teknis dan implementasi
sebuah perangkat lunak.
|
|
34
Output utama dari tahapan disain perangkat lunak
adalah spesifikasi disain.
Spesifikasi
ini
meliputi spesifikasi disain
umum yang akan disampaikan kepada
stakeholder sistem dan spesifikasi disain rinci yang akan digunakan pada
tahap
implementasi.
Spesifikasi
disain
umum hanya
berisi
gambaran
umum agar
stakeholder sistem mengerti
akan
seperti apa perangkat lunak yang akan
dibangun. Spesifikasi disain
rinci
atau
kadang
disebut disain
arsitektur
rinci
perangkat lunak diperlukan untuk merancang sistem sehingga memiliki
konstruksi yang baik, proses pengolahan data yang tepat dan akurat, bernilai,
memiliki aspek user friendly dan memiliki dasar-dasar untuk pengembangan
selanjutnya.
Desain
arsitektur
ini
terdiri
dari
desain
database,
desain
proses,
desain user
interface
yang mencakup desain
input, output form dan report, desain
hardware, software
dan jaringan.
Desain proses
merupakan
kelanjutan dari
pemodelan proses yang dilakukan pada tahapan analisis.
3. Konstruksi adalah tahapan menerjemahkan hasil disain logis dan fisik ke dalam
kode-kode program komputer.
4. Pengujian
sistem
melibatkan
semua
kelompok
pengguna
yang
telah
direncanakan pada tahap sebelumnya. Pengujian tingkat
penerimaan
terhadap
perangkat lunak akan berakhir ketika dirasa semua kelompok pengguna
menyatakan bisa menerima perangkat lunak tersebut berdasarkan kriteria-kriteria
yang telah ditetapkan.
5. Perawatan dan Konfigurasi. Ketika sebuah perangkat lunak telah dianggap layak
untuk dijalankan, maka tahapan baru menjadi muncul yaitu perawatan perangkat
lunak.
|