|
BAB 2
LANDASAN TEORI
2.1
Teknik Simulasi
Teknik Simulasi merupakan cara meniru suatu sistem nyata yang kompleks
dalam bentuk
model
untuk
dipelajari,
diuji,
dan
sebagainya. Banyak
ahli
memberikan
definisi mengenai simulasi seperti :
a. Shannon (1975)
Simulasi merupakan proses perancangan model dari sistem nyata yang
dilanjutkan dengan pelaksanaan eksperimen terhadap model untuk mempelajari
perilaku
sistem atau
evaluasi
strategi
(dalam batas-batas
yang
ditentukan
oleh
suatu kriteria atau serangkaian kriteria untuk operasi sistem).
b. Banks dan Carson (1984)
Simulasi
adalah
tiruan
dari
sistem nyata
yang
dikerjakan
secara
manual
atau
komputer yang kemudian diobservasi dan disimpulkan untuk
mempelajari
karakteristik sistem.
c. Hoover dan Perry (1990)
Simulasi merupakan proses perancangan model matematis atau logis dari sistem
nyata,
melakukan eksperimen
terhadap model
dengan
menggunakan
komputer
untuk menggambarkan, menjelaskan, dan memprediksi perilaku sistem.
d. Law dan Kelton (2000)
Simulasi yang dapat disebut juga pengimitasian adalah meniru atau
menggambarkan operasi-operasi yang terjadi pada berbagai macam fasilitas atau
|
 8
proses
yang
terjadi
pada
kehidupan
nyata dengan
menggunakan bantuan
komputer.
e. Harrel, dkk (2003)
Simulasi merupakan tiruan dari sistem dinamik
menggunakan model komputer
dalam mengevaluasi dan meningkatkan kinerja sistem.
Dari beberapa definisi di atas dapat disimpulkan bahwa simulasi adalah
teknik
meniru suatu sistem yang nyata/sesungguhnya dengan menggunakan bantuan perangkat
komputer sehingga sistem tersebut bisa dipelajari secara ilmiah dan diharapkan dapat
mengevaluasi dan meningkatkan kinerja sistem.
2.2
Kubus Rubik
Kubus rubik adalah permainan kubus 3x3x3 yang memiliki warna yang berbeda
pada keenam sisinya. Keenam sisi kubus akan dinamakan sebagai berikut : up (U), down
(D), front (F), back (B), left (L), dan right (R). Kubus ini
terdiri dari dua puluh enam
kubus kecil yang disatukan. Satu kubus kecil ditengah tidak dianggap karena berperan
sebagai sumbu kubus saat memutar sisi-sisinya.
Gambar 2.1 Ilustrasi Kubus Rubik
|
|
9
Kubus rubik diciptakan oleh seorang professor arsitektur asal negara Hungaria
yang bernama Erno Rubik pada tahun 1974. Di Jerman, pada tahun 1980 kubus rubik
mendapat
penghargaan
sebagai Games
of
The
Year
,
pada
tahun
1982
kubus
rubik
menjadi
kata tersendiri
yang
masuk
dalam
kamus The
Oxf
hingga
pada
tahun
2007
kubus rubik dinobatkan sebagai The Coolest Brand in The World (True Stories, 2011).
Sampai detik ini diperkirakan telah lebih dari 100.000.000 Kubus Rubik terjual di
seluruh dunia. Permainan
ini diklaim dapat
meningkatkan ketajaman kecerdasan visual
spasial
(kemampuan
visual
yang
diikuti
dengan kemampuan
persepsi
pandang
ruang
atau dimensi, kelebihan hal berpikir melalui gambar) dan daya nalar (proses yang cermat
dan
menyeluruh
dalam mempertimbangkan
segala segi
guna
menyelesaikan
masalah),
sehingga tak heran banyak orang tertarik memainkannya.
2.3
Algoritma
Ditinjau dari asal-usul katanya, kata Algoritma sendiri
mempunyai sejarah
yang
aneh. Orang
hanya
menemukan kata algorism
yang berarti proses
menghitung dengan
angka arab. Anda dikatakan algorist
jika Anda menghitung
menggunakan angka arab.
Para ahli bahasa berusaha menemukan asal kata ini namun hasilnya kurang memuaskan.
Akhirnya para ahli sejarah matematika menemukan asal kata tersebut yang berasal dari
nama penulis buku arab yang terkenal yaitu Abu Ja’far Muhammad Ibnu Musa Al-
Khuwarizmi.
Al-Khuwarizmi
dibaca
orang
barat
menjadi Algorism.
Al-Khuwarizmi
menulis buku yang berjudul Kitab Al Jabar Wal -
Muqabala yang artinya “Buku
pemugaran dan pengurangan” (The book of restoration and reduction). Dari judul buku
itu kita
juga memperoleh akar kata “Aljabar” (Algebra). Perubahan kata dari algorism
menjadi algorithm muncul karena kata algorism sering dikelirukan dengan arithmetic,
|
|
10
sehingga akhiran –sm berubah
menjadi –thm. Karena perhitungan dengan angka Arab
sudah menjadi hal yang biasa, maka lambat laun kata algorithm berangsur-angsur
dipakai
sebagai
metode
perhitungan
(komputasi) secara
umum, sehingga kehilangan
makna kata aslinya. Dalam bahasa Indonesia, kata algorithm diserap menjadi algoritma
(Alex Budiyanto, 2003).
Algoritma adalah urutan langkah-langkah logis penyelesaian masalah yang
disusun secara sistematis. Kata logis
merupakan kata kunci dalam algoritma. Langkah-
langkah
dalam
algoritma
harus
logis
dan
harus
dapat
ditentukan
bernilai
salah
atau
benar.
2.4 Algoritma Genetik
Algoritma genetik adalah suatu algoritma pencarian yang berbasis pada
mekanisme
seleksi alam
dan
genetika. Algoritma
genetik
merupakan salah
satu
algoritma yang sangat tepat digunakan dalam menyelesaikan masalah optimasi
kompleks, yang sulit dilakukan oleh metode konvensional (A. Desiani dan M. Arhami,
2006).
Secara
alamiah,
individu
di
dalam populasi
akan
saling
bersaing
untuk
mendapatkan sumber daya yang tersedia. Individu yang berhasil mendapatkan sumber
daya akan tetap bertahan hidup, sedangkan yang tidak, akan mati dan punah. Algoritma
genetik melakukan teknik pencarian untuk menemukan penyelesaian perkiraaan untuk
optimasi dan masalah pencarian. Selain itu, algoritma ini juga menggunakan teknik yang
terinspirasi oleh biologi revolusioner seperti warisan, mutasi, seleksi alam dan crossover.
Dalam hal
ini,
populasi
dari
kromosom
dihasilkan
secara
random dan
memungkinkan untuk berkembang biak sesuai dengan hukum yang berlaku untuk proses
evolusi
dengan
harapan
akan
menghasilkan
individu
dengan
kromosom
yang
prima.
|
|
11
Kromosom inilah
yang pada
kenyataannya
merupakan
penyelesaian
masalah
(solusi),
sehingga bila kromosom yang baik berkembang, maka solusi bagi masalahpun
diharapkan dapat dihasilkan.
Sifat algoritma genetik adalah mencari
kemungkinan-kemungkinan dari calon
solusi untuk mendapatkan yang optimal bagi penyelesaian masalah. Ruang cakupan dari
semua
solusi
yang
layak,
yaitu
objek-objek
di
antara solusi
yang
sesuai,
dinamakan
ruang pencarian.
Tiap titik
dalam ruang
pencarian
merepresentasikan satu solusi
yang
layak.
2.4.1 Struktur Dasar Algoritma Genetik
Algoritma genetik mempunyai struktur
dasar
yang
digunakan
dalam
penyelesaian suatu masalah. Menurut, Thiang,
dkk
(2001)
struktur
dasar
algoritma
genetik adalah sebagai berikut :
a. Membangkitkan populasi awal
Populasi awal
ini dibangkitkan secara random sehingga didapatkan solusi
awal.
Populasi
itu
sendiri
terdiri
atas
sejumlah
kromosom yang
merepresentasikan
solusi yang diinginkan.
b. Membentuk generasi baru
Untuk membentuk generasi baru, digunakan operator reproduksi/seleksi,
crossover, dan mutasi. Proses ini dilakukan berulang-ulang sehingga didapatkan
jumlah kromosom yang cukup untuk membentuk generasi baru dimana generasi
baru ini merupakan representasi dari solusi baru. Generasi baru ini dikenal
dengan istilah anak (off-spring).
|
 12
c. Evaluasi solusi
Proses
ini
akan
mengevaluasi
setiap populasi dengan
menghitung
nilai fitness
setiap kromosom dan
mengevaluasinya sampai
terpenuhi kriteria berhenti. Bila
kriteria berhenti belum terpenuhi maka akan dibentuk lagi generasi baru dengan
mengulangi langkah kedua. Beberapa kriteria berhenti yang sering digunakan
antara lain :
•
Berhenti pada generasi tertentu.
•
Berhenti setelah dalam beberapa generasi berturut-turut didapatkan
nilai
fitness tertinggi tidak berubah.
•
Berhenti bila dalam n generasi berikut tidak didapatkan nilai fitness yang
lebih tinggi.
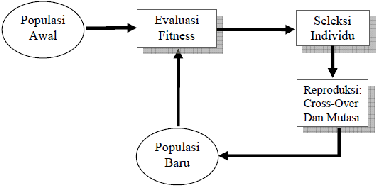
Gambar 2.2 Siklus Algoritma Genetik oleh David Goldberg Sumber :
its.edu/~entin/Kecerdasan%20Buatan/Buku/Bab%207%20Algoritma%20Geneti
ka.pdf
|
 13
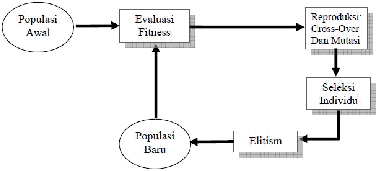
Siklus
ini
kemudian
diperbaiki oleh
beberapa
ilmuwan
yang
mengembangkan
algoritma
genetik,
yaitu Michalewicz
dengan
menambahkan
operator elitisim dan membalik proses seleksi setelah proses reproduksi.
Gambar 2.3 Siklus Algoritma Genetik oleh Michalewicz Sumber :
its.edu/~entin/Kecerdasan%20Buatan/Buku/Bab%207%20Algoritma%20Geneti
ka.pdf
2.4.2
Representasi Populasi Awal
Menurut Suyanto (2005), ada beberapa jenis representasi yang sering digunakan
yaitu:
a. Representasi Biner
Ini adalah representasi yang paling sederhana dan paling umum. Pada
representasi biner
ini, setiap
gen
hanya bisa
bernilai 0
atau
1.
Bilangan
biner
dapat digunakan untuk mempresentasikan “ya”
atau
“tidak”.
Representasi
ini
banyak digunakan karena
mempermudah pemrograman di dalam proses seperti
crossover dan mutasi.
|
|
14
b. Representasi Integer
Pada representasi
ini, setiap
gen bisa bernilai bilangan bulat (integer). Bilangan
bulat bisa digunakan untuk merepresentasikan nomor urut, posisi, jenis, atau
kualitas obyek. Dengan representasi ini, ukuran kromosom menjadi lebih
sederhana.
c. Representasi Real
Jika
representasi
biner
maupun
integer
tidak
bisa
mencapai
tingkat
ketelitian
yang diinginkan, maka bisa menggunakan representasi real.
d. Representasi Permutasi
Untuk masalah tertentu, kita mungkin saja tidak bisa menggunakan representasi
biner,
integer,
maupun
real.
Misalnya
dalam mencari
solusi
“urutan”
bukan
“nilai”.
2.4.3
Operator Genetik dalam Algoritma Genetik
Algoritma genetik mempunyai operator-operator genetik yang digunakan dalam
penyelesaian suatu masalah. Opeator-operator tersebut terdiri dari seleksi, rekombinasi
(crossover), dan mutasi.
2.4.3.1 Seleksi
Langkah pertama
yang
dilakukan dalam seleksi
adalah
pencarian
nilai fitness.
Dalam terminologi algoritma genetika kemampuan suatu individu (kromosom) untuk
bertahan hidup dapat diukur berdasarkan
nilai fitness-nya. Nilai fitness ditentukan dari
nilai objektif diri sendiri terhadap nilai objektif dari semua individu dalam wadah
|
|
15
seleksi. Semakin baik nilai fitness
suatu kromosom
maka akan semakin baik peluang
kromosom tersebut untuk bertahan hidup dan ikut dalam proses reproduksi.
Proses seleksi bertujuan
untuk
memilih kromosom yang akan dijadikan sebagai
parent (kromosom induk) pada proses crossover (pindah silang). Seleksi dilakukan
untuk mendapatkan calon induk yang baik. Induk yang baik akan menghasilkan
keturunan yang baik (Entin Martiana, 2011). Ada beberapa metode yang dapat dipilih
pada proses seleksi, antara lain :
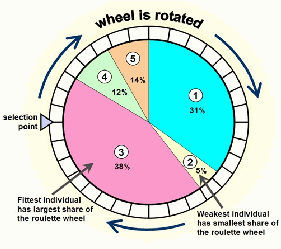
a. Roulette Wheel Selection
Pada
roulette
wheel
selection,
kromosom akan
dipilih
secara
acak
ditentukan
dengan memperhitungkan nilai fitness masing-masing kromosom. Semakin besar
nilai
fitness suatu
kromosom,
semakin
besar
pula peluang
kromosom
tersebut
untuk
terpilih
sebagai
parent
(kromosom induk).
Pengkodean
Roulette
Wheel
dapat dianalogikan seperti permainan roda putar. Pada permainan roda putar,
lingkaran roda dibagi menjadi beberapa wilayah. Pada Roulette Wheel Selection,
lebar suatu wilayah kromosom ditentukan menurut nilai fitness yang dimilikinya,
semakin besar
nilai
fitness maka akan semakin besar wilayahnya, dan semakin
besar pula peluang kromosom tersebut untuk terpilih.
b. Rank Selection
Pada
rank
selection, pemilihan kromosom
tidak
berdasarkan
pada
nilai fitness-
nya, namun diurutkan berdasarkan nilai rangking yang diberikan. Nilai rangking
dibuat berdasarkan urutan nilai fitness yang dimiliki setiap kromosom.
c. Tournament Selection
Pada tournament selection, 2 buah kromosom dipilih secara acak dari populasi.
Sebuah angka
r
dipilih
secara acak dari angka-angka diantara 0 dan 1. Sebuah
|
 16
parameter k ditentukan (misalnya k = 0,9). Jika r < k, maka kromosom dengan
nilai fitness yang lebih baik dipilih dan kemudian dikembalikan ke populasi dan
dapat dipilih lagi.
d. Elitism
Pada elitism, beberapa gen terbaik dari setiap generasi
diambil
dan
disimpan
dengan
tujuan
mencegah
hilangnya
gen-gen terbaik karena tidak dipilih untuk
melakukan crossover atau mutasi.
2.4.3.2 Rekombinasi (crossover)
Rekombinasi (crossover) adalah operator dari algoritma genetik yang melibatkan
dua
induk
untuk
membentuk
kromosom baru.
Individu
dipilih
secara
acak
untuk
dilakukan rekombinasi. Jika rekombinasi
tidak
dilakukan,
maka
nilai
dari
induk akan
|
 17
diturunkan
kepada
keturunan
(Entin
Martiana,
2011). Crossover
bertujuan
menambah
keanekaragaman string dalam satu populasi. Ada beberapa crossover, seperti :
a. Crossover satu titik
Crossover satu
titik
menggabungkan dua
genotipe
induk
dengan
memilih satu
titik pada parent dan menukar gen antara dua parent yang berada di luar titik.
b. Crossover dua titik
Prinsip crossover dua titik sama prinsipnya dengan crossover satu titik. Bedanya,
pada crossover dua titik, dipilih secara acak dua titik pada parent dan menukar
gen yang berada di antara dua titik.
c. Crossover banyak titik
Prinsipnya
memilih
titik-titik,
gen-gen
ditukar
antara
kromosom pada
titik
tersebut untuk menghasilkan kromosom baru.
Gambar 2.5 Ilustrasi Crossover Satu Titik
|
 18
2.4.3.3 Mutasi
Mutasi berperan untuk menggantikan gen yang hilang dari populasi akibat proses
seleksi yang memungkinkan munculnya kembali gen yang tidak muncul pada inisialisasi
populasi
(Entin
Martiana,
2011). Mutasi
dilakukan
dengan
cara
memilih
satu
atau
beberapa gen dalam kromosom dan kemudian mengganti nilainya.
Gambar 2.6 Ilustrasi Mutasi
2.4.4
Parameter Genetik dalam Algoritma Genetik
Algoritma genetik mempunyai parameter-parameter genetik berguna dalam
pengendalian operator-operator genetik. Penentuan parameter-parameter genetik sangat
berpengaruh
terhadap
kinerja
algoritma
genetik
dalam penyelesaian
suatu
masalah.
Parameter-parameter tersebut terdiri dari ukuran populasi (popsize), probabilitas
crossover (
), dan probabilitas mutasi (
?
).
2.4.4.1 Ukuran Populasi (popsize)
Ukuran populasi mempengaruhi ukuran efektivitas dan kinerja algoritma genetik.
Tidak ada aturan yang pasti tentang berapa nilai ukuran populasi. Apabila ukuran
populasi terlalu kecil, maka hanya terdapat sedikit solusi penyelesaian suatu
masalah.
|
|
19
Sebaliknya, ukuran populasi yang terlalu besar akan menurunkan kinerja algoritma
genetik. Ukuran populasi berkisar antara 20 – 30.
2.4.4.2 Probabilitas Crossover (?
?
)
Probabilitas
crossover
akan
mengendalikan
operator
crossover
dalam setiap
generasi dalam populasi
yang mengalami crossover. A. Desiani dan M. Arhami (2006)
menyatakan bahwa dari hasil penelitian algoritma genetika yang sudah pernah dilakukan
nilai
probabilitas
crossover
sebaiknya
tinggi,
yaitu
antara
0,8 -
0,9 agar
memberikan
hasil yang baik.
Jika
tidak terjadi crossover,
maka
keturunannya
akan
sama
persis
dengan
kromosom orangtuanya. Semakin besar probabilitas crossover, maka akan semakin
cepat struktur individu baru yang terbentuk ke dalam populasi. Namun, jika probabilitas
crossover terlalu besar, maka kandidat solusi terbaik
mungkin hilang
lebih cepat pada
generasi selanjutnya.
2.4.4.3 Probabilitas Mutasi (?
?
)
Probabilitas mutasi ( ) didefinisikan sebagai presentasi dari jumlah total
gen
pada populasi yang mengalami mutasi. Probabilitas mutasi akan mengendalikan operator
mutasi dalam setiap generasi dalam populasi yang mengalami mutasi. Probabilitas
mutasi biasanya lebih kecil dibanding dengan probabilitas crossover. Pada seleksi alam
murni,
mutasi
jarang
sekali
muncul.
A. Desiani
dan
M.
Arhami
(2006)
menyatakan
bahwa dari hasil penelitian yang sudah
pernah
dilakukan
menunjukkan
bahwa
nilai
probabilitas mutasi terbaik adalah antara 0.005 – 0.01.
|
 20
Jika peluang mutasi terlalu kecil, banyak gen yang mungkin berguna tidak
pernah dievaluasi. Tetapi bila peluang mutasi ini terlalu besar, maka akan terlalu banyak
gangguan acak, sehingga kemiripan dari induknya, dan juga algoritma
kehilangan
kemampuan untuk belajar dari histori pencarian.
2.4.5
Cara Kerja Algoritma Genetik
Proses algoritma
genetik
yang akan
dilakukan dalam
penyelesaian kubus rubik
adalah membangkitkan populasi awal secara acak, menghitung nilai fitness awal,
melakukan
proses crossover,
proses
mutasi,
menghitung
nilai fitness, dan melakukan
proses seleksi hingga menghasilkan populasi baru. Proses
ini akan berlangsung sampai
menemukan solusi yang diharapkan.
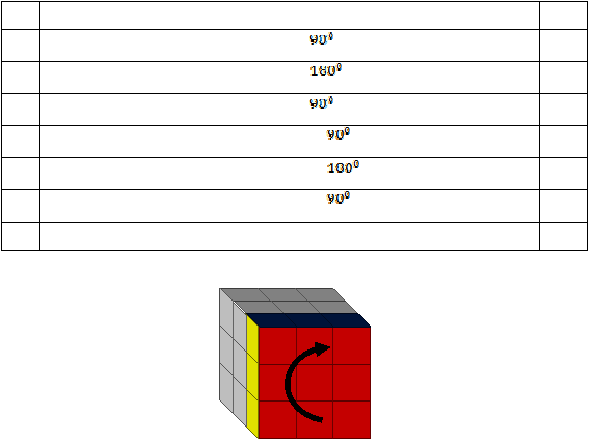
Tabel 2.1 Notasi Integer Pergerakan Kubus Rubik
F
Memutar seluruh sisi depan kubus sebesar
searah jarum jam
0
F2
Memutar seluruh sisi depan kubus sebesar
1
F’
Memutar seluruh sisi depan kubus sebesar
berlawanan arah jarum jam
2
L
Memutar seluruh sisi kiri kubus sebesar
searah jarum jam
3
L2
Memutar seluruh sisi kiri kubus sebesar
4
L’
Memutar seluruh sisi kiri kubus sebesar
berlawanan arah jarum jam
5
R
Memutar seluruh sisi kanan kubus sebesar
searah jarum jam
6
R2
Memutar seluruh sisi kanan kubus sebesar
7
R’
Memutar seluruh sisi kanan kubus sebesar
berlawanan arah jarum jam
8
B
Memutar seluruh sisi belakang kubus sebesar
searah jarum jam
9
B2
Memutar seluruh sisi belakang kubus sebesar
10
B’
Memutar seluruh kubus pada sisi belakang sebesar
berlawanan arah
11
|
 21
jarum jam
U
Memutar seluruh sisi atas kubus sebesar
searah jarum jam
12
U2
Memutar seluruh sisi atas kubus sebesar
13
U’
Memutar seluruh sisi atas kubus sebesar
berlawanan arah jarum jam
14
D
Memutar seluruh sisi bawah kubus sebesar
searah jarum jam
15
D2
Memutar seluruh sisi bawah kubus sebesar
16
D’
Memutar seluruh sisi bawah kubus sebesar
berlawanan arah jarum jam
17
T
Tetap
18
Gambar 2.7 Ilustrasi Perputaran Sisi Depan Kubus Rubik Searah Jarum Jam Sumber
rubik.html
|
 22
Contoh kasus :
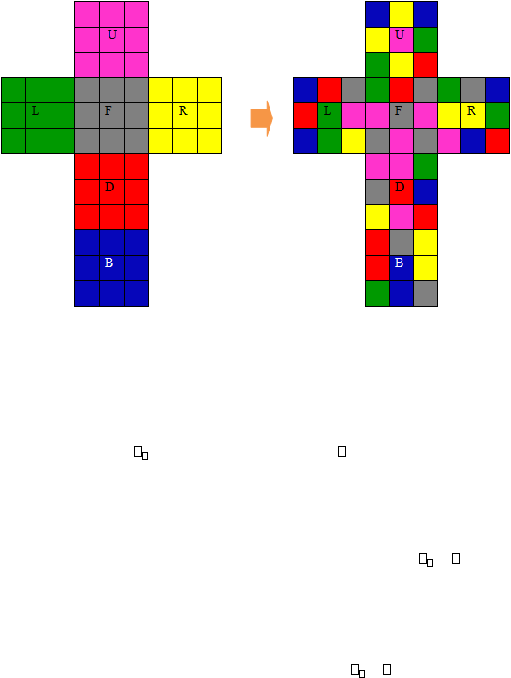
Apabila diketahui keadaan akhir dari suatu rubik yang akan diselesaikan seperti
pada gambar dibawah ini :
Gambar 2.8 Ilustrasi Keadaan Akhir Kubus Rubik
Untuk
penentuan
parameter
genetik
yaitu
ukuran
populasi
(popsize),
probabilitias
crossover
(
),
dan
probabilitas
mutasi (
?
), ada
beberapa rekomendasi
yang dapat digunakan, antara lain :
a. Untuk permasalahan yang memiliki kawasan cukup besar, De Jong (1975)
merekomendasikan untuk nilai parameter kontrol : (popsize :
:
?
)
=
(50 : 0.6
: 0,001).
b. Bila
rata-rata
nilai
fitness
setiap
generasi
digunakan
sebagai
indikator,
maka
Grefenstette (1986) merekomendasikan : (popsize :
:
?
) = (30 : 0.95 : 0,01).
|
 23
Pertama, kita hitung terlebih dahulu
nilai
fitness awal dari kondisi akhir kubus
rubik yang dilakukan dengan rumus :
Nilai fitness =
48-x
48
100%
Angka 48 didapat dari 54 sisi permukaan kubus rubik dikurang dengan enam(6). Enam
adalah enam warna yang berada pada sumbu kubus rubik. Enam warna ini tidak
diperhitungkan karena dianggap tidak bergerak. Dengan “x” adalah jumlah posisi
permukaan kubus kecil pada tiap sisi yang tidak sesuai pada tempatnya/yang memiliki
warna yang berbeda dengan sumbu tersebut.
Jika
nilai
fitness
=
100%
maka
kubus
rubik
sudah
selesai.
Jika
nilai
fitness
!=100%, terlebih dahulu kita bangkitkan populasi awal secara acak menggunakan
bilangan
random yang
dibangkitkan
tiap
gen dalam suatu
individu dengan
nilai dari
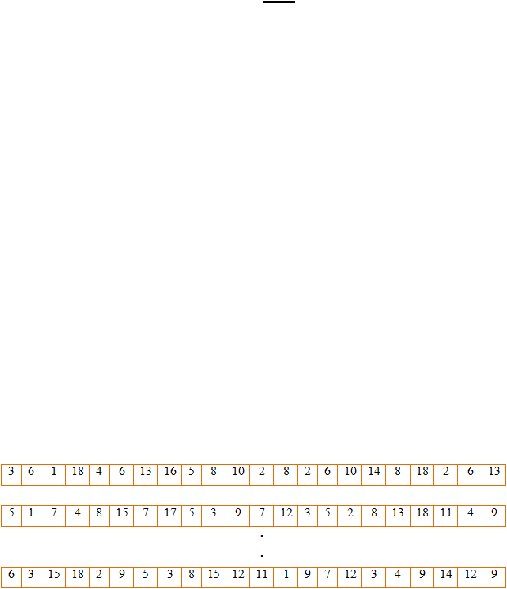
representasi integer kubus rubik, yaitu 0–18. Panjang kromosom yang digunakan adalah
22 karena pada Agustus 2008, Tomas Rokichi membuktikan bahwa langkah maksimum
untuk menyelesaikan kubus rubik adalah 22 langkah, sebanyak 30 buah kromosom.
Gambar 2.9 Ilustrasi Populasi Awal Secara Acak
|
 24
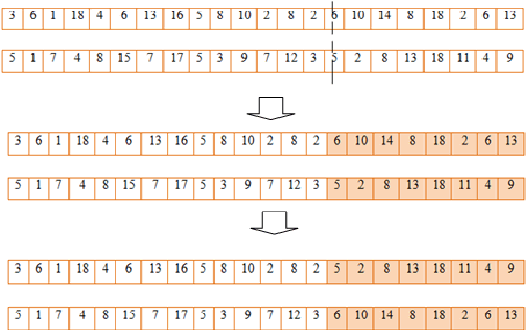
Setelah itu dilakukan rekombinasi(crossover). Misalkan
ditentukan probabilitas
crossover = 0,95 dan angka random crossover [0 -1] = 0,65. Maka letak posisi crossover
di luar titik 0.65 x 22 = 14.3 yaitu 15.
Gambar 2.10 Ilustrasi Crossover Satu Titik
Pada tahap mutasi, nilai gen yang lama akan diganti dengan nilai gen yang baru.
Jumlah
gen pada populasi adalah 22 x 30 = 660
gen. Apabila ditentukan probabilitas
mutasi = 0,01 dan angka random mutasi [0-1] = 0,1. Maka
tidak akan terjadi mutasi.
Tapi apabila angka random = 0,009. Maka banyak mutasi adalah 0,009 x 22 x 30 = 5,94
yang ditentukan secara acak dan menggantinya dengan nilai dari representasi integer
kubus rubik, yaitu 0 – 18.
|
 25
Gambar 2.11 Ilustrasi Mutasi
Dari hasil mutasi, kita cari nilai fitness. Sama seperti mencari nilai fitness diatas,
setelah
mutasi kita akan
mendapatkan 30
nilai fitness baru yang kemudian digunakan
untuk
menentukan rank
setiap kromosom karena
seleksi
yang
akan
dilakukan
dalam
pemilihan kromosom induk baru adalah rank selection.
Gambar 2.12 Ilustrasi Kromosom Baru
2.5
Model Rekayasa Piranti Lunak
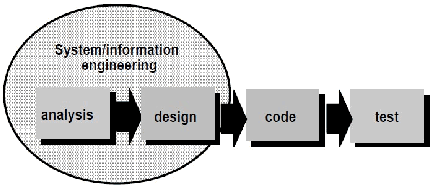
Model
sekuensial
linier
yang sering
disebut
juga
dengan
waterfall models
merupakan
paradigma
rekayasa
perangkat lunak
yang
mengusulkan
pada
pendekatan
proses yang sistematik dan sekuensial yang dimulai pada tingkat dan kemajuan sistem
pada seluruh analisis, design, kode, pengujian, dan pemeliharaan (Roger S Pressman,
1997), sebagai berikut:
|
|
26
a. Rekayasa Sistem/Informasi dan Pemodelan
Karena perangkat lunak selalu menjadi bagian dari sistem yang lebih besar, kerja
dimulai
dengan
membangun
syarat
semua
elemen
sistem dan
kemudian
mengalokasikan beberapa subset dari kebutuhan ke software.
b. Analisis Kebutuhan
Pada tahap ini merupakan analisis
kebutuhan perangkat lunak, Proses
pengumpulan kebutuhan diintensifkan dan difokuskan, khususnya pada software.
Untuk memahami sifat program
yang dibangun, analisis
harus
memahami
domain informasi, tingkah laku, unjuk kerja, dan interface yang diperlukan.
c. Desain/perancangan
Proses
desain
merepresentasikan
kebutuhan
ke
dalam bentuk
perangkat
lunak
sebelum dilakukan pengkodean.
d. Kode
Pada
tahapan
ini
mengkodekan
hasil dari desain/perancangan
ke
dalam
bahasa
pemrograman.
e. Pengujian/implementasi
Pengujian
software
dilakukan
untuk
memastikan bahwa software yang dibuat
telah sesuai dengan desain dan semua fungsi dapat dipergunakan dengan baik.
|
 27
Gambar 2.13 Waterfall Model
2.6
Unified Modelling Language (UML)
UML adalah bahasa standar yang digunakan untuk menjelaskan dan
memvisualisasikan artifak dari proses analisis
dan
disain
berorientasi
obyek.
UML
menyediakan standar pada notasi dan diagram yang bisa digunakan untuk
memodelkan
suatu system. UML menyediakan beberapa notasi dan artifak standar yang bias
digunakan sebagai alat komunikasi bagi para pelaku dalam proses analisis dan desain.
Artifak
di
dalam UML
didefinisikan
sebagai
informasi
dalam berbagai
bentuk
yang
digunakan atau dihasilkan dalam proses pengembangan perangkat lunak (Julius
Hermawan, 2004).
2.6.1
Use Case Diagram
Use Case Diagram menjelaskan apa yang akan dilakukan oleh sistem yang akan
dibangun dan siapa yang berinteraksi dengan sistem. Use case diagram pada umumnya
tersusun dari elemen actor, use case, dependency, generalization, dan association. Use
|
|
28
case diagram
ini memberikan
gambaran statis dari
sistem
yang sedang dibangun dan
merupakan artifak dari proses analisis (Julius Hermawan, 2004).
2.6.2
Sequence Diagram
Sequence diagram menjelaskan secara detail urutan proses yang dilakukan dalam
sistem
untuk mencapai
tujuan dari use case:
interaksi
yang terjadi antar class, operasi
apa saja yang terlibat, urutan antar operasi, dan informasi yang diperlukan oleh masing-
masing operasi (Julius Hermawan, 2004).
|