|
BAB II
LANDASAN TEORI
8
2.1
Teori Antrian
2.1.1
Pendahuluan
Antrian merupakan suatu fenomena yang timbul dalam aktivitas manusia.
Antrian yang muncul disebabkan oleh aktivitas pelayanan yang tidak diimbangi oleh
kebutuhan akan pelayanan sehingga pengguna layanan tersebut tidak terlayani
dengan segera. Menurut Donald Gross (2008: 1-2), sistem antrian
tercipta jika
pelanggan datang ke tempat pelayanan, pelanggan menunggu untuk dilayani jika
pelayanan tidak segera dilakukan dan pelanggan meninggalkan sistem pelayanan jika
sudah terlayani. Pelanggan yang dimaksud dalam sistem pelayanan ini bukan hanya
manusia, tetapi juga seperti suatu benda yang juga ingin dilayani, dalam kasus ini
adalah unit mobil yang ingin mendapatkan suatu jenis perbaikan di bengkel.
Teori antrian digunakan sebagai pembuktian suatu model untuk memprediksi
suatu tingkah laku sistem
antrian. Teori ini pertama kali diperkenalkan oleh A.K
Erlang dalam penemuannya yang berjudul “Solution of some problems in theory of
probabilities of significance in Automatic Telephone Exchange”. Beliau melakukan
perhitungan waktu keterlambatan operator telepon pada jaman itu ketika para
pelanggan yaitu para penelepon harus antri menunggu untuk dilayani.
Analisa dari teori antrian menyediakan informasi tentang kemungkinan yang
dapat membantu dalam mengambil keputusan untuk menciptakan sistem antrian
dengan tujuan untuk mengatasi permintaan pelayanan yang fluktuatif secara acak dan
menjaga keseimbangan antara biaya pelayanan dan biaya menunggu.
Dewasa ini,
teori antrian banyak digunakan dalam berbagai bidang. Menurut Hillier dan
Lieberman (2005: 771-772) sistem antrian terklasifikasi menjadi beberapa sistem
dimana teori antrian disimulasikan dan diterapkan secara luas. Klasifikasi sistem
antrian menurut mereka adalah sebagai berikut :
a)
Sistem Pelayanan Komersial, dimana aplikasi teori antrian dari model antrian
yang digunakan untuk kepentingan komersil seperti antrian pada toko,
supermarket, kafetaria dan sebagainya.
b)
Sistem Pelayanan Bisnis Industri, aplikasi teori antrian dari model antrian
yang digunakan dalam cakupan lini produksi seperti sistem material handling,
pergudangan dan sebagainya.
c)
Sistem Pelayanan Transportasi, aplikasi teori antrian dari model antrian yang
digunakan dalam proses transportasi seperti antrian pada kereta, antrian
pendaratan pesawat, dan sebagainya.
|
|
9
d)
Sistem Pelayanan Sosial, yaitu sistem pelayanan yang digunakan oleh
perusahaan atau instansi nasional, seperti registrasi SIM dan STNK, sistem
pelayanan di rumah sakit, dan sebagainya.
2.1.2
Karakteristik Dasar Sistem Antrian
Subyek penting yang berperan dalam
sistem antrian
ini adalah pelanggan
dan pelayan, di mana terdapat periode waktu antar pelanggan untuk mendapatkan
kebutuhan pelayanan dari pelayan. Menurut Donald
Gross (2008: 3-6) ada enam
karakteristik dasar dari proses antrian yang menyediakan deskripsi yang cukup dari
sistem antrian :
1.
Kedatangan
Setiap antrian timbul dari suatu kedatangan yang biasa disebut proses input.
Dalam sistem antrian, proses kedatangan pelanggan merupakan peristiwa secara
acak dan mempunyai peluang kejadian. Jumlah kedatangan bisa dikatakan tidak
terbatas jika jumlah pelanggan tidak tergantung pada jumlah pelanggan yang
telah ada sebelumnya didalam
sistem. Contoh dari jumlah kedatangan
tidak
terbatas pada kasus ini adalah unit mobil yang datang untuk mendapatkan suatu
pelayanan berupa perbaikan di bengkel. Dengan demikian diperlukan distribusi
probabilitas untuk menggambarkan antara kedatangan pelanggan berturut-turut
secara acak.
2.
Pelayanan
Pelayanan
merupakan salah satu faktor dalam sistem antrian, dimana ada
periode waktu yang dibutuhkan oleh seorang pelanggan untuk mendapatkan
pelayanan.
Mekanisme pelayanan dapat terdiri dari tunggal atau jamak
mengenai jumlah fasilitas pelayanan atau yang biasa disebut server. Proses
pelayanan mungkin tergantung pada jumlah pelanggan menunggu suatu layanan.
Sebuah antrian dapat bekerja lebih cepat jika jumlah server
banyak
namun
sebaliknya dapat mengakibatnya tidak efisiennya sistem antrian. Distribusi
probabilitas diperlukan untuk menggambarkan urutan waktu layanan pelanggan.
3.
Antrian
Sifat kedatangan dan proses pelayanan sangat mempengaruhi satu sama lain
sehingga dapat terbentuknya suatu antrian. Disiplin antrian berkaitan erat dengan
urutan pelayanan yang diterima pelanggan ketika memasuki fasilitas pelayanan.
Disiplin antrian ini terbagi menjadi empat bentuk, yaitu :
a)
FCFS (First Come, First Served/ Datang Pertama, Dilayani Pertama)
merupakan suatu peraturan dimana pelanggan yang dilayani terlebih dahulu
adalah pelanggan yang datang pertama kali. Contohnya seperti pelanggan
yang antri pada loket penjualan karcis.
|
 10
b) LCFS (Last Come, First Served/ Datang Terakhir, Dilayani Pertama)
merupakan antrian dimana pelanggan yang datang terakhirlah yang akan
dilayani terlebih dahulu. Contohnya seperti pada sistem antrian bongkar muat
barang dalam truk, dimana barang yang masuk terakhir akan keluar terlebih
dahulu.
c)
SIRO (Service in Random Number/ Pelayanan dalam Urutan Acak)
merupakan salah satu disiplin antrian dimana pelayanan dilakukan dengan
urutan acak (Random Order). Contohnya seperti dalam suatu kegiatan arisan,
dimana pemenangnya didasarkan pada proses undian.
d) Priority Queue
(Antrian Prioritas) merupakan prioritas pelayanan yang
dilakukan
khusus kepada pelanggan utama yang mempunyai prioritas tinggi
dibandingkan dengan pelanggan yang mempunyai prioritas rendah.
Contohnya seperti pada pasien rumah sakit yang mendapatkan prioritas
penanganan
terlebih dahulu dikarenakan mempunyai penyakit yang lebih
berat dibandingkan dengan pasien lain.
4.
Kapasitas antrian
Dalam beberapa proses antrian ada keterbatasan fisik mengenai jumlah ruang
tunggu, sehingga ketika jumlah pelanggan yang mengalami antrian mencapai
jumlah maksimal tertentu,
maka tidak ada lagi jumlah pelanggan yang diizinkan
masuk ke dalam sistem antrian sampai jumlah pelanggan dalam antrian tersebut
tidak mencapai batas maksimal. Sebuah antrian dengan ruang tunggu yang
terbatas dapat dikatakan sebagai balking
dimana pelanggan
dipaksa untuk
menolak jika hendak memasuki sistem antrian dengan jumlah pelanggan yang
sudah mencapai batas maksimal.
5.
Struktur Antrian
Menurut Eddy (2003: 105-107) struktur antrian dikategorikan menjadi empat
struktur dasar menurut fasilitas pelayanan dalam sistem antrian, yaitu:
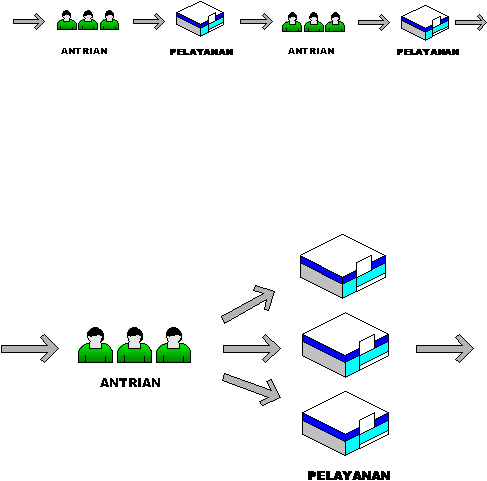
a) Single Channel Single Phase
Subjek
pemanggilan dalam pelanggan yang dilayani dalam sebuah antrian
akan membentuk
antrian tiap
satu barisan antrian
dan selanjutnya akan
berhadapan dengan satu fasilitas pelayanan. Contoh dari struktur antrian ini
adalah sistem antrian pada sebuah salon dimana masing-masing tukang cukur
mempunyai antrian pelanggan sendiri.
Gambar 2.1 Model Single Channel Single Phase
|
 11
b)
Single Channel Multi Phase
Subjek pemanggilan dalam pelanggan yang dilayani dalam sebuah antrian
akan masuk dan membentuk satu barisan antrian
dan selanjutnya akan
berhadapan dengan satu fasilitas pelayanan kemudian membentuk barisan
antrian lagi sampai pelayanan selesai. Contoh dari struktur antrian ini adalah
sistem antrian pada proses produksi dalam perusahaan manufaktur.
Gambar 2.2 Model Single Channel Multi Phase
c)
Multi Channel Single Phase
Subjek pemanggilan dalam pelanggan yang dilayani dalam sebuah antrian
akan masuk dan membentuk satu barisan antrian
dan selanjutnya akan
berhadapan dengan beberapa fasilitas pelayanan identik secara pararel.
Contoh dari struktur antrian ini adalah sebuah bengkel yang memiliki
beberapa stall dengan satu jalur antrian jenis perbaikan.
Gambar 2.3 Model Multi Channel Single Phase
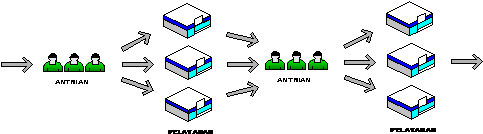
d)
Multi Channel Multi Phase
Subjek pemanggilan dalam pelanggan yang dilayani dalam sebuah antrian
akan masuk dan membentuk beberapa
barisan antrian dan selanjutnya akan
berhadapan dengan beberapa fasilitas pelayanan identik secara pararel
kemudian membentuk barisan antrian lagi sampai pelayanan selesai. Contoh
dari struktur antrian ini adalah pelayanan pasien dirumah sakit dari mulai
pendaftaran, diagnosa, peneyembuhan sampai dengan pembayaran.
|
 12
Gambar 2.4 Model Multi Channel Multi Phase
6.
Tingkat Pelayanan
Tingkat pelayanan memberikan tahap-tahap untuk melaksanakan suatu
pelayanan dalam suatu sistem antrian. Sebuah sistem antrian mungkin hanya
satu tahap pelayanan, atau biasa yang disebut sebagai tingkat pelayanan tunggal
seperti dalam salon rambut atau mungkin memiliki beberapa tahapan
atau yang
biasa disebut tingkat pelayanan ganda. Sebuah contoh dari sistem antrian tingkat
pelayanan ganda misalnya pasien yang menjalani perawatan di rumah sakit.
Perawatan ini memiliki prosedur pemeriksaan fisik
di mana pasien harus
melalui beberapa tahapan perawatan seperti sejarah medis, pemeriksaan telinga,
hidung, dan
tenggorokan, pemeriksaan darah,
elektrokardiogram, pemeriksaan
mata, dan sebagainya.
2.1.3
Notasi Sistem Antrian
Menurut Donald Gross (2008: 7-8) notasi pada sistem antrian atau yang
disebut sebagai notasi Kendall
digunakan sebagai singkatan untuk menggambarkan
proses antrian. Sebuah proses antrian digambarkan oleh serangkaian simbol dan garis
miring
seperti A/B/X/Y/Z,
dimana A
menunjukkan distribusi kedatangan, yaitu
jumlah kedatangan. B menunjukkan distribusi waktu pelayanan, yaitu selang waktu
antara satuan-satuan yang dilayani. X menunjukkan jumlah saluran layanan paralel.
Y menunjukan pembatasan kapasitas sistem
antrian
dan Z merupakan disiplin
antrian. Beberapa simbol standar untuk notasi Kendall ini disajikan dalam Tabel 2.1.
|
 13
Tabel 2.1. Simbol Standar Notasi Kendall
Karakteristik
Simbol
Penjelasan
M
Distribusi satuan unit
menggunakan Poisson
atau satuan waktu
menggunakan
ekponensial
D
Antar Kedatangan atau
waktu pelayanan tetap
G
Distribusi umum
pemberangkatan atau
waktu pelayanan
Jumlah Saluran
layanan pararel (X)
1,2,...8
kapasitas sistem
antrian (Y)
1,2,...8
FCFS
First Come, First Served
LCFS
Last Come, First Served
SIRO
Service in Random Number
PR
Priority Queue
Distribusi
Kedatangan (A)
Distribusi Waktu
Pelayanan (B)
Disiplin antrian (Z)
2.1.4 Karakteristik Operasi sistem antrian
Karaketristik
operasi menjelaskan
sistem bekerja dalam bentuk berbagai
ukuran
misalnya rata-rata banyaknya unit yang antri, rata-rata waktu menunggu, dan
lain-lain. Dalam menentukan karakteristik operasi sistem antrian, hal pertama yang
harus perlu dilakukan adalah menentukan notasi model dalam sistem antrian. Dalam
penelitian ini, notasi model antrian yang digunakan adalah notasi Multiple Channel
Model dengan notasi M/M/2/3/FCFS. Model M/M/2/3/FCFS adalah notasi model
antrian yang megungkapkan jumlah unit kedatangan mengikuti distribusi Poisson,
dan pelayananan mengikui distibusi Eksponensial. Sedangkan jumlah saluran
layanan pararel pada kondisi aktual berjumlah dua
(multiple channel) dan kapasitas
antrian ini berjumlah 3
dengan disiplin antrian First Come First Out
(FIFO).
Menurut
Donald Gross (2008:
69-73),
berikut adalah rumus dalam menenetukan
karakteristik operasi antrian dengan model M/M/2/3/FCFS adalah
1.
Tingkat intesitas kegunaan pelayanan
2.
Probabilitas tidak ada pengantri dalam sistem
|
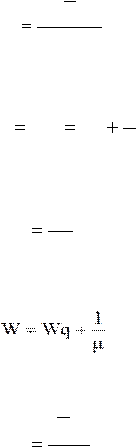 14
3.
Rata-rata banyaknya unit yang menunggu untuk dilayani
4.
Rata-rata banyaknya unit yang antri dalam sistem
5.
Rata-rata waktu menungggu sebelum dilayani
6.
Rata-rata waktu menunggu dalam sistem
7.
Probabilitas dari kedatangan kurang dari jumlah pelayanan (Po<k)
2.1.5 Kerangka Keputusan Masalah Antrian
Dalam menentukan solusi untuk mengatasi masalah timbulnya antrian, hal
yang penting dilakukan adalah bagaimana menentukan jumlah tingkat pelayanan
yang
tepat didalam sistem antrian.
Dikarenakan keputusannya adalah tingkat
pelayanan, variabel yang relevan dalam hubungannya dengan tingkat pelayanan
adalah total biaya
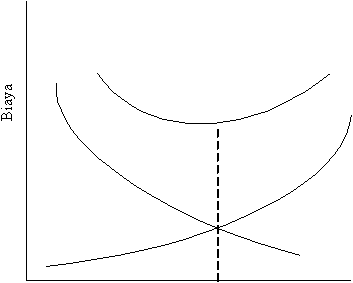
yang diharapkan. Hubungan variabel total biaya yang diharapkan
yang terdiri dari biaya pelayanan dan biaya menunggu dengan tingkat pelayanan
dapat terlihat di gambar 2.5. Solusi yang tepat dalam mengatasi masalah antrian
adalah bagaimana menentukan titik terendah dari total biaya yang diharapkan dengan
tingkat pelayanan yang bertambah seperti yang dijelaskan dalam garis putus pada
gambar 2.5.
2
s
o
p)
-
(1
s!
p
)
µ
?
(
P
Lq
µ
?
Lq
?W
L
?
Lq
Wq
)
(
n!
n
)
µ
?
(
Pn
Po
x
|
 15
Total Biaya yang diharapkan
Tingkat Pelayanan
Biaya pelayanan
Biaya menunggu
Gambar 2.5 Hubungan antara total biaya yang diharapkan dengan tingkat
pelayanan
Biaya pelayanan
akan bertambah seiring dengan tingkat pelayanan yang
bertambah. Sebagai contoh suatu bengkel jika ingin menambahkan stall perbaikan
dalam meningkatkan tingkat pelayanan pasti akan menambah biaya pelayanan seperti
menambah gaji mekanik baru. Tingkat pelayanan bertambah juga yang
mengakibatkan waktu menganggur pelayanan atau waktu non produktif yang
bertambah.
Biaya menunggu akan menurun sesuai dengan tingkat pelayanan yang
bertambah. Biaya menunggu juga dapat digambarkan sebagai biaya kehilangan
keuntungan bagi perusahaan, seperti pada penelitian ini adalah biaya lembur yang
sangat tinggi dibandingkan dengan biaya pelayanan. Biaya lembur ini berlaku pada
saat di luar jam kerja perusahaan. Hubungan antara biaya pelayanan dan menunggu
sehingga didapatkan total biaya yang diharapkan untuk keputusan masalah antrian
dapat dirumuskan sebagai :
Tc = Ec(Ci) + Ev(Cw)
dimana :
Ec = Jumlah server menganggur
Ci = Biaya pelayanan
Ev = Rata-rata waktu menunggu dalam sistem
Cw = Biaya menunggu
|
|
16
Biaya yang sudah diketahui dapat diuji kelayakannya melalui analisa
investasi.
Kelayakan investasi sangat diperlukan dalam penganggaran modal untuk
melaksanakan suatu investasi tertentu. Investasi yang tepat
adalah investasi yang
benar-benar memberi hasil pengembalian sesuai yang diinginkan perusahaan. Berikut
ini adalah metode yang digunakan untuk menilai kelayakan investasi yang dilakukan:
a)
Metode Masa Pengembalian Investasi (Payback Period Method)
Menurut Fuad (2000:
230) Payback Period
merupakan metode perhitungan
berapa lama arus kas yang masuk dapat menutupi biaya aliran kas yang dijadikan
biaya investasi awal.
b) Metode Net Present Value
Menurut Fuad (2000:
232) Net Present Value
merupakan metode perhitungan
dengan memperhatikan nilai waktu dari uang tersebut. Metode ini menggunakan
pengurangan dari suku bunga yang ditetapkan selama periode tertentu.
c)
Metode Profitability Index
Menurut Johar A. (2005:
97) Profitability Index
merupakan metode dengan
melakukan perbandingan nilai
keuntungan yang sudah dikurangi dengan suku
bunga dengan
nilai investasi. Metode ini dapat dikatakan diterima jika indeks
keuntungan yang diperoleh lebih dari 1%.
d) Metode Internal Rate of Return
Menurut Vincent.G (2005:
364)
Internal Rate of Return merupakan metode
menentukan suku bunga yang membuat nilai Net Present Value menuju nol.
2.2
Distribusi dalam karakteriskitik operasi antrian
Karakteristik dasar model antrian bergantung kepada faktor-faktor berikut:
2.2.1
Distribusi Kedatangan
Pola kedatangan dapat terjadi secara acak. Model antrian pada kasus ini
adalah model probabilitas karena variabel acak berpengaruh pada pola kedatangan
dalam proses antrian. Menurut Siagian (2000: 84) variabel acak merupakan bilangan
nyata yang variasinya ditentukan oleh percobaan acak. Terjadinya kedatangan
bersifat bebas dan tidak terpengaruh oleh kedatangan sebelum ataupun sesudahnya.
Variabel acak seringkali digambarkan terhadap distribusi probabilitas yang menurut
Montgomery (2009: 72)
adalah model matematika
yang berhubungan dengan nilai
variabel dengan probabilitas terjadinya nilai tersebut di dalam suatu populasi.
Pola Jumlah Kedatangan Menggunakan Distribusi Poisson
Distribusi ini pertama kali diperkenalkan oleh Siméon-Denis Poisson (1781–
1840) dalam karyanya mengenai “Penelitian Peluang Hukum Masalah Pidana dan
Perdata”. Karyanya
memfokuskan peubah acak N yang menghitung antara lain
jumlah kejadian diskret (kadang juga disebut "kedatangan") yang terjadi selama
interval waktu tertentu. Distribusi diskret menurut Montgomery (2009: 73) muncul
|
|
17
ketika parameter yang diukur hanya dapat mengambil nilai-nilai tertentu, seperti
bilangan bulat, dalam kasus ini adalah jumlah kedatangan. Percobaan yang
menghasilkan variabel acak X yang
menyatakan banyaknya probabilitas terhadap
jumlah kedatangan selama interval waktu tertentu dinamakan percobaan Poisson.
Asumsi dari distribusi peluang Poisson ini adalah kedatangan pelanggan sifatnya
acak dan mempunyai rata-rata kedatangan sebesar lamda (?) . Menurut Bocharov dkk
(2004:
8-9)
keterkaitan jumlah kedatangan waktu dalam distribusi Poisson
sebagai
berikut:
1.
Tidak
punya memori atau ingatan, yaitu banyaknya kedatangan
dalam
satu
interval waktu (atau daerah) tidak bergantung pada banyaknya kedatangan pada
waktu atau daerah yg lain.
2.
Probabilitas terjadinya satu kali jumlah kedatangan
dalam interval waktu (atau
daerah) yang sangat pendek (kecil) sebanding dengan lama waktu interval waktu
tersebut (atau luas daerahnya).
Berikut adalah persamaan
fungsi Peluang Poisson untuk jumlah kedatangan
adalah sebagai berikut :
P(x-kedatangan)
dengan :
P (x) = Peluang bahwa ada x pelanggan datang dalam sistem
? = Harga rata-rata tingkat kedatangan
e = Bilangan natural (e = 2,71828)
x = Frekuensi kedatangan pelanggan, dalam bilangan bulat (0,1,2,3,…)
Salah satu keterkaitan antara distribusi Poisson dengan Eksponensial adalah
bahwa jika banyaknya kedatangan per satuan waktu mengikuti distribusi Poisson
dengan rata-rata tingkat kedatangan, maka waktu antar kedatangan akan mengikuti
distribusi Eksponensial negatif .
2.2.2
Distribusi Pelayanan
Pola pelayanan pada model antrian ini juga menggunakan bentuk distribusi
probabilitas. Waktu pelayanan pada model antrian
ini didistribusikan secara acak,
maka harus ditentukan distribusi probabilitas yang paling
cocok untuk
menggambarkan karakter perilakunya.
Besaran ini bergantung
pada jumlah
pelanggan yang telah berada di dalam fasilitas tersebut. Pola
pelayanan ditentukan
oleh waktu pelayanan yang dibutuhkan untuk melayani pelanggan dalam suatu
fasilitas. Fasilitas pelayanan yang terdiri dari satu atau lebih biasa disebut dengan
|
|
18
server. Dalam kasus model antrian ini, pada sistem kondisi aktual hanya terdapat dua
server, sedangkan pada sistem usulan bertambah menjadi tiga server.
Pola Waktu Pelayanan Menggunakan Distribusi Eksponensial
Asumsi dari distribusi peluang Eksponensial
ini berguna untuk
mendeskripsikan waktu pelayanan dari variabel acak yang dilayani oleh server
dalam sistem antrian ini. Distribusi Eksponensial
termasuk ke dalam distribusi
kontinyu.
Distribusi kontinyu menurut Montgomery (2009: 73) muncul ketika
variabel yang diukur dinyatakan dalam skala kontinyu. Waktu pelayanan merupakan
sifat dari distribusi yang kontinyu.
Menurut Bocharov dkk
(2004 :6-7) keterkaitan
waktu pelayanan dalam distribusi Eksponensial sebagai berikut:
1.
Waktu antar pelayanan bersifat acak.
2.
Waktu antar pelayanan
berikutnya independen
terhadap waktu antar kejadian
sebelumnya.
3.
Waktu pelayanan dalam antrian tergantung dari unit yang dilayani.
Karena dalam distribusi Eksponensial memiliki standar deviasi sama dengan
rata-rata, distribusi probabilitas Eksponensial hanya cukup menggunakan pengujian
untuk melakukan perkiraan atau pun prediksi dengan hanya membutuhkan perkiraan
rata-rata populasi. Rumus umum density function probabilitas eksponensial adalah:
dengan :
P (x) = Peluang waktu pelayanan daam sistem
µ
= Rata-rata tingkat pelayanan
1/µ = Rata-rata waktu pelayanan
t
= Waktu pelayanan
e = Bilangan natural ( e = 2,71828 )
Asumsi yang biasa digunakan bagi distribusi waktu pelayanan adalah
distribusi Eksponensial negatif. Sehingga
jika waktu pelayanan mengikuti distribusi
Eksponensial negatif, maka tingkat pelayanan mengikuti distribusi Poisson.
2.2.3
Uji Goodness of Fit
Asumsi distribusi Eksponensial maupun Poisson sering kali harus diuji
keabsahannya. Menurut Lehmann dan
Romano (2005:
583-584)
hipotesa statistik
merupakan pernyataan atau dugaan mengenai satu atau lebih populasi. Pengambilan
secara acak oleh distribusi probabilitas dari suatu populasi harus diperiksa untuk
mengetahui benar atau salahnya suatu hipotesa.
Bukti dari contoh yang tidak
|
 19
konsisten dengan hipotesa akan membawa penolakan atau yang disebut Hipotesis
satu (H1), sedangkan bukti yang mendukung hipotesa tersebut akan membawa
penerimaan atau yang disebut hipotesis nol (H0). Pada penelitian ini digunakan Uji
chi kuadrat melalui test goodness of fit untuk menguji frekuensi dari variabel acak
pada jumlah
kedatangan atau data waktu pelayanan sudah sesuai atau menyimpang
dari
pola distribusi yang telah ditetapkan. Adapun kriteria penerimaan apakah data
tersebut
mengikuti pola distribusi atau tidak dilihat dari uji chi kuadrat
(
) yang
telah dilakukan. Perhitungan uji frekuensi teoritis atau yang diharapkan
ini didapat
dari
Dimana :
e
i
= frekuensi teoritis pada kelas interval ke-i
F
i
= probabilitas distribusi pada kelas ke-i
= total frekuensi pengamatan
Pengukuran mengenai perbedaan yang terdapat antara frekuensi yang
diharapkan dengan yang diamati melalui uji chi kuadrat adalah
Dimana :
= Uji chi kuadrat
Bila frekuensi pengamatan mendekati dari frekuensi teoritis akan
mengakibatkan nilai x lebih kecil dari nilai x pada tabel chi kuadrat sehingga
menunjukan adanya kesesuaian begitupun jika frekuensi pengamatan berbeda cukup
besar dari
frekuensi teoritis akan mengakibatkan nilai x lebih besar dari nilai x pada
tabel chi kuadrat sehingga menunjukan adanya penyimpangan.
2.3
Model Simulasi
2.3.1
Pendahuluan
Menurut Thomas J. (2004:
1), simulasi dapat diartikan sebagai suatu sistem
yang digunakan untuk memecahkan atau menguraikan persoalan-persoalan dalam
kehidupan nyata yang penuh dengan ketidakpastian baik dengan tidak atau
menggunakan model metode tertentu. Persoalan yang rumit akan lebih mudah
diselesaikan apabila kita membangun model percobaan dari suatu sistem melalui
pendekatan simulasi.
Seringkali dalam kasus pemilihan keputusan, contoh perilaku
|
|
20
yang dihasilkan oleh model percobaan sering dijadikan acuan dasar oleh pihak
manajemen atau pengambil keputusan. Melalui pendekatan simulasi, dampak dari
keputusan tersebut dapat dianalisa melalui hasil rekayasa tanpa merubah dari sistem
yang ada. Dengan demikian banyak sistem yang dapat disimulasikan dengan baik
guna memperoleh hasil yang optimal. Berikut adalah beberapa keuntungan yang bisa
dimanfaatkan oleh pendekatan simulasi menurut Charles H. (2001: 7) :
a)
Dapat menghemat waktu
b) Perilaku sistem dapat diamati secara menyeluruh
c)
Dapat dilakukan “trial” dan “error”
d) Percobaan dapat dilakukan setiap saat dan dapat diulang-ulang
2.3.2
Teknik Simulasi dengan ProModel ver 7.5
Semakin pesatnya perkembangan teknologi, pendekatan simulasi dapat
dilakukan dengan komputer sebagai alat bantu dalam menentukan keputusan.
ProModel
merupakan salah satu software
alat simulasi untuk pemodelan berbagai
bidang seperti
industri, bisnis, mulai dari toko-toko skala kecil sampai dengan mesin
produksi skala besar, pada sistem manufaktur, maupun sistem rantai pasokan.
ProModel adalah sistem berbasis Windows dengan antarmuka grafis dan pemodelan
yang berorientasi pada objek
konstruksi
mudah digunakan (Charles H. 2001: 80).
ProModel menggunakan optimasi tool bernama SimRunner yang melakukan analisis
dengan menjalankan desain kontruksi yang dibuat
pada model, sehingga dapat
memberikan jawaban terbaik mungkin kapabilitas dan kaya fitur (Charles H. 2001:
80).
2.3.3
Elemen ProModel
Menurut Charles H. (2001: 145-157), untuk membuat simulasi pada sistem,
terkebih dahulu kita harus menentukan beberapa elemen yang telah disediakan oleh
ProModel ver 7.5, yaitu :
a)
Lokasi
Lokasi dalam ProModel
merupakan objek yang ditempatkan tetap dalam
sistem (misalnya mesin, antrian, area penyimpanan, stasiun kerja, tangki,dan lain-
lain) di mana lokasi tersebut mengalami atau menunggu suatu proses dalam
simulasi. Jumlah lokasi dapat berupa unit tunggal lokasi (misalnya hanya satu
mesin) atau lokasi multi-unit (misalnya sekelompok mesin yang bersama-sama
melakukan yang operasi secara paralel. Berikut atribut-atribut lokasi yang terdapat
dalam ProModel pada gambar 2.6 :
|
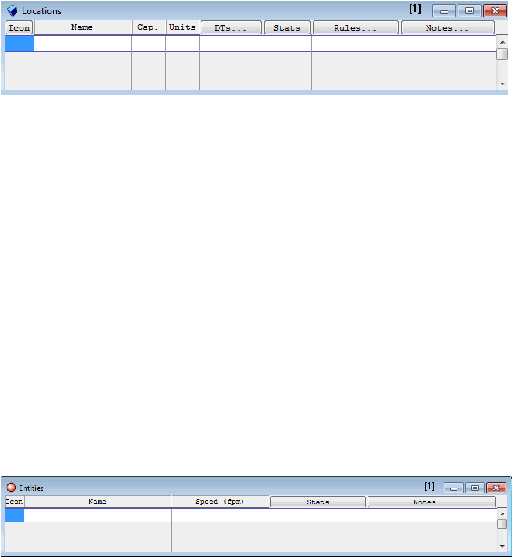 21
Gambar 2.6 Atribut dari elemen Location
i.
Icon,
merupakan perwujudan grafik yang menunjukkan lokasi yang
bersangkutan.
ii.
Name, merupakan nama dari lokasi
iii.
Capacity adalah jumlah kapasitas banyaknya produk dalam satu unit lokasi.
iv.
Unit, merupakan banyaknya unit lokasi.
v.
Dts (Down Times), merupakan pilihan perhitungan berdasarkan waktu, banyak
material yang masuk, ataupun lama pemakaian.
vi.
Stat, merupakan pencatatan secara statistik terhadap lokasi simulasi yang akan
dijalankan.
vii.
Rules,
merupakan aturan bagaimana entitas dalam proses akan masuk, keluar
dalam lokasi sesuai ketentuan disiplin antrian.
viii.
Notes, merupakan catatan tambahan mengenai detil lokasi.
b)
Entitas
Entitas mengacu pada barang yang diproses di sistem. Barang tersebut dapat
berupa barang jadi, bahan baku, ataupun
barang setengah jadi. Berikut atribut-
atribut entitas yang terdapat dalam ProModel pada gambar 2.7:
Gambar 2.7 Atribut dari elemen Entitas
i.
Icon,
merupakan perwujudan grafik yang menunjukkan entitas yang
bersangkutan.
ii.
Name, merupakan nama dari entitas
iii.
Speed (Fpm),
digunakan
untuk
menentukan kecepatan entitasnya sendiri.
iv.
Stat, merupakan pencatatan secara statistik terhadap entitas simulasi yang akan
dijalankan
v.
Notes, merupakan catatan tambahan mengenai detil entitas.
|
 22
c)
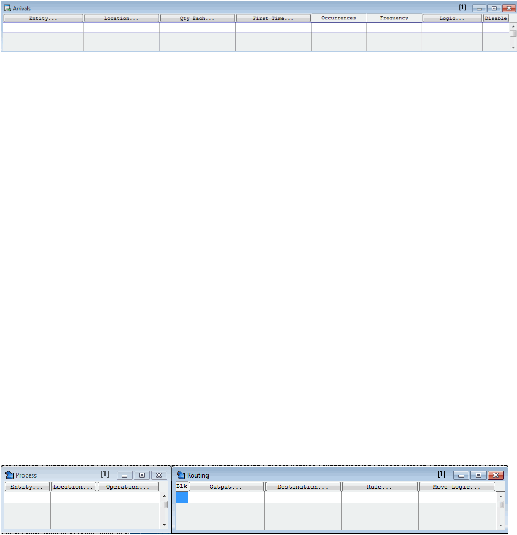
Kedatangan
Kedatangan merupakan suatu peristiwa masuknya entitas kedalam sistem.
Berikut atribut-atribut kedatangan yang terdapat dalam ProModel
pada gambar
2.8:
Gambar 2.8 Atribut dari elemen kedatangan
i.
Entity,
merupakan
jenis entitas yang akan diatur kedatanganya masuk ke
dalam sistem.
ii.
Locations, menunjukkan lokasi mana yang akan didatangi oleh entitas
iii.
Qty each, menunjukan jumlah entitas yang akan datang didalam sistem.
iv.
First Time, menunjukan waktu pertama kali entitas masuk kedalam sistem.
v.
Occurrences, merupakan jumlah entitas yang datang selama satu kali
simulasi.
vi.
Frequency, merupakan interval waktu dari antara jumlah dua kedatangan.
vii.
Logic, merupakan penambahan algoritma untuk mengatur kedatangan.
viii.
Disable, berguna untuk menonaktifkan atau mengaktifkan peristiwa
kedatangan.
d)
Proses
Proses mendefinisikan urutan pengolahan dan aliran logika entitas antara
lokasi yang satu dengan lainnya di dalam suatu sistem. Elemen proses
menentukan rute yang dilalui oleh tiap-tiap entitas
pada tiap-tiap lokasi yang
dilaluinya. Elemen ini akan terdiri dari dua bagian, yaitu window process
dan
window routing yang terlihat pada gambar 2.9:
Gambar 2.9 Atribut dari elemen proses
i.
Entity, merupakan
jenis entitas yang akan diatur prosesnya di dalam sistem.
ii.
Locations, menunjukkan lokasi mana yang akan didatangi oleh entitas
iii.
Operations,menunjukan perintah tambahan untuk menjalankan suatu proses.
iv.
Output, menunjukan entitas yang keluar setelah mengalami proses..
v.
Destination, menunjukan tujuan entitas masuk ke proses berikutnya.
vi.
Rule, berisi aturan sesuai dengan dispilin antrian.
vii.
Move logic, berisikan peraturan tentang perpindahan rute.
|
 23
2.3.4
Menjalankan Simulasi
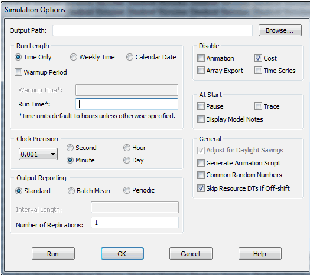
Setelah menentukan elemen untuk kontruksi simulasi dalam ProModel,
penting untuk melakukan pengaturan dalam menjalankan simulasi. Berikut ini adalah
beberapa peraturan dalam menjalankan simulasi ProModel ver 7.5:
Gambar 2.10 Peraturan dalam menjalankan simulasi ProModel ver 7.5
a)
Run Length, adalah penentuan dalam menjalankan simulasi berdasarkan
jangka waktu atau tanggal.
b)
Run Hours, menentukan jangka waktu lamanya pendataan statistik dilakukan.
c)
Warmup Hours, menentukan berapa lama simulasi akan dijalankan sebelum
pendataan statistik dicatat.
d)
Clock Precision, menentukan parameter interval waktu dalam pencatatan
statistik entah berdasarkan detik , menit, jam, atau hari.
e)
Output Reporting, menentukan format hasil laporan yang akan dibuat.
f)
Number of Replication, menyatakan berapa kali jumlah percobaan yang akan
disimulasikan.
g)
Disable
yaitu perintah menonaktifkan fitur
entah perhitungan statistik
berdasarkan waktu, animasi selama simulasi,
perhitungan biaya dalam
simulasi, perhitungan melalui susunan sistematis objek.
h)
Start,
memulai simulasi dari keadaan pause,
awal, atau pada saat mulai
menampilkan catatan.
i)
Display Note,
menampilkan catatan yang sudah dibuat pada elemen
ProModel.
|
|
24
2.3.5
Hasil Simulasi dari ProModel
Setelah melakukan simulasi, ProModel akan menghitung pendataan statistik
di dalam hasil laporannya. Hasil laporan inilah yang merupakan bagian terpenting
dalam melakukan analisa pengambilan keputusan.
Berikut ini adalah hasil laporan
dari simulasi ProModel ver 7.5:
a)
Grafik diagram batang dalam Location
Utilization, berguna untuk menjelaskan
tingkat utilisasi penggunaan dari setiap lokasi di dalam sistem.
b) Grafik diagram batang dalam Single Capacity Location States, berguna untuk
mengetahui komposisi tingkat produktifitas penggunaan fasilitas pelayanan
dengan tingkat non produktifitas penggunaan fasilitas tersebut.
c)
Grafik diagram batang dalam Entity States, berguna untuk mengetahui tingkat
waktu menunggu entitas yang antri dalam memasuki pelayanan fasilitas.
|