|
7
BAB 2
LANDASAN TEORI
2.1
Asuransi
2.1.1
Pengertian Asuransi
“Asuransi adalah suatu kemauan untuk menetapkan kerugian-kerugian
kecil (sedikit) yang sudah pasti sebagai pengganti/substitusi kerugian-kerugian
besar yang belum terjadi”.
[Salim, 2008: 1]
Menurut Undang-undang Nomor 2 Tahun 1992,
“Asuransi atau pertanggungan adalah perjanjian antara dua pihak atau
lebih, dengan mana pihak penanggung mengikatkan diri kepada tertanggung,
dengan menerima premi asuransi untuk memberikan penggantian kepada
tertanggung karena kerugian, kerusakan atau kehilangan keuntungan yang
diharapkan, atau tanggung jawab hukum kepada pihak ketiga yang mungkin
diderita tertanggung, yang timbul dari suatu peristiwa yang tidak pasti, atau untuk
memberikan suatu pembayaran yang didasarkan atas meninggal atau hidupnya
seseorang yang dipertanggungkan.”
[Satria, 2011: 12]
Pengertian asuransi menurut Kitab Undang-undang Hukum Dagang Pasal
246 adalah :
“Asuransi atau pertanggungan adalah suatu perjanjian, dengan mana
seorang penanggung mengikatkan diri kepada tertanggung dengan menerima
suatu premi, untuk memberikan penggantian kepadanya karena suatu kerugian,
|
|
8
kerusakan, atau kehilangan keuntungan yang diharapkan, yang mungkin terjadi
karena suatu peristiwa tak tertentu.”
[Satria, 2011: 13]
2.1.2
Prinsip-prinsip Asuransi
Dalam dunia asuransi terdapat enam prinsip dasar yang harus dipenuhi,
yaitu:
1.
Insurable Interest. Hak untuk mengasuransikan, yang timbul dari suatu
hubungan keuangan, antara tertanggung dengan yang diasuransikan dan
diakui secara hukum.
2.
Utmost Good Faith.
Suatu tindakan untuk mengungkapkan secara akurat
dan lengkap, semua fakta yang material (material fact) mengenai sesuatu
yang akan diasuransikan baik diminta maupun tidak.
3.
Indemnity.
Suatu mekanisme dimana penanggung menyediakan
kompensasi finansial dalam upayanya menempatkan tertanggung dalam
posisi keuangan yang ia miliki sesaat sebelum terjadinya kerugian (KUHD
Pasal 252, 253 dan dipertegas dalam Pasal 278).
4.
Proximate Cause. Suatu sebab aktif yang mengakibatkan terjadinya suatu
peristiwa secara berantai atau berurutan tanpa intervensi suatu kekuatan
lain.
5.
Subrogation. Hak penanggung yang telah memberikan ganti rugi kepada
tertanggung untuk menuntut pihak lain yang mengakibatkan kepentingan
asuransinya mengalami kerugian.
[Satria, 2011: 15]
|
|
9
2.1.3
Fungsi dan Tujuan Asuransi
Fungsi asuransi dibagi menjadi tiga, yaitu :
1.
Fungsi utama,
terdiri dari pemindahan risiko, pengumpulan dana, dan
premi yang seimbang.
2.
Fungsi sekunder, merangsang pertumbuhan usaha, keamanan, sehingga
tertanggung dapat berkonsentrasi pada usahanya, pencegahan kerugian
melalui identifikasi risiko-risiko potensial, pengendalian kerugian untuk
meminimalkan kerugian, manfaat sosial untuk mempercepat pemulihan
perekonomian dan tabungan (investasi).
3.
Fungsi tambahan, terdiri dari investasi dana dari premi yang terkumpul
dan invisible earnings.
[Nugraha, 2008: 8]
Tujuan dari asuransi, yaitu :
1.
Untuk memberikan jaminan perlindungan risiko yang diderita suatu pihak.
2.
Untuk meningkatkan efisiensi, karena tidak perlu
secara khusus
mengadakan pengamanan dan pengawasan untuk memberikan
perlindungan yang memakan banyak tenaga, waktu, dan biaya.
3.
Untuk membantu mengadakan pemerataan biaya, yaitu cukup hanya
dengan mengeluarkan biaya untuk premi saja yang jumlahnya sudah
tertentu secara tetap setiap periode.
4.
Untuk dasar pemberian kredit, terutama dalam sistem perkreditan yang
dilakukan oleh bank. Bank memerlukan jaminan atau agunan yang
diberikan oleh peminjam uang.
5.
Sebagai tabungan, bahkan lebih daripada itu karena yang dibayar kepada
asuransi akan diterima kembali.
|
|
10
6.
Untuk memupuk earning power
seseorang, badan usaha yang akan
digunakan pada waktu terjadi keadaan dimana ia tidak dapat berfungsi.
7.
Untuk modal investasi, bagi pihak lain melalui penggunaan dana yang
dikapitalisasi oleh asuransi.
[Salim, 2008: 29]
2.1.4
Jenis Asuransi
Jenis asuransi dibedakan menjadi empat, yaitu :
1.
Asuransi Jiwa (life insurance)
Yang dapat diasuransikan adalah kemampuan untuk mendapat penghasilan
setelah mengalami musibah/memasuki masa pensiun, biaya rawat
inap/pengobatan, biaya pendidikan dimasa depan dan biaya melunasi
agunan atau kredit bank.
2.
Asuransi Umum(general/non-life insurance)
Yang dapat diasuransikan adalah asset berupa bangunan berikut isi
bangunan, kegiatan konstruksi, kehilangan pekerjaan yang semestinya
diperoleh jika tidak terjadi musibah kendaraan/alat transportasi,
barang/mesin dalam perjalanan, barang pribadi, uang.
3.
Asuransi Sosial (social insurance)
Yang dapat diasuransikan adalah kemampuan untuk mendapat penghasilan
setelah mengalami musibah/memasuki masa pensiun, dan biaya rawat
inap/pengobatan.
4.
Asuransi Kesejahteraan Social (social security insurance)
Asuransi ini khusus untuk orang tidak mampu dan tidak terjamin oleh
sistem asuransi sosial pada umumnya yang berbasis pada kontribusi
peserta.
|
|
11
[Syahsono, 2010: 10]
2.1.5
Risiko yang Dapat Diasuransikan
Tidak semua risiko dapat diasuransikan, secara umum risiko yang dapat
diasuransikan memiliki ciri-ciri sebagai berikut :
1.
Loss-Unexpected. Terjadinya suatu peristiwa yang menimbulkan kerugian
adalah benar-benar tidak direncanakan sehingga tidak dapat diperkirakan
bahwa peristiwa tersebut benar-benar terjadi.
2.
Reasonable.
Risiko yang dapat dipertanggungkan adalah benda yang
memiliki nilai, baik dari pihak penanggung maupun pihak tertanggung.
3.
Catastrophic. Risiko yang tidak akan menimbulkan rugi sangat besar yang
terjadi bersamaan.
4.
Homogeneous. Barang yang akan dipertanggungkan homogen.
Dengan demikian risiko-risiko yang dapat diasuransikan adalah:
1.
Risiko yang dapat diukur dengan uang.
2.
Risiko homogen (risiko yang sama dan cukup banyak dijamin oleh
asuransi).
3.
Risiko murni (risiko ini tidak mendatangkan keuntungan).
4.
Risiko partikular (risiko dari sumber individu).
5.
Risiko yang terjadi secara tiba-tiba (accidental).
6.
Insurable interest
(tertanggung memiliki kepentingan atas obyek
pertanggungan).
7.
Risiko yang tidak bertentangan dengan hukum.
[Satria, 2011: 14]
|
|
12
2.2
Klaim, Premi, dan Polis
2.2.1
Pengertian Klaim
“Klaim adalah tuntutan ganti rugi sehubungan dengan peristiwa kerugian
terhadap objek asuransi dipertanggungkan”.
[Widiastuti, 2004: 24]
2.2.2
Pengertian Premi dan Polis
“Premi adalah pembayaran dari tertanggung kepada penanggung sebagai
imbalan jasa atas pengalihan risiko kepada penanggung”.
[Djojosoedarso, 2003: 127]
“Polis adalah surat
perjanjian yang mengatur segala hak dan kewajiban
dari masing-masing pihak”.
[Djojosoedarso, 2003: 72]
2.3
Proses Stokastik
Proses adalah runtunan perubahan (peristiwa) dalam perkembangan
sesuatu,rangkaian tindakan, pembuatan, atau pengolahan yang menghasilkan
produk dan stokastik adalah unsur peluang atau kemungkinan. Maka definisi dari
Proses Stokastik
adalah koleksi peubah acak dengan t
menyatakan indeks
waktu.
[KBBI, 2008]
Jika nilai suatu masa depan (future value) hanya dapat digambarkan dalam
suatu distribusi probabilitas maka time series
dikatakan sebagai stokastik time
series. Dengan demikian, jika dari pengalaman yang lalu keadaan yang akan
datang suatu barisan kejadian dapat diramalkan secara pasti, maka barisan
kejadian itu dinamakan deterministik. Sebaliknya jika pengalaman yang lalu
|
 13
hanya dapat menyajikan struktur peluang keadaan yang akan datang, maka
barisan kejadian yang demikian disebut stokastik.
[Halim, 2006: 2]
Proses stokastik
adalah suatu himpunan dari peubah
acak yang memetakan suatu ruang contoh O
ke suatu ruang state
S. Jadi, untuk
setiap t pada himpunan indeks T,
adalah suatu peubah acak. Setiap t
pada
himpunan indeks T juga sering diinterpretasikan sebagai waktu, dan
sebagai
state (keadaan) dari proses pada waktu t.
Suatu proses stokastik X
disebut proses stokastik dengan waktu kontinu
jika T
adalah suatu interval. Suatu proses stokastik dengan waktu kontinu
disebut memiliki inkremen
bebas jika untuk semua
, peubah acak
adalah bebas. Dengan kata
lain, suatu proses stokastik dengan waktu kontinu X
disebut memiliki inkremen
bebas jika proses berubahnya nilai pada interval waktu yang tidak tumpang tindih
(tidak overlap) adalah bebas.
Suatu proses stokastik dengan waktu kontinu
disebut
memiliki inkremen
stasioner jika
memiliki sebaran yang sama
untuk semua nilai t. Dengan kata lain, suatu proses stokastik dengan waktu
kontinu X
disebut memiliki inkremen
stasioner jika sebaran (distribusi) dari
perubahan nilai
antara sembarang dua titik hanya tergantung pada jarak
antara
kedua titik tersebut, dan tidak tergantung dari lokasi titik-titik tersebut.
[Ross, 2010: 84]
|
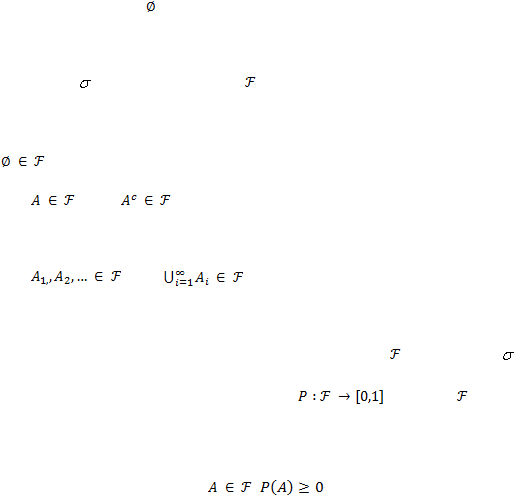 14
2.4
Ruang Contoh, Kejadian dan Peluang
Suatu percobaan yang dapat diulang dalam kondisi yang sama, yang
hasilnya tidak bisa diprediksi dengan tepat tapi kita bisa mengetahui semua
kemungkinan hasil yang muncul disebut percobaan acak.
[Hogg , McKean & Craig, 2012]
Ruang contoh adalah himpunan semua hasil yang mungkin dari suatu
percobaan acak, dan dinotasikan dengan
O. Suatu kejadian A
adalah himpunan
bagian dari O. Kejadian A
dan B
disebut saling lepas jika irisan dari keduanya
adalah himpunan kosong
.
[Pinsky & Karlin, 2011: 4]
Medan-
adalah suatu himpunan
yang anggotanya terdiri atas himpunan
bagian ruang contoh O, yang memenuhi syarat berikut:
1.
2.
Jika
, maka
3.
Jika
maka
[Pinsky & Karlin, 2011: 4]
Misalkan O adalah ruang contoh suatu percobaan dan
adalah medan-
pada
O. Ukuran peluang adalah suatu fungsi
pada (O,
) yang
memenuhi :
1.
P
tak negatif, yaitu untuk setiap
,
.
|
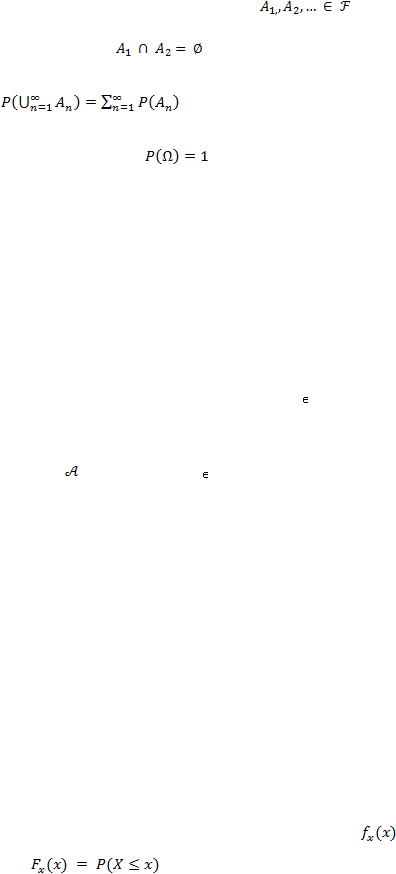 15
2.
P
bersifat aditif tak hingga, yaitu jika
adalah himpunan yang
saling lepas, yaitu
untuk setiap pasangan i
? j
, maka
3.
P
bernorma satu, yaitu
.
Pasangan (O, P) disebut ruang ukuran atau ruang probabilitas.
[Pinsky & Karlin, 2011: 4]
2.5
Peubah Acak dan Fungsi Sebaran
Misalkan O adalah ruang contoh dari suatu percobaan acak. Fungsi X yang
terdefinisi pada O yang memetakan setiap unsur ?
O
ke satu dan hanya satu
bilangan real X(?) = x disebut peubah acak. Ruang dari X adalah himpunan bagian
bilangan real
= {x : x = X(?), ?
O}. Peubah acak dinotasikan dengan huruf
kapital, misalnya X, Y, Z. Sedangkan nilai peubah acak dinotasikan dengan huruf
kecil seperti x, y, z.
[Pinsky & Karlin, 2011: 5]
Peubah acak X
dikatakan diskret jika semua himpunan nilai dari peubah
acak tersebut merupakan himpunan tercacah.
[Pinsky & Karlin, 2011: 8]
Catatan :
Suatu himpunan bilangan C disebut terhitung jika C terdiri atas bilangan terhingga
atau anggota C dapat dikorespondensikan 1-1 dengan bilangan bulat positif.
Peubah acak X dikatakan kontinu jika ada fungsi
sehingga fungsi
sebaran
dapat dinyatakan sebagai :
|
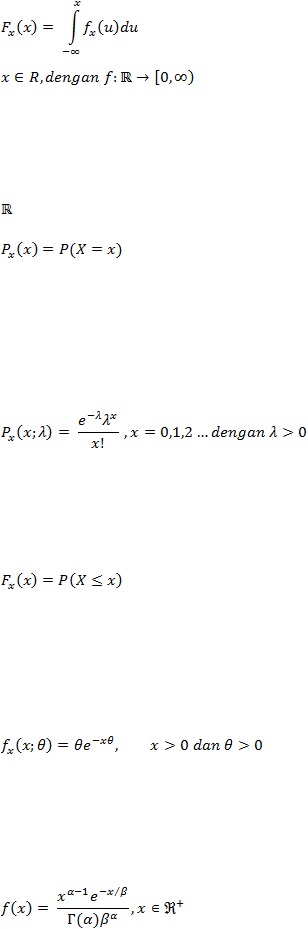 16
adalah fungsi yang terintegralkan. Fungsi f disebut
fungsi kepekatan peluang dari X .
[Pinsky
& Karlin, 2011: 8]
Fungsi kerapatan peluang dari peubah acak diskret X
adalah fungsi p
:
? [0,1] yang diberikan oleh :
[Pinsky & Karlin, 2011: 8]
Suatu peubah acak X disebut peubah acak Poisson dengan parameter ?, ? >
0, jika fungsi kerapatan peluangnya diberikan oleh :
[Pinsky & Karlin, 2011: 22]
Misalkan X adalah suatu peubah acak dengan ruang A. Fungsi sebaran dari
peubah acak X dinyatakan sebagai,
[Hogg, McKean, & Craig, 2012: 31]
Suatu peubah acak X dikatakan menyebar Eksponensial dengan parameter
?, jika X memiliki fungsi kepekatan peluang :
[Pinsky & Karlin, 2011: 28]
Suatu peubah acak X dikatakan menyebar Gamma dengan parameter a dan
ß, dinotasikan Gamma(a,ß), jika memiliki fungsi kepekatan peluang
|
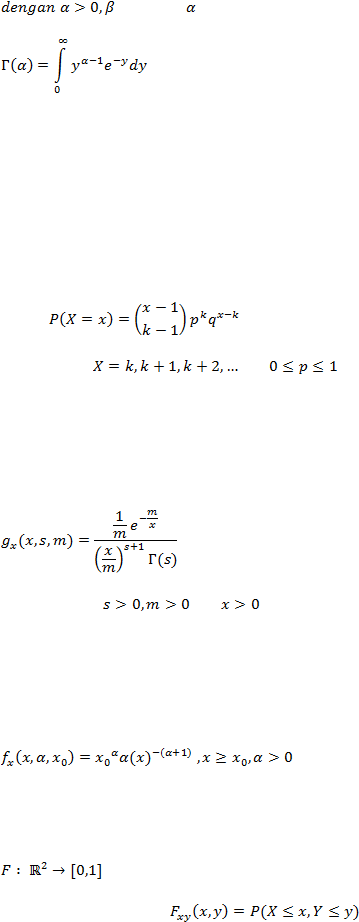 17
> 0 dan ?(
) > 0, dimana
[Pinsky & Karlin, 2011: 30]
Jika usaha yang saling bebas, dilakukan berulang kali menghasilkan
sukses dengan peluang p sedangkan gagal dengan peluang q = 1-p,
maka peubah
acak X
(yaitu banyaknya usaha yang berakhir tepat pada usaha ke-k) disebut
berdistribusi Binomial negatif jika dan hanya jika :
Untuk
dan
[Pinsky & Karlin, 2011: 21]
Suatu peubah acak X
dikatakan menyebar Invers-Gamma
dengan
parameter s dan m, jika memiliki fungsi kepekatan peluang :
Dengan
dan
[Hogg & Klugman, 2009]
Suatu peubah acak X dikatakan menyebar Pareto dengan parameter x
0
dan
a, jika memiliki fungsi kepekatan peluang :
[Ross, 2010]
Fungsi sebaran bersama dua peubah acak X dan Y merupakan suatu fungsi
yang didefinisikan oleh
|
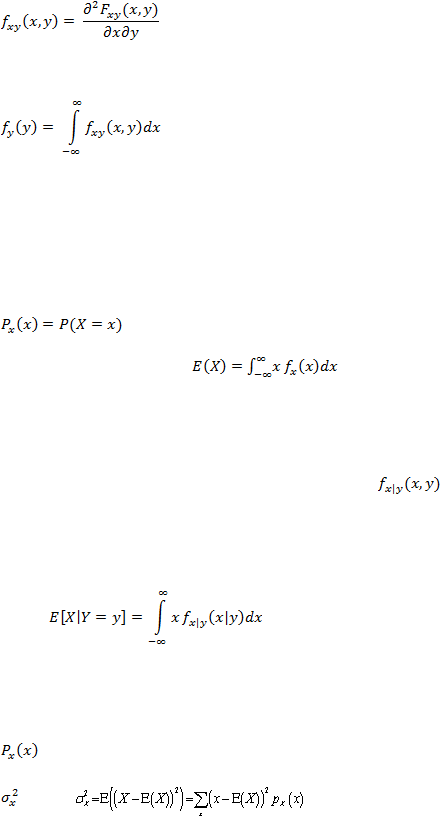 18
[Pinsky & Karlin, 2011: 501]
Misalkan X dan Y adalah peubah acak kontinu, maka fungsi kepekatan
peluang bersama dari X dan Y adalah
dan fungsi kepekatan peluang marjinal dari peubah acak Y adalah
[Pinsky & Karlin, 2011: 501]
2.6
Momen, Nilai Harapan, dan Ragam
Misalkan X adalah peubah acak diskret dengan fungsi kerapatan peluang
. Nilai harapan dari X, dinotasikan dengan E(X), adalah
jika jumlah di atas konvergen mutlak.
[Pinsky & Karlin, 2011: 7]
Misalkan X dan Y adalah peubah acak kontinu dan
adalah fungsi
kepekatan peluang bersyarat dari X
dengan syarat Y = y. Nilai harapan dari X
dengan syarat Y = y adalah
[Pinsky & Karlin, 2011: 7]
Misalkan X adalah peubah acak diskret dengan fungsi kerapatan peluang
dan nilai harapan E(X). Maka ragam dari X, dinotasikan dengan var (X) atau
,
adalah
|
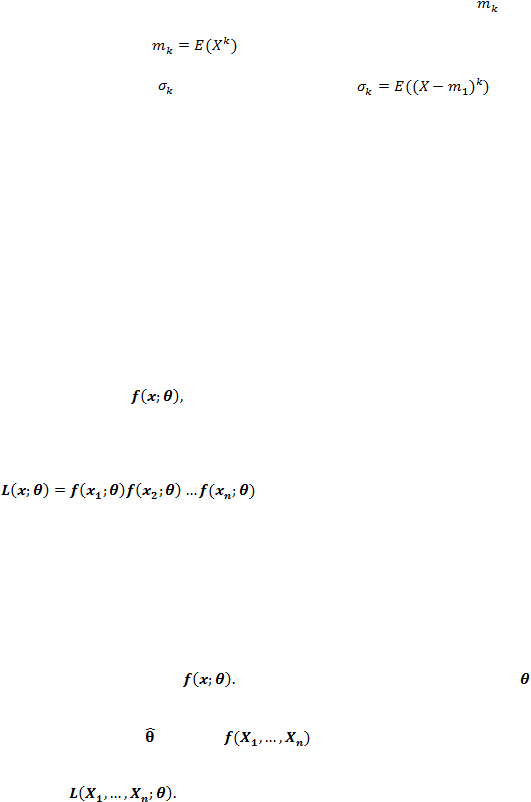 19
[Pinsky & Karlin, 2011: 7]
Jika k
adalah bilangan bulat positif , maka momen ke-k
atau
dari
peubah acak X adalah
.
Jika k
adalah bilangan bulat positif , maka
momen pusat ke-k atau
dari peubah acak X adalah
.
Nilai
harapan dari peubah acak X
juga merupakan rataan atau momen pertama dari X.
Nilai harapan dari kuadrat perbedaan antara peubah acak X
dengan nilai
harapannya disebut ragam atau variance dari X. Ragam merupakan momen pusat
ke-2 dari peubah acak X.
[Pinsky & Karlin, 2011: 7-8]
2.7
Likelihood
Misalkan X1
, X2, ..., X
n
adalah contoh acak dari suatu sebaran dengan fungsi
kepekatan peluang
dengan x merupakan realisasi dari peubah acak X.
Fungsi kepekatan peluang bersama dari X1, X2
, ..., X
n
(fungsi likelihood) adalah :
Fungsi kemungkinan maksimum merupakan bentuk maksimum dari fungsi
likelihood.
[Hogg, McKean, & Craig, 2012: 258]
Misalkan X1, X2
, ..., X
n
adalah contoh acak berukuran n dari suatu sebaran dengan
fungsi kepekatan peluang
Penduga kemungkinan maksimum bagi
dinotasikan dengan
,
adalah
yang memaksimumkan fungsi
likelihood
[Hogg, McKean, & Craig, 2012: 259]
|
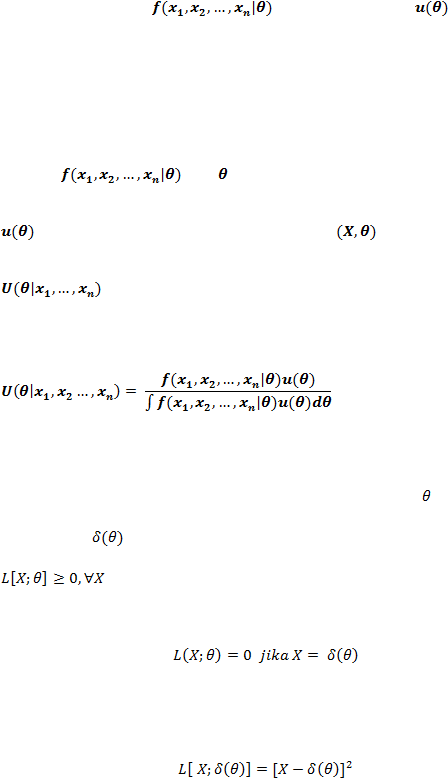 20
2.8
Pendekatan Bayes
Suatu peubah acak X
yang memiliki fungsi kepekatan peluang bersama yang
dilambangkan dengan
dan fungsi marjinal
, dinamakan
sebaran prior.
[Hogg, McKean, & Craig, 2012: 228]
Misalkan peubah acak X memiliki sebaran prior dengan fungsi kepekatan peluang
bersama
dan
memiliki fungsi kepekatan peluang marjinal
.
Fungsi kepekatan peluang gabungan dari
dilambangkan dengan
dinamakan fungsi kepekatan peluang dari sebaran posterior, dan
dinyatakan dengan :
[Hogg, McKean, & Craig, 2012: 228]
Misalkan X
adalah suatu peubah acak dengan parameter
dan penduga
parameternya
. Fungsi kerugian (loss function) dari parameter tersebut adalah
dan
Fungsi kerugian kuadratik
merupakan fungsi kerugian dengan kesalahan kuadrat
dari parameter tersebut yang dinyatakan dengan :
[Hogg, McKean, & Craig, 2012: 230]
|
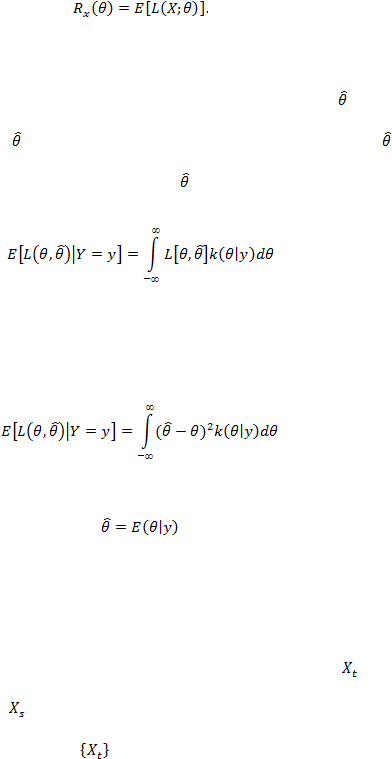 21
Fungsi resiko adalah nilai harapan dari fungsi kerugian, yang dinyatakan sebagai
berikut :
[Hogg, McKean, & Craig, 2012: 230]
Misalkan ? adalah suatu parameter dengan penduga parameternya
, dengan
fungsi kerugian L[?,
] dan nilai harapan dari fungsi kerugian tersebut E[L[?,
]],
dikatakan solusi Bayes jika penduga parameter
meminimumkan
Solusi Bayes
ini tergantung dari fungsi kerugiannya, jika diaplikasikan dalam
fungsi kerugian kuadratik (quadratic error loss) :
Sehingga menjadi :
[Hogg, McKean, & Craig, 2012: 229]
2.9
Rantai Markov
Proses stokastik yang memiliki sifat bahwa jika diberi nilai
, maka
untuk s > t, nilai
tidak dipengaruhi oleh nilai-nilai dari u < t
disebut
sebagai suatu proses Markov
. Dapat diartikan sebagai, peluang perilaku
tertentu di masa yang akan datang dari suatu proses, jika diketahui state
saat
|
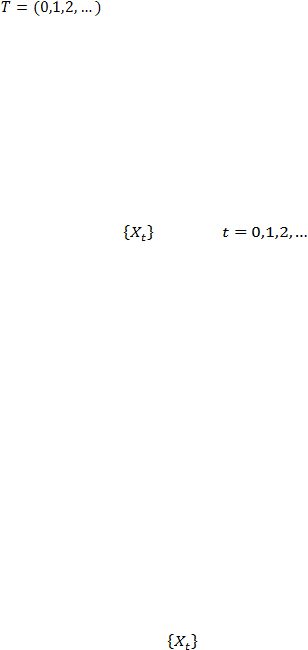 22
ini, tidak dapat dipengaruhi oleh informasi tambahan di masa yang sudah
lalu.
[Pinsky
& Karlin, 2011: 79]
Rantai Markov
diskrit
adalah suatu proses Markov
yang ruang state-
nya adalah gugus hingga atau gugus yang dapat dihitung dengan gugus
indeks
. Dapat dirumuskan sebagai berikut untuk semua titik
yang berada pada waktu n dan semua state :
Pr{X
n+1
= j|X
0
= i
0
, . . . , X
n
-1
= i
n
-1
, X
n
= i}
= Pr{X
n+1
= j|X
n
= i}
pada rantai Markov
dinyatakan sebagai bilangan bulat tak
negatif,
X
n
= 1
yang menyatakan bahwa
X
n
terdapat pada state
i
.
Proses stokastik
dengan
disebut rantai Markov
state hingga jika:
1. Memiliki sejumlah hingga state
2. Bersifat Markov
3. Peluang peralihan stasioner
4. Memiliki peluang awal P (X
0
= i)
untuk semua i.
[Pinsky & Karlin, 2011: 79]
Analisis Markov
merupakan suatu metode yang mempelajari sifat-sifat
suatu
variabel pada masa sekarang yang didasarkan pada sifat-sifatnya di masa
lalu dalam usaha menaksir sifat-sifat variabel yang sama di masa yang akan
datang.
Sebuah proses stokastik
dikatakan mempunyai sifat Markov
jika
peluang bersyarat dari kejadian yang akan datang P (X
t
= j|X
t
= i)
disebut
peluang peralihan. Dapat diartikan bahwa proses stokastik mempunyai sifat
(2.1)
|
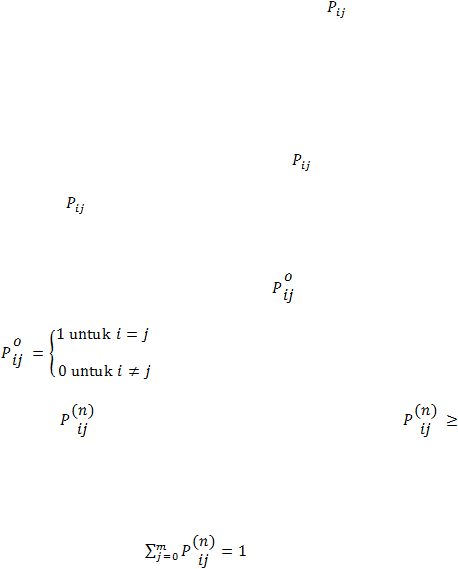 23
Markov
jika peluang bersyarat dari state
yang akan datang X
t+1
= j, jika
diberikan state
yang telah lalu dan sekarang X
t
= 1, tidak tergantung pada
state
sekarang dari sebuah proses. Peluang bersyarat P(X
t+1
= j|X
t
= i)
disebut
Peluang transisi.
Jika untuk setiap i
dan j
berlaku P(X
t+1
= j(X
t
= i) = P (X
t
= j|X
0
=
1)
untuk semua t = 0, 1, . . . , n
maka peluang transisi
satu langkah
dikatakan stasioner dan dilambangkan dengan
. Artinya peluang transisi
stasioner adalah peluang transisi
yang tidak berubah terhadap waktu (tidak
tergantung parameter t), sehingga untuk setiap i, j dan n, untuk n = 0, 1, . . .
, sehingga P (X
t+n
= j(X
t
= i) = P (X
n
= j|X
0
=1)
untuk t = 0, 1, . . . , n.
Peluang bersyarat ini dilambangkan oleh
dan disebut peluang transisi
n
langkah.
adalah peluang bersyarat variabel acak X
dimulai dari state i
hingga keadaan j
setelah n-langkah.
Untuk
n = 0 P(X
n
= j|X
0
= i) =
, dimana
Karena
adalah peluang bersyarat maka haruslah
0
untuk
semua i,j
dan n
= 0,1,….
dan karena proses membuat transisi
ke dalam
beberapa state maka :
, untuk semua i dan n = 0, 1, ….. ,
n
Peluang transisi
dapat juga ditulis dalam bentuk matriks untuk n = 0, 1,
. . . , n
:
Table 2.1 Peluang Peralihan Dalam Bentuk Matriks
|
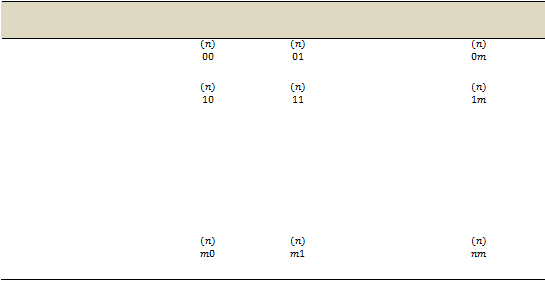 24
State
0
1
...
M
0
P
P
…
P
1
P
P
…
P
P
(n)
=
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
M
P
P
…
P
[Pinsky & Karlin, 2011: 95]
2.10
Sistem Bonus Malus
Bonus berasal dari bahasa latin yang memiliki arti hadiah karena kinerja
yang baik, sedangkan Malus
berasal dari bahas latin yang memiliki arti buruk,
jahat, merugikan.
Sistem Bonus-Malus
pertama kali diperkenalkan dan
dikembangkan di Eropa pada awal tahun 1960. Khususnya pada asuransi
kendaraan bermotor premi dasar ditentukan berdasarkan besar, harga atau
kapasitas dari kendaraan yang diasuransikan. Setelah masuk asuransi, penentuan
besar premi pada tahun berikutnya hanya dipengaruhi oleh banyaknya kecelakaan
dalam satu tahun periode sebelumnya. Perubahan premi kendaraan bermotor dari
tahun pertama ke tahun kedua, dengan tahun pertama tidak ada klaim, atau ada
satu klaim, atau dua klaim, dan seterusnya direalisasikan sebagai bentuk transisi
dari keadaan.
|
 25
Sistem Bonus-Malus (BMS) mempresentasikan banyaknya tarif grup yang
berhingga dan bergantung pada premi tahunan. Setiap tahun, tarif grup ditetapkan
sebagai tarif grup dari tahun sebelumnya dan banyaknya klaim yang tercatat dari
tertanggung asuransi pada perusahaan asuransi selama tahun itu. Jika tidak ada
klaim atau klaim tidak tercatat maka tertanggung tersebut akan mendapat Bonus
yang berbentuk pengurangan nilai premi. Sedangkan jika terjadi klaim, paling
sedikit satu klaim yang tercatat maka premi yang harus dibayar pada tahun
berikutnya oleh tertanggung akan naik. Dengan kata lain jika dalam satu tahun
periode terjadi klaim maka akan mendapat Malus.
Sistem Bonus-Malus dapat dinyatakan sebagai berikut:
1. Banyaknya tarif grup berhingga di awal periode dari asuransi dinotasikan
dengan Ci, dimana i = 1,2,….n. Sedangkan banyaknya tarif grup di akhir periode
asuransi dinotasikan dengan Cj, dimana
j = 1,2…n. Tarif grup terendah disebut
dengan super-Bonus
dan tarif grup tertinggi disebut dengan super-Malus. Premi
tahunan bergantung pada banyaknya tarif grup yang terjadi.
2. Persentase dari premi dasar
(dalam %) menotasikan persentase
yang akan
dikalikan dengan premi dasar sebagai premi berikutnya yang harus dibayar,
dengan
.
3. Perpindahan dari tarif grup sebelumnya (ke-i) ke tarif grup berikutnya (ke-j)
dengan k klaim yang tercatat, dinyatakan dengan :
t
ij
=
(2.9.1)
Untuk selanjutnya, misalkan untuk seorang pemegang polis, klaim yang
tercatat dalam satu tahun adalah berbentuk suatu barisan X1, X2
,…. X
m
dari suatu
peubah acak yang saling bebas dengan fungsi peluang bersama {q
k
}. Dinotasikan
|
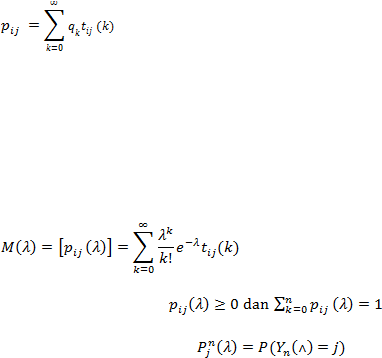 26
bahwa C1,C2,… adalah tarif grup dari tahun ke tahun dari pemegang polis. Tarif
grup tahun sebelumnya dengan banyaknya klaim yang tercatat. Dengan demikian
maka permasalahan sistem Bonus-Malus
dapat dipandang sebagai model rantai
Markov. Dengan menggunakan teori Markov, maka {C
n
} barisan peubah acak
dengan ruang tarif
grup berhingga. {C
n
} adalah Rantai Markov
yang memiliki
matrik M=(p
ij
)
sedemikian hingga untuk semua n = 1,2,… dan i
0
,i1
,…,i
n
,
Pr(C
n
= i
n
| C
n-1
= i
n-1
,…., C
0
= i
0
)
= P(i
n-1
,
i
n
)
(2.9.2)
Dimana,
Pr(C
n-1
= i
n-1
,…., C
0
= i
0
) > 0
Peluang transisi p
ij
merupakan peluang perpindahan dari tarif grup ke-i ke tarif
grup ke-j dari pemegang polis dapat dituliskan sebagai
Banyaknya klaim (k) yang terjadi dan tercatat oleh pemegang polis
diasumsikan memenuhi definisi proses Poisson
dengan laju ?. Dengan
menggunakan persamaan (2.9.1) maka matrik transisi p
ij
dari rantai Markov dapat
menjadi
Dengan,
Misal didefinisikan :
Dari persamaan (2.9.2) peluang untuk tidak ada klaim adalah positif, P
0
(?) < 0.
Dengan menggunakan sifat dari rantai Markov yang regular maka diperoleh
i.
Jika distribusi peluang untuk banyaknya klaim selama satu periode adalah
saling bebas terhadap periode, maka tarif grup untuk polisnya berbentuk
|
|
27
rantai Markov dengan matrik transisi M(?)
yang diberikan dalam persamaan
(2.9.2).
ii.
Jika peluang untuk tidak ada klaim dalam satu periode P
0
(?) > 0, maka
disebut dengan regular.
Akibatnya P
k
(?) > 0. Dengan demikian rantai Markov dari sistem Bonus-Malus
adalah regular. Artinya terdapat bilangan q = 1, sehingga {M(?)}
q
semua unsurnya
bernilai positif murni. Dalam kasus regular
dengan nilai eigen
satu yaitu nilai
eigen
dari matrik M. Distribusi stasioner, vektor
kolom p(?) merupakan solusi
tunggal dari persamaan dengan
[Supandi, 2010: 45-46]
2.11
Teori Risiko
Risiko adalah kemungkinan terjadinya hal-hal yang tidak diinginkan yang
menimbulkan kerugian. Risiko dalam industri perasuransian diartikan sebagai
ketidakpastian dari kerugian finansial atau kemungkinan terjadinya kerugian.
2.11.1
Klasifikasi Risiko
Risiko dapat diklasifikasikan sebagai berikut :
1.
Speculative Risks (Risiko Spekulatif)
Risiko spekulatif adalah risiko yang memberikan kemungkinan
untung (gain) atau rugi (loss) atau tidak untung dan tidak rugi (break
even). Risiko Spekulatif disebut juga risiko dinamis (dynamic risk).
2.
Pure Risks (Risiko Murni)
|
|
28
Risiko yang hanya mempunyai satu akibat yaitu kerugian.
Sehingga tidak ada orang yang akan menarik keuntungan dari risiko
ini.
3.
Fundamental Risk (Risiko fundamental)
Risiko yang sebab maupun akibatnya impersonal
(tidak
menyangkut seseorang). dimana kerugian yang timbul dari risiko
yang bersifat fundamental biasanya tidak hanya menimpa seorang
individu melainkan menimpa banyak orang.
4.
Particular Risks (Risiko Khusus)
Risiko khusus dimana risiko ini disebabkan oleh peristiwa-
peristiwa individual dan akibatnya terbatas.
5.
Perubahan Klasifikasi Risiko
Perubahan klasifikasi risiko dapat terjadi apabila penyebab
terjadinya risiko dan akibat dari risiko berubah atau dapat pula
disebabkan adanya cara pandang seseorang terhadap risiko tersebut.
6.
Guna Klasifikasi Risiko
Klasifikasi risiko berguna dalam rangka menetapkan apakah
suatu risiko dapat diasuransikan atau tidak dan untuk menentukan
apakah suatu risiko lebih tepat ditangani oleh pemerintah atau
diserahkan kepada lembaga asuransi komersial.
7.
Risiko Yang Dapat Diasuransikan dan Risiko Yang Tidak Dapat
Diasuransikan
|
|
29
Risiko spekulatif tidak dapat diasuransikan karena pada risiko
ini terdapat kemungkinan untuk mendapatkan keuntungan. Risiko
murni dapat diasuransikan karena hanya mempunyai satu
kemungkinan yaitu mendatangkan kerugian, tetapi berdasarkan
pertimbangan secara yuridis maupun komersial tidak semua risiko
murni dapat diasuransikan. Risiko fundamental biasanya asuransinya
dikelola oleh pemerintah, hal ini dikarenakan akibat dari risiko ini
dalam jumlah dan area yang luas.
[Griffin, & Lemmon, 2008]
2.11.2
Analisis Risiko
Dalam berbagai aspek kehidupan, terdapat perbedaan tingkatan pada
risiko. Hal-hal yang berpengaruh pada tingkatan risiko adalah aspek seringnya
kejadian terjadi (frekuensi) dan tingkat keparahan (severity). Kombinasi dari
kemungkinan munculnya suatu peristiwa dan besarnya kerugian (severity) yang
dialami peristiwa tersebut kita namakan risiko. Hubungan antara frekuensi dan
severity
adalah frekuensi tinggi severity
rendah, dan severity
tinggi
frekuensi
rendah.
[Salim, 2008]
2.12
Java Programming Language
Pemograman dengan bahasa Java dikembangkan oleh
Sun
Microsystems
sebagai bahasa
berorientasi objek
untuk tujuan umum
yaitu, aplikasi bisnis
interaktif, dan aplikasi internet berbasis web. Java
dapat dijalankan di
berbagai
komputer
karena tidak
mengeksekusi instruksi
pada
komputer secara langsung.
Sebaliknya, Java
berjalan pada
komputer
hipotetis
yang dikenal sebagai
Java
Virtual Machine.
|
|
30
[Farrell, 2012: 8]
Selain itu Java sendiri mempunyai karakteristik yang telah dikembangkan,
dimana karakteristik inilah yang menjadi ciri khas dari bahasa Java. Berikut
adalah karakteristik dari bahasa Java :
1.
Berorientasi Objek, Java
telah menerapkan konsep pemrograman
beorientasi objek dalam implementasinya.
2.
Robust, Java mendorong pemrograman yang bebas dari kesalahan dengan
bersifat strongly typed dan memiliki run-time checking.
3.
Portable, program Java
dapat dieksekusi di platform
manapun selama
tersedia JVM (Java virtual machine) untuk platform tersebut.
4.
Multithreading, Java
mendukung penggunaan multithreading
yang telah
terintegrasi secara langsung dalam bahasa Java.
5.
Dinamis, program Java
dapat melakukan suatu tindakan yang ditentukan
pada saat eksekusi program dan bukan pada saat kompilasi.
6.
Sederhana, Java
menggunakan bahasa yang sederhana dan mudah
dipelajari.
7.
Terdistribusi, Java
dirancang pada lingkungan yang terdistribusi seperti
halnya internet.
8.
Aman, aplikasi yang dibuat dengan bahasa Java
dapat dipastikan
keamanannya terutama untuk aplikasi internet.
9.
Netral secara arsitektur, Java
tidak terikat pada suatu mesin atau sistem
operasi tertentu.
10.
Interpreted, aplikasi Java
dapat dieksekusi pada platform
yang berbeda-
beda dengan melakukan interpretasi pada bytecode.
[Wintari & Purnama, 2011: 8-9]
|
|
31
Java merupakan bahasa pemrograman berorientasi objek atau OOP (object
oriented programming) karena semua aspek yang ada di Java adalah objek. Hal
tersebut
sangat memudahkan programmer
untuk merancang, membuat,
mengembangkan dan mengalokasikan kesalahan secara cepat, tepat, mudah dan
terorganisir. Elemen-elemen dari pemrograman Java itu diantaranya :
1.
Encapsulation, mekanisme pemrograman yang mengikat data dan program
bersama-sama dan mengamankannya dari penyalahgunaan dan intervensi
dari luar.
2.
Polymorphism, mengakses general class dalam prosesnya.
3.
Inheritance, proses dimana penurunan suatu objek terhadap objek lain
yang menjadi parent.
[Andriyanto, Adian, & Sofwan, 2011: 2]
2.13
Rekayasa Perangkat Lunak
Rekayasa perangkat
lunak adalah pembentukan dan penggunaan prinsip -
prinsip teknik suara dalam rangka untuk memperoleh perangkat lunak secara
ekonomis yang handal dan bekerja secara efisien pada mesin nyata. Definisi
rekayasa perangkat lunak adalah sebuah teknologi yang terdiri dari lapisan-lapisan
dan bertumpu pada komitmen organisasi kepada kualitas. Lapisan-lapisan dari
rekayasa perangkat lunak, yaitu:
1.
Fokus pada kualitas (quality focus)
2.
Proses (process)
3.
Metode (methods)
4.
Alat bantu (tools)
|
 32
Terdapat
empat
kegiatan
mendasar
yang umum untuk
semua proses
perangkat
lunak, yaitu:
1.
Spesifikasi,
merupakan kegiatan dimana customer mendefinisikan
perangkat lunak yang akan diproduksi dan kendala pada operasi.
2.
Pengembangan, merupakan kegiatan dimana
perangkat lunak ini
dirancang dan diprogram.
3.
Validasi,
merupakan kegiatan dimana perangkat lunak
tersebut akan
diperiksa
untuk memastikan
bahwa itu merupakan permintaan dari
customer.
4.
Evolusi,
merupakan kegiatan dimana
perangkat lunak tersebut
dimodifikasi untuk memenuhi keinginan customer dan persyaratan pasar.
[Pressman, 2010: 12-13]
2.14
Waterfall Model
Model
waterfall
adalah
model
yang
bersifat
sistematis dan sekuensial
dalam
pengembangan
perangkat
lunak yang melalui tahapan communication,
planning, modelling, construction, dan deployment. Disebut waterfall karena
tahap demi tahap yang dilalui harus menunggu selesainya tahap sebelumnya dan
berjalan secara berurutan. Tahapan pada model waterfall dapat dilihat pada
gambar 2.1.
|
|
33
Gambar 2.1 Model Waterfall
(Pressman, 2010: 39)
Berikut penjelasan dari tahapan-tahapan tersebut:
1.
Communication
Tahapan ini terdiri dari project initiation dan requirements gathering,
yaitu merupakan tahap pengumpulan informasi dan mencari kebutuhan
dari keseluruhan sistem yang akan diaplikasikan ke dalam bentuk
software.
2.
Planning
Tahapan ini terdiri dari estimating, scheduling dan tracking. Pada tahap ini
pengembang software
membuat perkiraan yang diperlukan serta
penjadwalan agar pembuatan software dapat selesai sesuai dengan waktu
yang diperkirakan.
3.
Modelling
Tahapan ini terdiri dari analysis dan design. Proses ini bertujuan untuk
mengubah kebutuhan-kebutuhan diatas menjadi representasi software
sebelum proses penulisan kode (coding) dimulai.
4.
Construction
Terdiri dari proses coding dan pengujian software, pada tahap ini design
software diterjemahkan menjadi bahasa yang dimengerti oleh mesin. Lalu
semua fungsi software
diuji coba agar software bebas dari error
dan
hasilnya sesuai dengan kebutuhan yang sudah didefinisikan sebelumnya.
5.
Deployment
|
|
34
Terdiri dari delivery, support dan feedback. Pada tahap ini software
digunakan langsung oleh customer. Pengembang juga menyediakan
dokumentasi untuk semua fitur dan fungsi, dan pengembang mendapatkan
umpan balik terhadap software untuk
kepentingan modifikasi fitur dan
fungsi.
[Pressman, 2010: 39]
2.15
Unified Modelling Language (UML)
UML adalah pemodelan yang digunakan untuk menggambarkan sebuah
sistem piranti lunak yang terkait dengan objek. UML terdiri dari beberapa tipe
diagram yaitu Use Case Diagram, Activity Diagram, Sequence Diagram, dan
Class Diagram.
2.15.1
Use Case Diagram
Use case
diagram
adalah diagram yang menggambarkan interaksi antara
sistem, eksternal sistem, dan pengguna. Diagram ini menyediakan informasi
mengenai siapa saja yang akan menggunakan sistem tersebut dan bagaimana cara
untuk menggunakannya.
Terdapat beberapa komponen kunci pada use case diagram, yaitu :
1.
Use cases, digunakan untuk menggambarkan deskripsi fungsional dari sistem
dari perspektif pengguna (user), yang berisi satu set perilaku terkait transaksi
yang biasanya dilakukan bersama-sama untuk menghasilkan nilai bagi
pengguna.
2.
Actors, mewakili peran orang, sistem lain, perangkat lain, ketika
berkomunikasi dengan kasus penggunaan tertentu dalam sistem.
|
|
35
3.
Relationships,
digambarkan sebagai garis antara dua simbol pada use case
diagram.
Arti dari setiap relationship
berbeda tergantung dari bagaimana
garis tersebut ditarik dan jenis simbol yang terhubung. Terdapat beberapa
jenis relationship pada use case diagram, yaitu :
a.
Associations, terjadi apabila hubungan antara actor
dan use case
tersebut
mendeskripsikan interaksi antara kedua belah pihak.
b.
Extends,
terjadi apabila terdapat hubungan antara extention use case dan
use case. Sebuah use case
diperbolehkan untuk mempunyai banyak
extends relationship, tetapi extension use case
hanya dapat dilakukan
apabila bersama dengan use case yang sedang berkembang
c.
Include, terjadi apabila ada urutan perilaku (use case) yang digunakan
dalam sejumlah kasus, dan user
ingin menghindari penyalinan deskripsi
yang sama ke dalam setiap use case yang digunakan. Include Relationship
biasa disebut sebagai penggambaran use case
yang memiliki perilaku dari
use case lain.
[Whitten & Bentley, 2007: 382]
|
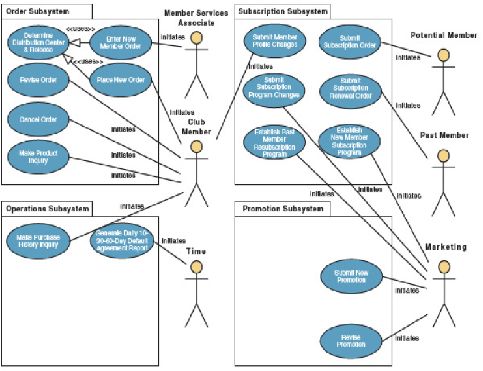 36
Gambar 2.2 Contoh Use Case Diagram
(Whitten & Bentley, 2007: 384)
2.15.2
Activity Diagram
Activity Diagram digunakan untuk menggambarkan aliran berurutan dari
sebuah proses use case atau business process. Selain itu, dapat juga digunakan
untuk logika model dengan sistem yaitu, menggambarkan tindakan (action) yang
akan dijalankan ketika suatu proses sedang berjalan dan beserta hasil dari proses
yang dijalankan tersebut.
Terdapat beberapa komponen dalam menggambarkan activity diagram,
yaitu :
1.
Initial Node,
bentuk lingkaran berisi penuh melambangkan awal dari suatu
proses.
|
|
37
2.
Actions,
bentuk persegi panjang yang mempunyai ujung lingkaran yang
melambangkan tahap-tahap per individu. Sequence dari actions
menunjukan
total dari aktivitas yang dilihat dari diagram.
3.
Flows, panah pada diagram mengindikasikan kemajuan
dari sebuah actions.
Kebanyakan flow tidak membutuhkan kata untuk mengidentifikasikan mereka
kecuali kata tersebut keluar dari decision.
4.
Decision, bentuk berlian dengan satu flow
masuk dan dua atau lebih flow
keluar. Flow keluar menandakan untuk indikasi sebuah kondisi.
5.
Merge, bentuk berlian dengan dua atau lebih flow masuk dan satu flow keluar.
Merupakan penggabungan flow yang sebelumnya dipisahkan oleh decision.
6.
Fork,
bar hitam dengan satu flow
yang masuk beserta dua atau lebih flow
yang keluar. Actions dengan flow pararel di bawah fork dapat terjadi dengan
adanya urutan secara bersamaan.
7.
Join, bar hitam dengan dua atau lebih flow yang masuk beserta satu flow yang
keluar, tercatat pada akhir dari proses secara bersamaan. Semua actions
yang
menuju join harus lengkap sebelum proses dapat berlanjut.
8.
Activity Final, lingkaran solid di dalam lingkaran berongga yang menandakan
akhir dari proses
Selain komponen –
komponen di atas, terdapat dua tambahan komponen dari
activity diagram, yaitu :
1.
Subactivity Indicator, simbol seperti sisir terbalik yang berada pada actions
mengindikasikan bahwa actions telah keluar menuju activity diagram
yang
lain. Hal ini dapat membantu activity diagram
agar tidak menjadi terlalu
kompleks.
|
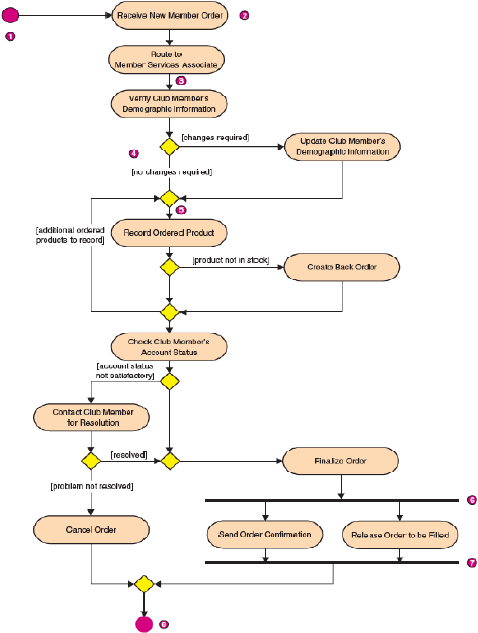 38
2.
Connector, huruf yang berada di dalam lingkaran dan memberikan alat untuk
mengarut kompleksitas. Flow
yang menuju connector
melompati flow yang
keluar dari connector dengan huruf yang sama.
[Whitten & Bentley, 2007: 382-392]
Gambar 2.3 Contoh Activity Diagram
(Whitten & Bentley, 2007: 392)
|
|
39
2.15.3
Sequence Diagram
Sequence Diagram adalah sebuah diagram
yang menggambarkan interaksi
antara actor
dengan sistem
dalam skenario use case
yang sedang berlangsung.
Diagram ini menggambarkan bagaimana pesan dikirim dan diterima antar objek
dan urutannya.
Terdapat 5 (lima) komponen penting dalam sequence diagram, yaitu :
1.
Actor : ditunjukkan dengan symbol aktor
2.
System : kotak yang mengindikasikan sistem sebagai ‘black box’ atau sebagai
keseluruhan. Tanda (:) adalah standar notasi sequence diagram
untuk
mendikiasikan sebuan ‘running instance’ sistem.
3.
Lifetimes : garis vertical
memanjang kebawah dari actor dan system symbols,
dimana mengindikasikan sequence.
4.
Activition bars
:
sebuah jalur yang menindikasikan lama waktu ketika
pengguna aktif dalam interkasi.
5.
Input messages : panah horisontal dari actor ke system yang mengindikasikan
masukan pesan.
6.
Output messages
: panah horizontal dari system
ke actor
yang ditandakan
dengan garis putus putus.
[Whitten & Bentley, 2007: 394-396]
|
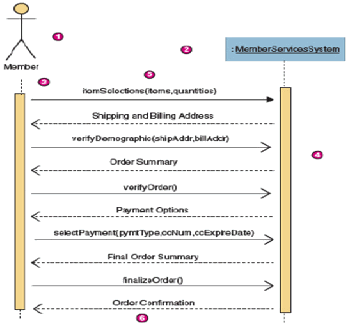 40
Gambar 2.4 Contoh Sequence Diagram
(Whitten & Bentley, 2007: 396)
2.15.4
Class Diagram
Class Diagram adalah sebuah diagram yang memberikan gambaran grafis
dari sistem struktur object statis, menunjukkan kelas objek bahwa sistem tersebut
tersusun atas hubungan – hubungan antara kelas object.
|
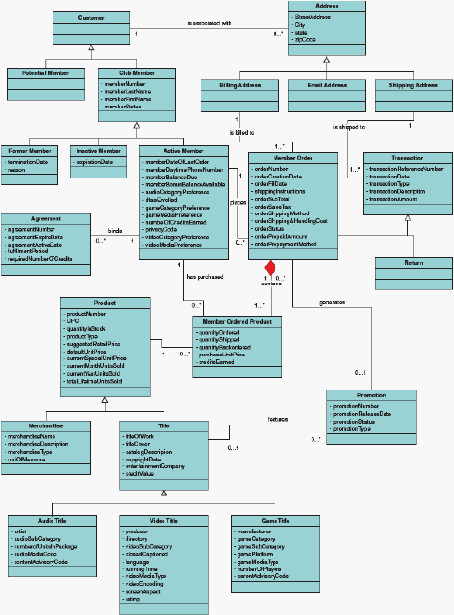 41
Gambar 2.5 Contoh Class Diagram
(Whitten & Bentley, 2007: 406)
Dalam penggunaannya, class diagram memiliki beberapa istilah, yaitu:
1.
Visibility
Fungsi dari visibility dalam class diagram
adalah untuk menentukan apakah
atribut atau operasi dari suatu kelas dapat digunakan oleh kelas lain
|
 42
Tabel 2.2 Penjelasan Visibility
Visibility
Simbol
Keterangan
Private
-
Hanya dapat digunakan oleh kelas yang
mendefinisikan
Protected
#
Dapat digunakan oleh kelas yang
mendefisinikan dan turunannya
Public
+
Dapat digunakan oleh kelas yang
berhubungan
2.
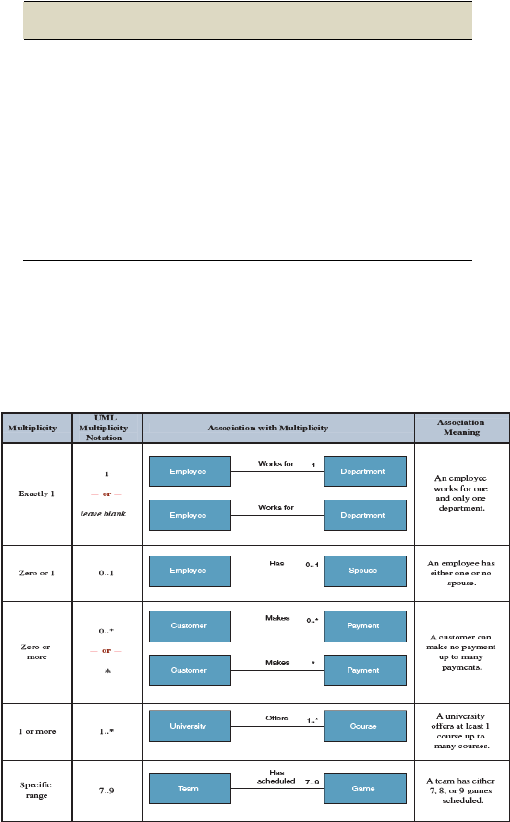
Multiplicity and Associations
Fungsi dari multiplicity
dalam class diagram
adalah untuk menentukan
banyaknya kelas yang berhubungan dengan kelas yang dimaksud.
Gambar 2.6 Contoh Multiplicity dan Associations
(Whitten & Bentley, 2007: 377)
|
 43
3.
Generalization
Fungsi dari generalization pada class diagram adalah untuk menggambarkan
hubungan antara superclass dan subclass.
Superclass
adalah bentuk umum
dari subclass, subclass adalah bentuk spesifik dari superclass
Gambar 2.7 Contoh Generalization
(Whitten & Bentley, 2007: 404)
4.
Aggregration
Fungsi dari aggregation adalah untuk menggambarkan hubungan dimana satu
kelas merupakan bagian dari kelas lain. Dalam agregasi tidak
menggambarkan sebuh inheritance, tetapi bersifat asimetris.
Misalnya
terdapat dua buah kelas team dan play, kelas player merupakan bagian kelas
dari team, tetapi team bukan bagian kelas dari player.
|
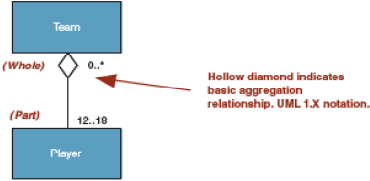 44
Gambar 2.8 Contoh Agregration
(Whitten & Bentley, 2007: 379)
[Whitten & Bentley, 2007: 379-406]
2.16
Object Oriented Programming
Object oriented programming (OOP)
merupakan cara programming yang
menggunakan obyek.
Objek
merepresentsaikan perancangan
software yang
berorientasi objek dilakukan dengan membagi fungsi-fungsi berdasarkan
pembagian
tanggung
jawab
yang
ditetapkan
kepada
setiap
kelas
yang
dibuat.
Setiap kelas
menyediakan
pelayanan
untuk
mengerjakan
operasi
tertentu dan
dilakukan oleh objek yang dibuat dari kelas tersebut.
Secara garis besar, suatu bahasa pemrograman dapat dikatakan sebagai
Object Oriented Programming
(OOP) apabila program tersebut
mendukung
konsep abstraksi (abstraction), enkapsulasi (encapsulation), polimorfisme
(polymorphism),
dan pewarisan (inheritance). Selain konsep-konsep ini, ada
beberapa konsep fundamental lainnya, seperti kelas, objek, dan message.
[Liang, 2011: 288]
|
|
45
2.17
8 Aturan Emas
8 (delapan) aturan emas dapat digunakan sebagai petunjuk dasar yang baik
untuk merancang suatu
user interface. Delapan aturan ini disebut dengan Eight
Golden Rules of Interface Design, yaitu :
1.
Konsistensi
Konsistensi dilakukan pada urutan tindakan, perintah, dan istilah yang
digunakan pada prompt, menu, serta layar bantuan.
2.
Memungkinkan pengguna untuk menggunakan shortcut
Ada kebutuhan dari pengguna yang sudah ahli untuk meningkatkan kecepatan
interaksi, sehingga diperlukan singkatan, tombol fungsi, perintah
tersembunyi, dan fasilitas makro.
3.
Memberikan umpan balik yang informatif
Untuk setiap tindakan operator, sebaiknya disertakan suatu sistem umpan
balik. Untuk tindakan yang sering dilakukan dan tidak terlalu penting, dapat
diberikan umpan balik yang sederhana. Tetapi ketika tindakan merupakan hal
yang penting, maka umpan balik sebaiknya lebih substansial. Misalnya
muncul suatu suara ketika salah menekan tombol pada waktu input data atau
muncul pesan kesalahannya.
4.
Merancang dialog untuk menghasilkan suatu penutupan
Urutan tindakan sebaiknya diorganisir dalam suatu kelompok dengan bagian
awal, tengah, dan akhir. Umpan balik yang informatif akan memberikan
indikasi bahwa cara yang dilakukan sudah benar dan dapat mempersiapkan
kelompok tindakan berikutnya.
|
|
46
5.
Memberikan penanganan kesalahan yang sederhana
Sedapat mungkin sistem dirancang sehingga pengguna tidak dapat melakukan
kesalahan fatal. Jika kesalahan terjadi, sistem dapat mendeteksi kesalahan
dengan cepat dan memberikan mekanisme yang sedehana dan mudah
dipahami untuk penanganan kesalahan.
6.
Mudah kembali ke tindakan sebelumnya
Hal ini dapat mengurangi keraguan pengguna karena pengguna mengetahui
kesalahan yang dilakukan dapat dibatalkan,
sehingga pengguna tidak takut
untuk mengeksplorasi pilihan-pilihan lain yang belum biasa digunakan.
7.
Mendukung tempat pengendali internal (internal locus of control)
Pengguna ingin menjadi pengontrol sistem dan sistem akan merespon
tindakan yang dilakukan pengguna daripada pengguna merasa bahwa sistem
mengontrol pengguna. Sebaiknya sistem dirancang sedemikan rupa sehingga
pengguna menjadi inisiator daripada responden.
8.
Mengurangi beban ingatan jangka pendek
Keterbatasan ingatan manusia membutuhkan tampilan yang sederhana atau
banyak tampilan halaman yang sebaiknya disatukan, serta diberikan cukup
waktu pelatihan untuk kode, mnemonic, dan urutan tindakan.
[Shneiderman & Plaisant, 2010: 88-89]
2.18
Kuesioner
Kuesioner adalah teknik pengumpulan data yang dilakukan dengan cara
memberi seperangkat pertanyaan atau pernyataan tertulis kepada responden untuk
dijawabnya. Penggunaan kuesioner ini dimaksudkan untuk mendapat informasi
yang diinginkan dan mendukung terhadap penelitian.
|
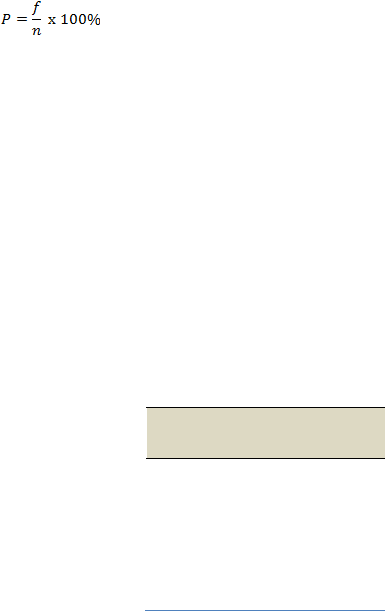  47
[Sugiyono, 2007: 199]
2.18.1
Analisis Kuesioner
Apabila form isian
kuesioner telah tersebar, terkumpul, dan terisi,
selanjutnya dianalisis dengan menyajikan data dalam bentuk tabel (tabulasi data)
dengan menggunakan rumus persentase yang merupakan teknik statistik
sederhana yang digunakan untuk melihat seberapa banyak kecenderungan
frekuensi jawaban yang diberikan responden, yaitu:
Dimana:
P
= persentase
f
= frekuensi dari setiap jawaban yang dipilih responden
n
= jumlah seluruh frekuensi alternatif jawaban yang menjadi pilihan responden
(jumlah sampel)
100% = konstanta
Tabel 2.3 Kategori Persentase
Persentase
Kategori
0%
Tidak seorang pun
1% - 24%
Sebagian kecil
25% - 49%
Hampir setengahnya
|
 48
50%
Setengahnya
51% - 74%
Sebagian besar
75% - 99%
Hampir seluruhnya
100%
Seluruhnya
[Santoso, 2001]
2.19
Bagan Alir (Flowchart)
Flowchart
merupakan teknik analisis yang digunakan untuk menjelaskan
aspek-aspek sistem informasi secara jelas, tepat, dan logis. Bagan alir
menggunakan serangkaian simbol standar untuk menguraikan prosedur
pengolahan transaksi yang digunakan oleh sebuah perusahaan, sekaligus
menguraikan aliran data dalam sebuah sistem.
2.19.1
Simbol-simbol Flowchart
Simbol dapat dikelompokan ke dalam empat kelompok sebagai berikut:
1.
Input/output. Yaitu simbol yang menggambarkan alat atau media yang
memberikan input kepada atau merekam output
dari kegiatan pengolahan
data.
2.
Processing. Merupakan simbol yang menunjukan jenis alat yang digunakan
untuk mengolah data (dengan komputer atau dikerjakan secara manual).
3.
Storage. Simbol yang menggambarkan alat yang digunkaan untuk
menyimpan data yang saat ini tidak dipakai oleh sistem.
|
 49
4.
Lain-lain. Simbol yang menunjukan arus data dan barang. Simbol ini juga
menggambarkan saat mulai dan berakhirnya flowchart, serta penjelasan-
penjelasan tambahan pada flowchart tersebut.
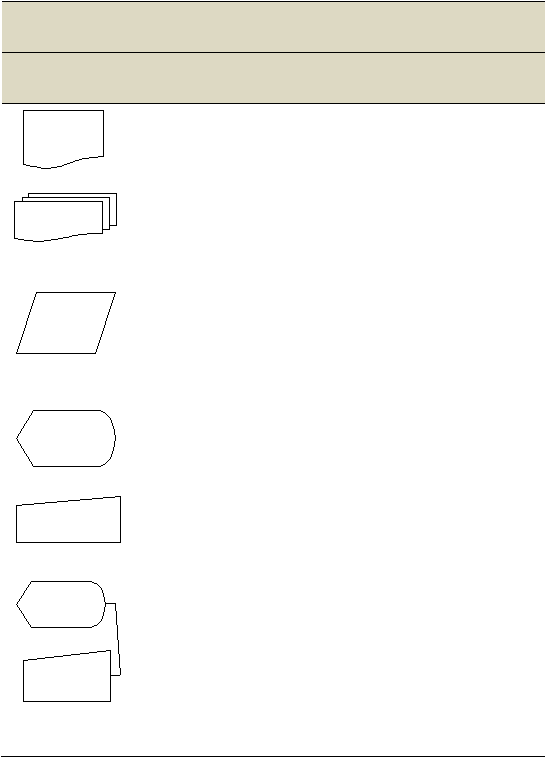
Tabel 2.4 Simbol-simbol Flowchart
Simbol
Nama
Penjelasan
Simbol-simbol Input/Output
Dokumen
Sebuah dokumen atau laporan, dokumen
dapat dibuat dengan tangan atau dicetak
oleh computer.
Dokumen rangkap
Digambarkan dengan menumpuk simbol
dokumen dan pencetakan nomor dokumen
di bagian depan dokumen pada bagian kiri
atas.
Input / Output,
Jurnal/Buku Besar
Digunakan untuk menggambarkan
berbagai media input dan output dalam
sebuah flowchart program.
Menggambarkan jurnal dan buku besar
dalam flowchart dokumen.
Tampilan
Informasi ditampilkan oleh alat output on-
line seperti terminal CRT atau monitor
computer PC.
Pemasukan data
on-line
Entri data oleh alat on-line seperti terminal
CRT atau komputer pribadi.
Terminal CRT,
Komputer Pribadi
Simbol tampilan dan entri data digunakan
bersama-sama untuk menggambarkan
terminal CRT dan computer pribadi
|
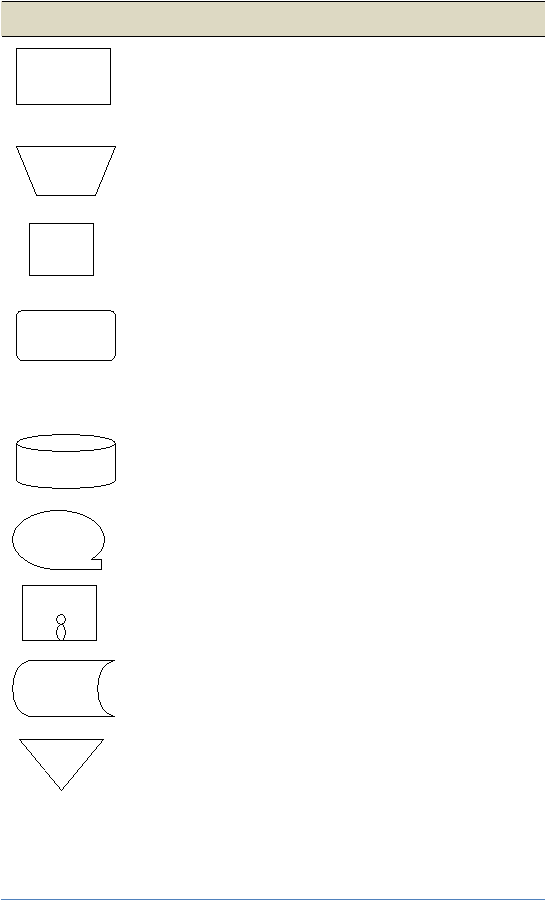 50
Simbol-simbol Pemrosesan
Pemrosesan
komputer
Sebuah fungsi pemrosesan yang
dilaksanakan oleh komputer biasanya
menghasilkan perubahan terhadap data
atau informasi.
Kegiatan manual
Sebuah kegiatan pemrosesan yang
dilaksanakan secara manual.
Kegiatan
campuran
Sebuah fungsi pemrosesan yang
dilaksakan dengan menggunakan alat
selain computer.
Kegiatan
pemasukan data
off-line
Sebuah kegiatan yang dilakukan dengan
menggunakan sebuah alat pemasukan data
off-line (entri data ke disket, register kas).
Disk bermagnit
Data disimpan secara permanen data disk
bermagnit, digunakan untuk
menyimbolkan file induk (master file).
Pita bermagnit
Data disimpan dalam sebuah pita
bermagnit
Disket bermagnit
Data disimpan dalam sebuah disket.
Penyimpanan on-
line
Data disimpan sementara dalam file on-
line dalam sebuah media direct access
seperti disket.
Arsip
Arsip dokumen disimpan dan diambil
secara manual. Huruf didalamnya
menunjukan cara pengurutan arsip: N =
Urut nomor; A = Urut abjad; T = Urut
tanggal
N
|
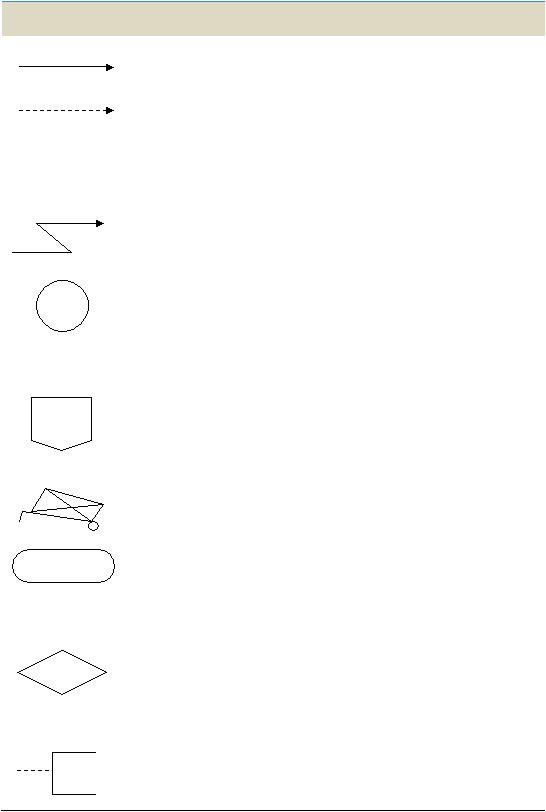 51
Simbol-simbol Arus dan Simbol lain-lain
Arus dokumen
atau pemrosesan
Arah arus dokumen atau pemrosesan, arus
normal adalah ke kanan atau ke bawah.
Arus data atau
informasi
Arah arus data atau informasi; sering
digunakan untuk menunjukan data yang
dikopi dari sebuah dokumen ke dokumen
lain.
Hubungan
komunikasi
Transmisi data dari sebuah lokasi ke lokasi
lain melalui saluran komunikasi.
Penghubung
dalam sebuah
halaman
Menghubungkan bagan alir pada halaman
yang sama. Simbol ini digunakan untuk
menghindari terlalu banyak anak panah
yang saling melintang dan
membingungkan.
Penghubung pada
halaman berbeda
Menghubungkan bagan alir yang berada
dihalaman yang berbeda.
Arus barang
Perpindahan fisik barang; digunakan
terutama dalam bagan alir dokumen
Terminal
Digunakan untuk memulai, mengakhiri,
atau titik henti dalam sebuah proses atau
program; juga digunakan untuk
menunjukan pihak eksternal.
Keputusan
Sebuah tahap pembuatan keputusan;
digunakan dalam bagan alir program
computer untuk menunjukan cabang bagi
alternative cara.
Anotasi
Tambahan penjelasana deskriptif atau
keternagan, atau catatan sebgaai
klarifikasi.
[Krismiadji, 2010: 71]
|