 8
BAB 2
2.1 Teori Graf
Adiwijaya (P47)
menyatakan bahwa teori graf
ditulis pertama kali
dalam makalah oleh Leonard Euler
matematikawan asal Swiss pada tahun
1736, yang digunakan untuk menyelesaikan masalah jembatan Königsberg
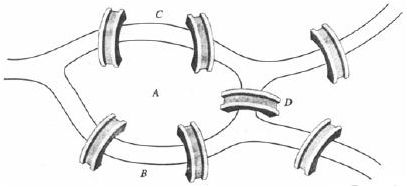
yang tertera pada gambar 2.1. Masalah tersebut adalah apakah bisa
melewati setiap jembatan tepat satu kali dan kembali lagi ke tempat asal
mula?.
Gambar 2. 1 Masalah Jembatan Königsberg
Gambar 2.2 adalah sketsa yang merepresentasikan ilustrasi jembatan
Königsberg yang pada gambar 2.1
|
 9
Gambar 2. 2 Representasi Graf dari Masalah Jembatan Königsberg
Jawaban atas masalah tersebut adalah tidak mungkin. Karena untuk
bisa melalui setiap jembatan tepat satu kali dan kembali lagi ke tempat asal
mula maka jumlah jembatan harus genap.
2.1.1
Definisi Graf
Adiwijaya (P48)
menjelaskan bahwa graf
merupakan struktur diskrit
yang terdiri himpunan sejumlah berhingga obyek yang disebut simpul dan
himpunan sisi
yang menghubungkan simpul-simpul tersebut. Notasi
sebuah graf adalah G = (V, E), di mana :
V merupakan himpunan tak kosong dari simpul-simpul misalkan V
= { v1 , v2 , ... , vn }
E merupakan himpunan sisi – sisi yang menghubungkan sepasang
simpul, misalkan E = {e1 , e2 , ... , en }
Contoh :
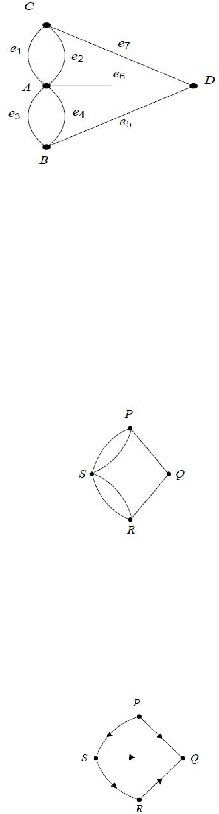
Graf dari masalah jembatan Königsberg dapat disajikan pada gambar 2.3 :
|
 10
Gambar 2. 3 Graf dari Masalah Jembatan Königsberg
2.1.2
Macam – macam Graf
Adiwijaya (P53) menjelaskan macam – macam graf yaitu :
1.
Graf
tidak berarah : Graf dengan sisi –
sisi penghubung simpulnya
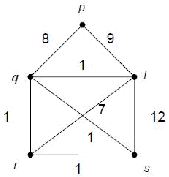
tidak memiliki arah. Contoh seperti pada gambar 2.4.
Gambar 2. 4 Graf Tidak Berarah
2.
Graf berarah: Graf dengan sisi – sisi penghubung simpulnya memiliki
arah. Contoh seperti pada gambar 2.5.
Gambar 2. 5 Graf Berarah
|
 11
3.
Graf berbobot : Graf yang sisi –
sisi penghubung simpulnya
mempunyai bobot. . Contoh seperti pada gambar 2.6.
Gambar 2. 6 Graf Berbobot
Adiwijaya (P71) menjelaskan bahwa graf bisa diaplikasikan pada suatu
permasalahan, salah satunya adalah travelling salesman problem.
2.1.3
Lintasan dan Sirkuit Hamilton
Lintasan hamilton suatu graf merupakan lintasan yang melalui setiap
simpul dalam graf tersebut tepat satu kali.
Jika lintasan tersebut kembali
kesimpul awal, sehingga membentuk lintasan tertutup (sirkuit) maka
lintasan ini dinamakan sirkuit hamilton.
Dengan demikian, sirkuit hamilton merupakan sirkuit yang melewati
masing-masing sisi tepat satu kali. Graf
yang memuat sirkuit hamilton
dinamakan graf
hamilton, sedangkan graf
yang memuat lintasan hamilton
dinamakan graf semi hamilton.
Contoh :
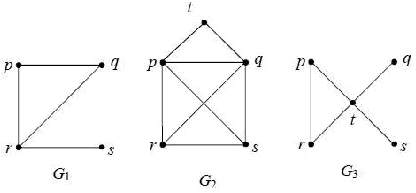
Perhatikan tiga graf pada gambar 2. 7 :
|
 12
Gambar 2. 7 Graf
Graf G1 merupakan graf semi hamilton, lintasan hamilton-nya adalah
s – r – p – q – r.
Sedangkan graf G2 merupakan graf hamilton, sirkuit hamiltonya adalah
t – p – r – q – p – s – q – t .
Sementara itu pada graf
G3 tidak terdapat lintasan maupun sirkuit
hamilton.
2.2 Optimasi
2.2.1
Definisi Optimasi
Optimasi merupakan suatu tindakan pengambilan keputusan terbaik
pada suatu masalah, keputusan tersebut berupa memaksimalkan faktor
yang diinginkan atau meminimumkan faktor yang tidak diinginkan
menurut batasan yang diberikan. Optimasi juga dijadikan solusi untuk
menentukan keputusan menyelesaikan suatu masalah. (Bidisha G, 2011).
|
|
13
2.2.2
Permasalahan Optimasi
Beberapa permasalahan dalam optimisasi adalah sebagai berikut:
Shortest Path Problem
: Suatu permasalahan untuk mencari
rute
terpendek dari suatu tempat ke tempat yang lain.
Traveling Salesman Problem
: Suatu permasalahan untuk mencari
rute perjalanan agar semua tempat dapat dilewati dengan jarak yang
optimal.
Assignment Problems
: Suatu permasalahan untuk mencari solusi
biaya pengeluaran agar seminimum mungkin dan memberikan tugas
pekerjaan kepada mesin-mesin yang tersedia.
Scheduling Problems
: Suatu permasalahan untuk mencari
jumlah
pekerja yang melakukan suatu proses kegiatan,
agar pengeluaran
biaya pekerja bisa diminimalkan dan hasil produksi tetap maksimal.
Routing Problems
: Mengatur routing
jaringan kabel agar biaya
pemasangan kabel tidak besar. (Vinnet C., Parveen K. Y., & Pawan
K. D., 2012:15)
2.3 Travelling Salesman Problem
Menurut Oloruntoyin S. T., Ojo J., Amao T., Salawudeen D., &
Oloruntoyin K. S. (2013: 1) menjelaskan bahwa travelling Salesman
Problem merupakan suatu masalah mencari rute terpendek dari satu tempat
melewati semua tempat dan kembali ke tempat asal. Penyelesaian masalah
ini menghasilkan
banyak rute
dengan jarak yang berbeda. Pencarian rute
terdekat dapat digunakan
dalam banyak hal, karena itu solusi untuk
|
|
14
masalah ini masih tetap dicari sampai sekarang. Banyak
metode yang ada
untuk menyelesaikan masalah ini.
2.4 Algoritma Semut
Algoritma semut diadaptasi dari tingkah laku semut mencari makanan
dari sarangnya. Dalam perjalanan mencari makanan, semut memberikan
feromon disetiap jejaknya. Tujuan pemberian feromon agar semut tersebut
dapat kembali saat menemukan dan membawa makanan ke sarangnya.
Feromon juga berfungsi sebagai komunikasi antar semut, sehingga semut
lain mengikuti jejaknya untuk membawa makanan. Dengan adanya
feromon, semut dapat menemukan rute perjalanan yang pendek dari sarang
ke sumber makanan (Thomas Stützle & Holger H. Hoos, 2000: 16).
2.5 Max – Min Ant System
Mann, A., Talwar, R., Bhushan, B., & Gupta, R. (2012:2)
memberikan penjelasan bahwa Max-Min
Ant System
yang dikembangkan
oleh Hoos pada tahun 1996 merupakan perluasan
dari algoritma Ant
System. Solusi dalam Max-Min
Ant System
dibangun dengan cara yang
persis sama seperti dalam Ant System.
Modifikasi utama dalam
Max-Min
Ant System
adalah untuk
mengeksploitasi solusi terbaik yang ditemukan, penambahkan feromon
diperbolehkan pada sisi –
sisi yang merupakan rute
terbaik. Lalu untuk
menghindari stagnasi semua semut melalui jalur yang sama, maka feromon
diberikan batasan dengan
interval [
,
]. Feromon diinisialisasi ke
|
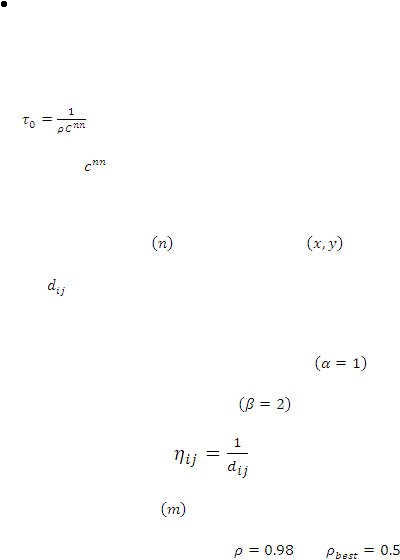 15
batas atas nilai feromon, untuk eksplorasi lebih tinggi pada awal algoritma.
Feromon diinisialisasi ulang jika tidak menemukan rute terbaik.
Bambang Y., Agus S. A., & Siswanto B. W. (2009) yang menjelaskan
bahwa “dalam algoritma semut, diperlukan beberapa variabel dan langkah
-
langkah untuk menentukan rute terpendek”. Berikut adalah langkah -
langkah dalam Max - Min Ant System:
Langkah 1 : Inisialisasi harga parameter – parameter algoritma
Parameter – parameter yang diinisialisasi adalah :
a)
Intensitas jejak semut antar titik dan perubahannya.
………………………………………………..…..….. (1)
Di mana
adalah panjang rute yang didapat dari metode nearest
neighbour heuristic
b)
Banyaknya titik
dan juga koordinat
atau jarak antar titik
(
)
c)
Titik berangkat (awal) dan titik tujuan
d)
Tetapan pengendali intensitas jejak semut
e)
Tetapan pengendali visibilitas
f) Visibilitas antar titik.
…………………….……. (2)
g)
Banyaknya semut
.
h)
Tetapan penguapan feromon (
dan
)
i) Jumlah iterasi maksimum (NCmax)
|
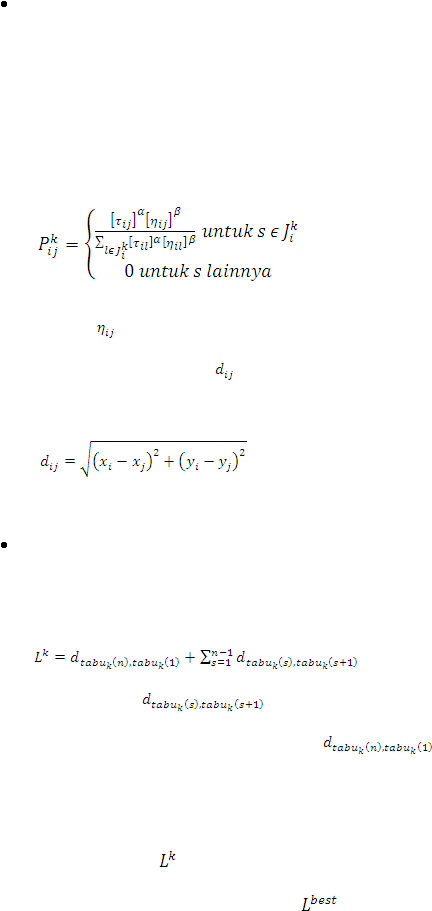 16
Langkah 2 : Penentuan kota tujuan
Semut diletakkan di masing masing kota sebagai tempat awal
sebelum memulai perjalanan. Semut akan memilih kota selanjutnya
berdasarkan persamaan probabilitas kota
yang bisa dilihat pada
persamaan (3) yaitu:
………………………. (3)
Di mana
yang didapat pada persamaan (2). Jika hanya diketahui
koordinatnya saja. Maka
bisa didapat dengan persamaan (4)
yaitu:
……………………………….. (4)
Dengan i sebagai indeks kota awal dan j sebagai indeks kota tujuan.
Langkah 3 : Menghitung panjang jalur setiap semut
Perhitungan panjang jalur tertutup setiap semut dilakukan
setiap pergantian siklus dengan persamaan (5) yaitu:
.
…………….. (5)
Di
mana
adalah jarak
dari kota
s sampai
kota
s+1 dalam tabu list pada
semut k dan
adalah
jarak dari kota n dan kota pertama dalam tabu list.
Kemudian perhitungan dilanjutkan dengan mencari jalur
terpendek. Setelah
dihitung, maka akan didapat jalur terpendek
dari setiap siklus yang dinyatakan dengan
.
|
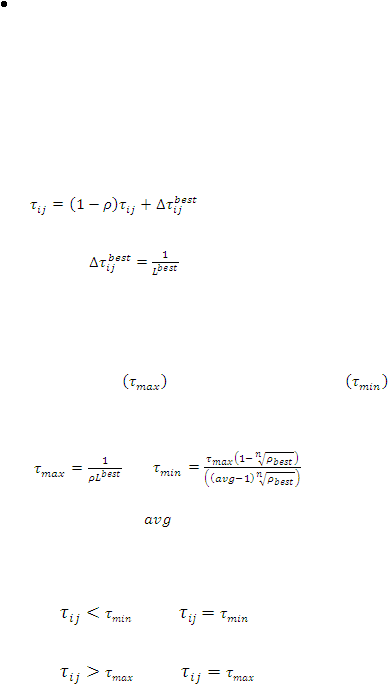 17
Langkah 4 : Perhitungan intensitas jejak kaki semut
Untuk siklus selanjutnya, semut yang akan melewati lintasan
tersebut harga intensitasnya telah berubah. Harga intensitas jejak kaki
semut antar kota untuk siklus selanjutnya dapat dihitung dengan
persamaan (6) yaitu:
…………….………………………….. (6)
Di mana
……………………………………….….. (7)
Jika semut menemukan jalur terbaik di awal atau pada iterasi siklus.
Harga intensitas jejak kaki semut dibatasi dengan batas atas
nilai feromon
dan batas bawah feromon
yang dihitung
dari dengan persamaan (8) yaitu:
.
dan
………………………. (8)
Di mana
merupakan rata-rata dari jumlah dari pilihan
yang berbeda pada semut untuk menemukan jalur terbaiknya.
Jika
, maka
Jika
, maka
Untuk mendekati optimal dalam Max-Min Ant System
maka
jumlah semut sama dengan jumlah kota
2.6 Metode Nearest Neigbour Heuristic
Nearest Neighbour Heuristic
merupakan solusi jalur
perjalanan
optimal secara sistematis dengan mencari kota
terdekat yang
belum
|
|
18
dikunjungi dari sebuah kota. Menurut Oloruntoyin S. T., Ojo J., Amao T.,
Salawudeen D., & Oloruntoyin K. S. (2013:1) untuk mengatasi masalah
travelling salesman problem dengan menggunakan nearest neighbour
heuristic dapat menggunakan langkah – langkah berikut ini.
Langkah 1
: Pilih simpul awal.
Langkah 2
: Lihat semua sisi yang keluar dari simpul awal, pilih simpul
berikutnya dengan nilai sisi yang terkecil.
Langkah 3
: Ulangi proses ini sampai semua simpul dikunjungi.
Langkah 4
: Periksa apakah semua simpul telah dikunjungi, jika sudah
maka kembali lagi ke simpul awal.
Langkah 5
: Hitung jarak rute perjalanan yang didapat
2.7 Unified Modelling Language (UML)
UML menggambarkan kebutuhan dan alur proses sistem. UML terbagi
atas beberapa jenis diagram, yaitu use case, activity
diagram, sequence
diagram,dan class diagram.
2.7.1
Use Case
Menurut Martin Fowler (2003: P99) menyatakan bahwa use case
adalah teknik untuk merekam persyaratan fungsional sebuah sistem. Use
case merupakan sebuah narasi tentang bagaimana sistem tersebut
digunakan.
Menurut Albertus Bayu Aji Priyono untuk lebih memperjelas use case,
lihat gambaran suatu peristiwa untuk sebuah klinik kesehatan di bawah ini
|
 19
Gambar 2. 8 Contoh use case
Pada gambar 2.8
menjelaskan bahwa “Pasien menghubungi klinik
untuk membuat janji (appointment) dalam pemeriksaan tahunan.
Receptionist
mendapatkan waktu yang luang pada buku jadwal dan
memasukkan janji tersebut ke dalam waktu luang itu.”
2.7.2
Activity Diagram
Menurut Martin Fowler (2003: P117) menyatakan bahwa activity
diagram
adalah teknik untuk menggambarkan logika prosedural, proses
bisnis, dan jalur kerja. Sebuah activity diagram
secara keseluruhan
menunjukkan aliran kontrol.
2.7.3
Sequence Diagram
Menurut Martin Fowler (2003: P53) menyatakan bahwa sequence
diagram menggambarkan interaksi diagram yang menunjukkan bagaimana
kelompok-kelompok objek saling berkolaborasi dalam beberapa aksi.
Menurut Albertus Bayu Aji Priyono
contoh dari sequence diagram
untuk pembuatan hotel reservation bisa dilihat di bawah ini. Objek yang
mengawali urutan pesan adalah ‘aReservation Window’.
|
 20
Gambar 2. 9 Contoh Sequence Diagram
Pada gambar 2.9 menjelaskan bahwa ‘Reservation window’ mengirim
pesan makeReservation() ke ‘HotelChain’. Kemudian ‘HotelChain’
mengirim pesan yang sama ke ‘Hotel’. Bila ‘Hotel’ punya kamar kosong,
maka dibuat ‘Reservation’ dan ‘Confirmation’.
2.7.4
Class Diagram
Menurut Martin Fowler (2003: P35) class diagram
mendeskripsikan
berbagai jenis objek dalam sistem dan macam -
macam hubungan statis
yang terdapat diantara mereka.
Class diagram
juga menunjukkan
properties
dan operasi dari kelas dan kendala yang berlaku pada objek
yang terhubung.
2.8 Personal Home Page (PHP)
Menurut Loka Dwiartara (2010: P3) menyatakan bahwa
PHP
ditemukan pertama kali
oleh seorang Software Developer bernama
Rasmus Lerdrof pada 1995. Awalnya Rasmus ingin mengetahui jumlah
|
|
21
pengunjung yang membaca resume
dalam website. Lalu dikembangkan
script
yang baru
dapat melakukan dua pekerjaan, yakni merekam
informasi pengunjung, dan menampilkan jumlah pengunjung dari suatu
website. Kemudian banyak orang di milis mendiskusikan script
buatan
Rasmus Lerdrof, hingga akhirnya rasmus mulai membuat
sebuah
tool/script, bernama Personal Home Page (PHP).
Keunggulan PHP :
Gratis
Cross platform
: Dapat di gunakan di berbagai sistem operasi,
mulai dari linux, windows, mac os dan sistem operasi yang lain.
Mendukung banyak database : PHP
telah mendukung banyak
database seperti MySQL, ODBC, Ovrimos, dan lain - lain.
On The Fly
: PHP
sudah mendukung on the fly, artinya dengan
PHP
anda dapat membuat dokumen seperti text, Word, Excel,
PDF, dan lain - lain.
2.9 Hyper Text Markup Language 5 (HTML5)
Menurut Yudha Yudhanto (2012) bahwa “HTML5 merupakan sebuah
bahasa markah untuk menstrukturkan dan menampilkan isi dari World
Wide Web, sebuah teknologi inti dari Internet. HTML5 adalah revisi kelima
dari HTML. Di
mana tujuan utama pengembangan HTML5 adalah untuk
memperbaiki teknologi HTML
agar mendukung teknologi multimedia
terbaru, mudah dibaca oleh manusia dan juga mudah dimengerti oleh
mesin”.
|
|
22
Berikut tujuan dibuatnya HTML5 :
Fitur baru harus didasarkan pada HTML, CSS, DOM, dan JavaScript.
Mengurangi ketergantugan untuk plugin eksternal (Seperti Flash).
Penanganan kesalahan yang lebih baik.
Lebih markup untuk menggantikan scripting.
HTML5 merupakan perangkat mandiri.
Proses pembangunan dapat terlihat untuk umum.
Fitur baru dalam HTML5 :
Unsur kanvas untuk menggambar.
Video dan elemen audio untuk media pemutaran.
Dukungan yang lebih baik untuk penyimpanan secara offline.
Elemen konten yang lebih spesifik, seperti artikel, footer, header, nav,
section.
Bentuk kontrol tampilan seperti kalender, tanggal, waktu, email, url,
search.
2.10
Model Waterfall
Pressman (2010: P39) menyatakan bahwa model waterfall, terkadang
disebut siklus model
klasik, dengan
pendekatan yang sistematis dan
sekuensial untuk pengembangan perangkat lunak.
Gambar 2.10 adalah fase model menurut Pressman (2010: P39)
|
 23
Gambar 2. 10 Model waterfall
Communication
Communication
merupakan proses tahap awal untuk analisis
terhadap kebutuhan perangkat lunak, dan tahap untuk mengadakan
pertemuan dengan konsumen
untuk mencari kebutuhan dari
keseluruhan sistem, serta pengumpulan data tambahan dari jurnal,
artikel, dan internet.
Planning
Setelah proses communication selesai maka dilanjutkan dengan
proses planning
yang akan menghasilkan dokumen user requirement
atau bisa dikatakan sebagai data
yang berhubungan dengan keinginan
user dalam pembuatan perangkat lunak, termasuk rencana yang akan
dilakukan.
Modeling
Proses modeling ini akan menerjemahkan syarat kebutuhan ke
sebuah perancangan perangkat lunak
yang dapat diperkirakan sebelum
dibuat coding. Proses ini berfokus pada rancangan struktur data,
arsitektur perangkat lunak, representasi interface, dan detail
(algoritma) procedural. Tahapan ini akan menghasilkan dokumen yang
disebut software requirement.
|
|
24
Construction
Construction merupakan proses membuat kode. Pengkodean
merupakan penerjemahan desain dalam bahasa yang bisa dikenali oleh
komputer. Programmer
akan menerjemahkan transaksi yang diminta
oleh user. Tahapan inilah yang merupakan tahapan secara nyata dalam
mengerjakan suatu perangkat lunak, artinya penggunaan komputer
akan dimaksimalkan dalam tahapan ini. Setelah pengkodean selesai
maka akan dilakukan testing terhadap sistem yang telah dibuat dengan
tujuan menemukan kesalahan-kesalahan terhadap sistem tersebut untuk
kemudian bisa diperbaiki.
Deployment
Tahapan ini bisa dikatakan final dalam pembuatan sebuah
perangkat lunak
atau sistem.
Setelah melakukan analisis, desain dan
pengkodean maka sistem yang sudah jadi akan
digunakan user.
Kemudian perangkat lunak
yang telah dibuat harus dilakukan
pemeliharaan secara berkala
|