|
5
BAB 2
TINJAUAN PUSTAKA
2.1.
Latar Belakang Teori Beban Ombak
Gelombang
pada revetment akan
menyebabkan
aliran yang
kompleks di
atasnya
dan di sepanjang
struktur revetment (menyaring dan menutupi lapisan).
Selama
arus
dan gelombang yang berlangsung, kekuatan
yang dihasilkan
oleh
gelombang
akan
berlawanan dengan
gaya
gravitasi. Gelombang
yang berlangsung
akan mengarah pada dua mekanisme penting :
1.
Air
yang
mengalir
ke bawah akan
menghasilkan
kekuatan
tarik
pada lapisan
penutup
dan
penurunan
tingkat
freatic
akan bertepatan
dengan
gradien
aliran
penurunan
filter. Mekanisme
pertama dapat
di skemakan
dengan aliran
bebas
pada filter dengan
gradien tertentu
yang sama dengan sudut kemiringan
lereng.
Hal ini dapat mengakibatkan pergeseran.
2.
Selama
gelombang
maksimum
berlangsung akan ada
sebuah gelombang yang
sesaat kemudian akan menimbulkan gelombang lanjutan. Sesaat sebelum dampak
gelombang terjadi, akan
ada
dinding
air
yang memberikan
tekanan tinggi
di
bawah
titik kerusakan maximum.
Di atas titik
berlangsungnya
hantaman
gelombang, permukaan struktur pelindung pantai hampir kering, itulah sebabnya
ada tekanan rendah pada struktur. Bagian depan yang terkena tekanan tinggi akan
menyebabkan aliran menuju ke atas filter. Aliran ini menuju ke arah aliran bawah
pada area terjadinya arus tersebut. Hasilnya adalah
gelombang yang
keluar dan
tekanan
gaya angkat
di dekat titik
maksimum
terjadinya
gelombang
(Gambar
2.2).
|
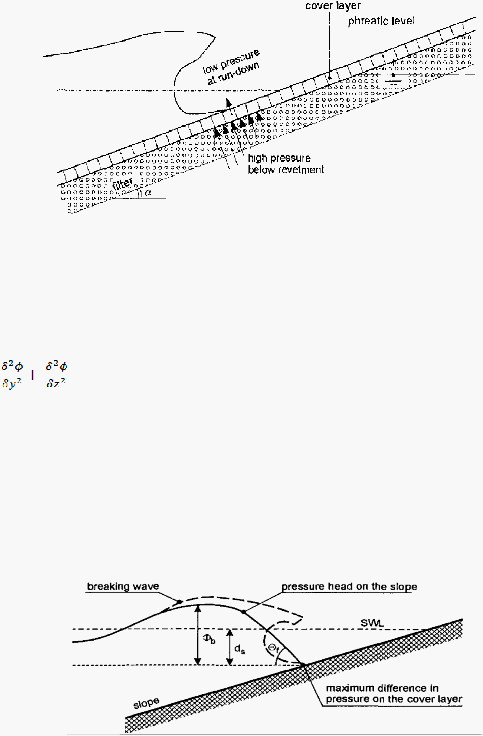 6
Gambar 2.1 Tekanan Yang Terjadi dalam struktur revetment.
(Sumber: Design Alternative Revetment, Pilarzyck)
Kondisi di atas dapat dihitung berdasarkan persamaan Laplace untuk aliran linier:
= 0 ......................................................................................................... (2.1)
Di mana:
?
= jarak titik tertinggi (potential head) dari titik benturan (m)
y = koordinat sejajar dengan lereng (m)
z = koordinat tegak lurus dengan lereng (m)
Gambar 2.2 Tekanan Utama Skematis Diatas Lereng
(Sumber: Design Alternative Revetment, Pilarzyck)
Setelah melalui perhitungan yang kompleks, tekanan gaya angkat pada filter
atau saluran dapat diderivasikan. Tekanan gaya angkat bergantung kepada
kecuraman dan tinggi
tekanan di bagian depan lapisan penutup (yang tergantung
|
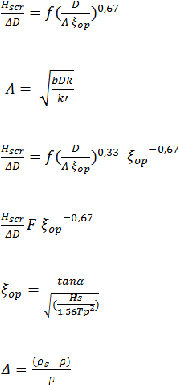 7
pada ketinggian gelombang, jangka waktu, dan sudut lereng, lihat Gambar 2.2),
ketebalan lapisan penutup, dan ketinggian
garis freatik pada filter dan saluran. Pada
saluran atau gorong-gorong, tekanan gaya angkat tidak bergantung pada
permeabilitas saluran jika permeabilitasnya lebih besar dari tanah dasar. Persamaan
gaya angkat dan gaya gravitasi menghasilkan rumus berikut (Pilarczyk et al., 1998):
................................................................................................... (2.2)
.............................................................................................................. (2.3)
.................................................................................... (2.4)
......................................................................................................... (2.5)
........................................................................................................ (2.6)
.
.............................................................................................................. (2.7)
Dimana:
Hscr
=
tinggi gelombang (m)
?
op
= breaker parameter
Tp
= periode gelombang saat di puncak spektrum (s)
?
=
panjang rembesan (m)
?
= massa relatif dari lapisan penutup
b
= ketebalan dari lapisan bawah (m)
D
= ketebalan matras beton (m)
k
= permeabilitas lapisan bawah (m/s)
|
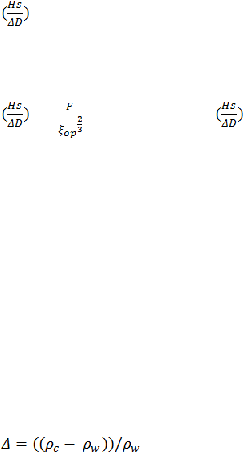 8
k’
= permeabilitas lapisan atas (m/s)
f
= koefisien stabilitas, umumnya tergantung dari tipe struktur, tan? dan friksi
F
= total faktor stabilitas
2.2.
Respon berdasarkan struktur
Ada dua metode desain praktis yang tersedia: metode black-box dan metode
analitis. Dalam kedua metode ini, bentuk akhir dari metode desain dapat ditampilkan
sebagai hubungan kritis dari beban dibandingkan dengan kekuatan, tergantung pada
jenis gelombang:
cr
= fungsi dari ?op
.......................................................................................... (2.8)
Untuk revetment, bentuk dasar dari persamaan ini adalah:
cr
=
dengan maksimum
cr
= 8,0 ........................................................ (2.9)
Dimana:
F
= konstanta stabilitas revetment
H
scr
=
tinggi gelombang (m)
?
= berat jenis relatif
D
= tebal lapisan atas (m)
?
op
= breaker parameter
Berat jenis relatif dihitung dengan cara berikut:
............................................................................................ (2.10)
Dimana:
?c
= berat jenis beton / material pelindung (kN/m³)
?
w
= berat jenis air (kN/m³)
|
 9
Untuk lapisan atas berpori, seperti pasir matras dan gabion, Kepadatan relatif lapisan
atas harus ditentukan, termasuk pori – pori yang berisi air (water-filled pores):
.
.................................................................................................... (2.11)
Dimana:
?t
= berat jenis relatif, termasuk pori-pori
n
= porositas material matras / material lapisan atas
breaker parameter didefinisikan sebagai berikut:
.
........................................................................................................... (2.12)
Kemiringan gelombang S
op
didefinisikan sebagai berikut:
S
op
.
.................................................................................................. (2.13)
Dengan Lop
........................................................................................... (2.14)
Dimana:
?
= kemiringan lereng (
0
)
L
op
= panjang gelombang pada periode puncak (m)
T
p
= periode gelombang pada puncak spektrum (s)
Keuntungan metode black-box ini adalah kemudahan dalam penggunaannya.
Bagaimanapun, kekurangannya adalah nilai F hanya diketahui pada beberapa tipe
struktur saja.
Metode analisa dilakukan berdasarkan teori penempatan blok batu revetment
pada material granular (blok dengan struktur yang saling mengunci). Di metode
perhitungan ini, sebagian besar
aspek fisik diperhitungkan.
Pada dasarnya, semua
|
 10
parameter fisik yang berhubungan dengan stabilitas telah dirangkum dalam
parameter “panjang rembesan”:
?
=
.
........................................................................................................... (2.15)
Hasil akhir dari metode analitis, sekali lagi dapat disajikan menjadi hubungan
seperti rumus berikut :
F = f(?). ................................................................................................................ (2.16)
Untuk pemasangan
yang tidak menggunakan filter
(langsung di atas pasir
atau tanah lempung, tanpa celah yang terbentuk di bawah
lapisan atas) permeabilitas
yang digunakan bukanlah permeabilitas lapisan filter, tetapi permeabilitas tanah
dasar yang digunakan.
Untuk bisa mengaplikasikan metode desain bagi penempatan batu revetment
di bawah beban gelombang pada kondisi lainnya, perlu memperhatikan adaptasi pada
faktor berikut :
Parameter revetment F.
Daya dukung parameter ? dan D.
Tinggi desain gelombang H
s
.
Panjang rembesan ?.
Faktor kenaikan kekuatan r.
Dalam Literatur ini hanya dapat ditunjukkan faktor –
faktor adaptasi di atas.
Formula dasar untuk analisa model tidak dijelaskan disini.
2.3.
Stabilitas Beban Aliran
Ada dua
pendekatan yang paling cocok
dalam
menentukan
stabilitas
bahan
revetment
yang terkena aliran gelombang. Salah satu pendekatan
yang paling cocok
berdasarkan jenis bebannya yaitu:
|
 11
Kecepatan aliran: untuk arus horizontal, di
mana aliran
jenisnya paralel
yang
sejajar dengan tanggul.
Debit:
aliran ke bawah pada lereng yang lebih curam dari 1:10, yang mengalir
tanpa gelombang; alirannya stabil.
Ketika kecepatan arus diketahui, atau bisa dikalkulasikan secara akurat,
Pilarczyk (pilarczyk 1998) memformulasikan:
? D = 0,035
.
.................................................................................... (2.17)
Dimana:
?
= berat jenis relatif
D
= karakteristik ketebalan matras (m)
g
= percepatan gravitasi (g = 9.81 m/s2
)
u
cr
= rata – rata kecepatan kritis dari aliran vertikal (m/s)
?
= parameter stabilitas
?
= parameter pelindung
K
T
= faktor turbulensi
K
h
= parameter kedalaman
K
s
= parameter kemiringan lereng
Parameter Stabilitas (?) :
Parameter stabilitas bergantung dari aplikasi di lapangan, berikut adalah data yang
digunakan :
|
 12
Tabel 2.1 Parameter Stabilitas, ?
Tipe Turap
Lapisan Atas
menerus
Tepi geosistem
dan Sambungan
Riprap dan blok beton
1
1.5
Blockmats, gorong - gorong,
0,5
0,75
geobags dan geomatras
(Sumber: Design Alternative Revetment, Pilarzyck)
Parameter pelindung (?) :
Dengan parameter pelindung kritis ?, tipe material dapat diperhitungkan,
berikut adalah nilai parameter pelindung:
Riprap, kantong kecil
? = 0,035
Penempatan blok, geobags
? = 0,05
Blockmats
? = 0,07
Gorong – gorong
? = 0,07 – 0,1
Geomatras
? = 0,07
Faktor turbulensi (K
T
)
:
Tingkat turbulensi dapat diperhitungkan dengan faktor turbulensi. Beberapa
panduan untuk nilainya adalah sebagai berikut :
Turbulensi Normal : penyangga dinding sungai, K
T
= 1,0
Turbulensi sedang : Tikungan dan posisi cekung bagian hilir sungai, K
T
= 1,5
Turbulensi besar : hydraulic jumps, tikungan tajam, dan gangguan local yang
kuat, K
T
= 2,0
Beban akibat semburan aliran air, K
T
= 3,0 – 4,0
Parameter Kedalaman K
h
:
|
 13
Parameter
kedalaman
air
perlu
diperhitungkan, sehingga kedalaman
air
berpengaruh
untuk mendapatkan kecepatan aliran
rata-rata
di atas
revetment.
Parameter
kedalaman juga tergantung pada
jenis
penampang aliran
dan
kekasaran
dari revetment. Rumus yang disarankan adalah sebagai berikut :
Penampang kecepatan aliran terbentuk penuh (fully developed velocity profile):
K
h
=
.
.................................................................................................... (2.18)
Penampang kecepatan aliran tidak terbentuk (non-developed profile) :
K
h
=
.
....................................................................................................... (2.19)
Aliran kasar (h/Ks < 5) :
Kh =
................................................................................................................ (2.20)
Dimana:
h
= kedalaman air (m)
K
s
= ekuivalen kekasaran menurut Nikuradse (m)
Pada kondisi di mana dimensi berasal dari revetment pada sebuah lereng, ketinggian
air pada dasar lereng harus digunakan untuk nilai h.
Ekuivalen kekasaran menurut Nikuradse bergantung dari jenis revetment atau
geosistem yang digunakan. Untuk riprap, K
S
sama dengan dua kali nilai dari diameter
batu yang digunakan, untuk karung setara dengan ketebalan batu, untuk matras
bergantung dari tipe yang digunakan, untuk tipe yang halus dapat menggunakan nilai
K
S
sebesar 0,05, sedangkan untuk matras kasar nilainya sebesar tebal matras.
Parameter stabilitas Ks:
Parameter stabilitas dari elemen revetment
juga bergantung pada
hubungan
besar sudut geser dalam revetment, sesuai jenis revetment yang digunakan. Pengaruh
|
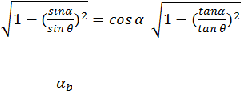 14
dari stabilitas ini di perhitungkan
dengan parameter kemiringan lereng, Ks, yang
ditentukan sebagai berikut:
K
s
=
.
........................................................ (2.21)
Atau K
s
= cos
Dimana:
?
= sudut geser pada material revetment
?
= kermiringan lereng (
o
)
?
b
= sudut lereng didasar sungai (
o
)
Angka ? bisa di asumsikan dengan
pendekatan pertama: 40
o
untuk riprap,
30
o
sampai 40
o
untuk sistem pengisian dengan pasir,
90
o
untuk matras beton
kaku
terangkur dan blockmats
(K
S
= cosa).
Bagaimanapun untuk matras fleksibel yang
tidak terangkur dan blockmats (yang jenisnya tidak terkunci satu sama lain)
nilai ini
jauh lebih rendah,
biasanya
sekitar
3/4 dari sudut geser
dalam lapisan tanah.
Jika
matras geotekstil dan blockmats
terhubung
dengan geotekstil yang dihamparkan di
atas filter geotekstil, nilai ? berkisar 15
0
-
20
0
.
Kelebihan dari rumus umum Pilarzyck yaitu bisa diterapkan pada beragam
situasi. Kekurangannya adalah penyebaran dalam hasil yang cukup luas, sebagai
akibat dari batasan parameter yang besar. Dengan aliran menurun disepanjang lereng
yang curam, sulit untuk memntukan atau memprediksi kecepatan aliran, karena
alirannya sangat tidak beraturan. Pada kondisi
seperti itu rumus yang berdasarkan
debit harus dikembangkan (Pilarzyck et al, 1998).
2.4.
Kriteria Stabilitas untuk Matras Beton
2.4.1
Matras Beton
|
 15
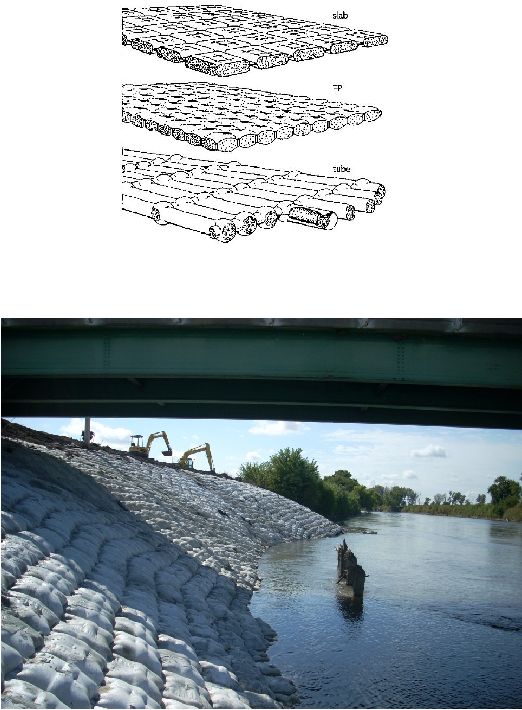
Karakteristik dari matras beton adalah semen atau beton yang berada diantara
lapisan geotekstil. Geotekstil bisa dihubungkan dengan banyak cara, yang
menghasilkan beragam bentuk matras, dengan bentuk dan ciri-cirinya masing-
masing. Beberapa contoh tampilan karakteristik matras beton dapat dilihat di Gambar
Gambar 2.3 Contoh Bentuk Matras Beton
(Sumber: Design Alternative Revetment, Pilarzyck)
Gambar 2.4 Matras Beton
|
 16
(Sumber: www.aspent.com)
Gambar 2.5 Matras Beton pada tepi sungai
(Sumber: www.aspent.com)
Permeabilitas dari matras adalah salah satu faktor yang
menentukan
stabilitasnya. Telah menjadi ketentuan
bahwa nilai permeabilitas yang diberikan
pihak penjual adalah permeabilitas dari geotekstil, atau biasa disebut filter points.
Pada kondisi sebenarnya, permeabilitas seluruh matras selalu lebih kecil.
Permeabilitas
matras yang tinggi dapat memastikan bahwa tekanan
yang terkumpul
dibawah matras dapat dihilangkan, sehingga tekanan yang mengangkat matras tetap
bernilai kecil.
Secara umum dengan tanah dasar berupa lempung dan lanau, permeabilitas
matras beton akan lebih tinggi dari tanah dasar. Oleh sebab itu air di bawah matras
beton dapat dibuang tanpa adanya gaya angkat yang berlebih pada matras.
Permeabilitas dari matras akan lebih rendah dibandingkan dengan permebilitas dari
tanah dasar jika menggunakan
filter granular, atau
lapisan pasir dan tanah
lempung
|
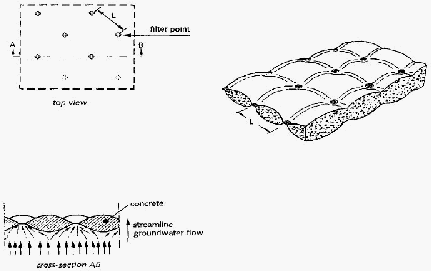 17
yang memiliki
permukaan tidak teratur (memunculkan rongga
antara
tanah dan
matras).
Hal ini
akan mengakibatkan
tekanan angkat/ geser yang berlebih di matras
selama gelombang berlangsung.
Gambar 2.6 Prinsip permeabilitas dari filter point pada matras
(Sumber: Design Alternative Revetment, Pilarzyck)
2.4.2
Fungsi dan Potensi Aplikasi
Suatu matras beton secara sederhana adalah suatu elemen konstruksi yang
dibentuk dengan cara menyuntikkan suatu bahan grout koloid ke dalam suatu cetakan
yang terbuat dari bahan fabric sintetik. Ketebalan matras ditentukan oleh
penyekat woven di dalam fabric tersebut. Sistem ini mengijinkan konstruksi dari
elemen-elemen yang berbeda, yang dapat digunakan untuk pencegahan erosi,
memperbaiki aliran air, atau sebagai bahan kedap air (waterproofing). Berbagai jenis
matras telah dipatenkan.
Matras beton digunakan untuk berbagai keperluan, antara lain : proteksi dan
konsolidasi lereng atau dasar kanal, sungai, saluran, tebing pantai, atau struktur-
struktur sejenis. Matras beton dapat disesuaikan untuk pelbagai keperluan yang
berbeda dalam badan air atau konstruksi maritim, dan kemudian dimensinya
|
 18
ditentukan menurut kebutuhan. Campuran beton yang biasa digunakan sebagai bahan
pengisi adalah semen (tipe V untuk aplikasi pada lingkungan maritim).
Menurut tipenya dikenal 2 kelompok :
Matras standar; yang biasanya digunakan jika tanah dasar keras, untuk
memenuhi fungsi perlindungan tebing dan dasar sungai atau untuk menyekat
struktur-struktur hidrolis.
Matras panel; memiliki kapasitas drainasi yang tinggi karena lubang-lubang
drain (weep hole) yang besar. Tersedia untuk panjang dan lebar dengan berat
luas sesuai rencana sehingga dapat dirakit sesuai dengan keperluan khusus.
Beberapa keuntungan penggunaan matras beton adalah sebagai berikut :
Kekuatan, yaitu berat dasar sesuai dengan keperluan.
Dapat dibuat dalam bentuk kaku atau lentur.
Dengan atau tanpa sambungan.
Tembus atau kedap air.
Relative tidak terpengaruh oleh kondisi cuaca buruk selama pelaksanaan.
Instalasi di bawah air juga dimungkinkan.
Tidak perlu ‘predraining’.
Pelaksanaan relative cepat.
Ketahanan hampir tidak terbatas.
Tidak memerlukan ‘sheet piling’.
Ekonomis.
Penyerdehanaan prosedur pelaksanaan karena hanya menggunakan satu proses
dan satu bahan (buatan) saja.
Berbagai tipe matras dapat dikombinasikan sesuai dengan keperluan.
Secara ekologis menguntungkan.
|
 19
Telah terbukti memuaskan dalam berbagai aplikasi.
Katergorisasi atas fungsi-fungsi tersebut dijelaskan dalam bagian berikut :
Daerah lepas pantai (offshore) :
Beberapa contoh aplikasi adalah sebagaimana berikut ini. Jaringan pipa yang
harus dipasang pada dasar laut dibungkus dengan batu dan matras panel. Batu-
batu penutup tersebut ditempatkan secara berhati-hati lewat suatu pipa vertikal
(semacam tremie) sedemikian sehingga material tersebut tidak tersapu oleh arus.
Pengujian telah menunjukkan bahwa matras dapat ditempatkan secara
memuaskan bahkan pada kedalaman 50 m. Pengisian batuan dan pemasangan
matras panel bahkan telah dapat dilakukan tanpa bantuan penyelam.
Sambungan fleksibel antara struktur padat dan matras panel digunakan untuk
mem-berikan proteksi dasar dapat terdiri dari batuan pengisi. Bergantung pada
permintaan, sambungan dapat juga digrout dengan mortar. Injeksi mortar dapat
juga mengeliminasi bahaya terjadinya penggerusan.
Jaringan pipa dan culvert dapat juga dibungkus rapat untuk mencegah
kerusakan, korosi, dan desakan ke atas.
Gambar 2.7 Matras Beton offshore
(Sumber : en.lvyangtj.com)
|
 20
Proteksi tebing (Bank & lock protection)
Di daerah pelabuhan, sebagai contoh matras diletakkan menutupi tebing pantai
yang sebagian besar dapat tertutup air dan ditempatkan sampai kedalaman 12 m.
Tujuan matras adalah untuk memproteksi tanah berpasir terhadap bahaya
gerusan.
Matras panel juga digunakan untuk melindungi pantai terhadap
gelombang pasang bertekanan kuat.
Gambar 2.8 Matras Beton Proteksi Lereng
(Sumber : www.hiwt.com)
Proteksi dasar saluran
Di daerah Nuremberg 2 pipa terowongan harus didorong di bawah Kanal Rhine-
Main-Danube untuk proyek kereta rel bawahtanah lokal. Untuk melindungi pipa
terowongan dan pekerja-pekerja konstruksi di dalamnya terhadap bahaya
keruntuhan dan rembesan air dari dasar kanal. Matras disiapkan di atas tanah,
diseret ke dalam air, kemudian ditempatkan secara teliti. Dengan ketebalan
tertentu
pada dasar kanal, matras tersebut memberikan proteksi yang andal
|
 21
karena beratnya dan karena karakter kedapair-nya. Ini adalah
metode yang
paling hemat dan sederhana yang tersedia.
Gambar 2.9 Matras Beton Proteksi Dasar Saluran
(Sumber : www.turbosquid.com)
Tabel 2.2 Contoh Spesifikasi Incomat Crib dan FP
Properties
Crib
10.100
Crib
10.200
FP C
60.149
Material
warp
PA
PA
PET
weft
PE
PE
PET
Tensile strength
warp
45 kN/m
45 kN/m
55 kN/m
weft
25 kN/m
25 kN/m
50 kN/m
Tear strength
warp
30 kN/m
weft
30 KkN/m
Elongation
warp
20%
20%
22%
weft
20%
20%
25%
Wtr.permeability
201/m²/sec
201/m²/sec
201/m
2
/sec
Pore size
330 ym
330 ym
330 ym
Unit weight
410 g/m²
410 g/m²
410 g/m²
Thickness after
filling
10 cm
20 cm
10 cm
|
|
22
Spesifikasi beberapa produk geotekstil untuk keperluan cetakan fleksibel
yang diproduksi oleh Huesker Synthetics adalah sebagai berikut :
Pendekatan deterministik biasanya diambil untuk keperluan perancangan
kasar dan digunakan di sini untuk memilih parameter-parameter gelombang yang
dapat diperoleh dari tiga jenis informasi, yaitu :
Pengukuran gelombang langsung. Pengukuran gelombang langsung memerlukan
penggunaan alat pengukur lepas pantai, misalnya pelampung gelombang (wave
rider buoy). Data dari pelampung pengukur tersebut di-konversikan ke dalam
kondisi pantai dan diekstrapolasikan untuk mem-berikan tinggi gelombang
rencana yang sesuai untuk usia rencana struktur yang ditinjau.
Data angin. Jika tidak diperoleh data pengukuran langsung, data angin dapat pula
dipergunakan untuk menaksir tinggi gelombang lepaspantai, menggunakan
berbagai persamaan empiris. Untuk tujuan perancangan, suatu prosedur yang
disederhanakan adalah sbb. :
A. Pilih periode ulang yang terkait dengan usia layanan struktur
B. Analisis data angina untuk menentuka rerata kecepatan angina setiap jam
menurut periode ulangnya
C. Tentukan fetch efektif untuk setiap arah kompas
D. Dapatkan kodisi gelombang lepas pantai
Dalam rangka menentukan kondisi-kondisi gelombang di lokasi, adalah perlu
untuk memperhitungkan efek-efek modifikasi akibat kedalaman air yang semakin
dangkal ketika gelombang semakin mendekati pantai.
|
 23
Gambar 2.10 Penentuan tinggi dan periode gelombang
(Sumber : moko1989.blogspot.com)
2.4.3
Aturan Desain Berdasarkan Beban Gelombang
Mekanisme kegagalan dari matras beton yang mungkin terjadi adalah sebagai
berikut :
Rongga bawah matras akan membentuk penurunan tanah yang tidak merata pada
lapisan tanah di bawahnya. Hal ini disebabkan karena matras ini cenderung kaku
akibat pengikatan benang antar jarak saringannya sehingga rongga akan melebar.
Dengan bentang
matras yang lebar, saat matras beton dihantam oleh gelombang
ombak, maka matras beton tersebut dapat mengalami kegagalan baik karena retak
pada beton atau putusnya sambungan antar saringan. Oleh sebab itu matras beton
harus dilapisi dengan geotekstil dalam penggunaanya.
Dengan
gelombang
yang cukup tinggi, perbedaan
tekanan gaya angkat
matras
akan terjadi selama gelombang terus berlangsung, yang akan mengangkat matras.
(Gambar 2.2)
|
 24
Efek pompa/naik turun dari pergerakan ini akan mengakibatkan tanah dasar
terlepas, yang menyebabkan terbentuknya profil S (rongga di tanah dasar) dan
revetment akan runtuh secara keseluruhan.
Adanya
asumsi
bahwa penurunan
tanah
setempat
akan menyebabkan
lepasnya tali penghubung antar matras beton. Kemudian
dampak gelombang juga
akan menyebabkan kerusakan dari tali penghubung tersebut, bila perbandingan dari
H
s
/D terlalu besar
untuk bentang tertentu.
Sebuah metode perhitungan diturunkan
berdasarkan rumus empiris dari tekanan benturan gelombang maksimum dan teori
balok sederhana. Keruntuhan pada jarak antar saringan yang pendek (lebih kecil dari
1 – 2 m) tidak diterima karena akan menyebabkan banyak keretakan.
Rumus empiris untuk dampak gelombang menurut Klein Breteler :
.
...................................................................................... (2.22)
Dimana:
F
impact
= gaya tekan per m revetment (N)
Dalam perhitungan telah diketahui bahwa jarak rata-rata antar retakan
hanya
sebesar 10 sampai 20 cm,
untuk tebal matras 10 cm dan tinggi
gelombang 2
m. Ini
berarti
bahwa pada
suatu
rasio
H
s
/D,
dampak
gelombang
dapat menghancurkan
matras secara keseluruhan. Untuk matras dengan tebal 15 cm dan tinggi
gelombang
1,5m, retakan akan ada di setiap
jarak 1
m.
Terlepas dari retakan akibat gelombang,
matras
juga harus
menahan tekanan
gaya angkat
akibat
hantaman
gelombang.
Tekanan
gaya angkat
tersebut
dihitung
dengan cara yang sama
seperti blok
revetment. Dalam
kebanyakan kondisi
kerusakan mekanisme
oleh
tekanan
gaya
angkat lebih berpengaruh daripada hantaman gelombang normal.
|
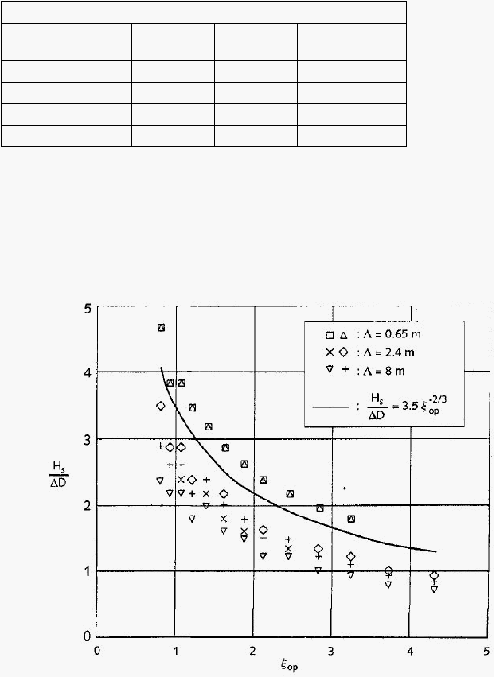 25
Nilai karakteristik dari panjang rembesan
untuk berbagai jenis matras dapat
diasumsikan sebagai berikut :
Tabel 2.3 Standar panjang rembesan yang diperbolehkan
Panjang Rembesan ? (m)
Matras
diatas
pasir (*)
diatas
pasir (**)
diatas
saringan
Standard -FP
1,5
3,9
2,3
FPM
1
3,9
2,3
Slab
3
9
4,7
Articulated (Crib)
0,5
1
0,5
(Sumber: Design Alternative Revetment, Pilarzyck)
*) matras dengan tanah dasar terhubung dengan baik (tidak ada celah /rongga di
bawah)
**) Perkiraan pesimis: pemadatan tanah dasar yang buruk dan adanya rongga
dibawah matras.
Gambar 2.11 Hasil perhitungan untuk matras beton ( H
s
/
?D < 4 karena jarak retakan
yang diperbolehkan berdasarkan benturan pada bentang)
(Sumber: Design Alternative Revetment, Pilarzyck)
|
 26
Dengan memperhitungkan mekanisme kegagalan di atas, formulasi
perhitungan stabilitas untuk matras (rumus 2.9) adalah sebagai berikut:
cr
=
dengan maksimum
max
= 4,0 .................................................... (2.23)
Dengan:
D
= tebal matras
?
= volum massa relatif dengan matras (?
s
– ?)/
?
s
= volum massa dari beton (kg/m³
)
F
= faktor stabilitas, dari tabel
Untuk
ketepatan
penentuan
dari
panjang
rembesan,
metode
ini
disebut
metode
analitis
Klein Breteler. Bagaimanapun selain tipe matras,
contoh tabung
matras
dengan nilai permeabilitas yang relatif
besar,
faktor
lain tidak terlalu
bermasalah dalam penentuan panjang rembesan. Hal ini
dapat
direkomendasikan
untuk menggunakan nilai F untuk perhitungan desainnya:
F = 2,5 atau (
=
3) untuk permeabilitas matras yang rendah di atas tanah granular.
F = 3,5 atau (
= 4) untuk permeab
ilitas
matras yang rendah di atas pasir yang
dipadatkan.
F = 4,0 atau (
= 5) untuk perm
eabilitas
matras di pasir atau tanah halus
(D
f15
<
2mm).
Nilai yang lebih besar dapat diterapkan jika
tanah lebih kuat terhadap
erosi
dan matras beton ditanamkan atau ditempatkan secara benar.
2.5
Stabilitas Geosistem
Penghalang utama dalam aplikasi geosistem adalah kurangnya kriteria desain
yang layak. Bagaimanapun, dari studi literature, kriteria stabilitas memiliki
|
 27
kemungkinan untuk diformulasikan dengan berdasarkan eksperimen skala kecil.
Dapat disimpulkan bahwa stabilitas struktur pinggir pantai yang tersusun dari
geosistem (karung, matras dan geotube) dapat disimulasikan serupa dengan batuan,
yaitu dalam istilah parameter H/?D.
Gambar 2.12 Aplikasi Geotube
2.5.1
Karung Berisi Pasir dan Mortar
Hingga saat ini, dapat disimpulkan bahwa stabilitas karung pasir dengan rasio
panjang-lebar tidak lebih besar dari 1-3 dan terisi dengan cukup (>70%), dapat
dihitung dengan cara perhitungan rip-rap. Dianjurkan untuk menghitung koefisien
stabilitas berdasarkan formula Pilarzyck (Pilarzyck, 1990) dengan koefisien stabilitas
c= 2,5. Berikut adalah rumusnya:
............................................................................................ (2.24)
(jika nilai ? > 3, nilai ? = 3 dapat dipergunakan)
Dengan:
|
 28
H
S
=
tinggi gelombang
?
= berat jenis matras
D
= tebal matras beton
c
= koefisien stabilitas ditentukan melalui
= 1
cos
?
=
sudut kemiringan (bisa diabaikan untuk lereng lebih kecil dari 1/3)
= parameter kesamaan surf setara dengan
=
............................................................................................................ (2.25)
L
0
=
panjang gelombang
Kepadatan kantong (?
s
) dapat diasumsikan 2000 dan 2300 kg/m3
pada
pasir dan beton. (
? = 1 dan 1
,3) .
Catatan: unit dengan bahan pengisi pasir yang terekspos benturan gelombang
langsung dapat diaplikasikan hingga Hs = 1,5 m (maksimal 2 m).
2.5.2
Stabilitas Matras Pelindung Pesisir Luar Termasuk Matras ProFix-mats
Pendekatan pertama mengenai stabilitas dari matras berisi mortar atau pasir
(seperti matras ProFix atau Fabriform) yang memiliki ketebalan seragam dilakukan
oleh Pilarzyck (1990) dengan rumus berikut:
untuk
<= 3 ................................................................... (2.26)
(jika nilai ? > 3, nilai ? = 3 dapat dipergunakan)
Dengan:
?
= berat jenis matras
D
eq
= tebal matras equivalent (rata – rata)
c
= koefisien stabilitas di tentukan bila
= 1
|
|
29
Nilai dari koefisien ‘c’ tergantung dari mekanisme kegagalan dan rasio
antara permeabilitas dari matras dan permeabilitas tanah dasar, km/ks :
c
= 3 – 4
ketika k
M
/k
S
< 1 dengan gaya angkat matras
dan deformasi tanah
dasar sebagai mekanisme kegagalan utama.
c
= 4 – 6
ketika k
M
/k
S
>= 1 ketika
deformasi tanah dasar sebagai mekanisme
kegagalan utama.
Kisaran nilai c berdasarkan pada penelitian proyek dari Delft Hydraulics
dengan menggunakan blok-blok revetment beton yang dipasang/block-mats
dan
beberapa tipe matras yang berbeda. Perlu dicatat bahwa gaya angkat dapat
muncul
bahkan saat nilai c=2, tetapi nilainya kecil dan berada pada jangka waktu yang
pendek sehingga tidak akan mengakibatkan kerusakan serius pada pelindung matras.
Sehingga nilai c=3 hingga 4 bisa digunakan sebagai parameter desain.
Pada kasus-kasus khusus di mana matras berukuran besar hanya digunakan
sementara dan/atau ketika deformasi tanah dasar dapat diterima atau tanah dasar
memiliki ketahanan lebih terhadap deformasi (contohnya tanah lempung) nilai c
yang lebih tinggi dapat dipergunakan (maks. C = 6). Di dalam riset yang disebutkan
(Delft hydraulics, 1975; pemasangan matras pada pulau berbentuk lingkaran) bisa
menjadi ilustrasi yang tepat untuk kondisi khusus tersebut. Dengan menggunakan
nilai c yang tinggi, perlu dilakukan pengecekan terhadap kemungkinan longsor pada
struktur, sehingga dapat muncul kebutuhan untuk penjangkaran khusus pada matras.
Material berisi pasir dapat diaplikasikan hingga Hs <= 1,5 m
2.6
Frekuensi
Frekuensi gelombang untuk membuat permodelan didalam plaxis 2D dengan
menggunakan rumus frekuensi :
|
 30
................................................................................................................. (2.28)
Dimana:
f
= frekuensi (Hz)
A
= amplitude per-s (s)
................................................................................................................. (2.29)
Dimana:
X
= total periode (s)
Y
= banyak periode yang terjadi
2.7
PLAXIS
PLAXIS (Finite Element Code For Soil and Rock Analysis) merupakan suatu
rangkuman program elemen hingga yang telah dikembangkan untuk menganalisa
deformasi dan stabilitas geoteknik dalam perencanaan-perencanaan sipil.
Berdasarkan prosedur input data yang sederhana, mampu menciptakan perhitungan
elemen hingga yang
kompleks dan menyediakan fasilitas output tampilan secara
detail berupa hasil-hasil perhitungan.
Dalam Penelitian ini data yang dibutuhkan adalah mengenai nilai-nilai
parameter pada pasir yang diambil dari data umum dari hasil penyelidikan pasir.
Data ini akan digunakan sebagai input,
adapun prosedur dari program PLAXIS
antara lain nilai parameter tanah antara lain ?
sand
?
beton
kohesi, modulus elastisitas
tanah, poisson ratio, dan sebagainya.
2.7.1
Pemodelan Perilaku Pasir
Pada program PLAXIS terdapat beberapa masukan dalam memodelkan
perilaku dari pasir, tanah dan batuan cenderung untuk berperilaku tidak linier saat
|
|
31
menerima pembebanan dari pondasi tiang maupun gempa (Dynamic Analysis).
Jumlah parameter yang diperlukan akan semakin banyak untuk tingkat pemodelan
yang semakin tinggi. PLAXIS juga mendukung beberapa model tanah tingkat lanjut
lainnya diantaranya adalah :
Model Mohr-Coulomb (MC)
Model Linear Elastic
2.7.2
Model Mohr-Coulomb (MC)
Model Mohr-Coulomb adalah model elastis-plastis yang terdiri dari lima buah
parameter, yaitu
E dan v untuk memodelkan elastisitas tanah :
?
dan c untuk
memodelkan plastisitas tanah dan ?
sebagai sudut dilatansi. Model Mohr-Coulomb
merupakan “ordo pertama” dari perilaku tanah dan batuan. Pada model Mohr-
Coulomb,
setiap lapisan tanah dimodelkan dengan sebuah nilai kekakuan rata-rata
yang konstan. Dengan nilai kekakuan yang konstan tersebut, maka perhitungan
cenderung cepat dan dapat diperoleh perkiraan awal dari bentuk deformasi dari
permodelan.
Model Mohr-Coulomb merupakan pemodelan tanah dengan nilai plastisitas
sempurna, dimana plastisitas mempunyai hubungan dengan terbentuknya regangan
yang tidak dapat kembali dengan semula. Untuk mengevaluasi apakah plastisitas
telah terjadi dalam perhitungan, sebuah fungsi leleh (yield function), f, digunakan
sebagai fungsi dari tegangan dan regangan. Sebuah fungsi leleh umumnya dapat
dinyatakan sebagai sesuatu bidang dalam ruang tegangan utama. Model plastis-
sempurna merupakan suatu model konstitutif dengan bidang leleh tertentu, yaitu
bidang leleh yang sepenuhnya didefinisikan oleh parameter model dan tidak
terpengaruh oleh peregangan (plastis). Untuk Kondisi tegangan yang dinyatakan oleh
|
 32
titik-titik yang berada di bawah bidang leleh, perilaku dari titik-titik tersebut akan
sepenuhnya elastis dan seluruh renganan dapat kembali seperti semula.
Gambar 2.13 Ide Dasar Dari Suatu Model Elastis Plastis- Sempurna
(Sumber: Manual Plaxis V8)
Modulus Elastisitas Young E
Ada 3 kondisi E yang berbeda, yang digunakan sesuai dengan kondisi
lapangannya. E
0
disebut sebagai E inisial, digunakan jika tanah memiliki rentang
elastis yang besar. Untuk tanah yang elastis E
0
berimpit dengan E
50
sehingga E
0
=
E
50
. E
50
adalah modulus elastisitas yang mengacu pada nilai 0.5
f (
f adalah
tegangan yang membuat tanah menjadi bersifat plastis sempurna). E
50
digunakan
jika kondisi tanah di lapangan dibebani (pembangunan upper Structure,
jalan,
embankment, dan sebagainya).
Poisson’s ration v
Cohesion c dan angle of friction ?
Untuk ?
yang biasanya pada tanah granulai, diambil batasan terbesar ?
= 35
0
(umumnya pasir padat). Alasannya adalah karena kecenderungan pelemahan kuat
geser setelah melewati kuat geser puncak (post-peak softening) pada tanah pasir.
Sudut Dilantansi ?
|
 33
Jika tanah menerima beban vertikal, butiran tanah akan bergulir ke samping
pada kondisit failure. Jika sudut geser dalam ?
adalah sudut gaya gesek antara
butir, maka ? = ? - 30
0
. ? bernilai negatif hanya realistis pada tanah pasir dalam
kondisi yang sangat lepas
2.7.3
Linear Elastic Model
Untuk setiap kenaikan tegangan dengan besar tertentu, regangan juga
bertambah dengan besar tertentu, dimana nilai keduanya membentuk garis yang
linier sesuai dengan prinsip hukum dari Hooke.
Parameter yang dibutuhkan :
Modulus Elastisitas Young
Poisson’s ratio v
Nilai v bervariasi antar 0.3 – 0.4. Semakin kecil nilai v berarti semakin kecil
regangan arah horizontal, tanah semakin padat atau kaku.
2.7.4
Model dan Input Parameter Material
Drained
Hanya menghitung tegangan pori initial u
O
. Tegangan pori ekses ?u tidak
akan dihitung pada kondisi ini. Digunakan untuk memodelkan tanah yang
kering, tanah yang memiliki porositas besar (tanah granular) dan tanah
yang telah mengalamai konsolidasi penuh dalam jangka waktu lama (air
pori telah terdisipasi semua sehingga ?u = 0).
Undrained
Perhitungan meliputi u
O
dan ?u bgahkan untuk material yang berada di
atas muka air tanah (penting untuk mengingat memasukkan parameter
|
|
34
efektif, bukan parameter jenuh untuk material di atas GWT). Untuk
perhitungan konsolidasi (Plastic Calcuulation) dimana ?u adalah
pemeran utamanya, diharapkan semua material yang mengalami
konsolidasi berada dalam kondisi undrained baik tanah granular di bawah
GWT maupun tanah kohesif yang berada di atas GWT. Ambil nilai
permeabilitas yang representative untuk pemodelan tersebut.
2.7.5
Pemodelan Beban dan Boundary Element
Pemodelan boundary element :
Standard fixities
Standard fixities adalah pilihan otomatis dimana vertical boundary
(koordinat x = koordinat x terendah dan koordinat x tertinggi) diberikan
horizontal fixities (Ux = 0), horizontal boundary (koordinat y = koordinat
y terendah) diberikan total fixites (Ux = Uy = 0), beams yang menyentuh
atau berpotongan dengan boundary yang memiliki fixities otomatis akan
diberikan fixed rotation pada titik potong tersebut.
Beban
Ada 2 tipe beban yang diberkan PLAXIS, masing-masing adalah beban
merata dan beban terpusat. Beban merata ditaruh dari titik ke titik
sementara beban terpusat pada suatu titik. Letak titik tersebut tidak harus
pada titik nodal karena akan terbentuk titik baru begitu beban
dimasukkan. Untuk masing-masing tipe beban disediakan 2 macam yaitu
A dan B jika membutuhkan pembebanan yang besarnya berbeda. Pada
beban merata kita bisa ubah tipe beban tersebut didalam menu PLAXIS
|
|
35
Loads – set Dynamic Load System – Load System A atau B untuk diubah
menjadi beban dynamic (gempa).
2.7.6
Pemodelan dan Aliran Muka Air
Phreatic Line
Phreatic Line adalah garis permukaan air dimana tegangan air adalah 0.
Tengan air akibat phreatic line adalah tengan air hidrostatik. Secara
umum phreatic line dapat kita tempatkan dimana saja, namun agar lebih
akurat sebisa mungkin harus melewati 2 titik nodal atau suatu garis antar
elemen. Ini dikarenakan tegangan air dihitung per titik nodal. Dalam
PLAXIS phreatic line dapat juga ditempatkan secara khusus per cluster,
untuk menggambarkan kondisi dimana beberapa elemen memliki phreatic
line yang berbeda misalnya sebagai akibat
dewatering pada pembuatan
basement.
Caranya dengan memilih dahulu cluster-cluster yang akan
diberi phreatic line,
sehingga tegangan akibat phreatic line hanya akan
berlaku pada cluster-cluster yan dipilih saja. Kemudian klik dua kali pada
masing-masing cluster untuk mendapatkan option pilihan. Berlakukan
user defined phreatic lines untuk tiap cluster, jika tidak maka perhitungan
secara otomatis akan menggunakan general phreatic line yang berada
pada boundary elemen bawah. Pilihan lain berupa interpolate adjacent
cluster or lines digunakan jika ada lapisan impermeable yang terletak di
antara 2 lapisan permeabel yang memiliki tinggi energy yang berbeda.
Untuk itu tegangan yang bekerja pada lapisan impermeable dihitung
berdasarkan interpolasi.
|
|
36
2.7.7
Pemodelan Perhitungan
Plastic Calculation
Analisis deformasi yang bersifat elastis plastis, tidak dipengaruhi oleh
waktu kecuali pada pemodelan soft soil creep. Jadi kondisi perhitungan
hanya ada 2 macam : fully undrained dan fully drained, yang mana diatur
berdasarkan parameter material yang diinput sejak awal. Ada 3 macam
variasi perhitungan dalam plastic calculation, yaitu load advanced
ultimate level, load advanced number of steps, manual control.
Consolidation analysis
Analisis konsolidasi yang menganalisis disipasi ekses tegangan pori
sebagai fungsi dari waktu. Variasi perhitungan hanta ada satu yaitu
automatic time stepping
Updated Mesh
Option ini memperhitungkan deformasi yang terjadi pada struktur sebagai
faktor yang mengurangi kekuatan tanah. Pada kenyataannya ini yang
terjadi pada lapangan, namun deformasi yang kecil biasanya tidak
memberikan dampak yang besar pada kekuatan tanah. Karena itu model
ini dianjurkan pada kondisi
yang riskan dan kita yakin akan terjadi
deformasi yang cukup besar pada struktur yang dimodelkan.
Reset displacement to zero
Digunakan untuk mengabaikan displacement / pergerakan yang terjadi
pada fase perhitungan sebelumnya sehingga perhitungan pada fase ini
dimulai dengan menganggap belum ada pergerakan. Contohnya,
pergerakan yang terjadi akibat berat sendiri biasa tidak perlu
diperhitungkan.
|
|
37
Ignored undrained behavior
Semua material yang bersifat undrained menjadi drained. Tegangan pori
ekses yang telah terjadi pada fase sebelumnya akan tetap ada, namun pada
fase dimana pilihan ini aktif tidak akan terjadi penambahan tegangan pori
ekses baru. Pilihan ini digunakan pada pembebanan gravity loading (berat
sendiri). Berat sendiri material yang bersifat undrained biasanya
menimbulkan tegangan pori ekses yang tidak realitis. Pada kenyataannya
tengangan pori ekses timbul akibat beban luar, bukan berat material itu
sendiri.
Delete intermediate steps
Menghilangkan step-step perhitungan sebelumnya, hanya menampilkan
hasil akhir yang paling relevan.
2.8
Korelasi Empiris Antar Parameter
Untuk mendapatkan data parameter tanah yang diperlukan dalam desain suatu
struktur Geoteknik, ada beberapa cara yang dapat dilakukan, yaitu : pengujian
langsung di lapangan, pengujian di laboratorium, ataupun dengan mengunakan
korelasi empiris antar parameter yang telah direkomendasikan oleh para tenaga ahli.
Pada umumnya, parameter tanah diperoleh dari hasil pengujian di lapangan dan
laboratorium. Sedangkan untuk korelasi empiris antar parameter biasanya digunakan
apabila data yang diperlukan untuk desain tidak tersedia dari hasil pengujian
langsung dilapangan ataupun laboratorium. Selain itu dapat juga digunakan untuk
verifikasi hasil data dengan data lainnya. Beberapa korelasi empiris yang telah
direkomendasikan oleh para ahli adalah sebagai berikut :
|
 38
1.
Nilai kisaran parameter pasir berdasarkan konsistensi tanah
Berikut adalah nilai kisaran parameter tanah pasir terutama untuk nilai sudut
geser dalam (f) :
Tabel 2.4
Interval Nilai Sudut Geser Dalam (f) Tanah Pasir
Cohesionless Soil
N-SPT
0 - 10
11 - 30
31-50
> 50
State
Loose
Medium
Dense
Very Dense
Angle of Friction (f)
25 - 32
28 - 36
30 - 40
> 35
Unit Weight (?)
12 - 16
14 - 18
16 - 20
18 - 23
(Sumber : Soil Mechanics, William T, Whitman, Robert V, 1962)
2.
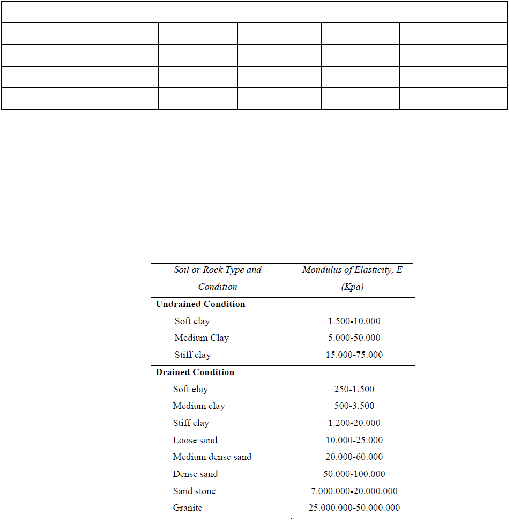
Korelasi beberapa jenis tanah dengan modulus elastisitas
Korelasi nilai kekakuan tanah dalam kondisi undrained
dan drained
berdasarkan konsistensi tanah :
Gambar 2.14 Interval Nilai Kekakuan Tanah Berdasarkan Konsistensi Tanah
(Sumber : Soil Mechanics, William T, Whitman, Robert V, 1962)
|