|
5
BAB 2
TINJAUAN KEPUSTAKAAN
2.1
Pondasi
Pondasi merupakan bagian dari struktur bangunan yang paling dasar yang
berfungsi untuk menanggung beban dan meneruskannya ke tanah. Dalam pembagian
secara umum, pondasi terbagi menjadi 2 macam menurut kedalamannya yaitu
pondasi dangkal dan pondasi dalam.
Pondasi dangkal adalah pondasi yang menanggung bebannya secara langsung
dan meneruskannya ke tanah. Kedalaman pondasi ini sangat dangkal dengan
perbandingan kedalaman dan lebar pondasi kurang dari 1 (L/B < 1, di mana L adalah
nilai kedalaman pondasi dan B adalah lebar pondasi). Pondasi dangkal terdiri dari
beberapa tipe seperti pondasi pasangan batu kali menerus, pondasi telapak
(footplate), pondasi telapak menerus, pondasi umpak, dan pondasi rakit.
Pondasi dalam adalah pondasi yang menanggung beban dan meneruskannya ke
tanah, tanah keras, atau batuan yang letaknya relatif cukup dalam jika diukur dari
permukaan tanah. Contoh dari pondasi ini adalah pondasi tiang yang terbagi menjadi
tiang pancang dan tiang bor. Nilai perbandingan antara kedalaman dengan lebar
pondasi pada pondasi dalam umumnya adalah lebih besar dari 4 (L/B
= 4).
Salah satu jenis pondasi dalam yaitu pondasi tiang. Dalam penggunaannya,
pondasi tiang umumnya terdiri atas tiang tunggal (single pile) dan kelompok tiang
(group piles)
Pemilihan penggunaan tiang tunggal dan kelompok tiang serta perencanaannya
relatif terhadap besar beban yang akan diterima, luas area pembebanan dan
parameter tanah yang dibebani. Kapasitas pembebanan kelompok tiang tidak selalu
|
|
6
sama dengan jumlah kapasitas pembebanan dari masing-masing tiang tunggal yang
ada dalam kelompok tiang tersebut.
Kapasitas pembebanan suatu kelompok tiang dipengaruhi oleh faktor efisiensi.
Biasanya pada jenis tanah lempung, kapasitas total dari kelompok tiang lebih kecil
daripada hasil kali kapasitas tiang tunggal dikalikan jumlah tiang dalam
kelompoknya. Hal-hal yang mempengaruhi efisiensi tiang di antaranya jumlah tiang
dalam suatu kelompok tiang, panjang atau kedalaman tiang, diameter tiang, susunan
tiang, jarak antar tiang, besarnya beban dan arah dari beban yang bekerja.
2.2
Beban Lateral
Beban lateral merupakan beban yang memiliki arah horizontal. Beban-beban
yang memiliki arah horizontal contohnya adalah beban angin, beban gempa, tekanan
tanah lateral, beban
hempasan ombak atau kapal pada sisi struktur bangunan, dan
lain-lain. Beban lateral yang diterima oleh pondasi tiang akan bergantung pada
struktur bangunan yang akan meneruskan gaya lateral yang diterima ke kolom bagian
paling bawah dari upper structure dan diteruskan kepada kelompok tiang pondasi.
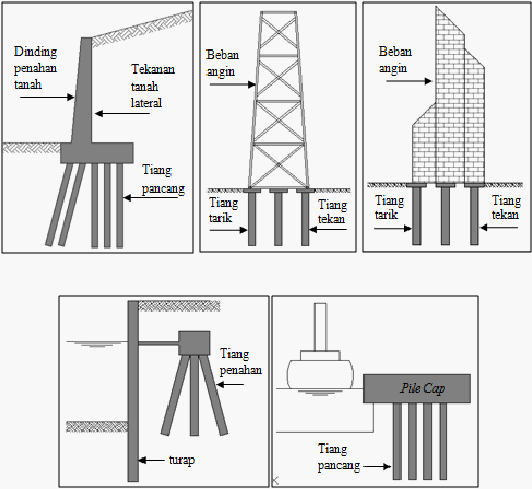
Pondasi tiang memiliki beberapa aplikasi untuk menahan beban lateral pada
struktur. Pondasi tiang dapat menahan beban lateral yang bekerja pada dinding
penahan tanah, di mana beban lateral berasal dari tekanan tanah lateral yang
mendorongnya seperti yang terlihat pada Gambar 2.1 (a). Pondasi tiang juga dapat
menahan beban lateral seperti beban angin yang bekerja pada struktur bangunan
tingkat tinggi seperti struktur rangka baja atau gedung pencakar langit seperti
yang
terlihat pada Gambar 2.1 (b) dan Gambar 2.1 (c) sehingga pondasi tiang mengalami
gaya tarik dan gaya tekan. Pondasi tiang juga dapat menahan dinding turap yang
menyangga pada pondasi tiang seperti Gambar 2.1 (d). Pondasi tiang juga
|
 7
menanggung beban lateral yang disebabkan gaya eksternal seperti hempasan
gelombang air laut, angin, dan benturan kapal pada konstruksi lepas pantai seperti
Gambar 2.1 (e).
(a)
(b)
(c)
(d)
(e)
Gambar 2.1 Aplikasi Pondasi Tiang dalam Menahan Beban Lateral
Pondasi tiang individu terdiri dari dua klasifikasi yaitu pondasi tiang pendek
dan pondasi tiang panjang. Pada tiang dengan kepala bebas, tiang panjang jika ß(L)
> 2,5 dan tiang pendek jika ß(L) < 2,5. Pada tiang dengan kepala terjepit, tiang
panjang jika ß(L) > 1,5 dan tiang pendek jika ß(L) < 1,5. Beban lateral yang bekerja
pada kedua jenis tiang tersebut akan menghasilkan pergerakan yang berbeda dari segi
defleksi dan mekanisme keruntuhan tiang. Perbedaan defleksi dan mekanisme
|
 8
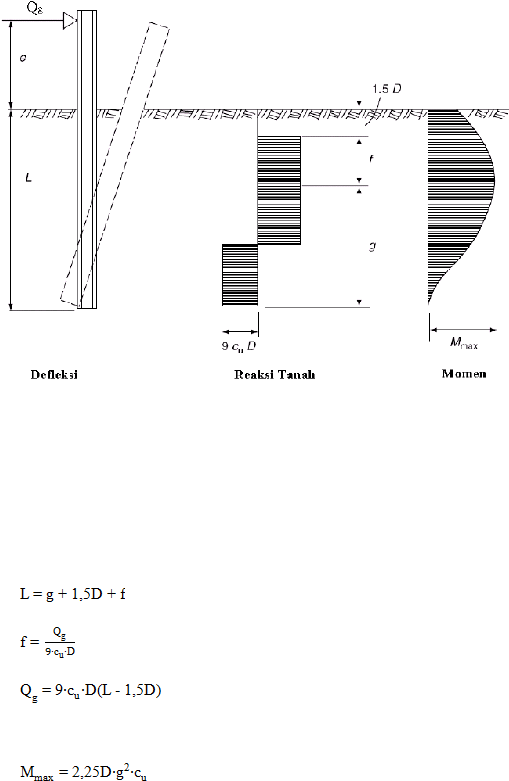
keruntuhan akibat beban lateral yang terjadi pada pondasi tiang pendek dan pondasi
tiang panjang dapat dilihat pada Gambar 2.2 dan Gambar 2.4.
Gambar 2.2 Defleksi dan Mekanisme Keruntuhan untuk Pondasi Tiang Pendek
dengan Kondisi Kepala Tiang Bebas Akibat Beban Lateral pada Tanah Kohesif
(Broms, 1964)
Panjang total tiang adalah sebesar:
..................................................................................... (2.1)
.................................................................................................. (2.2)
............................................................................ (2.3)
Momen maksimum yang terjadi:
................................................................................ (2.4)
|
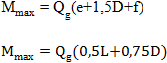 9
............................................................................ (2.5)
...................................................................... (2.6)
Di mana:
L
= Panjang tiang (m)
D
= Diameter tiang (m)
Qg
= Beban lateral (kN)
cu
= Kohesi tanah undrained (kN/m2)
f
= Jarak momen maksimum dari permukaan tanah (m)
g
= Jarak dari lokasi momen maksimum sampai dasar tiang (m)
|
 10
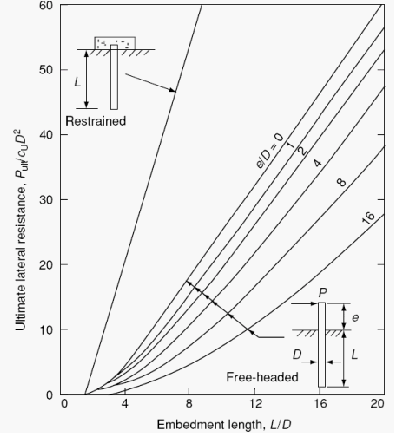
Nilai beban lateral (Qg = Pult) dapat ditentukan secara langsung melalui grafik
pada Gambar 2.3.
Gambar 2.3 Kapasitas Beban Lateral untuk Pondasi Tiang Pendek pada Tanah
Kohesif (Broms, 1964)
|
 11
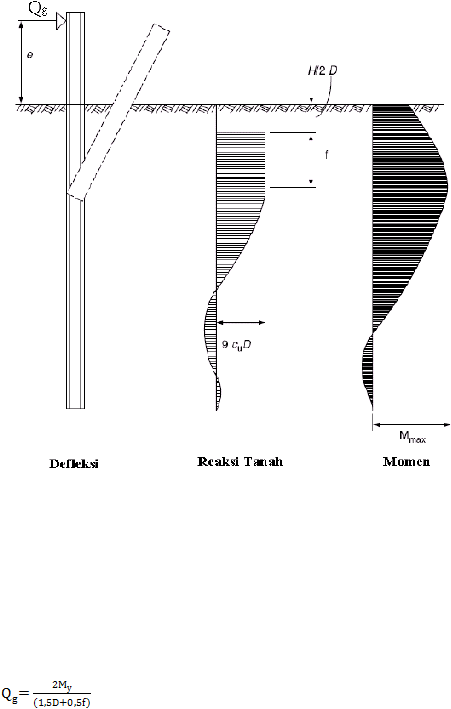
Gambar 2.4 Defleksi dan Mekanisme Keruntuhan untuk Pondasi Tiang Panjang
dengan Kondisi Kepala Tiang Bebas Akibat Beban Lateral pada Tanah Kohesif
(Broms, 1964)
Beban lateral yang ada pada pondasi tiang panjang adalah sebesar:
......................................................................................... (2.7)
Di mana:
Q
g
= Beban lateral (kN)
M
y
= Momen leleh (kN/m)
D
= Diameter tiang (m)
|
 12
f
= Jarak momen maksimum dari permukaan tanah (m)
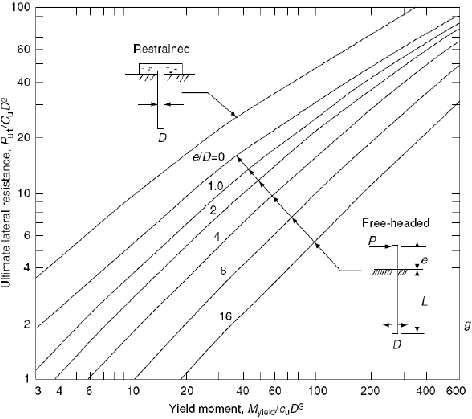
Untuk pondasi tiang panjang, nilai beban lateral (Q
g
= P
ult
) dapat diperoleh
berdasarkan grafik pada Gambar 2.5.
Gambar 2.5 Kapasitas Beban Lateral untuk Pondasi Tiang Panjang pada Tanah
Kohesif (Broms, 1964)
|
 13
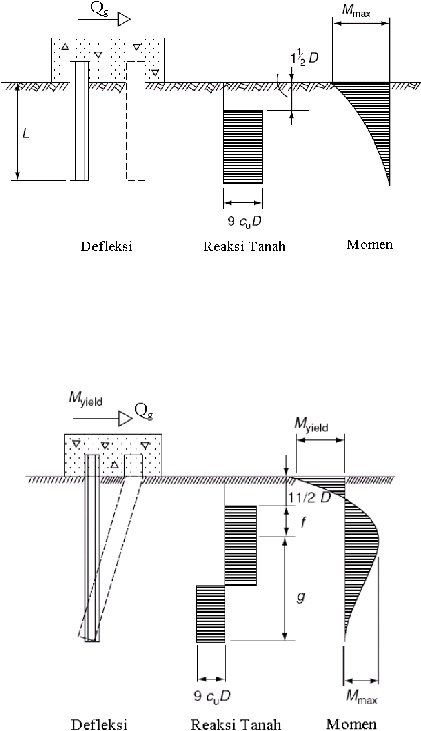
Mekanisme keruntuhan akibat beban lateral yang terjadi pada pondasi tiang
dengan kondisi kepala tiang terjepit dapat dilihat pada Gambar 2.6.
Gambar 2.6 (a) Defleksi Akibat Beban Lateral untuk Pondasi Tiang Pendek dengan
Kondisi Kepala Tiang Terjepit pada Tanah Kohesif (Broms, 1964)
Gambar 2.6 (b) Defleksi Akibat Beban Lateral untuk Pondasi Tiang Sedang dengan
Kondisi Kepala Tiang Terjepit pada Tanah Kohesif (Broms, 1964)
|
 14
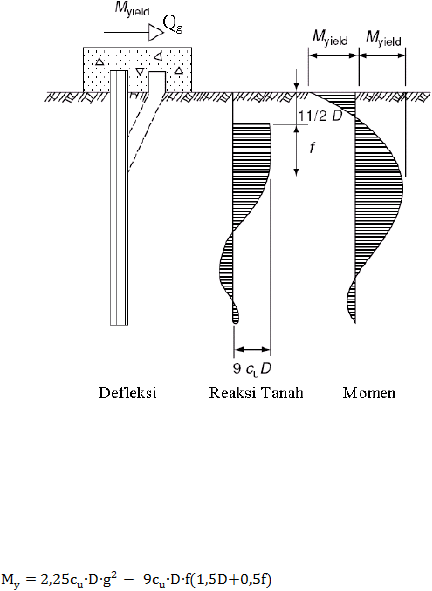
Gambar 2.6 (c) Defleksi Akibat Beban Lateral untuk Pondasi Tiang Panjang dengan
Kondisi Kepala Tiang Terjepit pada Tanah Kohesif (Broms, 1964)
Momen pada tiang:
............................................ (2.8)
Di mana:
L
= Panjang tiang (m)
D
= Diameter tiang (m)
Qg
= Beban lateral (kN)
cu
= Kohesi tanah (kN/m2)
f
= Jarak momen maksimum dari permukaan tanah (m)
g
= Jarak dari lokasi momen maksimum sampai dasar tiang (m)
|
 15
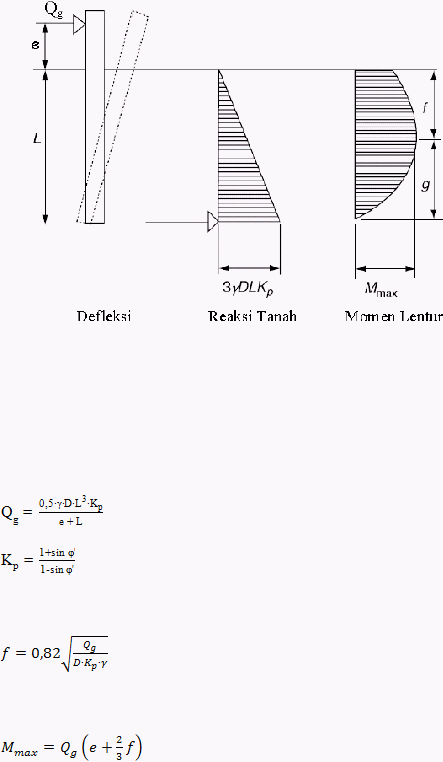
Gambar 2.7 Defleksi Akibat Beban Lateral untuk Pondasi Tiang Pendek dengan
Kondisi Kepala Tiang Bebas pada Tanah Non-kohesif (Broms, 1964)
Beban lateral untuk tiang pendek:
...................................................................................... (2.9)
............................................................................................. (2.10)
Lokasi momen maksimum:
..................................................................................... (2.11)
Momen maksimum:
............................................................................ (2.12)
|
 16
Di mana:
Q
g
= Beban lateral (kN)
M
max
= Momen maksimum (kN-m)
L
= Panjang tiang (m)
D
= Diameter tiang (m)
K
p
= Koefisien tekanan tanah pasif
f
= Jarak momen maksimum dari permukaan tanah (m)
= Berat isi tanah (kN/m³)
e
= Jarak beban lateral dari permukaan tanah (m)
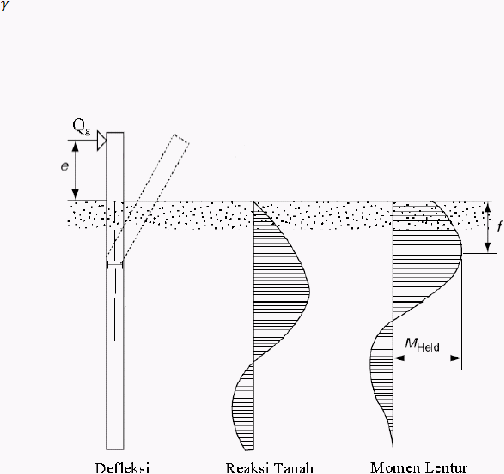
Gambar 2.8 Defleksi Akibat Beban Lateral untuk Pondasi Tiang Panjang dengan
Kondisi Kepala Tiang Bebas pada Tanah Non-kohesif (Broms, 1964)
|
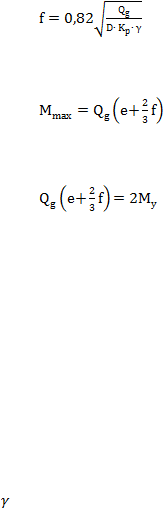 17
Lokasi momen maksimum:
...................................................................................... (2.11)
Momen maksimum:
................................................................................ (2.12)
Beban lateral untuk tiang panjang:
.................................................................................. (2.13)
Di mana:
Q
g
= Beban lateral (kN0
M
yield
= Momen leleh (kN-m)
L
= Panjang tiang (m)
D
= Diameter tiang (m)
f
= Jarak momen maksimum dari permukaan tanah (m)
= Berat isi tanah (kN/m³
)
e
= Jarak beban lateral dari permukaan tanah (m)
|
 18
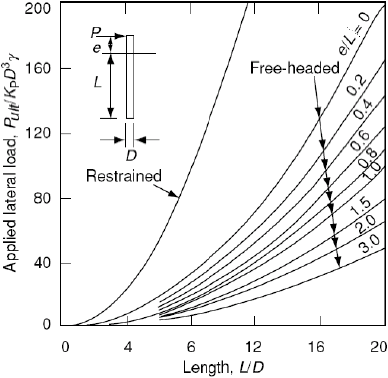
Untuk pondasi tiang pendek, nilai beban lateral (Qg = Pult) dapat diperoleh
berdasarkan grafik pada Gambar 2.9.
Gambar 2.9 Kapasitas Beban Lateral untuk Pondasi Tiang Pendek pada Tanah
Kohesif (Broms, 1964)
|
 19
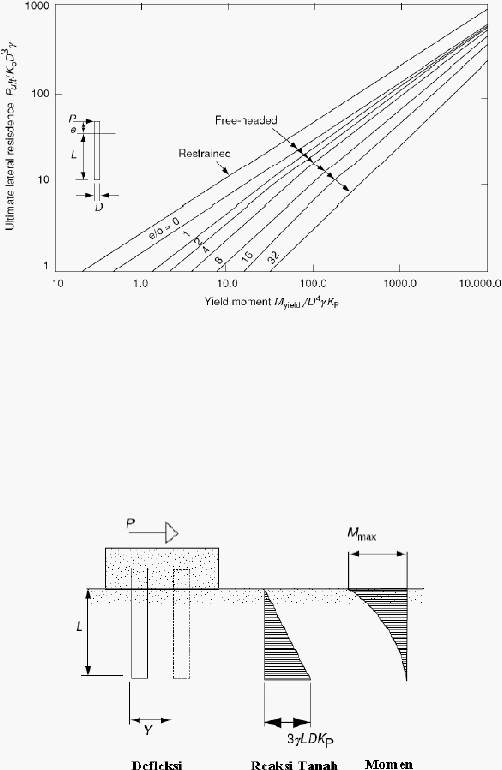
Nilai beban lateral (Qg = Pult) untuk pondasi tiang panjang dapat diperoleh
berdasarkan grafik Gambar 2.9.
Gambar 2.10 Kapasitas Beban Lateral untuk Pondasi Tiang Panjang pada Tanah
Non-kohesif (Broms, 1964)
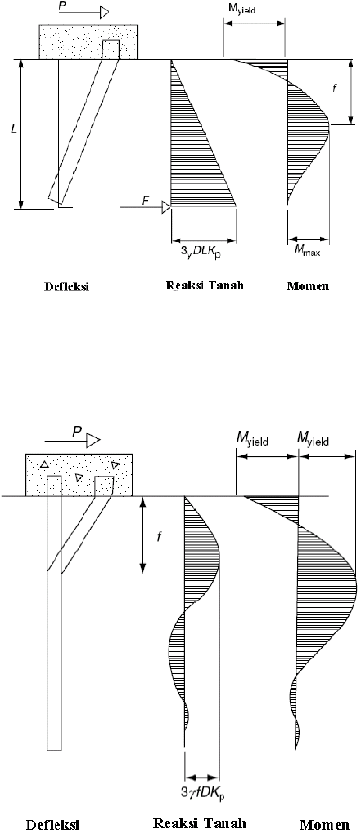
Mekanisme keruntuhan akibat beban lateral yang terjadi pada pondasi tiang
dengan kondisi kepala tiang terjepit dapat dilihat pada Gambar 2.11.
Gambar 2.11 (a) Defleksi Akibat Beban Lateral untuk Pondasi Tiang Pendek dengan
Kondisi Kepala Tiang Terjepit di Tanah Non-kohesif
|
 20
Gambar 2.11 (b) Defleksi Akibat Beban Lateral untuk Pondasi Tiang Sedang dengan
Kondisi Kepala Tiang Terjepit Di Tanah Non-kohesif
Gambar 2.11 (c) Defleksi Akibat Beban Lateral untuk Pondasi Tiang Panjang dengan
Kondisi Kepala Tiang Terjepit Di Tanah Non-kohesif (Broms, 1964)
|
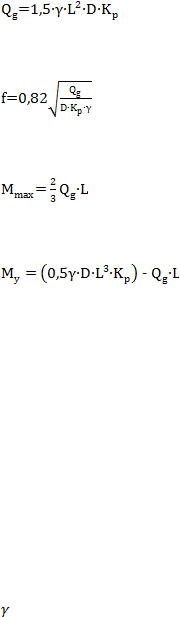 21
Persamaan beban lateral untuk kondisi kepala tiang terjepit:
.................................................................................. (2.14)
Lokasi momen maksimum:
......................................................................................... (2.11)
Momen maksimum:
.......................................................................................... (2.15)
Momen leleh:
................................................................... (2.16)
Di mana:
Q
g
= Beban lateral (kN)
K
p
= Koefisien tekanan tanah pasif
M
max
= Momen maksimum (kN-m)
M
y
= Momen leleh (kN-m)
L
= Panjang tiang (m)
D
= Diameter tiang (m)
f
= Jarak momen maksimum dari permukaan tanah (m)
= Berat isi tanah (kN/m³
)
e
= Jarak beban lateral dari permukaan tanah (m)
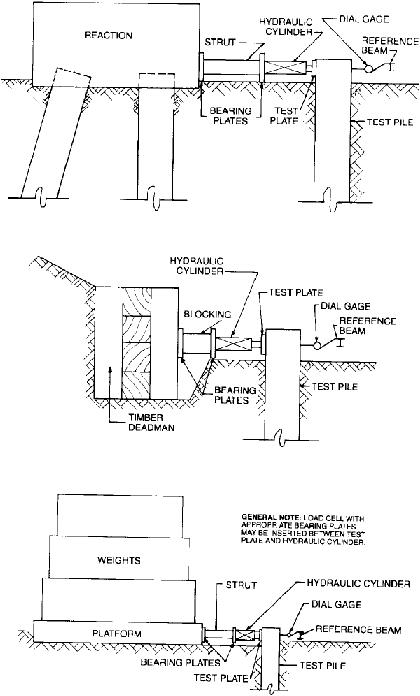
Dalam melakukan pengujian besarnya kapasitas tiang terhadap beban lateral,
digunakan bantuan dengan alat hydraulic jack. Digunakan juga plat baja yang cukup
kaku dengan ukuran tertentu yang pas dengan ukuran tiang agar dapat bersentuhan
secara keseluruhan dengan tiang pada saat uji kapasitas lateral tiang seperti terlihat
pada Gambar 2.12.
|
 22
(a)
(b)
(c)
Gambar 2.12 Beberapa Tipe Pengujian Kapasitas Lateral Tiang (a) Reaction Pile, (b)
Deadman, (c) Weighted Platform (ASTM D3966-81, 1989)
|
 23
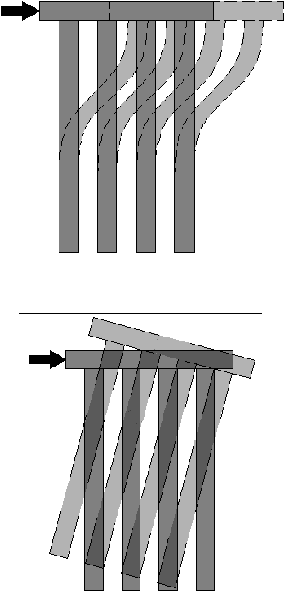
Beban lateral yang terjadi pada pondasi kelompok tiang dapat mengakibatkan
pergerakan pada keseluruhan kelompok tiang. Pergerakan yang dapat terjadi adalah
pergerakan translasi dan pergerakan rotasi. Pergerakan translasi pada kelompok tiang
adalah perubahan posisi pada kelompok tiang akibat timbulnya gaya aksial tarik dan
gaya aksial tekan sehingga pada satu sisi kelompok tiang terangkat naik dan di sisi
lainnya kelompok tiang tertekan ke bawah. Sedangkan pergerakan rotasi adalah
perubahan posisi tiang dalam bentuk perputaran kelompok tiang akibat kekakuan
tiang yang sangat besar.
Gambar 2.13 Pergerakan Translasi pada Kelompok Tiang Akibat Gaya Lateral
Gambar 2.14 Pergerakan Rotasi pada Kelompok Tiang Akibat Gaya Rotasi
|
 24
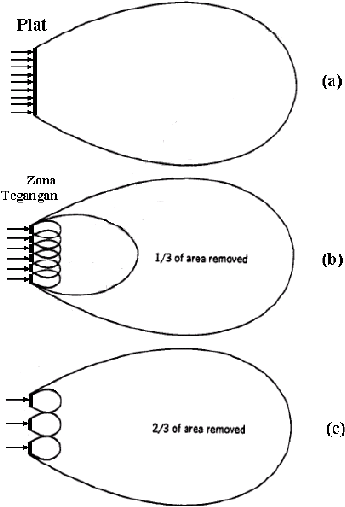
Pada sebuah plat yang diberi gaya lateral, akan muncul zona pengaruh beban.
Jika sepertiga bagian plat dihilangkan, maka akan terjadi overlap pada zona
tegangan. Overlap yang terjadi akan mereduksi kapasitas dari sebuah elemen. Agar
tidak terjadi overlap, maka jarak antar elemen harus diperbesar dengan
menghilangkan lagi sepertiga bagian plat. Hal ini ditunjukkan pada Gambar 2.15.
Gambar 2.15 Zona Tegangan Plat
|
 25
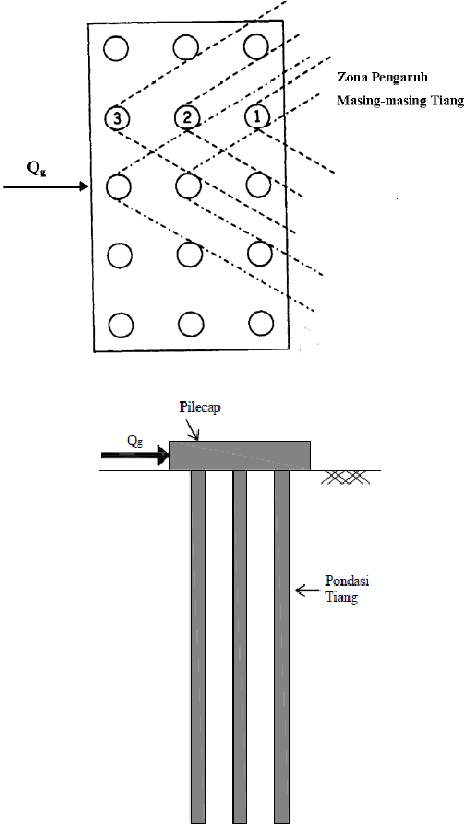
Gambar 2.16 Zona Pengaruh Kelompok Tiang
|
 26
2.3
Teori Dasar Solusi Elastik (Reese dan Matlock)
Metode non-dimensional untuk analisis beban lateral terhadap tiang elastis
berdasarkan penelitian oleh Reese dan Matlock (1956). Untuk tiang yang sangat
panjang, panjang,nilai L akan berkurang pengaruhnya akibat defleksi yang semakin
mendekati nol sesuai panjang tiang. Apabila asumsi sifat elastis diterapkan terhadap
tiang, dan defleksi terlampau kecil apabila dibandingkan dengan panjang tiang, maka
pondasi tiang yang dibebani secara lateral dapat bergerak secara elastis sesuai beban
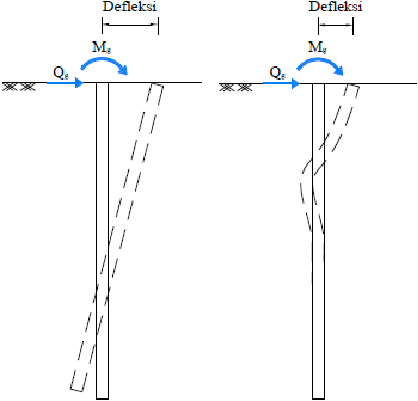
yang diterima. Perbedaan defleksi antara tiang pendek yang kaku dan tiang panjang
yang elastis dapat dilihat pada Gambar 2.17.
Gambar 2.17 Defleksi pada Pondasi Tiang Kaku dan Pondasi Tiang Elastis
|
 27
2.3.1
Tanah Granular
Momen dan perpindahan dari suatu pondasi tiang yang tertanam di tanah
granular
berdasarkan beban lateral dan momen yang terjadi di permukaan tanah
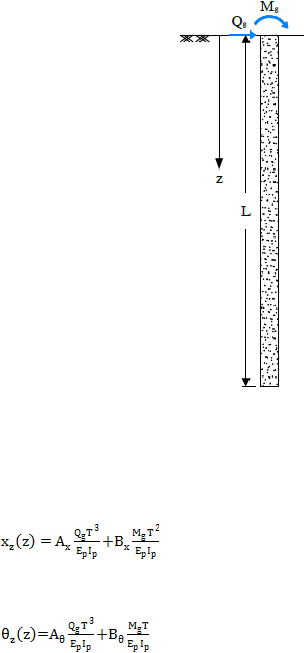
ditentukan oleh metode umum oleh Matlock dan Reese (1960). Pada Gambar 2.18
dapat dilihat pondasi tiang dengan panjang
L diberikan gaya lateral Q
g
dan Momen
M
g
pada permukaan tanah (z=0)
Gambar 2.18 Beban Lateral dan Momen pada Pondasi Tiang
Defleksi pada tiang (x
z
):
........................................................................ (2.17)
Tekuk pada tiang (?
z
):
.......................................................................... (2.18)
|
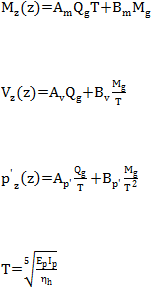 28
Momen pada tiang (M
z
):
.......................................................................... (2.19)
Gaya geser pada tiang (V
z
):
................................................................................ (2.20)
Reaksi pada tanah (p’
z
):
............................................................................. (2.21)
Karakteristik panjang tiang:
................................................................................................. (2.22)
Di mana:
E
p
= Modulus elastisitas tiang
I
p
= Momen inersia penampang tiang
Q
g
= Beban lateral
M
g
= Momen
z
= kedalaman
?
h
= k/Z = Modulus konstan reaksi tanah
k
= Modulus reaksi tanah dalam arah horizontal
A
x
, B
x
, A
?
, B
?
, A
m
, B
m
, A
v
, B
v
, A
p’
, B
p’
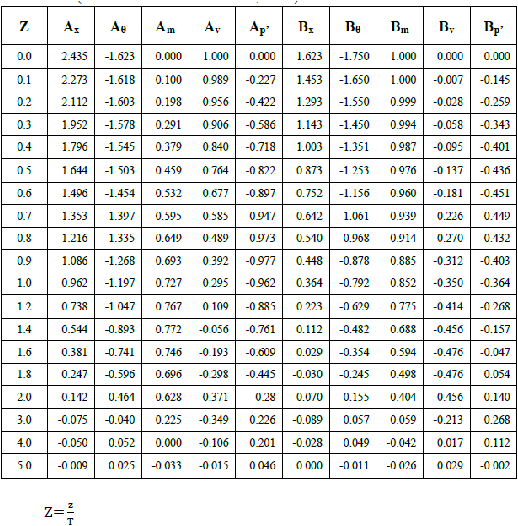
adalah koefisien yang dapat dilihat pada tabel
2.1.
|
 29
Tabel 2.1 Koefisien A dan B pada Pondasi Tiang Panjang Vertikal pada Tanah
Granular dengan Asumsi E
s
= ?
h
x
Di mana
................................................................................................... (2.23)
|
 30
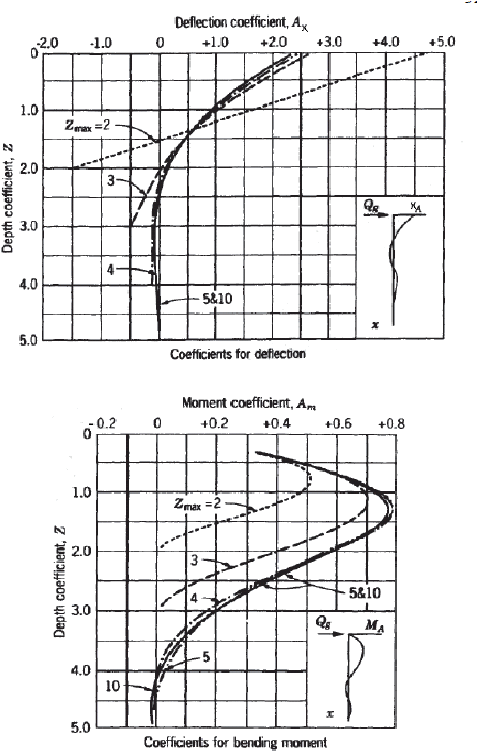
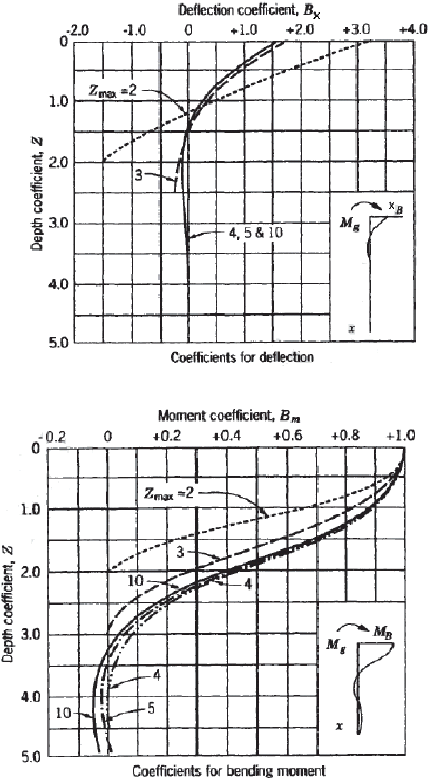
Gambar 2.19 Koefisien A
x
dan A
m
Pondasi Tiang (Broms, 1964)
|
 31
Gambar 2.20 Koefisien Bx dan Bm Pondasi Tiang (Broms, 1964)
|
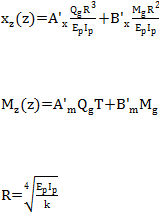 32
2.3.2 Tanah Kohesif (Cohesive Soil)
Menurut Davidson dan Gill (1963), persamaan solusi elastis untuk tiang yang
tertanam di tanah granular menyerupai dengan persamaan solusi elastis untuk tiang
yang tertanam di tanah kohesif.
Defleksi pada tiang (x
z
):
........................................................................ (2.24)
Momen pada tiang:
........................................................................ (2.25)
Karakteristik panjang tiang:
................................................................................................. (2.26)
Di mana:
E
p
= Modulus elastisitas tiang
I
p
= Momen inersia penampang tiang
Q
g
= Beban lateral
M
g
= Momen
z
= Kedalaman
k
= Modulus reaksi tanah dalam arah horizontal
Nilai A’
x
, B’
x
, A’
m
, dan B’
m
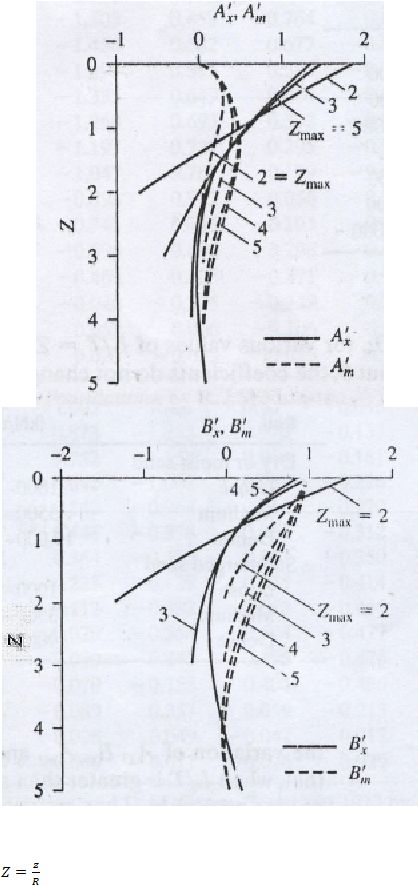
diambil berdasarkan grafik pada Gambar 2.21.
|
 33
Gambar 2.21 Nilai A’
x
, B’
x
, A’
m
, dan B’
m
(Davidson dan Gill, 1963)
Di mana:
............................................................................................... (2.27)
|
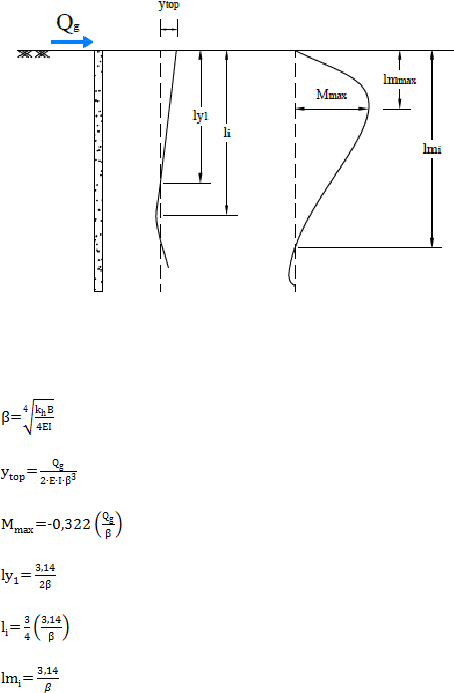 34
2.4
Teori Dasar Metode Chang
Berdasarkan metode Chang, kondisi pondasi tiang dibedakan menjadi dua
macam,
yaitu kondisi kepala tiang bebas (free head pile) dan kondisi kepala tiang
terjepit (fixed head pile).
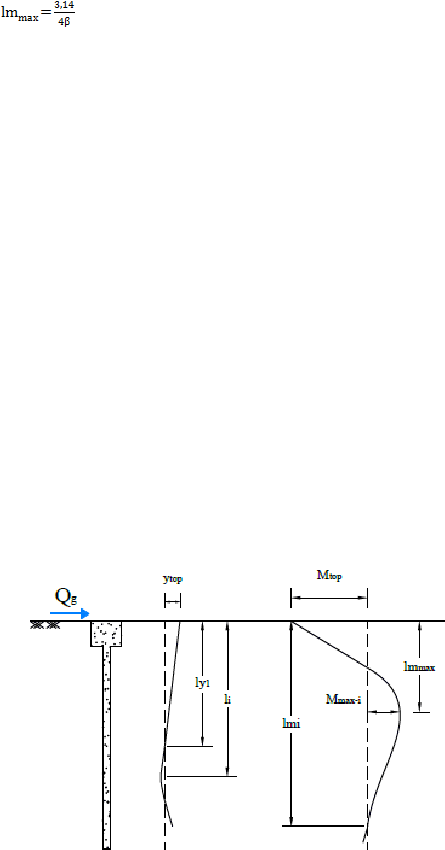
2.4.1. Kondisi Kepala Tiang Bebas (Free Head Pile)
Gambar 2.22 Kondisi Kepala Tiang Bebas (Free Head Pile)
.................................................................................................. (2.28)
............................................................................................ (2.29)
................................................................................. (2.30)
.................................................................................................. (2.31)
.............................................................................................. (2.32)
................................................................................................. (2.33)
|
 35
............................................................................................. (2.34)
Di mana:
k
h
= Modulus reaksi tanah dalam arah horizontal (kN/m³
)
B
= Lebar atau diameter tiang (m)
E
= Modulus elastisitas tiang (kN/m
2
)
I
= Momen inersia penampang tiang (m
4
)
Q
g
= Gaya horizontal pada tiang (kN)
M
max
= Bending momen maksimum pada kedalaman lm
max
lm
max
= Kedalaman dari M
max
lm
i
= Kedalaman dari momen titik nol pertama
y
top
= Perpindahan kepala tiang
ly1
= Kedalaman dari perpindahan titik nol pertama
l
i
= Kedalaman sudut defleksi titik nol pertama
2.4.2. Kondisi Kepala Tiang Terjepit (Fixed Head Pile)
Gambar 2.23 Kondisi Kepala Tiang Terjepit (Fixed Head Pile)
|
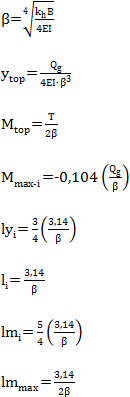 36
.................................................................................................. (2.35)
.............................................................................................. (2.36)
................................................................................................. (2.37)
............................................................................... (2.38)
............................................................................................ (2.39)
.................................................................................................... (2.40)
........................................................................................... (2.41)
............................................................................................. (2.42)
Di mana:
k
h
= Modulus reaksi tanah dalam arah horizontal (kN/m³)
B
= Lebar atau diameter tiang (m)
E
= Modulus elastisitas tiang (kN/m²
)
I
= Momen inersia penampang tiang (m
4
)
Q
g
= Gaya horizontal pada tiang (kN)
M
top
= Bending momen maksimum pada kepala tiang
M
max-1
= Bending momen maksimum pada kedalaman lm
max
lm
max
= Kedalaman dari M
max-1
lm
i
= Kedalaman dari momen titik nol kedua
y
top
= Perpindahan kepala tiang
ly1
= Kedalaman dari perpindahan titik nol pertama
l
i
= Kedalaman sudut defleksi titik nol kedua
|
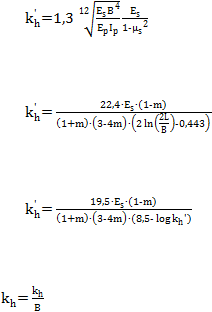 37
Untuk mencari nilai k
h
dapat dipakai beberapa metode, antara lain:
1.
Metode Vesic (1961)
.......................................................................... (2.43)
2.
Metode Glick (1948)
........................................................... (2.44)
3.
Metode Francis (1964)
................................................................ (2.45)
Untuk keseluruhan metode dapat ditentukan nilai kh dengan rumus:
..................................................................................................... (2.46)
Di mana:
E
s
= Modulus elastisitas tanah
E
p
= Modulus elastisitas tiang
I
p
= Momen inersia penampang tiang
µ
s
= Poisson ratio tanah
L
= panjang tiang
B
= Lebar atau diameter tiang
|
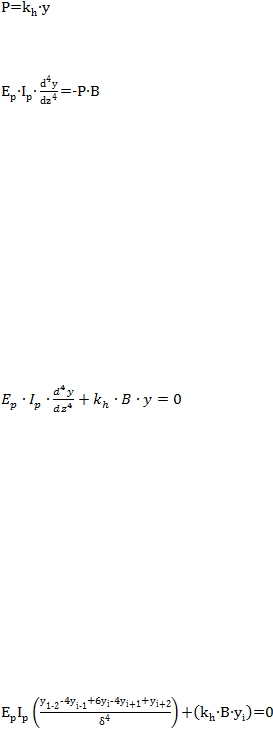 38
2.5
Teori Dasar Metode Finite Difference
Reaksi yang terjadi pada tiang pondasi sebanding dengan perpindahan menurut
model Winkler (1867). Tekanan (P) dan defleksi (y) pada suatu titik direlasikan
dengan koefisien reaksi tanah dalam arah horizontal (k
h
) menjadi:
................................................................................................... (2.47)
Tiang biasanya dianggap batang tipis yang memenuhi persamaan:
....................................................................................... (2.48)
Di mana:
E
p
= Modulus elastisitas tiang
I
p
= Momen inersia penampang tiang
z
= Kedalaman
B
= Lebar atau diameter tiang
Dari persamaan (2.47) dan (2.48) didapat persamaan defleksi tiang dengan beban
lateral sebagai berikut:
.................................................................. (2.49)
Solusi dari persamaan differensial di atas dapat diperoleh baik secara analitis
maupun secara numerik. Solusi secara analitis mudah dilakukan bila nilai k
h
konstan
sepanjang tiang. Apabila harga k
h
bervariasi, maka dapat diselesaikan dengan cara
numerik menggunakan metode finite difference
(Palmer dan Thompson, 1948;
Gleser, 1953)
Dalam metode tersebut, persamaan differensial dasar (2.49) ditulis dalam
bentuk finite difference untuk titik i sebagai berikut:
........................................... (2.50)
|
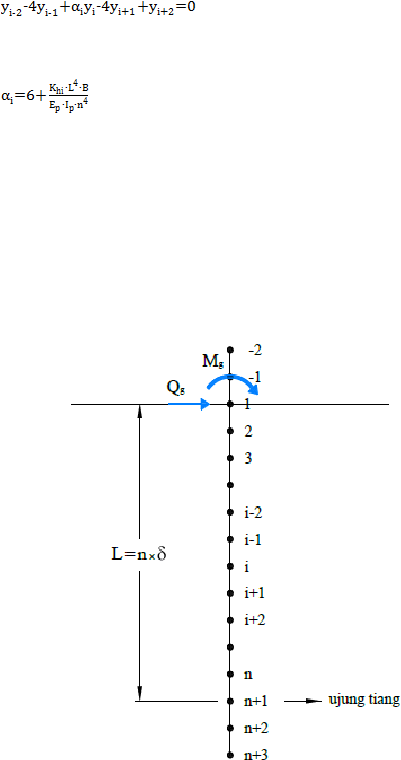 39
Dari persamaan (2.50) diperoleh:
............................................................... (2.51)
Dengan:
......................................................................................... (2.52)
Di mana:
n
= Banyaknya interval sepanjang tiang
K
hi
= Koefisien reaksi tanah dalam arah horizontal di titik i.
Persamaan (2.52) dapat ditetapkan dari titik 2 sampai n sehingga memberikan (n-1)
persamaan.
Gambar 2.24 Analisa Finite Difference untuk Tiang dengan Beban Lateral
|
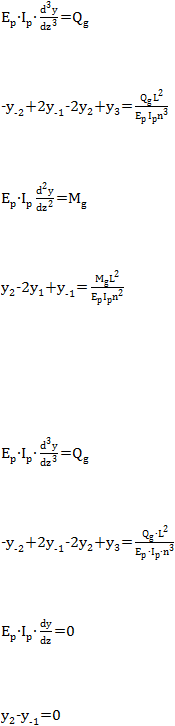 40
Persamaan-persamaan selanjutnya dapat diperoleh dari syarat-syarat batas pada
ujung kepala tiang.
Pada kepala tiang ada dua keadaan yang harus diperhatikan:
1.
Kondisi kepala tiang bebas (free head pile)
Gaya geser:
................................................................................... (2.53)
Sehingga didapat persamaan:
............................................................... (2.54)
Momen:
.................................................................................... (2.55)
Sehingga didapat persamaan:
........................................................................... (2.56)
2.
Kondisi kepala tiang terjepit (fixed head pile)
Gaya geser:
................................................................................... (2.57)
Sehingga didapat persamaan:
............................................................... (2.58)
Rotasi:
....................................................................................... (2.59)
Sehingga didapat persamaan:
.......................................................................................... (2.60)
|
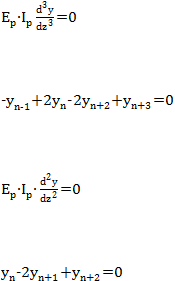 41
Dasar tiang dianggap bebas, sehingga:
Gaya geser:
...................................................................................... (2.61)
Sehingga didapat persamaan:
.............................................................. (2.62)
Momen:
..................................................................................... (2.63)
Sehingga didapat persamaan:
........................................................................... (2.64)
Dua persamaan yang masih dibutuhkan didapat dari persamaan keseimbangan
gaya horizontal dan momen. Persamaan simultan n+5 diperlukan untuk menghitung
n+5 perpindahan yang tidak diketahui (pada titik -2, -1, n+2, dan n+3).
Cara lain dari prosedur di atas adalah dengan mengabaikan persamaan gaya
geser pada ujung (tip) dan kepala tiang (top) yaitu persamaan (2.54) atau (2.58) dan
(2.62), jadi mengabaikan dua perpindahan variabel pada titik -2 dan n+3. Dalam hal
ini hanya n+3 persamaan
yang harus dipecahkan. Prosedur ini memberikan hasil
yang hampir sama dengan prosedur sebelumnya.
|
 42
2.6
Efisiensi Kelompok Tiang
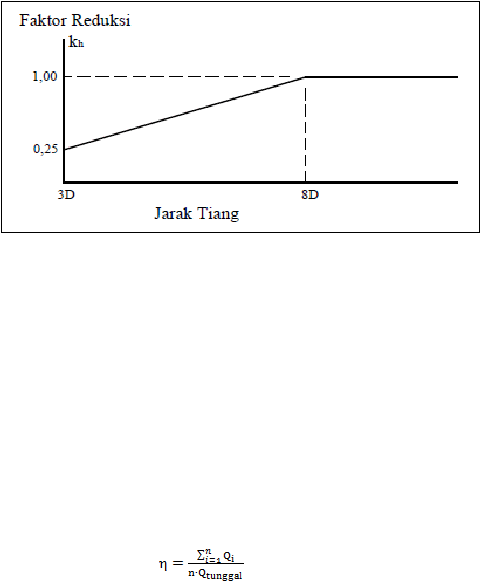
Berdasarkan Prakash (1962), nilai faktor reduksi untuk kelompok tiang
ditentukan berdasarkan besarnya jarak antar tiang.
Gambar 2.25 Faktor Reduksi Kelompok Tiang (Prakash, 1962)
Faktor reduksi tersebut digunakan untuk mencari nilai modulus reaksi tanah
dalam arah horizontal dari suatu kelompok tiang. Yang kemudian dapat digunakan
untuk mencari nilai kapasitas lateral dari suatu kelompok tiang.
Dalam perhitungan efisiensi kelompok tiang di penelitian ini, digunakan
perhitungan efisiensi dengan cara pada rumus 2.xx. Rumusan efisiensi ini merupakan
hasil dari pembagian antara beban yang dapat ditanggung kelompok tiang dengan
jumlah perkalian beban tiang tunggal dengan total tiang.
……………………..……………. (2.65)
?
= efisiensi kelompok tiang
n
= jumlah tiang
Qi
= beban lateral pada tiang ke-i
Q
tunggal
= beban lateral pada tiang tunggal
|
|
43
2.7
PLAXIS 3D
PLAXIS 3D adalah program finite element
tiga dimensi yang dikembangkan
untuk analisa deformasi, stabilitas, dan aliran air tanah dalam ilmu geoteknik.
PLAXIS 3D adalah bagian dari produk PLAXIS yang merupakan program finite
element yang digunakan secara luas untuk ilmu dan desain geoteknik. Pengembangan
PLAXIS dimulai tahun 1987 di Delft University of Technology sebagai inisiatif dari
Dutch Ministry of Public Works and Water Management (Rijkswaterstaat). Tujuan
awal pengembangan adalah untuk menciptakan program elemen hingga 2 dimensi
untuk analisis bantaran sungai yang terdiri dari tanah lunak pada dataran rendah di
Belanda. Dalam beberapa tahun, PLAXIS dikembangkan untuk mengatasi sebagian
besar area geoteknik. Karena pertumbuhan yang sangat pesat dan berkelanjutan,
perusahaan PLAXIS (Plaxis bv) dibentuk tahun 1993.
Di tahun 1998, PLAXIS 2D pertama untuk Windows dirilis. Pada waktu yang
sama, pengembangan untuk perhitungan elemen hingga 3 dimensi dilakukan
sehingga program 3DTunnel dapat dirilis tahun 2001. 3DFoundation adalah program
tiga dimensi kedua yang dirilis tahun 2004. Kedua program tersebut tidak mampu
untuk mendefinisikan bentuk geometri 3 dimensi yang lebih kompleks karena
keterbatasan geometris. Baru pada tahun 2010 program PLAXIS 3D dirilis. PLAXIS
3D adalah program PLAXIS dengan permodelan penuh 3 dimensi yang
mengkombinasikan interface yang mudah dengan fasilitas permodelan 3 dimensi.
|
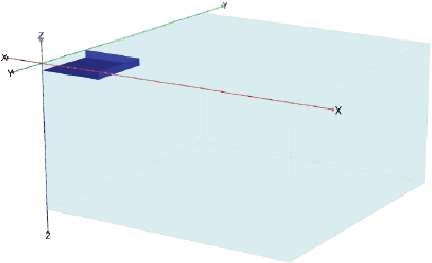 44
Gambar 2.26 Sumbu Koordinat pada PLAXIS 3D
2.8
Penelitian Sebelumnya
Penelitian ini mengacu pada laporan atau jurnal dari penelitian yang sudah
pernah dilakukan sebelumnya. Berikut ini adalah rangkuman dari jurnal-jurnal
tersebut:
A.
Analisa Kapasitas Kelompok Tiang Terhadap Beban Lateral dengan
Menggunakan PLAXIS 3D Foundation (Sri Dewi dan Gouw Tjie-Liong,
2009)
Salah satu faktor penting dalam perencanaan pondasi adalah daya
dukung lateral pondasi yang timbul akibat gempa, beban angin, dan lain-
lain. Kapasitas pembebanan lateral dari suatu kelompok tiang bukan
merupakan penjumlahan dari kapasitas lateral masing-masing tiang. Maka
dalam suatu perhitungan kapasitas pembebanan lateral tiang diperlukan
adanya faktor pengali untuk mengetahui kapasitas kelompok tiang yang
efektif. Faktor pengali tersebut biasa dikenal dengan sebutan faktor
|
|
45
efisiensi atau faktor reduksi. Agar diperoleh desain yang ekonomis maka
diperlukan faktor efisiensi kelompok tiang yang sesuai.
Di dalam literatur
geoteknik yang ada sangat jarang dibahas secara
mendetail mengenai faktor efisiensi kelompok tiang ini. Faktor efisiensi
yang terdapat di dalam literatur-literatur
tersebut pada umumnya tidak
membahas efek jumlah tiang dalam kelompok tiang, kekakuan tanah, dan
konfigurasi tiang. Penelitian ini bertujuan untuk mencari apakah terdapat
pengaruh efek-efek tersebut terhadap faktor efisiensi. Hasil penelitian
menunjukkan bahwa efek jumlah tiang dalam kelompok tiang, kekakuan
tanah, dan konfigurasi tiang berpengaruh terhadap faktor efisiensi
kelompok tiang. Semakin banyak jumlah tiang dalam suatu kelompok
tiang, faktor efisiensi semakin kecil. Semakin besar kekakuan tanah, faktor
efisiensi semakin besar.
B.
Lateral Bearing Capacity of Piles in Cohesive Soils Based on Soils’
Failure Strength Control (R. Ziaie Moayed, A. Judi, dan B. Khadem Rabe,
2008)
Penelitian ini memberikan presentasi hasil dari analisis numerik
pada penelitian pondasi tiang pada tanah kohesif. Broms (1964a)
memberikan grafik untuk mendapatkan kapasitas daya dukung lateral pada
tiang sejenis. Namun, grafik tersebut tidak memberikan data untuk seluruh
tiang dengan panjang berbeda. Dalam studi ini, sebuah program elemen
hingga yang diperuntukan khusus bagi pondasi tiang digunakan. Investigasi
ini dilaksanakan dengan variasi pada panjang dan diameter tiang pancang
pada tiga jenis tanah lempung yang berbeda.
|
|
46
Tujuan dari penelitian ini adalah untuk menghasilkan beberapa
grafik yang menunjukkan area di antara tiang panjang dan tiang pendek
yang tidak dipertimbangkan oleh Broms. Selanjutnya, pada penelitan
Broms, efek beban vertikal
terhadap kapasitas daya dukung tiang tidak
diperhitungkan. Pada penelitian ini, efek beban vertikal juga dipelajari, dan
grafik hasil perhitungan dittampilkan untuk mempermudah prosedur desain
pada tanah kohesif.
C.
Studi Model Setrifugal dari Grup Tiang yang Dibebani Beban Lateral pada
Lapisan Lempung: Karakteristik Bending Momen (T. Ilyas dan Budi S.
Soepandji, 2008)
Sebuah seri percobaan dengan alat sentrifugal dilaksanakan pada
lapisan lempung untuk mengetahui karakteristik bending momen dari grup
tiang akibat pembebanan lateral statis. Grup tiang mempunyai denah
simetris dengan konfigurasi tiang tunggal 2 x 1, 2 x 2, 3 x 3, dan 4 x 4.
Grup tiang memiliki jarak antar tiang 3 kali lebar tiang. Pile cap terbuat
dari bahan aluminium masif yang terletak di atas permukaan tanah
digunakan untuk mengikat tiang di dalam grup.
Pada studi ini didapatkan kesimpulan bahwa formula empiris untuk
menentukan kapasitas bending momen untuk grup tiang dengan denah
simetris dapat dipergunakan untuk desain praktis.
D.
Behaviour of Laterally Loaded Rigid Piles
in Cohesive Soils Based on
Kinematic Approach
(V. Padmavathi, E. Saibaba Reddy, dan R. Madhav,
2008)
|
|
47
Pondasi tiang adalah pondasi yang berguna untuk area dataran
rendah di mana karakteristik tanahnya perlu diperbaiki. Beberapa metode
tersedia untuk memprediksi batas ketahanan lateral dari tiang kaku pada
tanah lempung. Solusi yang ada untuk batas ketahanan pondasi tiang pada
lempung antara lain perhitungan semi-empiris atau berdasarkan analisis
pendekatan dengan beberapa penyederhanaan. Pada sebagian besar metode
ini, tanah diasumsikan bersifat plastis dan dianalisa melalui analisa pada
titik rotasi. Meskipun batas beban lateral yang didapatkan dari metode ini
cukup sesuai dengan nilai yang diukur, distribusi beban lateral tidak
konsisten. Pendekatan baru yang berdasarkan respon non-linear
(hiperbolik) telah dikembangkan untuk mempelajari respon perpindahan
bebandari pondasi individu tiang kaku dengan kepala bebas pada tanah
kohesif. Batas kapasitas lateral yang diprediksi dari tiang dan distribusi
tekanan tanah lateral sepanjang tiang memiliki perbandingan yang baik
sesuai teori dan hasil pengujian eksperimen.
E.
Studi Perilaku Tiang Pancang Kelompok Menggunakan Plaxis 2D pada
Tanah Lunak (Wildan Firdaus, 2011)
Dengan mengacu pada jurnal “Numerical Analysis of Load Test on
Bored Piles, 2004”, didapatkan dari hasil penelitiannya tersebut kesimpulan
bahwa model material Mohr Coulomb
lebih kaku daripada model material
Hardening, dan model material Soft soil lebih kaku lagi dari model material
Mohr Coulomb. Hal ini karena perbedaan dari rumus yang dipakai dari
masing-masing metode tersebut.
|
|
48
Studi ini membandingkan beberapa bentuk konfigurasi dari tiang
pancang kelompok, yang terdiri dari 2, 3, 4, 6, dan 8 tiang pancang dalam 1
konfigurasi dengan jarak anttar tiang pancang antara 2D sampai 4D, dalam
menahan beban aksial dan lateral menggunakan bantuan program dalam
pengerjaannya yaitu Plaxis 2D versi 8 dengan model material Mohr
Coulomb, Hardening, Soft Soil.
Berdasarkan hasil perhitungan menggunakan Plaxis 2D diperoleh
hasil akibat berubahnya jarak antar tiang pancang berupa penambahan
kemampuan tiang pancang dalam menahan beban aksial dan lateral, untuk
beban yang sama, perubahan jarak antar tiang dapat mengurangi penurunan
dan defleksi tiang pancang.
F.
In-situ Static Lateral Loading Test On 9 x 7 Group Pile Foundation
(S.
Teramoto, M. Kimura, T. Akitsu, S. Kubota, T. Nishizaki, dan T. Niimura,
2013)
Beban lateral seperti gempa bumi sangat mempengaruhi stabilitas
dari infrastruktur penting yang diharuskan untuk bertahan lebih kuat
dibanding struktur lain saat terjadi gempa. Pengujian dilakukan pada
kelompok pondasi tiang pada kondisi sebenarnya di lapangan. Penelitian ini
mengabaikan friksi yang terjadi antara pile cap dengan permukaan tanah.
Dari hasil penelitian ini didapatkan bahwa nilai Load Sharing Factor (LSF)
atau yang biasa disebut faktor distribusi gaya dari grup tiang memiliki trend
variasi di mana nilai LSF terbesar ada pada tiang depan dan belakang dan
semakin ke tengah semakin menurun pembagian gaya yang ada.
|