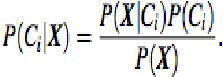
19
Jadi memaksimalkan P (Ci | X). Ci kelas yang P (Ci | X)
dimaksimalkan disebut hipotesis posteriori maksimal. Dengan teorema
Bayes:
Gambar 2.12: Rumus Classifier Naïve Bayesian (2)
Sumber: Han dan Kamber (2011, p351)
Keterangan :
P(Ci|X) = Probabilitas hipotesis Ci jika diberikan fakta atau record X
(Posterior probability)
P(X|Ci) = mencari nilai parameter yang memberi kemungkinan yang
paling besar (likelihood)
P(Ci) = Prior probability dari X (Prior probability)
P(X) = Jumlah probability tuple yg muncul
1.
Ketika P (X) adalah konstan untuk semua kelas, hanya P (X | Ci) P
(Ci) butuh dimaksimalkan. Jika probabilitas kelas sebelumnya
tidak diketahui, maka umumnya diasumsikan ke dalam kelas yang
sama, yaitu, P (C1) = P (C2) = · · · = P (Cm), maka dari itu akan
memaksimalkan P (X | Ci). Jika tidak, maka akan memaksimalkan
P (X | Ci) P (Ci). Perhatikan bahwa probabilitas sebelum kelas
dapat diperkirakan oleh P (Ci) = | Ci, D | / | D |, dimana | Ci, D |
adalah jumlah tuple pelatihan kelas Ci di D.
2.
Mengingat dataset
mempunyai banyak atribut, maka akan sangat
sulit dalam mengkomputasi untuk menghitung P(X|Ci). Agar
dapat mengurangi
perhitungan dalam mengevaluasi P(X|Ci),
asumsi naïve independensi kelas bersyarat dibuat. Dianggap
bahwa nilai-nilai dari atribut adalah kondisional independen satu
sama lain, diberikan kelas label dari tuple
(yaitu bahwa tidak ada
hubungan ketergantungan diantara atribut ) dengan demikian :