|
BAB 2
TINJAUAN PUSTAKA
2.1. Support Vector Machine
Support Vector Machine (SVM) dikembangkan oleh Boser, Gu yon,
dan Vapnik, pertama kali diperkenalkan pada tahun 1992 di Annual
Workshop on Computational Learning Theory. Konsep dasar metode SVM
sebenarn ya merupakan gabungan atau kombinasi dari teori-teori komputasi
yang telah ada pada tahun sebelumnya, seperti marginhyperplane (Dyda dan
Hart, 1973; Cover, 1965; Vapnik, 1964), kernel diperkenalkan oleh Aronszajn
tahun 1950, Lagrange Multiplier yang ditemukan oleh Joseph Louis Lagrange
pada tahun 1766, dan demikian juga dengan konsep-konsep pendukung lain.
Menurut Fachrurrazi (2011) SVM merupakan suatu teknik untuk
melakukan prediksi, baik prediksi dalam kasus regresi maupun klasifikasi.
Teknik SVM digunakan untuk mendapatkan fungsi pemisah (hyperplane)
yang optimal untuk memisahkan observasi yang memiliki nilai variabel target
yang berbeda (William, 2011). Hyperplane ini dapat berupa line pada tw o
dimension dan dapat berupa flat plane pada multiple dimension.
Menurut Nugroho (2003), karakteristik SVM secara umum dirangkum
sebagai berikut:
1. Secara prinsip SVM adalah linear classifier.
2. Pattern recognition dilakukan dengan mentransformasikan data
pada ruan g input (input space) ke ruang yang berdimensi lebih
tinggi (feature space), dan optimisasi dilakukan pada ruang vector
yang baru tersebut. Hal ini membedakan SVM dari solusi pattern
recognition pada umumnya, yan g melakukan optimisasi
parameter pada hasil transformasi yan g berdimensi lebih rendah
daripada dimensi input space.
3. Menerapkan strategi Structural Risk Minimization (SRM).
4. Prinsip kerja SVM pada dasarn ya han ya mampu menangani
klasifikasi dua kelas, namun telah dikembangkan untuk klasifikasi
lebih dari dua kelas den gan adan ya pattern recognition.
|
|
Metode Support Vector Machine memiliki beberapa keuntungan
yaitu:
1. Generalisasi
Generalisasi didefinisikan sebagai kemampuan suatu metode
untuk mengklasifikasi suatu pattern atau pola, yang tidak
termasuk data yang dgunakan dalam fase pembelajaran metode
itu.
2. Curse of dimensionality
Curse of dimensionality didefinisikan sebagai masalah yang
dihadapi suatu metode pattern recognition dalam
mengestimasikan parameter dikar enakan jumlah sampel data yang
relatif lebih sedikit dibandingkan dengan dimensional ruang
vektor tersebut.
3. Feasibility
SVM dapat diimplementasikan relatif lebih mudah, karena proses
penentuan support vector dapat dirumuskan dalam Quadratic
Programing (QP) problem (Nugroho, 2003).
Adapun kerugian dari metode Support Vector Machine adalah sebagai
berikut:
1. Sulit dipakai pada problem berskala besar. Dalam hal ini
dimaksudkan dengan ju mlah sampel yang diolah.
2. SVM secara teoritik dikembangkan untuk problem klasifikasi
dengan dua kelas. Namun dewasa ini SVM telah dimodifikasi
agar dapat men yelesaikan masalah dengan lebih dari dua kelas
(Nugroho, 2003).
2.1.1. Support Vector Regression (SVR)
SVR merupakan penerapan SVM yang digunakan untuk kasus regresi,
yang outputnya berupa bilangan riil atau kontinue. SVR merupakan metode
yang d apat mengatasi overfitting, sehingga akan menghasilkan perfomansi
yang bagus (Smola dan Scholkopf, 2004). Overfitting merupakan kondisi
dimana suatu model tidak menggambark an hubungan utama anatara variabel
|
 input dan output melainkan menggambarkan random error atau noise,
kondisi ini akan mengakibatkan hasil prediksi yang buruk.
Misalnya ada set data training, ( , )
x y dimana j=1,2,.., dengan
j j
x x x x R
{
, .., y }
y y R
= .
{
, , }... n
= dan output yang bersangkutan 1
input 1 2 3
Dengan SVR, akan ditemukan suatu fungsi ( )
f x yang mempunyai deviasi
y untuk semua data training. maka dengan
paling besar e dari target aktual i
SVR, manakala e sama dengan 0 akan didapatkan regresi yang sempurna.
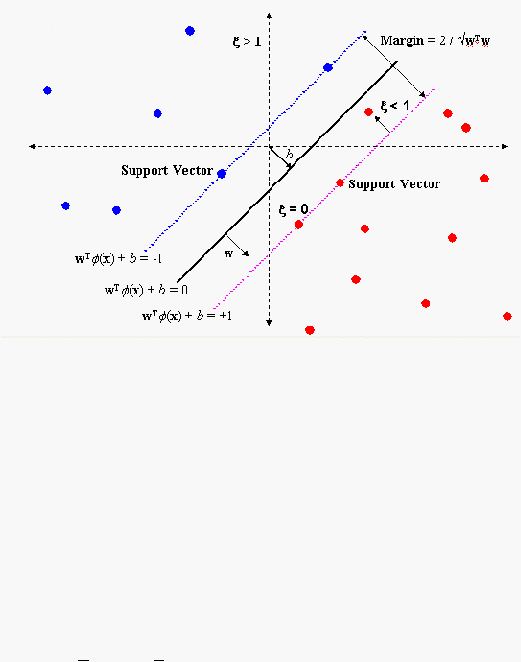
Sumber: Anandan, Varma, Joy, 2014
Gambar 2.1 Support Vector Machine
Ilustrasi fungsi hyperplane seperti pada Gambar 2.1. Misal terdapat
fungsi berikut sebagai garis regresi
f
( ) ( ) b
f x w x
= +
(2.1)
T
Dimana ( ) x
f menunjukkan suatu titik didalam feature space F hasil
pemetaan x di dalam input space. Koefisien w dan b diestimasi dengan cara
meminimalkan fungsi resiko (risk function) yang didefinisikan dalam
persamaan
1 1
+
min || || ( , ( ))
w C L y f x
2
2
i i
(2.2)
1
i
=
|
 Subject to
( )
y w x b
f e
-
-
=
i i
( )
1,2,...,
w x y b + =
f e
- + =
i i
i =
Dimana
e
( , ( )) | ( ) | | ( ) | 0
L y f x y f x y f x
= - - - = (2.3)
i i i i i i
|| ||
w adalah reguralisasi. Agar kapasitas fungsi dapat
Faktor 2
dikontrol maka fungsi harus dibuat setipis mungkin dengan cara
|| ||
w .Faktor kedua dalam fungsi tujuan adalah kesalahan
meminimalkan 2
empirik (empirical error) yang diukur dengan e -insensitive lossfunctio n.
Dengan menggunakan ide e -insensitive lossfunction norm dari w harus
diminimalkan agar mendapatkan generalisasi yang baik untuk fungsi regresi f.
Karena itu diperlukann ya menyelesaikan problem estimasi berikut:
1
min || ||
2
2 w
(2.4)
Subject to
( )
y w x b
f e
-
-
=
i i
( )
1,2,...,
w x y b + =
f e
- + =
i i
i =
ˆ
(y y)
e
= -
2 2
(y (b b ))
x
= - +
2
0 1
Asumsikan bahwa ada suatu fungsi f yang dap at men gaproksimasi
semua titik ( , )
x y dengan presisi e . Diasumsikan bahwa semua titik ada
i i
dalam rentang f e atau disebut feasible. Sedan gkan infeasible merupakan
± atau disebut feasible. Sedan gkan infeasible merupakan
kondisi dimana ada beberapa titik yang keluar dari rentang f e
± , titik yang
,
untuk mengatasi masalah
infeasible ini bisa ditambahkan variabel slack *
pembatas yang tidak layak (infeasible constrain) dalam masalah optimasi.
Selanjutnya masalah optimasi diatas bisa diformulasikan sebagai berikut:
1 1
min || || ( , )
w C
+
(2.5)
2 *
=
2 i i
i
1
|
|
Subject to
( ) , 1,2,...,
y w x b i
f
-
-
-
= =
T
i i i
( ) , 1, 2,...,
w x y b i + - = =
f - + - = =
*
T
i i i
, 0
=
*
i i
Kostanta C menentukan tawar menawar (trade of) antara ketipisan
fungsi f dan batas atas deviasi lebih dari e yang masih ditoleransi. Semua
deviasi lebih besar daripada e akan dikenakan penalti sebesar C. Dalam
SVR, e ekuivalen dengan akurasi dari aproksimasi terhadap data training.
nilai e yang kecil akan dikaitkan dengan nilai yang tinggi pada variabel slack
(*)
dan akurasi aproksimasi yang tinggi. Sebaliknya, nilai yang tinggi untuk
i
yang kecil dan aproksimasi yan g rendah.
e berkaitan dengan nilai (*)
i
Menurut persamaan (2.5) nilai yang tinggi untuk variabel slack akan
membuat kesalahan empirik mempunyai pengaruh yang besar terhadap faktor
regulasi. Dalam SVR, support vector adalah data training yang terletak pada
dan diluar batas f dari fungsi keputusan, karen a itu jumlah support vector
menurun dengan naiknya e .
Dalam formulasi dual, problem SVR adalah sebagai berikut:
1
max ( )( ) K( , ) ( ) ( )
x x y
a a a a a a a a
-
-
-
+ - - -
* *
* *
2 i i j j i j i i i i i
1 1
= =
1 1
i j
i i
= =
(2.6)
Subject to
a a
( ) 0 - =
*
i i
1
i
=
a
a
= = =
= = =
0 , 1, 2, ..,
0 , 1, 2, ..,
C i
i
C i
*
i
K( , )
x x adalah dot-product kernel
Dimana C didefinisikan oleh user, 1
j
K( , ) ( ) ( )
x x x x
f f
= . Dengan menggunakan
T
yang didefinikan sebagai 1
j i j
lagrange multiplier dan kondisi optimalitas, fungsi regresi secara eksplisit
dirumuskan sebagai berikut
a a
( ) ( ) K( , )
f x x x b +
= - +
*
i i i j
(2.7)
1
i
=
|
 2.1.2. Lagrange
Menurut Smith (2004) Lagrange merupakan suatu metode matematika
untuk memecahkan masalah optimasi dengan adanya constrains atau batasan.
f x x R R
untuk dicari nilai minimum
Misal apabila ada fungsi 1
( , ..., ) : n
n
( , ..., ) 0
g x x = . Inti dari persamaan
atau maksimumnya dengan constrain 1
n
Lagrange Multiplier ini adalah
( ) ( )
f x g x
=
(2.8)
Dimana gradian dari f sama dengan ( Lagrange Multiplier) dikali dengan
gradian dari g. Dan bentuk dari persamaan constrains
( ) 0
g x =
(2.9)
Dalam konteks SVM, kedua persamaan diatas digabung menjadi satu
persamaan yang biasa disebut Lagrangian:
L x f x g x
L x
= -
=
( , ) ( ) ( )
( , ) 0
(2.10)
Berdasarkan teori dari Support Vector Machine, diketahui bahwa persamaan
yang harus di optimasi adalah
1
( ) || ||
f w w =
2
2
( , ) [ , ] 1 0 =
g w b y w x b - =
= + - =
i i i
Dan ( , )
g w b dapat di pecah menjadi
i
( , ) [ , ] 1 0 =
g w b w x b
g w b w x b
= + -
1 1
( , ) [ , ] 1 0 - =
= - + - =
(2.11)
2 1
Kemudian masukkan persamaan ke dalam Lagrangian
( , , ) ( ) ( , ) ( , )
L w b f w g w b g w b
= - -
1 1 2 2
1 || || ([ , ] 1) ( [ , ] 1)
2
1 || || ([ , ] 1) ([ , ] 1)
2
w w x b w x b
= - + - - - + -
(2.12)
2
1 1 2 2
w w x b w x b
= - + -
+ + +
2
1 1 2 2
Untuk gradian pada Lagrangian
( , , ) ( ) ( , ) ( , ) 0
L w b f w g w b g w b
= - - =
1 1 2 2
Digunakan
|
 = - + =
( , , ) 0
L w b w x x
w
1 1 2 2
= - + =
( , , ) 0
L w b
b
1 2
(2.13)
= + - =
( , , ) [ , ] 1 0
L w b w x b
1
1
= + + =
( , , ) [ , ] 1 0
L w b w x b
2
2
Dengan keempat persamaan turunan pada Langrangian diatas dapat
ditemukan vektor weight w , bias b, dan nilai dari Langrangian Multiplier ( )
2.1.3.
Kernel
Menurut Murfi (2014) fungsi kernel adalah suatu fungsi k yang mana
untuk semua vektor input x,z akan memenuhi kondisi
f f
( , ) ( ) ( )
k x z x z
=
(2.14)
T
Dimana (.)
f adalah pemetaan dari input space ke feature space. Dengan kata
lain fungsi kernel adalah fungsi inner product pada feature space.
( , ) ( , )
k x z x z
,
x z R
dan
T
Misal 2
= adalah fungsi kernel untuk 2
( , )
x x x
( , )
z z z
= . Maka
= dan 1 2
1 2
= +
= + +
=
=
( ) ( )
x z x z x z
2 2
T
1 1 2 2
( 2 )
( , 2 , ) ( , 2 , )
x z x z x z x z
x x x x z z z z
2 2 2 2
1 1 1 1 2 2 2 2
2 2 2 2
T
1 1 2 2 1 1 2 2
( ) ( )
x z
f f
T
( , ) ( )
k x z x z
= adalah suatu fungsi kernel dengan
T
Sehingga 2
( ) ( , 2 , )
x x x x x
R
f = , yaitu suatu fungsi pemetaan dari 2
R ke 3
pemetaan 2 2
1 1 2 2
seperti pada Gambar 2.2.
|
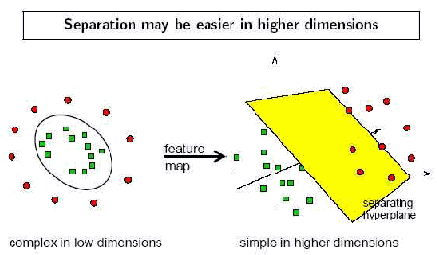 Fungsi kernel dapat menghitung inner product pada feature spase
secara langsung dari ruang input tanpa secara eksplisit menghitung koordinat
proyeksi masing-masing vektor input pada feature space.
Inner product adalah operasi yang sangat penting karena sangat erat
kaitannya dengan persoalan geometri dari data pada ruang fitur, misal untuk
menghitung jarak:
f f f f f f f f
2
|| ( ) ( ) || ( ) ( ) (z) (z) 2 (x) (z)
T T T
x z x x
-
= + -
( , ) ( , ) 2 ( , )
k x x k z z k x z
= + -
Ada 3 jenis fungsi kernel
•
Linear
k x x x x
=
(2.15)
( , ) T
i j i j
•
Polynomial
( , ) ( )
k x x x x r
= + , dimana >0
(2.16)
T d
i j i j
•
Radial Basis Function
( , ) exp( || || )
k x x x x
= - -
(2.17)
2
i j i j
|
|
Tujuan dari penggunaan kernel ini ialah untuk mengimplementasikan
suatu model pada ruang dimensi yang lebih tinggi (feature space) tanpa harus
mendefinisikan fungsi pemetaan dari ruang inpu t ke feature space, sehingga
untuk kasus yan g non lineary separable pada ruang input diharapkan menjadi
lineary separable pada feature space. Selanjutnya dapat digunakan
hyperplane sebagai decision boundary secara efisien.
2.2. Peak Ground Acceleration (PGA)
PGA merupakan besaran ukuran yang digunakan untuk mengukur
kecepatan pergerakan pada permukaan tanah. Ir wansyah dan Winarko (2012)
men yatakan bahwa karakteristik PGA dapat diperoleh melalui rekaman PGA
pada kejadian gempa-gempa sebelumnya. Perekaman Ground Acceleration,
dimungkinkan untuk mengekstrasi karakteristik utama dari rekaman ground
motion seperti peak ground velocity. Percepatan gempa dapat dihitu ng
sebagai percepatan dibatuan dasar, maupun percepatan gempa dipermukaan
tanah.
Nilai nilai PGA dapat ditentukan dengan fungsi atenuasi. Fungsi
atenuasi adalah suatu fungsi yang menggambarkan korelasi antara intensitas
tanah setempat, Magnitude gempa, serta jarak suatu titik dari pusat gempa.
Para ahli telah banyak merumuskan banyak fungsi atenuitasi, dimana fungsi
atenuitasi yang berlaku di suatu tempat belum tentu berlaku ditempat lain.
Karena fungsi atenuitasi sangat bergantung dari kondisi alam ditempat
tersebut (Irsyam et al ,2010). Menurut Irwansyah dan
Winarko(2012)pemilihan fungsi atenuitasi ditentukan oleh kondisi geologi
dan lapisan tektonik disuatu tempat. Besarnya kekuatan PGA yang terjadi di
Indonesia bisa dijelaskan dari Gambar 2.3. Dari gambar bisa diketahui nilai
PGA dari kota Aceh sebesar 0,3-0,4g.
|
 Sumber: Irsyam et al (2010)
Gambar 2.3 Peta Hazard Gempa Indonesia Dibatuan Dasar pada
Kondisi PGA (T = 0 Detik) untuk 2% PE 50 Tahun
2.3. PerancanganAplikasi Program
Teknologi informasi merupakan suatu rangkaian kegiatan yang
difasilitasi oleh peralatan elektronik yang mencakup pen golahan, transmisi,
dan penyajian informasi. Teknolo gi ini dikembangk an untuk menciptakan
kemudahan dalam menjalankan suatu rangkaian kegiatan. TIK (Teknologi
Informasi dan Komunikasi) merupakan konvergensi dari tiga wilayah yaitu
teknologi informasi, data dan informasi, serta masalah-masalah sosial
ekonominya. Perkembangan TIK dap at diukur berdasarkan empat dimensi
yaitu keterhubungan, akses, kebijakan dan penggunaan (Hermana, 2007).
2.4. R
R adalah bahasa pemograman yang open source untuk mengolah data
statistik dan grafik. Bahasa pemrograman ini dikembangkan di B ell
Laboratories oleh Rick Becker, John Chambers dan Allan Wilks. R
men yediakan berbagai teknik statistika dan teknik grafik yang sangat bisa
dipergunakan secara luas, terbukti dari banyaknya library d ari teknik-teknik
statistik maupun grafis yang dikembangkan oleh banyak peneliti lainnya. R
dapat dijalankan untuk Unix, Windows, dan Macintosh.
Menurut Theodorick (2013) R mampu melakukan manipulasi data,
perhitungan statistik dan pemograman grafik dengan kelebihan-kelebihan
seperti:
•
Penanganan data dan fasilitas pen yimpanan yang efektif
|
|
•
R angkaian perhitungan dalam array, terutama matrix
•
Koleksi tools yang besar, koheren dan berintegrasi untuk data
analisis
•
Menggunakanbahasa programming S yang simple dan efektif yang
menggunakan syarat, perulangan dan fungsi rekursif.
2.5. Java Programming
Yang dimaksud b erbasis komputer dalam p enelitian ini adalah
membuat interface program untuk pengaplikasian metode Support Vector
Regression. Penelitian ini merubah perhitungan yang dilakukan secara
manual menjadi otomatis dengan komputer.
Pemograman dengan bahasa java dikembangkan oleh Sun
Microsystems sebagai bahasa berorientasi objek. Tujuan umumn ya yaitu
untuk aplikasi bisnis interaktif, dan aplikasi internet berbasis web. Java tidak
mengeksekusi instruksi pada komputer secara langsung sehingga dapat
dijalankan di b erbagai komputer. Sebaliknya, Java berjalan pada computer
hipotetis yang dikenal sebagai Java Virtual Machine (Farrell, 2010).
Java merupakan bahasa pemrograman yang popular dikalangan para
programmer, dengan demikian sangat ideal untuk membuat suatu proyek.
(Wild, 2011).
Kelebihan menggunakan Java menurut Campione (2001) dan Badley
(2002):
-
Multiplatform. Java dapat dijalankan di beb erapa sistem operasi.
Sistem Operasi yang mendukung java adalah Microsoft Windows,
Linux, Mac OS.
-
Object Oriented Programming. Java merupakan salah satu bahasa
pemrograman berbasis objek secara murni. Semua tipe data
diturunkan dari kelas dasar yang disebut object. Kelebih an ini
menjadikan Java sebagai salah satu bahasa pemograman termudah,
bahkan untuk fungsi-fungsi yang advance seperti komunikasi antara
komputer sekalipun.
-
Library yang banyak, sehingga memudahkan pro grammer
mengembangkan aplikasi.
|
|
-
Mudah didekompilasi. Dekompilasi adalah proses memb alikkan dari
kode jadi menjadi kod e sumber. Ini dimungkinkan karena kode jadi
Java merupakan bytecode yang menyimpan banyak atribut bahasa
tingkat tinggi, sep erti nama-nama kelas, metode, dan tipe data.
Kekuran gan dari Java:
-
Masih ada beberapa hal yang tidak kompatibel antara platform satu
dengan platform lain. Untuk J2SE, misalnya SWT-AWT bridge yang
sampai sekarang tidak berfungsi pada Mac OS X.
-
Penggunaan memori untuk program berbasis Java jauh lebih besar
daripada bahasa tingkat tinggi generasi sebelumny
seperti C/C++
dan Pascal (lebih spesifik lagi, Delphi dan Object Pascal).
2.6. NetBeans
NetBeans adalah sebuah open-source project yang berperan sebagai
alat mengembangkan atau develope kit untuk membuat program yang
berbasis Java. Pada Juni 2000 Netbeans dibuat menjadi open-source oleh Sun
Microsystems, yan g menjadi sponsor sampai Januari 2010. Dua produk dari
NetBeans adalah NetBeans IDE dan NetBeans Platform. NetBeans IDE
(Integrated Development Environment) adalah sebuah proyek open-source
yang memungkinkan pengguna men gemban gk an Java Desktop, Mobile,
aplikasi web, dan menyediakan peralatan untuk para pengembang PHP dan
C/C++. NetBeans ditulis dalam Java dan dapat dijalankan dalam berbagai
macam system operasi (Anonim, 2013). NetBean dapat diunduh secara gratis
di netbeans.org/downloads/index .html
Fitur- Fitur NetBeans adalah sebagai berikut (An onim, 2013):
-
Module System, sifat modular NetBeans memberikan developer
kekuatan untuk memenuhi persyaratan yang kompleks dengan
menggabungkan b eberapa modul kecil atau sederhana. Apabila
developer menggunakan salah satu modul standar NetBeans, maka
develope dapat mengintegrasikan modul pihak ketiga atau
mengembangkan sendiri.
|
|
-
Lifecycle Management, Seperti server aplikasi lainnya, NetBeans
menyediakan layanan siklus hidup ke aplikasi java desktop. Aplikasi
server mengerti bagaimana men yusun modul web, modul EJB, dan
artefak yang terkait, kedalam aplikasi web. Modul NetBeans
melakukan hal yang serupa dan menyusun aplikasi java desktop.
NetBeans juga menyediakan main method sehingga pengembang
tidak perlu membuatnya lagi
-
Pluggability, Service Infrastructure, and File System, Ini adalah salah
satu fitur unggulan NetBeans, user bisa langsung menginstal modul
yang mereka inginkan di aplikasi yang sedang mereka jalankan.
NetBeans juga men yediakan infrastructure untuk mendaftarkan dan
menarik service, memungkinkan pengembang menurunkan
ketergantungan terhadap modul individual.
-
Window System, Standarized UI Toolkit, and Advance Data-Oriented
Components, NetBeans memungkinkan pengembang memaksimalkan
dock dan window tanpa perlu melakukan coding yang
rumit. Swing
dan JavaFX adalah toolkit UI Standar java dan bias digunakan pada
NetBeans
-
Miscellaneous Features, Documentation, and Tooling Support,
NetBeans IDE, yang merupakan pengembanga
perangkat lunak
(SDK) dari NetBeans Platform, menyediakan banya
template dan
alat-alat, sep erti memen angkan penghargaan Matiss
GUI Builder
yang memungkinkan pengembang untuk dengan muda
mendesain
tataletak aplikasi pengembang.
2.7. Interaksi Manusia dan Ko mputer
Setiap manusia yan g menjadi penggun a komputer, berkomunikasi
dan berkolaborasi dengan komputer melalui antarmuka (Shneiderman ,
2010). Terdapat delapan aturan (8 Golden Rules) yang harus diperhatikan
dalam membuat desain antarmuka, yaitu :
1. Berusaha untuk konsisten
Tindakan-tindakan kon sisten diperlukan seper
konsisten pada
pemakaian warna, layout, jenis tulisan, dan pembuatan menu.
|
|
2. Menyediakan fungsi yang bersifat umum
Rancangan perlu memiliki fungsi-fungsi yang mudah dikenali
penggun a yang beragam atau penjelasan pemakaian aplikasi juga
memiliki fungsi tambahan yang mendukung aplikasi tersebut untuk
para ahli. Fungsi yang
bersifat umum diperlukan karena jenis
penggun a yang beragam dari yang baru mengenal komputer hingga
yan g sudah ahli dengan komputer.
3. Memberikan umpan balik yan g informatif
Sistem harus memberikan umpan balik dengan respon yang berbeda di
setiap kondisi yang ada untuk segala aksi yan g dilakukan pengguna.
4. Merancang dialog untuk menghasilkan penutupan
Dialog penutupan dibuat sebagai tanda bahwa langkah-langkah yan g
dilakukan sudah benar.
5. Memberikan pencegahan terhadap k esalah an yang sederhana
Aplikasi harus dapat mendeteksi kesalahan yang dilakukan oleh
penggun a dan langsung memberikan penanganan kesalahan dengan
cara yang mudah dipahami dan instruksi yang spesifik untuk
penanganannya.
6. Memungkinkan pengembalian aksi sebelumnya
Diperlukan pengurangan kecemasan dari pengguna karena kesalahan
yan g dilakukannya. Penguran gan kecemasan ini dapat dilakukan
dengan memungkinkan pengguna kembali ke k eadaan sebelumnya
sehingga pengguna d apat mengeksplorasi secara leluasa.
7. Mendukung pengendalian internal
Pengguna dapat mengontrol sistemnya sehingga dapat merespon
tindakannya sendiri. Pengguna juga tidak akan merasa dirinya yan g
dikendalikan oleh sistem.
8. Mengurangi beban ingatan jangk a pendek
Perancang harus menghindari antarmuk
dimana pengguna harus
mengingat informasi dari satu tampilan yan
akan dipakai di tampilan
lainnya karena terbatasnya kapasitas ingata
manusia dalam hal
|
 2.8. Waterfall Model
Menurut Sommervile (2011), Waterfall Model adalah dasar dari
aktivitas proses yang terdiri dari spesifikasi, pengembangan, validasi,
evolusi. Semua aktivitas direpresentasikan dalam tahapan proses yan g
terpisah seperti spesifikasi kebutuhan, perancangan perangkat lunak,
implementasi, pengujian dan sebagainya.
Gambar 2.4Waterfall Model
Tahapan dari Waterfall Model seperti pada Gambar 2.4 merefleksikan
pokok-pokok dari aktivitas pengemban gan :
1. Requirements Definition
Pada tahap ini, didefinisikan mengenai layanan yang diberikan oleh
sistem, batasan sistem, dan
tujuan ditetapkan setelah melakukan
konsultasi dengan pengguna sistem. Definisi ini dilakukan secara rinci
dan dibuat sebagai spesifikasi dari sistem
2. System and Software Design
Perancangan sistem menyediakan kebutuhan peran gkat keras atau
perangkat lunak dengan menyediakan arisitektur dari keseluruhan
sistem. Proses perancangan sistem melibatkan pengidentifikasian dan
penjelasan abstraksi sistem dan hubungannya.
3. Implementaion and Unit Testing
Perancangan sistem direalisasikan menja
sebuah program atau unit
program. Pengujian melibatkan verifika
untuk memastikan apakah
setiap unit memenuhi spesifikasi sistem.
|
|
4. Integration and System Testing
Setiap program yang sudah ada diintegrasikan dan di uji sebagai salah
satu keutuhan sistem untuk memastikan apakah kebutuhan sistem
sudah terpenuhi. Setelah pengujian dilakuk an, sistem baru disebarkan
ke pengguna.
5. Operation and Maintenance
Pada tahap ini dilakukan instalasi terhadap sistem dan digunakan
dalam praktiknya. Perbaikan melibatkan koreksi terhadap kesalahan
yan g tidak ditemukan sebelumnya, memperbaiki implementasi unit
sistem, dan meningkatkan kinerja sistem.
|