|
5
BAB 2
LANDASAN
TEORI
2.1 Gelombang
Bunyi
Gelombang
bunyi
merupakan gelombang longitudinal
yang
terjadi
karena
perapatan dan
perenggangan dalam medium
gas, cair,
atau
padat (Tipler, 1998,
p505).
Gelombang itu dihasilkan ketika sebuah benda, seperti garpu tala atau senar biola, yang
digetarkan
dan
menyebabkan gangguan
kerapatan
medium.
Gangguan
dijalarkan
di
dalam
medium
melalui
interaksi
molekul-molekulnya. Getaran
molekul
tersebut
berlangsung sepanjang arah penjalaran gelombang. Seperti dalam kasus gelombang pada
tali,
hanya
gangguan
yang
dijalarkan,
sementara
molekul-molekul itu
sendiri
hanya
bergetar ke belakang dan ke depan di sekitar posisi kesetimbangan.
Di
dalam
gas,
kerapatan
dan
tekanan
terkait
erat.
Oleh
karena
itu,
gelombang
bunyi
dalam
gas,
seperti
udara,
dapat
dipandang sebagai
gelombang
kerapatan
atau
gelombang
tekanan.
Di
dalam
gelombang
pada
tali,
simpangan
transversal tali
dinyatakan dengan fungsi
gelombang y(x ±
vt). Fungsi
gelombang
untuk
gelombang
bunyi
yang
analog
dengan
simpangan transversal
tali adalah simpangan longitudinal
molekul-molekul gas dari posisi kesetimbangannya s(x ± vt) atau
fungsi yang berkaitan
perubahan tekanan gas p(x ± vt).
|
 6
2.1.1 Kenyaringan dan
Tingkat
Intensitas
Karena rentang intensitas yang dapat ditangkap telinga demikian luas dan karena
rangsangan
psikologis
kenyaringan
tidak
berubah-ubah secara
langsung
terhadap
intensitas,
tetapi
lebih
mendekati
logaritmik, maka
suatu
skala
logaritmik
digunakan
untuk menyatakan tingkat intensitas gelombang bunyi. Tingkat intensitas ß yang diukur
dalam desibel didefinisikan oleh
ß
=
10 log
I
I
0
Dengan I adalah
intensitas bunyi dan I
0
adalah intensitas acuan, yang akan di
ambil sebagai ambang pendengaran:
I
0
=
10
-12
W/m²
Pada skala ini, ambang pendengaran adalah
ß
=10 log
I
=
0 dB
I
0
dan ambang sakit adalah
ß
=10 log
I
=
10 log 10¹²
=
120 dB
10
12
Jadi, rentang intensitas bunyi dari 10
-12
W/m² hingga 1 W/m²
bersesuaian dengan
rentang intensitas dari 0 dB hingga 120 dB.
|
 7
2.1.2 Frekuensi
Jika
disimpangkan
sebuah
benda
dari
kesetimbangannya dan
melepaskannya,
benda
itu
akan
berosilasi
bolak-balik
di
sekitar
kedudukan
setimbang.
Waktu
bagi
benda untuk melakukan satu osilasi penuh disebut periode T. Kebalikan periode disebut
frekuensi f, yang merupakan banyaknnya osilasi setiap detik. Dirumuskan sebagai
berikut:
f
=
1
T
Satuan frekuensi adalah kebalikan sekon (s
-1
), yang disebut hertz(Hz).
2.1.3 Gerak Harmonik Sederhana
Gerak Harmonik sederhana memiliki rumus dasar sebagai berikut:
X = A cos (?t +
)
dengan A, ?,
merupakan konstanta. Berdasarkan definisi, gerak dengan
perubahan posisi
terhadap
waktu
menuruti
persamaan di
atas
disebut
dengan
gerak
harmonik
sederhana.
Perhatikan
bahwa
cos
(?t
+
)
=
sin
(?t
+
+
p/2).
Apakah
persamaan
diungkapkan
sebagai
fungsi
konsinus
atau
fungsi
sinus
semata-mata
bergantung
pada
kapan
dipilih
t
=
0.
Simpangan
maksimum
dari
kesetimbangan disebut amplitudo
A.
Argumen
fungsi
kosinus,
?t +
disebut
fase
gerak,
dan
konstanta
disebut konstanta fase.
Selama satu
siklus
gerak penuh,
fase
bertambah sebesar 2 p pada akhir siklus. Benda memiliki posisi dan kecepatan yang sama
lagi, seperti yang dimiliki pada permulaan siklus karena cos(?t +
+ 2p) = cos (?t +
). Kita
dapat
menentukan periode
T
dari
kenyataan
bahwa
fase
pada
waktu
t
+
T
tidak lain hanya 2 p ditambah fase pada waktu t.
|
|
8
2.2 Pengertian
Sinyal
Untuk
membuat
program mengenai
pemrosesan
sinyal
analog
menjadi
sinyal
digital,
kita
haruslah
mengetahui apa
itu
sinyal.
Menurut
J.G.
Proakis
dan
D.G.
Manolakis
(1995,
p2)
sinyal
adalah
besaran
fisik
yang
berubah-ubah
menurut
waktu,
ruang,
atau
variable
bebas
atau
variabel-variabel lainnya.
Secara
matematis
dideskripsikan sinyal sebagai fungsi dari satu atau lebih variabel bebas. Sebagai contoh:
S1
(t) = 5t
S1
(t) = 20t²
mendeskripsikan dua buah sinyal, salah satu berubah-ubah secara
linear
menurut
variable
bebas
t
(waktu)
dan
yang
kedua
berubah-ubah secara
kuadratik
menurut
t.
Contoh lainnya:
s(x,y) = 3x + 2xy + 10y²
fungsi
ini
mendeskripsikan sinyal dua variable bebas
x
dan
y
yang dapat mewakili dua
koordinat yang berhubungan.
Sinyal-sinyal
yang
dideskripsikan pada
dua
persamaan
diatas
termasuk
kelas
sinyal
yang
secara
presisi
didefinisikan dengan menetapkan ketergantungan fungsional
pada variable bebas. Namun, terdapat beberapa kasus yaitu hubungan fungsional seperti
itu tidak diketahui atau terlalu rumit untuk setiap penggunaan praktis.
Sebagai contoh , suatu sinyal suara tidak dapat dideskripsikan secara fungsional
dengan
pernyataan
seperti
di
atas.
Pada
kenyataanya, salah
satu
cara
untuk
menginterpretasikan
isi
informasi
atau pesan
yang
disampaikan dengan
setiap
segmen
waktu yang pendek dari sinyal suara adalah dengan mengukur amplitudo, frekuensi, dan
fase yang terdapat dalam segmen waktu sinyal yang pendek.
|
|
9
Pembangkitan sinyal biasanya berhubungan dengan sebuah sistem yang memberi
respons terhadap suatu stimulus dorongan atau gaya. Pada sinyal suara, sistem ini terdiri
dari
tali
vokal,
yang
disebut
juga
dengan
vokal.
Perangsang dorongan
yang
dikombinasikan dengan sistem dinamakan sumber sinyal.
Dalam
hal
ini,
sistem
dapat
juga
didefinisikan sebagai
suatu
perangkat
yang
melakukan operasi pada suatu sinyal. Saat kita melewatkan
sinyal melalui sebuah
sistem,
maka
sistem
tersebut
akan
melakukan beberapa
operasi
pada
sinyal,
yang
mempunyai
pengaruh
mengurangi kegaduhan
dan
interferensi dari
sinyal
pembawa
informasi. Operasi-operasi seperti itu biasanya disebut sebagai pemrosesan sinyal.
Dalam pemrosesan sinyal-sinyal digital pada sebuah komputer digital, operasi-
operasi yang dilakukan pada sinyal terdiri dari sejumlah operasi matematis seperti yang
ditetapkan oleh program perangkat lunak.
2.2.1. Sinyal
Waktu-Kontinu Versus Sinyal
Waktu-Diskrit
Sinyal-sinyal selanjutnya dapat diklasifikasikan menjadi empat kategori berbeda
yang tergantung pada karakteristik variabel (bebas) waktu dan
nilai-nilai yang mereka
ambil. Sinyal
waktu-kontinu atau
sinyal analog didefinisikan untuk setiap nilai waktu
dan diambil pada nilai-nilai dalam selang kontinu (a,b), dengan a dapat menjadi -8 dan
b dapat
menjadi
8.
Secara
matematis,
sinyal-sinyal
ini
dapat dideskripsikan dengan
fungsi dari suatu variabel kontinu. Contoh dari sinyal analog adalah sebagai berikut :
sinyal X1 (t) = cos
t
, sinyal X2 (t) = e
-|t|
Sinyal waktu-diskrit didefinisikan hanya pada nilai-nilai waktu khusus tertentu. Sinyal
X(t
n
)
=
e
-|t|
,
n
=
0,
1,
2, … memberikan sebuah contoh sinyal waktu-diskrit. Jika kita
|
|
10
menggunakan indeks
n
pada
waktu-diskrit
sesaat
sabagai
variabel
bebas,
nilai
sinyal
menjadi
suatu
fungsi
variabel
integer
(yaitu,
suatu
barisan
angka).
Jadi
sinyal
waktu-
diskrit
dapat
digambarkan
secara
matematis dengan
suatu
barisan
bilangan
riil
atau
bilangan kompleks. Untuk menegaskan sifat alamiah waktu-diskrit dari sinyal, kita akan
menunjukkan suatu sinyal seperti itu dengan x(n) sebagai ganti x(t). Jika waktu sesaat t
n
adalah
ruang
yang
sama
(dengan
kata
lain,
t
n
=
nT),
notasi
x(nT)
juga
digunakan.
Sebagai contoh, barisan
x(n) = { 0,8
n
, jika n
0 // 0, yang lainnya }
Dalam aplikasi ini, sinyal waktu-diskrit dapat muncul dengan dua cara:
1. Dengan memilih nilai-nilai suatu sinyal analog pada waktu diskrit sesaat. Proses
ini
dinamakan
pencuplikan. Seluruh
instrument
pengukuran yang
mengambil
pengukuran pada selang waktu reguler memberikan sinyal waktu-diskrit. Sebagai
contoh, sinyal x(n) pada
gambar 2.2 dapat diperoleh dengan pencuplikan sinyal
analog x(t) = 0,8
t
, t
0 dan x(t) = 0, t < 0 sekali setiap detik.
2. Dengan mengumpulkan sebuah variabel melalui periode waktu tertentu. Sebagai
contoh, perhitungan
jumlah
nada-nada sama dalam
suatu komposisi, atau
merekam ketukan drum pada suatu permainan.
2.2.2. Sinyal Bernilai
Kontinu Versus
Nilai Diskrit
Nilai-nilai
sinyal
waktu-diskrit dapat
menjadi
kontinu
atau
diskrit.
Jika
suatu
sinyal
diambil
dengan
seluruh
nilai
yang
mungkin dengan
interval
terbatas
atau
tak
terbatas,
hal
itu dikatakan
menjadi sinyal
bernilai-kontinu.
Alternatifnya,
jika
sinyal
|
|
11
diambil
pada
nilai-nilai
dari
suatu
himpunan terbatas
nilai
yang
mungkin, hal
itu
dikatakan
menjadi sinyal bernilai-diskrit.
Biasanya,
nilai-nilai
ini
seimbang dan karena
itu
dapat
dinyatakan sebagai suatu kelipatan integer dari jarak
antara
dua
nilai
yang
berurutan. Sinyal waktu-diskrit yang mempunyai himpunan nilai-nilai diskrit dinamakan
sinyal digital.
Agar suatu sinyal diproses secara digital, sinyal harus diskrit waktunya dan nilai-
nilainya harus diskrit (dengan kata lain, hal itu harus sebagai sinyal digital). Jika sinyal
yang akan diproses berbentuk analog, sinyal dikonversikan menjadi sinyal digital
dengan pencuplikan
sinyal
analog pada saat
waktu-diskrit, untuk
menghasilkan sinyal
waktu-diskrit
dan
kemudian
dengan
mengkuantisasi
nilai-nilainya
ke
suatu
himpunan
nilai diskrit. Proses
mengkonversi suatu sinyal bernilai-kontinu menjadi sinyal bernilai-
diskrit
dinamakan
kuantisasi,
adalah
dasar
suatu
proses
pendekatan. Hal
itu
dapat
diselesaikan
secara
sederhana
dengan
pembulatan
atau
pemotongan.
Sebagai
contoh,
jika
nilai-nilai sinyal
yang
diijinkan
dalam
sinyal
digital
adalah
integer,
misalnya
0
sampai 15, sinyal yang bernilai-kontinu dikuantisasi menjadi nilai-nilai integer ini. Jadi,
nilai
sinyal 8,58
akan didekati dengan
nilai
8
jika
proses kuantisasi dilakukan dengan
pemotongan
atau
dengan
9 jika
proses kuantisasi
dilakukan
dengan
pembulatan ke
integer terdekat.
2.2.3. Konsep
Frekuensi Dalam
Sinyal
Waktu-Kontinu Dan Waktu-Diskrit
Dari
fisika, diketahui
bahwa
frekuensi
berhubungan lebih
erat
dengan
bentuk
khusus dari gerak periodic, yang dinamakan osilasi harmonik, yang dideskripsikan oleh
fungsi-fungsi sinusoida. Konsep frekuensi ini berbanding langsung dengan konsep
waktu. Sesungguhnya,
frekuensi mempunyai dimensi kebalikan waktu. Jadi kita akan
|
 12
mengharapkan bahwa
sifat
waktu
(kontinu
atau
diskrit)
akan
mempengaruhi
sifat
frekuensi tersebut.
2.2.4. Sinyal Sinusoidal
Waktu-Kontinu
Osilasi harmonic sederhana secara
matematis dideskripsikan dengan sinyal
sinusoida waktu kontinu berikut ini :
X
a
(t) = A sin (
t
+
), -8 < t < 8
Subskrip a yang digunakan dengan x(t)
menunjukkan sinyal analog. Sinyal ini dicirikan
secara
lengkap
dengan
tiga
parameter: A
adalah
Amplitudo
sinusoida,
adalah
frekuensi dalam radian persekon (rad/s), dan
adalah fase dalam radian. Sebagai ganti
dari
,
kita sering menggunakan frekuensi F dalam putaran per sekon atau
Hertz(Hz),
dengan
= 2
F
Ditinjau dari F, sinyal sinusoidal waktu-kontinu dapat ditulis sebagai berikut
X
a
(t) = A sin (2
f t +
), -8 < t < 8
Kita
akan
menggunakan
persamaan-persamaan di
atas
dalam
menyajikan
sinyal-sinyal
sinusoida.
|
 13
2.3 Elemen-Elemen
Dasar Sistem Pemrosesan Sinyal
Digital
Dalam
melakukan pemrosesan
sinyal
secara
digital,
dibutuhkan dua
interface
yang
dinamakan
pengkonversi
analog
menjadi
digital (A/D).
Keluaran pengkonversi
A/D adalah sinyal digital yang sesuai dengan masukan terhadap prosesor digital.
Sinyal
Sinyal
Masukan
Analog
Konverter
A/D
Proses
Sinyal
Digital
Konverter
D/A
Keluaran
Analog
Sinyal
Sinyal
Masukan
Masukan
Digital
Digital
Gambar 2.1 Diagram Blok Dari Sinyal Digital Proses Sistem
(Sumber : Digital Signal Processing, 1995, p4)
Prosesor sinyal digital dapat merupakan sebuah komputer yang dapat diprogram,
atau sebuah mikroprosesor kecil yang diprogram untuk melakukan operasi-operasi yang
diinginkan pada sinyal
masukan.
Mungkin
juga dapat berupa perangkat keras prosesor
digital
yang
dikonfigurasi untuk
melakukan
sekumpulan
operasi
tertentu pada
sinyal
masukan.
Untuk
pemakaian dengan
keluaran
digital
dari
prosesor,
sinyal
digital
akan
disampaikan kepada pemakai dalam bentuk analog. Karena itu perlu disediakan interface
lainnya
dari
daerah
digital
ke
daerah
analog.
Interface
ini
dinamakan
pengkonversi
digital
menjadi analog
(D/A).
Jadi
sinyal
tersebut
disediakan
untuk
pemakai
dalam
bentuk analog, seperti contohnya dalam komunikasi suara.
Walaupun demikan, ada beberapa aplikasi praktis lainnya yang ingin
disampaikan dalam bentuk digital dan tidak
memerlukan pengkonversi
D/A.
Sebagai
|
 14
contoh, pada pemrosesan digital sinyal radar. Informasi yang didapat dari sinyal radar,
misalnya posisi pesawat terbang dan kelajuan, dapat secara
mudah dicetak pada kertas.
Dalam kasus ini pengkonversi D/A tidak diperlukan.
2.3.1 Pencuplikan Sinyal Analog
Ada beberapa cara untuk mencuplik sinyal analog. Dalam skripsi
ini digunakan
pencuplikan periodik atau pencuplikan seragam yang merupakan tipe pencuplikan yang
sering digunakan dalam praktek. Ini dideskripsikan dengan hubungan
x(n)= x
a
(nT), -8<n<8
dengan
x(n)
adalah
sinyal
(waktu-diskrit) yang
didapat
dengan
mengambil
cuplikan-
cuplikan sinyal
analog
x
a
(t) setiap T detik. Yang dimaksud sinyal analog disini adalah
sinyal dari
instrumen akustik. Selang
waktu T
adalah periode pencuplikan atau
selang
pencuplikan, dan
kebalikannya 1/T
=
F
s
dinamakan
laju
pencuplikan (cuplikan
per
second) atau frekuensi pencuplikan (Hz).
Pencuplikan periodik menetapkan suatu hubungan antara variabel waktu t dan n
dari sinyal waktu kontinu dan dari sinyal waktu diskrit. Sesungguhnya variabel-variabel
ini berhubunggan secara linear melalui periode pencuplikan t atau ekuivalennya, melalui
n
laju pencuplikan 1/T = F
s
sebagai t = nT =
F
s
Sebagai konsekuensi dari persamaan t
=
nT =
n
,
terdapat hubungan antara
F
s
variabel frekuensi F (atau ?) untuk sinyal analog dan variabel frekuensi f (atau ?) untuk
sinyal
waktu diskrit. Untuk
menetapkan hubungan ini
kita
akan terapkan dalam
sinyal
sinusoida analog yang berbentuk:
|
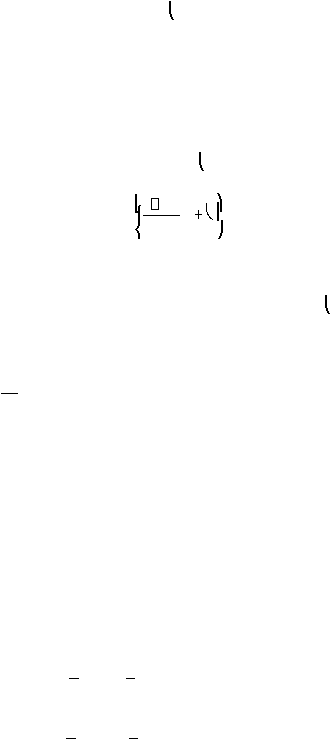 15
X
a
(t) = A sin (2pFt +
)
yang bila dicuplik secara periodik pada laju 1/T = F
s
cuplikan per sekon menghasilkan
X
a
(nT) = x(n) = A sin (2pFnT +
)
=
A sin
2
nF
F
s
Jika kita bandingkan antara rumus diatas dengan rumus x(n) = A sin (2pfn +
), maka
variabel frekuensi F dan f berhubungan secara linear yaitu
f
=
F
atau ekivalennya yaitu ? = ?T
F
s
Sedangkan
jika kita
lihat
interval
variabel
frekuensi F
atau ?
untuk sinusoida
waktu
kontinu adalah:
-8 < F < 8
-8 < ? < 8
Namun
hal ini akan berbeda pada sinyal waktu-diskrit. Pada sinyal waktu diskrit
kita
menggunakan:
-
1
<
f
<
1
2
2
-
1
<
?
<
1
2
2
Dari kedua rumus diatas dapat kita ambil kesimupulan, yaitu bila frekuensi sinusoida
waktu-kontinu dicuplik pada laju 1/T = F
s
, harus berada dalam interval dengan kisaran:
|
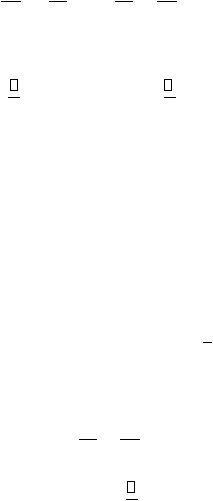 16
s
-
1
=
-
F
s
2T
2
=
F =
F
s
=
1
2
2T
atau ekuivalennya:
-
=
-p F
T
=
?
=
p
F
s
=
T
Dari persamaan yang kita dapat diatas
maka kita dapat
mengambil kesimpulan bahwa
perbedaan
yang
mendasar antara
sinyal
waktu-kontinu dan
sinyal waktu-diskrit berada
dalam interval nilai-nilai variabel frekuensi F dan f, atau ? dan ?
mereka. Pada sinyal
waktu-kontinu interval
frekuensi mereka tak berhingga
untuk variabel F(atau ?),
lalu
menjadi interval frekuensi berhingga untuk variabel f(atau ?). Ini dikarenakan frekuensi
tertinggi dalam
sinyal waktu-diskrit adalah ?
=
p
atau f =
1
.
Jika didapat
nilai
laju
2
pencuplikan F
s
,
maka nilai F dan ? tertinggi yang sesuai adalah:
F
maks
=
F
s
=
1
2
2T
?
maks
=
p
F
s
=
T
namun
hal
ini
akan
menimbulkan
ambigu,
karena
frekuensi
tertinggi
sinyal
waktu-
kontinu yang dapat dibedakan adalah sinyal yang dicuplik dengan laju 1/T = F
s
dengan
F
maks
=
F
s
/2 atau ?
maks
=
p
F
s
. Untuk lebih jelasnya akan dicontohkan sebagai berikut.
Ada dua buah sinyal analog sebagai berikut:
x
1
(t) = cos 2 p (10) t
x
2
(t) = cos 2 p (50) t
kedua sinyal ini akan dicuplik dengan laju F
s
=
40 Hz. Sinyal waktu-diskrit yang sesuai
adalah :
|
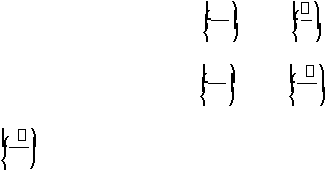 17
10
x
1
(n) = cos 2 p
n = cos
n
40
2
50
5
x2(n) = cos 2 p
n = cos
n
40
2
5
maka, cos
n
=
cos (2 pn + pn/2) = cos pn/2. Dengan demikian dapat disimpulkan
2
bahwa
x2
(n)
=
x
1
(n) yang
berarti
bahwa
kedua sinyal
tersebut
identik
dan
tidak
dapat
kita bedakan.
Jika
kita
berikan
nilai
yang
dimunculkan
dengan cos
(p/2)n, kita
harus
memeriksa
ulang apakah nilai
x
2
(t) dan
x1
(t) karena nilai
x2
(t) akan
sama dengan
x1
(t)
bila keduanya dicuplik pada frekuensi F2
= 50 Hz dan F1
= 10 Hz dengan laju
pencuplikan 40 cuplikan per sekon.
Jika kita
ambil
contoh
lagi
dengan
frekuensi
F3 = 90 Hz dengan
laju
pencuplikan 40
cuplikan per sekon maka hasilnya akan identik pula dengan hasil dari F1
.
Jika demikian
dapat diambil kesimpulan bahwa semua sinyal sinusoida dengan rumus
cos
2
p
(F1
+
40k)t,
dengan
k
=
1,2,3,4,
dan
seterusnya adalah
identik
pada
laju
pencuplikan 40 cuplikan per sekon.
2.3.2 Gangguan Pada Sinyal Nada
Instrumen Musik Akustik
Sinyal
nada
instrumen
akustik
yang
masuk
ke
dalam
sistem
pengenalan
nada,
tidak
selalu bersih walaupun sedikt pasti ada
gangguan yang berupa
noise atau derau.
Noise adalah
semua bentuk besaran,
yang
bukan
merupakan
bagian
dari
besaran atau
sesuatu
yang diinginkan. Noise ada dua
macam yaitu
internal
noise dan external noise.
Internal
noise dihasilkan oleh efek panas pada amplifier. Banyaknya noise yang
masuk
ke dalam
sinyal
tergantung bandwidth
dari
amplifier
masukan. Pada
umumnya cara
|
|
18
untuk
menekan
Internal
Noise adalah
memilih
amplifier
yang
memiliki
bandwidth
mendekati bandwidth
sinyal
masukan.
Jenis
noise
yang
kedua
adalah external
noise.
Noise
jenis
ini
dihasilkan
dari berbagai
macam
sumber.
Salah
satu
contohnya
adalah
sinyal
hand
phone,
pada
saat
kita
rekam
suara
kita
melalui
microphone,
hand
phone
disekitar kita mendapat sinyal masukan, maka jalur elektris dalam microphone tersebut
akan terganggu. Hal
ini
dikarenakan sinyal pada hand phone ditambahkan pada sinyal
elektris
microphone. Jika
kita
dengarkan
melalui
speaker
maka
akan
terdengah
suara
patah-patah. Salah satu
solusi dari
gangguan
noise
ini
adalah
menjauhkan hand phone
tersebut
dari
jalur
elektris
microphone. Sedangkan
jika
melalui
piranti,
noise
dapat
dikurangi dengan cara memfilter sinyal masukan tersebut.
Filter dapat digunakan untuk menekan adanya noise pada sinyal. Aplikasi
akuisisi
data
menggunakan low-pass
filter.
Low-pass
filter
melewatkan
komponen
frekuensi yang lebih rendah tetapi melemahkan komponen dengan frekuensi lebih tinggi.
Cut-off frekuensi dari filter harus cocok dengan frekuensi sinyal yang diinginkan saat ini
serta sampling rate
yang digunakan
untuk pengubahan sinyal analog ke
sinyal digital.
Antialiasing
filter
adalah
low-pass
filter
yang
mencegah
frekuensi
lebih
tinggi
yang
dapat men-distorsi sinyal digital.
2.4. Pengertian Notasi
Musik
Sebelum mengenal apa
itu notasi
musik, terlebih dahulu
harus mengerti apa itu
musik. Pengertian
musik adalah apresiasi
seni yang
terungkap dalam suara dan
ditangkap
oleh
indera
pendengaran. Musik
ditulis agar
dapat
dibaca,
dipelajari,
diteruskan kepada orang lain atau disimpan sebagai notasi musik, sehingga dapat
|
 19
memberikan kontribusi bagi perkembangan dunia
musik. Notasi musik ditulis dengan
dua sistematika penulisan, yaitu:
1. Sistem Penulisan Notasi Balok
Notasi balok digambarkan dengan lima garis para nada, yang setiap garisnya
mewakili tiap nada yang berbeda dimulai dari nada a hingga g. Penulisan dan
pengucapan
nada-nada
pada
notasi
balok
menggunakan huruf
alphabet,
dengan urutan C, D, E, F, G, A, B. Untuk mengetahui nada-nada tersebut ada
pada oktaf ke
berapa,
biasanya ditambahkan angka
yang
mewakili
tingkat
oktaf nada tersebut. Contohnya penulisan nada-nada pada oktaf ketiga : C3,
D3, E3, F3, G3, A3, B3
=
Not penuh. Nilainya 4 ketukan
=
Not setengah. Nilainya 2 ketukan
=
Not seperempat. Nilainya 1 ketukan
=
Not seperdelapan. Nilainya
1
/2 ketukan
|
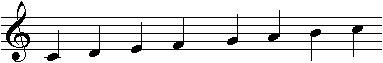 20
C3
D3
E3
F4
G3
A3
B3
C4
2. Sistem Penulisan Notasi Angka
Pada dasarnya penulisan
notasi angka tidak jauh berbeda dengan notasi
balok.
Pada
notasi
angka,
penulisan
nada
menggunakan angka
(angka
1
sampai dengan 7).
Angka kedelapan
merupakan perulangan dari
nada
pertama atau dasar, tetapi
lebih tinggi oktafnya. Cara penulisan ini disebut
solmisasi.
1
2
3
4
5
6
7
1’
Do
Re
Mi
Fa
Sol
La
Si
Do’
Pada musik dikenal tiga jenis tangga nada, yaitu :
1. Tangga Nada Diatonis :
a. Tangga Nada Mayor
Tangga nada dengan jarak nada 1 1
1
/2
1
1
1
1
/2 , dengan penulisan C D E
F G A B C.
b. Tangga Nada Minor
Tangga nada dengan jarak nada 1 ¹
/2
1 1 ¹/2
1
1, dengan penulisan C D
Eis F G Ais Bes C.
2. Tangga Nada Pentatonis
|
|
21
Tangga nada yang terdiri dari lima nada, yang pada umumnya terdapat pada
musik-musik etnik.
2.5. Rekayasa Piranti Lunak
Salah
satu
model
Rekayasa Piranti
Lunak
menurut Pressman
(1997,
p31-32)
adalah classic
life
cycle
yang
menggunakan pendekatan
yang
sistematis dan
berurutan
dalam mengembangkan sebuah piranti lunak. Aktivitas yang dilakukan dalam classic life
cycle terdiri dari beberapa tahapan, yaitu :
1. Analisa dan rekayasa sistem (System engineering and analysis)
Pada
tahap
ini
perancang
mulai
mengetahui dan
menetapkan kebutuhan-
kebutuhan
semua
elemen
sistem
dan
mengalokasikan beberapa
bagian
dari
kebutuhan-kebutuhan ini ke piranti lunak. Hal ini diperlukan karena piranti lunak
berhubungan
dengan elemen
yang
lain
seperti
perangkat
keras, pengguna,
dan
database.
2. Analisis kebutuhan piranti lunak (Software requirement analysis)
Proses
penetapan kebutuhan sistem
difokuskan
pada
piranti
lunak.
Untuk
memahami alur
program yang
akan
dibuat,
perancang harus
memahami
information domain
dari
piranti
lunak,
fungsi-fungsi
yang
diperlukan, kinerja.
Kebutuhan-kebutuhan sistem
dan
piranti
lunak
didokumentasikan
dan
dikonfirmasikan dengan customer atau user.
3. Perancangan (Design)
Perancangan
piranti
lunak
adalah
proses
yang
memfokuskan
pada
tiga
atribut
dari program : struktur data, arsitektur piranti lunak, dan detil prosedur. Proses
|
|
22
perancangan
menterjemahkan kebutuhan
sistem
ke
dalam
suatu
representasi
piranti lunak.
4. Pengkodean (Coding)
Pada
tahap
ini
rancangan
diterjemahkan ke
dalam
bahasa
mesin
(machine-
readable code).
5. Pengujian (Testing)
Dilakukan pengujian
terhadap
statement-statement
yang
ada
dari
fungsi-fungsi
eksternal, yaitu
menguji apakah input yang dimasukkan dapat memberikan hasil
yang diharapkan.
6. Pemeliharaan (Maintenance)
Perancang
melakukan
perubahan-perubahan pada
program
yang
sudah
ada.
Perubahan
ini
dapat
terjadi
karena
adanya kesalahan-kesalahan (error).
Piranti
lunak harus beradaptasi terhadap perubahan pada lingkungan.
2.6. Flowchart
Flowchart atau bagan alir merupakan alat bantu yang biasanya digunakan dalam
pemrograman. Bagan alir
membantu programmer dalam
mengorganisasikan pemikiran
mereka
dalam
pemrograman, terutama
bila
dibutuhkan
penalaran
yang
tajam
dalam
logika prosedur suatu program (Jone, 1980).
Simbol-simbol yang sering digunakan untuk bagan alir adalah sebagai berikut:
1. Proses
Berupa proses atau pengolahan
|
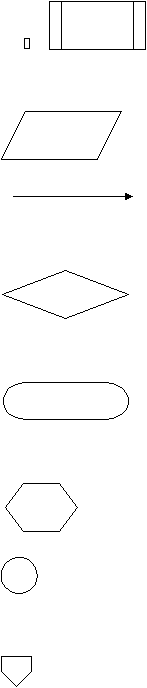 23
Untuk predefined process atau modul
2.
Operasi input/output
3.
Menghubungkan antar komponen dan
menunjukkan arah
4.
Decision, berupa pertanyaan atau penentuan suatu
keputusan
5.
Terminal, untuk
menandai awal atau
akhir
suatu
proses
6.
Preparation, untuk inisiasi suatu nilai
7.
Connector, sebagai penghubung dalam satu
halaman
8.
Off Page Connector, sebagai penghubung antar
halaman
|