|
BAB 2
LANDASAN TEORI
2.1 AI sebagai Pengenal
Pola
Banyak pemakaian AI
yang diterapkan pada berbagai aplikasi berbasis komputer,
salah
satunya
adalah
dalam pengenalan pola. Pola
yang
dimaksud
dapat
berupa
citra
(image), karakter, data dan yang lainnya. Pola tersebut baik citra, karakter, maupun data
sebenarnya
semuanya
merupakan
kumpulan
suatu
nilai,
permasalahannya adalah
bagaimana
menerjemahkan suatu
pola
tersebut
menjadi suatu
nilai
tertentu
yang
dapat
diproses pada sistem komputer.
Banyak bagian di dalam
AI dengan kelebihannya
masing-masing seperti
Expert
Systems(ESs),
Artificial
Neural
Networks
(ANNs), Fuzzy
Logic
dan
sebagainya.
Semuanya adalah termasuk dalam soft computing, dimana soft computing adalah koleksi
dari
beberapa
metodologi
yang
bertujuan
untuk
mengeksploitasi adanya
toleransi
terhadap ketidaktepatan, ketidakpastian, dan kebenaran parsial untuk diselesaikan
dengan mudah dan biaya penyelesaiannya murah. Definisi ini pertama kali diungkapkan
oleh Prof. Lotfi A. Zadeh pada tahun 1992 [Kusumadewi, 2003, p8].
Soft
computing merupakan inovasi baru dalam membangun sistem cerdas.
Sistem cerdas ini merupakan sistem yang memiliki keahlian seperti manusia pada
domain tertentu, mampu beradaptasi dan belajar agar dapat bekerja lebih baik jika terjadi
perubahan lingkungan. Bidang AI yang sering digunakan untuk pengenalan pola adalah
Artificial
Neural
Networks
(ANNs), karena
metode
ini
menggunakan
proses
pembelajaran setiap pola data dengan jaringan seperti syaraf biologis yang menyimpan
suatu
informasi / nilai tertentu sebagai pengenal dari pola data yang dimaksud.
7
|
|
8
Sebagai
contoh
bila
pada
pengenalan
pola
wajah
seseorang,
pengambilan
nilai
yang dilakukan bisa dengan
mengukur
geometri
wajah orang tersebut
untuk dijadikan
suatu
nilai
atau
dengan
ekstraksi
lainnya. Nilai
tersebut
yang
akan
disimpan
untuk
dipelajari
polanya
sampai
hasil
pembelajaran dan
pola
datanya
memiliki
kesalahan
/
error yang cukup kecil sehingga pembelajaran tersebut berhasil mengenali pola wajah
seseorang.
Perkembangan
ANN dalam
pengenalan
pola
sangat
luas,
dari
pengenalan
karakter,
pengenalan
wajah,
pengenalan
retina,
sampai
pengenalan pola
data
untuk
aplikasi peramalan. Semua itu menggunakan metode, model dan ekstraksi yang berbeda-
beda sesuai kebutuhan,
namun semuanya berpedoman pada sistem pembelajaran
jaringan untuk menghasilkan pengenalan pola yang dimaksud.
2.2 Artificial Neural
Network / ANN
ANN merupakan
simulasi
atau tiruan
dari
cara kerja syaraf
manusia,
terutama
dalam
proses
pembelajaran.
Simulasi
ini
dilakukan
dengan
menggunakan program
komputer yang melakukan pembelajaran melalui sejumlah proses perhitungan.
ANN
tersusun
dari sejumlah syaraf tiruan. Sebuah
sel syaraf
tiruan (selanjutnya
akan disebut neuron/node/unit) pada dasarnya adalah model elektronik logis dari sebuah
sel syaraf biologis. Jumlah neuron yang digunakan tergantung pada masalah yang ingin
dipecahkan, bisa hanya tiga dan bisa pula beribu-ribu.
Tiap
input
kedalam
sebuah
neuron
memiliki
nilai
bobot
(weight). Nilai bobot
inilah
yang terus
disesuaikan dalam proses
pembelajaran
ANN.
Pada
umumnya, bobot
ini
dapat
bernilai
baik
negatif
maupun
positif,
sehingga
dapat
merupakan peredam
maupun peningkat bagi tiap input. Setiap input yang memasuki neuron akan dikalikan
|
 9
dengan
nilai
bobotnya, dan
nilai-nilai baru
dari
tiap
input
tersebut
akan
dijumlahkan
sebagai
nilai
fungsi
aktivasi.
Nilai
ini
akan
dimasukkan kedalam
fungsi
aktivasi
yang
akan menghasilkan nilai baru dari input dan bobot tersebut yang disebut nilai output dan
neuron tersebut akan
meneruskan output
ke
neuron berikutnya. Untuk jelasnya
lihat
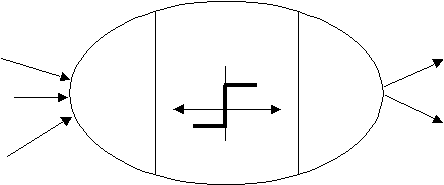
gambar 2.1 berikut :
output
dari
neuron-
neuron
bobot
Fungsi Aktivasi
S
Output
bobot
output ke
neuron-
neuron
yang lain
yang lain
Gambar 2.1 Struktur Neuron / Node Artificial Neural Network
Pada ANN, neuron-neuron dikelompokkan kedalam
lapisan-lapisan. Umumnya
neuron-neuron yang terletak pada lapisan yang sama akan memiliki keadaan serta fungsi
aktivasi
yang
sama.
Apabila neuron-neuron
dalam
suatu
lapisan
akan
dihubungkan
dengan neuron-neuron pada lapisan lain, maka setiap neuron antar kedua lapisan
tersebut harus terhubung.
Dalam
ANN
untuk melakukan perhitungan diperlukan suatu iterasi yang disebut
epoch. Dalam melakukan suatu pembelajaran dilakukan sebanyak epoch yang
ditentukan atau sampai target error minimum yang diharapkan sudah tercapai.
Dalam
ANN juga
banyak
faktor
yang
mempengaruhi
kecepatan
pembelajaran
diantaranya arsitektur jaringan ANN, konstanta
laju
belajar (learning rate), konstanta
|
|
10
momentum, fungsi aktivasi, pasangan
data
masukan
(training pairs) dan sebagainya,
namun
pada
penelitian
difokuskan
untuk
faktor
pada
topologi
atau
arsitektur
jaringan
dari ANN, karena
arsitektur
jaringan
merupakan
langkah
awal
penentuan
interkoneksi
bobot antar neuron dalam proses pembelajaran. Untuk
lebih jelasnya, hal
ini akan lebih
diuraikan pada bab 4.
2.2.1 Arsitektur ANN
Seperti yang telah dijelaskan sebelumnya bahwa
neuron-neuron
dikelompokkan
dalam
lapisan-lapisan (layers).
Kelakuan
dan
keadaan
neuron
ini
pada
tiap
lapisan
biasanya sama, baik fungsi
aktivasinya maupun pola bobotnya. Karena sebagian besar
jaringan
adalah berupa
neuron-neuron,
maka
neuron
tersebut dikelompokkan pada tiap
layer dengan arsitektur yang berbeda.
Arsitektur jaringan
dari ANN ini
menjadi
faktor
yang
penting dalam
performa
proses pembelajaran.
Beberapa arsitektur dari ANN antara lain:
a. Single Layer Net
Jaringan dengan
lapisan tunggal hanya
memiliki satu lapisan dengan bobot-
bobot
terhubung.
Jaringan
ini
hanya
menerima input
kemudian
secara
langsung
akan
mengolahnya menjadi
output
tanpa
harus
melalui
lapisan
tersembunyi. Seberapa
besar
hubungan antara
dua
neuron
ditentukan
oleh
bobot yang bersesuaian. Sebagai contoh lihat gambar 2.2
|
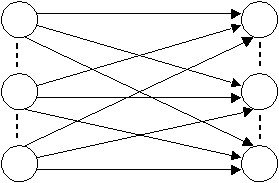 11
w
11
x1
w
1j
Y1
w
1m
x
i
w
n1
w
i1
w
ij
Y
j
w
im
w
nj
x
n
w
nm
Y
m
Input
Units
One Layer
of Weights
Output
Units
Gambar 2.2 Single Layer Neural Net
Sumber
:
Fausett, 1994, p13
b. Multi Layer Net
Jaringan dengan banyak lapisan, memiliki satu atau lebih lapisan yang
terletak di
antara lapisan
input dan lapisan output (memiliki satu atau
lebih
lapisan tersembunyi). Umumnya, ada
lapisan bobot-bobot yang terletak
antara
dua
lapisan
yang
bersebelahan. Jaringan
dengan banyak
lapisan
ini
dapat
menyelesaikan permasalahan
yang
lebih
rumit
seperti
prediksi,
pengenalan pola, pengklasifikasian, dan sebagainya daripada jaringan dengan
lapisan
tunggal,
tentu
saja
dengan
pembelajaran yang
lebih
rumit
juga
[Mganapathy, 2003].
Sampai
saat
ini
belum
ada
yang
menentukan
jumlah
lapisan
tersembunyi (hidden
layer) ataupun banyak sel
neuron
/
node
yang
terdapat
didalamnya.
Namun
beberapa
sumber
mengatakan penentuan
banyak
sel
neuron dalam
lapisan
tersembunyi
ini
dapat
menentukan
kecepatan suatu proses pembelajaran. Bila terlalu banyak, bobot yang diatur
akan dibuat untuk mencocokkan data input sebagai pengganti pola dasarnya.
Sayangnya hal
ini akan
menimbulkan overfitting. Bila terlalu sedikit, maka
|
 12
data
yang
dipelajari
tidak
akurat
karena
kurang
mendapat
bobot
(weight)
yang
beragam,
sehingga
membutuhkan proses
pelatihan
yang
banyak.
Beberapa sumber
mempertimbangkan pemilihan
jumlah
hidden
node dapat
dilakukan dengan bereksperimen dengan kisaran nilai
tertentu.
Hal
ini
akan
lebih diuraikan pada bab 3. Untuk
lebih jelas tentang multi layer
net dapat
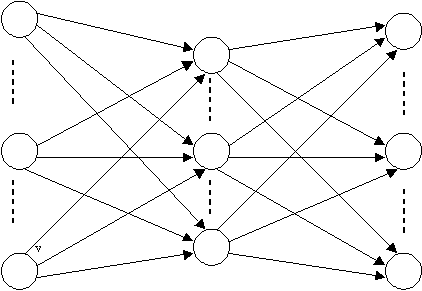
dilihat pada gambar 2.3.
v
11
x1
v
1j
v
1p
v
i1
x
i
v
ij
v
ip
Y
1
w
11
z1
w
1k
w
1m
w
j1
z
j
w
jk
Y
k
w
jm
v
n1
nj
w
p1
z
p
w
pk
w
pm
x
n
Input
Units
v
np
Hidden
Units
Y
m
Output
Units
Gambar 2.3 Multi Layer Neural Net
Sumber
:
Fausett, 1994, p13
c. Competitive Layer Net
Pada Competitive Layer
Net, neuron output dari jaringan berlomba diantara
mereka sendiri untuk menjadi aktif (diaktivasi), pada jaringan
ini hanya ada
satu neuron yang aktif pada saat yang sama.Untuk jelasya lihat gambar 2.4.
|
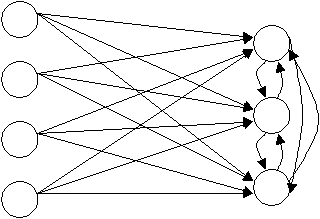 13
X1
X2
X3
X
4
Input
Units
Output
Units
Gambar 2.4 Competitive Layer Net Sederhana
Sumber
:
Haykin, 1999, p59
Proses
pembelajaran ANN
merupakan proses
penyesuaian nilai
bobot
bagi
tiap
input.
Nilai
bobot
akan
bertambah jika
informasi
yang
diberikan
oleh
neuron
yang
bersangkutan
tersampaikan, sebaliknya
jika
informasi
tidak
disampaikan
oleh
suatu
neuron
ke
neuron
yang
lain,
maka
nilai
bobot
yang
menghubungkan
keduanya
akan
dikurangi. Pada saat pembelajaran dilakukan pada input yang berbeda, maka nilai bobot
akan diubah secara dinamis hingga mencapai suatu nilai yang cukup seimbang. Apabila
nilai
ini telah tercapai,
maka
mengindikasikan bahwa tiap-tiap
input telah berhubungan
dengan output yang diharapkan [Kusumadewi, 2003, p220].
Arsitektur dasar ANN paling
sedehana
yang
melakukan
klasifikasi
pola
terdiri
dari sebuah layer input (dengan neuron
/
unit
yang disesuaikan dengan pola yang akan
diklasifikasikan) dan sebuah output layer [Fausett, 1994, p40]. Untuk lebih jelasnya lihat
gambar 2.5.
|
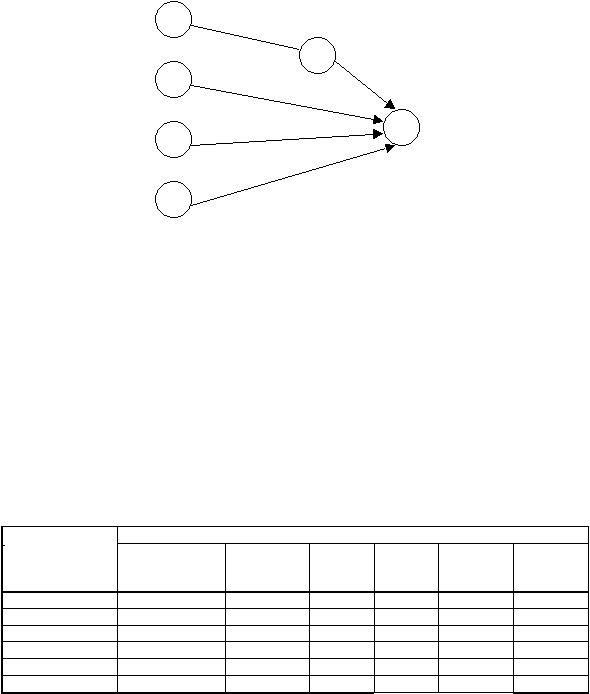 14
1
b
X1
w1
X
i
w
i
Y
w
n
X
n
Input
Unit
Gambar 2.5 Jaringan
Single Layer untuk klasifikasi pola
Sumber
:
Fausett, 1994, p40
Secara umum, banyak aplikasi permasalahan yang
menggunakan tipe dari
ANN
yang berbeda. Hal ini dapat dilihat pada tabel 2.1 yang menunjukkan aplikasi ANN
pada
banyak permasalahan.
Application
Problem Type
ANN
Type
Backpropagation
Adaptive
Resonance
Feature
Map
Routing
Radical
Basis
Recurrent
Temporal
Difference
Classification
X
X
X
X
X
Math Modelling
X
X
X
Forecasting
X
X
X
Reconstruction
X
Clustering
X
X
Routing
X
Sumber : Neural
Network Utility: Installation
and
User’s Giude, Ver. 3.1, p.90, IBM Corporation,
1994
Tabel
2.1 Tipe dari
ANN dan Aplikasinya
Sumber
:
DeLurgio, 1998, p673
|
|
15
Pada tabel 2.1 di atas tipe dari aplikasi meliputi :
-
Classification Problem seperti proses persetujuan kredit (tolak atau terima) dan
identifikasi cacat (baik atau buruk).
-
Mathematical Modelling
pada saat ANN digunakan untuk mengenali atau
membandingkan fungsi matematik.
-
Forecasting termasuk
aplikasi
estimasi
dengan
metode
Univariate dan
Multivariate.
-
Reconstruction/Recognition
melibatkan
tentang
mengenali
sebuah
pola
pada
sinyal yang tidak jelas. Sebagai contoh, aplikasi pengenalan karakter
merupakan indikasi reconstruction.
Metode pengenalan karakter pada
scanner
computer dan mesin fax menggunakan ANN.
-
Clustering
melibatkan
tentang
menemukan
pengelompokan logika
dari
nilai
dalam
data.
Sebagai
contoh,
dalam
pemasaran, ketika
mencoba
untuk
mengelompokkan tipe konsumen dan tanggapan mereka kedalam tipe promosi
yang berbeda.
-
Routing berisi
tentang
menentukan
rute
yang
terbaik
sampai
nilai
tujuan.
Sebagai contoh masalah traveling salesman
Seperti
dijelaskan
di atas, salah satu pendekatan
ANN yang relevan
kepada
estimasi adalah dengan metode ANN backpropagation,
yang akan diuraikan pada
penelitian ini dalam bab-bab selanjutnya.
2.2.2 Fungsi
Aktivasi
Seperti telah dijelaskan sebelumnya, operasi perhitungan dasar dari ANN
adalah
menjumlahkan sinyal input yang terbobot dan meneruskannya ke output, atau aktivasi.
|
 16
Aktivasi inilah yang memiliki fungsi yang menghasilkan output yang berbeda-beda pula.
Adapun
beberapa fungsi
aktivasi
yang sering digunakan dalam desain arsitektur ANN,
antara lain :
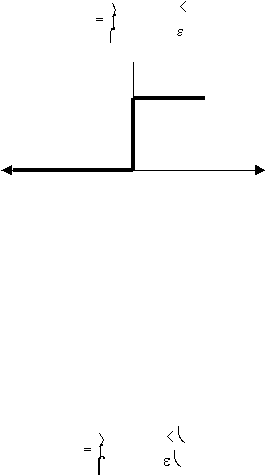
a. Fungsi Biner (Hard Limit)
Jaringan
dengan
lapisan
tunggal
sering
menggunakan fungsi
undak
(step
function)
untuk
mengkonversikan input
dari
suatu
variabel
yang
bernilai
kontinyu ke suatu output biner (0 atau 1) seperti terlihat pada gambar 2.6.
Fungsi undak biner (hard limit) dirumuskan sebagai :
0
,
y
1,
jika
jika
x
0
x
0
y
1
0
x
Gambar 2.6 Fungsi aktivasi : Undak Biner (Hard Limit)
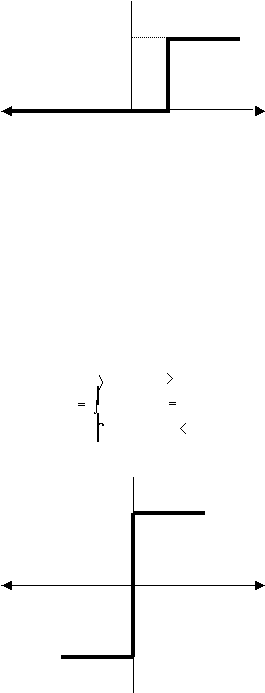
b. Fungsi Biner (Threshold)
Fungsi biner dengan menggunakan nilai ambang sering juga disebut dengan
nama fungsi nilai ambang (threshold) atau fungsi Heaviside (gambar 2.7).
Fungsi undak biner (dengan nilai ambang ?) dirumuskan sebagai :
0 jika
, jika
y
1,
jika
x
x
|
 17
y
1
0
?
x
Gambar 2.7 Fungsi aktivasi : Undak Biner (threshold)
c. Fungsi Bipolar (Symetric Hard Limit)
Fungsi bipolar sebenarnya
hampir
sama
dengan
undak
biner,
hanya
saja
output yang dihasilkan berupa 1, 0, atau –1 (gambar 2.8).
Fungsi Symetric Hard
Limit dirumuskan sebagai :
1,
y
0
,
jika
jika
x
0
x
0
1, jika
x
0
y
1
0
x
-1
Gambar 2.8 Fungsi aktivasi : Bipolar (symetric hard
limit)
|
 18
y
1
0
?
-
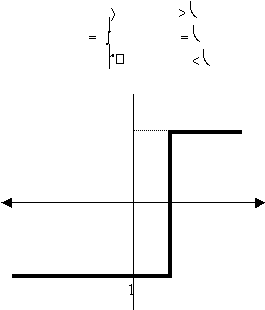
d. Fungsi Bipolar (dengan threshold)
Fungsi bipolar
sebenarnya hampir sama dengan
fungsi undak biner dengan
threshold,
hanya saja output
yang dihasilkan berupa 1, 0, atau –1 (gambar
2.9).
Fungsi bipolar (dengan nilai ambang ?) dirumuskan sebagai :
1,
y
0
,
jika
jika
x
x
1,
jika
x
x
Gambar 2.9 Fungsi aktivasi : Bipolar (dengan threshold)
e. Fungsi Linear (identitas)
Fungsi linear
memiliki nilai output yang sama dengan nilai inputnya (gambar
2.10).
Fungsi linear dirumuskan sebagai :
|
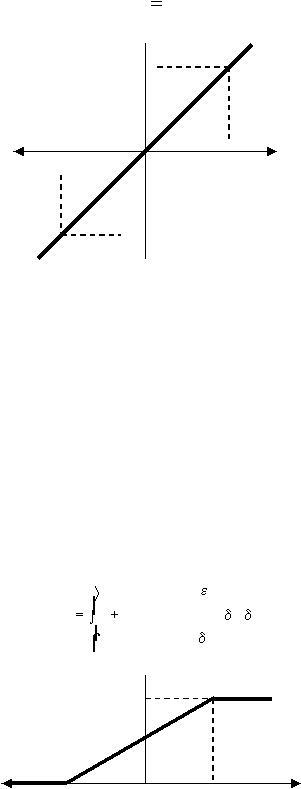 19
y
x
y
1
-1
0
1
x
-1
Gambar 2.10 Fungsi aktivasi : Linear (identitas)
f.
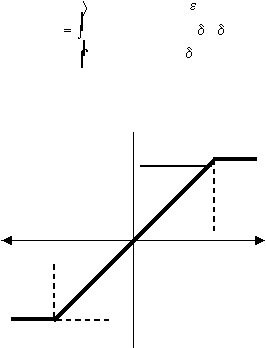
Fungsi Saturating Linear
Fungsi ini akan bernilai 0 jika inputnya kurang dari -½, dan akan bernilai 1
jika
inputnya
lebih dari ½. Sedangkan jka nilai input terletak antara -½ dan
½, maka outputnya akan bernilai sama dengan nilai input ditambah ½
(Gambar 2.11).
Fungsi saturating
linear dirumuskan sebagai :
1;
y
x
0,5;
0;
jika x
0,5
jika
0,5
x
0,5
jika x
0,5
y
1
-0,5
0
0,5
x
Gambar 2.11 Fungsi aktivasi : Saturating
Linear
|
 20
g. Fungsi Symetric Saturating Linear
Fungsi ini akan bernilai –1 jika inputnya kurang dari –1, dan akan bernilai 1
jika inputnya lebih dari 1. sedangkan jika nilai input terletak antara –1 dan 1,
maka outputnya akan bernilai sama dengan nilai inputnya (gambar 2.12).
Fungsi symetric saturating
linear dirumuskan sebagai :
1;
y
x;
1;
jika x
1
jika
1
x
1
jika x
1
y
1
-1
0
1
x
-1
Gambar 2.12 Fungsi aktivasi : Symetric Saturating
Linear
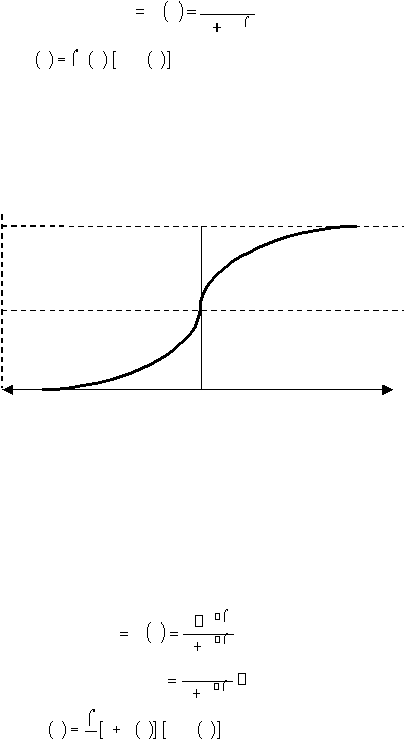
h. Fungsi Sigmoid Biner
Fungsi
ini
banyak
digunakan
pada
jaringan syaraf yang dilatih dengan
menggunakan
backpropagation.
Fungsi
sigmoid biner
memiliki
nilai
pada
rentang antara 0 sampai 1. Oleh karena itu, fungsi ini sering digunakan untuk
jaringan syaraf yang membutuhkan nilai output yang terletak pada interval 0
sampai 1. Namun, fungsi ini juga bisa digunakan oleh jaringan syaraf
yang
nilai ouputnya 0 atau 1 (gambar 2.13).
|
 21
Fungsi sigmoid biner dirumuskan sebagai :
y
f
x
1
1
e
x
dengan :
f
'
x
f
x
1
f
x
Dimana
e adalah bilangan
natural e = 2,718281828459 dan s
adalah
kecuraman kurva sigmoid yang biasanya bernilai 1.
f(x)
1
0,5
0
x
0
Gambar 2.13 Fungsi aktivasi : Sigmoid Biner
i.
Fungsi Sigmoid Bipolar
Fungsi sigmoid bipolar hampir sama dengan fungsi sigmoid biner, hanya saja
output dari fungsi ini memiliki rentang antara –1 sampai 1 (gambar 2.14).
Fungsi sigmoid bipolar dirumuskan sebagai :
y
f
x
1
e
x
1
e
x
2
1
1
e
x
dengan :
f
'
x
1
f
x
1
f
x
2
|
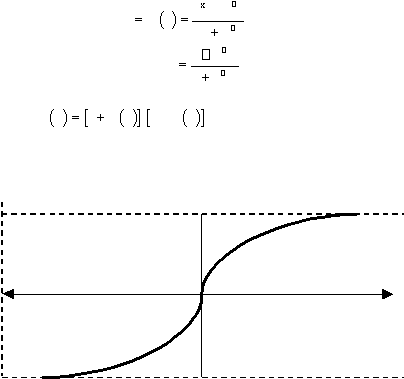 22
Fungsi
ini
sangat
dekat
dengan
fungsi
hyperbolic
tangent. Keduanya
memiliki rentang antara –1 sampai 1. Untuk fungsi hyperbolic tangent,
dirumuskan sebagai :
y
f
x
e
e
x
e
x
e
x
1
e
2
x
1
e
2
x
dengan :
f
'
x
1
f
x
1
f
x
f(x)
1
0
x
-1
0
Gambar 2.14 Fungsi aktivasi : Sigmoid Bipolar
2.2.3 ANN Backpropagation
Pembelajaran pada
ANN
secara
umum
terbagi
menjadi
dua, yaitu pembelajaran
terawasi (supervised
learning)
dan
pembelajaran tak
terawasi
(unsupervised
learning).
Pada supervised learning,
output yang diharapkan sudah diketahui dan dijadikan acuan
bagi
proses pembelajaran.
Sedangkan
pada unsupervised
learning tidak ada hasil
yang
dijadikan acuan. Masalah-masalah yang diselesaikan dengan metode pembelajaran ini
adalah masalah-masalah yang tidak memiliki suatu nilai output harapan, misalnya untuk
proses klasifikasi.
|
|
23
ANN
Backpropagation
merupakan
metode pembelajaran yang termasuk kedalam
kategori supervised learning, metode ini diperkenalkan oleh David Rumelhart dan James
McClelland pada tahun 1986 [Fausett, 1994, p289]. Pada dasarnya, apabila pada proses
pembelajaran dihasilkan output yang tidak sesuai dengan hasil yang diharapkan, maka
harus ada nilai bobot yang disesuaikan. Penyesuaian ini dilakukan mulai secara mundur
dari satu neuron ke neuron-neuron sebelumnya.
Sistem
ini dibagi
menjadi dua bagian
yaitu tahap pelatihan (training)
dan
tahap
pengujian (testing). Dalam
tahap pelatihan ini
data dibaca dari
suatu
file
yang berupa
urutan
masukan
(input)
dan
keluaran
(output)
atau
yang
diberi
nama
Training
pairs.
Hasil
dari
proses
pelatihan
ini
adalah
menentukan
bobot
(weight) dari
input
neuron
sebelumnya.
Sedangkan pada tahap pengujian diberi
sejumlah data masukan untuk diuji
berdasarkan hasil dari pelatihan jaringan tersebut, data yang diuji dapat berasal dari data
yang
telah
dilatih
atau
diluar
data
pelatihan
(out
of
sample
data).
Pada
saat
proses
langkah
maju (feedforward),
neuron-neuron
diaktifkan dengan menggunakan fungsi
aktivasi
sigmoid, bisa berupa sigmoid biner
maupun
bipolar
sesuai
dengan kebutuhan
penggunaan input atau output. Adapun arsitektur jaringan backpropagation dapat dilihat
pada gambar 2.15.
|
 24
X1
v
11
v
1n
v
21
X2
v
2n
Y1
w
11
Z1
w
12
w
1q
Y2
v
31
X
p
v
pn
w
n1
Z
n
w
n2
w
nq
Y
q
Gambar 2.15 Arsitektur jaringan backpropagation
Sumber
:
Kusumadewi, 2003, p236
Keterangan simbol :
x
Vektor input pelatihan
x
= (x1,…,x
i
,…,x
n
).
t
Vektor output target
t = (t1 ,…,t
k
,…,t
m
).
d
k
Porsi koreksi error/kesalahan penyesuaian bobot untuk w
jk
yang berasal
dari
unit output
Y
k
;
juga
informasi tentang error pada unit
Y
k
yang di
balikkan (backpropagate) ke hidden unit yang memberikan pada unit Y
k
.
d
j
Porsi koreksi error/kesalahan penyesuaian bobot
untuk v
ij
yang berasal
dari
informasi
error backpropagation dari
lapisan
output
menuju
unit
tersembunyi Z
j
.
a
Konstanta Laju belajar (Learning Rate)
X
i
Unit input i :
Untuk sebuah unit input, sinyal input dan sinyal output sama dinamakan
x
i
v
0j
Bias pada hidden unit j.
Z
j
Hidden unit j:
Sinyal input menuju Z
j
dinyatakan dengan z_in
j
:
z
_
in
j
v
0
j
x
i
v
ij
i
1
Sinyal output (aktivasi) dari Z
j
dinyatakan dengan z
j
:
z
j
f
z
_
in
w
0k
Bias pada unit output k.
Y
k
Unit output k :
Sinyal input menuju Y
k
dinyatakan dengan y_in
k
:
p
y
_ n
in
k
w
0
k
z
j
w
jk
j
1
|
 25
Sinyal output (aktivasi) dari Y
k
dinyatakan dengan y
k
:
y
k
f
y
_
in
k
Pada
algoritma
pelatihan
backpropagation
terdiri
atas dua tahap,
yaitu
tahap
feedforward
dan
tahap
backward
dimana
pada
tahap feedforward merupakan proses
perhitungan
nilai
input
ke dalam
jaringan
sedangkan
pada
tahap
backward
merupakan
penyesuaian
bobot
didalam jaringan
yang
berdasarkan
hasil
perhitungan
pada
feedforward.
Pelatihan ini dilakukan untuk menyesuaikan nilai-nilai bobot interkoneksi
jaringan dengan target
output / referensi sebagai acuan hasilnya. Proses penyesuaian
bobot
ini
mempunyai batasan / kriteria
untuk berhenti, dimana batasan tersebut diatur
oleh target
error
yang diinginkan. Pada tahap feedforward jaringan
menghasilkan nilai
hasil
perhitungan
yang
kemudian
dibandingkan
dengan target
outputnya
sehingga
menghasilkan
selisih error
untuk kemudian
dilakukan
penyesuaian
bobot pada
tahap
backward dengan mengirimkan informasi selisih error tersebut.
Algoritma pelatihan ANN backpropagation adalah sebagai berikut :
Langkah 0 : Inisialisasi bobot
(bangkitkan nilai bilangan acak yang kecil)
Langkah 1 : Selama kondisi berhenti false, lakukan langkah 2-9
Langkah 2 : Untuk setiap pasangan data pelatihan, lakukan lagkah 3-8
Feedforward (langkah maju):
Langkah 3 : Setiap unit input (X
i
,
i
= 1,…,n) menerima sinyal
input
x
i
dan
meneruskan
sinyal
tersebut
ke
semua
unit pada lapisan diatasnya (hidden layer).
Langkah
4
:
Setiap
unit
tersembunyi
(Z
j
,
j
=
1,…,p)
menjumlahkan sinyal-sinyal input terbobot,
n
z
_
in
j
v
0
j
x
i
v
ij
i
1
|
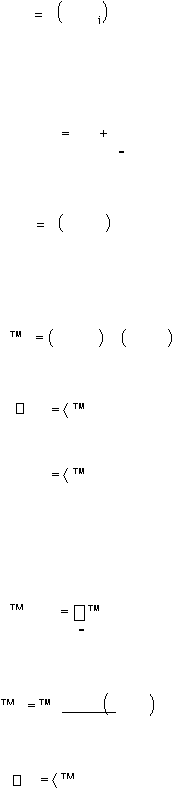 26
j
'
gunakan fungsi aktivasi untuk menghitung sinyal
outputnya,
z
j
f
z
_
in
dan kirimkan sinyal tersebut ke semua unit di lapisan
atasnya (unit-unit output).
Langkah 5 : Setiap
unit output (Y
k
,
k
=
1,…,m) menjumlahkan
sinyal-sinyal input terbobot,
p
y
_
in
k
w
0
k
z
j
w
jk
j
1
Gunakan fungsi aktivasi untuk menghitung
sinyal
outputnya,
y
k
f
y
_
in
k
Backward (langkah mundur):
Langkah 6 : Tiap-tiap unit output (Y
k
,
k
=
1,…,m) menerima pola
target
yang berhubungan dengan pola input
pembelajaran, hitung informasi errornya,
k
t
k
y
k
f
y
_
in
k
hitung koreksi bobot (yang nantinya akan digunakan
untuk memperbaiki nilai w
jk
),
w
jk
k
z
j
hitung juga koreksi bias (yang nantinya akan
digunakan untuk memperbaiki nilai w
0k
),
w
0
k
k
dan kirimkan nilai
d
k
ke unit-unit yang ada di lapisan
bawahnya.
Langkah 7 : Tiap-tiap hidden unit (Z
j
,
j
=
1,…,p) menjumlahkan
delta
inputnya (dari
unit
yang
berada
pada
lapisan
atasnya),
_
in
j
m
k
w
jk
k
1
kalikan
nilai
ini
dengan
turunan
dari
fungsi
aktivasinya untuk menghitung informasi errornya,
j
in
f
'
z
in
j
kemudian
hitung koreksi bobot (yang nantinya
digunakan untuk memperbaiki nilai v
ij
),
v
ij
j
x
i
|
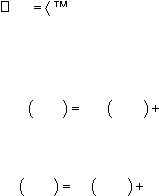 27
hitung
juga koreksi
bias
(yang
nantinya
digunakan
untuk memperbaiki nilai v
oj
),
v
0
j
j
perbaikan bobot dan bias :
Langkah
8
:
Setiap
unit
output
(Y
k
,
k
= 1,…,m) memperbaiki
bobot dan biasnya (j = 0,…,p),
w
jk
baru
w
jk
lama
w
jk
Setiap unit tersembunyi (Z
j
,
j
=
1,…,p)
memperbaiki
bobot dan biasnya (i = 0,…,n),
v
ij
baru
v
ij
lama
v
ij
Langkah 9 : Tes kondisi berhenti
Untuk lebih jelasnya, proses pelatihan pada algoritma backpropagation
digambarkan dalam diagram alir berikut :
|
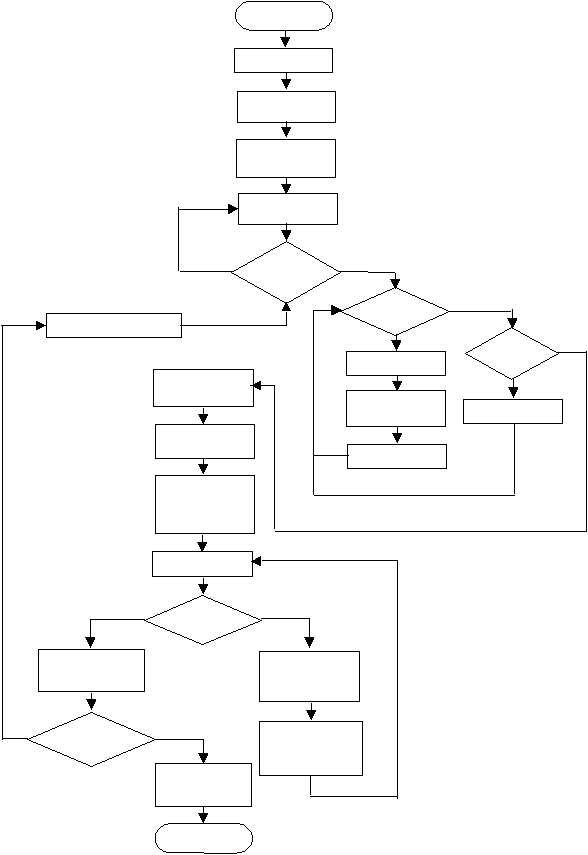 28
MULAI
Baca data Input
Masukkan data
sebagai vektor
Skalakan data vektor
input
Baca record pertama
pada vektor
Record selanjutnya pd vektor
true
Tiap record
vektor =
akhir
?
false
node hidden
layer = akhir?
false
Hitung
Sx.w
+ bias
true
Output
layer?
true
Hitung selisih error dari
hasil feedforward dg
target
Masukkan ke fungsi
aktivasi
false
Layer Selanjutnya
Hitung porsi error
d
output layer
Node Selanjutnya
Hitung koreksi bobot
delta rule ? utk
semua bobot ke
output layer
Layer sebelumnya
true
Input layer
?
false
Lakukan perbaikan
semua bobot w(baru)
=
w(lama) + ? w
Hitung porsi error
d
hidden layer dari
layer sesudahnya
false
Target error /
epoch tercapai ?
true
Simpan vektor-
vektor bobot akhir
pelatihan
Hitung delta rule
?
utk semua bobot ke
hidden layer dan
simpan hasilnya
SELESAI
Gambar 2.16 Diagram
Alir pada
Algoritma Pelatihan
(Training) Backpropagation
|
 29
Epoch
adalah
satu
iterasi
/
putaran
sampai
semua
vektor
data pelatihan telah
dilatih.
Biasanya
diperlukan
banyak
epoch
dalam
proses
pembelajaran ANN
backpropagation.
Dasar
matematis untuk
algoritma backpropagation
adalah
teknik
optimisasi
yang dikenal
sebagai
gradient
descent
(kecuraman penurunan). Kecuraman
dari fungsi (dalam
hal
ini, fungsi adalah error
dan variabel adalah bobot dari jaringan)
memberikan
arah
yang
mana
fungsi
tersebut
akan
meningkat
dengan cepat
[Fausett,
1994, p296].
Pada
algoritma
pengujian
ANN hanya
terdapat
satu
tahap,
yaitu
tahap
feedforward. Tahap ini sama seperti tahap feedforward pada algoritma pelatihan dimana
tahap
tersebut
memberikan
nilai
input
ke
dalam
jaringan.
Yang
membedakan
adalah
pada
algoritma pengujian tidak
ada
tahap
backward
sebab
jaringan
pada
algoritma
pengujian ini merupakan jaringan yang sudah melalui tahap pelatihan.
Bobot interkoneksi
jaringan
merupakan
nilai akhir bobot setelah melakukan
tahap
pelatihan
sehingga
jaringan
untuk
pengujian
mempunyai arsitektur
yang
tetap
seperti pada tahap pelatihan dengan nilai bobot akhir hasil pelatihan tersebut.
Algoritma pengujian ANN backpropagation adalah sebagai berikut
Feedforward (langkah maju):
Langkah
1
:
Setiap unit input (X
i
,
i
= 1,…,n) menerima sinyal
input
x
i
dan
meneruskan
sinyal
tersebut
ke
semua
unit pada lapisan diatasnya (hidden layer).
Langkah
2
:
Setiap
unit
tersembunyi
(Z
j
,
j
=
1,…,p)
menjumlahkan sinyal-sinyal input terbobot,
n
z
_
in
j
v
0
j
x
i
v
ij
i
1
gunakan fungsi aktivasi untuk menghitung sinyal
outputnya,
z
j
f
z
_
in
|
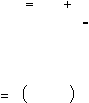 30
dan kirimkan sinyal tersebut ke semua unit di lapisan
atasnya (unit-unit output).
Langkah 3 : Setiap
unit output (Y
k
,
k
=
1,…,m) menjumlahkan
sinyal-sinyal input terbobot,
p
y
_
in
k
w
0
k
z
j
w
jk
j
1
Gunakan fungsi aktivasi untuk menghitung
sinyal
outputnya,
y
k
f
y
_
in
k
2.3 Metode-metode Estimasi
Mengestimasikan masa depan merupakan salah satu keinginan yang paling kuat
dalam
kehidupan manusia
modern.
Tujuannya telah
dihasilkan secara
ilmiah
yang
berdasarkan estimasi,
seperti
kesehatan
manusia,
tingkah
laku,
perekonomian,
pembelajaran, cuaca,
perlombaan
balap
kuda,
penjualan
perusahaan, saham
dan
sebagainya [DeLurgio, 1998, p4].
Bagi kebanyakan organisasi, estimasi sangat diperlukan untuk menentukan
tujuan
kerja
organisasi
dimasa
depan
atau
disebut
perencanaan, namun
sebuah
perencanaan tersebut membutuhkan suatu alasan yang baik agar hasil yang didapat pada
kenyataannya tidak
menyimpang jauh
dari
yang
diharapkan. Berdasarkan hal
tersebut,
estimasi
merupakan sesuatu
yang
penting
dalam
mengatur
rencana
ke
depan
suatu
organisasi.
2.3.1. Tahapan-tahapan Proses
Estimasi
Sistem estimasi sangat penting
untuk mencegah terjadinya hal yang tidak perlu
seperti
pemadaman pembangkit listrik,
tidak
ada
penjualan, tidak
ada
konsumen,
kelebihan beban dan sebagainya. Walaupun hasil estimasi dengan kenyataan tidak selalu
|
|
31
tepat, namun sistem ini tetap sangat penting dan sangat diperlukan sebagai acuan proses
yang akan dilakukan pada masa depan. Banyak perusahaan, distributor, organisasi yang
terbaik di dunia menggunakan sistem
estimasi yang canggih dalam melakukan rencana
proses kerjanya [DeLurgio, 1998, p5].
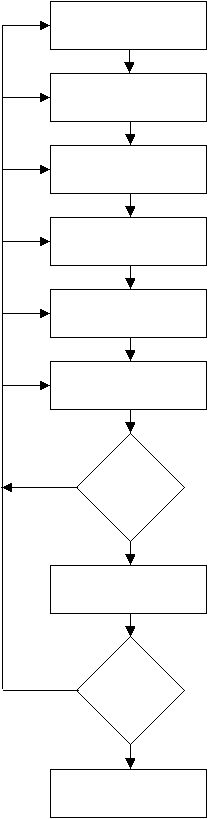
Berkut
merupakan
tahapan-tahapan dalam
proses
estimasi
yang
digambarkan
dalam diagram alir :
|
 32
Definisi Masalah
Pencarian Informasi
Hipotesis/Teori/Model
yang dipakai
Rancang Sistem
Estimasi
Menguji Sistem
Estimasi
Analisa Hasil
I. Definisi Masalah
A. Rencana, sasaran, keputusan
B. Batasan sistem
II. Pencarian Informasi
A. Mendefinisikan sistem
B. Mendefinisikan akibat dan
efek
III. Hipotesis/Teori/Model
A. Model Causal
B. Eksplorasi Grafik
C. Teori dari Model Causal
D. Pertimbangkan metode yang
sesuai
IV. Rancang
Sistem
Estimasi
A. Memilih
data
in-sample
B. Memilih data out-sample
V. Menguji Sistem Estimasi
A. Memasukkan data in-sample
B. Prakirakan data out-sample
Tidak
Tidak
Hasil
Benar?
Ya
Pemeliharaan dan
Verifikasi berkelanjutan
Sistem
Terkendali
?
VI. Analisa Hasil
A. Apa asumsi benar?
B. Lakukan teori pendukung
C. Persetujuan Ahli?
D. Melaksanakan tes out-sample
VII. Pemeliharaan dan Verifikasi
berkelanjutan
A. Menyertakan percobaan
real-time
B. Menerapkan Model/Sistem
C. Memeriksa Model/Sistem
Ya
Teruskan Pemakaian
Sistem
Gambar 2.17 Diagram
Alir Metode Ilmiah dalam Proses
Estimasi
Sumber
:
DeLurgio, 1998, p27
|
 33
Namun
secara keseluruhan
proses
estimasi,
untuk
mendapatkan estimasi
yang
aktual dibutuhkan data
lalu
/
histori data yang aktual
juga. Sistem mempelajari model
pola data
yang
lalu (backcast)
untuk menentukan pola tersebut kedepan
(forecast), dan
menurut DeLurgio [1998, p17] “A
good forecast requires a good backcast”.
2.3.2 Metode Estimasi
yang Mengacu
pada
Rangkaian Waktu
Pada proses estimasi terdapat beberapa metode yang digunakan, metode tersebut
mengacu
kepada
rangkaian
waktu
(time
series)
dari
suatu
pola
data.
Metode-metode
yang umum digunakan pada pola ini adalah :
a. Metode estimasi time series (univariate)
Merupakan
metode
yang
menggunakan
model
time series
sebagai
fungsi
dirinya
sendiri
tanpa
ada
variabel
luar
lain
yang
bergantung, singkatnya
konsep dasar
dari
model
estimasi
Univariate adalah
estimasi
data
waktu
depan
merupakan fungsi
matematis
(f)
dari
data
waktu
yang
lalu.
Secara
matematik dapat ditulis :
Nilai Estimasi = f (Nilai yang lalu)
Sebagai contoh,
asumsikan
model
estimasi
sederhana
untuk
rata-rata
dua
bulan :
Estimasi penjualan bulan Juni =
penjualanbulan April
penjualanbulan Mei
2
600
500
=
2
=
550
Model-model yang termasuk metode estimasi Univariate :
-
Moving Average
-
Exponential Smoothing
-
Classic Decomposition
|
|
34
-
Fourier Series
-
ARIMA
-
Multimodel simulation methods
b. Metode estimasi causal (Multivariate)
Model
ini
menggunakan konsep
hubungan
sebab
akibat
dalam
perhitungannya. Model ini mengestimasikan data ke depan berdasarkan suatu
rangkaian dan
rangkaian lain,
sebagai
contoh
penjualan perabot
rumah
mungkin dipengaruhi oleh
faktor ekonomi seperti harga rumah, pendapatan
seseorang, jumlah pengantin baru, dan sebagainya. Variabel-variabel
eksternal
ini
disebut
predictor
atau
variabel
independen, dan
variabel
penjualan
perabot
dapat
disebut
predicted
atau
variabel
dependen. Secara
matematis, fungsi ini dapat ditulis :
Variabel dependen = f
(variabel predictor independen)
atau
Nilai estimasi = f (nilai yang lalu, nilai variabel
yang lain)
Sebagai
contoh,
asumsikan
estimasi
penjualan
perabot rumah dengan
tiga
model variabel :
Estimasi penjualan Juni = 50 + 0,2 x PPL + 1 x PRR + 0,5 x PRB
=
50 + 0,2 x 600 + 1 x 250 + 0,5 x 200 =
520
dimana
:
PPL = Penjualan perabot rumah bulan lalu
PRR = Pendapatan rata-rata seseorang
PRB = Pembelian rumah baru
Model-model yang termasuk dalam metode estimasi multivariate / causal:
-
Multiple Regression
|
 35
-
Econometric
-
Cyclical
-
State Space
-
Vector Autoregression
-
Input/Output Models
c. Metode estimasi kualitatif
Metode ini berdasarkan atas pendapat dan penilaian dari estimasi lainnya dan
perubahan teknologi. Metode ini banyak digunakan untuk membuat prediksi
jangka panjang ketika
hanya sedikit data yang objektif
yang
mengacu pada
pola
atau
hubungan yang
lalu
untuk
mendukung
metode
kuantitatif.
Contohnya, asumsikan prediksi estimasi dari tiga panel eksekutif :
Estimasi Juni =
prakiraanM
anager 1
prakiraanM
anager 2
prakiraanM
anager
3
3
400
600
600
=
=
533
3
Pada dunia
bisnis,
metode
ini digunakan
untuk
memprakirakan permintaan
produk
baru, teknologi baru, pasaran baru, strategi kompetitif yang
terbaik.
Dalam sektor
publik,
metode
ini
digunakan
untuk memprakirakan pengaruh
perubahan kebijakan publik, permintaan layanan dan sebagainya. Metode ini
tidak banyak digunakan seperti Univariate dan Multivariate karena biayanya
mahal, keakuratan yang rendah dan keterbatasan data untuk metode yang lain
[DeLurgio,
1998,
pp22-23].
Model-model yang
digunakan
dalam
metode
estimasi kualitatif :
-
Panel Consensus
-
Sales Force Composite
-
DELPHI
|
|
36
-
Relevance Trees
d. Metode estimasi kuantitatif lainnya
Metode-metode
yang
telah
diuraikan
di
atas
semuanya
merupakan
bagian
dari
Quantitative
Forecasting
Methods. Semuanya
menggunakan
data
kuantitatif dari
suatu pola
masukan
/
input
dan
diolah dengan
melakukan
perhitungan analitis
secara
persamaan
matematik.
Selain
itu
ada
metode
kuantitatif
yang
tidak
menggunakan persamaan
matematis
dalam
sistem
estimasinya, namun
hanya
mengenali
pola
data
masukan
tersebut
yang
kemudian
secara
logis
dapat
menemukan persamaan
fungsi
matematiknya,
metode ini
merupakan
metode kuantitatif yang lain selain diatas, metode ini
menggunakan pola
data
yang
lalu
yang
diubah
menjadi suatu
fungsi
linear
maupun
non-linear
sebagai
fungsi
perhitungan dalam
metode
estimasinya.
Singkatnya, pada metode
ini
menggunakan Artificial Intelligence (AI) untuk
melakukan perhitungan dalam estimasinya. Pada estimasi dengan metode AI
tidak
terdapat
rumus
yang
menghitung hasil
estimasi
seperti
metode
sebelumnya, intinya hanya menggunakan data masukan / input untuk dikenali
polanya.
Metode
ini
akan
menghasilkan suatu
fungsi
sendiri
yang
dipakai
untuk
mengestimasikan data
yang
lain. Model-model
yang
termasuk
dalam
metode estimasi kuantitatif lainnya :
-
Expert Systems (ESs)
-
Artificial Neural Networks (ANNs)
-
Genetic Algorithms (GAs)
|
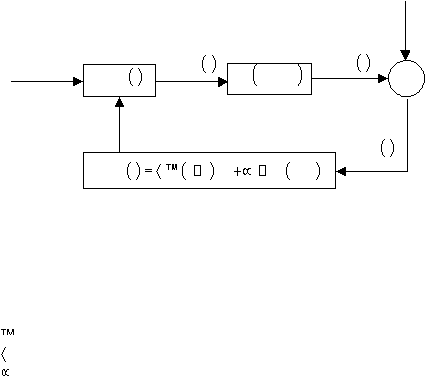 37
2.3.3 Estimasi
dengan Metode
ANN Backpropagation
Keunggulan yang utama dari
ANN adalah kemampuan untuk belajar dari contoh
yang
diberikan. Algoritma belajar
yang digunakan
adalah
algoritma
backpropagation.
Pada algoritma
ini
digunakan data
referensi dari luar (sebagai pengajar) dibandingkan
dengan data keluaran ANN, hasilnya berupa sinyal kesalahan / selisih error
yang
kemudian dilakukan proses perbaikan error
untuk mengubah nilai bobot di setiap
interkoneksi pada ANN.
Y
r
(referensi)
input
x
w
t
z
_
in
t
f
z
_
in
O
j
t
-
+
i ij
j
keterangan :
w
ij
t
t
1
x
j
w
ij
t
1
e
t
Sinyal
error
x
vektor input pelatihan
x
=
(x1
,
…x
i
)
o vektor output pelatihan
o = (o1,…,o
j
)
Y
vektor output target (referensi)
Y
=
(Y1,…,Yr)
j
porsi koreksi kesalahan untuk pengaturan bobot w
ij
konstanta laju belajar(learning rate)
konstanta momentum
w
ij
bobot koneksi antara neuron i ke neuron j
Gambar 2.18 Blok Diagram Algoritma Pembelajaran
Backpropagation
Gambar
di
atas
merupakan urutan
data
dalam
proses
pembelajaran
backpropagation
pada ANN. Di bawah ini merupakan contoh langkah dalam
membangun sistem estimasi dengan metode backpropagation.
|
 38
O1
I
1
1
w
13
I
3
w
03
O
0
w
13
O
1
O
1
3
1
e
3
I3
O3
w
34
I
4
w
34
O
3
w
24
O
2
O
1
4
1
e
I
4
O
4
O
0
w
03
I
0
0
I
3
3
O2
I
2
2
I
4
4
w
24
Neuron Bias
Input
Hidden
Output
Input
Output yang
Diharapkan (D
4
)
I
0
I1
I2
0
0
1
0,50
0
1
1
0,25
1
1
1
0,75
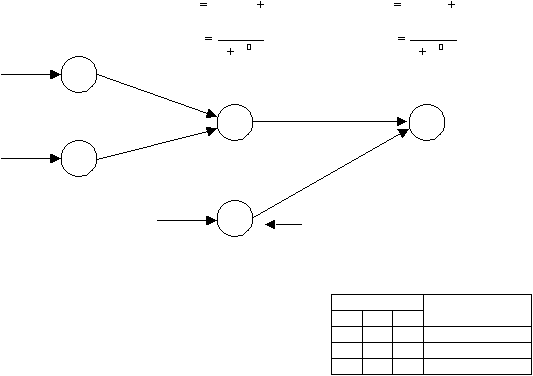
Gambar 2.19 ANN sederhana
2x1x1
Sumber
:
DeLurgio, 1998, p678
a. Tentukan
struktur jaringan
ANN berdasarkan
teori pendukung tentang
apa
yang
mempengaruhi variabel
dependen.
Sebagai
contoh,
struktur
jaringan
pada gambar
2.19.
Pada
umumnya,
hal
ini
menyangkut
pemilihan
variabel
input, jumlah
node
input, jumlah
hidden
layer dan
nodenya, fungsi aktivasi,
dan jumlah output node.
b. Bagi data input dan data output menjadi dua bagian, yang pertama digunakan
untuk melatih ANN, dan yang kedua digunakan untuk menguji jaringan
dengan contoh percobaan diluar sampel atau estimasi.
c. Menyekalakan semua variabel input dan output yang diharapkan dalam
rentang 0 sampai 1. Karena struktur matematis dari
jaringan, maka penting
|
|
39
untuk menyekalakan variabel antara 0 sampai 1. hal ini tidak mempengaruhi
pola aslinya atau nilainya.
d. Inisialisasi bobot dan mulai epoch pembelajaran menggunakan pasangan data
pelatihan (pada gambar 2.19 terdapat 3 data) dengan mengulangi langkah (e)
sampai (m). Satu epoch merupakan perhitungan dari error atau kesalahan dan
perubahan penyesuaian bobot dengan memproses pada semua pasangan data
pelatihan. Pada langkah ini nilai inisialisasi juga diberikan pada semua bobot
w
ij
dalam ANN. Nilai ini mempengaruhi kecepatan dan hasil RMS dari proses
pelatihan.
Kebanyakan
percobaan
menggunakan inisialisasi
bobot
dengan
semua 0, bilangan acak dengan rentang -1 sampai 1 atau dari -0,5 sampai 0,5.
e. Input dari pasangan data pelatihan yang sudah diskalakan diberikan ke node
1 dan 0 pada contoh gambar 2.19.
f.
Distribusikan input-input terskala ke setiap node
tersembunyi (dalam contoh
ini
hanya terdapat satu hidden node). Pada umumnya, tiap node tersembunyi
menerima
semua
variabel
input
terskala,
yang
menyebabkan pengolahan
semua input
pada beberapa
node. Pada
layer input, output O
j
sama dengan
nilai input I
j
.
O
0
=
I
0
O1
=
I1
g. Hitung dan jumlahkan input pada node penerima. Pada tiap node tersembunyi
(pada contoh
node 3), output dari input node (node 0 dan 1) akan dikalikan
dengan bobot lalu dijumlahkan, maka input ke node 3:
I
3
w
03
O
0
w
13
O
1
|
 40
h. Ubah input pada hidden node menjadi output. Pada setiap hidden node, input
terbobot diubah dengan fungsi aktivasi dalam rentang 0 sampai 1.
O
1
3
1
e
I3
i.
Hitung dan jumlahkan output pada hidden node sebagai input untuk output
node.
Ouput pada
hidden
node
O3 dan
pada
bias (pada
contoh
node
2)
dikalikan dengan bobot dan dijumlahkan.
I
4
w
24
O
2
w
34
O
3
j.
Ubah
input pada outut
node. Pada
node output 4,
input
terbobot
I
4
diubah
menjadi output O
4
dalam rentang 0 sampai 1. ini adalah hasil akhir dari ANN.
O
1
4
1
e
I
4
k. Hitung
error output.
Nilai
output
terskala O
4
dibandingakan dengan
nilai
output yang diharapkan D
4
,
dan error dihitung :
e
i
D
4
O
4
dimana i adalah nomor data pada pasangan data pelatihan (training set)
l.
Backpropagate error
untuk pengaturan bobot. Berdasarkan error
pada
langkah (k), bobot pada keseluruhan jaringan disesuaikan untuk mengecilkan
/
meminimisasi nilai error
RMS (Root Mean Square).
Ini merupakan proses
backpropagation
yang akan lebih diuraikan pada bab 3.
m.
Lanjutkan
epoch.
Ulangi
langkah
(e)
sampai
(l)
untuk
semua
pengamatan
pada
data
pasangan input
(pada
gambar
2.19
hanya
ada
3).
Setiap
data
pengamatan yang sudah dilalui dinamakan epoch. Saat semua data
|
 41
pengamatan telah diproses (contoh
:
satu epoch selesai),
lanjut ke
langkah
(n).
n. Hitung nilai error RMS tiap epoch. Jika nilai RMS ini sudah cukup rendah,
berhenti
dan
lanjut
ke
langkah
(o). Jika
RMS
tidak
cukup
rendah,
ulangi
langkah (e) ke (n) sampai kondisi berhenti tercapai.
e
2
RMS
i
nt
dimana :
RMS = perkiraan sisa error
e
i
=
error yang terjadi setiap pengamatan pada epoch terakhir
nt = jumlah data pelatihan / training set
o. Tentukan keabsahan data out-of-sample. Setelah melatih ANN menggunakan
satu set data input / pelatihan, sekarang ANN diuji dengan menggunakan data
pengujian (validate).
Pada
contoh,
gunakan
ANN
yang
telah
dilatih dengan
langkah (a)
sampai
(n)
untuk
mendapatkan output. Jika
RMS pada
contoh
out-of-sample
konsisten
dengan
RMS pada
pelatihan,
maka
model
tersebut
valid. Jika model tidak valid, ulangi percobaan setelah :
1) mencoba nilai inisial yang lain untuk bobot
2) desain ulang ANN (seperti melebihi/mengurangi layer/node)
3) mencoba metode ANN yang lain
4) jangan gunakan ANN sebagai metode untuk peramalan
|