|
BAB 2
LANDASAN TEORI
2.1
Algoritma
Algoritma adalah logika, metode dan tahapan (urutan) sistematis yang digunakan
untuk memecahkan suatu permasalahan (Wahono et al, 2003). Penemu algoritma adalah
seorang ahli
matematika dari
uzbekistan yang bernama Abu
Abdullah Muhammad Ibn
Musa al-Khwarizmi (770-840) (Wahono et al, 2003). Di literatur barat dia lebih terkenal
dengan sebutan Algorizm (Wahono et al, 2003). Panggilan inilah yang kemudian dipakai
untuk
menyebut
konsep
algorithm
yang
ditemukannya. Dalam
bahasa
Indonesia
kemudian disebutkan dengan algoritma.
Suatu
algoritma
yang
baik
harus memenuhi
beberapa
syarat
(Wahono
et
al,
2003), yaitu:
Susunan langkah yang dilaksanakan harus jelas.
Harus memiliki suatu titik awal dan minimal satu titik akhir.
Harus berhenti setelah beberapa langkah yang terhingga.
Setiap pernyataan harus jelas.
2.2
Steganografi
Selama
beratus-ratus
tahun, sejarah
membuktikan
bahwa
menjaga kerahasiaan
sebuah informasi
sangatlah
penting.
Berbagai
cara dan metode
guna menjaga
kerahasiaan telah ditempuh. Efeknya pun luar biasa.
Salah satu contohnya adalah metode kuno yang bernama steganografi.
Steganografi adalah teknik penyembunyian data rahasia ke dalam sebuah wadah (media)
6
|
|
7
sehingga data
yang
disembunyikan sulit dikenali oleh
indera
manusia
(Mdesian, 2005).
Pengamanan
dengan
menggunakan
steganografi
membuat
seolah-olah
pesan
rahasia
tidak
ada
atau
tidak
nampak, padahal
pesan tersebut ada.
Hanya saja
kita
tidak
sadar
bahwa ada pesan tersebut di sana.
Kata
steganografi (steganography)
berasal
dari
bahasa
Yunani
(Budi,
2002).
Steganos
artinya
'tersembunyi/terselubung',
dan
graphein,
'menulis'
sehingga
kurang
lebih artinya "menulis
(tulisan) terselubung" (Budi, 2002).
Teknik
ini meliputi banyak
sekali
metoda komunikasi untuk menyembunyikan pesan rahasia (Budi, 2002). Metoda
ini termasuk tinta yang tidak tampak,
microdots, pengaturan kata, tanda tangan digital,
jalur tersembunyi dan komunikasi spektrum lebar (Budi, 2002).
Steganografi
membutuhkan dua
properti,
yaitu
wadah
penampung
dan
data
rahasia
yang akan
disembunyikan (Mdesian, 2005). Steganografi digital
menggunakan
media
digital
sebagai
wadah
penampung,
misalnya
citra,
suara,
teks, dan
video.
Data
rahasia yang disembunyikan juga dapat berupa citra, suara, teks, atau video. Penggunaan
steganografi
antara
lain
bertujuan
untuk
menyamarkan eksistensi
(keberadaan)
data
rahasia sehingga sulit dideteksi, dan melindungi hak cipta suatu produk.
Steganografi
dapat
dikatakan
mempunyai hubungan
yang
erat
dengan
kriptografi. Akan
tetapi
metoda
ini
sangat
berbeda
dengan
kriptografi. Kriptografi
mengacak pesan
sehingga tidak
dimengerti,
sedangkan
steganografi
menyembunyikan
pesan
sehingga
tidak
terlihat
(Budi,
2002).
Pesan
dalam
cipherteks mungkin
akan
menimbulkan kecurigaan sedangkan pesan
yang dibuat dengan steganografi tidak akan.
Kedua
teknik
ini
dapat
digabungkan
untuk
mendapatkan
metoda
pengiriman
rahasia
yang sulit dilacak. Pertama pesan dienkrip, kemudian cipherteks disembunyikan dengan
cara steganografi pada
media
yang tampak tidak
mencurigakan (Budi, 2002). Cara ini
|
 8
sangat berguna jika
digunakan pada cara steganografi komputer karena banyak
format
file
digital
yang dapat
dijadikan
media
untuk
menyembunyikan
pesan. Format
yang
biasa digunakan diantaranya:
•
Format image: bitmap (bmp), gif, pcx, jpeg, dll.
•
Format audio: wav, voc, mp3, dll.
•
Format lain: teks file, html, pdf, dll.
Gambar 2.1. Komunikasi Steganografi Modern (Provos, 2003)
2.2.1
Sejarah
Steganografi
Teknik
steganografi sudah digunakan sejak
ribuan
tahun
yang
lalu. Saat
itu,
ada
seorang
Yunani
bernama
Demaratus yang
sedang
berada
Persia.
Dia
menjadi
saksi
bahwa
Raja
Persia
Xerxes
tengah
membangun
armada
perang
yang sangat besar. Armada perang tersebut akan digunakan Xerxes
menginvasi
|
|
9
Yunani dan Spartans. Selain akan datang dengan armada yang lengkap dan besar,
Xerxes
akan
menyerang secara
cepat
dan
tiba-tiba.
Demaratus sebagai
orang
Yunani
merasa
terpanggil
untuk
membela
bangsanya. Namun
tentu
saja
bukan
hal
yang
mudah
melarikan
diri
dari
wilayah
Persia
dan
melaporkan hal
ini ke
Yunani
dan
Spartan.
Resiko
hukuman
mati
pasti
didapat
seandainya dia
tertangkap (Adi, 2004).
Demaratus
lalu
mengambil
kulit
kayu
yang
mengandung lilin.
Dibersihkannya kayu
itu dari
lilin dan ditulisnya pesan di bawah kulit kayu
itu.
Setelah itu, kayu itu kembali diberi lilin sehingga pesannya menjadi tidak
terbaca.
Dikirimkanlah
kulit kayu
itu
ke
Yunani dan ketika
melewati
prajurit-
prajurit penjaga Persia, pesan itu tetap aman karena tidak
terbaca dan disangka
hanya
sebagai
kulit
kayu
biasa.
Akhirnya
Yunani
menerima
pesan
Demaratus
dan
segera
mempersiapkan bala
tentaranya
untuk
mengantisipasi invasi
Persia.
Dan
datanglah
waktu
yang
ditunggu-tunggu.
Waktu
itu
Persia
sangat
terkejut
karena
ternyata
Yunani
sudah
mengantisipasinya. Peperangan
tersebut
mengakibatkan kekalahan di pihak Persia (Adi, 2004).
Dalam
perkembangannya
teknik
steganografi
tidak
hanya
melalui
kulit
kayu
yang
mengandung lilin
tapi
juga
berkembang
melalui
tinta
khusus
yang
hanya
dapat
dibaca
dengan
penambahan cairan
khusus
(Adi,
2004).
Ada
juga
dengan trik berupa pesan biasa namun kata-kata tertentunya diberi tanda khusus,
sehingga penerima
pesan
tidak
membaca pesan
secara keseluruhan
tapi
hanya
pesan yang diberi tanda saja (Adi, 2004). Namun begitu, teknik steganografi ini
tidak
efisien.
Dalam beberapa
kasus
teknik
ini
mudah dipatahkan bagi
orang-
orang yang sudah berpengalaman (Adi, 2004).
|
|
10
Selain
itu ada beberapa kasus yang melibatkan penggunaan teknik
steganografi, diantaranya adalah:
•
Di jaman Histalaeus, pesan disembunyikan dengan cara membuat tato di
kepala
budak
yang
telah
digunduli. Kemudian
ditunggu
sampai
rambut
budak tersebut mulai tumbuh baru sang budak dikirim melalui penjagaan
musuh.
Ketika
diperiksa di
pintu
gerbang memang
sang
budak
tidak
membawa pesan apa-apa. Sesampainya di
tujuan baru
sang
budak
dicukur oleh sang penerima pesan untuk dapat dibaca pesannya
(Budi,
2005).
•
Bangsa
Romawi
mengenal steganografi
dengan
menggunakan
tinta tak-
tampak (invisible ink) untuk menuliskan pesan. Tinta tersebut dibuat dari
campuran sari
buah, susu, dan
cuka. Jika tinta digunakan untuk
menulis
maka tulisannya tidak tampak. Tulisan di atas kertas dapat dibaca dengan
cara memanaskan kertas tersebut (Budi, 2005)
.
•
Pesan rahasia dapat juga dikirimkan dengan mengirim surat pembaca ke
sebuah surat kabar. Huruf awal setiap kalimat (atau bisa juga setiap kata)
membentuk
pesan
yang
ingin diberikan.
Cara
lain
adalah dengan
membuat puisi dimana huruf awal dari setiap baris membentuk kata-kata
pesan sesungguhnya (Budi, 2005).
•
Hal
yang
sama
dapat
dilakukan
dengan
membuat
urutan
gambar
buah
dimana pesan
tersebut
merupakan
gabungan
dari
huruf
awal dari
nama
buah tersebut (Budi, 2005).
|
|
11
•
Pengarang
Dan Brown dalam buku
novelnya
yang
berjudul
“The
Da
Vinci
Code”
memberikan
pesan
di
sampul
bukunya
dengan
membuat
beberapa
huruf
dalam
cetakan
tebal
(bold).
Jika
disatukan, huruf-huruf
yang ditulis dalam cetakan tebal tersebut membuat berita yang dimaksud
(Budi, 2005).
•
Dalam peristiwa penyerangan
gedung WTC tanggal 11 September 2001
disebutkan oleh "pejabat pemerintah dan para ahli dari pemerintahan AS"
yang
tidak disebut
namanya bahwa
"para teroris
menyembunyikan peta-
peta dan foto-foto target dan juga perintah untuk aktivitas teroris di ruang
chat
sport,
bulletin
boards
porno
dan
web
site
lainnya". Isu
lainnya
menyebutkan
bahwa
teroris
menyembunyikan pesan-pesannya
dalam
gambar-gambar porno
di
web
site
tertentu.
Walaupun
demikian
sebenarnya
belum
ada
bukti
nyata
dari
pernyataan-pernyataan
tersebut
diatas (Budi, 2002).
Di
dunia digital,
steganografi
muncul
dalam
bentuk
digital
watermark,
yaitu tanda digital yang disisipkan dalam gambar (digital image) atau suara. Hak
cipta
(copyright)
dari
gambar
dapat
disisipkan
dengan
menggunakan
high-bit
dari pixel yang membentuk gambar tersebut (Budi, 2005). Gambar terlihat tidak
berbeda -
karena kemampuan, atau
lebih
tepatnya ketidakmampuan
mata
manusia
yang
tidak
dapat
membedakan satu
bit
saja,
akan
tetapi
sebenarnya
mengandung pesan-pesan tertentu.
|
 12
Gambar 2.2. Syndrome tanpa data sisipan
Gambar 2.3. Syndrome yang disisipkan Chapter 2 dari
”Harry
Potter and The Sorcerer’s Stone”
2.2.2
Kriteria
Steganografi yang Baik
Steganografi
yang dibahas
di
sini
adalah
penyembunyian data
di
dalam
citra digital. Meskipun demikian, penyembunyian data dapat juga dilakukan pada
wadah berupa suara digital, teks, ataupun video.
|
|
13
Penyembunyian data rahasia ke dalam citra digital akan mengubah
kualitas
citra tersebut. Kriteria
yang
harus diperhatikan
dalam
penyembunyian
data adalah:
1.
Mutu citra penampung tidak jauh berubah (Mdesian, 2005). Setelah
penambahan
data
rahasia,
citra hasil
steganografi masih
terlihat dengan
baik.
Pengamat
tidak
mengetahui kalau
di
dalam
citra
tersebut
terdapat
data rahasia.
2.
Data yang disembunyikan
harus tahan terhadap manipulasi yang
dilakukan pada
citra
penampung
(Mdesian, 2005).
Bila
pada
citra
dilakukan operasi pengolahan citra, maka data yang disembunyikan tidak
rusak.
3.
Data
yang disembunyikan
harus
dapat diungkapkan kembali (recovery)
(Mdesian, 2005).
2.2.3
Teknik
Penyembunyian
Data
Penyembunyian data
dilakukan dengan
mengganti
bit-bit
data
di
dalam
segmen
citra dengan
bit-bit data
rahasia
(Mdesian, 2005).
Salah
satu
metode
penyembunyian data yang sederhana adalah LSB Modification. Contoh:
11010010
LSB = Least Significant Bit
MSB = Most Siginificant Bit
MSB LSB
|
|
14
Bit
yang cocok
untuk diganti
adalah bit
LSB, sebab perubahan tersebut
hanya
mengubah
nilai
byte
satu
lebih
tinggi
atau
satu
lebih
rendah
dari
nilai
sebelumnya. Misalkan byte tersebut
menyatakan
warna keabuan
tertentu,
maka
perubahan satu bit LSB tidak mengubah warna keabuan
tersebut secara berarti.
Selain itu, mata manusia tidak dapat membedakan perubahan yang kecil.
Untuk
memperkuat teknik penyembunyian data, bit-bit data rahasia tidak
digunakan
mengganti
byte-byte yang
berurutan,
namun
dipilih
susunan
byte
secara
acak.
Misalnya
jika
terdapat
50
byte dan
6
bit
data
yang
akan
disembunyikan,
maka
maka
byte yang diganti bit
LSB-nya
dipilih
secara
acak,
misalkan byte nomor 36, 5, 21, 10, 18, 49.
Bilangan
acak
dibangkitkan dengan
pseudo-random-number-generator
(PRNG)
kriptografi
(Mdesian,
2005).
PRNG
kriptografi
sebenarnya adalah
algoritma
kriptografi
yang digunakan untuk
enkripsi. PRNG
dibangun dengan
algoritma
DES
(Data
Encryption Standard),
algoritma
hash
MD5,
dan
mode
kriptografi CFB (Chiper-Feedback Mode) (Mdesian, 2005). Tujuan dari enkripsi
adalah
menghasilkan sekumpulan
bilangan acak
yang
sama
untuk
setiap kunci
enkripsi
yang sama. Bilangan acak dihasilkan dengan
cara
memilih bit-bit dari
sebuah blok data hasil enkripsi.
2.2.4
Struktur File Image
Pada
komputer, suatu
gambar
adalah
array
dari
bilangan
yang
merepresentasikan intensitas terang pada point yang bervariasi
(pixel). Pixel ini
menghasilkan raster data gambar.
Suatu
gambar yang berdimensi 640
x
480
|
|
15
pixel dengan 256 warna (atau 8 bit per warna per pixel). akan berisi kira-kira 900
kilobyte data.
Gambar digital disimpan juga secara khusus di dalam file 24-bit atau 8-
bit.
Gambar
24-bit
menyediakan lebih
banyak
ruang
untuk
menyembunyikan
informasi;
bagaimanapun, ukurannya
dapat
menjadi
sangat
besar
(dengan
perkecualian
gambar JPEG).
Semua
variasi
warna
untuk
pixel
yang
diperoleh
dari
tiga
warna
dasar:
merah, hijau
dan
biru.
Setiap
warna
dasar
direpresentasikan dengan
1
byte;
gambar
24-bit
menggunakan 3
byte per
pixel
untuk
merepresentasikan
suatu
nilai
warna.
3
byte
ini
dapat
direpresentasikan
sebagai
nilai
hexadesimal, desimal,
dan
biner.
Dalam
banyak
halaman
Web,
warna
latar
belakang
direpresentasikan
dengan
bilangan
6
digit
hexadesimal,
yang
merupakan
tiga
ikatan
representasi warna
merah,
hijau
dan
biru.
Latar
belakang
putih akan
mempunyai nilai
FFFFFF: 100%
merah (FF), 100%
hijau
(FF)
dan
100%
biru
(FF).
Nilai
desimal-nya 255,255,255
dan
nilai
biner-nya
adalah 11111111, 11111111, 11111111.
Pixel
merepresentasikan kontribusi
dari
ukuran
file.
sebagai
contoh,
andaikan kita mempunyai gambar 24-bit dengan lebar 1,024 pixel dan panjang
768 pixel, yang merupakan resolusi umum untuk grafik beresolusi tinggi, gambar
tersebut akan mempunyai
lebih dari dua juta
pixel, dan akan menghasilkan file
berukuran
lebih
dari
2
Mbyte, yang
tentu
saja
menjadi
penyebab
utama
ketidakpopulerannya di internet.
|
|
16
2.2.5
Steganografi pada
file image
Seperti terlihat diatas bahwa file 8-bit merepresentasikan satu warna pada
satu pixel
menggunakan 1
byte data, yang
berarti
satu
warna
direpresentasikan
dengan skala 255, yang berarti pula bahwa file 24-bit yang menggunakan 3 byte
data memiliki skala sampai 16,581,375.
Steganografi
pada
file image
didasarkan
pada
kenyataan
bahwa
mata
manusia
tidak
mampu
membedakan
perubahan
warna
yang terlalu
kecil,
misalnya perubahan 1
nilai dalam skala 255,
yang berarti bahwa
mata
manusia
tidak
dapat
membedakan
warna
biru
yang
bernilai
255
dan
yang
bernilai
254.
Kenyataan ini kemudian dimanfaatkan untuk menyisipkan data rahasia ke dalam
tiap
warna per pixel sebanyak 1 bit dengan cara mengubah
LSB
(Least
Significant
Bit)
dari
nilai
warna dengan
data
yang
akan
disisipkan. Walaupun
demikian perubahan 1 bit tersebut berpengaruh terhadap ganjil-genap nilai warna
yang kemudian dapat dideteksi oleh serangan visual.
2.3
Kompresi JPEG
Beberapa
tahun
yang
lalu, JPEG (Joint Photographic Experts Group)
membuat
standar teknik kompresi internasional pertama untuk format file citra tidak bergerak (still
image)
yang
kini
digunakan
secara
luas.
Standar
yang
pada
waktu
itu
diajukan
oleh
JPEG
bertujuan
agar
bersifat
umum
sehingga
dapat
memenuhi kebutuhan berbagai
aplikasi yang bekerja dengan file image (Guillermito, 2004) .
Lebih lanjut akan dijelaskan secara singkat tahapan dalam proses kompresi yang
diajukan dalam standar JPEG.
|
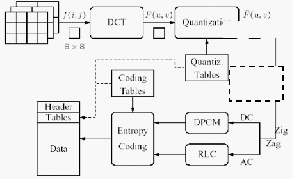 17
YCbCr
Kuantisasi
Tabel
Kuantisasi
Gambar 2.4. Tahap – tahap dalam kompresi JPEG (Leung, 2004)
2.3.1
Konversi
dari
RGB Menjadi YCbCr
Format warna
RGB
(Red,
Green,
Blue) adalah format yang digunakan
dalam
file bitmap, dimana
setiap pixel terdiri atas
komposisi tiga
variabel
yang
berisi
nilai
masing –
masing
warna. JPEG
mengubah
format
tersebut
menjadi
satu koefisien
luminance (nilai
Y
:
intensitas
warna keseluruhan pada
gambar)
yang
berupa
bentuk
hitam/putih dari
gambar,
dan
dua
koefisien
chrominance
(nilai
Cb
dan
Cr
:
Cb
merupakan
kombinasi warna
dari
Biru/Kuning dan
Cr
merupakan
kombinasi
warna
dari
Merah/Hijau) melalui
rumus
berikut
(Anonymous, 2004):
|
 18
Gambar 2.5. Rumus Perkalian Matriks untuk mengubah RGB menjadi YcbCr
(Anonymous, 2004)
Tujuan
dari
pengubahan
ini
karena
mata
manusia
pada
dasarnya
lebih
peka
terhadap
intensitas
(luminance) dibanding
terhadap
warna
(chrominance)
(Guillermito, 2004), sehingga untuk alasan penghematan ruang, beberapa metode
JPEG mampu menggunakan hanya satu pixel warna untuk mewakili empat pixel
lainnya tanpa
menyebabkan perubahan
yang berarti
pada
gambar.
Berikut
ini
contoh dari gambar yang dikonversi menjadi YCbCr :
Red
Green
Blue
Y
(Luminance)
Cr
(Chrominance)
Cb
(Chrominance)
Gambar 2.6. Perubahan dari format RGB menjadi YcbCr (Anonymous, 2004)
2.3.2
DCT (Discrete Cosine
Transform)
DCT
merupakan fungsi
yang digunakan
untuk
mengubah
nilai
YCbCr
pada setiap pixel
menjadi
koefisien
DCT.
Pada
bulan
Juni
1987,
JPEG
melakukan studi terhadap 12
proposal
yang
membahas tentang kualitas gambar
yang melalui proses DCT, dan pada bulan Januari 1988 ditemukan bahwa
|
 19
proposal
yang
menggunakan 8
x
8
DCT,
telah
menghasilkan gambar dengan
kualitas
paling
baik,
namun
demikian
penggunaan teknik
ini
tetap
memiliki
kekurangan yaitu
efek
isolasi
antara
blok –
blok pixel yang
saling berdekatan,
inilah alasan
mengapa gambar
JPEG yang dikompres dengan
rasio
yang tinggi
akan terlihat terkotak – kotak (Wallace, 2004).
Gambar 2.7. JPEG image dengan rasio kompresi tinggi (Leung, 2004)
Pada
tahap
ini
keseluruhan gambar
pertama
–
tama
dibagi
menjadi
berukuran 8 x 8 pixel,
kemudian blok – blok pixel tersebut satu persatu diproses
menjadi 64 koefisien DCT melalui rumus berikut :
Jika
Sebaliknya
Gambar 2.8. Persamaan DCT (Leung, 2004)
Tujuan dari tahap ini adalah karena pada gambar “alami” nilai koefisien
DCT rata – rata berukuran amat kecil dan banyak yang dapat dihilangkan dengan
|
 20
tetap
mempertahankan
keakuratan
gambar.
Pada
gambar
berikut
akan
diperlihatkan perubahan dari nilai warna menjadi koefisien DCT :
Gambar 2.9. Perubahan nilai warna menjadi koefisien DCT (Guillermito, 2004)
Koefisien
DCT
pertama
dari
tiap
blok
memiliki nilai
paling
besar
dibanding
63
koefisien
lainnya
karena
merupakan nilai
rata
–
rata
dari
keseluruhan blok,
koefisien pertama
ini
disebut
dengan koefisien
DC
dan 63
koefisien
lainnya
disebut
dengan
koefisien AC.
Jika
blok
DCT
tersebut
dikembalikan melalui
tahap
Inverse
DCT,
maka
akan
didapat
kembali
64
nilai
pixel yang mengalami sedikit perubahan sehingga tahap ini disebut sebagai tahap
lossy.
2.3.3
Kuantisasi
Kuantisasi
juga
merupakan
tahap
lossy dalam
kompresi
JPEG
karena
kuantisasi sendiri
berarti
pembagian
antara
setiap
koefisien
DCT dengan
koefisien kuantisasi dan pembulatan sesudahnya (Guillermito, 2004). Berikut ini
adalah tabel kuantisasi
untuk koefisien luminance dan chrominance
yang sudah
ditetapkan sebagai
standar oleh
JPEG
dengan
rasio
kompresi paling
baik
dan
penurunan kualitas gambar paling rendah :
|
 21
Gambar
2.10. Tabel Kuantisasi Luminance dan Tabel Kuantisasi
Chrominance(Leung, 2004)
Tabel
koefisien
ini
sendiri
pada
implementasinya akan
berubah
sesuai
rasio kompresi yang ditentukan oleh user, oleh karena itu tabel tersebut disimpan
di awal file gambar dan akan digunakan kembali untuk mengembalikan koefisien
frekuensi
menjadi
koefisien
DCT
(Inverse
Quantization). Semakin
tinggi
rasio
kompresi pada gambar maka semakin tinggi pula nilai pada tabel kuantisasi dan
kualitas gambarpun akan semakin rendah.
Keragaman warna pada satu blok ternyata juga sangat berpengaruh pada
penurunan
kualitas
yang
disebabkan oleh
dua
tahap
lossy tersebut
(DCT
dan
Kuantisasi)
(Leung,
2004).
Pada
dua
gambar
berikut akan
diperlihatkan
perbedaan pada blok
yang memiliki warna variatif dengan
blok
yang memiliki
warna cenderung sama :
|
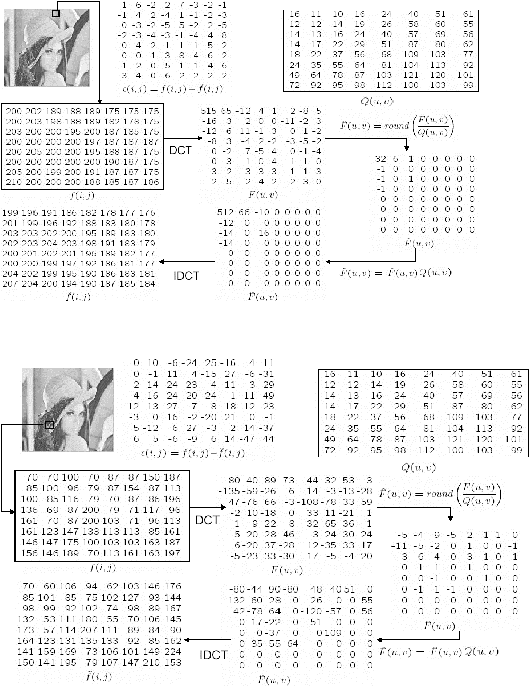 22
Kesalahan
Tabel
Kuantisasi
Kuantisasi
Inverse Kuantisasi
Gambar 2.11. Perubahan pada blok dengan warna cenderung seragam (Leung, 2004)
Kesalahan
Tabel Kuantisasi
Kuantisasi
Inverse Kuantisasi
Gambar 2.12. Perubahan pada blok dengan warna cenderung variarif (Leung, 2004)
2.3.4
DPCM (Differential
Pulse Code
Modulation)
Pada tahap ini, koefisien DC dari tiap – tiap blok disatukan untuk
memasuki tahap Entropy Coding, teknik DPCM digunakan karena
nilai – nilai
|
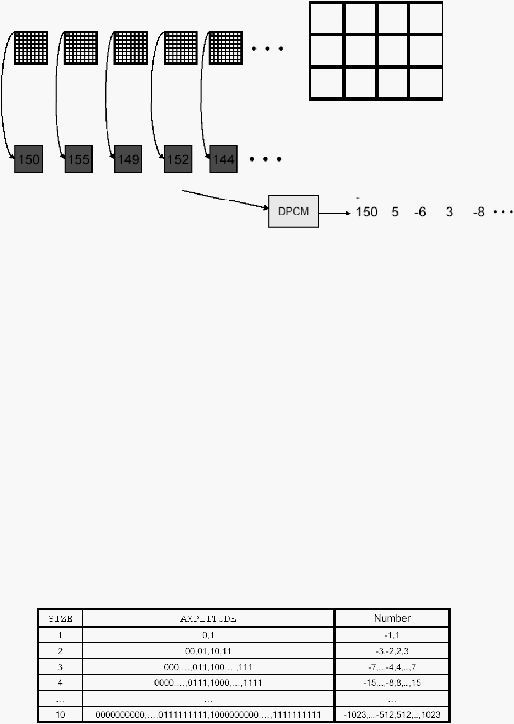 23
koefisien DC antara blok satu dengan lainnya tidak jauh berbeda (Leung, 2004).
Berikut ini akan digambarkan lebih rinci :
Blok
1
Blok
5
Blok
2
Blok
3
Blok
4
Koefisien
Koefisien Koefisien
Koefisien
Koefisien
DC
Blok 1
DC
Blok 2
DC
Blok 3
DC
Blok 4
DC
Blok 5
Gambar 2.13. Proses DPCM (Leung, 2004)
2.3.4.1 Entropy coding pada
Koefisien DC
Koefisien DC
yang
sudah
melalui
tahap
DPCM
kemudian
dikompresi
menggunakan kompresi
huffman, sebelumnya deretan
angka
DPCM
tersebut
dirubah
bentuknya menjadi
pasangan
–
pasangan
(size,amplitude), dimana
size
menyatakan
jumlah
bit
yang
diperlukan
untuk merepresentasikan angka DPCM dan amplitude menyatakan angka
tersebut dalam bentuk
bit
(Leung, 2004).
Tabel
berikut
menyatakan
hubungan antara size, amplitude dan angka :
Gambar 2.14. Hubungan size, amplitude dan angka (Leung, 2004)
|
 24
Seperti
yang
terlihat
diatas bahwa
amplitude dapat
menyatakan
nilai absolut dari angka DPCM, yang berarti amplitude dapat berisi angka
positif
maupun
negatif
(dalam
bentuk
komplemen satu dari
positifnya).
Dalam
tahap
Entropy coding
yang
mengalami kompresi
huffman
hanya
size-nya saja, karena perubahan pada size tidak terlalu jauh sedangkan
amplitude sangat bervariasi. Lebih lanjut dijelaskan pada gambar berikut
Gambar 2.15. Entropy coding pada koefisien DC (Leung, 2004)
2.3.5
RLC (Run Length
Coding)
Pada
tahap
ini
koefisien AC
dari
tiap
–
tiap
blok
disatukan untuk
memasuki tahap Entropy Encoding, teknik
RLC digunakan karena nilai –
nilai
koefisien AC memiliki banyak nilai berurut, yaitu nilai nol yang urutannya rata –
rata
panjang
(Guillermito,
2004).
Berikut
ini
contoh
dari
blok
koefisien
DCT
yang telah dikuantisasi :
Gambar 2.16. Koefisien DC ter-Kuantisasi (Leung, 2004)
|
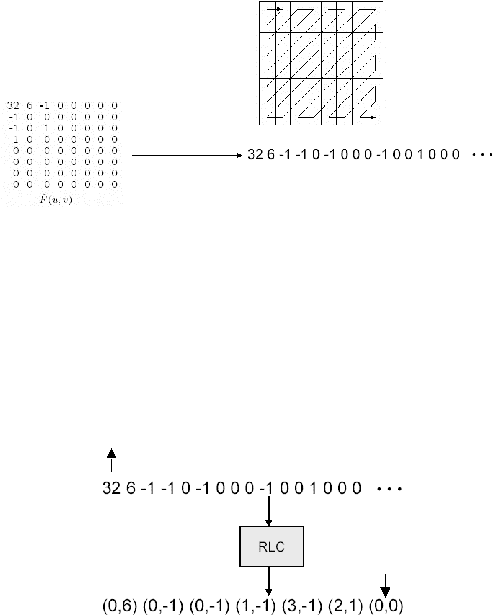 25
Pada gambar diatas terlihat bahwa nilai – nilai nol cenderung berdekatan
dari kiri/atas ke kanan/bawah, oleh karena
itu
untuk
membuat semakin banyak
nilai 0 yang berurutan maka urutan koefisien diubah dalam bentuk zig - zag yang
lebih rinci dijelaskan pada gambar berikut (Leung, 2004):
Koefisien DCT ter-Kuantisasi
Koefisien AC
Gambar 2.17. Koefisien AC dalam urutan zig – zag (Leung, 2004)
Setelah
diubah
urutannya, nilai
–
nilai
AC
tersebut
kemudian
diubah
bentuknya
menjadi pasangan
–
pasangan (runlength,
value), dimana
runlength
adalah
jumlah
0
yang
berurutan dan
value
adalah
nilai
non
-
0
yang
terletak
sesudahnya. Dalam hal ini koefisien DC tidak diperhitungkan dalam RLC.
Koefisien DC
Tidak diproses
Akhir Blok
Gambar 2.18. Proses RLC (Leung, 2004)
|
 26
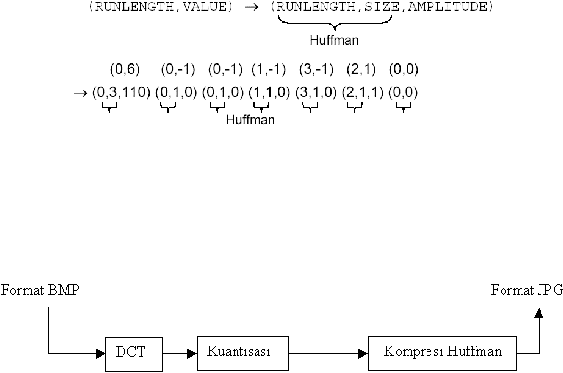
2.3.5.1 Entropy coding pada
koefisien AC
Koefisien AC
yang
sudah
melalui
tahap
RLC
juga
kemudian
dikompresi
menggunakan kompresi
huffman,
sebelumnya
deretan
pasangan –
pasangan (runlength,
value)
tersebut
dirubah
bentuknya
menjadi
pasangan
–
pasangan
(runlength,
size, value),
sama
seperti
koefisien DC (Leung,
2004).
Dalam
hal
ini
yang
mengalami kompressi
huffman
hanya
runlength
dan
size-nya saja
untuk
alasan
yang
sama
dengan koefisien DC. Lebih lanjut dijelaskan dalam gambar berikut :
Gambar 2.19. Entropy coding pada koefisien AC (Leung, 2004)
2.4
Steganografi pada
JPEG
Secara umum proses kompresi diatas dapat digambarkan seperti dibawah ini :
Gambar 2.20. Proses Kompresi secara umum (Westfeld, 2004)
Seperti dijelaskan diatas bahwa tahap DCT dan kuantisasi merupakan tahap lossy
yang menyebabkan turunnya kualitas pada gambar namun tidak demikian halnya pada
|
 27
tahap Huffman. Kondisi
ini kemudian dimanfaatkan untuk
melakukan penyisipan data
dengan melihat bahwa koefisien – koefisien DCT yang ditransfer antara tahap kuantisasi
dan
Huffman
dapat
dikembalikan persis
ke
bentuk
semula
melalui
proses dekompresi
karena tidak melalui tahap lossy.
Koefisien
DCT
tersebut
pun
memiliki
karakteristik sendiri,
yang
harus
tetap
dijaga agar tidak menimbulkan kecurigaan pada pendeteksian steganografi, dengan kata
lain bahwa algoritma steganografi yang baik dapat mempertahankan sifat – sifat
yang
dimiliki koefisien DCT. Lebih lanjut dijelaskan dalam gambar berikut :
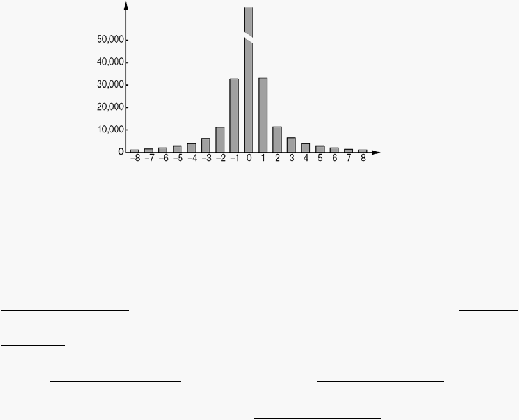
Gambar 2.21. Frekuensi Kemunculan Koefisien DCT (Westfeld, 2004)
Dari gambar diatas dapat kemudian disimpulkan beberapa karakteristik :
1. Jumlah kemunculan berkurang dengan meningkatnya nilai absolut dari koefisien
frekuensi.
2. selisih jumlah kemunculan antara antara dua koefisien frekuensi berkurang
dengan meningkatnya nilai absolut dari koefisien frekuensi.
Steganografi menyisipkan data steganografi dengan mengubah nilai – nilai dari
koefisien frekuensi tersebut.
|
|
28
2.5
Pendeteksian Terhadap
Steganografi ( Steganalysis )
Berbagai
usaha telah dilakukan
untuk
mendeteksi keberadaan data tersembunyi
dalam file image untuk alasan keamanan oleh berbagai pihak. Seperti sempat terjadi di
Amerika
pada
sekitar
bulan
Februari 2001, sebuah media
lokal
USA TODAY
yang
memuat berita tentang steganografi yang digunakan oleh
teroris
untuk berkomunikasi,
sempat
membuat
kepanikan
massal
dan
memaksa
pemerintah mendanai
sebuah
perusahaan
teknologi
informasi,
WetStone
Technologies, untuk
menyelidiki
kemungkinan penyisipan data rahasia
dalam file –
file image
yang
terdapat pada
situs
pelelangan yang sangat terkenal yaitu eBay.com.
WetStone
akhirnya mengumumkan hasil
penyelidikannya bahwa
mereka
hanya
menemukan sekitar 1 diantara 100.000 gambar yang dicurigai memiliki data rahasia, dan
sekitar 1 diantara 1 – 2 juta
gambar
yang diyakini
memiliki data rahasia,
jumlah
yang
terlalu kecil untuk menjadi ancaman besar dan tidak sebanding dengan kepanikan yang
dialami
masyarakat, karena
memang,
pada
sekitar
bulan
Maret
2004
USA
TODAY
mengakui bahwa
wartawan
yang
memuat
berita tersebut
memalsukan
hampir seluruh
ceritanya dan kemudian memberhentikannya dengan tidak hormat
2.5.1
Visual attack
Visual attack adalah teknik pertama yang pernah dipublikasikan terhadap
file
image
untuk
mendeteksi
keberadaan
data
tersebut.
Visual attack
memungkinkan
mata
manusia
melihat
keberadaan
data
tersembunyi
dalam
file
image karena data tersembunyi tersebut menimpa struktur gambar secara visual.
File
image pada umumnya memiliki nilai
warna yang sama pada pixel-
pixel yang berdekatan. Penyisipan data rahasia yang memiliki bit tidak beraturan
|
 29
akan
menyebabkan
pixel-pixel
yang
saling
berdekatan
tersebut
memiliki
nilai
warna
yang bervariasi
dalam
bentuk
ganjil-genap
walaupun
tidak
terlihat
oleh
manusia
karena
perbedaanya terlalu
kecil.
Teknik
visual
attack
memperbesar
perbedaan tersebut
sehingga
terlihat
oleh
mata
manusia
dengan
cara
membuat
nilai
warna
ganjil
menjadi
ekstrim
maksimum (255)
dan
nilai
warna
genap
menjadi ekstrim minimum (0) sehingga setiap pixel hanya memiliki nilai warna 0
atau 255 saja (Guillermito, 2003). berikut ini diberikan contoh :
Sisipan Data
File Asli
Visual attack
Keterangan
Tidak disisipkan apapun
Terlihat bahwa warna
putih tidak mengalami
perubahan, warna putih
yang saling berdekatan
cenderung memiliki
LSB yang sama (semua
pixelnya memiliki nilai
warna 255)
Disisipkan 1kB data
File image yang
disisipkan data terlihat
penuh dibawah, ini
terjadi Karena nilai
warna pertama pada
struktur file BMP adalah
pixel terakhir pada
gambar.
|
 30
Disisipkan 5 kB data
Data terlihat semakin
penuh oleh data sisipan
Gambar 2.22. Perbandingan Image pada Visual Attack (Guillermito, 2003)
2.5.2 Analisis
Histogram DCT
Seperti
telah
dijelaskan
sebelumnya,
pada
umumnya
pixel –
pixel
yang
berdekatan pada file image memiliki nilai LSB yang sama, dengan kata lain pixel
–
pixel yang
berdekatan
umumnya
memiliki
nilai-nilai
warna
yang
sama,
kemudian setelah penyisipan data LSB dari nilai – nilai warna tersebut berubah
menjadi
sangat bervariasi dengan perbedaan yang
sangat kecil yaitu
hanya satu
nilai
warna.
Menurut
Guillermito (Anonymous,
2004)
LSB
dari
data
yang
disisipkan
tersebut,
pada
setiap
kasus,
ternyata
memiliki
distribusi
yang
mendekati 50/50, yang berarti pada data yang disisipkan, LSB bernilai 1
memiliki jumlah yang hampir sama dengan LSB bernilai 0 (Guillermito, 2003).
Pada algoritma JSteg,
yang
mengalami perubahan bukanlah nilai –
nilai
warna
pada
pixel melainkan
koefisien
DCT
pada
saat
kompresi,
seperti
telah
dijelaskan bahwa JSteg menyisipkan LSB data rahasia pada koefisien DCT. Hal
tersebut memberikan pengaruh yang sama seperti halnya nilai – nilai warna pada
|
 31
BMP, koefisien DCT yang memiliki LSB bernilai 1 juga memiliki jumlah yang
hampir sama dengan LSB bernilai 0.
Westfeld dan Pfitzmann (Westfeld, 2003) kemudian
merumuskan suatu
teknik pendeteksian berdasarkan kenyataan tersebut. Mereka menyebut pasangan
LSB 0 dan 1 yang hampir sama jumlahnya dengan Pair of Values (PoV).
0010
PoV pertama,
koefisien DCT bernilai 2 dan 3 memiliki jumlah hampir sama.
0011
0100
PoV kedua,
koefisien DCT bernilai 4 dan 5 memiliki jumlah hampir sama.
0101
0110
PoV ketiga,
koefisien DCT bernilai 6 dan 7 memiliki jumlah hampir sama.
0111
1000
PoV keempat,
koefisien DCT bernilai 8 dan 9 memiliki jumlah hampir sama.
1001
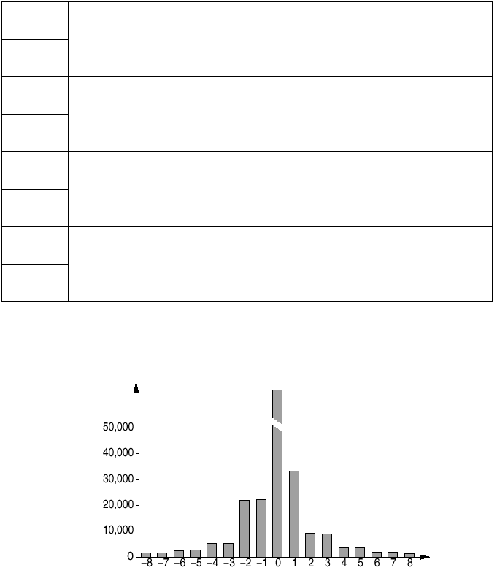
Lebih lanjut dalam histogram koefisien DCT berikut :
Gambar 2.23. Koefisien DCT file image setelah disisipi data oleh Jsteg
(Westfeld, 2003)
|
|
32
Seperti
terlihat
diatas
jumlah
koefisien DCT
bernilai
1
dan
0
tidak
mengalami
perubahan,
ini disebabkan
karena
0 dan 1 merupakan PoV
(pasangan), karena
koefisien
DCT
bernilai
0
tidak
bisa
digunakan dalam
steganografi (oleh algoritma apapun)
maka 1 pun
menjadi tidak bisa digunakan
(Westfeld, 2004).
2.6
Algoritma
Steganografi pada
File JPEG
2.6.1
Algoritma
JSteg
JSteg
dibuat
oleh
Derek
Upham
dan
merupakan algoritma
steganografi pertama yang dipublikasikan secara
umum untuk
format JPEG.
Algoritma
JSteg
menyisipkan data
ke
dalam
koefisien
DCT
JPEG
secara
sekuensial dangan cara mengganti
LSB (Least Significant Bit) dengan
LSB
dari
data
yang
akan disisipkan.
Algoritma
ini
tidak
menggunakan password
sehingga siapapun yang mengetahui algoritma JSteg dapat memperoleh data
rahasia tersebut (Provos, 2003).
File JPEG,
dalam
hal
ini
yang
menggunakan algoritma steganografi
apapun,
tidak
terdeteksi
oleh
visual
attack
karena
tidak
mengubah
struktur
visual (Provos, 2003)
melainkan koefisien DCT (lebih lanjut dijelaskan pada
kompresi
JPEG)
dan
cenderung berukuran jauh
lebih
kecil
dari
BMP,
oleh
karena
itu
sangat
populer
di
internet dan
mengalami
perkembangan pesat
dalam hal algoritma steganografi.
JSteg menyisipkan data
ke
dalam koefisien
DCT yang tidak bernilai
nol,
sama
seperti
algoritma
steganografi JPEG
pada
umumnya,
tanpa
mempertahankan sifat-sifat koefisien DCT (lebih lanjut dijelaskan pada
|
|
33
kompresi JPEG). Hal tersebut menyebabkan
algoritma ini sangat rentan
terdeteksi melalui pengamatan histogram DCT.
2.6.2
Perkembangan Algoritma
F5
Algoritma
F5
dikembangkan secara
bertahap
dari
bentuknya
yang
pertama yaitu algoritma F3,
namun dalam
implementasinya hanya algoritma
F5 yang digunakan dalam aplikasi. Algoritma F3 dan F4
yang
akan
dijelaskan
berikut
hanya
dimaksudkan
untuk
memperjelas proses
perkembangannya.
2.6.2.1
Algoritma
F3
Algoritma
F3
mengatasi
kelemahan pada
JSteg
namun
belum cukup sempurna
untuk diimplementasikan
menjadi sebuah
aplikasi, untuk selanjutnya akan dibahas perkembangan algoritma
F3 dan proses penyempurnaanya sampai menjadi F5.
F3 memiliki 2 sifat yang membedakannya dari Algoritma
JSTEG :
1.
Tidak
seperti
JSTEG
yang
menggunakan algoritma
LSB
(menimpa LSB dari bit host dengan bit steganografi),
F3
hanya
melakukan
pengurangan terhadap
nilai
absolut
dari
koefisien DCT ketika LSB dari bit host tidak sama dengan bit
steganografi (Westfeld,
2004).
Hal
ini
dilakukan
untuk
mengatasi kelemahan JSTEG yang merusak sifat –
sifat
|
 34
histogram
DCT
(Westfeld, 2004).
Lebih
rinci
dijelaskan
dalam diagram berikut :
Koefisien DCT host
Data steganografi
Koefisien DCT steganogram
Data steganografi
Tidak
Digunakan
Gambar 2.24. Penyisipan data steganografi pada F3 (Westfeld, 2004)
2. Koefisien DCT yang bernilai 1 atau -1 mengalami penyusutan
dalam
jumlah
besar.
F3
otomatis
memproses
koefisien lain
ketika menghasilkan nilai 0 karena penerima pesan tidak dapat
membedakan
antara
nilai
0
yang
memang
tidak
digunakan
oleh
F3
dengan
nilai
0
yang
dihasilkan
oleh
pengurangan
1
atau
-1.
Penyusutan terjadi ketika F3
terus
menerus
mengurangi koefisien yang bernilai 1 atau -1 menjadi 0 sambil
beralih ke koefisien berikutnya.
3.
Terjadi
Peningkatan koefisien
jumlah
genap
sehingga
melebihi jumlah
koefisien ganjil
dalam
tingkat
yang
mencolok. Hal
ini
terjadi
karena
pemrosesan
koefisien
lain
yang
selalu
menghasilkan
nilai
genap
setelah
terjadi
penyusutan
yang
hanya
mungkin terjadi
ketika
data
|
 35
steganografi bernilai 0, oleh karena itu F3 tidak efektif untuk
data steganografi
yang
memiliki lebih
banyak
nilai
0,
lebih
rinci dijelaskan dalam diagram berikut :
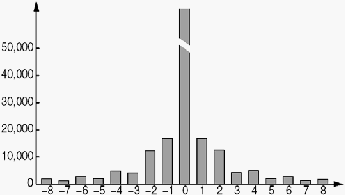
4.
Jumlah Kemunculan
Koefisien DCT
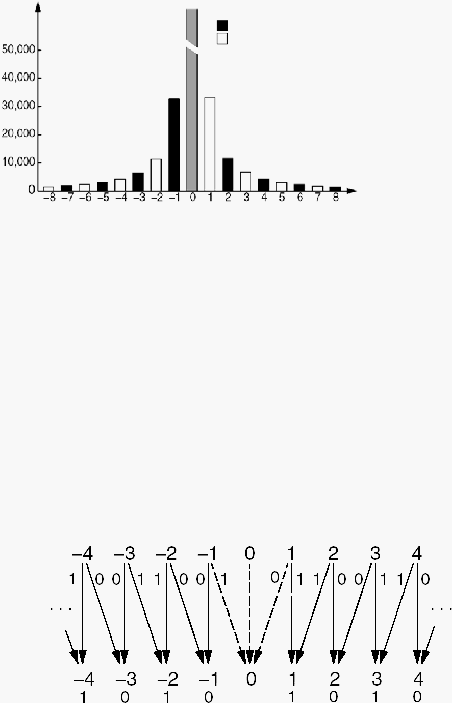
Gambar 2.25. Jumlah kemunculan koefisien DCT pada image yang disisipkan pesan
dengan algoritma F3 (Westfeld, 2004)
2.6.2.2
Algoritma
F4
F4
mengatasi
kelemahan F3
dengan
cara
memetakan
koefisien DCT
menjadi
4
bagian
:
koefisien negatif
ganjil
dan
positif
genap
memiliki
data
steganografi bernilai
0,
sedangkan
koefisien negatif
genap
dan
positif
ganjil
memiliki data
steganografi bernilai
1
(Westfeld,
2004).
Lebih
rinci
dijelaskan
dalan diagram berikut :
|
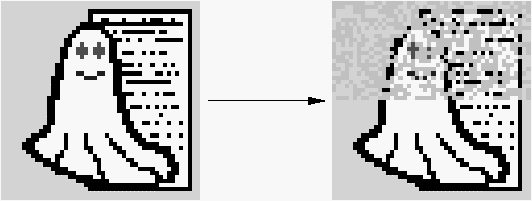
 36
Jumlah Kemunculan
Data steganografi 0
Data steganografi 1
Koefisien DCT
Gambar 2.26. Jumlah kemunculan koefisien DCT pada image yang disisipkan pesan
dengan algoritma F4 (Westfeld, 2004)
Dalam
diagram
diatas
terlihat
bahwa
penyusutan dapat
dikurangi karena
koefisien bernilai
absolut
1
tidak
hanya
mengalami pengurangan oleh data steganografi 0 saja namun
dapat
juga oleh data
steganografi
1. Nilai koefisien
genap pun
tidak lagi melonjak karena pengurangan setelah penyusutan dapat
terjadi tidak hanya pada koefisien ganjil namun terhadap koefisien
genap juga.
Koefisien DCT host
Data steganografi
Koefisien DCT steganogram
Data steganografi
Tidak
Digunakan
Gambar 2.27. Penyisipan data steganografi pada F4
(Westfeld, 2004)
|
|
37
F4
juga
membentuk diagram koefisien
dengan
menjaga
sifat
-
sifat
pada
diagram aslinya,
misalkan
kita
memiliki
dua
variabel
X,Y
yang
masing
–
masing
mewakili nilai
koefisien
sebelum
dan
sesudah
F4
menyisipkan data
steganografi
(Westfeld,
2004).
P(X
=
x)
untuk
mewakili
kofisien
frekuensi
yang
dihasilkan
JPEG
encoder,
dan
P(Y =
y)
untuk
mewakili
koefisien DCT
yang
dihasilkan F4
(Westfeld,
2004).
Kita dapat
menuliskan dua sifat berikut berdasarkan diagram :
P(X = 1) > P(X = 2) > P(X = 3) > P(X = 4) (1)
P(X = 1) - P(X = 2) > P(X = 2) - P(X = 3) > P(X = 3) - P(X = 4) (2)
Jika
data
steganografi disebarkan
secara
seragam
maka
didapat :
P(Y = 1) = ½ P(X = 1) + ½ P(X = 2) (3)
P(Y = 2) = ½ P(X = 2) + ½ P(X = 3) (4)
P(Y = 3) = ½ P(X = 3) + ½ P(X = 4) (5)
Dengan pengurangan persamaan diatas maka didapat :
P(Y = 1) – P(Y = 2) = ½ P(X = 1) - ½ P(X = 3)
(7)
P(Y = 2) – P(Y = 3) = ½ P(X = 2) - ½ P(X = 4)
(8)
Dari persamaan (1) kita dapat simpulkan bahwa :
P(Y = 1) > P(Y = 2) >
P(Y = 3) > P(Y = 4)
(9)
Jika kita tambahkan P(X = 2) – P(X = 3) ke persamaan (2)
maka akan didapat :
P(X = 1) - P(X = 3) > P(X = 2) - P(X = 4) > P(X = 3) - P(X = 5) (10)
|
 38
Sehingga :
½ P(X = 1) - ½ P(X = 3) > ½ P(X = 2) - ½ P(X = 4)
(11)
P(Y = 1) – P(Y = 2) >
P(Y = 2) – P(Y = 3)
(12)
Dari
persamaan (12)
dapat
terlihat
bahwa
sifat
diagram
koefisien
sebelum dan
sesudah
peyisipan
data
oleh
F4
tidak
mengalami perubahan.
Diagram
berikut
akan
menggambarkan lebih
rinci
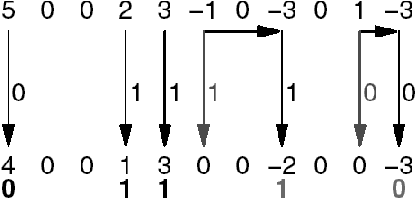
bagaimana F4 memasukkan data steganografi bernilai ”01110” :
Gambar 2.28. Penyisipan data steganografi pada F3 (per bit)
(Westfeld, 2004)
Dapat
terlihat
bahwa
bit 5 mengalami
pengurangan
menjadi
4
karena
data
steganografi yang
disisipkan
bernilai
0,
sedangkan penyisipan koefisien -1 atau
1
akan
menyebabkan F4
secara otomatis mencari koefisien lain.
|
 39
2.6.2.3
Algoritma
F5
Dalam banyak
kasus,
data
steganografi tidak
menempati
seluruh kapasitas
yang disediakan oleh
steganogram, oleh
karena
itu F4 hanya
menyisipkan data di
awal
file dan data steganografi
terpusat hanya
di awal
file (Westfeld, 2004), seperti ditunjukkan
gambar berikut :
Gambar 2.29. Penyebaran Data yang disisipkan pada image dengan algoritma F4
(Westfeld, 2004)
Algoritma
F5
menyisipkan data
tidak
dengan
mengubah
LSB
(Least
Significant
Bit)
melainkan
melakukan
pengurangan
(decrement)
terhadap
koefisien
DCT,
hal
ini
dilakukan
agar
steganogram (image yang disisipi oleh steganografi) tidak
merusak sifat-sifat histogram DCT.
|
 40
Gambar 2.30. Tahapan kompresi file JPEG (Westfeld, 2004)
2.6.2.3.1
Permutative
Straddling pada
F5
F5
menggunakan mekanisme
straddling
yang
fungsinya mengacak letak
semua
koefisien
DCT
terlebih
dahulu
dengan
menggunakan
permutasi
(Westfeld,
2004).
F5 kemudian menyisipkan data steganografi menurut urutan
permutasi
tersebut
dan
mengirimkannya kepada
tahap
Huffman
dalam
urutan
sebenarnya sesudah
penyisipan
selesai,
urutan
permutasi
itu
sendiri
didapat
dari
password
yang
dimasukkan
oleh
user.
Dengan password
yang
benar,
user
lain
akan mendapatkan urutan permutasinya dan
dapat
membaca data yang tersembunyi dengan benar.
Java
menyediakan
kelas
SecureRandom yang
memiliki kemampuan
untuk menghasilkan bilangan
random
antara –128 sampai 127 berdasarkan password
user,
namun
pada
kenyataannya image
JPEG
berukuran
relatif
kecil
(16Bit, 283 x 212) saja dapat memiliki ratusan ribu koefisien
DCT, jumlah koefisien DCT
ini selain ditentukan oleh
ukuran
image dan rasio kompresi ditentukan juga oleh
|
|
41
jumlah kombinasi
warna. Untuk
mendapatkan jumlah
yang
mencukupi kebutuhan
aplikasi
akan
merandom
32
bit
bilangan, yaitu 4 bilangan yang
masing-masing berjumlah 8
bit
yang
di-random
bersamaan, sehingga
menghasilkan
bilangan random antara -4.294.967.296 sampai
4.294.967.295 :
c6 = d[10] x Math.pow(2,24) + d(Wallace,
2004) x Math.pow(2,16) + d(Westfeld,
2003)
x
Math.pow(2,8)
+ d(Westfeld,
2004);
Jumlah
bilangan random
diatas
ternyata
dapat
mencukupi
kebutuhan
sebagian
besar
image
JPEG,
namun
urutan
koefisien
DCT
tidak
menggunakan bilangan
minus
dan
pada
banyak
kasus nilai
random diatas
terlalu
besar
untuk
jumlah
koefisien DCT
pada
image
sehingga dapat
dikatakan
tidak efisien.
Oleh
karena
itu
dilakukan operasi
modulo
(%)
terhadap
nilai
random
sehingga
nilainya
tidak
akan melebihi jumlah koefisien DCT dan nilai random
yang
lebih kecil dari nol akan ditambahkan jumlah koefisien DCT
sehingga tidak terdapat nilai minus.
c6 %= cntr;
if (c6<0) c6 += cntr;
|
 42
Proses
pengacakan akan
dimulai
dengan
membuat
array
berisi
indeks
terlebih
dulu,
array
ini
pada
awalnya
akan
diisi terurut dan pada
akhir
proses
akan
berisi
indeks
yang
sudah
teracak. Pertama-tama aplikasi akan
merandom
satu bilangan antara 1 hingga posisi indeks teratas,
kemudian
nilai
dari
posisi
indeks
random tersebut
akan
ditukar dengan nilai pada posisi indeks teratas, lebih lanjut
dijelaskan dengan gambar berikut :
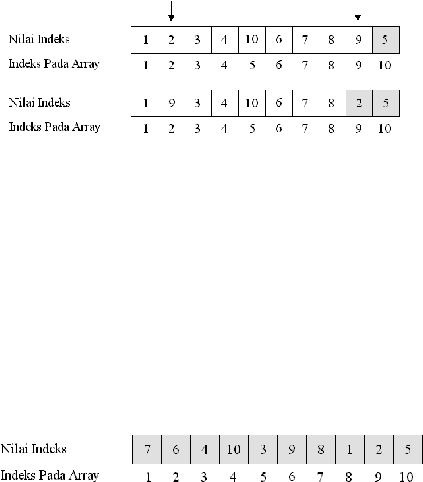
Gambar 2.31. Proses Random pada Putaran Pertama
Pada
gambar
diatas
aplikasi
menukar nilai
pada
posisi
random (5)
dengan
nilai
pada
posisi
indeks
teratas
(10),
kemudian pada
putaran
kedua
aplikasi
akan
mengurangi posisi
indeks
teratas, yang berarti pada contoh
diatas
aplikasi
hanya
akan
merandom bilangan
1–9,
oleh
karena itu
array
pada
indeks terakhir tidak
akan
diikut-
sertakan
dan
digambarkan berwarna
abu-abu,
nilai
pada
posisi random
berikutnya
kemudian
akan ditukar
dengan
|
 43
nilai pada posisi
indeks
teratas
(9),
lebih lanjut dijelaskan
dengan gambar berikut :
Gambar 2.32. Proses Random pada Putaran Kedua
Proses
ini akan
terus berlanjut hingga
indeks teratas
berada
pada
posisi
2,
dalam keadaan ini
nilai
dari
semua
indeks
sudah
teracak,
lebih
lanjut
dijelaskan pada
gambar
berikut :
Gambar 2.33. Keadaan pada Akhir Proses
Pada
contoh diatas
semua
nilai
dari
setiap
indeks
sudah
teracak.
Pengurangan posisi
indeks
teratas
dimaksudkan
agar
nilai
indeks
tidak
akan
dirandom
lebih
dari satu kali, dengan memperkecil jangkauan
indeks
maka
proses permutasi akan berjalan lebih cepat.
|
 44
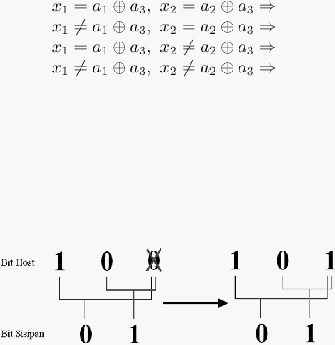
2.6.2.3.2
Matrix Encoding
pada
F5
Matrix
encoding
pertama
kali
ditemukan oleh
Ron
Crandall. Teknik ini memungkinkan perubahan bit host yang
minimum jika
terdapat
sisa
kapasitas
dalam
steganogram
(Westfeld, 2004). Dalam contoh berikut akan dijelaskan
lebih
rinci,
jika
kita
ingin
menyisipkan
dua
bit
x1,x2 ke
dalam 3 bit host a1,a2,a3
dengan mengubah maksimal satu
bit maka terdapat 4 kemungkinan :
Tidak merubah apapun
Merubah a1
Merubah a2
Merubah a3
Dalam
contoh
berikut
akan dijelaskan
lebih rinci,
jika kita ingin menyisipkan dua bit (01)
ke dalam tiga bit
host (100) maka akan dilakukan perubahan terhadap bit a3 :
Gambar 2.34. Perubahan pada bit a3
Jika kita
ingin
mendapatkan kembali
nilai
x1
maka
lakukan operasi xor
terhadap a1 dan a3, dan jika kita
ingin
mendapatkan nilai x2
maka lakukan operasi xor terhadap a1
dan a2.
|
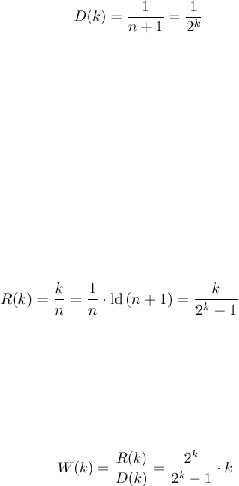 45
Pada
contoh
diatas
kita
tidak
mengubah
lebih
dari
satu bit, pada fungsi (dmax,n ,k) n bit host akan diubah oleh
k
bit data steganografi tidak
lebih dari jumlah dmax. Untuk
fungsi
(1,n,k) bit host
mempunyai panjang
n
=
2
k
–
1,
dari
persamaan
panjang tersebut maka didapat persamaaan
”kerapatan perubahan” (change density)-nya yaitu :
Kerapatan
perubahan
dapat
didefinisikan sebagai
proporsi
dari
bit
yang
sudah
dirubah, bahkan
teknik
yang
mampu
menyimpan 100%
data
pun
memiliki
kerapatan
perubahan
50% (karena
diasumsikan
bahwa
½ dari LSB
data host sudah sesuai dengan LSB data steganografi). Lalu
didapat juga ”tingkat penyisipan”(embedding
rate) :
Menggunakan persamaan
dari
”tingkat
penyisipan”
dan
”kerapatan
perubahan” maka
didapat
”efisiensi
penyisipan” (embedding efficiency) :
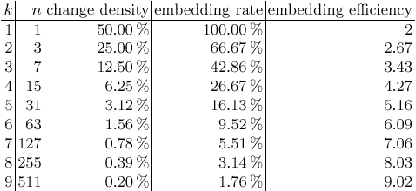
”Efisiensi penyisipan” pada (1,n,k) selalu lebih besar
dari
k, tabel
berikut
akan
menjelaskan
lebih
rinci
bahwa
semakin rendah ”tingkat penyisipan” maka semakin tinggi
|
 46
efisiensinya, oleh
karena
itu
penyisipan data
dalam
jumlah
kecil dapat dilakukan se-efisien mungkin.
Sebagai
contoh,
jika
kita
ingin
menyisipkan pesan
sebesar
1000 bit
ke
dalam
carrier
dengan kapasitas
50000
bit, maka embedding rate yang dibutuhkan adalah R = 1000
:
50000 = 2%. Nilai ini berada di antara R(k = 8) dan R(k =
9)
pada
tabel
di
atas.
Kita
pilih
k =
8,
sehingga
mampu
meyisipkan 50000 : 255 = 196 code words dengan nilai n =
255. Kode (1, 225, 8) dapat menyisipkan 196 x 8 = 1568 bit,
sedikit diatas 1000 bit. Tetapi jika kita memilih k = 9, maka
kita tidak dapat menyisipkan pesan dengan sempurna.
Kasus
pada
gambar
2
menggunakan desain
(1,3,2)
yang
berarti
1
perubahan pada
setiap
3
bit
carrier
untuk
mendapatkan 2
bit
data.
Terdapat
banyak
desain
lain
tergantung
pada
rate dan
change density
yang
diinginkan,
desain
(1,7,3)
misalnya,
digunakan pada
7
bit
data
yang
menyimpan 3 bit data sisipan dengan rate 42 % dan change
|
|
47
density
12.5 %, desain
(1,31,5) memiliki
rate 16
%
dan
change density 3 %.
Kapasitas
penyisipan dapat
diperbesar dengan
memperbanyak perubahan yang
dilakukan pada
bit
carrier,
desain
(2,13,6)
yang
menggunakan 13
bit
carrier
untuk
menyimpan 6 bit data memiliki rate 46 % dan change
density 13.5 %, bandingkan dengan desain (1,7,3) dimana 14
bit
carrier
digunakan
untuk
menyimpan
6
bit
data dengan
maksimum 2 perubahan pada data.
Algoritma F5
hanya
menggunakan desain (1,n,k)
yang
berarti
membatasi
hanya
1
perubahan saja,
hal
ini
dilakukan karena desain (1,n,k)
adalah
desain
yang
paling
baik
untuk
penyisipan
data
berkapasitas kecil
atau
sangat
kecil,
dan
pada
banyak
kasus,
data
yang
disisipkan oleh
steganografi adalah
pesan
rahasia
berukuran
kecil.
Desain
(1,n,k)
misalnya,
dapat
mencapai rate
9,5%
pada
k
=
6,
sedangkan desain (2,n,k), pada k = 6
masih memiliki rate
46%.
Jika
perubahan pada
bit
yang
menyimpan data
(change
density) semakin
kecil
maka
kapasitasnya
pun
semakin kecil pula (rate), oleh karena itu pada algoritma F5
semakin kecil data yang disisipkan maka semakin kecil pula
perubahan yang dilakukan pada koefisien DCT dan semakin
sulit pula dideteksi.
|
 48
2.6.3
Pembatasan Ukuran
File Sisipan
Ukuran
file
yang
dapat
ditampung
oleh steganogram
sangat
bergantung jumlah koefisien DCT
yang tidak bernilai nol
yang dimiliki oleh
image. Jumlah koefisien DCT
ini bergantung kepada kualitas kompresi jpeg,
dimensi
image
dan
keragaman
variasi
warnanya, semakin
besar
dimensi
image, semakin tinggi kualitas kompresinya dan semakin beragam warnanya
maka semakin besar pula kapasitasnya.
Gambar 2.35. Dua image yang diamati : final.jpg dan nature.jpg
Dua
image
yang
diamati diatas
menunjukkan perbedaan yang
cukup
besar, image nature.jpg memiliki 174.829 koefisien DCT
yang tidak bernilai
nol
sedangkan
image
final
jpg
hanya
memiliki 66.922
koefisien
DCT
saja.
Pengamatan juga dilakukan terhadap image yang seluruhnya hanya berwarna
hitam dan putih, kedua image tersebut ternyata tidak memiliki koefisien DCT
yang tidak bernilai nol yang berarti bahwa kedua image tersebut tidak dapat
digunakan sebagai media penyisipan data.
|
|
49
Jumlah
koefisien
DCT
tersebut
menujukkan
kapasitas dalam
satuan
bit yang mampu ditampung oleh steganogram, jika suatu image memiliki 800
koefisien DCT
yang
tidak
bernilai
0
berarti
image
tersebut mampu
menampung 800 bit atau 100 byte data. Namun kapasitas steganogram
pada
algoritma
F5
tidak
dapat
diperkirakan dengan
pasti
karena
adanya
proses
penyusutan pada saat penyisipan walaupun dalam jumlah yang kecil.
Image final.jpg diatas berukuran 196.608 byte sedangkan image
nature
berukuran 409.600
byte,
yang
berarti
bahwa
final.jpg
dapat
menampung
sekitar
4.25%
dari
size-nya yaitu
8.365
byte
data
sedangkan
image
nature.jpg dapat
menampung sekitar 5.33% dari size-nya atau 21.853
byte
data.
Menurut
Westfeld
sendiri
(Westfeld, 2004)
algoritma F5
pada
beberapa
kasus
tertentu
dapat
memiliki
kapasitas
maksimum
sampai
13%
dari size steganogram-nya.
2.7
Flowchart (Bagan
Alir)
Flowchart adalah suatu metoda untuk menggambarkan proses kerja suatu sistem
yang
terorganisir
dengan
menggunakan diagram.
Grafik
diagram
tersebut
digunakan
karena pada dasarnya grafik lebih mudah dimengerti oleh manusia daripada keterangan
dalam bentuk tabel ataupun serangkaian kode – kode algoritma.
Flowchart itu terdiri dari dua bagian utama yaitu bentuk (shape) dan garis (line),
dimana bentuk adalah bagian yang mewakili setiap langkah atau keputusan dalam proses
dan
direpresentasikan dalam
bentuk
lingkaran,
persegi
panjang
dan
sebagainya,
sedangkan
garis
menunjukkan
urutan
proses
dan
menggambarkan langkah –
langkah
yang harus diikuti. Adapun simbol-simbol dasar flowchart adalah sebagai berikut :
|
 50
Terminator
:
menggambarkan awal (“Start”
atau
“Begin”)
atau akhir (“End” atau “Stop”) dari sebuah proses.
Process
:
menggambarkan beberapa
aktivitas
atau
proses
dengan menuliskan teks di dalam simbol tersebut.
Decision
:
menggambarkan suatu
titik percabangan dimana
keputusan harus
dibuat.
Terdapat
dua
alur
garis,
satu
menunjuk ke bawah dan yang lain menunjuk ke sebelahnya.
Setiap
garis
ditandai dengan
satu
jawaban yang
mungkin,
seperti “Yes” dan “No”, atau “Benar” dan “Salah”.
Arrow : menunjukkan urutan langkah-langkah aktivitas (alur
proses)
Connector
: menggambarkan
hubungan
antara
bentuk-
bentuk dalam
flowchart
tanpa
menggunakan
garis.
Sebuah
huruf atau nomor dalam lingkaran ini menghubungkan huruf
atau nomor yang saling berhubungan tersebut.
Data
:
menggambarkan data
yang
masuk
atau
keluar
dari
sebuah aktivitas.
Predefined
process
:
menggambarkan suatu
proses
yang
sudah
didefinisikan sebelumnya, seperti
modul
atau
subrutin.
Preparation : menggambarkan modifikasi seperti setting
dari tombol atau inisialisasi suatu rutin.
|