|
BABII
LANDASAN
TEORI
2.1
Tinj:man Pustaka
2.1.1
Pengertian dan Tujuan Perawatan
Pemeliharaan
merupakan
suatu
fungsi
dalam suatu perusahaan
manufaktur
yang
sama pentingnya
dengan
fungsi-fungsi
lainnya
seperti
kegiatan
produksi.
Hal ini
karena
apabila
kita
memiliki
suatu
peralatan
atau
fasilitas,
maka biasanya
kita
akan
berusaha
untuk tetap
mampergunakan
fasilitas
itu untuk
jangka
wa.lrtu yang panjang.
Demikian
pula
halnya dengan
perusahaan
manufaktur,
dimana
pimpinan
perusahaan
tersebut
akan selalu berusaha
agar fasilitas/peralatan
produksinya
dapat terns
digunakan
sehingga
kegiatan produksinya dapat berjalan lancar.
Maintenance
dapat
diartikan
sebagai
kegiatan
untuk
memelihara atau
menJaga
fasilitas/peralatan
pabrik dan
mengadalcan
perbaikan
atau penyesuaianlpenggantian
yang diperlukan
agar supaya
terdapat
suatu keadaan
operasi
produksi
yang
memuaskan sesuai
dengan
apa
yang
direncanalcan.
Jadi
dengan
adanya
kegiatan
maintenance
ini
malca
fasilitas/peralatan
pabrik
dapat
dipergunalcan
untuk
produksi
sesuai
dengan
rencana,
dan
tidak
mengalami
kerusalcan
selama
fasilitas/peralatan
tersebut
dipergunakan
untuk
proses
produksi
atau
sebelum
jangka
waktu
tertentu
yang telah direncanakan tercapai.
|
|
Tujuan
utama fungsi pemeliharaan
adalah
:
1. Kemampuan
produksi
dapat
memenuhi
kebutuhan
sesuai dengan
rencana
produksi
2.
MerJaga
kualitas
pada tingkat
yang tepat untuk
memenuhi
apa
yang
dibutuhkan
oleh produk
itu
sendiri
dan
kegiatan
produksi
yang
tidak
terganggn
3.
Untuk
membantu
mengnrangi
pemakaian dan
penytmpangan
yang di
Iuar
batas dan
menjaga
modal yang
diinvestasikan
dalam
perusahaan
selama
waktu
yang
ditentukan
sesuai
dengan
kebijaksanaan
perusahaan
mengenai
investasi
tersebut
4.
Untuk
mencapai
tingkat
biaya
peme!iharaan
serendah
mungkin,
dengan
melaksanakan
kegiatan
pemeliharaan
secara
efektif dan
efisien
keseluruhannya
5.
Menghindari
kegiatan
pemeliharaan
yang
berbahaya
bagi
keselamatan para
pekerja
6.
Mengadakan
suatu kerja sama
yang erat dengan
fungsi-fungsi
utama
lainnya
dari suatu perusahaan
dalam
rangka
untuk
mencapai tujuan
utama
perusahaan
,
yaitu tingkat keuntungan atau
return of investment
yang
sebaik
mungkin
dan
total
biaya yang terendah
|
|
2.1.2
Jenis-jenis Pemelihaman
2.1.2.1 Preventive Maintenace
Yang
dimaksudkan
dengan
preventive maintenance
adalah
kegiatan
pemeliharaan
dan
perawatan
yang di!alrukan untuk
mencegah
timbu!nya
kerusakan-kerusakan
yang
tidak
terduga
dan
menemukan
kondisi
atau
keadaan
yang dapat
menyebabkan
fasilitas
produksi
mengalami kerusakan
pada
waktu digunalmn da!am proses.
Dengan
demikian
semua fasilitas
produksi
yang
mendapatkan
preventive
mantenance
akan terjamin
kelancaran
kerjanya
dan selalu
diusahalcan
dalam kondisi
atau keadaan
yang siap
dipergunakan
untuk setiap operasi
atau proses produk:si
pada
setiap saat. Preventive
maintenance
ini
sangat
penting
karena
kegunaannya
yang
sangat
efektif di dalam
menghadapi
fasilitas-fasilitas
produksi
yang
termasuk
dalam
go!ongan
"critical
unit".
Sebuah
fasilitas/peralatan
produksi
akan
termasuk:
dalam
"critical unit", apabila
:
"
Kerusakan
fasilitas
atau peralatan
tersebut akan
membahayakan
k:esehata11
atau
k:eselamatan para
pekerja
"
Kerusal<an
fasilitas
ini
akan mempengaruhi kualitas
produk
yang
dihasilkan
"
Kerusakan fasilitas tersebut akan menyebabkan
k:emacetan
seluruh
proses
produksi
"
Modal yang
ditanamkan dalam fasilitas
tersebut adalah cukup besar atau
mahal
|
|
Apabila
preventive
maintenance
dilaksanakan
pada fasilitas-fasilitas atau peralatan
yang
termasuk
dalam "critical
unit", mal<a tugas-tugas
maintenance
dapatlah
dilakukan
dengan
suatu perencanaan
yang
intensif
untuk
unit
yang
bersangkutan,
sehingga
rencana
produksi
dapat dicapai
dengan
jumlah
basil
produksi
yang
lebih
besar dalam waktu
yang
relatiflebih
singkat.
2.1.2.2
Conective Maintenance
Corrective
maintenance
adalah
kegiatan
pemeliharaan
dan perawatan
yang
dilakukan
setelah
terjadinya
suatu kerusakan
atau
kelainan
pada
fasi!itas
atau
peralatan
sehingga
tidal< dapat
berfungsi
dengan
baik.
Kegiatan
corrective
maintenance
sering disebut
kegiatan
perbaikan atau reparasi.
Maksud
dari
tindakan
perbaikan
ini
adalah
agar
fasilitas
atau
peralatan
tersebut
dapat dipergunakan
kembali
dalam proses
produksi,
sehingga
operasi
atau
proses
produksi
dapat
berjalan
lancar
kembali.
Dengan
demikian,
apabila
suatu
perusahaan
menerapkan
kebijal<an
untuk
melakukan
corrective
maintenance
saja,
maka terdapat
faktor
ketidakpastian (uncertainty)
dalam
kelancaran
proses
produksinya
akibat
ketidakpastian akan kelancaran bekerjaynya
fasilitas/peralatan
produksi yang ada.
2.1.3
Tugas-tugas atau kegiatan dalam maintenance
Semua
tugas
atau
kegiatan
dari
maintenance
dapat
digolongkan
da!am
salah
satu
dari
lima
tugas pokok berikut ini :
1. Inspeksi
(Inspection)
yang
merupakan
tindakan
pemeriksaan
terhadap
mesin
untuk mengetahui
berada
atau
tidaknya
keadaan
dari mesin
tersebut
dalam
persyaratan yang diinginkan.
|
|
2.
Kegiatan
teknik
(Engineering)
yang
meliputi
kegiatan
percobaan
atas
peralata11. yang
barn
dibeli, kegiatan-kegiatan
pengembangan
peralatan
atau
komponen
peralatan
yang perlu
diganti,
serta
melakukan
berbagai
penelitian
terhadap kemungkinan pengembangan tersebut.
3.
Keriat&>
Produksi
{Production) merupakan
kegiatan
maintenance
yang
sebenarnya,
yaitu memperbaiki
dan
mereparas1
mesin-mesin
dan
peralatan
pabrik
4. Pekerjaan
administrasi
(Clerical
work)
merupakan
kegiatan
yang
berhubungan
dengan
pencatatan-pencatatan
mengenai
biaya-biaya
yang
terjadi dalam
melakukan
pekerjaan-pekerjaan
maintenance
dan
biaya-biaya
yang berhubungan
dengan
kegiatan
maintenance,
komponen
yang
dibutuhkan,
progress
report
tentang
hal-hal
yang dikerjakan,
waktu
dilakukannya
inspeksi
dan perbaikan,
serta lamanya
perbaikna
tersebut,
dan
komponen
yang
trersedia di
bagian
maintenance.
5.
Pemeliharaan
Bangunan
(House
Keeping)
yang
merupakan
kegiatan untuk
menjaga
agar
bangunan
tetap terpelihara dan
terjamin
kebersihannya.
2.1.4
Konsep Ke:mdalan
(Reliability)
Keandalan
menurut
Ebeling
(1997,
p5)
adalah
peluang
suatu
komponen
atau
sistem alcan dapat beroperasi
sesuai
dengan
fungsi
yang diinginkan
untuk
suatu
periode
tertentu
keti.ka digunakan
dibawah kondisi
operasi
yang
ditetapkan.
|
|
Jadi
meialui
definisi
di
atas,
dapat
disimpulkan
bahwa
keandalan
atau
reliability
menunjukkan
tingkat
kerewelan
suatu
mesin atau
peralatan.
Semakin
besar
nilai
reliability,
maka
semakin jarang
mesin atau
peralatan tersebut
mengalami gangguan.
2.1.5
Konsep Keterawatan (Maintainability)
Menurut
Ebeling
(1997,
p5)
keterawatan
merupakan
probabilitas
bahwa suatu
komponen
atau
sistem
yang
rusak
akan
diperbaiki
atau
direparasi
kepada
kondisi
yang
telah
ditentukan
dalam
periode
waktu
tertentu
saat
pemeliharaan
yang
dilakukan
telah sesuai dengan tata cara yang
telah
ditentukan.
2.Ui
Konsep Ketersediaan (Availability)
Menurut
Ebeling
(1997,
p6),
ketersediaan
yaitu
peluang
suatu
komponen
atau
sistem
dapat
beroperasi
sesuai
dengan
fungsinya
pada
waktu
tertentu
ketika
digunakan
pada
kondisi
operasi
yang
telah
ditetapkan.
Sedangkan
menurut Kapur
(1997,
p226),
ketersediaan
atau
availability
merupakan
suatu
konsep
yang
berhubungan
erat
dengan
probabilitas suatu
peralatan untuk
melakukan
operasi
secar
memuaskan pada kondisi tertentu.
Ada
beberapa
macam
cara
yang berbeda untuk
mengemukakan availability
ini
diantaranya :
l.
Inherent
Availability (Ketersediaan Inheren)
Keterediaan
inberen
1111
merupakan
ketersediaan
yang
hanya
mempertimbangkan faktor
kerusakan
dan
perbaikan
dan
umumnya
digunakan
|
|
untuk
mengukur
ketersediaan
pada
perusahaan
yang
menerapkan
kebijaksanaan
corrective
maintenance.
Ketersediaan
inheren ini
dirumuskan
sebagai
berikut
:
Ainh
=
l'v!TBF
MTBF+MTTR
Dimana:
Anh
=
Ketersediaan Inheren
MTBF =Rata-rata
waktu antara kegagalan (M:ean
Time Between Failure)
MTTR =Rata-rata
waktu antar perbaikan (M:ean
Time to
Repair)
2.
Achieved
Availability
(Ketersediaan
Tercapai)
Ketersediaan
tercapai
ini
merupakan
pengukuraxr
ketersediaan yang telah
mempertimbangkan
faktor
peme!iharaan
dan
pada
umumnya
digunakan
oleh
perusahaan
yang
menerapkan
metode
proactive
maintenance.
Rumus
yang digunakan
:
MTBM
Aa=----
MTBM+M
Dirnana:
Aa
=
Ketersediaan Tercapai
MTBM =
Mean Time Between Maintenance
M
=Rata- rata waktu peme!iharam, yang dihitung dengan rumus:
|
|
m(td
)MTTR
+
(
d
)MPMT
M=
1pm
Ia
m
(
[d)+lpm
Peme!iharaan
yang
tidak
te1jadwal dan
pemeliharaan
pencegahan
terrnasuk
dalam MTBM ini,
dimana
MTBM
dihitung dengan
menggunakan rumus :
MTBM=
td
td
m(td)+ ·
1pm
Dimana:
td= waktu ekonomis
Tpm =rata-rata
selang waktu antar preventive maintenance yang
digunal<an
J\!IPMT
=
rata-rata
waktu
preventive
maintenance
(Mean
Preventive
Maintenance Time)
3.
Operational
Availability
(Ketersediaan
operasional)
Operational availability
merupakan
ketersediaan
yang
telah
mempertimbangkan
aspek
keterlambatan
pemeliharaan yang
disebabkan
oleh
karena
maintenance
delay
dan
supply
delay,
dihitung
dengan
rumus
:
MTBM
Ao=--- =
MTBM+M
Dimana:
A,
=
ketersediaan
operasional
MTBM
=
rata-rata
waktu
antar
peme!iharaan
(Mean
.
Time
Between
Maintenance)
|
|
M
=rata- rata
downtime
pemeliharaan
2.1.7
Konsep Downtime
Dovmtime
merupakan
waktu
menganggur
atau waktu dimana suatu unit tak dapat
lagi menjalankan
fungsinya sesuai dengan
yang
diharapkan.
Hal
ini dapat teljadi
apabila
suatu unit mengalami
masalab
seperti
kerusakan
mesin
yang dapat
mengganggu
performasi
dari
mesin secara
keselumhan
termasuk
kualitas
produk
yang
dihasilkan
atau
kecepatan
produksinya
sehingga
membutuhkan
waktu
tertentu
untuk mengembalikan fungsi unit
tersebut
pada
kondisi semula.
Downtime terdiri dari
beberapa unsur :
.,
Supply
delay
yaitu
waktu
yang dibutuhkan
oleh
personel
maintenance
untuk
memperoleh
komponen
yang dibutuhkan
dalam
proses
perbaikan.
Supply
delay dapat terdiri dari lead time administrasi,
lead time produksi,
dan
waktu
transportasi komponen pada lokasi perbaikan.
"
Maintenance delay yaitu
waktu yang dibutuhkan
untuk
menunggu
ketersediaan
sumber daya maintenance
untuk
melakukan
suatu proses
perbaikan.
Sumber
daya
maintena11ce
dapat
bempa
personel,
alat
bantu,
alat
tes.
"
Access time
yaitu
waktu untuk
mendapatkan
akses ke komponen
yang
mengalami
kerusakan.
|
|
,.
Diagnosis
time yaitu
waktu yang dibutuhkan
untuk
menentukan
penyebab
kerusakan
dan
langkah
perbaikan
yang
harus
ditempuh untuk
memperbaiki
kerusakan.
,.
Repair
or Replacement
time
yaitu waktu
aktua!
yang dibutuhkan
untuk
menyelesaikan
proses
pemu!ihan
setelah
permasalahan dapat diidentifikasi
dan akses ke
komponen
yang rusak dapat dicapai.
,.
Verification an.d
alignment
yaitu waktu
untuk
memastikan
bahwa
fungsi
dari
suatu unit telah kembali pada
kondisi
operasi semula.
Supply
delay
dan
maintenance
delay
tidak tennasuk
kedalam
inherent
repair time
yang
merupakan
waktu
perbaikan
yang benar-benar
merefleksikan
maintainability
dari sebuah
unit.
Hal ini
dikarenakan
keduanya
dipengaruhi
oleh
parameter
ekstemal
yang bukan
merupakan bagian dari
sisem itu
sendiri.
2.1.8
Fungsi
Distril:msi Kemsakan
Yang dimaksud
dengan
distribusi
kerusakan
yaitu
ekspresi
matematis
usia
dan
pola
kerusakan
peralatan.
Karakteristik
kerusal<an
dari
setiap
peralatan akan
mempengaruhi bentuk
kedekatan
yang
digunakan
dalam
menguji
kesesuaian
dan
menghitung parameter
fungsi distribusi
kerusakan.
Keputusan
yang
berhubungan dengan
penentuan
kebijakan
perawatan
seperti
kebijakan
perawatan
pencegahan
memerlukan
infonnasi
tentang
selang
waktu
suatu
peralatan
akan
mengalami
kerusakan
lagi.
Umumnya
saat terjadi
perubahan
kondisi
|
 peralatan dari baik
menjadi rusak
dan tidak dapat diketabui dengan pasti namun dapat
diketailUi
probabi!itas terjadinya
perubahaan tersebut.
2.1.9
Fungsi Kepadatan
Pelmmg
Bila
x menyatakan
continuous
random variable
sebagai waktu kerusakan
dari
suatu
sistem dari
jumlah kerusakan
pada
suaiu waktu,
dan
mempunyai fungsi
distribusi
fx
yang
kontinyu
disetiap
titik
sumbu
nyata
maka
fx
dikatakan
sebagai
fungsi
kepadatan
peluang
dari
variabel
x. Jika
x
dapat
bemilai
nyata (x
2:
0)
pada
interval waktu t,
hams memenuhi persyaratan sebagai berikut :
Fx(t)2:0; untuk t 2: 0
Sehingga,
2.1.10 Fnngsi Distribnsi Kumnlatif
Menurut
Ebeling
(!997,
p23)
funsi
distribusi kumulatif
adalah
fungsi
yang
menggambarkan probabilitas atau
peluang terjadinya kemsakan sebelum waktu
t
dan
hal
ini
dapat
dinyatakan
sebagai
berikut
:
F(t)
=
P(x
<
t)
atau
t
F(t)
=
f(t)dt; dimana t 0
0
|
|
t
Keterangan
rumus
:
F(t)
=
Fungsi
Distribusi
Kumulatif
f(t) = Fungsi
kepadatan
peluang
nilai probabilitas
fungsi
distribusi
kumulatif
ini berkisara antara 0
:<: F(t)
:<: I dan jika
terdapat nilai
t--+
oo, maka
F(t) = 1
2.1.11
Fungsi Reliability
Saat
menentukan
keandalan
dari suatu
peralatan,
terdapat
hal
penting
yang
harus
diperhatikan
yaitu spesifikasi
fungsi yang diharapkan
dari
peralatan
tersebut.
Keandalan harus diterjemahkan da!am satuan fungsi waktu.
Fungsi
keanda!an
merupakan
probabi!itas
suatu
pera!atan
dapat
beroperasi
dengan
baik
tanpa mengalami
kerusakan
da!am
periode
waktu
tertentu.
Menurut
Ebeling
(1997,
p23), probabi!itas dari kemungkinan
peralatan
akan
memenuhi fungsinya
paling tidak hingga waktu tertentu (t),
dapat didefinisikan
sebagai
berikut
:
"
R(t)
=
P
(x:,.
t); dengan
R(t) merupal<an
distribusi
keanda!an.
Bi!a di!ihat
dari waktu
kerusakan
atau
kegaga!an
variabel
x yang
memi!iki
fungsi kepadatan f(t),
maka dapat didefinisikan sebagai
berikut
:
"
R(t)=1-F(t)
"
R(t)
=
1-
f
tf(t)dt untuk t 0
0
w
"
R(t)= Jrct)dt
0
|
|
Luas area
keseluruhan
kurva
sama
dengan
l
sehingga
dapat
dikatakan
bahwa
nilai
dari
probabilitas
fungsi
keandalan
dan
fungsi distribusi kumulatif berada diantara
0
hingga
l, yakni
:
0
:SR(t) :S 1
0
:S F(t)
:S
l
2.Ll2
Mean Time to Failure
Menurut Ebeling
(1997,
p26),
Mean
Time to
Failure (MTTF) atau
nilai
tengah
dari
distribusi
kerusakan
adalah
nlai
rata-rata
atau
nilai
yang
diharapkan
dari
suatu
distribusi
kerusakan
yang
didefinisikan
oleh f{t)
sebagai
berikut
:
w
MTTF
=
E(t)
=
J
tf{t)dt
0
dan
menurut
Ebeling (1997,
p24), terdapatrumus:
f(t)
=
dF(t)
=
_
dR(t)
dt
dt
sehingga
diperoleh
:
MTTF
=
1-
dR(t) tdt
0
dt
w
MTTF
=-
tR(t)l:+ JR(t)dt
0
00
MTTF
=
JR(t)dt
0
|
|
f
2.1.13 Fungsi Laju Kerusakan
Mennrut
Jardine (1993,
pl9),
laju kerusakan
suatu
peralatan
pada waktu t
merupakan
probabilitas
dimana
peralatan
akan mengalami
kerusakan
pada se!ang
wal<tu berikutnya
dan
diketahui kondisinya baik
pada
awal
interval.
Laju kerusalcan sesaat
(hazard
rate)
merupakan
limit atau batas dari laju kerusakan
dengan
panjang
interval
waktu yang
mendekati
no!. Simbol dari
laju
kerusakan
sesaat
adalah A(t) dan fungsinya:
A,(t)
=
f{t)
R(t)
Menurut
Ebeling (1997,
p28), jika A(t) Lit merupakan
probabilitas
saat
peralatan
.
menga!ami
kerusakan
selama
interval
wal'1u
yang pendek
Lit, dan
diketahui
bahwa
peralatan
tersebut
tidak mengalami kerusakan
sampai waktu
t,
maka notasi dari
probabilitas dapat ditulis
sebagai berikut
:
"
Kemungkinan kegagalan
atau kerusakan antara
waktu t dan
Lit
:
t-':-8\
P[t 5 T 5
t+
Lit]=
f(t)dt = R(t)- R(t- Lit)
0
"
Kemungkinan sistem bekerja pada
saat
t
:
P(t5T5HL1t]
R(t)-R(t+Lit)
P
[
t
5
T
5
t+
Lit
I
T
;:> t
J
=
[
j
=
P
T
d
R(t)
Fungsi
dari
laju kerusakan
merupakan
unit dari laju
kerusakan
dengan
Lit
-+
0,
dengan
demikian
fungsi
laju
kerusakan
sesaat
dan
fungsi
laju
kerusakan dapat
didefinisikan sebagai berikut
:
|
|
A(t)
=
lim
-
[R(t+ ll.t)- R(t)]
'HO
R(t)ll.t
lc(t) =-
dr(t). _I_
dt
R(t)
A(t)
=
f(t)
R(t)
Dimana:
@
A(t)
=
fungsi
laju
Kerusakan fasilitas
ini
,.
f(t) =
fungsi
ketepatan
peluang
"
R(
t)
=
fungsi
keandalan
2.1.14 Distrilmsi untuk mengllitung keanda!an
Pendekatan
yang
digunakan
untuk
mencari
kecocokan
antara
distribusi
keandalan
dengan data
kerusakan terbagi dalam
dua
cara
yaitu
:
1.
Menurunkan distribusi keandalan
secara empms langsung dari
data
kerusakan.
Jadi
dengan
kata
lain
kita
menentukan
model
matematis untuk
keandalan,
laju
kerusakan dan
rata-rata
waktu
kerusakan
secara
Iangsung
berdasarkan
pada
data
kerusakan.
Cara
ini disebut juga
dengan
non-
parametric
method.
Hal
ini
dikarenakan metode
ini
tidak
membutuhkan
spesifikasi
dari distribusi teoritis tertentu
dan
selain
itu
juga tidak
membutuhkan
penaksiran
dari
parameter
untuk distribusi.
2.
Mengidentifikasi
sebuah
distribusi
keandalan
secara
teoritis,
menaksir
parameter
dan kemudian
melakukan
uji kesesuaian
distribusi.
Metode
ini
akan
|
|
menggunakan
distribusi
teoritis
dengan
tingkat
kecocokan
tertinggi
dan data
kerusakan
sebagai
model distribusi
reliabilitas
yang digunakan
untuk
menghitung
keanda!an, laju
kerusakan,
dan
rata-rata waktu
kerusakan.
Berdasarkan kenyataan
bahwa
hampir
semua
data
kerusakan
umum
memiliki
kecocokan
yang tinggi
terhadap
suatu
distribusi teoritis
tertentu,
maka cara
kedua
umumnya lebih
disukai
daripada
cara
pertama.
Cara
kedua
juga
memiliki
beberapa
keunggulan
(Ebeling,
1997,
p358-359):
1.
Model
empiris
tidak
menyediakan
informasi
di
luar range dari data
sampel,
sedangkan
dalam model distribusi
teoritis,
ekstrapo!asi
melebihi
range
data
sample
adalah
mungkin
untuk
dilakukan.
2.
Yang
ingin
diprediksi
adalah
data kerusakan
secara
keseluruhan
bukan
hanya
terbatas
pada sampel saja
karena
sampel
hanya
merupakan
sebagian
kecil dari
populasi
yang diambi! secara acak sehingga
model kerusakan
tidal< cukup bila
hanya dibentuk
berdasarkan
data sampel
saja.
3.
Distribusi
teoritis
dapat digunakan
untuk
menggambarkan
berbagai
macam
laju
kerusakan.
4. Uk:uran
sampel
yang kecil
menyediakan informasi
yang sedikit
rnengenm
proses kegagala11.
Akan tetapi
jika
sampel
konsisten
terhadap
distribusi
teoritis
maka hasil
prediksi
yang
lebih kuat
dapata diperoleh.
5.
Distribusi teoritis
lebih
mudah
untuk
digunakan
dalam
menganalisa
proses
kegagalan yang
kompleks.
|
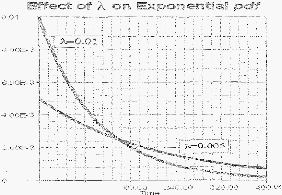 Adapun
distribusi
statistik
yang pada umumnya
digunakan
sebagai
model
distribuso
keandalan
yaitu :
1. Distribusi
Eksponensial
(Exponential Distribution)
2. Distribusi Weibull
(Weibull
Distribution)
3. Distribusi
Nonna!
(Normal Distribution)
4.
Distribusi
Lognormal
(Lognormal
Distribution)
2.1.14.1
Exponential Distribution
Menurut
Steven
Nahmias
(2001,
p721),
distribusi
eksponensia! ini
memiliki
laju
kerusakan
yang
konstan
terhadap
waktu
(Constant
Failure
Rate
Model).
Menurut
Ebeling
(1997, p41), jika terdapat
peralatan
yang
memiliki !aju kerusakan
tetap, maka
dapat dipastikan
tennasuk dalam distribusi
eksponensial.
Distribusi ini
merupakan
distribusi
yang paling populer
digunakan
dalam teori keandalan.
Gambar 2.1
Distribusi Eksponentsial
|
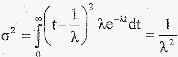 Distribusi
eksponensial
merupakan
distribusi
yang
paling
mudah
untuk
dianalisa
(Ebeling,
1997,
p41).
Parameter
distribusi
eksponensial adalah A (laju
kerusakan).
Menurut
Ebeling
(1997,
p42),
fungsi-fungsi
dari
distribusi eksponensial:
®
Fungsi
kepadatan
peluang
f(tjA)
=
Aexp(-At)
f(t) =A
eC·>ct); untuk
t
0,
/, > 0,
dan
dengan t
=
waktu
Fungsi
Distribusi Kumulatif
F(t)=l-exp(-At)
F(t)
=
1-
e'"':
Fungsi
Keanda!an
R(t)
=
eC-A<l
Ni!ai
rata-rata dari dstribusi
eksponensia!
MTTF
=
_1_
lc
Variansi (c?)
dan
standar deviasi
(a)
1
a=-
lc
|
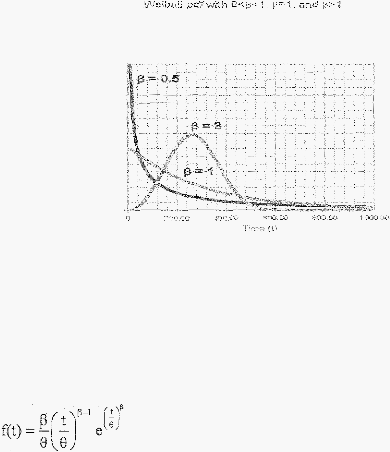 2.1.14.2
Weibull Distribution
Distribusi
Weibull
ini
merupakan
distriusi
yang
muncul
pada
hampir
semua
karakteristik
kegagalan produk
(Ebeling,
1997,
p58).
Distribusi
Weibull
yang
banyak
digunakan
adalah
dalam
dua
parameter yaitu
parameter
skala
(6) dan
parameter
bentuk
CB).
Gambar
2.2
Distribusi
Weibull
Menurut
Ebeling
(1997,
p58-59), fungsi-fungsi
dalam
distribusi
weibull
yaitu:
0
Fungsi
kepadatan
peluang
untuk
t
2':
0
|
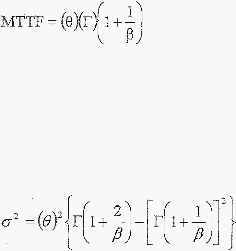 (
t
\
Fungsi
dist1ibusi kumulatif
-
-I
F(t)=l-e
'
8
'
Keandalan
(
t
R(t)
=
e
-le-J
(t
y-1
)c(t)
=
eleJ
Nilai
rata-rata
waktu
kerusakan
dalam
distribusi
weibull
f(x)
=
(x-l)r(x-1)
dimana
f(x)
=
fungsi gamma
Variansi
2.1.14.3
Normal Distribution
Nonnal
distribution seringkali
disebut
juga
dengan
Gaussian
(Gaussian
Distribution),
dimana
distribusi
ini
memiliki
ciri-ciri
simetris
di
sekitar
rataan
dengan
sebaran
di
distribusi yang ditentukan oleh cr.
Distribusi
normal
ini
sangat
cocok
untuk
menggambarkan
fenomena
kelelahan akibat
kondisi
wear
out
di suatu
item.
|
 .-.....
·:·
T=T=Ti
Gambar 2.3
Distribusi
Normal
Sebenamya
distribusi
ini
bukanlah
distribusi
reliabilitas
mumi karena variabel
acaknya
memiliki
range antara minus tak
hingga sampai
plus tak
hingga. Akan tetapi,
karena hampir untuk semua nilai
fL
dan
cr, peluang
untuk variabel acak yang memiliki
nilai
negatif dapat
diabaikan,
maka
distribusi
nonnal
dapat
digunakan
sebagai
pendekatan
yang
baik
untuk proses kegagalan.
Menurut
Ireson
(1995, pl7),
fungsi-fungsi
yang digunakan
dalam
distribusi
nonnal
yaitu :
®
Fungsi
kepadatan
peluang
f(t)
=
1
cr.J2ri
(c··")''
e
za' '
untuk- oo
<
t
<
oc, dimana t
=
waktu
Fungsi distribusi kumulatif
|
|
Fungsi
keandalan
R(t)
=
¹- F(t)
R(t)=l-<:f:)
Fungsi
laju kerusakan
2(t)
=
_cJ>_,_U_ _Jl_c_)
GR(t)
Nilai
rata-rata waktu kerusakan
MTTF=
2.1.14.4
Lognormal Distribution
Lognormal
Distribution
mengenal
dua parameter
yaitu s sebagai
parameter
bentuk
(shape
parameter)
dan
tmed
sebagai
parameter lokasi (location
parameter)
yang
merupakan
nilai
tengah dari
waktu
kerusakan.
Distribusi
ini
didefinisikan
hanya
intuk nilai
t
positif, oleh sebab
itu lebih sesuai
sebagai
distribusi
kerusakan.
Lognormal
distribution
mernpunyai
beberapa
bentuk
dan
menurut
Ebeling
(1997,
p73), seringkali
juga
dijurnpai
data
yang
sesuai dengan
Weibull Distribution
sesuai pula
untuk
distribusi ini.
|
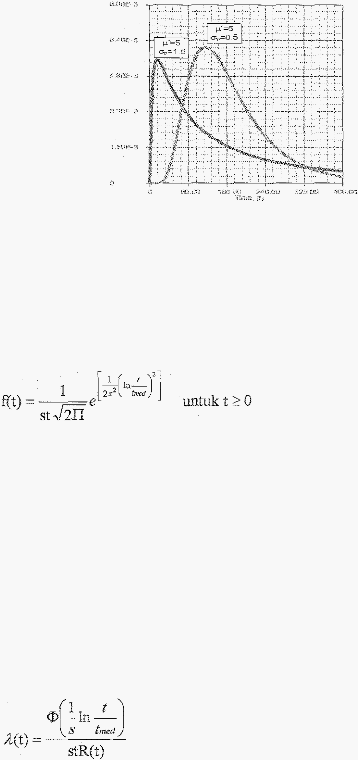 -
t:ff'eet
of cr ,,
on
L.ognonrnd
_r.x:H
Gambar 2.4 Distribusi Lognormal
Fungsi-fungsi
yang
sering
digunakan
dalam
distribusi
ini
menurut
Ebeling
(1997,
p73), yakni
•
•
Fungsi
kepadatan
peluang
Fungsi
distribusi kumu!atif
F(t)
=
q,(.!.rn -
1
)
S
fmed
Fungsi
keandalan
R(t)
=
1F(t)
Laju
kerusakan
|
|
Nilai
rata-rata
-
,'l
MTTF
=
tm,ae 2
Variansi
2.1.15 Identifikasi Distrilmsi
Menurut
Ebeling
(1997,
p359), identifikasi
distribusi
dilakukan
melalui tiga
tahap,
yaitu identifikasi
awal,
penaksiran
parameter,
dan
uji goodness
of
fit.
Perindan
ketiga
tahap tersebut
diberikan
pada
uraian
berikut.
2.1.15.1 Identifikasi Awal
Identifikasi
awal dapat
dibedakan
dengan
dua
metode,
yaitu
probability
plot
dan
metode
least
square.
Dengan
probability
plot
dibuat
grafik dengan
titik-titik
(ti,
F(ti)).
Bila
data
tersebut
menghampiri
suatu
distribusi,
maka
grafik yang terbentuk
akan
berbentuk garis
!urns.
Namun
demikian,
tingkat
subjektifitas
untuk
menilai
kelurusan garis menyebabakan
metode ini
tidak terlalu
populer
digunakan.
Dengan
metode
least
square,
dicari nilai
index of
fit
(nilai korelasi)
antara ti
(atau
ln
ti) sebagai
x
dengan
y
yang
merupakan
fungsi dari distribusi
teoritis
terhadap
x.
Kemudian
distribusi
yang
terpilih adalah
distribusi
yang
memiliki
nilai
index of
fit
terbesar.
|
 i-0.³
""" .,
Perhitungan
umum
pada
metode lest
square yaitu
:
N
J
r
.
ar
.
tenga
hk
erusa
k
an
=
F(
tr
')
=
---'-
n+0.4
Dimana:
i
=
data waictu
ke
-
t
n
=
jumlah
data
kem.sakan
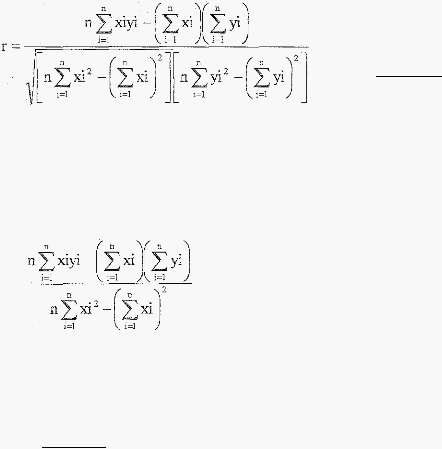
Menurut Walpole (1995, p664), perhitungan index offit memiliki
cara
yang
sama
dengan perhitungan korelasi Pearson.
Jxy
JxxJyy
Dimana =
n
adalah jumlal1 kerusakan
yang terjadi.
Gradien:
b
untuk distribusi
Weibull, Normal, Lognormal
n
nI;x:iyi
b
i-l
n
nL.xr
i=l
untuk
distribusi
Exponensial
Intersep: a=
y-
bx
|
|
1
)
Menurut
Ebeling
(1997,
p364),
metode least square
memiliki
rumus
sebagai
berikut:
@
Untuk Exponensial Distribution
n
Lxiyi
Parameter: A = b =
-"'i "---
n
Lxi2
i=l
Dimana:
.
d
1
}
Yl
=
nl[l-F(ti)]
xi=
ti
1
Dan:MTTF=
b
Dimana : ti adalal1 data
ke- i
Untuk Weibull Distribution
Xi=Inti
1
yi
=lnlnl
L
1-
F(ti
]
Dimana
:
ti adalal1 data
ke -
i
Parameter:
a
fJ=b
dan
{)=e
f3
Untuk Normal Distribution
xi= ti
|
|
yi =
zi
=
<J)
1
[F (
ti)] =
ti -
f.1
0'
Dimana
:
ti
adalah
data ke
-
i
Parameter
1
0'=-
b
a
f.l=
b
Untuk Lognonnal
Distribution
xi
=Inti
Parameter:
1
S=-
"tneci=e-sa
b
Dimana
:
ti adalah data
ke - i
2.1.15.2
Pendngaan
Parameter
Setelah
kandidat
distribusi teoritis
ditemukan,
maka
langkah
berikutnya
adalah
menaksir
parameter
dari data
tersebut.
Parameter
dari suatu
distribusi
hanya
dapat
diduga
(diestimasi)
dan
tidak dapat secara
tepat diketahui,
karena
tidak ada
suatu
metode
yang dapat
mengetahui
dengan
tepat parameter dari suatu distribusi
berdasarkan data sampel yang diambil.
Pada
penjelasan
sebelumnya,
pendugaan
parameter
dapat
dihitung
bersama-sama
dengan
identifikasi
awal distribusi,
yaitu
dengan
menggunakan
metode
least
square
|
|
fit,
tetapi
metode
tersebut
umumnya
kurang
disukai.
Metode
pendugaan
parameter
yang
lebih sering digunakan adalah
Maximum Likelihood Estimator
(MLE).
Secara
umum, untuk
menemukan
:MLE dari
setiap distribusi
teoritis,
kita
hru1.1s
mencari nilai
maksimum
dari
likehood
fUnction
berikut
yang
mengandung
sejumlah
parameter
81. ........,ek
yang
tidal< diketahui
(Ebeling,
p375).
n
L(L(e, ....
,a)=
Tif(ttle,_
...
,a;
i=l
Tujutan
:MLE adalah menentukan
nilai parruneter
81,. ....... ,ek
yang
dapat
memberikan
likehoodfunction
yang sebesar
mungkin
untuk setiap nilai
t
1,
h,........
tn.
Oleh
karena bentuk
perkalian
daripada
!ikehood
function
pada
umumnya
lebih
mudah untuk memecahkan
logaritma dari
likehood
function.
Nilai
maximum
likehood
function
dapat diperoleh
dengan
mengambil
turunan
pertama
dari logaritma
likehood function=
0,
yaitu
:
31nL(8L. ,ll)
ae,
i
1,2,.......,
k
Exponential:MLE
Nilai
:MLE untuk parameter
dengan distribusi
ini
adalah :
r
},=-
T
dimana:
r
=
n
=
jumlah data
kerusakan
T
=
L
'
i=l
t1
yang
mempakan
jumlah
waktu
kemsalcan
|
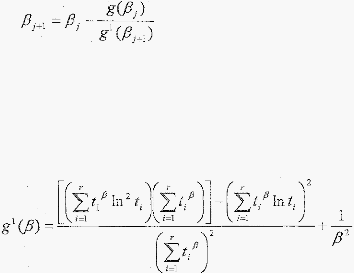 Weibull
MLE
Turunan
pertama dari
!ikehood
function dari
distribusi ini
:
'
)/In
tt
g(fJ)
=
-"'io]'-i" -
)JJ
1=1
1
1
--lntt =
0
f3
r
Tujuan
dari MLE
yaitu memperoleh
nilai
!3
dari persamaan
diatas" Namun
terdapat
pennasalahan
dalam hal
ini yakni persamaan
diatas
tersebut
tidak
dapat
diselesaikan
dengan cara matematis" Jadi
metode
Newton
Rhapson
dapat
digunakan untuk
memecahkan
persamaan
non
linear
yaitu
dengan
menggunakan
persamaan
:
dimana
g'(x)
=
dg(x)
dx
Persamaan
ini
hams
dipecahkan
dengan cara iterasi
hingga
mencapai
nilai
!3i yang
maksimum
atau dengan kata lain yaitu nilai g(f:l) yang
mendekati
noL
Oleh karena
itulah, terlebih
dahulu
akan
dicari turunan
pertama dari
g(f:l):
Untuk
dapat
mempermudah
penyelesaian
iterasi
dengan
Newton
Rhapson
maka
disarankan
nilai
f:liawal yang
digunakan
adalah
nilai
f:lyang
diperoleh
melalui
metode least square"
|
 Kemudian
nilai
MLE
untuk
e
diperoleh
dari persamaan di
bawah ini
:
NormalMLE
Nilai
MLE untuk
parameter dari
distribusi
normal :
!1=x
2
(n
-l)s²
0'
=
n
Lognormal
MLE
Nilai
MLE untuk
parameter dari
distribusi
ini
:
c
In(
f.F
=
L.-'
1=I
n
t
me d -
e
fi
'V"
(ln
t
-
)2
s- -
I
L.='-
'
"._:
:_'_f.l :
-,
n
2.1.15.3
Goodness of
Fit
Goodness of Fit
merupakan
langkah
terakhir dalmn pemilihan
distribusi
seara teori
yang biasa dapat
disebut
pula
dengan
uji
kesesuaian
secara
statistik
yang didasarkan
pada sampel waktu
kerusakan.
Uji ini
dilakukan
dengan
membandingkan
H
0
(hipotesis
no!) dan
H1
(hipotesis
alematif).
I-Ia akan
menyatakan
bahwa
waktu
kerusakan
yang berasal
dari distribusi
tertentu
dan
H1
akan menyatakan bahwa
waktu
kerusakan tidak berasal dari distribusi
|
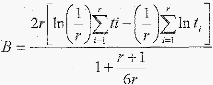 terentu.
Apabila
Ho
diterima,
maka
hal
itu
berarti
bahwa
pengujian
statistik
ini berada
di
luar nilai
kritik.
Dalam hal
ini
terdapat dua
jenis
goodness
of
fit test
yaitu
general tests
(uji
umum)
dan
spesific tests
(uji
khusus).
Yang
merupakan
uji
umum
yaitu uji
chi square
dan
uji
khusus
yaitu
Barlett's
test
untuk
exponential
distribution, Mann's
test
untuk
Weibull
distribution,
Kolmogorov
Smimov
test
untuk
normal
distribution
dan
lognormal
distribution.
Uji
umum
dapat
digunakan
untuk
menguji
beberapa
distribusi,
akan tetapi
uji
khusus
masing-masing hanya
dapat
menguji satu
jenis
distribusi.
Lagipula
dibandingkan
dengan
uji umum, uji
khusus
lebih
akurat
dalam
menolak
suatu
distribusi yang
tidak
sesuai.
e
>-
Barlett's test
untuk
exponential distribution
Menurut
Ebeling (1997,
p399),
hipotesa
untuk uji
ini
yaitu
:
o
Ho :
Data
berdistribusi eksponensial.
>-
o
H1
:
Data tidal<
berdistribusi
eksponensial.
Uji
statistiknya
:
Keterangan
rumus
:
o
t,
=
data waktu kerusakan ke- i
|
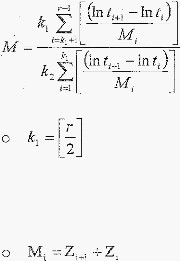 5{r-1
o
r
=
jumlah kerusakan
o
B
=
nilai
uji
statistik
untuk uji
Barlett's test
);- I-Io
diterima bila
ni!ai B jatuh dalam wilayah kritik :
x'
<B
<
x2
1-:Vz.r-1
o
Dimana distribusi chi
square
merniliki ®-1
derajat kebebasan.
Mann 's Test
untuk
Weibull distribution.
Perlu diketahui
bahwa pada
tahun !974,
distribusi
ini
dikembangkan
oleh
Mann,
Schafer, dan
Singpurwalla.
);-
Menurut
Ebeling (1997,
p400), hipotesis untuk
me!akukan uji
ini
yaitu :
o
H
0
:
Data berdistribusi
Weibull.
o
H1
:
Data tidak berdistribusi
Weibull.
>
Uji
statisiknya
:
;
dengan:
0
k2=[r;
1
]
|
|
1
o
Z,
=ln-l-ln(l-
i-O.S
)]
n+0.25
Keterangan Rumus
:
o
M
=
nilai
uji
statistik
untuk
Mann's test.
o
t, = data
waktu kerusakan
ke- i
o
t
1
_
1
=data
waktu
kerusakan ke- (i +1)
o
[x] = bilangan
integer dari
x
o
r
=
n
yaitu jumlah unit
yang
diamati
o
i
=
nomor data kerusakan (1, 2, 3,..., n)
bila
M
<
F,m
malm
Ho
diterima. Nilai Fcnt diperoieh
dari tabel distribusi F
dengan
v
1
<>
Kolmogorov-Smirnov
test
untuk
normal
distribution
dan
lognormal
distribution.
Uji
ini
dikembangkan
oleh
H.W. Lilliefors pada
tahun 1967.
');;>
Menurut Ebeling (1997, p402), hipotesa untuk
melakukan
uji ini
yaitu :
o
Ho : Data
terdistribusi
normal (lognonnal)
o
H1
:
Data tidak
terdistribusi
normal (lognormal)
Uji statistiknya :
Dn =max {D1
,
D2};
dengan
:
o
Dl
=max{w(tl
-l)-
}
blo;n
s
n
|
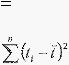 f
f
0
Dz
=max{ -lt,
-ll}
IS1Sn
n
\
S
)
-
t
0
t
L..
...2.._
i=I
n
o
s2
=
i= '---
n-1
keterangan
rumus
:
o
ti
=data waktu antar kerusakan ke-i
o
s =
standar
deviasi sample.
o
n
=
banyaknya data kerusa.kan
Bila
Dn
<
D,,.;,
maim
Ho diterima.
Nilai
Dcrit
diperoleh
dari ta.bel
critical value
fr
the
Kolmogorov-Smirnov testfor
normality (Lilliefors test).
2.1.16 Mean Time to Repair (MTTR)
Untuk
da.pa.t
menentuka.n
nilai
tengah
da.ri fungsi
probabi!itas
untuk
wa.ktu
perbaikan,
ma.ka perlu diketa.hui
terlebih
da.hulu
distribusi
data
waktu
perbaikannya..
Penentuan
a.tau pengujian dila.kukan dengan
cara yang sama. dengan
yang telah
dijelaskan
sebelumnya. Menurut
Ebeling
(1997,
pl92),
MTTR
diperoleh
dengan
mengguna.kan rumus
:
w
00
MTTR
=
th(t)dt
=
(1-H(t))
0
0
|
 med
Dimana:
h(t)
=
fungsi
kepadatan
peluang untuk
data
waktu perbaikan
H(t)
=
fngsi distribusi kumu!atifuntuk
ata
data waktu perbaikan
Adapun perhitungan MTTR
untuk masing-masing
distribusi
ada!ah sebagai
berikut
:
*
Distribusi
eksponensial.
t
-t!A1TTR
H(t)=
Je
l-e-tfMITR
MTTR
0
MTTR
=
!_;
dimam
:
A
=
laju
perbaikan
A
<>
Distribusi
lognormal
dan
normal
lvfTTR
=
t
e''
12
Dimana:
t
mod
=
nilai
tengah waktu perbaikan dan
s
=
standar deviasi dari In t
,.
Distribusi
Weibull
Dimana:
Nilai
r
dapat
diperoleh
dari tabe!
Gamma Function
2.1.17 Interval
Waktu
Penggantian Pencegahan Kemsakan untuk
Meminimasi
Total
Downtime
Penggantian pencegahaJl di!akukan
untuk
menghindari
terhentinya
mesin
akibat
kerusakan
komponen.
Untuk
melakukan
tindakan
perawatan
ini,
maka hams
|
|
diketahui
interval
waktu antara
tindakan
penggantian
(tp)
yang
optimal
dari
suatu
komponen sehingga
dicapai
minimasi downtime
yang maksimal.
Perawatan jenis ini
memerlukan suatu metode perhitungan sebagai
berikut
:
0
Block Replacement
Jika pada selang
waktu
tp tidalc
terdapat
kerusakan,
maka
tindakan
penggantian
dilalcnkan
pada
suatu interval
tp
yang
tetap. Jika sistem rusak sebelum
jangka
waktu tp,
maka
dilalcnkan penggantian
kerusakan
dan
penggantian
selanjutnya
alcan
tetap
dilakukan
pada
saat
tp
dengan
mengabaikan
penggantian perbaikan
sebelumnya.
"'
Age
Replacement
Dalam
metode
ini
tindakan
penggantian
dilakukan
pada
saat
pengoperasiannya
sudah
mencapai
umur
yang ditetapkan
yaitu sebesar
tp. Jika pada selang
waktu
tp
tidalc terdapat
kerusakan,
maka
dilakukan
penggantian
sebagai
tindakan korektif
Perhitungan
umur tindakan
penggantian
tp dimulai
dari
awal
lagi dengan
mengambil
acuan
dari waktu
mulai bekerjanya
sistem
kembali
setelah
dilakukan
tindakan
perawatan
korektif
tersebut.
Rumus yang
digunalcan dalam
metode ini adalah
:
D(tp) = (Total
ekspektasi
downtime per
siklus)/(Ekspektasi panjang
walcn
siklus)
Rumus dari
total
ekspektasi
downtime per
siklus
yaitu :
Total ekspektasi downtime
per
siklus
=
TP · R(tP)
+
Tr ·
(1-
R(tp))
|
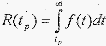 Keterangan rumus : Tp
=
interval waktu tindakan penggantian pencegahan
R(tp)
=
probabilitas suatu
sildus tindakan
pencegahan
Tr
=
interval waktu tindakan perbaikan kerusakan
Reliabilitas
waktu
siklus
pencegahan sama
dengan
probabilitas
dari
kerusakan
yang
terjadi
setelah waktu tp, yaitu
:
Jadi probabilitas dari
suatu
siklus rusak
=
1-
R(ti).
Ekspektasi
panjang
siklus
pencegahan
adalah
panjang
siklus
pencegahan
dika!i
dengan
probabilitas
siklus
pencegahan,
kemudian
ditambah dengan ekspektasi
panjang siklus
kegagalan
yang
dikalikan
dengan
probabilitas siklus
kegagalan.
Rumus dari
ekspektasi
panjang waktu
siklus
yaitu
:
Ekspektasi
panjang waktu
siklus
=
(tP
+
TP ).R(tp)
+
(ekspektasi
panjang siklus
kegagalan).(l- R(tP))
Untuk
menentukan
ekspektasi
panjang
sik!us
kegagalan,
perlu
diperhatika11waktu
rata-rata kegagalan atau
MTTF (Mean Time to Failure), dimana untuk preventive
maintenance
diperoleh
:
|
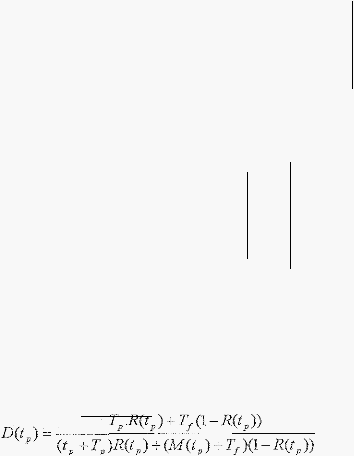 f
f
=
(tp +
Tp)R(tp)
+
f
tf(t)dt
+
T
00
MTTF
=
0
if(t)dt
Nilai
tengah
distribusi
kerusakan adalah
:
f
00
if(t)dt
M(t
)
-
0
-----,
p
1-
R(tp)
Sehingga
ekspektasi
panjang
siklus
kegagalan
adalah
:
s
if(t)dt
Ekspektasi
panjang siklus
kegagalan
=
r
0
+
T
.
ll-
R(tp)
1
Dengan
demikian
ekspektasi
panjang waktu
siklus
adalah
:
=(t
+Tp)R(t
)+
I
t,
if(t)dt
0
+T
.(1-R(t
))
'
p
l-
R(t )
I
p
L
t,
1
1
p
(l-
R(tp))
0
Total downtime per satu
siklus (D(tp))
adalah :
D(tp)
=
TpR(t p)
+
T
1
(1- R
(tp))
c
.
-
,,
'---"---"-----
(tp
+
Tp)R(tp) +I t.f(t)dt +Tf(l-R(tp))
0
|
|
Keterangan Rumus :
Tr
=
waktu
untuk
meltaakukan
penggantian
kerusakan
komponen.
TP =
waktu untnk melakukan penggantian preventif
tp
=
fungsi
kepadatan
pelnang
dari
waktu
kegagalan
komponen. f(t)
=
fungsi
kepadatan
peluang
dari waktu
kegagalan komponen. R(tp)
=
probabilitas terjadinya
penggantian
pencegahan
pada saat
tp.
2.1.18 Interval Waktn Pemeriksaan
Optimal
Benlasarkan
Kriteria Minimasi
Downtime
Selain
tindakan
penggantian
pencegahan,
juga
perlu dilakukan
tindakan
pemeriksaan
yang
dilakukan
secara
teratur.
Hal
ini dilakukan agar
dapat
meminimasi
downtime
mesin
akibat
kerusakan yang terjadi secara tiba-tiba
(Jardine,
1993,
p
J
08).
Konstruksi
model
interval
waktu
pemeriksaan
optimal
tersebut
adalah :
J
.
_!:._
=
waktu rata -rata perbaikan.
f1
2.
=
waktu rata- rata
pemeriksaan.
l
Menurut
Jardine
(1993,
p109),
total
downtime
per
unit
waktu merupakan fungsi
dari
frekuensi
pemeriksaan (n)
dan
dinotasikan
dengan D(n),
yakni
:
D(n)
=
downtime
untuk
perbaikan kerusakan
+
downtime
untuk
pemeriksaan.
|
|
Keterangan :
A(n)
=
laju
kerusakan
yang
terjadi.
n
=
jum!ah pemeriksaan
per
satuan waktu.
f.L
=
berbanding terbalik dengan
1/f.L.
i= berbanding
terbalik
dengan
1/i.
Diasumsikan
bahwa
laju
kerusakan
berbanding
terbalik
dengan
jumlah
pemeriksaan :
2(n)
=
':_
n
dan karena
D(n) =
;t(n)
+.'?_
f.l
l
maka
A,(n)
k
=--
n'
dan
D(n)=--4--+!
n f.1
1
dimana
:
k
=
nihti
konstan dari
jumlah
kerusakan per satuan waktu.
sehingga
diperoleh :
n=t;i
|
|
2.1.19 Perhitungan
Reliability Pada
Mean
Time
to Failure (MTTF) tanpa dan
dengan Perawatan Pencegaban
Peningkatan
keandalan dapat
ditempuh dengan
cara
pemeliharaan
pencegahan.
Perawatan pencegahan dapat
mengurangi pengaruh
wear out
dan
menunjukkan
hasil
yang
signifikan terhadap
umur
mesin. Model
keandalan
berikut
ini
mengasumsikan
sistem kembali ke kondisi baru setelah menja!ani pemeliharaan pencegahan. Menurut
Ebeling (1997, p204), keandalan pada saat
t
dinyatakan sebagai berikut:
Rm(t)
=
R(t)
Rm(t)
=
R(T).R(t-T)
untuk 0
:<:
t
<
T
untuk T
:<:
t
<
2T
Dimana:
T
=
interval waktu penggantian pencegahan kerusakan.
Rm(t)
=
keandalan (reliability)
dari sistem denga.n pemeliharaan pencegahan.
R(t)
=
keandalan sistem tanpa pemeliharaan pencegahan.
R(T)
=
peluang dari keandalan hingga pemeliharaan pencegal1an pertama.
R(t-T)
=
peluang dari
keandalan antara waktu (t-T) sete!ah sistem dikembalikan pad a
kondisi awal pada saat T.
Secara umum persamaannya adalah sebagai berikut :
Rn,(t)
=
R(T)"R(t-nT)
untuk nT
:<:
t < (n+
l)T dan n
=
0,
I, 2,.
Keterangan rumus :
R(t)"
=
probabilitas keanda!an hingga n
selang waktu pemeliharaan.
R(t-nT)
=
probabilitas keandalan untuk walctu (t-nT) dari pemeliharaan yang terakhir.
|
|
Untuk laju kerusakan yang
konstan:
R(t)
=
e
xc
maka:
Rm(t)
=
(e "')" .e 1c t nT)
Rm
(t)
=
e
l.nt .e
i.t
.e l.nt
=
e
'"'
=
®(t)
Ini
membuktikan
bawa
bila
dilakukan preventive
maintenance
pada
distribusi
eksponensia! (laju kerusakan konstan), maka tidak akan
menghasilkan dampak
apapun atau tidak ada
peningkatan reliability seperti yang diharapkan.
Menurut
Ebeling (1997, p204), MTTF untukpreventive maintenance:
T
ro
r
R(t)dt
MTTF
=
r
R"' (t)dt
=
0
------
0
1-R(T)
|